Pseudosymmetry as viewed using charge density analysis

Abstract

Peculiarities of chemical bonding in crystalline 3-isopropyl-4-thiomethyl-N6-benzoylsidnone imine with four independent molecules were investigated by means of R. Bader's “Atoms in Molecule” theory. For the fist time the pseudosymmetry phenomenon was explored at both the molecular (charge density within the molecular species) and supramolecular (network of intermolecular interactions) level.

---

“Pseudosymmetry” is the spatial arrangement of species that feigns symmetry without fulfilling it.¹ A classical example is the crystalline tolan, where the local symmetry element (pseudo-2₁-axis) between its two crystallographically nonequivalent species was fist identified.² Since then, crystals with several independent molecules in an asymmetric unit and in general the phenomenon of pseudosymmetry have been subject of a vast number of studies. Usually the search for an explanation of the occurrence of such systems (e.g. with Z′ > 1) has been based on the statistical analysis of various crystal structures.^3–10 Using this approach, several principles governing the formation of structures with Z′ > 1 were derived (dense packing and H-bonding requirements,^4,6,10 strength of the chemical binding between independent molecules¹¹). However, the degree of similarity between independent molecules was only a minor point of the study. Comparison of the geometrical parameters was mainly used to estimate to what extent the chemically identical but symmetry independent moieties are identical.

A more powerful approach is the analysis of the electron density distribution function ρ(r) in a crystal^12–14 within the “Atoms in Molecules” theory proposed by Bader.¹⁵ It allows a comparison of the topological characteristics of chemical bonds, atomic charges and volumes, and is substantially more sensitive to the difference in the intermolecular interaction patterns as compared to the classical approach based on the comparison of geometric parameters. However, charge density studies of such crystals are scarce and limited to systems with only two independent molecules.^16–22 Moreover, in the majority of investigations the two species were a priori assumed to be fully identical and additional constaints were applied to their electron densities. The others demonstrated that the ρ(r) distributions within independent molecules are different due to the variation of their bonding patterns, although with no quantitative description of the latter.^20,22

In this context, even more intriguing are the crystals where the independent species are related by a pseudosymmetry element. It should impose additional constraints on the molecules involved. To check this, in the first place, one should consider the molecular densities of all the species independently and, secondly, a reference point, i.e. non-pseudosymmetric “twin” (in the asymmetric unit of the same crystal), is needed. In the case of only two independent molecules the second requirement cannot be fulfilled. Nevertheless, if the asymmetric unit contains several molecules in an ABBA manner (the molecules of the same (A or B) type are symmetry-connected, A and B species are not), one can explore the differences between the pseudosymmetry-related species and those without it in a similar crystalline environment. The crystal structure of 3-isopropyl-4-thiomethyl-N6-benzoylsidnone imine (1, Fig. 1) meets the above conditions. Herein we present the results of the topological analysis of the ρ(r) function of the respective crystal. According to our X-ray diffraction data this compound crystallizes with four symmetry-independent molecules (Fig. 2). Hereinafter they will be referred to according to the color scheme of Fig. 2, i.e. the green, the blue (atoms are labelled with A), the red (atoms are labelled with B), and the orange species (atoms are labelled with C). The geometrical parameters of the independent species in the crystal are similar and are reproduced well by the DFT (M052X/6-311++G**) calculations. The variation of the bond lengths does not exceed 0.04 Å, and when only the independent molecules in the crystal are compared the differences in bond lengths are only 0.007 Å (see Table S1 of the ESI).† The major difference is observed in the position of the phenyl group. When all independent species in the crystal of 1 are superimposed (Fig. S1 of the ESI),† it is somewhat rotated around the C(7)–C(9) line. The angle between the phenyl planes in the independent molecules ranges from ca. 0° (between the green and the blue molecules) up to 11.6° (between the red and the orange molecules), although no apparent deviation of other atoms is observed.

Fig. 1 General view of molecule 1 in representation of atoms via thermal ellipsoids at 50% probability level.

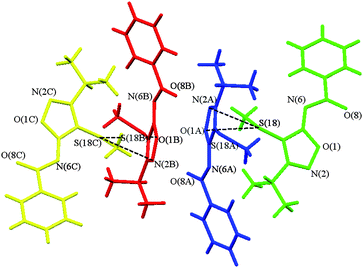Fig. 2 Fragment of the crystal packing of 1 representing its four independent species. The first (green) molecule is the one containing the S(18) atom. Atoms labelled with A, B, and C correspond to the second (blue), third (red), and fourth (orange) molecule, respectively.

There is a pseudo-inversion center located between the red and the blue species in the asymmetric unit of 1; it is displaced from the exact symmetry element (|Δr|¹⁰) by 0.42 Å. Although the mutual disposition of the green and blue molecules and that of the red and orange ones suggests also the presence of the pseudo-2₁-axis, the examination of the supramolecular organization in 1 reveals that there are two pairs of molecules (green – orange and blue – red) with different binding patterns. All four species are involved in the formation of the infinite zigzag chains (Fig. S2 of the ESI)†via the C–S⋯π interactions interlinking the green molecules with the blue ones and the red ones with the orange moieties; the corresponding S⋯O separation is 3.176(2)–3.290(2) Å, being slightly bigger in the latter case. However, the distinction between the green–orange and the blue–red pairs becomes clear when the weaker intermolecular binding in the crystal of 1 is considered. The C–H⋯O contacts hold together the blue and the red molecules related by the pseudo-inversion, while the green and the orange species form the centrosymmetric dimer with their symmetry-equivalents (C(15)⋯O(8) distances are 3.123(2)–3.148(3), 3.384(2) and 3.115(2) Å, respectively). Furthermore, interatomic contacts of the green–orange type are not detected at all.

As a rough measure of the variation in the binding patterns one can consider the number of species bound to a particular molecule. Based on the geometric criteria (Mercury²³ program's thresholds) for all independent molecules the intermolecular contacts with the following species [number and “color” of the molecules bound] can be located:

green: 2 blue + 1 green +1 red = 4(3),

red: 1 green + 2 blue + 2 red + 3 orange = 8(6),

blue: 2 green + 2 red + 1 orange = 5(5),

orange: 1 blue + 3 red + 2 orange = 6(4),

where the number of species, except for those of the same type with the reference molecule, is given in parentheses. Although the general observation is that the two largest numbers of bound species (self-assembly excluded) are found for the red–blue pair and the smallest values for the green and orange species, there is a marked difference between the molecules within the pairs. In other words, the analysis of the routine X-ray structure is not enough to thoroughly explore the pseudosymmetry relationship between the independent species of 1. As a result, the crystalline 1 was subjected to the detailed analysis of the electron density distribution to explore the pseudosymmetry on both molecular (charge density within the species) and supramolecular (interaction energy) levels. The latter is possible owing to an additional advantage of the above approach, which is the opportunity to locate all attractive interactions based on the presence of critical points (3, −1) or BCPs in ρ(r)¹⁵ and to estimate their energy from the X-ray diffraction data.^24,25 The efficiency of this scheme was confirmed by a successful recovery of the total energy of all intermolecular interactions for a molecule in a crystal that reproduced the sublimation enthalpy with high accuracy.^26,27

The charge density distribution for the independent molecules in crystal 1 is qualitatively similar, although there is a slight variation in the ρ(r) parameters of the chemical bonds. The deformation electron density (DED) function in the plane of the heterocycle (Fig. 3) in the four species exhibits the same expected features. These are the maxima in the vicinity of the oxygen, nitrogen, and sulfur atoms, attributed to their electron lone pairs (LPs), and the DED accumulation in the area of covalent bonds with a certain depletion in the case of the O–N bond, which is a well-known feature.^28,29 However, the degree of this depletion is clearly different, being small for the green and the blue molecules and more pronounced in the other two species. Hence, despite the geometrical similarity, which encourages one to consider all independent molecules fully identical, even the visual inspection of the DED sections reveals the weakness of this assumption and is an evidence of pseudosymmetry in the above pairs.

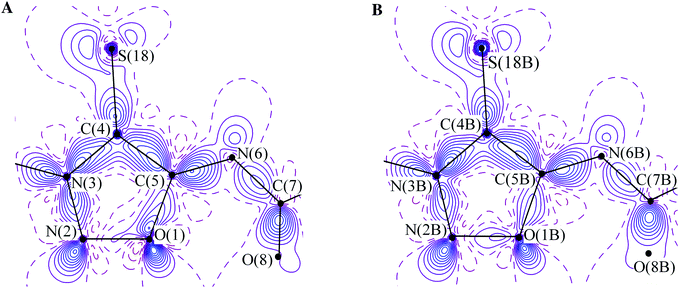Fig. 3 (A) The DED distributions in the mesoionic cycle of the green molecule in the crystal of 1. The contours are drawn with 0.1 e Å⁻³ interval, the non-positive contours are dashed. (B) DED distributions in the mesoionic cycle of the red molecule in the crystal of 1. The contours are drawn with 0.1 e Å⁻³ interval, the non-positive contours are dashed.

This agrees with the topological parameters of the electron density distribution function within the molecules. The difference in the ρ(r) and ∇²ρ(r) values in the BCPs of the chemical bonds in the mezoionic cycle reaches up to 0.134 e Å⁻³ for the N–C bond and 2.8 e Å⁻⁵ for the O–C one. Other bonds which include heteroatoms, such as C–S and those with and within the NC=O group, are more persistent. The corresponding difference averages 0.035 e Å⁻³ and 0.8 e Å⁻⁵. Ellipticity (ε), which serves as a measure of the π component input, also varies in a relatively wide range (up to 0.08). The latter, though, has only little effect on the character of the charge density delocalization over the independent molecules. In all cases, the ε values indicate that N–N, C–N, and C–C bonds have a partial double-bond character (0.20–0.28), while the O–N and O–C bonds (0.06–0.16) are almost single ones. The NC=O fragment (ε = 0.10–0.13) and the phenyl group (the ε value for the N(6)–C(7) bond is 0.15–0.18) are not involved in this delocalization [the intramolecular bonding peculiarities for 1 will be discussed in detail elsewhere].

The above parameters are in agreement with the different degree of electron density concentration in the O–N interatomic area of the green (orange) and the blue (red) species. Indeed, the N–O bonds in the green and the blue molecules are characterized by the ρ(r), ∇²ρ(r), and ε values being close to those for their pseudosymmetric partners. The corresponding ρ(r) values for the green and orange molecules are equal to 2.106 and 2.115 e Å⁻³, respectively, whereas in the blue and the red species they are 2.131 and 2.156 e Å⁻³. Likewise, the ∇²ρ(r) [ε] values at the same BCPs are equal to 6.62 [0.06] and 7.00 [0.07] e Å⁻⁵ for the green and the blue molecules, respectively. In the remaining two cases, these values are 5.98 [0.10] and 5.73 [0.10] e Å⁻⁵. For comparison, the DFT-computed (M052X/6-311++G**) ρ(r), ∇²ρ(r), and ε values at the BCP of the N–O bond in the isolated molecule of 1 are equal to 2.447 e Å⁻³, 3.5 e Å⁻⁵, and 0.109, respectively, with the corresponding interatomic distance equal to 1.348 Å. Both in the crystal and in the isolated state, the N–O bond (h_e(r) values range from –0.51840 to –0.38930 a.u.) corresponds to the intermediate type of interactions.

A similar trend is observed for the net charges of the molecules in the asymmetric unit. To calculate the latter we estimated the atomic charges (q_at) by the integration of ρ(r) over Ω, the atomic basins surrounded by a zero-flux surface.¹⁵ The obtained q_at values (Table S2 of the ESI)† for the independent species vary only slightly (up to 0.10 e for the carbon atoms). In particular, the difference in the charges of the heterocyclic atoms is in the range of 0.01–0.05 e. The charge of the sulfur atom differs only by 0.03 e; it, however, changes its sign. The main difference between the independent molecules was found in the case of the phenyl and the S-Me groups. The corresponding net charges vary from 0.02 to 0.16 e and from 0.05 to 0.18 e, respectively. The variation of the net charge on the heterocycle, NC=O, and i-Pr fragments does not exceed 0.08 e.

The differences in the atomic volumes, calculated via a similar procedure, for the four independent species are even smaller. Although the molecular volumes are almost the same (333.4–337.2 ų), there is a substantial variation of the total charge of independent molecules. The summation of the q_at values for the green, blue, red and orange species leads to 0.03, −0.12, −0.12, and 0.19 e (Table 1). Accordingly, the charge of the blue and the red species is negative; moreover, it is the same within an experimental error of 0.02 e. The other two molecules are positively charged, although to a different extent. This affects the dipole moment of the independent species. The dipole moment was calculated for the model density, which was composed only from pseudoatoms of each independent molecule, while all other atoms were excluded from the total electron density. Although this method provides rather reliable values,³⁰ such approximation may cause some uncertainties in the molecular properties. The calculated dipole moments are 7.9, 9.9, 9.7, and 11.8 D for the green, blue, red, and orange species, respectively. In agreement with the above discussion of the total charges, the values computed for the blue–red pair are very close to each other, whereas those for the green and orange molecules differ by more than 30%. Note that the only value of the dipole moment computed for the green molecule, which is practically neutral, is meaningful. Indeed, its dipole moment equals that for the isolated state (7.9 D).

Table 1 The net charges and the total interaction energies for the independent molecules of 1.^a

Molecule	Σqat/e	ΣEint^b/kcal mol^−1
a The green and orange molecules, as well as the blue and red ones, are pseudo-symmetry related. b The values with the self-assembly excluded are given in parentheses.
Green	+0.03	23.7 (20.0)
Blue	−0.12	26.6 (26.6)
Red	−0.12	28.3 (26.9)
Orange	+0.19	25.2 (18.9)

---

From the analysis of the above molecular properties, one can see the qualitative similarity between the molecules within pseudosymmetric pairs and the distinction between those of different pairs. The latter effect is most likely caused by the different bonding patterns of the independent molecules (see above). To describe this variation on the quantitative level we performed a search for the BCPs in the intermolecular area and then estimated the energy (E_int) of thus located interactions using the correlation scheme proposed by Espinosa et al.^24,25 which introduced the relationship between the energy of an interatomic interaction E_int and the value potential energy density function v(r) at the BCP.^24,25 As a result, in addition to the S⋯π (Fig. 4A) and C–H⋯O contacts expected on the basis of the geometrical criteria, a large number of weaker intermolecular interactions, such as π⋯π (Fig. 4B), C–S⋯H, C–H⋯N, C–H⋯π(phenyl), and H⋯H ones, was found in the crystal of 1. Among them, there are two contacts that link the green and the orange species. In addition, there is at least one interaction between the molecules of each type. No binding of the blue molecule with its symmetry equivalents was detected. In line with the topological parameters at the corresponding BCPs, all intermolecular interactions are of the “closed-shell” type. The values of ∇²ρ(r) and h_e(r) function, which is the electron energy density, vary from 0.18 to 1.01 e Å⁻⁵ and from 0.0005 to 0.0019 a.u., respectively.

Fig. 4 (A) The DED section in the plane of S⋯π interaction between the orange and red moieties. Contours are drawn with 0.1 e Å⁻³ step, the non-positive contours are dashed. (B) DED section in the plane of π⋯π interactions between the blue and red moieties. Contours are drawn with 0.1 e Å⁻³ step, the non-positive contours are dashed.

The energy of the intermolecular interactions (E_int) in the crystal of 1 is in the range of 0.3–2.2 kcal mol⁻¹. The smallest and the largest values correspond to the C–H⋯N and the above C–H⋯O contacts, respectively (see Table S3 of the ESI).† The summation of the E_int for all independent interactions yields 57.7 kcal mol⁻¹, which falls into the range of sublimation enthalpies typical for molecular crystals of similar composition.³¹ Similar to the above atomic charges and volumes of the four species, the E_int values for the identical contacts formed between the independent molecules are slightly different. The energy of the S⋯π interactions within the red–yellow and the green–blue chains varies from 1.3 to 1.5–1.6 kcal mol⁻¹. The differences in the E_int values for other contacts in 1 are of the same order of magnitude.

The total energy of interactions formed by each of the independent species reaches 23.7, 26.6, 28.3, and 25.2 kcal mol⁻¹ for the green, blue, red, and orange molecules, respectively (Table 1). One can see that these values closely follow the trend observed for their charges. This effect most likely results from the charge transfer accompanying the formation of intermolecular interactions in 1, even though there are no unambiguous data in the direction of the charge transfer. For instance, the disposition of the DED maxima (Fig. 4A) in the S⋯π section allows the conclusion that that the charge is transferred either from the LP of the sulfur atom to the σ*-orbital of the N–O bond or from the LP of the corresponding oxygen atom to the σ*-orbital of the C–S bond. Despite this uncertainty, the sum of interaction energies with self-assembly excluded (20.0, 26.6, 26.9, and 18.9 kcal mol⁻¹ for the green, blue, red, and orange species, respectively) correlates with the molecular charges (Table 1).

The total energy of interactions formed by the independent molecules illustrates the quantitative similarity between the binding patters of the species within the pseudosymmetric pairs. Indeed, the variation of the corresponding values for the pseudosymmetric partners (Table 1), i.e. between the green and orange species and between the blue and red ones, does not exceed 1.7 kcal mol⁻¹ (for all interactions) or even 1.1 kcal mol⁻¹, when the self-assembly is excluded. Otherwise the difference reaches ca. 3–8 kcal mol⁻¹ (the largest variation is observed for the ΣE_int values, excluding self-assembly, of the red and orange species), which is approximately the energy of several C–H⋯O contacts. Although this was anticipated based on the number of bound molecules, in the case of total interaction energies the observed tendency is more pronounced.

Consequently, the high-resolution X-ray diffraction study of crystalline 1 with four independent molecules allowed exploring, for the fist time, the pseudosymmetry phenomenon based on the charge density within the species (molecular level) and interaction energies (supramolecular level). Its results showed that the independent molecules, which are not symmetry and/or pseudosymmetry related, are not obliged to be identical, because their crystalline surrounding can be slightly different. From a methodological point of view this means that, when dealing with systems with Z′ > 1, one should not a priori constrain the molecular charge density parameters of the independent species. However, the presence of pseudosymmetry implies the resemblance of not only the geometry of the species, but also their charges, volumes, and interaction energies. As a result, the similarity between independent molecules is not because their chemical nature is the same, but is rather the reflection of the pseudosymmetric relationship between them.

Experimental

The crystals of 1 (C₁₃H₁₅N₃O₂S, M = 277.34) are triclinic, space group P-1, at 100 K: a = 10.2520(4), b = 11.2447(4), c = 23.8900(8) Å, α = 103.240(5), β = 91.368(5), γ = 90.574(5)°, V = 2679.75(17) ų, Z = 8 (Z′ = 4), d_calc = 1.375 g cm⁻³, µ(MoKα) = 2.43 m⁻¹, F(000) = 1168. Intensities of 384 485 reflections were measured with a Bruker SMART APEX2 CCD diffractometer [λ(MoKα) = 0.71072 Å, ω-scans, 2θ < 90°] and 43 867 independent reflections [R_int = 0.0354] were used in further refinement. The structure was solved by the direct method and refined by the full-matrix least-squares technique against F² in the anisotropic–isotropic approximation. Hydrogen atoms were located from the Fourier synthesis of the electron density and refined in the isotropic approximation. For 1 the refinement converged to wR2 = 0.1239 and GOF = 1.004 for all independent reflections (R1 = 0.0396 was calculated against F for 35309 observed reflections with I > 2σ(I)). All calculations were performed using SHELXTL PLUS 5.0.³²

The multipole refinement for 1 was carried out within the Hansen–Coppens formalism³³ using the XD program package¹² with the core and valence electron density derived from wave functions fitted to a relativistic Dirac–Fock solution.³⁴ Before the refinement, the C–H bond distances were normalised to a standard value of 1.08 Å. The level of multipole expansion was octupole for all non-hydrogen atoms. The D₁₀ term was refined for all hydrogen atoms. The κ and κ′ parameters were the same for identical atoms of the independent molecules. The refinement was carried out against F. For 1 it converged to R = 0.0299, Rw = 0.0286 and GOF = 1.6504 for 35 410 merged reflections with I > 3σ(I). All bonded pairs of atoms satisfy the Hirshfeld rigid-bond criteria. The potential energy density v(r) was evaluated through the Kirzhnits approximation³⁵ for the kinetic energy density function g(r). Accordingly, the g(r) function is described as (3/10)(3π²)^2/3[ρ(r)]^5/3 + (1/72)|∇ρ(r)|²/ρ(r) + 1/6∇²ρ(r), in conjunction with the local virial theorem (2g(r) + ν(r)=1/4∇²ρ(r)) leading to the expression for v(r) and, thus, for the electron energy density h_e(r). The total electron density function for 1 was positive everywhere. The residual electron density was not more than 0.310 e Å⁻³. Analysis of topology of the ρ(r) function was carried out using the WinXPRO program package.³⁶

DFT calculations of the isolated molecule 1 were performed with the Gaussian98 ³⁷ program package using M052X functional.^38,39 Full optimization of the molecule at C1 point group was carried out with the 6-311++G** basis set starting from the X-ray structural data. As convergence criteria, the extremely tight threshold limits of 2 × 10⁻⁶ and 6 × 10⁻⁶ au were applied for the maximum force and displacement, respectively. The topological analysis of computed electron density was performed using AIMall program package.⁴⁰

Acknowledgements

This study was financially supported by the Russian Foundation for Basic Research (Project 06-03-32557), the Foundation of the President of the Russian Federation (Federal Program for the Support of Leading Scientific Schools, Grant NSh 3019.2008.3, and Young Doctors, Grant MK-1054.2005.3) and the Russian Science Support Foundation. Authors also thank Dr. E. Pidko for fruitful discussion.

Notes and references

1. M. Ruck, Z. Kristallogr., 2000, 215, 148–156.
2. P. M. Zorkii and V. K. Bel'skii, Proceedings of the Fedorov Yubilee Session (in Russian), Leningrad, 1972, p. 79.
3. N. Padmaja, S. Ramakumar and M. A. Viswamitra, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 725–730.
4. J. W. Steed, CrystEngComm, 2003, 5, 169–179.
5. A. J. C. Wilson, Acta Crystallogr., Sect. A: Found. Crystallogr., 1993, 49, 795–806.
6. C. P. Brock and J. D. Dunitz, Chem. Mater., 1994, 6, 1118–1127.
7. A. Gavezzotti and G. Filippini, J. Phys. Chem., 1994, 98, 4831–4837.
8. G. R. Desiraju, CrystEngComm, 2007, 9, 91–92.
9. K. M. Anderson and J. W. Steed, CrystEngComm, 2007, 9, 328–330.
10. L. N. Kuleshova, M. Y. Antipin and I. V. Komkov, J. Mol. Struct., 2003, 647, 41–51.
11. A. Gavezzotti, CrystEngComm, 2008, 10, 389–398.
12. T. S. Koritsansky, S. T. Howar, T. Richter, P. R. Mallinson, Z. Su and N. K. Hansen, 1995.
13. C. Gatti, Z. Kristallogr., 2005, 220, 399–457.
14. V. G. Tsirelson and R. P. Ozerov, Electron density and Bonding in Crystals: Principles, Theory and X-Ray Diffraction experiments in Solid State Physics And Chemistry, IOP Publishing Ltd., Bristol and Philadelphia, 1996.
15. R. F. W. Bader, Atoms In molecules. A Quantum Theory, Clarendron Press, Oxford, 1990.
16. V. Pichon-Pesme and C. Lecomte, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 485–493.
17. I. Bytheway, B. N. Figgis and A. N. Sobolev, J. Chem. Soc., Dalton Trans., 2001, 3285–3294.
18. J. Overgaard, B. Schiott, F. K. Larsen and B. B. Iversen, Chem.–Eur. J., 2001, 7, 3756–3767.
19. C. Gatti, E. May, R. Destro and F. Cargnoni, J. Phys. Chem. A, 2002, 106, 2707–2720.
20. J. Overgaard, M. P. Waller, J. A. Platts and D. E. Hibbs, J. Phys. Chem. A, 2003, 107, 11201–11208.
21. P. Munshi and T. N. G. Row, J. Phys. Chem. A, 2005, 109, 659–672.
22. P. Munshi and T. N. G. Row, Cryst. Growth Des., 2006, 6, 708–718.
23. UK. Program MERCURY 1.4.2 Cambridge Crystallographic Data Center.
24. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
25. E. Espinosa, I. Alkorta, I. Rozas, J. Elguero and E. Molins, Chem. Phys. Lett., 2001, 336, 457–461.
26. K. A. Lyssenko, A. A. Korlyukov, D. G. Golovanov, S. Yu. Ketkov and M. Yu, J. Phys. Chem. A, 2006, 110, 6545–6551.
27. K. A. Lyssenko, A. A. Korlyukov and M. Y. Antipin, Mendeleev Commun., 2005, 15, 90–92.
28. K. A. Lyssenko, M. Y. Antipin and V. N. Khrustalev, Russ. Chem. Bull., 2001, 50, 1539–1549.
29. I. S. Bushmarinov, M. Y. Antipin, V. R. Akhmetova, G. R. Nadyrgulova and K. A. Lyssenko, J. Phys. Chem. A, 2008, 112, 5017–5023.
30. K. A. Lyssenko, Y. V. Nelyubina, R. G. Kostyanovsky and M. Y. Antipin, ChemPhysChem, 2006, 7, 2453–2455.
31. J. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, Oxford, 2002.
32. G. M. Sheldrick. SHELXTL v. 5.10, Structure Determination Software Suit; Bruker AXS: Madison, Wisconsin, USA.
33. N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1978, 34, 909–921.
34. Z. W. Su and P. Coppens, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 27–32.
35. D. A. Kirzhnits, J. Exp. Theor. Phys., 1957, 5, 54.
36. A. Stash and V. Tsirelson, J. Appl. Crystallogr., 2002, 35, 371–373.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. A. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, 1998.
38. Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364.
39. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
40. T. A. Keith. AIMAll (Version 08.01.25), 2008, http://aim.tkgristmill.com.

---

Footnote

† Electronic supplementary information (ESI) available: Additional experimental details. CCDC reference number 737013. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/b912147a

---