Crime scene investigation: The effect of drug contaminated bloodstains on bloodstain pattern analysis

Abstract

We explore for the first time the relationship between the drug content of blood and its corresponding physical property, viscosity, and examine whether this effect can lead to the miss-interpretation of the Bloodstain Pattern Analysis (BPA) of drug contaminated bloodstains found at crime scenes. The viscosity of amphetamine spiked blood was measured using a capillary tube viscometer with amphetamine concentrations explored over the range 3.0 × 10⁻⁷ to 4.1 × 10⁻³ mol dm⁻³ equating to therapeutic and potentially fatal levels respectively, which are commonly found in Crime Scene Investigation and were found to result in a viscosity change; the range of 0.5–11.0% respectively. Based on these observations the estimation of variances within BPA was calculated by introducing the variability of the viscosity into previously derived equations. We find with increasing amphetamine concentrations an increase in the percentage change (corresponding to a decrease in dynamic viscosity) of blood viscosity occurred; this variation theoretically induces a 0.61 mm diameter alteration (2.9%) of resultant bloodstains. The effect of drug contaminated bloodstains on BPA is currently an under explored area within the field of forensic science which requires further investigation due to BPA's inclusion in legal proceedings.

---

Introduction

Bloodstains are the most significant and frequently encountered type of evidence associated with nearly all deaths and violent crimes.¹ Bloodstain Pattern Analysis (BPA) focuses upon the analysis of the size, shape, and distribution of bloodstains resulting from bloodshed,¹ providing crucial information to forensic criminal investigators such as: possible events that have occurred during the act of a particular crime; indication to the order in which these events occurred; and identification of the individuals involved.^2,3 As with all forensic evidence, it is imperative that any evidence examined within connection to the law must be as accurate as possible to reduce any likelihood of doubt and potentially false convictions. BPA is as relevant within today's society as any other piece of forensic evidence and must not be overlooked.⁴

Research conducted by Herbert Leon MacDonell¹ stated that bloodstains produced as a result of an intoxicated individual were not significantly different or altered as a result of their blood alcohol level.¹ This claim was based upon the fact that the alcohol concentration required to significantly alter the viscosity of blood, leading to an alteration in BPA, was within a range of concentrations up to 1%, which is two times the recognised fatal level. Therefore, the consumption of a dose significant enough to affect analysis would be deadly, and it is highly likely this would never be practically encountered. Additionally, this assumption was not scientifically supported. Research conducted in 1983, prior to MacDonell, studied the effects of alcohol on thrombotic disease⁵ conducting in vitro and in vivo experiments focusing upon the relationship between alcohol and blood viscosity. It was found that the in vitro addition of alcohol did not significantly change the viscosity of blood at concentrations of 0.1, 0.2, and 0.3% (w/v). However at 0.4% it was found that the viscosity was depressed by 1.2%. Results for the in vivo addition of alcohol showed that on average, a 7.4% increase in blood viscosity occurred after an average of 64 g (1.12 g kg⁻¹ body weight) alcohol consumption. While research involving alcohol in relation to blood is not unknown;⁵ never before has the effect of drugs on BPA been explored.

Owing to their stimulating mildly hallucinogenic and aphrodisiac properties, amphetamines are extremely popular in certain social settings. The toxic effects of drug use, such as hallucinations and drug induced psychosis, can lead to all forms of aggressive antisocial behaviour, including violence, and therefore this research is enormously relevant within modern-day Forensic Science, and with the misuse of drugs on the rise and the ever-presence of blood at violent crime scenes, with time this study will no doubt become more significant.⁶ Based on the above insights, we explore for the first time the effects of amphetamine on blood viscosity and estimate the variance caused upon the BPA of drug contaminated stains, concluding whether or not the Forensic use of BPA needs to be reconsidered.

Experimental section

All chemicals used were of analytical grade and used as received from Sigma-Aldrich without any further purification. Blood was obtained from TCS-Biosciences Limited (defibrinated horse blood; P.C.V. 40%) and Oxoid Limited (laked horse blood; lysed with saponin). The viscosity calibration fluid obtained from Rheoteck Ltd was used as received and came provided with standard viscosity values dependent upon temperature.

Viscosity measurements were carried out using a capillary tube viscometer (U-Tube Viscometer, Type BS/U, nominal overall length 283 mm, sample volume 13.5 mL, Size C, nominal constant 0.03). The viscometer was filled in a vertical position with the fluid sample and the free flow time of blood from an upper reservoir line to a lower reservoir line measured in seconds. Afterwards, the experimentally determined viscometer constant was used to convert the free flow times into values of dynamic viscosity (mPa.s). All measurements were performed at 37 °C to simulate body temperature. For the purpose of accurate temperature control, the capillary tube viscometer was secured within a transparent glass enclosed bath system, in which the viscometer stood in the same position throughout all tests. A thermostated bath system with a peristaltic pump (Lauda water circulator) was used to maintain a constant temperature but was momentarily turned off during viscosity measurements to eliminate water fluctuations disturbing the viscometer in the form of shaking. Additionally the viscometer was kept away from exposure to direct sunlight or airflow as recommended in previous literature.⁷ After each successive analysis the viscometer was washed through with hot water, deionised water, and finally acetone before being allowed to air dry.

The viscometer was calibrated using the calibration standard so that the raw data obtained from the tests (free flow time (seconds)) could be accurately converted into dynamic viscosity (mPa.s). The calibration fluid was consequentially run through the viscometer at varying temperatures corresponding to the known viscosity values of the fluid and a calibration plot of ‘run time (seconds)’ verses ‘dynamic viscosity, ‘V’, (mPa.s)’ plotted; producing a highly linear response (seconds = 41.385 [seconds/mPa.s] + 16.515 s; R² = 0.999). This allows the calibration constant, ‘C’ of the viscometer to be deduced from the following equation:

where V is dynamic viscosity (mPa.s), C is the calibration constant of the viscometer and t is the free flow time (seconds). Consequently from this plot a value of 42.94 was deduced as the calibration constant for the given viscometer.

Results and discussion

The effect of amphetamine upon the viscosity of blood was explored by calculating the dynamic viscosity of unadulterated blood and comparing this to the dynamic viscosity of amphetamine spiked blood. For unadulterated defibrinated horse blood the dynamic viscosity value of 3.3 mPa.s was obtained which is in excellent agreement with 4.8 mPa.s and is as expected.⁸ A range of relevant amphetamine concentrations were chosen: 3.0 × 10⁻⁷ mol dm⁻³, taken as the therapeutic blood concentration;⁹ 4.1 × 10⁻⁶ mol dm⁻³, as expected after taking an average dose¹⁰ and the fact that studies have found this level to produce only ‘mild affects’;¹¹ 4.1 × 10⁻⁵ and 4.1 × 10⁻⁴ mol dm⁻³, concentrations within the believed fatal range;⁹ and finally 4.1 × 10⁻³ mol dm⁻³, above the stated fatal concentration,⁹ however it must be noted that some studies suggest there is no fatal dose of amphetamine.¹² Note also that two forms of blood were used, laked and defibrinated horse blood, to ensure that any variation observed was applicable to blood as a whole and not just one experimental form.¹³

The blood samples were consequentially spiked with amphetamines and the dynamic viscosities measured. The observed results are depicted in Table 1 and for convenience Fig. 1 presents a graphical representation where it can be readily observed that the presence of amphetamine significantly alters the dynamic viscosity value of defibrinated horse blood. A negative correlation is apparent, suggesting that with increasing amphetamine concentrations a decrease in the viscosity value of blood is observed within the range of 0.5–11.0% (±0.001%: N = 3), which represents a change in dynamic viscosity of between 0.02–0.36 mPa.s respectively. Fig. 2 is a diagrammatical representation that can be summarised to depict that an increase in amphetamine concentration results in an increase in the percentage change of viscosity, resulting in an overall decrease in the dynamic viscosity value of the sample in question.

Table 1 The effect observed from the addition of amphetamine to both defibrinated and laked horse blood

Amphetamine Concentration/M	Defibrinated Horse Blood		Laked Horse Blood		Corresponding Dose Level
	Dynamic Viscosity/mPa.s	Δ Viscosity Observed/%	Dynamic Viscosity/mPa.s	Δ Viscosity Observed/%
0	3.29	0.0	2.74	0.0	Unadulterated
3.0 × 10^−7	3.27	0.5	2.72	0.6	Therapeutic
4.1 × 10^−6	3.15	4.1	2.70	1.5	Average Dose
4.1 × 10^−5	3.12	5.1	2.67	2.4	Within Fatal Range
4.1 × 10^−4	3.09	5.7	2.66	2.8	Within Fatal Range
4.1 × 10^−3	2.93	11.0	2.65	3.4	Above Fatal Range

---

Fig. 1 Relationship between: log₁₀ amphetamine concentration and log₁₀ viscosity of defibrinated horse blood (square); and laked horse blood (circle).

Fig. 2 A diagrammatic representation of the observed increase in percentage change that is apparent with an increase in the concentration of amphetamine within the blood sample.

Upon detailed analysis of the results shown in Table 1, it is apparent that the addition of an average dose of amphetamine (4.1 × 10⁻⁶ mol dm⁻³)¹⁰ to defibrinated horse blood resulted in a decrease in dynamic viscosity of 4.1% representing an alteration from 3.29 to 3.15 mPa.s. Considering the average standard deviation of ±0.001% (N = 3) it can be stated that the decrease in viscosity observed is significant and most probably due to the addition of amphetamine to the defibrinated horse blood rather than experimental deviation. Furthermore, the largest alteration observed within the range tested was a viscosity change of 11.0%, when tests were performed at an amphetamine concentration of 4.1 × 10⁻³ mol dm⁻³ (above the believed fatal range),⁹ however, it must be born in mind that with amphetamine (as well as other narcotics) desensitisation occurs with prolonged use, and therefore doses much higher than those examined here may be encountered, thus the effects within these specific individuals may be higher still.

As expected defibrinated and laked horse blood display similar trends (both exhibit negative correlations), however, these trends are not to the same extent; with the addition of amphetamine laked horse blood exhibits a percentage change corresponding to a decrease in viscosity within the range of 0.6–3.4%, of which is dramatically less than the alterations observed with defibrinated blood (0.5–11.0%). This may likely reflect the extensive pre-treatment of the blood by the manufacturer. We have demonstrated that the addition of amphetamine to horse blood causes a decrease in its dynamic viscosity, thus we now turn our attention to determining whether this variation results in a significant alteration when performing BPA.

When calculating the variances within BPA we understand that the flight characteristics and resultant stain characteristics of blood are a function of its physical properties, viscosity being one of the three most important contributing factors. Due to the properties of blood it is possible to determine the height from which a blood drop has fallen, the direction it was travelling upon impact with a surface, its velocity and the angle at which it impacted.^1,14,8 The following equation⁸ depicts the length and width (or the diameter – which is used to estimate the height or impact velocity) of a vertical impact as a subject of viscosity:

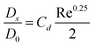where D_S is the final stain diameter, D_o the drop diameter (taken as 4.4 mm),⁸C_d is a constant (using experimental data, the value of 1.11),⁸ and Re is the Reynolds number as defined by:⁸where μ is the viscosity as determined in this paper, ρ the density (taken as 1062 kgm⁻²),³ and V_o the impact velocity (taken as 3.8 ms⁻¹).⁸

Using eqn (2) we now introduce variable viscosity values (as appropriate to the viscosity change of blood due to the addition of amphetamine) and determine the discrepancy this brings with regards to whether this change is sufficient to mislead BPA experts. The results of this analysis are depicted in Table 2 for determining the final stain diameter, D_S which is essential for calculating the drop height and impact velocity of the bloodstain. As identified above, only the results for defibrinated horse blood are considered although similar trends were apparent within the data set of laked horse blood.

Table 2 The observed variation within the calculated stain diameter deduced from introducing variable viscosity values into eqn (2). The variable values were taken from the results of the addition of amphetamine to defibrinated horse blood (Table 1)

Corresponding Dose Level	Dynamic Viscosity of Blood Sample/mPa.s	Final Stain Diameter, DS Calculated/mm	Variation in Calculated Stain Diameter/%
Unadulterated	3.29	20.94	0.0
Therapeutic	3.27	20.96	0.1
Average Dose	3.15	21.17	1.0
Within Fatal Range	3.12	21.22	1.3
Within Fatal Range	3.09	21.26	1.5
Above Fatal Range	2.93	21.55	2.9

---

The data presented in Table 2 represents the bloodstain diameters calculated when the alterations within the dynamic viscosity of blood due to the addition of amphetamine are incorporated into eqn (2); these values are also compared to unadulterated blood, based upon the assumption that all other values remain constant. When considering the effects of the average dose (4.1 × 10⁻⁶ mol dm⁻³),¹⁰ and the extreme alteration that occurs when an amphetamine concentration of above the fatal range is incorporated (4.1 × 10⁻³ mol dm⁻³)⁹ it is apparent that at these concentrations, amphetamine causes a diameter alteration of 0.23 mm (1.0%) and 0.61 mm (2.9%) respectively, both of which are equivalent to a drop height of ∼6 ft.¹ Considering this, upon first appearances one would assume that an alteration of 2.9% is highly significant, however, when taking into consideration that both of the raw data values obtained are equivalent to a drop height of ∼6 ft,¹ it would appear that the alteration is not highly significant.

Let us now ‘theoretically’ consider the effect that a change in the viscosity value of blood has upon the stain pattern produced when a single drop impacts upon a solid/smooth angled surface. If we assume that two small droplets of blood are falling through the air under identical conditions such as the same volume, and velocity, except that one of the droplets contains amphetamine, and as shown above has a slightly decreased viscosity, then we can presume that the droplets travel through the air in the same Newtonian motion. The differences between these two spherical blood drops only become apparent when each drop impacts upon the surface.¹⁵ As the blood impacts the surface it proceeds to flow in the direction that it was travelling upon impact. The extent to how far the blood flows in a particular direction is dependent upon its angle of impact, velocity and other factors (viscosity). However, upon ceasing momentum, the resultant bloodstain is routinely examined using trigonometry; which incorporates the length and width of the stain to determine the angle ‘θ’ of impact via the following equation:¹

Consequentially it would be fair to state that if both of the above blood droplets impacted upon a surface at an identical angle, they would then proceed to exhibit different lengths because of their differences in viscosity. The blood containing amphetamine would have a reduced viscosity and resultantly ‘flow’ a longer distance along the surface before coming to a halt and alternatively the ‘normal’ blood drop would exhibit a slightly more viscous texture and hence cease momentum quicker – resulting in differential stain lengths orientating from the same angle of impact. This concept is diagrammatically represented in Fig. 3 where it is shown that a difference in viscosity will result in an alteration to the length of a stain and as a consequence a different angle of impact will be calculated based upon the calculation in eqn (4). Previous literature has shown viscosity to be an important variable affecting the impact process of fluids upon hard surfaces.¹⁵ The theoretical perspective highlighted above is in excellent agreement with Mao et al.,¹⁵ who considered the effect of a range of parameters on the spread and rebound of liquid droplets impacting flat surfaces. The authors¹⁵ considered (among many) the effect of viscosity upon the impacting process and demonstrated that as the impact droplets reach their maximum spread, the rate of spread reduces and viscosity starts to become significant.¹⁵ Additionally a droplet with a high viscosity produces a smaller maximum spread (travel) and consequently has less energy for recoil/rebound than the less viscous blood droplet.¹⁵

Fig. 3 A diagrammatic representation of how the length of a bloodstain is dependent upon the viscosity of the blood in question.

Considering the data (and theoretical argument) represented above, it is apparent that a change in blood viscosity causes alterations resulting in changes to the calculated angles (theoretically), heights and impact velocities of resultant bloodstains when using BPA to construe these values, and perhaps in light of this revelation one must suggest that this data is highly significant and that the deduced alterations are also significant, meaning they must be accounted for when undertaking BPA interpretation. However, questions must also be asked whether it is plausible that an alteration by such a small scale (for an average concentration: 0.23 mm) could cause such an immense and inconceivable misinterpretation of evidence, and it is with this that we suggest more research be needed within this field before any audacious claims are made.

Last it is illuminating to consider the possible effect of surface tension when undertaking BPA analysis. The Weber number, We is given by:⁸

where σ is the surface tension. This is then related to the number of spines, N, from an impacting bloodstain:where C_N is a constant of 0.955 for blood. For curiosity, if we assume that the surface tension, assumed to be constant above, is indeed affected to a similar degree as that observed for the viscosity (see above), which is ∼4% for an average dose of amphetamine, we can deduce the Weber number assuming that the surface tension, taken to be 0.0056 Nm⁻¹,⁸ varies by ±4%. From this we can then deduce the change on the N of a blood spatter impact which is consequently 103 for a +4% difference and 107 spines for a −4% difference in surface tension. As the number of spines is used to deduce the impact angle, θ, of the impacting blood as given by the following relationship:⁸

N = 0.76We^0.5sin³θ (7)

and when computed through this does not appear to have a significant affect on the impact angle when using the number of spines as an indicator as governed by eqn (7). As identified above (Fig. 3) it is likely that the change in viscosity from the inclusion of drugs will likely affect the spread (travel) of the blood droplet. However, at this stage, the role of surface tension is unknown and we wish to simply highlight that BPA, while at first glance may be simple, has many factors which, left overlooked, could have a potentially detrimental impact in interpreting blood stains; further work is underway to try and elucidate the role of drug contained blood upon surface tension and BPA.

Conclusions

We have demonstrated that the presence of amphetamine within blood significantly alters its viscosity with the effect of increasing amphetamine concentrations resulting in an increase in the percentage change of blood viscosity. At times the changes in viscosity are shown to be as large as 11.0%, with the average dose of amphetamine increasing blood viscosity by 4.1%. When introducing these variables into an equation for the calculation of BPA we demonstrate that this variation induced up to a 0.61 mm (2.9%) bloodstain diameter alteration. Note that this is undertaken using commercially available blood and it is not clear, what deviation, if any, there might be in the case of real human blood. In terms of the alteration of the bloodstain diameter, this might not be significant enough to lead to the miss-interpretation of such evidence at crime scenes, but diligently, where BPA is employed in the case of a positively identified drug taker, adequate control experiments will need to be performed; more research into this field is required to give a definitive answer as we believe we have merely touched the surface.

References

1. S. H. James, P. E. Kish, and T. P. Sutton, Principles of Bloodstain Pattern Analysis: Theory and Practice, CRC Press, Taylor and Francis Group, USA, 2005.
2. S. H. James, Interpretation of Bloodstain Evidence at Crime Scenes, 2 edn, CRC Press, London, 1998.
3. M. A. Raymond, E. R. Smith and J. Liesegang, Sci. Justice, 1995, 36, 153.
4. http://www.guardian.co.uk/uk/2006/feb/10/ukcrime.sandralaville .
5. T. Hamazaki and H. Shishido, Thromb. Res., 1983, 30, 587.
6. http://www.merck.com/mmpe/sec15/ch198/ch198k.html .
7. Y. Çinar, A. Şenyol and K. Duman, Am. J. Hypertens., 2001, 14, 433.
8. C. Knock and M. Davison, J. Forensic Sci., 2007, 52, 1044.
9. V. DiMaio, and D. DiMaio, Forensic Pathology, 2 edn, CRC Press, LLC, USA, 2001.
10. Dollery, within: Inchem, http://www.inchem.org/documents/pims/pharm/pim934.htm%23PartTitle%3A3.%20%20PHYSICOCHEMICAL%20PROPERTIES, 2010.
11. I. Gustavsen, J. Mørland and J. Bramness, J. Acc. Anal. Prev., 2006, 38, 490.
12. M. Verschraagen, A. Maes, B. Ruiter, I. Bosman, B. Smink and K. Lusthof, For. Sci. Int., 2007, 170, 163.
13. H. Bate and M. Grande, Med. Biol. Eng. Comput., 1979, 17, 177.
14. A. Emes, and C. Price, Chapter 5 from: P. White, Crime Scene to Court: The Essentials of Forensic Science, 2 edn, RSC, Cambridge, 2004.
15. T. Mao, D. C. S. Kuhn and H. Tran, AIChE J., 1997, 43, 2169.

---