DOI:
10.1039/C0AY00300J
(Paper)
Anal. Methods, 2010,
2, 1918-1926
Self-weighted alternating normalized residue fitting algorithm with application to quantitative analysis of excitation-emission matrix fluorescence data†
Received
7th May 2010
, Accepted 4th September 2010
First published on
15th October 2010
Abstract
In this paper, a novel algorithm named as self-weighted alternating normalized residue fitting (SWANRF) has been proposed for quantitative analysis of excitation-emission matrix fluorescence data. The proposed algorithm can obtain satisfactory solutions for the analytes of interest even in the presence of potentially unknown interferences, fully exploiting the second-order advantage. By comparing the performance of the alternating trilinear decomposion (ATLD) algorithm, and PARAFAC-ALS on one simulated and two real fluorescence spectral data arrays, SWANRF can deal with higher collinearity problems, obtain improved convergence rate through shuffling the computational matrices, and partially reextract valid information from the residue and further remove invalid information to the residue. In addition, SWANRF can only behave more stably, independent of the used initial values unlike PARAFAC, but also achieves very smooth profiles at high noise level, where ATLD may be helpless with the actual component and has to resort to additional component(s) to fit noise, yielding rough profiles. Based on these attractive merits, such a novel method may hold great potential to be extended as a promising alternative for three-way data array analysis.
Introduction
With the rapid development of modern analytical instruments, second-order calibration is gaining more and more widespread acceptance in many scientific fields, such as chemistry, medicine, food, environmental and single-cell science.1–6 It highlights a new avenue to enhance the wealth of available information from a large amount of collected second-order instrumental data. Moreover, since the trilinear decomposition of three-way data arrays is unique, it can directly extract relative concentrations and profiles (in the spectral, time, pH, or other modes) of individual components, and accurately quantify the components of analytical interest in a complex system, even in the presence of unknown and uncalibrated complicated interferences. This characteristic is commonly known as “second-order advantage”, which mathematically makes it easy to carry out the final aim of analytical chemistry without the aid of tedious separation procedures.7,8 Attracted by this merit derived from three-way data arrays, it has led to a resurgence of interest in the development of second-order calibration-based analytical methodologies.
In the last two decades, several algorithms for the decomposition of three-way data arrays have been proposed, and they can be generally sorted into three main types. The approaches of the first sort resolve the data arrays based upon eigenanalysis or generalized eigenanalysis, with the generalized rank annihilation method (GRAM)9–11 and the direct trilinear decomposition (DTLD) method12–14 as the well-known examples. These methods can give rise to direct solution to the component profiles in each order. Unfortunately, for GRAM, its use is constrained to only one standard and one mixture samples at a time, and for DTLD, the necessary construction of two pseudo-samples unavoidably incurs a loss of information in multiple samples. In addition, the algorithm for these methods may occasionally yield imaginary solutions and exhibit inflated variance, only when the signal-to-noise is high, can it work well. The approach of the second sort is mainly bilinear least squares (BLLS),15,16 which is recently proposed and built upon a direct least-squares procedure, also preserving the important second-order advantage. The last type of method is based on an iterative least squares principle,17–24 and fits a trilinear model through iterative decomposition of the three-way data cube stacked with a serial of response matrices measured for each sample including calibration and unknown samples. These methods provide a judicious way to extract useful information from multiple samples, and have been most widely employed because of their lesser sensitivity to instrumental noise and model deviations. The most representative example is the parallel factor analysis (PARAFAC) first proposed by psychometricians in the early 1970s,21,22 which can provide a unique solution independent of rotation and reliably solve many chemical problems. However, the success of this algorithm is dependent on the trilinear degree of three-way data, the choice of the number of components and the signal-to-noise ratio. Furthermore, this method suffers from annoyingly slow convergence. This may be due to that leastways mild degrees of multicollinearity as a result of the rather large size of at least two modes of data arrays causes PARAFAC-ALS to require numerous iterations before convergence, and the size of intermediate data is too large and excessively wastes physical memory of the computer. Subsequently, a series of second-order calibration methods, such as alternating trilinear decomposition (ATLD)23 and its various variants, were developed to avoid the above relatively strict constraint. These methods not only resist the influence of the excess factors selected, but also achieve fast convergence. However, sometimes it is difficult for ATLD to produce an accurate solution by Moore–Penrose generalized inverse when encountering rank deficient cases, which often occurs in the practical analytical processing and the kinetic system. Furthermore, the application of ATLD is restricted when the noise level is too high. All of the above-mentioned results suggest that all methods have their respective advantages and shortcomings, but there is no perfect alternative with all the advantages to successfully resolve different second-order data problems, up until to now. Related works on second-order calibration are therefore worthy of further study.
In this paper, a new second-order calibration method, self-weighted alternating normalized residue fitting (SWANRF), was developed with some improved properties. The proposed algorithm minimizes three new residues based on two steps of least squares, which overcomes to some extent the disadvantages associated with those above mentioned methods. Compared with PARAFAC-ALS, it is able to deal with higher collinearity problems, behave more stably independent of the used initial values, obtain improved convergence rate through shuffling the computational matrices, and partially reextract valid information from the residue and further remove invalid information to the residue based on truncated least squares method. In addition, SWANRF can also achieve very smooth profiles at high noise level, where ATLD may be helpless with the actual component and have to resort to additional component(s) to fit noise, yielding rough profiles. In the present paper, a simulated data arrays and two real chemical data arrays were employed to reveal the performance of the proposed algorithm.
Nomenclature
Throughout this paper, scalars are represented by lower-case italics; bold lower-case characters mean vectors; bold capitals designate two-way matrices; underlined bold capitals symbolize three-way arrays, and the superscript T denotes the transpose of a matrix, the superscript + means the Moore–Penrose generalized inverse of a matrix. Before reading the following parts of this paper, readers are recommended to refer to the nomenclature for detailed information. The details are as follows: ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) , three-way data array; I, J, K, the dimensions of three modes of
, three-way data array; I, J, K, the dimensions of three modes of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) ; xijk, the ijkth element of
; xijk, the ijkth element of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) ; AI×N, BJ×N, CK×N, the three underlying profile matrices of
; AI×N, BJ×N, CK×N, the three underlying profile matrices of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) with I × N, J × N, K × N, respectively (which will be simply represented by A, B and C, respectively, in this paper); ain, bjn, ckn, the inth, jnth and knth elements of the three underlying profile matrices A, B and C, respectively; a(i), b(j), c(k), the ith, jth, kth row vectors of profile matrices A, B and C, respectively; diag(a(i)), diag(b(j)), diag(c(k)), diagonal matrices with elements equal to the elements of a(i), b(j) and c(k), respectively; Xi‥, X.j., X‥k, the ith horizontal, jth lateral and kth frontal slices of
with I × N, J × N, K × N, respectively (which will be simply represented by A, B and C, respectively, in this paper); ain, bjn, ckn, the inth, jnth and knth elements of the three underlying profile matrices A, B and C, respectively; a(i), b(j), c(k), the ith, jth, kth row vectors of profile matrices A, B and C, respectively; diag(a(i)), diag(b(j)), diag(c(k)), diagonal matrices with elements equal to the elements of a(i), b(j) and c(k), respectively; Xi‥, X.j., X‥k, the ith horizontal, jth lateral and kth frontal slices of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) respectively; Ei‥, E.j., E‥k, the ith horizontal, jth lateral and kth frontal slices of the three-way array residue
respectively; Ei‥, E.j., E‥k, the ith horizontal, jth lateral and kth frontal slices of the three-way array residue ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) , respectively; eijk, the ijkth element of the three-way residue array
, respectively; eijk, the ijkth element of the three-way residue array ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) ; ‖ · ‖F, the Frobenius matrix norm; ⊙, the Khatri-Rao product.
; ‖ · ‖F, the Frobenius matrix norm; ⊙, the Khatri-Rao product.
Theory
Trilinear model for second-order calibration
Second-order data are usually obtained from hyphenated instruments, such as an excitation-emission matrix spectrofluorometer and HPLC with a diode array detector. In the case of excitation-emission matrix (EEM) fluorescence, a three-way data array, ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) , can be stacked by a set of EEMs measured under I excitation wavelengths and J emission wavelengths for each of the K samples, which consist of calibration samples and prediction samples. A trilinear model for such a three-way array,
, can be stacked by a set of EEMs measured under I excitation wavelengths and J emission wavelengths for each of the K samples, which consist of calibration samples and prediction samples. A trilinear model for such a three-way array, ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) , as depicted in Fig. 1, can be expressed as follows:
, as depicted in Fig. 1, can be expressed as follows:| |  | (1) |
| where i = 1,2,...,I; j = 1,2,...,J; k = 1,2,...,K. |
 |
| | Fig. 1 The graphical representation of trilinear model of three-way data array ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) . . | |
For the sake of more conveniently and clearly understandable data for chemometricians, the three-way data array ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) can be sliced along the three different modes and represented in matrix form by three symmetrical expressions:23
can be sliced along the three different modes and represented in matrix form by three symmetrical expressions:23
| | | Xi‥ = Bdiag(a(i))CT + Ei‥, i = 1,2,…,I | (2) |
| | | X.j. = Cdiag(b(j))AT + E.j., j = 1,2,…,J | (3) |
| | | X‥k = Adiag(c(k))BT + E‥k, k = 1,2,…,K | (4) |
Provided that k1 + k2 + k3 ≥ 2N + 2 (where k1, k2 and k3 are the k-ranks of A, B and C, respectively), the decomposition of trilinear model proposed above is unique up to some scaling and permutation indeterminacy.
Due to the cyclic symmetry of the trilinear model,23 the three above-mentioned expressions are mathematically equal to each other. According to eqn(2)–(4), the loss function to be minimized is the sum of the squares of the elements of the residual matrix, which may be represented as
| |  | (5) |
| |  | (6) |
| |  | (7) |
The ATLD algorithm minimizes alternately one of the three objective functions over C on fixed A and B, then over A on fixed B and C, and then over B on fixed C and A. The updates for A, B and C from eqn(5)–(7) are
| | | aT(i) = diagm(B+Xi‥(CT)+), i = 1,2,…,I | (8) |
| | | bT(j) = diagm(C+X.j(AT)+), j = 1,2,…,J | (9) |
| | | cT(k) = diagm(A+X‥k(BT)+), k = 1,2,…,K | (10) |
where diagm(·) denotes a column
N-vector whose elements are diagonal elements of a square matrix. ATLD holds the fastest convergence, which is attributed to the operation based on sliced matrices with less size and two other major strategies. One is the truncated least squares method which uses the tolerance to truncate the small singular values in the singular value
decomposition, the other is the operation of selecting diagonal elements which also makes ATLD retain trilinearity property and indeed be insensitive to the component number. Unfortunately, the optimal strategy of selecting diagonal elements inevitably induces some floats of the loss function of ATLD rather than monotonous decrease. Moreover, the diagonal elements may suffer from such serious influence at high noise level that ATLD only recurs to additional component(s) to fit noise to realize an accurate resolution, but the spectral loadings are still rough.
The idea of PARAFAC-ALS is based on the following equations obtained through three stretched matrices,
| | | XI×JK = A(C⊙B)T + EI×JK, | (11) |
| where XI×JK = [X‥1, X‥2, X‥k], EI×JK = [E‥1, E‥2, E‥k], |
| | | XJ×KI = B(A⊙C)T + EJ×KI, | (12) |
| where XJ×KI = [X‥1, X‥2, X‥k], EI×JK = [E‥1, E‥2, E‥k ], |
| | | XK×IJ = C(B⊙A)T + EK×IJ, | (13) |
| where XK×IJ = [X‥1, X‥2, X.J.], EK×IJ = [E‥1, E‥2, E.J.], |
And the corresponding least squares loss function can be written as
| | | σ(A) = ‖XI×JK − A(C⊙B)T ‖2F | (14) |
| | | σ(B) = ‖XJ×KI − B(A⊙C)T ‖2F | (15) |
| | | σ(C) = ‖XK×IJ − C(B⊙A)T ‖2F | (16) |
In terms of above-mentioned loss functions, the PARAFAC-ALS method has identified a solution of A for fixed B and C, or B for fixed A and C, or C for fixed A and B, then A, B and C are updated through using the strict least squares principle as follows:
Obviously, PARAFAC provides a strict least squares solution in mathematical sense, whose loss function is a monotonic decline and smooth spectral profiles. However, in each iterative procedure, there exists more or less deviations between the two loading matrices A and B as well as the score matrix C and their corresponding underlying matrices, respectively. These deviations which will be retained and transferred through each iteration, may reduce the convergence speed, cause perturbations to PARAFAC and even make PARAFAC occur two-factor degeneracy problem, especially if encountering serious collinearity. Furthermore, PARAFAC will leave some trashy errors in the three loadings or lose some valid information to the residue in order to ensure the sum of squares of residue minimum.
SWANRF algorithm
For a trilinear model XI×JK = A(C⊙B)T + EI×JK, one can obtain the following new residue:| | | XI×JKP+ = APP+ + EI×JKP+, P = (C⊙B)T | (20) |
Similarly,
| | | XJ×KIQ+ = BQQ+ + EJ×KIQ+, Q = (A⊙C)T | (21) |
| | | XK×IJR+ = CRR+ + EK×IJR+, R = (B⊙A)T | (22) |
In order to overcome some shortcomings of the aforementioned algorithms, the self-weighted alternating normalized residue fitting (SWANRF) algorithm makes use of these three new residues to construct three objective functions, respectively. One can solve the trilinear model based on truncated least squares by alternatively optimizing the following three objective functions rather than those utilized in PARAFAC-ALS.
| | | S(C) = ‖(XK×IJR+ − CRR+) × WBA‖2F | (23) |
| | | S(A) = ‖(XI×JKP+ − APP+) × WCB‖2F | (24) |
| | | S(B) = ‖(XJ×KIQ+ − BQQ+) × WAC‖2F | (25) |
where
WCB = diag(sqrt(1./diagm(
PPT))),
WAC = diag(sqrt(1./diagm(
QQT))), and
WBA = diag(sqrt(1./diagm(
RRT))) as weight factors, which is an accompanying outcome of the Moore–Penrose generalized inverse operation on the stretched matrices. That is,
C minimizes
S(
C) (
eqn (23)) for fixed
A and
B;
A minimizes
S(
A) (
eqn (24)) for fixed
B and
C;
B minimizes
S(
B) (
eqn (25)) for fixed
A and
C. Hence, three equations can be obtained below:
| | | C = (XK×IJR+WBA·WBA(RT)+RT)·(RR+WBA·WBA(RT)+RT) + | (26) |
| | | A = (XI×JKP+WCB·WCB(PT)+PT)·(PP+WCB·WCB(PT)+PT) + | (27) |
| | | B = (XJ×KIQ+WAC·WAC(QT)+QT)·(QQ+WAC·WAC(QT)+QT) + | (28) |
It is worth indicating that any matrix S, only when it is column or row full rank, respectively S+S or SS+ is equal to identity matrix, but the condition number of S is much large, namely serious collinearity occurs, the non-diagonal elements of S+S or SS+ can not be simply regarded as zeros, otherwise, it will incur some perturbations.
Having derived the updated equations for these parameter matrices, the general algorithm for the SWANRF method can be described as follows:
1. Estimate the correct component number;
2. Initialize matrices A and B;
3. Compute matrix C using eqn (26);
4. Compute matrix A using eqn (27);
5. Compute matrix B using eqn (28);
6. Scale A and B to be columnwise normalized, respectively;
7. Compute matrix C using eqn (26);
8. Repeat steps 4–8 until a stopping criterion is satisfied.
Iterative stop criterion of the new algorithm is
| | 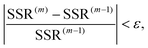 | (29) |
Here  ; m denotes the iteration number in the decomposition of the three-way array and ε is some arbitrary small value (ε = 10−6 in this paper).
; m denotes the iteration number in the decomposition of the three-way array and ε is some arbitrary small value (ε = 10−6 in this paper).
Theoretically, the convergence rate and stability of the SWANRF algorithm will be improved through shuffling the computational matrices. The redistribution of residue will increase the ability to grasp the valid information. In the meantime, it is expected that SWANRF can solve the collinear problem to some extent by introducing weight terms. In the following sections, the performance of the algorithm will be demonstrated in detail using simulated and real fluorescence data arrays.
Simulated and experimental
In order to investigate the performance of the proposed method, a simulated and two real excitation-emission spectral data arrays have been employed as examples. The SWANRF and other two representative methods such as ATLD and PARAFAC-ALS were adopted to treat these data arrays for comparison. The simulated data were collected with MATLAB. All computer programs were written in-house in MATLAB and all calculations were carried out on a personal computer Pentium IV processor with 512 MB RAM under Windows XP operating system.
A three-way data array produced by a fluorescence spectrophotometer on twelve samples with four species was simulated. The excitation spectral profiles a1–a4 were produced by
| a1,i = 0.8*gs(2i − 1,30,30) + 0.1*gs(2i − 1,60,10) |
| a2,i = 0.5*gs(2i − 1,20,20) + 0.1*gs(2i − 1,50,30) |
| a3,i = 0.8*gs(2i − 1,30,15) + 0.1*gs(2i − 1,60,20) |
| a4,i = 0.3*gs(2i − 1,40,10) + 0.1*gs(2i − 1,20,25) |
with i = 1,2,…,50, where gs(x, a, b) refers to the value at x of a Gaussian function with centre a and standard deviation b, i.e. gs(x,a,b) = exp[−(x − a)2/2b2].The emission spectral profiles b1–b4 were generated by
| b1,j = 0.6*gs(2j − 1,40,10) + 0.1*gs(2j − 1,60,10) |
| b2,j = 0.8*gs(2j − 1,30,10) + 0.1*gs(2j − 1,70,25) |
| b3,j = 0.7*gs(2j − 1,40,20) + 0.1*gs(2j − 1,60,25) |
| b4,j = 0.5*gs(2j − 1,20,10) + 0.1*gs(2j − 1,50,25) |
with j = 1,2,…,25.
The first seven samples only including species 1–3 were simulated as the calibration set, while the other samples including all four species as the predicted set. Their concentrations were randomly produced. According to eqn (1), the three-way responses were exactly generated with an additive random error, which was normally distributed with mean zero and standard deviation 0.5%.
For further insight into the capability of the proposed method dealing with higher collinearity, the simulated data was treated as below. The excitation and emission spectra of the fourth component has been reproduced by the equation:
| b4 = norm(b4 + acollinearity × b3) |
where norm is a function normalizing vectors to unit length;
b3 and
b4 indicate the original
spectra of component 3 and 4, respectively;
acollinearity designed as 2.4 is a term regulating the degree of collinearity.
Real sample analysis
Real excitation-emission matrix fluorescence data I.
Honokiol (HK) and Magnolol (ML) are the primary active components extracted from magnolia co-existing in human plasma as traditional Chinese medicine.24 Fifteen samples with different concentration levels of HK and ML in plasma were analyzed using excitation-emission matrix fluorescence. The first eight samples only containing HK and ML were used as a calibration set with concentrations listed in Table 1, while the other samples containing HK, ML and plasma diluted with water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100) as a prediction set with concentrations shown in Table 2. All of the spectral surfaces were recorded at excitation wavelengths varying from 250 to 300 nm in 2 nm steps, and emission wavelengths varying from 330 to 420 nm in 2 nm steps with a scanning rate of 1200 nm min−1. The slit width was 5.0/5.0 nm. The effect of Rayleigh and Raman scatterings were roughly reduced by subtracting the response matrix of an average blank solution from all sample response matrices. Therefore, a 26 × 46 × 15 three-way data array was yielded, and then treated using the SWANRF as well as other two traditional methods such as ATLD and PARAFAC-ALS, to acquire the spectral profiles of each component and the HK and ML concentrations in the presence of human plasma.
100) as a prediction set with concentrations shown in Table 2. All of the spectral surfaces were recorded at excitation wavelengths varying from 250 to 300 nm in 2 nm steps, and emission wavelengths varying from 330 to 420 nm in 2 nm steps with a scanning rate of 1200 nm min−1. The slit width was 5.0/5.0 nm. The effect of Rayleigh and Raman scatterings were roughly reduced by subtracting the response matrix of an average blank solution from all sample response matrices. Therefore, a 26 × 46 × 15 three-way data array was yielded, and then treated using the SWANRF as well as other two traditional methods such as ATLD and PARAFAC-ALS, to acquire the spectral profiles of each component and the HK and ML concentrations in the presence of human plasma.
Table 1 The concentrations (ng ml−1) of calibration samples in both excitation-emission fluorescence experiments
| In the first excitation-emission fluorescence experiment |
| No. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| HK |
31.2 |
0.0 |
62.4 |
93.6 |
124.8 |
156.0 |
187.2 |
234.0 |
| ML |
0.0 |
26.8 |
40.2 |
67.0 |
93.8 |
107.2 |
134.0 |
160.8 |
|
In the second excitation-emission fluorescence experiment
|
| No. |
1 |
2 |
3 |
4 |
5 |
|
| TP |
43.6 |
348.8 |
436.0 |
523.2 |
610.4 |
|
Table 2 Resolved concentrations of the first real excitation-emission fluorescence data set using SWANRF, ATLD and PARAFAC-ALS when component number was chosen as threea
| No. |
Actual concentration/ng ml−1 |
Predicted concentration/ng ml−1 |
| SWANRF |
ATLD |
PARAFAC-ALS |
| HK |
ML |
HK |
ML |
HK |
ML |
HK |
ML |
|
s S.D. between the actual and predicted concentrations; Ma Average iteration numbers of SWANRF, ATLD and PARAFAC-ALS in 100 runs; The recoveries (%) are indicated in square brackets.
|
| 1# |
62.4 |
134.0 |
64.2 [102.9] |
135.2 [100.9] |
50.8 [81.3] |
132.9 [99.2] |
64.1 [102.7] |
135.2 [100.9] |
| 2# |
93.6 |
107.2 |
97.4 [104.0] |
108.4 [101.1] |
87.8 [93.8] |
103.3 [96.3] |
97.3 [104.0] |
108.4 [101.1] |
| 3# |
124.8 |
80.4 |
126.2 [101.1] |
79.3 [98.6] |
129.5 [103.8] |
72.7 [90.4] |
126.2 [101.1] |
79.3 [98.6] |
| 4# |
156.0 |
53.6 |
155.0 [99.4] |
55.2 [103.0] |
161.5 [103.5] |
55.5 [103.5] |
155.1 [99.4] |
55.2 [103.0] |
| 5# |
78.0 |
107.2 |
81.5 [104.5] |
99.2 [92.5] |
85.5 [109.6] |
102.6 [95.7] |
81.2 [104.1] |
99.2 [92.5] |
| 6# |
93.6 |
80.4 |
94.7 [101.2] |
72.6 [90.3] |
98.6 [105.3] |
73.9 [92.0] |
94.5 [101.0] |
72.6 [90.3] |
| 7# |
124.8 |
53.6 |
124.1 [99.4] |
50.3 [93.9] |
128.5 [102.9] |
53.2 [99.3] |
123.9 [99.3] |
50.3 [93.8] |
|
s
|
2.6 |
5.3 |
7.9 |
5.3 |
2.5 |
5.3 |
| Ma |
143 |
8 |
322 |
Real excitation-emission matrix fluorescence data II.
Testosterone propionate (TP), a shortest ester of testosterone, can be transformed into a highly fluorescent derivative through oxidation reaction with concentrated sulfuric acid (H2SO4), as depicted in Fig. 2. Twelve samples with different concentrations of TP in two different cosmetics were analyzed through the excitation-emission matrix fluorescence measurement of highly fluorescent oxidation derivative of TP. All of the spectral surfaces were recorded at excitation wavelengths varying from 282 to 400 nm in 5 nm steps, and emission wavelengths varying from 402 to 548 nm in 5 nm steps with a scanning rate of 1200 nm min−1. Hence, a three-way data array of 24 × 30 × 12, here the number 12 correspond to five calibration samples plus seven actual samples spiked with cosmetics, was obtained. The first five initial concentrations of TP, the pseudo-sample concentrations, are shown in Table 1. The effect of Rayleigh and Raman scatterings were roughly reduced by subtracting the average response matrix of three different blank pseudo-samples.
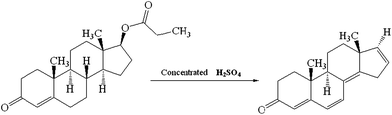 |
| | Fig. 2 Principle of oxidation reaction for TP. | |
Results and discussion
With a view to investigate the feasibility of the proposed method to resolve three-way data arrays, a simulated excitation-emission matrix fluorescence data was designed with high collinearity. Like PARAFAC-ALS, the simulated data showed that SWANRF was sensitive to the estimated component number. However, when the model dimensionality is correctly estimated, the new algorithm can work better. Hence, in the following analysis of this simulated data, the number of components was chosen to be 4, which was the true dimensionality of the underlying model. The resolved excitation spectral, emission spectral and concentration profiles were plotted together with the actual profiles in Fig. 3 (A1, B1 and C1). For comparison the ATLD and PARAFAC-ALS algorithms were also performed on the simulated data, the resolved profiles in the three modes were depicted against the actual ones in Fig. 3 (A2, B2 and C2) and (A3, B3 and C3), respectively. An inspection of the results in Fig. 3 reveals that the spectral profiles resolved by the SWANRF algorithm are slightly smoother and more similar to the actual ones than those of PARAFAC-ALS, but the spectral profiles extracted by the ATLD algorithm are crude. The consistency values between resolved and actual profiles are 1.0000, 0.9998 and 0.9999 for the first component by using SWANRF, ATLD and PARAFAC-ALS, respectively. These consistency values are calculated using the following equation:  where â and
where â and  are the actual profiles of the component and a, b are the resolved profiles. In addition, the concentration profiles indicate that our proposed method can perform better than ATLD and PARAFAC-ALS. The root mean square errors of prediction (RMSEP) are 0.0220, 0.0838 and 0.0266 for SWANRF, ATLD and PARAFAC-ALS, respectively. This is due to the SWANRF algorithm which makes redistribution between the valid information and residue by using the first step of least squares. However, the PARAFAC-ALS algorithm provides an inaccurate judgement of the amount of residue in order to keep the least squares meaning, and ATLD seems useless when encountering high level noise.
are the actual profiles of the component and a, b are the resolved profiles. In addition, the concentration profiles indicate that our proposed method can perform better than ATLD and PARAFAC-ALS. The root mean square errors of prediction (RMSEP) are 0.0220, 0.0838 and 0.0266 for SWANRF, ATLD and PARAFAC-ALS, respectively. This is due to the SWANRF algorithm which makes redistribution between the valid information and residue by using the first step of least squares. However, the PARAFAC-ALS algorithm provides an inaccurate judgement of the amount of residue in order to keep the least squares meaning, and ATLD seems useless when encountering high level noise.
 |
| | Fig. 3 Resolved (solid line) and actual (dashed line) profiles using three algorithms on simulated data set with N = 4: (A1), (B1) and (C1) for SWANRF; (A2), (B2) and (C2) for ATLD; (A3), (B3) and (C3) for PARAFAC-ALS. | |
The SWANRF algorithm as another symmetric three-way data array decomposition method can overcome serious collinear problems to some extent. With the condition number of excitation and emission spectral profiles which are 14.1673 and 12.1981, respectively, the performance of SWANRF is more stable independent of the used initial values than that of ATLD and PARAFAC-ALS. For 1000 replicated analyses, the error probability of SWANRF is a third part of that of PARAFAC-ALS which is 4.2%, and much less than that of ATLD 10.4%. Furthermore, the standard deviations of each component under 1000 replicates, 0.0024, 0.0007, 0.0003 and 0.0005 for SWANRF are less than 0.0191, 0.0078, 0.0009 and 0.0008 for PARAFAC-ALS, respectively. This may be in agreement with the fact that the success of ATLD depends on the noise level, in this simulated data, ATLD can resort to one or more component to fit noise to avoid the dilemma, but the resolved profiles with N = 5 are still rough and RMSEP equal to 0.0850 is larger than that with N = 4. As for PARAFAC-ALS, the tolerance is limited to high degree of collinearity, which may make PARAFAC-ALS trap into swamp or need more iterative time to cast off two-factor degeneracies. When treating the simulated data with acollinearity equal to 2.4, both PARAFAC-ALS and ATLD are helpless, even if ATLD recurs to one or more component numbers. Whereas, under this circumstance, SWANRF can not only realize reliable spectral resolution but also provide accurate concentration prediction with RMSEP equal to 0.0731. The reason for this may be that the action of mixing the computational matrices, is just like shuffling cards, and the weighted term introduced into object functions can improve the stability of the SWANRF algorithm. Subsequently, another surprise is that the convergence speed of SWANRF is simultaneously increased to some extent.
The same simulated data array was employed to examine the convergence rate of the SWANRF algorithm. Random initialization was implemented to start the iterative optimization procedures of SWANRF as well as the other two algorithms. In this set of data array, the results demonstrated that the convergence rate of SWANRF was faster than that of PARAFAC-ALS but much slower than that of ATLD. The average iteration number of 1000 runs for SWANRF was 721, slightly less than that for PARAFAC-ALS (IT = 893) and much more than that for ATLD (IT = 14). Although the convergence rate is only improved to some extent, SWANRF may highlight a new avenue to scan the essence of slow convergence and reduce the number of iterations.
Real excitation-emission matrix fluorescence data I.
For the analysis of the first real data array without high condition number, the component number has been estimated to be three. So far, there are several methods to select the appropriate component number, from the literature.25,26 For comparison, the SWANRF and the other two algorithms were employed to decompose the three-way data array with size of 26 × 46 × 15, respectively. Each algorithm was started from an initial estimate of concentration matrix with the elements randomly distributed in the range from 0 to 1, and was run 100 times separately. The three algorithms worked well each time. However, the average iterative cycles of 143 attained by using SWANRF is much less than 322 iterations for PARAFAC-ALS. This fact further confirmed that the convergence rate of SWANRF was improved by comparison with PARAFAC-ALS.
In the practical analysis process, the most important issue is to accomplish reliable resolution of spectra and accurate quantification of individual components of interest. In validating the resolution results, the actual excitation and emission spectra for every species are measured individually by two solutions of pure species involved. Fig. 4 shows the resolved spectral profiles together with the actual ones by using SWANRF (A1 and B1), ATLD (A2 and B2) and PARAFAC-ALS (A3 and B3), respectively. It can be observed that SWANRF and PARAFAC-ALS provide more precise resolution than ATLD, which indicates the proposed algorithm can be used to decompose the real three-way data array and achieve satisfactory resolutions for excitation and emission spectral profiles almost the same as PARAFAC-ALS when the degree of collinearity is not high. Furthermore, the predicted concentrations of Honokiol (HK) and Magnolol (ML) in human plasma using the three algorithms are summarized in Table 2. It is appreciated that all three algorithms can yield good results, but the SWANRF method performs slightly better than ATLD in extracting concentrations of prediction samples, almost similar to PARAFAC-ALS.
 |
| | Fig. 4 Resolved (solid line) and actual (dashed line) profiles of the first real excitation-emission fluorescence data set using the three algorithms when component number was chosen as three: (A1), (B1) SWANRF; (A2), (B2) ATLD; (A3), (B3) PARAFAC-ALS. | |
Real excitation-emission matrix fluorescence data II.
In this section, the determination of testosterone propionate (TP) in two cosmetics with the aid of the newly developed second-order method has been discussed, based on the measurement of highly fluorescent oxidation derivative of TP obtained through oxidation reaction with concentrated sulfuric acid (H2SO4). The first five pseudo-samples were used as calibration samples and the remaining seven spiked with two different cosmetics as concentration prediction samples. Prior to analysis, the component number of the second real data array has been estimated to be three. Subsequently, the developed SWANRF method as well as the other two methods were used to analyze the data array of 24 × 30 × 12 for comparison in the same way. Fig. 5 displays the resolved excitation and emission profiles using SWANRF (A1, B1), ATLD (A2, B2) and PARAFAC-ALS (A3, B3), respectively. From Fig. 5, it can be observed that the resolved profiles of oxidation derivative of TP are almost identical and match the expected spectral properties. In addition, it should be noted that the resolved profiles of the third component by using the ATLD method is different from those of SWANRF or PARAFAC-ALS, whose relative concentrations are near to zero. This indicates that due to the presence of high noise, ATLD is accustomed to employ an additional component to release this predicament. However, the relative concentrations of the third component resolved by SWANRF and PARAFAC-ALS are so high that it can not be considered as noise. It may be explained that in the analysis of cosmetics, though the ingredients are different from cosmetic to cosmetic, the extracted components from cosmetics may be analogous and some of them have such highly similar fluorescent properties after oxidation reactions that ATLD can not resolve these into separated factors, or there may be serious interference from non-linear factors, which makes ATLD unsatisfactory namely from some deviations between predicted and actual concentrations. Fortunately, no matter what it is, the proposed algorithm can resort to the third component to fit this part in order to ease the problem like PARAFAC-ALS and provide better stability when encountering the collinearity problem. In 100 replicates starting with random initial values, the probability to occur two-factor degeneracy problem for SWANRF is less than that of PARAFAC-ALS. Though the convergence rate of ATLD (IT = 55) is much faster than that of SWANRF, the average iteration number for SWANRF (IT = 910) and the standard deviation among iteration numbers was less than those for PARAFAC-ALS (IT = 1012), suggesting that the convergence speed and stability are improved, respectively.
 |
| | Fig. 5 Resolved (solid line) and actual (dotted line) profiles of the second real excitation-emission matrix fluorescence data set by using the three algorithms when the component number was chosen as three: (A1), (B1) SWANRF; (A2), (B2) ATLD; (A3), (B3) PARAFAC-ALS. Roman numerals 1, 2 and 3 indicate the oxidation derivative of TP, the first interference and second interference, respectively. | |
Assisted by the spectral profiles resolved by these algorithms, the corresponding column in absolute concentration modes to the TP oxidation derivative as a function with the initial TP concentrations is found to evaluate the actual concentrations in cosmetics by linear regression, which is called pseudo-calibration. The prediction concentrations of pseudo-samples extracted by SWANRF, ATLD and PARAFAC-ALS are listed in Table 3. These results demonstrate that the proposed algorithm can retract some valid information from the residue and allow for better prediction capacity than ATLD and PARAFAC-ALS in the presence of unknown complicated interference and high collinearity or non-linear factor.
| No. |
Actual concentration/ng ml−1 |
Resolved concentration/ng ml−1 |
| SWANRF |
ATLD |
PARAFAC-ALS |
|
Mb The iteration of SWANRF, ATLD and PARAFAC; The recoveries (%) are indicated in square brackets.
|
| 1# |
87.2 |
79.2 [90.8] |
98.0 [112.4] |
77.9 [89.4] |
| 2# |
218.0 |
214.0 [98.2] |
244.9 [112.3] |
212.6 [97.5] |
| 3# |
392.4 |
392.8 [100.1] |
427.8 [109.0] |
391.6 [99.8] |
| 4# |
566.8 |
580.6 [102.4] |
612.9 [108.1] |
579.5 [102.3] |
| 5# |
87.2 |
83.3 [95.6] |
89.0 [102.1] |
82.8 [94.9] |
| 6# |
218.0 |
229.4 [105.2] |
242.1 [111.1] |
229.0 [105.1] |
| 7# |
392.4 |
384.6 [98.0] |
402.0 [102.5] |
384.2 [98.0] |
| Mb |
910 |
55 |
1012 |
Conclusions
A novel algorithm, self-weighted alternating normalized residue fitting (SWANRF), has been developed for three-way data resolution and for second-order calibration, which can fully exploit the second-order advantage. For comparison, one simulated and two real excitation-emission spectral data arrays have been treated by SWANRF and other algorithms, such as ATLD and PARAFAC-ALS. The results suggest that the SWANRF method can obtain simultaneously satisfactory solutions for the analytes of interest and provide better stability and improved convergence speed than those of the PARAFAC-ALS method. It is further appreciated that the SWANRF method can overcome the serious collinear problem to some extent which makes ATLD and PARAFAC-ALS trap in meaningless solution, and ensure the smoothness of the resolved spectral profiles unlike ATLD in some cases, especially when the level of noise is very high. Such a method shows several advantages over the traditional methods and may possess great potential to be further tailored as a general and promising alternative for the study of complex chemical systems or processes.
Acknowledgements
The authors would like to acknowledge financial support from The National Natural Science Foundation of China (Grant No. 20775025) and the Program for Changjiang Scholars and Innovative Research Team in University (PCSIRT).
References
- G. M. Escandar, N. M. Faber, H. C. Goicoechea, A. Muñoz de la Peña, A. C. Olivieri and R. J. Poppi, TrAC, Trends Anal. Chem., 2007, 26, 752–765 CrossRef CAS.
- J. H. Christensen, A. B. Hansen, J. Mortensen and O. Andersen, Anal. Chem., 2005, 77, 2210–2217 CrossRef CAS.
- M. L. Naborniak, G. A. Cooper, Y. C. Kim and K. S. Booksh, Analyst, 2005, 130(1), 85–93 RSC.
- A. C. Olivieri, J. A. Arancibia, A. Muñoz de la Peña, I. Durán Merás and A. Espinosa-Mansilla, Anal. Chem., 2004, 76, 5657–5666 CrossRef CAS.
- P. C. Damiani, I. Durán-Merás, A. García-Reiriz, A. Jimé nez-Girón, A. Muñoz de la Peña and A. C. Olivieri, Anal. Chem., 2007, 79, 6949–6958 CrossRef CAS.
- H. Shirakawa and S. Miyazaki, Biophys. J., 2004, 86, 1739–1752 CrossRef CAS.
- E. Sanchez and B. R. Kowalski, J. Chemom., 1988, 2, 265–280 CAS.
- P. J. Gemperline, K. H. Miller, T. L. West, J. E. Weinstein, J. G. Hamilton and J. T. Bray, Anal. Chem., 1992, 64, 523A–532A CrossRef CAS.
- E. Sanchez and B. R. Kowalski, Anal. Chem., 1986, 58, 496–499 CrossRef CAS.
- S. Li, C. Hamilton and P. Geperline, Anal. Chem., 1992, 64, 599–607 CrossRef CAS.
- B. Wilson, E. Sanchez and B. R. Kowalski, J. Chemom., 1989, 3, 493–508 CAS.
- M. Gui, S. C. Rutan and A. Agbodjan, Anal. Chem., 1995, 67, 3293–3299 CrossRef CAS.
- K. S. Booksh, Z. Lin, Z. Wang and B. R. Kowalski, Anal. Chem., 1994, 66, 2561–2569 CrossRef CAS.
- E. Sanchez and B. R. Kowalski, J. Chemom., 1990, 4, 29–45 CAS.
- M. Linder and R. Sundberg, Chemom. Intell. Lab. Syst., 1998, 42, 159–178 CrossRef CAS.
- M. Linder and R. Sundberg, J. Chemom., 2002, 16, 12–27 CrossRef CAS.
- C. J. Appellof and E. R. Davidson, Anal. Chem., 1981, 53, 2053–2056 CrossRef CAS.
- P. Geladi, Chemom. Intell. Lab. Syst., 1989, 7, 11–25 CrossRef CAS.
-
R. Bro, Multi-way Analysis in the Food Industry: Model, Algorithms and Applications. Doctoral Thesis, University of Amsterdam, 1998 Search PubMed.
- A. K. Smilde and D. A. Doornbos, J. Chemom., 1991, 5, 345–360 CAS.
- R. A. Harshman, Foundations of the PARAFAC Procedure: models and conditions for an ‘exploratory’ multimode factor analysis, UCLA Working Papers in Phonetics, 1970, 1–84 Search PubMed.
- J. D. Carroll and J. J. Chang, Psychometrika, 1970, 35, 283–319 CrossRef.
- H. L. Wu, M. Shibukawa and K. Oguma, J. Chemom., 1998, 12, 1–26 CrossRef CAS.
- Y. C. Lee, C. Y. Huang and K. C. Wen, J. Chromatogr., A, 1995, 692, 137–145 CrossRef CAS.
- Z. P. Chen, Z. Liu, Y. Z. Cao and R. Q. Yu, Anal. Chim. Acta, 2001, 444, 295–307 CrossRef CAS.
- R. Bro and H. A. L. Kiers, J. Chemom., 2003, 17, 274–286 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: MATLAB for SWANRF algorithm. See DOI: 10.1039/c0ay00300j |
|
| This journal is © The Royal Society of Chemistry 2010 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) , three-way data array; I, J, K, the dimensions of three modes of
, three-way data array; I, J, K, the dimensions of three modes of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) ; xijk, the ijkth element of
; xijk, the ijkth element of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) ; AI×N, BJ×N, CK×N, the three underlying profile matrices of
; AI×N, BJ×N, CK×N, the three underlying profile matrices of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) with I × N, J × N, K × N, respectively (which will be simply represented by A, B and C, respectively, in this paper); ain, bjn, ckn, the inth, jnth and knth elements of the three underlying profile matrices A, B and C, respectively; a(i), b(j), c(k), the ith, jth, kth row vectors of profile matrices A, B and C, respectively; diag(a(i)), diag(b(j)), diag(c(k)), diagonal matrices with elements equal to the elements of a(i), b(j) and c(k), respectively; Xi‥, X.j., X‥k, the ith horizontal, jth lateral and kth frontal slices of
with I × N, J × N, K × N, respectively (which will be simply represented by A, B and C, respectively, in this paper); ain, bjn, ckn, the inth, jnth and knth elements of the three underlying profile matrices A, B and C, respectively; a(i), b(j), c(k), the ith, jth, kth row vectors of profile matrices A, B and C, respectively; diag(a(i)), diag(b(j)), diag(c(k)), diagonal matrices with elements equal to the elements of a(i), b(j) and c(k), respectively; Xi‥, X.j., X‥k, the ith horizontal, jth lateral and kth frontal slices of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) respectively; Ei‥, E.j., E‥k, the ith horizontal, jth lateral and kth frontal slices of the three-way array residue
respectively; Ei‥, E.j., E‥k, the ith horizontal, jth lateral and kth frontal slices of the three-way array residue ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) , respectively; eijk, the ijkth element of the three-way residue array
, respectively; eijk, the ijkth element of the three-way residue array ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) ; ‖ · ‖F, the Frobenius matrix norm; ⊙, the Khatri-Rao product.
; ‖ · ‖F, the Frobenius matrix norm; ⊙, the Khatri-Rao product.
![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) , can be stacked by a set of EEMs measured under I excitation wavelengths and J emission wavelengths for each of the K samples, which consist of calibration samples and prediction samples. A trilinear model for such a three-way array,
, can be stacked by a set of EEMs measured under I excitation wavelengths and J emission wavelengths for each of the K samples, which consist of calibration samples and prediction samples. A trilinear model for such a three-way array, ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) , as depicted in Fig. 1, can be expressed as follows:
, as depicted in Fig. 1, can be expressed as follows:

![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) .
.![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) can be sliced along the three different modes and represented in matrix form by three symmetrical expressions:23
can be sliced along the three different modes and represented in matrix form by three symmetrical expressions:23


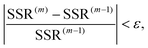
 ; m denotes the iteration number in the decomposition of the three-way array and ε is some arbitrary small value (ε = 10−6 in this paper).
; m denotes the iteration number in the decomposition of the three-way array and ε is some arbitrary small value (ε = 10−6 in this paper).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100) as a prediction set with concentrations shown in Table 2. All of the spectral surfaces were recorded at excitation wavelengths varying from 250 to 300 nm in 2 nm steps, and emission wavelengths varying from 330 to 420 nm in 2 nm steps with a scanning rate of 1200 nm min−1. The slit width was 5.0/5.0 nm. The effect of Rayleigh and Raman scatterings were roughly reduced by subtracting the response matrix of an average blank solution from all sample response matrices. Therefore, a 26 × 46 × 15 three-way data array was yielded, and then treated using the SWANRF as well as other two traditional methods such as ATLD and PARAFAC-ALS, to acquire the spectral profiles of each component and the HK and ML concentrations in the presence of human plasma.
100) as a prediction set with concentrations shown in Table 2. All of the spectral surfaces were recorded at excitation wavelengths varying from 250 to 300 nm in 2 nm steps, and emission wavelengths varying from 330 to 420 nm in 2 nm steps with a scanning rate of 1200 nm min−1. The slit width was 5.0/5.0 nm. The effect of Rayleigh and Raman scatterings were roughly reduced by subtracting the response matrix of an average blank solution from all sample response matrices. Therefore, a 26 × 46 × 15 three-way data array was yielded, and then treated using the SWANRF as well as other two traditional methods such as ATLD and PARAFAC-ALS, to acquire the spectral profiles of each component and the HK and ML concentrations in the presence of human plasma.

 where â and
where â and 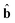 are the actual profiles of the component and a, b are the resolved profiles. In addition, the concentration profiles indicate that our proposed method can perform better than ATLD and PARAFAC-ALS. The root mean square errors of prediction (RMSEP) are 0.0220, 0.0838 and 0.0266 for SWANRF, ATLD and PARAFAC-ALS, respectively. This is due to the SWANRF algorithm which makes redistribution between the valid information and residue by using the first step of least squares. However, the PARAFAC-ALS algorithm provides an inaccurate judgement of the amount of residue in order to keep the least squares meaning, and ATLD seems useless when encountering high level noise.
are the actual profiles of the component and a, b are the resolved profiles. In addition, the concentration profiles indicate that our proposed method can perform better than ATLD and PARAFAC-ALS. The root mean square errors of prediction (RMSEP) are 0.0220, 0.0838 and 0.0266 for SWANRF, ATLD and PARAFAC-ALS, respectively. This is due to the SWANRF algorithm which makes redistribution between the valid information and residue by using the first step of least squares. However, the PARAFAC-ALS algorithm provides an inaccurate judgement of the amount of residue in order to keep the least squares meaning, and ATLD seems useless when encountering high level noise.



