Ionic mobility of the solvated proton and acid–base titration in a four-compartment capillary electrophoresis system

Abstract

Although H⁺ and OH⁻ are the most common ions in aqueous media, they are not usually observable in capillary electrophoresis (CE) experiments, because of the extensive use of buffer solutions as the background electrolyte. In the present work, we introduce CE equipment designed to allow the determination of such ions in a similar fashion as any other ion. Basically, it consists of a four-compartment piece of equipment for electrolysis-separated experiments (D. P. de Jesus et al., Anal. Chem., 2005, 77, 607). In such a system, the ends of the capillary are placed in two reservoirs, which are connected to two other reservoirs through electrolyte-filled tubes. The electrodes of the high-voltage power source are positioned in these reservoirs. Thus, the electrolysis products are kept away from the inputs of the capillary. The detection was provided by two capacitively coupled contactless conductivity detectors (C⁴D), each one positioned about 11 cm from the end of the capillary. Two applications were demonstrated: titration-like procedures for nanolitre samples and mobility measurements. Strong and weak acids (pK_a < 5), pure or mixtures, could be titrated. The analytical curve is linear from 50 μM up to 10 mM of total dissociable hydrogen (r = 0.99899 for n = 10) in 10-nL samples. By including D₂O in the running electrolyte, we could demonstrate how to measure the mixed proton/deuteron mobility. When H₂O/D₂O (9 : 1 v/v) was used as the solvent, the mobility was 289.6 ± 0.5 × 10⁻⁵ cm² V⁻¹ s⁻¹. Due to the fast conversion of the species, this value is related to the overall behaviour of all isotopologues and isotopomers of the Zundel and Eigen structures, as well as the Stokesian mobility of proton and deuteron. The effect of neutral (o-phenanthroline) and negatively charged (chloroacetate) bases and aprotic solvent (DMSO) over the H⁺ mobility was also demonstrated.

---

Introduction

Water and its related ions (solvated proton and hydroxide) are ubiquitous in science as well as in real life: from living cells to fuel cells. Approximately two centuries ago, even before Avogadro had determined the composition of water, Grotthuss tried to explain the ability of water particles to conduct electricity.¹ Despite the importance of the subject and the centuries of studies, some questions remain and new ones arise from biochemistry and technological endeavours, for example. Computational modelling is an important approach nowadays,² but instrumental assistance remains of fundamental importance.³ Here, we introduce a capillary electrophoresis technique to be considered among them.

Electrophoresis comes along with electrolysis of water. This fact has led to the use of buffers to keep a constant pH. This practice, however, precludes the observation of proton and hydroxide as ionic species, because they are neutralized as soon as they start to migrate in the buffer region. Thus, capillary electrophoresis—an important analytical technique used nowadays—cannot be used, in its usual form, to study these ubiquitous species. We have demonstrated, however, that reproducible experiments can be carried out in non-buffered solutions by using equipment with four-compartments, which keeps electrolysis products away from the ends of the capillary.⁴

The idea consists of splitting each reservoir into two new ones that are connected through a salt bridge. The high-voltage electrode is kept in one of them, while the end of the capillary is kept in the other one. In fact, the salt bridge, as well as both of the vials, is filled with the running electrolyte. Thus, during an electrophoresis run, the end of the bridge replenishes the end-capillary vial with the same species and at the same rate that they are transported through the main capillary.

Although electrolysis of water is the main concern, one should note that several other electroactive species might undergo changes. In addition, the charge transfer through the capillary is responsible for significant change in the electrolyte composition. For example, in a previous paper,⁴ we described the composition changes in a typical electrolyte for anion analysis: the chromate/Tris (tris(hydroxymethyl)amino methane) buffer. Although pH may be kept nearly constant at 8.5 by Tris/TrisH⁺ system, there is a significant change in concentration of chromate, which is the species that allows the indirect UV detection of anions. Because of the high mobility of chromate (compared to TrisH⁺), its depletion at the cathode reservoir occurs not only by electrochemical reduction, but also by charge transport. The rates of both processes are similar, i.e., for each mol of chromate reduced to Cr³⁺, another one is transferred to the other reservoir.

The four-compartment equipment allows the use of electrolytes as simple as NaCl and then the electrophoretic migration of the proton can be monitored by capacitively coupled contactless conductivity detection (C⁴D).^5–7 Such a detector is suitable, because the signal depends on the difference between the mobilities of the proton (the fastest cation in aqueous medium) and the co-ion in the electrolyte (Na⁺, in the given example). Thus, there is no requirement about optical absorptivity of the species. A similar assertion can be made about hydroxide, because it is one of the fastest anionic species in aqueous medium. Thus, almost any anion that is not prone to hydrolysis may be used as the co-ion.

The setup originally used for the electrolysis-separated experiments is not appropriate for routine analysis.⁴ Thus, we worked on some implementations until we could reach the design proposed on the present paper. The described system allows the measurement of proton and hydroxide mobilities in aqueous and organic media as well as titration-like determinations in volumes as low as 10 nL.

Experimental

The equipment

Fig. 1 shows the two reservoirs used to separate the end of the column from the neighbourhood of the electrode. Essentially, the setup is composed of a machined PMMA cylinder and other standard parts. The usage of glue and septa allows the confinement of the inner atmosphere and, thus, the control over the pressure. Moreover, it prevents high-voltage discharges. Replenishing of the solution inside the salt bridge is accomplished by applying different pressures to the reservoirs. It is worthwhile to note that this salt bridge is composed of two sections: one wide-bore and long polyethylene (PE) tube and one small-bore and short capillary. As previously demonstrated,⁴ this setup improves the isolation of the vials by combining good control over contamination by diffusion and electrophoretic migration of the electrolysis products.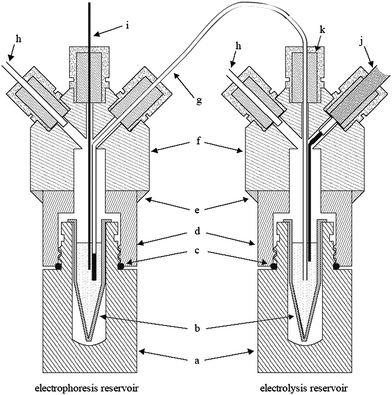

Fig. 1 Cross-section view of the electrolysis separated arrangement. Removable scintillation vials (a) are used as support for dischargeable 1.5-mL vials (b). Similar volumes of running electrolyte are loaded in the vials to keep the level of liquids. A flexible polyethylene tube with a small piece of 250-μm i.d. silica capillary is used as the salt bridge (g). The housing for the vials is made up of PMMA cylinders (f) glued with epoxy (e) to the caps of the scintillation vials (d). Neoprene o-rings (c) and silicone septa (k) are used to seal the reservoirs, which allow the pressurization of them through air inlets (h). With this setup, the end of the capillary (i) and the high-voltage electrode (j) are placed in different vials.

In the previous study,⁴ we demonstrated the importance of preventing the flow of solution between the reservoirs connected by the salt bridge, because the electrolysis products can be led to the main reservoir and, thus, the advantage of the electrolysis-separated system would be lost. The solution adopted in the present setup is to submit both reservoirs to the same pressure by connecting their air inlets together and putting the same solution volume in the polypropylene vials. The same electrolyte solution was used to fill up the reservoirs, salt bridges, and the capillary.

The similarity of the reservoirs allows one to replace the salt-bridge end by the electrode in the electrophoresis reservoir (Fig. 1). Such an operation converts the electrolysis-separated system into a conventional CE equipment. Thus, one can opt between the simpler conventional mode and the elaborated but powerful electrolysis-separated mode.

Fig. 2 shows the electrophoretic compartment of the equipment and the main resources available. The first remarkable feature is the symmetry of the setup, which allows the sample to be introduced in any end of the capillary, because two C⁴D (550 kHz 2 V_pp) are used. This means that, using a unipolar high-voltage source, the separation of cations or anions can be carried out by introducing the sample in the positive or negative side. Hydrodynamic injection (typically at 1.0 kPa for 20 s) was used. The experiments were carried out with an adjustable 30-kV high-voltage power supply model 30A12-P4-STD (Ultravolt, Long Island, NY). The temperature was controlled with a set of nine temperature sensors, three fans, and three dissipative elements.

Fig. 2 Front side of the electrophoresis equipment. Air inlets (a–d) are used to pressurize or depressurize a couple of reservoirs. The high-voltage power source is connected through cables e and f. Two C⁴D (g and h) are positioned close to both ends of the capillary, which is fixed on the grounded stainless steel grid (i) of a box containing three 6-cm fans. This box also acts as the support for the thermal marker (j).

To improve the accuracy, a double thermal marker was used to estimate the electroosmotic flow (EOF) and compensate its effect on the effective mobility of the species.⁸

A significant extent of the external side of the capillary is in contact with a grounded stainless steel grid. The purpose of such a grid is to keep the control over the capillary outside potential, because there is a significant difference on the EOF if the capillary is in an isolated environment (floating potential) or it is grounded (zero volts).⁹ This grid also acts as a support for the thermal marker.

Reagents and solutions

All reagents were of analytical grade. Phosphoric acid 85% and acetic acid were obtained from Merck (Rio de Janeiro, Brazil). Hydrochloric acid 37%, sulfuric acid 95%, citric acid, chloroacetic acid, potassium nitrate, sodium chloride, lithium hydroxide, lithium chloride, o-phenanthroline, sodium hydroxide and potassium hydrogenphtalate were purchased from Merck (Darmstadt, Germany). Caesium sulfate, ammonium chloride, phenol, and dimethylsulfoxide (DMSO) were obtained from Sigma (St Louis, MO, USA). Deuterium oxide 99.9 atom % D was purchased from Aldrich (Milwaukee, WI). All solutions were prepared by dissolving or diluting the reagents in deionized water (Barnstead/Thermolyne, Dubuque, IA, USA).

The study about the effect of chloroacetate and o-phenanthroline on the mobility of the proton was carried out in an electrolyte obtained by mixing aqueous solutions of LiOH, HCl, and LiCl in order to obtain an ionic strength equal to 10 mM and pH 5.0. The sample, HCl 0.5 mM, was injected hydrodynamically. Each experiment was performed at two different running potentials: +21 kV and +26 kV, in order to compensate thermal effects.

Capillary electrophoresis

The experiments were performed using a silica capillary (J&W Scientific, Folson, USA) with 75 μm I.D. and 360 μm O.D. The capillary total length was typically 56 cm, with 11 cm and 45 cm of effective length for the 1st and 2nd detectors, respectively. The capillary column was preconditioned before use by washing with 0.1 M NaOH solution (10 min), deionized water (10 min), and background electrolyte (10 min). Before the first injection, high-voltage was applied for approximately 10 min. The samples were injected hydrodynamically (1.0 kPa for 20 s).

Titration

Each stock solution (sulfuric, hydrochloric, citric, phosphoric and acetic acids, phenol and ammonium chloride) at ca. 50 mM was standardized by potentiometric titration (pH meter Quimis, QA 338-ECV, Diadema, São Paulo, Brazil) using NaOH as secondary standard and potassium hydrogenphtalate as primary standard. Solutions from 50 μM to 10 mM were prepared by dilution with deionized water of the standardized stock solutions and then injected in the capillary electrophoresis equipment. The calibration curves were obtained using the peak area for H⁺.

Theoretical model

Digital simulations were performed to clarify the chemical phenomena taking place inside the capillary when a hydronium zone migrates in an unbuffered environment. The model employed here is an extension of a previously described simulator.⁵ In brief, the coupled, non-linear differential equations describing the time evolution of the concentration distributions of the different species along the capillary (eqn (1)) are numerically integrated using a finite difference scheme for space discretization and the 4th order Runge-Kutta method with adaptive step control for the time evolution.where x is the position along the capillary, v_EOF is the electroosmotic flow rate (assumed uniform throughout the capillary), E is the local electric field, c_i, D_i, and μ_i are the ith species local concentration, diffusion coefficient, and electrophoretic mobility respectively.

The above model was supplemented by considering also fast chemical reactions. To do so, a chemical equilibrium calculation is performed at each time step on each point of the space grid. The chemical equilibrium equations (mass action laws with stoichiometric constraints) are solved by the SEQEx2 algorithm.¹⁰ Although it allows generic reactions with an arbitrary number of chemical species in an arbitrary number of phases to be considered, only acid–base equilibriums were treated here. Species distribution profiles at representative times were taken from the simulation data and used to help the interpretation of experimental results.

Results and discussion

Fundamentals and titration

The proposed system can potentially be used in two kinds of experiments: quantitation of ionizable hydrogen in the injected sample and studies about proton migration in the medium that is filling up the capillary.

The first application can be envisioned as a titration method for nanolitre volumes. When the electric field is applied, H⁺ starts to migrate speedily toward the negative electrode, and can, thus, be determined like other cationic species. This phenomenon tends to exhaust the H⁺ from the region occupied by the sample. Thus, if there is a weak acid in this sample, it dissociates, and the new H⁺ ions generated by the dissociation migrate away from the sample region. The continuous process of dissociation and migration eventually exhausts the H⁺ stock provided by the weak acid. Thus, not only free H⁺, but all dissociable hydrogen at that environment migrates as a band and is quantified, which corresponds to the complete titration of the sample.

Simulated and experimental results help to enlighten the features of this process. Fig. 3 contains the simulated profiles of H⁺ concentration along the capillary for two different background electrolytes (pH 6.0 and 9.0). In both of them, a plug containing 1 mM acetic acid in pure water was placed at the head of the column (covering the initial 2-mm portion of it) and allowed to migrate at the same electric field strength into an unbuffered background electrolyte (BGE). Of course, in both cases, the concentration of free H⁺ at the initial position of the sample is only 0.124 mM, because of the partial dissociation of the acetic acid. The first snapshot (at 1 simulated second) shows that the already completely dissociated band migrated away from its original position. The shape is very similar for both pH values and a significant electrodispersion, caused by the use of a co-ion (Na⁺) with dissimilar mobility, is apparent. However, a small difference at the front of the band can be noted, because of significant consumption of H⁺ at pH 9.0. This attenuation at the front of the band systematically became more and more evident as the H⁺ zone migrates. This continuous consumption leads to the complete neutralization before the detector is reached.

Fig. 3 Simulated hydronium concentration profiles along the capillary for BGE pH 6 (left column) and 9 (right column). Snapshots correspond to 1, 3, and 5 simulated seconds. Injection plug is 1 mM acetic acid in water and electric field intensity is 250 V cm⁻¹.

The result of this simulation is in good agreement with experimental results using alkaline BGE, whose electropherograms do not indicate a peak for hydronium. Thus, neutral to acid BGE should be used, because OH⁻ acts as an effective scavenger of protons. Another proton scavenger is HCO₃⁻ usually present in water used to prepare the solution. This is the reason that the pH is adjusted to 6.0 or below, because the availability of such a base is minimum.

The importance of the nature of the sample was also investigated. Solutions of different acids and mixtures were analysed, using a 10-mM LiCl BGE (pH adjusted to 5.5 with HCl). Potassium (100 μM KCl) was used as an internal standard.

The parameters of the analytical curves are shown in Table 1. The correlation coefficients indicate good linearity. The intercepts are not statistically different from zero, which indicates the absence of systematic errors. The slopes are clearly separated in two different levels. This tendency is made clearer with the relative slope taking that one for HCl as the reference. Hydrochloric acid was chosen because it is a strong monoprotic acid. This relative slope should be 1 for a monoprotic acid, 2 for a diprotic acid, and so on. By comparing the relative slope with the pK_a values,^11,12 one can observe that one acid group of citric acid (pK_a 6.39) and two groups from phosphoric acid (pK_a 7.20 and 12.15) were not titrated. The same occurs with phenol (pK_a 9.98) and NH₄⁺ (pK_a 9.24), because no peak for hydronium was observed. Thus, there is a threshold pK_a value of about 5, which is near to the pH of the electrolyte.

Table 1 Analytical curves for pure acids and mixtures ^ab

Acid	Correlation coefficient (n = 4)	Intercept	Slope/mM^−1	Slope/slopeHCl	pKa values
a Analytical concentration was used for the calibration of pure acids. For the last two rows, the total amounts of dissociable acid were considered, i.e., H2SO4 and H3PO4 have, respectively, two and one dissociable H^+. Thus, the amounts of these acids were converted in the corresponding amounts of HCl and HAc and summed up the monoprotic acids for purposes of preparation of the analytical curves. b The margins for the numerical results correspond to the 95% confidence limits.
HCl	0.9995	−0.1 ± 0.8	8.2 ± 0.8	1	−6.2
Acetic (HAc)	0.9994	−0.2 ± 0.9	8.3 ± 0.9	1.0 ± 0.1	4.76
H2SO4	0.99998	−0.2 ± 0.8	16.5 ± 0.4	2.0 ± 0.2	−2.0, 1.99
H3PO4	0.99999	0.0 ± 0.1	8.6 ± 0.1	1.0 ± 0.1	2.15, 7.20, 12.32
Citric (H3Cit)	0.99998	0.0 ± 0.3	15.2 ± 0.3	1.9 ± 0.2	3.13, 4.76, 6.40
HCl + H2SO4	0.9997	0 ± 2	8.2 ± 0.6	1.0 ± 0.1
HAc + H3PO4	0.99997	0.2 ± 0.5	8.5 ± 0.2	1.0 ± 0.1

---

The last two rows of Table 1 show the results for two equimolar mixtures of weak and strong mono- and polyprotic acids. In both cases, the same performance of a simple solution was kept.

These results were obtained at four concentration levels only. However, detailed analytical curve for a prototypic acid (HCl) was obtained. The coefficient of correlation (n = 10) was 0.99899 (from 50 μM up to 10 mM), using 10 mM NaCl (pH adjusted with HCl to 6.0) as the background electrolyte. The LOD, estimated by 3× the baseline noise, was 5 μM. These are impressive results if we consider that samples of ca. 10 nL were titrated. Obviously, a large volume of sample must be handled.

Proton and deuteron mobilities

The second application is the measurement of proton mobility in different solvents and electrolytes. Fig. 4 shows the electropherograms of a sample containing H⁺ and Cs⁺ using a LiCl solution prepared in a mixture of water and deuterium oxide as the background electrolyte. The electropherogram of the first detector shows two positive peaks related to hydronium and caesium, as expected. There are two additional signals at the electropherogram of the second detector, because of the use of a double thermal marker.⁸ Taking the distances, times, and electric field into account, one can calculate the mobilities, from which the EOF mobility should be subtracted. In the case shown in Fig. 4, the thermal markers were 50-mm apart, thus the EOF mobility was 38.43 × 10⁻⁵ cm² V⁻¹ s⁻¹.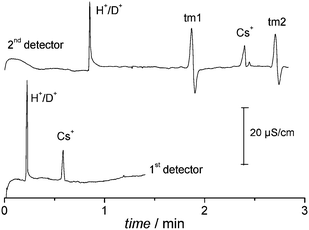

Fig. 4 Electropherograms of a 25 μM Cs₂SO₄ and 90 μM HCl sample in a 10 mM LiCl running electrolyte (pH 4.95), using water/deuterium oxide 9 : 1 (v/v) as solvent. Running potential: +15 kV. The thermal marks (tm1 and tm2) were recorded only by the second detector, because of the position of the thermal marker and the direction of the electroosmotic flow (see Fig. 2).

When pure water was used as the solvent, the obtained values for mobilities (×10⁻⁵ cm² V⁻¹ s⁻¹, 26 °C) were 306 ± 2 for hydronium and 75.1 ± 0.3 for caesium. On the other hand, when H₂O/D₂O (9 : 1 v/v) was used as the solvent, these mobilities changed to 289.6 ± 0.5 for hydronium and 74.4 ± 0.3 for caesium. It is worth to note that deuterium oxide has a small effect on the mobility of Cs⁺, because of changes of viscosity and solvation. On the other hand, the hydronium mobility was reduced by 5%.

This behaviour can be understood by taking the proton transfer in water into account. According to a modern model for proton transfer in water,^13–16 the stable H₃O(3H₂O)⁺ species (the so-called Eigen cation) is converted into the transition structure H₂O–H–OH₂⁺ (or Zundel cation), which is finally converted to a new Eigen cation. This is known as Eigen–Zundel–Eigen (EZE) mechanism. Naturally, these species are involved in other hydrogen bonds not considered here, which results in larger and complex structures. However, the net result is the propagation of protons along the direction determined by the electric field. Thus, the starting proton from the injected sample is exchanged by other ones along the capillary. There is, however, a significant amount of deuterium in the solvent used in the experiment from Fig. 4. Thus, one should consider all the possible isotopologues and isotopomers in the EZE mechanism of proton/deuteron transfer.

Although EZE is by far the most important transport mechanism of proton in water, the Stokesian mechanism should be also considered. Based on conductivity measurements in aprotic solvents, Gileadi and Kirowa-Eisner³ estimated the Stokesian mobility of proton to be similar to the lithium mobility, i.e., a contribution of ca. 40 × 10⁻⁵ cm² V⁻¹ s⁻¹. Therefore, one can say that protons migrate ca. 10% of the time as a conventional species, i.e., without the proton transfers (or hopping).

As a consequence of this double mechanism, the assumption of a prompt and complete exchange of H⁺ from the sample by the proton/deuteron isotopic composition of the solvent is not strictly valid: the species starts migrating mainly as it is in the sample and gradually becomes a new species whose composition is determined by the solvent. Thus, there is a systematic error in calculating the proton/deuteron mobility from effective length of the capillary and migration time, because the velocity is not constant. Fortunately, the Stokesian contribution to the migration is small, and thus velocity should stabilize after a few centimetres from the injection point. For example, considering a 5-mm length sample and that the mobilities of proton and deuteron are similar, the average composition of the plug after a travelling path of 5 mm should reflect roughly the proton/deuteron content of the solvent and sample at the rate of 90 : 10, respectively. After another 5 mm travel, the average composition becomes 99 : 1, and so on. Of course, this is only an approximation, but it makes clear that the composition and consequently the velocity of the band should be stabilized before it comes to the first detector, at 8 cm from the injection point. That is why the mobilities are calculated by taking into account the migration time between the two detectors, instead of the injection point and second detector. This procedure allows the use of a non-deutered acid in the preparation of the sample, which considerably simplifies the experiment.

It is also worthwhile to note that the proton mobility obtained for pure water is significantly lower than the limiting value for H⁺, which is in agreement with the Onsager model for ions in solution. The aims of this experiment were: (1) to show that the composition of the acid inside the sample is not important, because the propagation of protons and deuterons along the capillary will determine the mobility; (2) introducing a non-spectroscopic method for evaluating the behaviour of the mobility of proton and deuteron in liquid phase; and (3) to be a proof of concept of an electrophoretic method for the determination of isotopic composition of water, because this composition can be inferred from the mobility measurement. Of course, an exhaustive study about these possibilities is out of the scope of the present paper.

Weak bases and organic solvents

Although some parts of the equipment are made in poly(methyl methacrylate), the solutions come in contact only with silica, polypropylene, and polyethylene. Thus, experiments with pure or mixed organic solvents can be carried out. The system allowed us to study other protic and aprotic organic solvents and the effect of weak ionic or neutral bases in the electrolyte.

Fig. 5 shows the effect of chloroacetate (a negatively charged base) and o-phenanthroline (a neutral base) on the proton mobility in aqueous medium. In both cases, the base reduced the mobility of proton. This behaviour can be explained by considering the dynamic equilibrium of association of H⁺ and the base and the time sharing of the proton between the faster (hydrated proton) and slower (protonated base) species. In this case, the stronger the base, the higher will be the time spent by the proton in this form. Thus, although chloroacetic acid is a neutral species and protonated o-phenanthroline is a positively charged species, chloroacetate is less effective for retarding proton because it is a weaker base (pK_b = 11.1) than o-phenanthroline (pK_b = 9.1). The overall effect is a ten times greater reduction of mobility for the o-phenanthroline.

Fig. 5 Effect of chloroacetate and o-phenanthroline on the proton mobility in aqueous solution (10 mM LiCl, pH 5.0, 26 °C).

Migration in an aprotic solvent is shown in Fig. 6. The electropherogram of a solution containing H⁺ and Li⁺ was obtained using KNO₃ in DMSO as the electrolyte. In this case, the main mechanism of proton transport is the Stokesian migration. In DMSO, proton transport by EZE mechanism occurs only through the residual water remaining in the solvent. The H⁺ mobility is higher than the Li⁺ mobility, but it is lower than that of K⁺. This is evidenced by the negative peak observed for the proton when K⁺ is used as co-ion in the background electrolyte. The mathematical model for conductivity detection in electrophoresis using 1 : 1 strong electrolytes shows that negative peaks should be obtained in this case.¹⁷

Fig. 6 Electropherogram of a sample containing HCl and LiCl (2 mM each) and 10 mM KNO₃ running electrolyte in DMSO. Running potential: +26 kV.

Similar principles and technique shown to proton can be also applied to hydroxide. Of course, the sample should be injected in the opposite end of the capillary (negative side). Although quantitation and mobility measurement of OH⁻ are possible, the behaviour of the electrophoretic peak suggests that hydroxide interacts with the silica wall, which diminishes the perspective of such uses.

Fig. 7 shows the electropherograms for reproducibility tests. While peak shape and migration time for H⁺ hold for several runs, three to five runs are enough to observe a considerable change in the electropherograms of hydroxide samples. Most likely, the increase of the chloride migration time is related to the increase of the EOF, because hydroxide and chloride are migrating against the electroosmotic flow. The results suggest that each time hydroxide migrates, it deprotonates the wall and increases the EOF.

Fig. 7 Electropherograms of a sample containing (a) 1 mM NaOH and 0.1 mM KCl and (b) 0.19 mM HCl and 0.1 mM KCl. Experimental conditions: (a) Running electrolyte: 10 mM lithium trifluoroacetate (pH 8.9), −26 kV, capillary length: 56.0 cm (45.0 cm effective). (b) Running electrolyte: 10 mM LiCl (pH 5.5), +10 kV, capillary length: 67.4 cm (12.0 cm effective).

Conclusions

The electrophoresis system presently introduced, naturally, has some limitations, as well as any other approach. However, it is a viable and complementary technique. The main feature to be explored in mobility experiments of proton and deuteron in liquid phase is the possibility of using complex environment containing different ions, solvents, and other neutral species. Beside the low sample volume, another important feature of the nanolitre acid–base titrations is the possibility of determining the total amount of dissociable hydrogen in complex mixtures of weak acids, which could be explored in environmental and biological applications.

Acknowledgements

Authors thank Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) and Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for the financial support and fellowships and Dr Z. G. Richter for the English revision.

Notes and references

1. S. Cukierman, Biochim. Biophys. Acta, Bioenerg., 2006, 1757, 876.
2. J. A. Morrone, K. E. Hasllinger and M. E. Tuckerman, J. Phys. Chem. B, 2006, 110, 3712.
3. E. Gileadi and E. Kirowa-Eisner, Electrochim. Acta, 2006, 51, 6003.
4. D. P. de Jesus, J. G. A. Brito-Neto, E. M. Richter, L. Angnes, I. G. R. Gutz and C. L. do Lago, Anal. Chem., 2005, 77, 607.
5. J. G. A. Brito-Neto, J. A. F. da Silva, L. Blanes and C. L. do Lago, Electroanalysis, 2005, 17, 1198.
6. J. A. F. da Silva and C. L. do Lago, Anal. Chem., 1998, 70, 4339.
7. P. Kuban and P. C. Hauser, Anal. Chim. Acta, 2008, 607, 15.
8. R. M. Saito, C. A. Neves, F. S. Lopes, L. Blanes, J. G. A. Brito and C. L. do Lago, Anal. Chem., 2007, 79, 215.
9. V. Kasicka, Z. Prusik, P. Sazelova, M. Chiari, I. Miksik and Z. Deyl, J. Chromatogr., B: Biomed. Sci. Appl., 2000, 741, 43.
10. R. N. Mioshi and C. L. do Lago, Anal. Chim. Acta, 1996, 334, 271.
11. P. W. Atkins, Physical Chemistry, Oxford University Press, Oxford, 4th edn., 1990, p. 951.
12. J. A. Dean, Lange's Handbook of Chemistry, McGraw Hill, New York, 15th edn., 1999, pp. 8.18–8.72.
13. N. Agmon, Chem. Phys. Lett., 1995, 244, 456.
14. D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601.
15. M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925.
16. O. Markovitch, H. Chen, S. Izvekov, F. Paesani, G. A. Voth and N. Agmon, J. Phys. Chem. B, 2008, 112, 9456.
17. M. Jaros, T. Soga, T. van de Goor and B. Gas, Electrophoresis, 2005, 26, 1948.

---