A field theory for ions near charged surfaces valid from weak to strong couplings
Marius M.
Hatlo
and
Leo
Lue
*
School of Chemical Engineering and Analytical Science, University of Manchester, PO Box 88, Sackville Street, Manchester, United Kingdom M60 1QD. E-mail: leo.lue@manchester.ac.uk
First published on 17th November 2008
Abstract
A theory is developed to model the behavior of mobile ions around a fixed charged distribution in the presence of dielectric bodies. By treating the short and long-wavelength fluctuations of the electric potential within different approximation schemes, this approach combines the strengths of the mean field approximation and the strong coupling expansion, while retaining the simplicity of the commonly used Poisson-Boltzmann theory. It is capable of accurately describing ion-correlation induced phenomena, such as the attraction between two like charged plates, the repulsion between two oppositely charged plates, and overcharging. The theory is compared with Monte Carlo simulation data for various systems of charged plates with their associated counterions and added electrolyte. Good agreement is found for nearly all conditions examined.
1 Introduction
To understand biological and colloidal systems, such as DNA, charged micelles or membranes immersed in a water solution, it is crucial to have a good understanding of electrostatic interactions. In these systems, charged macromolecules or surfaces are always surrounded by neutralizing counterions in solution, and often they are also accompanied by electrolyte. The interaction between these charged structures can in many cases be understood by only considering the behavior of the counterions.1 However, certain phenomena, such as oscillations in the force profile and overcharging,2 are due to the presence of salt. In the case where the electrostatic interactions are weak, the properties of the system are well described by the Poisson-Boltzmann (PB) theory. PB theory is a key ingredient in DLVO theory, which is fundamental to colloidal and biological science. Unfortunately, in many practical situations, the assumptions that underpin the PB theory are invalid, and the theory cannot be expected to work well. To systematically improve the accuracy of the PB theory, which is a mean field (MF) theory, perturbation approaches, such as the loop expansion, can be applied; however, the results at one-loop level often offer only a tiny improvement over the mean field approximation.1,3,4 Higher-order loop corrections are increasingly complicated, and practically intractable for inhomogeneous systems. Integral equations can be used,2,5–7 and they have the advantage that they can be very accurate; however, integral equations are often complicated, computationally intensive, and can, in many cases, be difficult to interpret physically.When the charge density on the particles in a system is sufficiently high, the system is said to be in the strong coupling regime, which means that the average electrostatic interactions are much stronger than the thermal energy (kBT). By particles we mean both large macromolecules, as well as the neutralizing counterions or co-ions. Within this strong coupling regime, it has been found that multivalent counterions can generate attractive forces between similarly charged objects8,9 and repulsive forces between oppositely charged surfaces.10,11 This phenomenon has also been observed experimentally, where examples are the attraction between similarly charged silica plates,12 the repulsion between oppositely charged plates,13 the condensation of DNA molecules,14 bundle formation of filamentous actin,15 and aggregation of colloidal particles. Also, the like-charge attraction is found in Monte Carlo simulations,8 integral equation theories,2,5,6 modified Poisson-Boltzmann theories,16 and field theoretic methods.17,18
If electrolyte is added to a system in the high-coupling regime, interesting phenomena, such as overcharging and oscillations in the force profile, can occur. These phenomena have been observed in simulations and integral equation theories for planar2 and cylindrical geometries.19
To understand the difference between the strong and the weak coupling regimes, it is helpful to look at the simplest Coulomb system: the one component plasma (OCP). The OCP consists of a system of point charges in a uniformly distributed, neutralizing background charge. In the weak coupling regime, the OCP is well described by a Debye–Hückel theory, which is a natural extension of the Poisson-Boltzmann theory, when going from an inhomogeneous system to a bulk system. However, as the coupling between ions increases, other more sophisticated theories must be used, where one of the most successful is the hypernetted chain (HNC) approximation.20 It is interesting to note that other, much simpler, theories yield almost the same level of accuracy, and, more importantly, offer more physical insight. One such approach is the correlation hole corrected Debye–Hückel theory (CCDH),21 which incorporates a correlation hole around each ion. This correlation hole represents a region close to each ion, where it is energetically unfavorable for other ions to be located, and, consequently, this region can be considered free of ions. When incorporating the correlation hole into the simple Debye–Hückel theory, the results are within 10% of Monte Carlo simulations of the 3D OCP from weak to strong coupling.21,22 Another related theory is the Gaussian field theory (GFT) which incorporates a high wave-vector cut-off.23,24 With an appropriately chosen value for the cut-off, it is in excellent agreement with Monte Carlo simulations for the internal energy over the full range of coupling parameters tested.
In the OCP, the neutralizing background is uniformly distributed throughout the system; however, more physically important cases are systems where the neutralizing background is concentrated in planar, spherical or cylindrical objects, and the counterions are distributed around them. This is the common coarse-grained model used to study charged colloids and biological macromolecules (i.e.DNA). For these systems, theories such as the HNC approximation5 and the modified Poisson-Boltzmann theory25 have been applied successfully, with good agreement with Monte Carlo simulations. However, there is a need for simpler and more transparent approaches that can easily be generalized to different geometries and different systems, analogously to the CCDH and the GFT for the OCP discussed above. Several theories have taken steps in this direction; examples include the density functional CCDH theory26 and the correlation corrected Poisson-Boltzmann theory.16
In the limiting case where the average distance between the ions a⊥ is much larger than the average distance between the ions and the fixed charged object (z < a⊥), a single particle theory is sufficient to describe these systems. This leads to the strong coupling (SC) theory, which is exact in the limit when lB/µ→∞,17 where the Bjerrum length, lB = βq2/ε, is the distance at which two counterions interact with energy kBT, and the Gouy-Chapman length (µ = q/2πlBΣ) is the distance at which the interaction between a counterion and the charged surface equals kBT, where Σ is the surface charge.
Monte Carlo simulations show that the ions obey the strong coupling theory when z ≪ a⊥, and a mean field theory when z ≫ a⊥.1 Based on this observation, theories that split the interaction between the ions at short and long-range have been developed.16,27,28 The long-range interactions are treated within a mean field theory, and the short range interactions are treated separately with an alternate method that captures the strong correlations between the counterions (e.g., liquid state theory or computer simulation). With an appropriate value for the scale at which it is possible to distinguish between long and short wavelengths, these theories can successfully describe the Monte Carlo results for the full range of coupling parameters. However, they lack a consistent way to calculate the length at which to differentiate between the long and the short wavelengths.
In this work, we present a self-consistent theory that is in good agreement with Monte Carlo simulations from the weak to intermediate and strong couplings. The resulting approach can be evaluated with a similar level of ease as the Poisson-Boltzmann equation. This theory can describe systems with only counterions, but also works well even for systems with added electrolytes. In addition, the theory can successfully describe the influence of dielectric bodies on free ions in the system, which cannot be captured successfully by either the PB or the SC expansion. The theory can also be systematically improved.
The remainder of this article is organized as follows. In Section 2, we develop a field theory for treating systems with electrostatic interactions. This approach is applied to the case of a single, uniformly charged plate in Section 3. The approach is then applied, in Section 4, to ions confined between two charged plates. Finally, the main points of the article and directions for future work are presented in Section 5.
2 Theory
In this work, we consider a system at temperature T composed of a fixed charge distribution Σ(r) immersed in a continuous medium with a spatially varying dielectric constant ε(r). The fixed charge distribution is surrounded by an electrolyte solution consisting of mobile particles with point charges of magnitude qα; the chemical potential of particles of type α is held fixed at µα. The charge density q(r) of the mobile particles is: | (1) |
The grand partition function ZG for this system is given by:7
 | (2) |
The total electrostatic energy Eelec of the system is given by:29
 | (3) |
 | (4) |
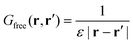 | (5) |
To separate short and long-wavelength phenomena, we split27,28,30 the Green's function G0 into a short wavelength Gs and a long wavelength Gl component:
| G0(r, r′) = Gs(r, r′) + Gl(r, r′) | (6) |
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) )G0, and Gl =
)G0, and Gl = ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) G0. The operator
G0. The operator ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) filters out the short wavelengths; its specific form is arbitrary, and in this work we use:
filters out the short wavelengths; its specific form is arbitrary, and in this work we use:![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) = [1 − σ2∇2 + σ4∇4]−1 = [1 − σ2∇2 + σ4∇4]−1 | (7) |
In order to emphasize the distinction between the long and short-wavelength contributions to the energy, we rewrite the Hamiltonian as:
 | (8) |
| Ese = ½∫drdr′Σ(r)Gs(r,r′)Σ(r′) | (9) |
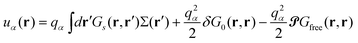 | (10) |
In the approximation scheme we pursue, the one-particle contribution to the partition function is treated exactly, while the interaction between the particles is treated approximately.
By performing a Hubbard-Stratonovich transformation31,32 twice (once with respect to Gl and another time with respect to Gs), the grand partition function of the system can be written as a functional integral:
 | (11) |
 | (12) |
The functional ZrefG is the grand partition function of the reference system, which is the system in the absence of electrostatic interactions. In the remainder of this article, we consider a system of point charges, so that Eref = 0. In this case, the reference system is an ideal gas, which has a grand partition function:
 | (13) |
Two fields are introduced in eqn (11): ψl that fluctuates at large wavelengths and is associated with Gl, and ψs that fluctuates at short wavelengths and is associated with Gs. The long-wavelength field is assumed to be weakly fluctuating (terms of order Ξλl are small), so a mean field approximation should be sufficient. The short-wavelength modes are expected to be strongly fluctuating (terms of order Ξλs are large) and coupled between themselves as well as to the large wavelength modes.
Performing the path integral over ψs, we get an effective field theory for the long-wavelength system. The expression for the grand partition function ZG is:
 | (14) |
 | (15) |
The quantity ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) G is a coarse-grained grand partition function of the reference system, which is defined as:
G is a coarse-grained grand partition function of the reference system, which is defined as:
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) G[γ] = 〈ZrefG[γ − qiψs]〉s G[γ] = 〈ZrefG[γ − qiψs]〉s | (16) |
To evaluate the functional integral over ψs, we use a cumulant expansion:
ln ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) G[γ] ≈ 〈lnZrefG[γ − qiψs]〉s + ½{〈ln ZrefG[γ − qiψs]ln ZrefG[γ − qiψs]〉s − 〈ln ZrefG[γ − qiψs]〉2s} + ⋯ G[γ] ≈ 〈lnZrefG[γ − qiψs]〉s + ½{〈ln ZrefG[γ − qiψs]ln ZrefG[γ − qiψs]〉s − 〈ln ZrefG[γ − qiψs]〉2s} + ⋯ | (17) |
This leads to an approximation similar to the SC expansion of Moreira and Netz.17,33 In this work, we use the ideal gas reference state and truncate the cumulant expansion at first order, which yields:
 | (18) |
 | (19) |
The average value of the field ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l(r) is determined by solving the Poisson equation:
l(r) is determined by solving the Poisson equation:
 | (20) |
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) −1i
−1i![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l, and the density distribution ρα(r) is given by:
l, and the density distribution ρα(r) is given by: | (21) |
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l =
l = ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) ϕ, rather than the electric potential itself, enters into the expression for the density.
ϕ, rather than the electric potential itself, enters into the expression for the density.
The Helmholtz free energy F is given by:
 | (22) |
The first term is related to the “entropic” contribution of the counterions. The second term is the energy of the electrostatic field. The third term is the contribution of the one-body interactions of the mobile particles. The final term is the short-wavelength contribution to the self energy of the fixed charges.
The free energy should be independent on the parameter σ; however, because the theory is approximate, it will have a dependence on σ. Based on this, we determine the value of σ by requiring that the free energy is stationary with respect to this parameter (i.e. ∂F[ρ]/∂σ = 0). This is similar to the optimized random phase approximation.34
3 Counterions surrounding a single charged plate
We now apply the theory developed in the previous section to a system of counterions confined to one side of a uniformly charged plate (i.e.z > 0). The fixed charge density is Σ(r) = Σδ(z), where Σ is the surface charge density, and z is the distance from the surface of the plate. The dielectric constant of the plate (i.e. for z < 0) is ε′. The counterions, which are point charges of magnitude q, are immersed in a continuum medium of dielectric constant ε (i.e. for z > 0).There are two key length scales in this system: the Bjerrum length lB and the Gouy-Chapman length µ. The key dimensionless parameter for this system is the coupling constant Ξ = lB/µ = 2πβ2q3Σ/ε, which is the ratio of these two length scales. In the weak-coupling regime, where Ξ ≪ 1, and the Poisson-Boltzmann theory is expected to work well. In the strong coupling regime, where Ξ ≫ 1, ion-ion correlations are significant, and the Poisson-Boltzmann theory is expected to fail. In this case, the strong coupling expansion, developed by Moreira and Netz,17 is expected to apply.
The one-particle interaction potential for the counterions is:
 | (23) |
 | (24) |
The parameter σ separates short from long-wavelength phenomena. One estimate for the value of σ is that it is related to lB.27 Another estimate for σ is that it is directly related to the average distance between the counterions.16,28 The average distance between the counterions confined to a 2D surface (e.g., collapsed on a charged surface) is  . This suggests that the value of σ should follow the same trend, and it should scale as
. This suggests that the value of σ should follow the same trend, and it should scale as  when Ξ ≫ 1, since in this case all the counterions are confined in a 2D layer near the surface. The dependence of the parameter σ on the coupling parameter Ξ, as predicted by our theory, for various values of Δ is plotted in Fig. 1. The value of σ increases with increasing coupling in agreement with the arguments above.
when Ξ ≫ 1, since in this case all the counterions are confined in a 2D layer near the surface. The dependence of the parameter σ on the coupling parameter Ξ, as predicted by our theory, for various values of Δ is plotted in Fig. 1. The value of σ increases with increasing coupling in agreement with the arguments above.
 | ||
| Fig. 1 Dependence of the parameter σ on the coupling parameter Ξ for (i) Δ = 0.1 (solid line), (ii) Δ = 0.5 (dashed line), and (iii) Δ = 0.95 (dotted line). The thick lines are from the full theory, and the thin lines are from eqn (26). | ||
For σ ≫ 1, the electric potential ϕ is almost constant, and the electrostatic contribution to the free energy Fref can be approximated as:
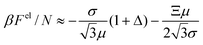 | (25) |
 | (26) |
This yields the same dependence of σ on the coupling as argued above. As can be seen in Fig. 1, this approximation is extremely accurate for low values of Δ but worsens as the difference between the dielectric constant of the plate and the solvent increases.
The deviation of the counterion density profile from the predictions of the Poisson-Boltzmann theory is plotted in Fig. 2 for the case where there is no dielectric interface (i.e. Δ = 0). The thick lines are the predictions of this work, the symbols are the simulation data of Moreira and Netz,17 and the thin dotted line is the strong coupling limit.17 The theory is able to quantitatively describe the counterion distribution from the weak-coupling to the strong coupling regimes.
 | ||
| Fig. 2 Counterion density profile near a single charged plate with (i) Ξ = 0.5 (solid line, circles), Ξ = 10 (dashed line, squares), and (ii) Ξ = 100 (dotted line, triangles). The symbols are Monte Carlo simulation data.42 The thick lines are from the present work. The thin dotted line is the strong coupling limit.38 | ||
In Fig. 3, the density profile of counterions near a charged surface is plotted on a log-log scale. Near the surface, the density profile is well described by the strong coupling theory. Further from the surface at roughly z > σ, however, the strong coupling theory breaks down. At these distances, mean field behavior is observed, and the counterion density profile can be fitted to the PB solution, although with an effective, or rescaled, Gouy-Chapman length µeff:28
 | (27) |
 | ||
| Fig. 3 The ion density profile close to a charged surface: (i) Ξ = 10 (dashed line) and (ii) Ξ = 100 (solid line). The circles are the SC expansion, and the dotted and the dashed-dotted lines are a best fit of the PB theory to the long-range tail for Ξ = 10 and Ξ = 100, respectively. | ||
In many situations, the substance carrying the surface charge has a low dielectric interior, which gives rise to repulsive image charge interactions between it and the counterions. The attraction between the surface charge and the counterions is opposed by this repulsive image charge interaction between the counterions and the dielectric interface. This effect has been studied extensively in the weak coupling regime, with results that compare well with Monte Carlo simulations.35–37
The counterion density profiles near a charged plate with different values of the dielectric constant are plotted for Ξ = 10 in Fig. 4(a) and for Ξ = 1000 in Fig. 4(b). The thick lines are predictions of the present work, and the thin lines are predictions of the strong coupling expansion, and the symbols are simulation data of ref. 38. We observe that even for Ξ = 1000, which is well in to the strong coupling regime, the SC expansion fails to accurately describe the Monte Carlo data. The failure of the SC expansion is due to the fact that the average distance between ions and the average distance from an ion to the charged plate become of the same order of magnitude, and the criterion for the SC is no longer fulfilled. On the other hand, the present theory is able to quantitatively describe the simulation data.
 | ||
| Fig. 4 Counterion density profile for Ξ = 10 (a) and Ξ = 1000 (b) near a single charged, dielectric plate with (i) Δ = 0.1 (solid lines, circles), (ii) Δ = 0.5 (dotted lines, triangles), and Δ = 0.95 (dashed line, squares). The symbols are the Monte Carlo simulation data of Moreira and Netz.43 The thin lines are the predictions of the strong coupling expansion,38,43 and the thick lines are from the present work. | ||
4 Ions confined between two charged plates
In this section, we consider the situation where ions are confined between two plates separated by a distance d. One plate is located at z = 0 and has a surface charge density of Σ1 and counterions of charge q1; the other plate is located at z = d and has a surface charge density of Σ2 with counterions of charge q2. The counterions associated with each plate may also differ from each other in magnitude as well as sign. Note that in this case, the total fixed charge density is:| Σ(r) = Σ1δ(z) + Σ2δ(z − d). |
There are two Gouy-Chapman lengths: µ1 = |2πβq1Σ1|−1 and µ2 = |2πβq2Σ2|−1.
For the two-plate system the self energy of the fixed charges is:
 | (28) |
 | (29) |
In the following, we apply the theory to three different situations.
4.1 Similarly charged plates: counterions only
Now we examine the case of counterions confined between two uniformly charged plates, both with surface charge density Σ = Σ1 = Σ2 and separated by a distance d. The counterions associated with each plate are identical (i.e.q = q1 = q2).The variation of σ with plate spacing for different values of the electrostatic coupling is plotted in Fig. 5, together with the approximation for σ based on the approximate free energy (thin lines). Again, as for the one plate case, we can obtain an approximate expression for σ by assuming that the electric potential is uniform. In this case, the electrostatic contribution to the free energy is approximately:
 | (30) |
 | ||
| Fig. 5 Dependence of the parameter σ on the distance d between charged plates for the coupling parameter: (i) Ξ = 10 (solid lines), (ii) Ξ = 20 (dashed lines), and (iii) Ξ = 100 (dotted lines). The thick lines are from the full theory, and the thin lines are from eqn (26). | ||
Making this stationary with respect to σ must generally be done numerically, however, the process is computationally much easier than solving the full problem. For d = 0, this approximation leads to  , which appears to be very accurate, according to Fig. 5. The approximate value for σ is in fairly good agreement with the actual value for all separations, however, the agreement is best only at very small and very large separations. As seen from Fig. 5, the value of σ decreases with decreasing plate-plate separation, which is due to the overlap of the ion atmospheres which leads to a decrease in the average distance between the ions.
, which appears to be very accurate, according to Fig. 5. The approximate value for σ is in fairly good agreement with the actual value for all separations, however, the agreement is best only at very small and very large separations. As seen from Fig. 5, the value of σ decreases with decreasing plate-plate separation, which is due to the overlap of the ion atmospheres which leads to a decrease in the average distance between the ions.
In Fig. 6(a), we compare the predictions of the present theory for the counterion density distribution between the charged plates with the Monte Carlo simulation data of Moreira and Netz.17 The counterion density profile becomes increasingly flat as the strength of the electrostatic coupling (Ξ) increases. In the strong coupling limit (Ξ → ∞, denoted by the thin solid line), the counterions are uniformly distributed between the plates.
 | ||
| Fig. 6 Counterion density profile (a) and force between the plates (b) for counterions confined between two uniformly charged plates separated by a distance d. The symbols are the simulation data of Moreira and Netz,17 the thick lines are the predictions from this work, and the thin lines are the SC limit. | ||
A comparison of the predictions of the present theory for the pressure between the two plates with MC simulation data of Moreira and Netz17 is given in Fig. 6(b). We find the theory to be in quantitative agreement with the simulation data. The strong coupling result is only approached at very high-coupling or at small plate-plate separations. According to our theory, attraction between the plates will start at a coupling Ξ ≈ 10.0, which is a slightly lower coupling value than what is found in simulations where attraction is found for Ξ ≈ 12.0.
4.2 Similarly charged plates: counterions with added electrolytes
Here, we consider two similarly charged plates, as in the previous section, but now with added electrolytes. The strong coupling expansion of Moreira and Netz17 was original developed for systems with only counterions. Li and Ma have extended39 the SC expansion to the case with added electrolytes. In addition, this same system has been studied by Li and Ma using computer simulation.39 In this section, we compare the predictions of our theory to their simulation data, as well as to the predictions of the PB theory and the SC expansion.For a monovalent electrolyte (e.g., NaCl) in water, the coupling parameter is seldom higher than Ξ = 5.0,39 which will be the case when the electrolyte is in contact with highly charged surfaces. In this regime, we would not expect any attractive forces between like charged objects; however, there may be significant ion binding to the surface, as seen in the previous section, making the force between the plates much smaller than what is expected from a mean field analysis. In Fig. 7, the pressure between two plates of surface charge Σ−1 = −50 Å2/e (which is representative of a silica plate11) is plotted in the presence of a 1:1 electrolyte of bulk concentration of c = 10 mM. This leads to a coupling of Ξ ≈ 6, which is among the highest couplings which is physically relevant for monovalent ions in water at room temperature. The dashed line in Fig. 7 is the corresponding PB result, which overestimates the repulsion between the plates. However, by using an effective surface charge of Σ−1 = −190 Å2/e, the Poisson-Boltzmann theory is in good agreement with the full theory (see the symbols in Fig. 7).
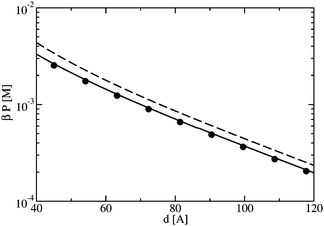 | ||
| Fig. 7 The force as a function of plate-plate separation for two plates with surface charge density Σ−1 = −50 Å2/e in the presence of c = 10 mM of 1:1 electrolyte: the solid line is this work, the dashed line is the prediction of the Poisson-Boltzmann theory, and the symbols are the prediction of the PB theory with an effective charge density of Σeff−1 = −190 Å2/e. | ||
In Fig. 8, the predictions of the theory developed here are compared to Monte Carlo simulation data39 and the SC expansion by Li and Ma.39 From Fig. 8, we see that the theory developed here is in quantitative agreement with the Monte Carlo simulation data, as opposed to the SC expansion by Li and Ma which is at best in qualitative agreement. Within the approximation used in this paper, we do not include the solvation force felt by electrolytes, where salt ions would rather be in an environment where they are maximally screened,35,40 giving rise to a repulsion from any low salt regions. This effect can be included by going beyond the mean field approxmation for the long-wavelength field, by using, for example, a loop expansion or a variational theory. However, this is only a minor effect, especially at low salt concentrations or high fixed charge density.
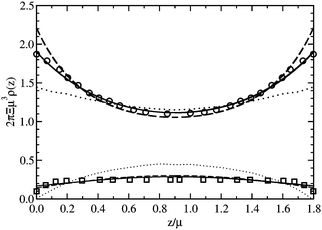 | ||
| Fig. 8 Counterion and co-ion density profiles between two uniformly charged plates for Ξ = 1.0: (i) counterions (thick lines, circles) and (ii) co-ions (thin lines, squares). The solid lines are the predictions of this work, the dashed lines are the predictions of the Poisson-Boltzmann theory, and the dotted lines are the predictions of the SC expansion of Li and Ma.39 The symbols are the MC data of Li and Ma.39 | ||
4.3 Oppositely charged plates
In this section, we examine the properties of ions confined between two oppositely charged plates. We compare the predictions of the present theory with the simulation data of Trulsson and coworkers,11 who consider a system of oppositely charged plates with surface charge Σ1−1 = −50 Å2/e and Σ2−1 = 100 Å2/e, in contact with a v:1 electrolyte at different bulk electrolyte concentrations c. This system was intended to mimic the experimental system studied by Besteman and coworkers,13 where the interaction between a silica sphere and an amine-terminated surface is studied. The simulations11 were found to agree well with experimental results.13In Fig. 9, the force between the plates is plotted for a 2:1 electrolyte and compared with simulation data.11 We find that the pressure is always negative for the case when the bulk electrolyte concentration is c = 10 mM, however, it becomes repulsive for c = 50 mM, in good agreement with simulations.
 | ||
| Fig. 9 The force as a function of plate-plate separation in the presence of 2:1 electrolyte: (i) c = 10 mM (solid line, circles) and (ii) c = 50 mM (dotted line, squares). The surface charges of the plates are Σ1−1 = 50 Å2/e and Σ2−1 = 100 Å2/e. The lines are this work, and the symbols are MC data of Trulsson and coworkers.11 | ||
In Fig. 10, the same system is studied with trivalent counterions (v = 3), however, for a lower bulk salt concentration, as a lower salt concentration is needed to observe repulsive forces between the surfaces. The agreement between theory and simulation is slightly worse in this case, but is still fairly good. The agreement between the theory and simulation results is only qualitative for the case of a 4:1 electrolyte, which is shown in Fig. 11. We find that for 2:1 electrolytes the force becomes repulsive for a bulk salt concentration of c = 50 mM, for 3:1 at a bulk salt concentration of c = 5 mM, and for 4:1 at a concentration of c = 0.5 mM, all in agreement with simulation data.11
 | ||
| Fig. 10 The force as a function of plate-plate separation in the presence of 3:1 electrolyte: (i) c = 0.1 mM (dotted line, diamonds), (ii) c = 1.0 mM (dashed line, squares), and (iii) c = 5.0 mM (solid line, circles). The surface charges of the plates are Σ1−1 = 50 Å2/e and Σ2−1 = 100 Å2/e. The lines are this work, and the symbols are MC data of Trulsson and coworkers.11 | ||
 | ||
| Fig. 11 The force as a function of plate-plate separation in the presence of 4:1 electrolyte: (i) c = 0.01 mM (dotted line, diamonds), (ii) c = 0.10 mM (dashed line, squares), and (iii) c = 0.50 mM (solid line, circles). The surface charges of the plates are Σ1−1 = 50 Å2/e and Σ2−1 = 100 Å2/e. The lines are this work, and the symbols are MC data of Trulsson and coworkers.11 | ||
The theory developed here becomes less accurate when the asymmetry of the ions becomes large and as the added electrolyte concentration increases. However, it is in qualitative agreement with the simulations in all cases, and in quantitative agreement for low salt and low levels of asymmetry. The reason why the current theory cannot capture the asymmetric case is most likely due to the fact that the value of the correlation length σ should vary with the position between the plates. In particular, the value of σ near plate 1 should differ from the value near plate 2, as the surface charge and the valency of the counterions are different for both surfaces. The theory can be generalized to include a spatially varying split between the long-range and short-range Green's functions, unfortunately, this would complicate its evaluation.
One cause of the disagreement at high electrolyte concentration is probably due to excluded volume effects, which are not accounted for in the calculations performed in this article. Again, these effects can be included within the framework of the theory (by using a different reference system, see Section 2), but that would complicate the numerical calculations.
Another cause of the discrepancy is related to the level approximation used in theory. The mean field approximation is not sufficient to properly describe a bulk electrolyte system; fluctuations in the long-wavelength field need to be included with a variational approximation or loop expansion. In addition, the second cumulant term is required in the short range system to balance the ion self energy. Therefore, as the added electrolyte in the system increases in the plate system, these additional terms, which are missing from the current calculations, will become more significant.
Trulsson and coworkers conclude11 that overcharging is not a prerequisite for repulsion between oppositely charged plates. To check if our theory predicts the same trends, we examine the apparent charge density of the plate with charge density Σ1 (which has the high valency counterions):
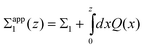 | (31) |
In Fig. 12, the apparent charge density is plotted for different plate separations for the 3:1 electrolyte at bulk ion concentration of 5 mM. For all separations plotted in Fig. 12, the plates are repelled from each other (see Fig. 10); however, not all of the separations show overcharging (i.e. a positive value of Σapp1), in agreement with the findings of the simulation study.11 The repulsion found between the plates is due to a large accumulation of ions in between the plates, effectively pushing the plates apart. The number of ions between the plates can be much larger than what is predicted by PB theory, an effect that increases with increasing electrostatic coupling.11
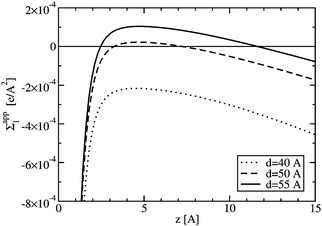 | ||
| Fig. 12 The apparent charge density (see eqn 31) for different plate-plate separations with c = 5 mM of 3:1 electrolyte: (i) d = 40 Å (dotted line), (ii) d = 50 Å (dashed line), and (iii) d = 55 Å (solid line). The surface charges of the plates are Σ1−1 = 50 Å2/e and Σ2−1 = 100 Å2/e. A positive value corresponds to charge inversion. | ||
5 Conclusions
We have developed a field theoretic approach to model the behavior of counterion and co-ions around charged objects. This approach is able to extend beyond the weak coupling regime by treating the long-wavelength and short-wavelength fluctuations in different manners. In this work, short-wavelength fluctuations are handled by a cumulant expansion that is truncated at first order, and long-wavelength fluctuations are handled by the mean field approximation.The length scale σ which divides short and long-wavelength phenomena is found by consistently making the free energy stationary with respect to this parameter. The value is mainly determined by the interplay of the short-wavelength self energy of the ions, the short-wavelength self energy of the plates and the short-wavelength interaction between the ions and the plates.
The approximate theory developed here was compared against simulation data for systems containing ions near a single charged plate and for systems with ions confined between charged plates. The theory was found to give quantitative agreement, as long as most of ions in the system were counterions (i.e. there is relatively little added electrolyte). As the amount of added electrolyte increases, the quality of the predictions of the theory decreases.
The accuracy of the theory can be improved in several different manners. For example, the value of σ could be allowed to vary throughout the system. As discussed briefly in Section 4.3, this could improve the results for systems with asymmetric electrolytes, where we have found our approach to be less accurate. Another improvement would be to use a different reference system to account for excluded volume interactions. These interactions would become important when total ion concentration between the plates becomes substantial (c ≈ 0.1–1.0 M). However, the excluded volume effects are not so important in the strong coupling regime, although they are more important for systems with 1:1 electrolytes at highly charged surfaces.41 A final way to improve the theory is to increase the level of approximation used to evaluate the functional integrals of the long and short-wavelength fields.
Acknowledgements
MM Hatlo acknowledges support from an EC Marie Curie Fellowship (MEST-CT-2004-503750).References
- A. Naji, S. Jungblut, A. G. Moreira and R. R. Netz, Physica A, 2005, 352, 131–170 CrossRef.
- R. Kjellander, T. A. Kesson, B. Jönsson and S. Marcelja, J. Chem. Phys., 1992, 97, 1424 CrossRef CAS.
- R. Podgornik, J. Phys. A, 1990, 23, 275 CrossRef.
- P. Attard, D. J. Mitchell and B. W. Ninham, J. Chem. Phys., 1988, 88(8), 4987–4996 CrossRef CAS.
- R. Kjellander and S. Marèelja, Chem. Phys. Lett., 1984, 112, 49 CrossRef CAS.
- R. Kjellander and S. Marèelja, J. Chem. Phys., 1985, 82, 2122 CrossRef CAS.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, London, 2nd edn, 1986 Search PubMed.
- L. Guldbrand, B. Jönsson, H. Wennerstrom and P. Linse, J. Phys. Chem., 1984, 80, 2221 CrossRef CAS.
- J. Z. Wu, D. Bratko, H. W. Blanch and J. M. Prausnitz, J. Chem. Phys., 1999, 111(15), 7084–7094 CrossRef CAS.
- J. Z. Wu, D. Bratko, H. W. Blanch and J. M. Prausnitz, Phys. Rev. E, 2000, 62(4), 5273–5280 Search PubMed.
- M. Trulsson, B. Jonsson, T. Akesson and J. Forsman, Phys. Rev. Lett., 2006, 97 Search PubMed 068302.
- O. Zohar, I. Leizerson and U. Sivan, Phys. Rev. Lett., 2006, 96, 177802 CrossRef.
- K. Besteman, M. A. G. Zevenbergen, H. A. Heering and S. G. Lemay, Phys. Rev. Lett., 2004, 93, 170802 CrossRef CAS.
- V. A. Bloomfield, Biopolymers, 1997, 44, 269–282 CrossRef CAS.
- J. Tang and P. A. Janmey, J. Biol. Chem., 1996, 271, 8556–8563 CrossRef CAS.
- J. Forsman, J. Phys. Chem. B, 2004, 108, 9236–9245 CrossRef CAS.
- A. G. Moreira and R. R. Netz, Phys. Rev. Lett., 2001, 87(7), 078301 CrossRef CAS.
- A. Naji, A. Arnold, C. Holm and R. R. Netz, Europhys. Lett., 2004, 67(1), 130–136 CrossRef CAS.
- M. Deserno, F. Jimenez-Angeles, C. Holm and M. Lozada-Cassou, J. Phys. Chem. B, 2001, 105, 10983–10991 CrossRef CAS.
- M. Baus and J.-P. Hansen, Phys. Rep., 1980, 59, 1–94 CrossRef CAS.
- S. Nordholm, Chem. Phys. Lett., 1984, 105, 302–307 CrossRef CAS.
- Y. Levin, Rep. Prog. Phys., 2002, 65(11), 1577–1632 CrossRef CAS.
- N. V. Brilliantov, Contrib. Plasma. Phys., 1998, 38, 489–499 CrossRef CAS.
- A. G. Moreira and R. R. Netz, Eur. Phys. J. D, 2000, 8(1), 145–149 CAS.
- A. W. Outhwaite, L. B. Bhuiyan and S. Levine, J. Chem. Soc. Faraday Trans. 2, 1980, 76, 1388 RSC.
- A. Diehl, M. Tamashiro, M. C. Barbosa and Y. Levin, Physica A, 1999, 274, 433–445 CrossRef.
- C. D. Santangelo, Phys. Rev. E, 2006, 73, 041512 CrossRef.
- Y.-G. Chen and J. D. Weeks, Proc. Nat. Acad. Sci. (USA), 2006, 103, 7560–7565 CrossRef CAS.
- J. D. Jackson, Classical Electrodynamics, Wiley, New York, 1975 Search PubMed.
- J. M. Rodgers, C. Kaur, Y.-G. Chen and J. D. Weeks, Phys. Rev. Lett., 2006, 97, 097801 CrossRef.
- J. Hubbard, Phys. Rev. Lett., 1959, 3, 77 CrossRef.
- R. L. Stratonovich, Dokl. Akad. Nauk SSSR, 1957, 115, 1097.
- A. G. Moreira and R. R. Netz, Europhys. Lett., 2000, 52(6), 705–711 CrossRef CAS.
- H. C. Andersen and D. Chandler, J. Chem. Phys., 1972, 57, 1918–1929 CrossRef CAS.
- M. M. Hatlo, R. A. Curtis and L. Lue, J. Chem. Phys., 2008, 128, 164717 CrossRef CAS.
- L. B. Bhuiyan, C. W. Outhwaite, D. Henderson and M. Alawneh, Mol. Phys., 2007, 105, 1395–1402 CrossRef CAS.
- D. Henderson, T. Gillespie and D. NagyBodas, Mol. Phys., 2005, 103, 2851–2861 CrossRef CAS.
- A. G. Moreira and R. R. Netz, Europhys. Lett., 2002, 57, 911–917 CrossRef CAS.
- C. Li and H. Ma, J. Chem. Phys., 2004, 121, 1917 CrossRef CAS.
- R. R. Netz, Phys. Rev. E, 1999, 60(3), 3174–3182 Search PubMed.
- L. Lue, N. Zoeller and D. Blankschtein, Langmuir, 1999, 15(11), 3726–3730 CrossRef CAS.
- A. G. Moreira and R. R. Netz, Eur. Phys. J. E, 2002, 8, 33–58 CAS.
- A. G. Moreira, Charged systems in bulk and at interfaces, PhD thesis, Max-Planck-Institut fur Kolloid und Grenzflachenforschung, Golm, 2001.
| This journal is © The Royal Society of Chemistry 2009 |


