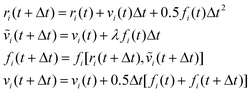DOI:
10.1039/B809751H
(Paper)
Soft Matter, 2009,
5, 98-103
Lamellar-in-lamellar self-assembled C–b–(B–b–A)m–b–B–b–C multiblock copolymers: Alexander–de Gennes approach and dissipative particle dynamics simulations
Received
9th June 2008
, Accepted 17th September 2008
First published on 20th October 2008
Abstract
A simple theoretical analysis of the lamellar-in-lamellar self-assembled state of ternary C–b–(B–b–A)m–b–B–b–C multiblock copolymer melts in the strong segregation limit is presented using the Alexander–de Gennes approximation. For a given value of m, the influence of the chain length of the various blocks and the value of the Flory–Huggins χAB and χBC interaction parameters on the number k of internal domains is discussed in detail. The theoretically predicted tendencies are corroborated by computer simulations using the dissipative particle dynamics technique.
1. Introduction
During the past decades hierarchically ordered block copolymers and block copolymer based systems have been an attractive subject for experimental1–15 and theoretical16–22 investigations. The growing interest in this class of systems is due to the possibilities of creating periodic structures combining different periodicities. One of the first observations of a double-periodic behavior concerned the self-assembly in a melt of comb-shaped supramolecules consisting of polystyrene–block–poly(4-vinylpyridine) (PS–b–P4VP) diblock copolymers with hydrogen-bonded pentadecylphenol (PDP) side chains attached to the P4VP blocks.1,2 The two different periods are connected to the two different intrinsic length scales: the long length scale period of the diblock copolymer and the short length scale period of the repeat motive of the comb-shaped P4VP(PDP) blocks. Depending on the relative volume fraction of the polystyrene block, lamellar-in-lamellar, lamellar-in-spheres, spheres-in-lamellar, etc. are formed.
Binary PS–b–(PI–b–PS)4–b–PI–b–PS and ternary P2VP–b–(PI–b–PS)4–b–PI–b–P2VP linear undecablock copolymers are the first examples of block copolymers with a linear architecture where double-periodic behavior has been observed experimentally.4,5 Here P2VP, PI and PS denote poly(2-vinylpyridine), polyisoprene and polystyrene, respectively. For these multiblock copolymers all chemically different species are mutually immiscible. A 3-layered and a 5-layered lamellar-in-lamellar structure was observed for the binary, resp. ternary multiblock copolymer system. In these cases the long length scale period involves phase separation between the “long” PS resp. P2VP end-blocks and the middle multiblock, whereas the short length scale results from the microphase separation within the internal (PI–b–PS)4–b–PI part of the multiblock containing much shorter blocks.
Both linear and graft-like multiblock copolymers have been extensively studied theoretically in the frameworks of self-consistent field calculations,16,17 the weak segregation Landau approach18–20 and strong segregation theory.21,22 The copolymer composition, the architecture, the length of the different blocks and the values of the Flory–Huggins interaction parameters are the essential parameters. In our own theoretical work21 on ternary C–b–(B–b–A)m–b–B–b–C multiblock copolymers the number k of internal A and B lamellar domains was addressed as a function of parameter m using self-consistent field considerations in the strong segregation limit. In ref. 22 we also analyzed and explained the essential difference between ternary C–b–(B–b–A)m–b–B–b–C and binary A–b–(B–b–A)m–b–B–b–A multiblock copolymers. The theoretical predictions obtained were in excellent agreement with the few experimental data available.4,5
In this paper we reconsider the C–b–(B–b–A)m–b–B–b–C multiblock copolymer melt using a much simpler theoretical approach based on the Alexander–de Gennes approximation.23,24 Thus a very simple expression [eqn (12)] for the free energy is obtained which clearly demonstrates the influence of the number of internal layers k. We show that this simplified approach provides results that are virtually identical to the results obtained by the far more elaborated treatment. Using it we analyze and discuss the domain formation in ternary C–b–(B–b–A)m–b–B–b–C multiblock copolymers in much more detail than before as a function of the chain length of the blocks and the Flory–Huggins χAB and χBC interaction parameters, limiting ourselves to the lamellar-in-lamellar self-assembled state. To corroborate the theoretically predicted tendencies, we performed computer simulations using the well-known dissipative particle dynamics (DPD) technique.25–33
2. Theoretical model
Considering the ternary C–b–(B–b–A)m–b–B–b–C multiblock copolymer melt in the Alexander–de Gennes approximation implies that we assume all 2m + 1 middle A- and B-blocks as well as the outer C-blocks to be stretched uniformly inside their respective layers. We assume that the 2m + 1 short middle blocks self-assemble into k internal layers confined between the outer C-layers.
In general, a global multiblock conformation can be either a bridge or a loop as illustrated in Fig. 1. Both global bridges and global loops consist in turn of local loops and bridges. In the spirit of the Alexander–De Gennes approximation,23,24 we will not distinguish between global bridge and global loop conformations, assuming half of the global loop to be equivalent to half of the global bridge.
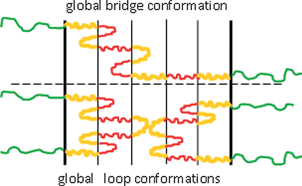 |
| | Fig. 1 A schematic representation of a global bridge (top) and a global loop (bottom) conformation for a C–b–(B–b–A)4–b–B–b–C multiblock copolymer. A-, B- and C-blocks are denoted by red, yellow and green, respectively. In the illustration m = 4 and k = 5. | |
3. Theoretical analysis
Let n denote the degree of polymerization of the internal A- and B-blocks alike and N denote the degree of polymerization of the outer C-blocks, with N ≫ n. The statistical segment length and monomer volume are denoted as a and υ, respectively, and are assumed to be equal for all chemically different components. The thickness of the internal layers and the outer layer are denoted as h and H (Fig. 2). Furthermore Σ is used to denote the interfacial area per multiblock copolymer chain. The Flory–Huggins interaction parameters χAB, χBC and χAC are taken as positive, implying unfavourable interactions between all the chemically different species.
 |
| | Fig. 2 A schematic representation of a global bridge conformation of a C–b–(B–b–A)m–b–B–b–C copolymer for m = 6. h and H denote the thickness of the internal layers and half of the outer layers, respectively. | |
Incompressibility implies:
The total free energy per multiblock copolymer chain can be written as:
| | | F = 2FBC + (k−1)FAB + mF0A + (m + 1)F0B + 2FC + Fconf | (3) |
Here FAB and FBC are the interfacial free energies related to the interfacial tensions and the average interfacial area Σ per multiblock copolymer by:
| | | FAB = γABΣ, FBC = γBCΣ | (4) |
with interfacial tensions

and
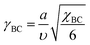
The elastic free energies of uniformly stretched short A- and B-blocks F0A and F0B are the same and in a scope of the Alexander–de Gennes approximation are:
| | 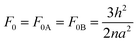 | (5) |
Likewise, the elastic free energy F0C for the outer C-blocks is given by:
| |  | (6) |
The conformational term Fconf takes into account the global stretching of the middle multiblock chain. In our previous paper this conformational energy was approximated by Fconf = kln2.21 Here we introduce an improved expression obtained in the following way. The middle multiblock chain is divided into three parts, namely into two tail sections of type (B + A/2) containing one B-block and half of the A-block and a middle part consisting of (2m − 2) sections of type (A/2 + B/2) which contain half of an A- and half of a B-block. For the global bridge conformation the middle part of the multiblock chain starts at the centre of the second thin domain which is an A-domain and finishes at the centre of the (k − 1)th A-domain. Its conformation can be described by a random walk with drift on a periodic one-dimensional lattice with steps ending at the centres of the A- and B-domains. Assuming that the walk consists of k+ steps in the positive direction and k− steps in the opposite direction (here we do not take into account the boundary conditions) so that k+ + k− = 2m − 2 and k+ − k− = k − 3, the conformational free energy (in kBT energetic units) is given by:
| | 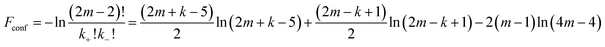 | (7) |
A comparison with the very simple expression Fconf = kln2 used before,21 shows that the latter slightly overestimates the combinatorial contribution.
Taking into account eqn (1), (2), (4)–(7), the free energy expression (3) transforms into:
| |  | (8) |
with:
| | | γ* = 2γBC + (k − 1)γAB | (9) |
| |  | (10) |
Note that eqn (8) is very similar to the corresponding equation for lamellar self-assembled diblocks. The main differences are the additional combinatorial terms and the obvious k-dependence of both the interfacial (γ*Σ) and the elastic stretching (Q/Σ2) contributions. Minimization of the free energy (8) with respect to Σ yields the equilibrium interface area:
| |  | (11) |
which results in the final expression for the total free energy:
| |  | (12) |
4. Results and discussions
We consider first the only system investigated experimentally so far, i.e., P2VP–b–(PI–b–PS)4–b–PI–b–P2VP. It corresponds to χBC = 0.4, χAB = 0.1, χBCN = 340, χABn = 17, m = 4 and n/N = 0.2. The free energy [eqn (12)] as a function of the number of internal layers k is presented in Fig. 3a. The minimum occurs for k = 5 precisely as found experimentally.4 The results for the values m = 3, 5 and 6 are presented in Fig. 3b, c and d. The values of k found are 5, 7 and 7. These results are in excellent agreement with the ones obtained from a much more elaborated mean-field calculation using the same set of parameters.21
 |
| | Fig. 3 The free energy F of the lamellar-in-lamellar self-assembled C–b–(B–b–A)m–b–B–b–C multiblock copolymer melt as a function of the number k of internal layers for χBCN = 340, χABn = 17, n/N= 0.2. (a) m = 4, (b) m = 3, (c) m = 5, (d) m = 6. | |
In order to investigate the effect of the interfacial tension, numerical calculations were performed for different values of the Flory–Huggins χBC-parameter for m = 3, 4, 5 and 6, χAB = 0.1 and a fixed length of the internal blocks n = 200. Throughout the rest of this section the length N of the outer blocks is assumed to satisfy (2m + 1)n = 2N, thus assuring an equilibrium lamellar structure. The results are summarized in Table 1. Fig. 4a–d shows the free energy as function of k for m = 4 and Flory–Huggins parameter values χBC = 0.04, 0.4, 2.5 and 9.5, where the minima are found at k = 3, 5, 7 and 9, respectively.
Table 1 The number of internal domains kopt as a function of χBC for χAB = 0.1 and n = 200
|
k
opt
|
χ
BC
|
|
m = 3, N = 700 |
m = 4, N = 900 |
m = 5, N = 1100 |
m = 6, N = 1300 |
m = 7, N = 1500 |
| 3 |
≤0.16 |
≤0.08 |
≤0.06 |
≤0.045 |
≤0.042 |
| 5 |
0.17–2.6 |
0.09–0.64 |
0.07–0.3 |
0.05–0.18 |
0.043–0.13 |
| 7 |
≥2.7 |
0.66–6.7 |
0.31–1.76 |
0.19–0.83 |
0.13–0.48 |
| 9 |
|
≥6.8 |
1.77–13.2 |
0.84–3.75 |
0.49–1.82 |
| 11 |
|
|
≥13.3 |
3.77–22.4 |
1.83–6.85 |
| 13 |
|
|
|
≥22.5 |
6.9–34.5 |
| 15 |
|
|
|
|
≥35 |
 |
| | Fig. 4 Free energy F of lamellar-in-lamellar self-assembled C–b–(B–b–A)4–b–B–b–C multiblock copolymer melt as a function of the number k of internal layers for n = 200, N = 900, χAB = 0.1 and (a) χBC = 0.04, (b) χBC = 0.4, (c) χBC = 2.5, (d) χBC = 9.5. | |
Larger χBC values force a reduction in the equilibrium BC interfacial area which in turn forces the internal short blocks to become more stretched. To relief this stretching the system starts to create more AB interfaces, i.e. larger values of k. Of course, in reality the values of the Flory–Huggins interaction parameters hardly ever exceed unity. The calculations for larger values are nevertheless useful to track and understand the tendencies in the layer formation in ternary C–b–(B–b–A)m–b–B–b–C multiblock copolymers.
To see how these results depend on the elastic stretching of the blocks, the length of the internal blocks was decreased with a factor 2 to n = 100. Since we maintain the assumption (2m + 1)n = 2N, the length N of the outer blocks is likewise decreased by a factor of 2. We first consider fixed χAB = 0.1 and determine the equilibrium number of internal domains kopt as a function of m and χBC. The results are presented in Table 2. A comparison with Table 1 shows that the decreased length of the blocks, implying “stiffer” springs, indeed requires larger values of χBC to obtain the same number of internal layers. As an explicit example we observe that for n = 100, resp. 200, 5 layers are found for 0.094 ≤ χBC ≤ 0.76 resp. 0.09 ≤ χBC ≤ 0.64.
Table 2 The number of internal domains kopt as a function of χBC for n = 100 and χAB = 0.1
| |
χ
BC
|
|
k
opt
|
m = 3, N = 350 |
m = 4, N = 450 |
m = 5, N = 550 |
m = 6, N = 650 |
m = 7, N = 750 |
| 3 |
≤0.17 |
≤0.09 |
≤0.06 |
≤0.05 |
≤0.04 |
| 5 |
0.18–3.55 |
0.094–0.76 |
0.06–0.34 |
0.05–0.20 |
0.04–0.13 |
| 7 |
≥3.56 |
0.77–9.25 |
0.35–2.15 |
0.21–0.95 |
0.14–0.55 |
| 9 |
|
≥9.3 |
2.2–18.6 |
1.0–4.7 |
0.56–2.2 |
| 11 |
|
|
≥18.7 |
4.8–32.2 |
2.3–8.9 |
| 13 |
|
|
|
≥32.3 |
9.0–50.5 |
| 15 |
|
|
|
|
≥51 |
Numerical calculations were also performed for a constant χBC = 0.1 as a function of χAB with internal block lengths of n = 200 and n = 100. The results are collected in Fig. 5 and 6. For the given value of χBC = 0.1, the minimal number of k = 3 internal layers is found for χAB to be sufficiently large, at smaller values a transition to a 5-layered and even a 7-layered structure (more A–B interface) is observed. Of course, 2nχAB has to be considerably larger than 10 to really have a strongly segregated lamellar-in-lamellar self-assembled state.
 |
| | Fig. 5 The number of domains kopt of lamellar-in-lamellar self-assembled C–b–(B–b–A)m–b–B–b–C as a function of χAB and m for n = 200 and χBC = 0.1. Dashed lines delineate the range of χAB-values used. | |
 |
| | Fig. 6 The number of domains kopt of lamellar-in-lamellar self-assembled C–b–(B–b–A)m–b–B–b–C as a function of χAB and m for n = 100 and χBC = 0.1. Dashed lines delineate the range of χAB-values used. | |
The interfacial contribution to the free energy is given by Finterface = 2FBC + (k − 1)FAB, which can be simply rewritten as  where eqn (2) and (4) have been used. From this expression it follows straightforwardly that when χAB > 4χBC or equivalently γAB > 2γBC a 3-layered structure has a lower interfacial free energy than a 5-layered one. The results presented in the various tables, however, show that in reality a 3-layered structure is already formed at considerably smaller values of χAB, thus demonstrating in particular the importance of the conformational contribution [see eqn (8)].
where eqn (2) and (4) have been used. From this expression it follows straightforwardly that when χAB > 4χBC or equivalently γAB > 2γBC a 3-layered structure has a lower interfacial free energy than a 5-layered one. The results presented in the various tables, however, show that in reality a 3-layered structure is already formed at considerably smaller values of χAB, thus demonstrating in particular the importance of the conformational contribution [see eqn (8)].
The tendencies observed are corroborated by the results of computer simulations obtained by using dissipative particle dynamics simulation technique. The results are described in the next section, whereas the computational details are presented in the Appendix.
5. Dissipative particle dynamic simulations
In the dissipative particle dynamics simulation technique a large series of monomers are collected into a few bead-and-spring (DPD) particles in order to simulate the molecular behavior at longer time and length scales. The first situation simulated resembles the experimentally studied ternary P2VP–b–(PI–b–PS)4–b–PI–b–P2VP linear undecablock copolymer system, i.e.m = 4.5Fig. 7 shows the corresponding self-assembled state observed for C4–(B1A1)4B1–C4 with the energy parameters representing the soft repulsion [see eqn (A2)] equal to aBA = 85, aBC = 320. Using eqn (A10) in the Appendix for the relation between these energy parameters and the familiar Flory–Huggins parameters, this corresponds to  and
and  . Fig. 7 demonstrates that a self-assembled lamellar state is formed with 5 “thin” internal layers as observed experimentally4 and calculated theoretically (Fig. 3a and ref. 21). The same result is obtained for internal blocks that are twice as long C4–(B2A2)4 B2–C4 (the subscripts of A, B and C denote the number of DPD particles taken for the calculations).
. Fig. 7 demonstrates that a self-assembled lamellar state is formed with 5 “thin” internal layers as observed experimentally4 and calculated theoretically (Fig. 3a and ref. 21). The same result is obtained for internal blocks that are twice as long C4–(B2A2)4 B2–C4 (the subscripts of A, B and C denote the number of DPD particles taken for the calculations).
 |
| | Fig. 7 An image of C4–(B1A1)4B1–C4 for aBA = 85, aBC = 320. | |
Subsequently, we address the issue of the dependence of the number of internal layers on the interfacial tension. For this purpose we take m = 5, as reasonable variations in the values of the Flory–Huggins parameters are theoretically predicted to induce transitions between a different number of internal layers. That this is also the case in the simulations is shown in Fig. 8, where 3 images of the same system C4–(B1A1)5 B1–C4 are presented for different energy parameters aAB, aBC. Fig. 8 demonstrates that when the A–B interaction becomes less unfavourable and the B–C interaction becomes more unfavourable, indeed transitions are observed from 3 to 5 to 7 internal layers. There is the obvious tendency to decrease the BC interface with a corresponding increase in the AB interface.
 |
| | Fig. 8 Images of the self-assembled C4–(B1A1)5 B1–C4 multiblock copolymer melt for: (a) aAB = 250, aBC = 50; (b) aAB = 75, aBC = 120; (c) aAB = 65, aBC = 300. | |
That the number of internal layers also depends on the length of the blocks is illustrated by a simulation of C3–(B1A1)3 B1–C3 and C3–(B2A2)3 B2–C3 using the same energy parameter values. Fig. 9 shows that in the former case 3 internal layers are formed and 5 in the latter. Although this example can not be directly compared with the theoretical examples given, it confirms that shorter blocks, the rest being equal, push the system towards a smaller number of internal layers.
 |
| | Fig. 9 Images of (a) C3–(B1A1)3 B1–C3 and (b) C3–(B2A2)3 B2–C3 for aAB = 75 and aBC = 120. | |
6. Summary
In this paper, we presented a simple theoretical analysis of the strongly segregated lamellar-in-lamellar self-assembled state of ternary C–b–(B–b–A)m–b–B–b–C multiblock copolymers using the Alexander–de Gennes approach. This simplified description results in a very simple expression for the free energy clearly demonstrating the influence of the number of internal layers k on the various contributions. It allowed us to discuss in detail the influence of the pertinent parameters on the number of internal layers formed. The main observation concerns the sensitivity of k on the interfacial tension between the outer C-layers and the adjacent internal B-layers. The theoretically observed general tendencies were corroborated by the results of computer modeling using the dissipative particle dynamics technique. Experiments to verify these predictions are underway.
Computational Details
The dissipative particle dynamics (DPD) simulation method was introduced by Hoogerbrugge and Koelman25 and first successfully applied by Groot and Madden26 to AB diblock copolymer melts. The time evolution for a set of interacting particles is found by solving Newton's equations of motion. The force acting on the ith particle  due to particle j is the sum of a conservative force
due to particle j is the sum of a conservative force  , a dissipative force
, a dissipative force  , and a random force
, and a random force  is given by:
is given by:| |  | (A1) |
where the sum is over all other particles within a certain cut-off radius rC. Since rC is the only length scale it is used as the unit of length and thus set equal to 1. The conservative force  is a soft repulsive force given by:
is a soft repulsive force given by:| |  | (A2) |
where aij is the repulsive interaction parameter between particles i and j,  ,
, ,
, 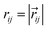 . The dissipative force
. The dissipative force  is a hydrodynamic drag force and is defined by:
is a hydrodynamic drag force and is defined by:| |  | (A3) |
where γ is a friction parameter, ωD is a r-dependent weight function. The random force  describes thermal noise:
describes thermal noise:| |  | (A4) |
where σ is the noise amplitude, ωR is a weight function, and θij is a random variable with normal distribution, Δt is a time-step. The dissipative force slows down the particles by removing the kinetic energy from them and this effect is balanced by the random force due to thermal fluctuations. Friction γ and noise σare related by:27| | σ2 = 2γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kBT kBT | (A5) |
The associated weight functions satisfy the fluctuation–dissipation theorem if the following relation is satisfied:28
The standard choice for ωD is:
| | 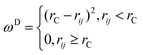 | (A7) |
The spring force  that acts on bead i due to its connection with beads j satisfies:
that acts on bead i due to its connection with beads j satisfies:
| |  | (A8) |
where
C is a harmonic type spring constant, which is chosen to be equal to 4 (in terms of
kBT).
27
A modified version of the velocity–Verlet algorithm is used to solve Newton's equations of motion:29
| | 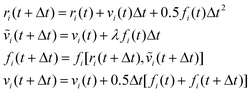 | (A9) |
Groot and Warren
27 presented a detailed investigation of the effect of
λ on the steady state temperature and showed that for a particle density
ρ = 3 and noise
σ = 3, the optimum value is given by
λ = 0.65 for which the temperature control can be maintained even at large time-steps of Δ
t = 0.06. For our calculations we took accordingly
λ = 0.65, Δ
t = 0.06,
ρ = 3 and
σ = 3.
The DPD simulations are performed in a cubic box of L3 grids with periodic boundary conditions. Since the particle density ρ is set equal to 3, the total number of simulated DPD beads equal 3L3. As reported in ref. 30–32, the morphology obtained by DPD simulations may depend on the finite size of the simulation box. In our simulations we have periodic structures with large periods and to exclude finite size effects we have to take the simulation box sufficiently large. The number of DPD beads per chain is in the range 9–17. The size of the simulation box volume used was taken in the range V = 1 × 103–3 × 103, in such a way that for each case considered L exceeded the length of the chains. All simulations were started from random positions.
Following the work of Groot and Warren,27 the repulsive parameters between the same types of particles is taken as aii = 25. For different types of particles aij can be chosen from the relation between the energy parameter aij and the Flory–Huggins interaction parameter χij
| | | aij = aii + 3.497χij | (A10) |
References
- J. Ruokolainen, R. Mäkinen, M. Torkkeli, T. Mäkelä, R. Serimaa, G. ten Brinke and O. Ikkala, Science, 1998, 280, 557 CrossRef CAS.
- O. Ikkala and G. ten Brinke, Science, 2002, 295, 2407 CrossRef CAS.
- J. Ruokolainen, G. ten Brinke and O. Ikkala, Adv. Mater., 1999, 11, 777 CrossRef CAS.
- J. Masuda, A. Takano, Y. Nagata, A. Noro and Y. Matsushita, Phys. Rev. Lett., 2006, 97, 098301 CrossRef.
- Y. Nagata, J. Masuda, A. Noro, D. Cho, A. Takano and Y. Matsushita, Macromolecules, 2005, 38, 10220 CrossRef CAS.
- C. C. Evans, F. S. Bates and M. D. Ward, Chem. Mater., 2000, 12, 236 CrossRef CAS.
- A. F. Thünemann and S. General, Macromolecules, 2001, 34, 6978 CrossRef.
- C. Osuji, C. Y. Chao, I. Bita, C. K. Ober and E. L. Thomas, Adv. Funct. Mater., 2002, 12, 753 CrossRef CAS.
- I. A. Ansari, V. Castelletto, T. Mykhaylyk, I. W. Hamley, Z. B. Lu, T. Itoh and C. T. Imrie, Macromolecules, 2003, 36, 8898 CrossRef CAS.
- G. O. R. Alberda van Ekenstein, E. Polushkin, H. Nijland, O. Ikkala and G. ten Brinke, Macromolecules, 2003, 36, 3684 CrossRef CAS.
- C. Y. Chao, X. Li, C. K. Ober, C. Osuji and E. L. Thomas, Adv. Mater., 2004, 14, 364 CAS.
- O. Ikkala and G. ten Brinke, Chem. Commun., 2004, 2131 RSC.
- C. S. Tsao and H. L. Chen, Macromolecules, 2004, 37, 8984 CrossRef CAS.
- I. W. Hamley, V. Castelletto, P. Parras, Z. B. Lu, C. T. Imrie and T. Itoh, Soft Matter, 2005, 1, 355 RSC.
- B. Nandan, C. H. Lee, H. L. Chen and W. C. Chen, Macromolecules, 2005, 38, 10117 CrossRef CAS.
- R. Nap, C. Kok, G. ten Brinke and S. I. Kuchanov, Eur. Phys. J. E, 2001, 4, 515 CrossRef CAS.
- R. Nap, N. Sushko, I. Ya. Erukhimovich and G. ten Brinke, Macromolecules, 2006, 39, 6765 CrossRef CAS.
- Y. Smirnova, G. ten Brinke and I. Ya. Erukhimovich, J. Chem. Phys., 2006, 124, 054907 CrossRef.
- S. I. Kuchanov, V. E. Pichugin and G. ten Brinke, e–Polym., 2006, 012 Search PubMed.
- S. I. Kuchanov, V. E. Pichugin and G. ten Brinke, Europhys. Lett., 2006, 76, 959 CrossRef CAS.
- A. Subbotin, T. Klymko and G. ten Brinke, Macromolecules, 2007, 40, 2915 CrossRef CAS.
- T. Klymko, A. Subbotin and G. ten Brinke, J. Chem. Phys., 2008, 129, 114902 CrossRef.
- P. G. de Gennes, J. Phys., 1976, 37, 1443.
- S. Alexander, J. Phys., 1977, 38, 977 CAS.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155 CrossRef.
- R. D. Groot and T. J. Madden, J. Chem. Phys., 1998, 108, 8713 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423 CrossRef CAS.
- P. Espanol and P. B. Warren, Europhys. Lett., 1995, 30, 191 CrossRef CAS.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon, Oxford, 1987 Search PubMed.
- U. Micka and K. Binder, Macromol. Theory Simul., 1995, 4, 419 CrossRef CAS.
- Y. Bahbot-Raviv and Z. G. Wang, Phys. Rev. Lett., 2000, 85, 3428 CrossRef CAS.
- Q. Wang, P. F. Nealey and J. J. de Pablo, Macromolecules, 2001, 34, 3458 CrossRef CAS.
- C.-I. Huang and C.-M. Chen, ChemPhysChem, 2007, 8, 2588 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. 

 and
and 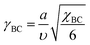
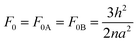

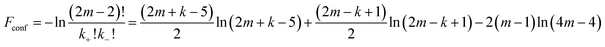








 where eqn (2) and (4) have been used. From this expression it follows straightforwardly that when χAB > 4χBC or equivalently γAB > 2γBC a 3-layered structure has a lower interfacial free energy than a 5-layered one. The results presented in the various tables, however, show that in reality a 3-layered structure is already formed at considerably smaller values of χAB, thus demonstrating in particular the importance of the conformational contribution [see eqn (8)].
where eqn (2) and (4) have been used. From this expression it follows straightforwardly that when χAB > 4χBC or equivalently γAB > 2γBC a 3-layered structure has a lower interfacial free energy than a 5-layered one. The results presented in the various tables, however, show that in reality a 3-layered structure is already formed at considerably smaller values of χAB, thus demonstrating in particular the importance of the conformational contribution [see eqn (8)]. and
and  . Fig. 7 demonstrates that a self-assembled lamellar state is formed with 5 “thin” internal layers as observed experimentally4 and calculated theoretically (Fig. 3a and ref. 21). The same result is obtained for internal blocks that are twice as long C4–(B2A2)4 B2–C4 (the subscripts of A, B and C denote the number of DPD particles taken for the calculations).
. Fig. 7 demonstrates that a self-assembled lamellar state is formed with 5 “thin” internal layers as observed experimentally4 and calculated theoretically (Fig. 3a and ref. 21). The same result is obtained for internal blocks that are twice as long C4–(B2A2)4 B2–C4 (the subscripts of A, B and C denote the number of DPD particles taken for the calculations).



 due to particle j is the sum of a conservative force
due to particle j is the sum of a conservative force  , a dissipative force
, a dissipative force  , and a random force
, and a random force  is given by:
is given by:
 is a soft repulsive force given by:
is a soft repulsive force given by:
 ,
, ,
,  . The dissipative force
. The dissipative force  is a hydrodynamic drag force and is defined by:
is a hydrodynamic drag force and is defined by:
 describes thermal noise:
describes thermal noise:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kBT
kBT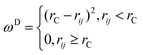
 that acts on bead i due to its connection with beads j satisfies:
that acts on bead i due to its connection with beads j satisfies: