Influence of droplet properties on the formation of microemulsion-ABA-triblock copolymer networks

Abstract

Structural equilibrium properties of transient networks formed by microemulsion droplets and ABA triblock copolymers in solution have been studied by Monte Carlo simulation. The droplets were represented by soft spheres and the polymers by junctions connected by harmonic bonds with an angular potential regulating the intrinsic chain stiffness. The interaction parameters were selected such that the end A-blocks were localized inside the droplets and the middle B-block in the continuous phase. The influence of (i) the droplet volume fraction, (ii) the droplet radius, and (iii) the contour length of the middle B-block on the formation and the structure of the microemulsion-polymer network at three-fold excess of the polymers were investigated by using polymer end-to-end separation probability distribution functions, droplet radial distribution functions, and network connectivity indicators. A universal behavior of the properties investigated was found when examining the results versus the length ratio of the polymer end-to-end separation and the surface-to-surface separation between neighboring droplets for a hypothetical homogeneous droplet distribution. At a length ratio of 0.5, few polymer bridges between droplets were established and only clusters with a small number of droplets were found. However at a length ratio of ca. 1.5 a connected network was formed and most of the polymers formed bridges between two droplets.

---

1 Introduction

Solutions composed by microemulsion droplets and hydrophobically modified end-capped triblock copolymers have gained significant importance in technological applications such as paints, cosmetics, and pharmaceutical formulations. Two characteristics of these solutions contribute to this interest. A microemulsion solution allows for the coexistence of hydrophobic and hydrophilic additives, establishing a delivery or encapsulation tool for a large variety of molecules. At the same time, the addition of triblock copolymers allows an easy control of the viscoelastic properties of the solution.

These solutions show fluid or gel-like properties depending on the balance among the droplet volume fraction, droplet size, polymer length, and polymer concentration. In systems composed of triblock copolymers and microemulsion droplets, the changes in the viscoelastic behavior are explained by the formation of a transient network^1,2 of the polymers using the oil droplets as physical crosslinkers.^3–7 To minimize the free energy of the system, the hydrophobic end segments tend to be located inside the oil droplets. This restrains the polymer conformations to essentially two arrangements: loops where both ends are located inside the same droplet and bridges where the ends reside inside different droplets. The positions of the droplets are restrained by the bridging polymers, and at a sufficient amount of bridges a network spanning throughout the whole solution is established. In case the network becomes sufficiently triangulated, the system displays a fluid to a gel-like transition. A deeper understanding of the aspects controlling the properties of such systems is thus of great importance, not at least to optimize their characteristics for technological applications. We also note that the present systems have some aspects in common with those corresponding to aqueous solutions of A-B-A triblock copolymers, with aggregating hydrophobic A blocks (see e.g.ref. 8). However, the influence of droplet properties and concentration cannot be extrapolated to the latter.

The influence of the midblock length on the formation of the network has been examined in a large number of studies.^5,9–13 The results presented by different authors appear, however, to be contradictory. While it has been mentioned that the midblock length has a relatively small significance in the dynamics of the system,¹² other authors have observed that with increasing midblock length the viscosity presents a non-trivial behavior increasing at low droplets concentrations and decreasing at higher concentrations.¹³ The effect of the increase in the midblock length was argued in ref. 13 to be in opposition to that observed in ref. 5. It has also been proposed that the increase of the midblock length leads to a shielding of the end blocks thus reducing the probability of the formation of bridges as the chain length is increased.³ According to these authors, the bending energy and the steric constraints of the smaller chains would favour the formation of bridges.

The influence of the droplet size on the properties of the systems has been focused in a few communications.^10,13,14 It was observed that an increased droplet size, at constant droplet volume fraction and polymer concentration, leads to an increase in the viscosity,¹³ which was explained by a larger number of polymers per droplet.

Also, the influence of the droplets volume fraction on the formation of a transient network has been examined experimentally.^9,10,12–17 It has been observed that the increase in the oil volume fraction, keeping the droplet radius constant, leads to an increase in the fraction of chains involved in bridging.¹⁵ However, it has also been reported that above a certain microemulsion number density the viscosity may decrease with increasing the droplet volume fraction, maintaining the droplet radius and keeping the polymer-droplet number ratio constant.¹² Furthermore, an increase in the droplet volume fraction leads to an increase in the fraction of chains involved in bridging. For example, 1/3 of chains formed bridges at a droplet volume fraction of 10%, which raised to essentially all at a volume fraction of 20%.¹⁵

Simulation,^14,18–24 numerical and analytical,^{16,17,25–27} and statistical²⁸ studies have also been undertaken to gain further understanding regarding these systems. However, a large part of the models make use of a simplifying approach where the surfaces to which the polymer ends are linked are considered as fixed parallel planes (e.g.ref. 19,21,29–31). A comparison between a polymer between two flat surfaces and two fixed spherical droplets¹⁶ showed that the repulsion caused by the polymers when linking two spheres is smaller than when confined between two flat surfaces. Furthermore, polymers attached to curved surfaces have a lower free energy relative to polymers attached to flat surfaces. This observation may have a correspondence in the increased size of the droplets, as larger droplets have a smaller curvature.

Thus, although a large body of work regarding the microemulsion solutions with added triblock copolymers has been performed, a systematic study including a rationalization of the factors governing the connectivity, and thus the structural and dynamic properties, is still lacking. In this work we focus on the influence of droplet volume fraction and droplet size at different polymer lengths on the structure of the solution and on the propensity for forming networks. We are employing a coarse-grain model solved using Monte Carlo simulations. Our main outcome is that the properties of the solution can be rationalized by a single reduced parameter.

2 Model and simulation details

We have employed a coarse-grain approach to model solutions containing oil-in-water microemulsions and hydrophobically end-capped hydrophilic polymers. The droplets are represented by soft spheres characterized by the radius R_d. The ABA-triblock copolymer is built up of segments connected by harmonic bonds. An end A-block is represented by one hydrophobic segment, and the middle B-block by N_B hydrophilic segments. Since the excluded-volume effect of the polymer segments is unimportant in the present investigation, the polymer description is further simplified by representing each segment by a point. The stiffness of the polymers is regulated using an angular potential.

In more detail, the total potential energy of the solution is composed of five terms as follows

U = U_seg,seg + U_seg,d + U_d,d + U_bond + U_ang (1)

where the three first terms represents intermolecular contributions and the last two intra-polymer contributions.

First, we have assumed U_seg,seg = 0; thus, no segment–segment interaction and in particular no effective attraction between the end-blocks in the aqueous phase. In these systems, the solvation of the end-blocks inside the oil droplets dominates over the polymer self-association.

The total segment–droplet potential energy U_seg,d is given by

where N_p denotes the number of polymers, N_seg = 2 + N_B the number of segments in one polymer, N_d the number of droplets, and r_ij the center-to-center separation between segment i and droplet j. Furthermore, in eqn (2) the minus sign applies to A-segments and the plus sign to B-segments. Throughout, we have used ε_seg,_d = 30 kJ/mol. Thus, we assume the same potential energy cost (i) to transfer a hydrophobic A-segment from the oil droplet to the continuous aqueous phase and (ii) to transfer a hydrophilic B-segment from the aqueous phase to a droplet. With the experimental value of 1.2k_BT for transferring a CH₂group from oil to water, our value of ε_seg,_d implies that one A-segment energetically represents a block of 10 CH₂groups.

The droplets interact through a soft repulsive potential, for simplicity employing the same functional form as used for the B segment–droplet interaction. The total droplet–droplet potential energy U_d,_d is given by

where r_ij denotes the center-to-center separation between droplet i and droplet j and ε_d,_d = 100 kJ/mol. Experimentally, microemulsion solutions display a slow change of the droplet number density and droplet size through different processes. Here, we assume the number density and size to be constant.

The total bond potential energy U_bond is given by

where N_bond = N_p(N_seg − 1) is the number of bonds in the system, r_m,bond the bond length of bond m, k_bond = 0.4 N/m² the harmonic force constant, and r₀ = 15 Å the equilibrium bond distance.

Finally, the total angular potential energy U_ang is given by

where N_ang = N_p(N_seg − 2) is the number of angles formed by three consecutive segments in a chain in the system, α_m,ang the value of angle m, k_ang = 3.4 × 10⁻²⁴ J deg⁻² the angular force constant, and α₀ = 180° the equilibrium angle.

Each investigated system is specified by the droplets and polymers involved. Two sets of droplet solution have been used, viz. (i) solutions with different droplet volume fraction ϕ at constant droplet radius R_d and (ii) solutions with different droplet radius R_d at constant droplet volume fraction ϕ. Beside volume fractions and radii, Table 1 provides droplet number density ρ, nearest-neighbor droplet–droplet separation for droplets distributed on a primitive cubic lattice R_d,_d = ρ^−1/3, and corresponding surface-to-surface separation R_d,d^surf = R_d,d − 2R_d of the droplet solutions. Three types of chains with different length of the middle B-block, N_B, have been used. These values are given in Table 2 as well as the resulting root-mean-square (rms) end-to-end separation <R_ee²>^1/2 and rms radius of gyration <R_g²>^1/2. All combinations of droplet solutions and chains have been investigated. All systems contain N_d = 20 droplets and N_p = 60 polymers; hence, the polymers are in excess with a polymer-droplet number ratio β = N_p/N_d = 3. Throughout, the temperature T = 298 K has been used.

Table 1 Parameters and key properties of investigated droplet solutions.

ϕ	R d /Å	ρ × 10^8/Å^−3	R d,d /Å	R d,d ^surf/Å	L/Å
0.05	80	2.31	350.9	190.9	952.4
0.07	80	3.24	313.6	153.6	851.4
0.10	80	4.63	278.5	118.5	755.9
0.12	80	5.56	262.1	102.1	711.4
0.15	80	6.99	242.7	82.7	658.8
0.10	50	19.1	173.6	73.6	471.4
0.10	60	11.0	208.9	88.9	567.0
0.10	80	4.63	278.5	118.5	755.9
0.10	90	3.25	313.3	133.3	850.4
0.10	100	2.37	348.1	148.1	944.9
0.10	110	1.78	382.9	162.9	1039.4

---

Table 2 Chain parameters and key properties of investigated droplet-free polymer solutions.^a

Chain type	N B	<Ree^2>^1/2/Å	<Rg^2>^1/2/Å
a Since the polymers are non-interacting, these results were obtained by simulating a single polymer.
I	10	104.3 (0.2)	38.2 (0.1)
II	15	131.5 (0.3)	48.8 (0.1)
III	20	155.0 (0.3)	50.4 (0.1)

---

The properties of the systems were obtained by performing Metropolis Monte Carlo simulation in the canonical ensemble (constant number of particles, volume, and temperature), using the Molsim package.³² The systems investigated were confined in a box with the edge length L specified in Table 1 and with periodic boundary conditions applied. All particles (droplets and segments) were subjected to independent translational trial moves. Furthermore, pivot rotations of a subchain of the polymer and translations of whole chains were also made. Finally, to further improve the sampling efficiency, cluster moves involving droplets and end-segments confined in that droplet were also used. Equilibration runs comprised at least 2.5 × 10⁵ steps, corresponding to a large excess in terms of the convergence of both energy and conformation indicators and production runs involved 5 × 10⁵ steps. One step encompasses N trial moves, where N = N_d + N_pN_seg is the total number of particles in the system. Sampling results indicate a good coverage of the distances accessible to the ends of the chains and a large displacement of the particles representing droplets, substantiating a good coverage of configurational space. Also, a relatively large acceptance rate of the pivot rotations suggests frequent chain exchange between droplets, confirmed by direct observation of the evolution of the connectivity indicators for specific droplets. These observations suggest also that the final results are essentially independent from the initial configuration.

A polymer was classified in one of four conformations: (i) loop characterized by both end-blocks residing in the same droplet, (ii) bridge in which the two end-blocks reside in different droplets, (iii) tail where one end-block resides in a droplet and the other in the aqueous phase, and (iv) nonadsorbed where both end-blocks are in the aqueous phase. The fraction of polymers in conformation x will be denoted by f_x with x = loop, bridge, tail, or nonads. Generally, the fraction of nonadsorbed polymersf_nonads was negligible, and the fraction of tails was small f_tail < 0.02.

The connectivity of the systems has been characterized by using four connectivity indicators. Two droplets were considered to belong to the same cluster if they were connected directly or indirectly by at least one bridging polymer linking pairs of droplets. A cluster was classified according to how many droplets it contained. From the frequency of clusters with different sizes, two normalized cluster size distributions P_iⁿ and P_i^m were calculated according to

andwhere <n_i> is the average number of clusters containing i droplets. Note, that P_iⁿ is a “number”-weighted measure of the cluster size distribution representing that any given cluster, randomly selected, will contain i droplets, whereas P_i^m is a “mass”-weighted measure representing the probability that any droplet chosen randomly will be found in a cluster containing i droplets. The first two connectivity indicators areandrepresenting the average cluster size, again “number”- and “mass”-weighted. Furthermore, the local connectivity was characterized by two indicators. They are the average number of droplets that are linked to a droplet, <N_d^link>, and the (related) average number of bridging polymers establishing the link between two linked droplets, <N_p^link>, also referred to as bond order. Obviously, we have the relation <N_p^link> = 2βf_bridge/<N_d^link>. Moreover, the smallest value of <N_p^link> is unity and hence the maximal value of <N_d^link> is 2βf_bridge, which are achieved when all linked droplet pairs are connected with only one bridging polymer per link.

3 Results

3.1 Effect of droplet volume fraction

The solution structure for systems with varying droplet volume fraction at constant droplet radius and chains of type III with N_B = 20 will first be examined. In addition, some properties of droplet-free and of polymer-free solutions will be considered.

The polymer end-to-end separation probability distribution P(R_ee) for systems with ϕ = 0.05, 0.10, and 0.15 and for a droplet-free polymer solution is shown in Fig. 1(a). With polymers only, P(R_ee) displays a nearly Gaussian behavior with < R_ee² > ^1/2 = 155 Å. In the presence of droplets, two maxima appear; hence, P(R_ee) changes character. We make the following observations: i) The first maximum at the location R_ee = 55 Å decreases in magnitude at increasing ϕ, whereas the second one is shifted to smaller R_ee and increases in magnitude at increasing ϕ; ii) Table 1 shows that the droplet surface-to-surface distance for a regular droplet distribution R_d,d^surf is decreasing at increasing ϕ; iii) Table 3 shows that the fraction of loop conformations f_loop decreases from 0.78 to 0.45 and the fraction of bridge conformation f_bridge increases from 0.21 to 0.54 as ϕ is increased from 0.05 to 0.15. From observations i)-iii), we infer that the maximum of P(R_ee) appearing at R_ee = 55 Å originates from chains possessing a loop conformation, whereas the other maximum appearing at larger R_ee arises from chains forming bridges between droplets. From geometrical arguments, it is reasonable that a polymer with an unperturbed rms end-to-end separation of 155 Å attains a typical end-to-end separation of ≈ 55 Å when forming a loop on a sphere with the radius 80 Å. Thus, (i) all chains are doubly connected to droplets either in loop or bridge conformations, (ii) the spatial extensions of polymers in these two conformations are well separated, and (iii) the probabilities of the chain conformations depend on the droplet volume fraction.

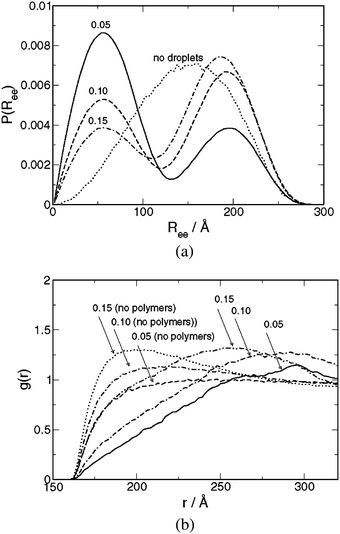Fig. 1 (a) Polymer end-to-end separation probability distribution P(R_ee) and (b) droplet–droplet radial distribution function g(r) for systems containing chains of type III at droplet radius R_d = 80 Å and indicated droplet volume fractions ϕ. The corresponding distribution for droplet-free polymer solution is given in (a) and for polymer-free droplet solutions in (b).

Table 3 Fraction of chains in loop, bridge, and tail conformations and connectivity indicators for systems with different chain types and droplet volume fractions ϕ.

Chain type	ϕ	f loop	f bridge	f tail	<Nd^n>	<Nd^m>	<Nd^link>	<Np^link >	γ
I	0.05	0.776	0.212	0.012	1.84	2.60	0.90	1.42	0.55
	0.07	0.697	0.291	0.013	2.49	5.27	1.22	1.45	0.68
	0.10	0.635	0.356	0.010	3.84	9.24	1.57	1.39	0.88
	0.12	0.551	0.440	0.010	6.70	14.42	1.94	1.40	1.02
	0.15	0.448	0.544	0.009	11.31	18.34	2.48	1.30	1.26
II	0.05	0.724	0.260	0.017	2.31	4.60	1.14	1.38	0.69
	0.07	0.615	0.371	0.015	4.04	10.40	1.64	1.33	0.86
	0.10	0.537	0.451	0.012	8.67	16.67	2.14	1.25	1.11
	0.12	0.436	0.554	0.011	11.92	18.52	2.64	1.27	1.29
	0.15	0.366	0.626	0.009	13.96	19.09	3.02	1.25	1.59
III	0.05	0.655	0.326	0.017	3.19	7.74	1.43	1.39	0.81
	0.07	0.555	0.428	0.017	6.70	14.61	1.98	1.31	1.01
	0.10	0.402	0.585	0.013	11.85	18.55	2.80	1.26	1.31
	0.12	0.363	0.626	0.011	13.96	19.14	3.08	1.22	1.52
	0.15	0.295	0.695	0.010	13.20	18.98	3.40	1.23	1.87

---

Fig. 1(b) shows the droplet–droplet radial distribution function g(r) for systems with different droplet volume fraction in the presence and the absence of polymers. Throughout, g(r) = 0 for r ≈ < 160 Å, which is consistent with the droplet radius R_d = 80 Å. In the absence of polymers, g(r) displays a weak maximum that grows at increasing number density, and then g(r) smoothly approaches unity; a typical behavior for a dilute solution of soft spheres possessing excluded-volume interactions only. With polymers being present, the maximum in g(r) is shifted to larger droplet separations, and the location of these maxima appears at larger separations at decreasing ϕ. The locations of the maxima at ϕ = 0.15 and 0.10 agree with R_d,d, representing the nearest-neighbor droplet–droplet separation for droplets distributed on a primitive cubic lattice, given in Table 1. The absence of such an agreement at ϕ = 0.05 is consistent with the smaller fraction of bridging conformations. Furthermore, with polymers present the rise of g(r) after r = 160 Å is much slower, indicating an additional effective repulsion between the droplet, which we attribute to an effectively larger radius originating from the polymers attached onto the droplets in loop conformations. Thus, we conclude that the distribution of the droplets in the solution undergoes a drastic change upon the addition of the triblock copolymers.

The cluster size probability distribution P_i^m at some selected values of ϕ is shown in Fig. 2. At the lowest droplet volume fraction ϕ = 0.05, we have a broad and, essentially, decaying distribution with 17% of the droplets being unconnected to other droplets. At ϕ = 0.07 clusters involving most of the droplets dominate, and at ϕ = 0.10 nearly all droplets reside in a single cluster.

Fig. 2 Cluster size probability distribution P_i^m for systems containing chains of type III at droplet radius R_d = 80 Å and indicated droplet volume fractions ϕ.

The fraction of chains in different conformations and the connectivity indicators presented in Table 3 give further information on the network established at increasing droplet volume fraction. Here, data for all chain types are given. For the longest chain (type III), we find that the average cluster size increases at increasing ϕ. At the largest droplet volume fraction <N_d^m> is nearly equal to N_d, the number of droplets in the system. The average number of droplets linked to a given droplet is increasing with ϕ, being 1.4 at ϕ = 0.05 and 3.4 at ϕ = 0.15. The bond order decreases from 1.4 to 1.2 at increasing ϕ, showing that the average number of polymers linking two droplets reduces at increasing droplet volume fraction. The general pattern remains for shorter chains (types I and II). However, the fraction of loop conformations f_loop is larger, the fraction of bridge conformations f_bridge is smaller, and the droplets are less linked to each other. We will return to the reasons for these differences appearing for shorter polymers in section 4.

3.2 Effect of droplet size

We will continue by examining the influence of the droplet radius at constant droplet volume fractions with chains of type III on the solution structure. Again, some properties of droplet-free and of polymer-free solutions will be discussed.

Fig. 3(a) displays the polymer end-to-end separation probability distribution for systems with R_d = 50, 80, and 110 Å. Again two maxima appear at all conditions. The maximum at the smaller separation increases in magnitude, the other maximum decreases in magnitude, and the location of both maxima are shifted to larger separation at increasing R_d. The variation in amplitude is corroborated by the changes in the fraction of loop and bridge conformations given in Table 4, which state that the largest fraction of bridges appears for the smallest droplets. The increase of R_ee of the first maximum of P(R_ee), representing polymers in loop conformations, at increasing R_d is expected, since the average distance between the two anchoring points of the loops becomes larger. The shift of the second maximum is related to the larger droplet surface-to-surface separation of neighboring droplets appearing at increasing R_d at constant ϕ, see Table 1.

Table 4 Fraction of chains in loop, bridge, and tail conformations and connectivity indicators for systems with different chain types and droplet radii R_d.

Chain type	R d	f loop	f bridge	f tail	<Nd^n>	<Nd^m>	<Nd^link>	<Np^link>	γ
I	50	0.300	0.692	0.009	15.76	19.42	3.18	1.31	1.42
	60	0.424	0.567	0.009	10.01	17.68	2.45	1.37	1.17
	80	0.635	0.356	0.010	3.84	9.24	1.57	1.39	0.88
	90	0.697	0.293	0.010	2.76	6.10	1.26	1.39	0.78
	100	0.723	0.268	0.010	2.46	5.15	1.18	1.38	0.70
	110	0.770	0.220	0.010	2.02	3.58	1.02	1.29	0.64
II	50	0.216	0.775	0.010	15.69	19.46	3.75	1.24	1.79
	60	0.325	0.665	0.011	12.82	18.99	3.16	1.26	1.48
	80	0.537	0.451	0.012	8.67	16.67	2.14	1.25	1.11
	90	0.588	0.401	0.012	5.60	12.86	1.81	1.34	0.99
	100	0.629	0.359	0.013	4.16	9.92	1.59	1.36	0.89
	110	0.706	0.281	0.013	2.71	5.94	1.28	1.33	0.81
III	50	0.220	0.769	0.010	6.31	15.97	3.21	1.39	2.11
	60	0.262	0.727	0.012	11.53	18.59	3.43	1.26	1.74
	80	0.402	0.585	0.013	11.85	18.55	2.80	1.26	1.31
	90	0.484	0.503	0.014	9.02	17.34	2.40	1.26	1.16
	100	0.577	0.407	0.016	5.62	13.52	1.89	1.30	1.05
	110	0.644	0.340	0.015	3.90	9.29	1.58	1.32	0.95

---

Fig. 3 (a) Polymer end-to-end separation probability distribution P(R_ee) and (b) droplet–droplet radial distribution function g(r) for systems containing chains of type III at droplet volume fraction ϕ = 0.05 and indicated droplet radii R_d in Å. The corresponding distribution for droplet-free polymer solution is given in (a) and for polymer-free droplet solutions in (b).

The droplet–droplet radial distribution functions g(r) for the systems with different droplet radius R_d are shown in Fig. 3(b). Here, the radial extension of the regions with g(r) = 0 varies, since the droplet radius varies among the systems. In the absence of the polymers, the three distributions functions become the same when represented as g(r/R_d), as expected, since g(r/R_d) depends only on the droplet volume fraction. With polymer present, the solution containing droplets with radius R_d = 110 Å follows the behavior of solutions with droplets with radius R_d = 80 Å discussed above, viz the frequency of small separations decreases and the maximum of g(r) is shifted to larger separation but is yet smaller than R_d,d owing to a relative small fraction of bridging polymers (f_bridge = 0.34). For the smallest droplets, R_d = 50 Å, the maximum of g(r) is shifted to a shorter separation and a second maximum appears at r = 200 Å. We will return to this appearance in section 4.

Fig. 4 displays the cluster size probability distribution P_i^m at some selected values of R_d. With the largest droplet radius the probability of finding a droplet in a cluster of a given size is fairly uniform. At decreasing droplet radius, the cluster size increases. With the droplet radius R_d = 80 Å there is a strong dominance of large clusters involving nearly all droplets, which remains visible for even smaller radii (not represented).

Fig. 4 Cluster size probability distribution P_i^m for systems containing chains of type III at droplet volume fraction ϕ = 0.05 and indicated droplet radii R_d in Å.

Table 4 provides the fraction of chains in loop, bridge, and tail conformation and connectivity indicators for the systems at increasing droplet radius. Again, data for all chain types are presented. For the longest chain (type III) the fraction of chains forming bridges, as well as the connectivity indicators <N_dⁿ>, <N_d^m>, and <N_d^link> increase with decreasing R_d. As in the previous subsection, the bond order decreases as the connectivity increases. The only exception appears (again) for R_d = 50 Å. The general pattern remains for shorter chains (types I and II), but with a smaller fraction of bridging polymers and smaller connectivity as in the previous subsection. Furthermore, with the shorter chains the systems with droplet size R_d = 50 Å fall in the regular pattern.

4 Discussion

We have so far examined the structure of a microemulsion solution containing oil droplets and triblock copolymers, where three parameters have been varied: (i) midblock length of the copolymer, (ii) the droplet volume fraction at constant droplet radius, and (iii) the droplet radius at constant droplet volume fraction. The first two properties have been varied by a factor of three and the last one by a factor of two. We have observed that the structure of the microemulsion in most cases is drastically affected with triblock copolymers present in three-fold excess. Frequently a network involving essentially all droplets was formed. Furthermore, the polymers could be divided into two populations, one possessing a loop conformation and the other exhibiting a bridge conformation.

It is anticipated the system could be described with a smaller number of parameters than the number of physical ones. In fact, we will now describe the system using only one single reduced parameter involving two length scales, one characterizing the polymers and other the droplet solution. More specifically, we will consider the length ratio

where <R_ee²> ^1/2 was the rms end-to-end separation of the polymers and R_d,d^surf the surface-to-surface distance between neighboring droplets uniformly distributed in the droplet solution.

Fig. 5 displays the fraction of chains bridging two droplets, f_bridge, the average cluster size, <N_d^m>, the average number of droplets linked to a droplet, <N_d^link>, and the percolation probability, P_percolation as a function of the length ratio γ across all the 33 systems. (The length ratios for the systems were given in Tables 3 and 4). We find a gratifying master behavior of all the four properties as γ is increased from 0.5 to 2. This observation provides a very strong argument that this length ratio is an important parameter characterizing our systems. We do not yet exclude that additional reduced parameters are needed to characterize the main features of the system when other physical parameters than those three used here are varied.

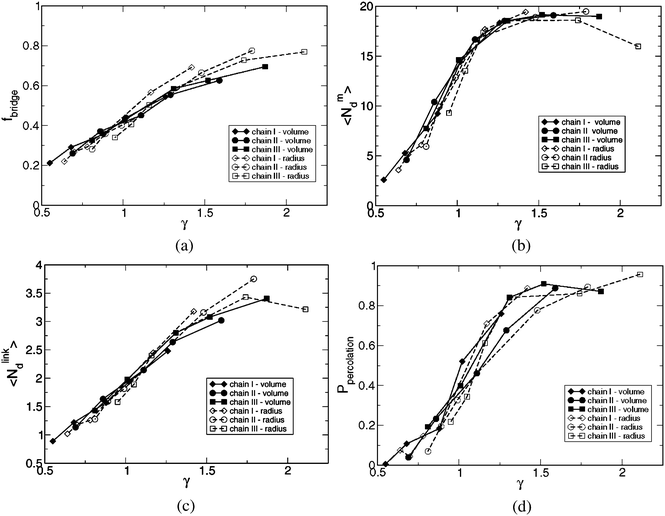Fig. 5 (a) Fraction of chains bridging two droplets f_bridge, (b) average cluster size <N_d^m>, (c) average number of droplets linked to a droplet <N_d^link>, and (d) percolation probability P_percolation as a function of the length ratio γ = <R_ee²>^1/2/R_d,d^surf for all 33 systems studied.

In more detail, Fig. 5(a) shows that the fraction of chains in bridge conformations increases from 0.2 to 0.7 as γ is increased from 0.5 to 2. When the chains are short relative to the surface-to-surface distance between neighboring droplets only a small fraction of the chains form bridges. Such a bridge formation requires the establishment of a pair of neighboring droplets, which is entropically costly. Since the end-blocks are strongly hydrophobic, the alternative is that the two ends of a polymer have to reside in the same droplet and hence the polymer attains a loop conformation. Noticeable, at γ = 2, f_bridge amounts about 0.7, and still 30% of the chains appear in loop conformations.

Fig. 5(b) shows that the average cluster size <N_d^m> increases from about 2 at γ = 0.5 to nearly the maximal value 20 at γ = 1.25, where it levels off. Thus, as the fraction of bridges is increasing (at increasing γ), the average cluster size is growing. When about half of the polymers are forming bridges, corresponding to 1.5 bridging polymer per droplet (remember β = 3), the cluster size is fully developed.

As expected, the average number of droplets linked to a droplet <N_d^link> increases also monotonically with γ, as shown in Fig. 5(c). At γ = 0.5 in average a droplet is linked to less than one other droplet. At γ = 1.25, where <N_d^m> has leveled off, a droplet is linked to two other droplets. Interestingly, <N_d^link> continues to increase after γ = 1.25 implying an increased triangulation of the already established cluster comprising essentially all droplets. The largest value obtained is <N_d^link> = 3.5, which should be compared with the maximal one 2βf_bridge = 4.2. The ratio 4.2/3.5 = 1.2 is just the bond order, which displays a weak reduction from 1.4 to 1.2 as γ is increased from 0.5 to 2 (see Tables 3 and 4).

Fig. 5(d) depicts the behavior of the percolation probability as a function of γ. The percolation probability P_percolation is defined as the fraction of conformations for which a system is percolated in at least one dimension. At γ = 0.5 the probability of a percolated system is basically zero. The probability increases monotonically to about 0.8 at γ = 1.5, and levels off at larger γ. Noticeably, the percolation probability levels off at larger value of γ as compared to the average cluster size. The intermediate probability P_percolation = 0.5 is observed to occur about γ = 1.1.

Despite these general trends, we have one system that has a different behavior calling for some attention. In the droplet solution characterized by ϕ = 0.10 and R_d = 50 Å, we found with the longest chains (type III) several deviating features. This system had the longest chain as compared to the droplet surface-to-surface separation, γ = 2.1. Fig. 3(b) displayed a shift of the maximum in the droplet–droplet radial distribution function to shorter distances upon the addition of the polymer; in Fig. 5(b) a lower value of <N_d^m> than expected was encountered; and in Fig. 5(c) a lower value of <N_p^link> than expected was found. Briefly, in this system a depletion attraction between the droplets mediated by the polymers starts to become important, leading to an effective attraction between the droplets competing with network formation. This tendency of a droplet–polymer segregation is discussed in more detail in a separate publication, where also the effect of the polymer stiffness is examined.³³

5 Summary

On the basis of Monte Carlo simulations, structural properties of solutions containing microemulsion droplets and semi-flexible ABA triblock copolymers have been investigated at a fixed number ratio of polymers and droplets. The end-blocks were assigned properties representing an alkyl chain with 10 carbon atoms. Our focus has been on the formation of transient networks with the droplets constituting the nodes and the polymers forming the bridges between the nodes. The network formation has been examined on a global level through cluster size and percolation analyses and on a local level through the number of droplets linked to a given droplet and the bond order.

It was found that the structural properties obtained for (i) different droplet volume fraction, (ii) different droplet radius, and (iii) different polymer contour length could be collapsed on a universal behavior when examined as a function of the length ratio of the unperturbed polymer root-mean-square end-to-end separation and the surface-to-surface distance between neighboring droplets for a uniform droplet distribution. At a small length ratio, most polymers formed loops and the droplets were unconnected or connected to other droplets in small clusters. At unity length ratio appreciable sized clusters were formed and ca. 40% of the polymers formed loops. At a length ratio of 1.5, an infinite network of connected droplets had been established, where each droplet on average were connected to three other droplets involving ca. 60% of the polymers. Finally at a length ratio exceeding 2, a new regime is entered in which the depletion attraction between droplets mediated by the polymers starts to become visible; this regime is currently under further investigation.

6 Acknowledgments

Financial support by the Fundação para a Ciência Tecnologia (FCT), Portugal, through grant SFRH/BD/17440/2004 and the Swedish Research Council (VR) through the Linnaeus Center of Excellence on Organizing Molecular Matter (OMM) are gratefully acknowledged.

7 References

1. M. S. Green and A. V. Tobolski, J. Chem. Phys., 1955, 14(2), 80–92.
2. A. S. Lodge, Trans. Faraday Soc., 1956.
3. H. Eicke, C. Quellet and G. Xu, Colloids and Surfaces, 1989, 36, 97–107.
4. C. Quellet, H. Eicke, G. Xu and Y. Hauger, Macromolecules, 1990, 23, 3347–3352.
5. R. P. W. J. Struis and H. Eicke, J. Chem. Phys., 1991, 95, 5989–5996.
6. U. Zölzer and H. Eicke, J. Phys. II France, 1992, 2, 2207–2219.
7. D. Vollmer, J. Vollmer, B. Stühn, E. Wehrli and H. Eicke, Phys.Rev. E: Stat. Phys., 1995, 52, 5146–5155.
8. L. Guo and E. Luijten, J. Polym. Sci. part B: Polym. Phys., 2005, 43, 959–969.
9. F. Molino, J. Appell, M. Filali, E. Michel, G. Porte, S. Mora and E. Sunyer, J. Phys.: Condens. Matter, 2000, 12, 491–498.
10. M. Filali, M. J. Ouazzani, E. Michel, R. Aznar, G. Porte and J. Appell, J. Phys. Chem. B, 2001, 105, 10528–10535.
11. E. Michel, L. Cipelletti, E. d'Humieres, Y. Gambin, W. Urbach, G. Porte and J. Appell, Phys. Rev. E: Stat. Phys., 2002, 66 031402–1,7.
12. F. E. Antunes, K. Thuresson, B. Lindman and M. G. Miguel, Colloids Surf. A: Physicochem. Eng. Apects, 2003, 215, 87–100.
13. I. Lynch and L. Piculell, J. Phys. Chem. B, 2004, 108, 7515–7522.
14. M. Surve, V. Pryamitsyn and V. Ganesan, J. Chem. Phys., 2006, 125 064903.
15. H. Bagger-Jörgenssen, L. Coppola, K. Thuresson, U. Olsson and K. Mortensen, Langmuir, 1997, 13, 4204–4218.
16. S. R. Bhatia and W. B. Russel, Macromolecules, 2000, 33, 5713–5720.
17. A. Zilman, J. Kieffer, F. Molino, G. Porte and S. A. Safran, Phys. Rev. Letters, 2003, 91 015901–1,4.
18. S. Misra, M. Nguyen-Misra and W. L. Mattice, Macromolecules, 1994, 27, 5037–5042.
19. M. Nguyen-Misra, S. Misra and W. L. Mattice, Macromolecules, 1996, 29, 1407–1415.
20. P. G. Khalatur, J. N. Kovalenko and A. R. Khokhlov, Macromol. Theory Simul., 1999, 8, 309–320.
21. K. Karastasos, S. H. Anastasiadis, T. Pakula and H. Watanabe, Macromolecules, 2000, 33, 523–541.
22. M. Vacatello, Macromolecules, 2001, 34, 1946–1952.
23. J. Li, C. Peng, H. Liu and Y. Hu, European Polymer Journal, 2005, 41(3), 627.
24. M. Surve, V. Pryamitsyn and V. Ganesan, Langmuir, 2006, 22, 969–981.
25. R. Nagarajan, J. Chem. Phys., 1989, 90, 1980–1994.
26. S. T. Milner and T. A. Witten, Macromolecules, 1992, 25, 5495–5503.
27. M. Björling and P. Stilbs, Macromolecules, 1998, 31, 9033–9043.
28. G. Hed and S. A. Safran, EUR. Phys. J. E, 2006, 19, 69–76.
29. S. Misra and W. L. Mattice, Macromolecules, 1994, 27, 2058–2065.
30. M. M. Santore, W. B. Russel and R. K. Prud'homme, Macromolecules, 1990, 23, 3821–3832.
31. J. Huh and A. C. Balazs, J. Chem. Phys., 2000, 113, 2025–2031.
32. P. Linse, Molsim, version 4.0.3, 2004.
33. J. M. G. Sarraguça, A. A. C. C. Pais and P. Linse, Langmuir, 2008, 24, 11153–11163.

---