Isomeric colloidal clusters with shape-dependent mobility

Abstract

Colloidal clusters were assembled into discrete isomeric shapes and their translational and rotational mobility were measured by single-particle tracking as the shape deviated from linear to the most compact.

---

Colloidal particles stand at the cross-section of chemistry, biology, and engineering; they underpin technology in fields that span pharmaceuticals, foodstuffs, and chemical sensors.¹ It has been a challenge to understand their mobility under conditions where their shape does not fall into simple geometrical idealizations such as sphere, rod, ellipsoid, and so forth. As a result, computation-based methods have been developed that enable the solution of fluid dynamics equations for objects with complex shapes,² however the need to compute each case separately with appropriate software renders these techniques specialized. As an alternative, we present here experiments in which colloidal spheres are assembled into explicitly discrete isomeric shapes and their mobility is tracked individually under a microscope.

Considering translation and rotation in the surface plane, parallel to a wall after particles sediment in water to near the bottom of a sample cell, we focus on trimers as the simplest chain structure that can provide insight into how isomerization matters. As is well known, in this situation lubrication forces slow translational diffusion relative to that in the bulk,³ and in a prior related study we considered this quantitatively.⁴ However, in-plane symmetry of the surface causes lubrication forces to affect equally those translational motions parallel and perpendicular to the surface; the absolute magnitudes are reduced but not their ratios, which are the main point of the present study. Using CCD detection we have accumulated large statistical samples; this enables us to contrast, without concern even in principle about sample heterogeneity, the influence of isomerization on translational and rotational diffusion for rigid assemblies whose masses are identical but whose shapes differ.

To produce colloidal isomers, we build upon methods developed by many previously to form close-packed colloidal monolayers,⁵ except that to produce isomers, instead we form submonolayers onto which a thin (30 nm) layer of silicon oxide is coated by electron beam deposition. This produces coherent, bridged objects that are easy to remove by mild ultrasonication, and the resulting objects present a large family of different cluster sizes and shapes. The parent particles, from which the colloidal isomers were formed, are colloidal silica spheres, 1.57 µm in diameter (Duke Scientific). During experiments, salt (3 mM NaCl) is added to keep the electrostatic screening length negligible relative to the particle diameter. Single-particle tracking codes described previously⁴ are used to quantify the trajectories observed for Brownian diffusion. After allowing the trimer isomers to sediment to near the bottom of a sample cell, copious statistics regarding their Brownian diffusion parallel to the surface are accumulated by phase contrast microscopy using a CCD camera with 30 ms resolution (Andor Ixon). Of course, the particles also fluctuate slightly in their position from the bottom of the sample cell. However, the standard deviation of the Boltzmann distribution of the position of the center of mass from the bottom of the sample cell (75 nm in these experiments) was just 2.5% of the particle diameter. Detailed investigation of the consequences of such fluctuations of elevation shows that while they could broaden the tails of displacement distribution functions when considering the interactions between neighboring particles (not the subject of the present paper), the rotation and translation of dilute particles, reported below, was unaffected. Furthermore, we note that in a prior study of spherical colloids that had sedimented in this way, we found that the in-plane translational diffusion coefficient was slowed down relative to predictions from the Stokes–Einstein equation, in quantitative agreement with expectations for lubrication forces at the calculated distance from the wall.⁶ This prior study also showed the in-plane rotational diffusion coefficient to be quantitatively described by the Debye equation, unmodified by lubrication forces, which is understandable because hydrodynamic forces from rotation are short-range.

To quantify isomerization, we introduce the bending angle (θ) between adjacent elements of these trimer clusters, shown in Fig. 1a (schematic) and Fig. 1b (phase contrast image). As bending angle varies, so the isomerization also varies.

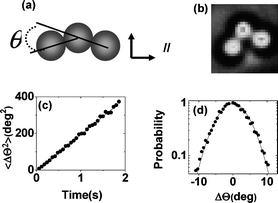Fig. 1 (a) Colloidal trimers can be discriminated by the bending angle (θ) defined in this panel. (b) Experimental example of an isomer with θ = 85°. (c) Raw data illustrated: mean-squared angular displacement is plotted against time for a linear trimer. The slope of the line defines the rotational diffusion coefficient. (d) More raw data illustrated, for the same system as for panel (c). The histogram of rotation is plotted versus the amount of rotation for an observation time of 30 ms. The distribution follows a Gaussian function (line through the data) and the breadth of the distribution implies the rotational diffusion coefficient.

Placing into perspective the numbers that follow, first we illustrate the raw data from which they come. The slope of the mean-square displacement, plotted against time, defines the diffusion coefficient—this, in Fig. 1c, is illustrated for the rotational diffusion coefficient of the sample defined in the figure caption. Alternatively, from the large statistical data set, Fig. 1d shows the histogram of angular motion during an observation time of 30 ms, and from the breadth of the distribution the diffusion coefficient follows. For all of the data presented below, these alternative approaches gave consistent findings. The findings presented below concern translational and rotational diffusion coefficients, D_T and D_R respectively, determined in this manner for dilute concentrations of these isomeric clusters.

Our central findings describe how colloidal isomers diffuse at substantially different rates. For clarity of presentation, diffusion coefficients of all the isomers were normalized by those measured for the most compact one. Fig. 2a summarizes how this ratio depends on deviations from linear shape—notice that rotational diffusion of the most compact-shaped isomers speeds up by 90% and translational diffusion by 10%.

Fig. 2 Dependence of translational (D_T) and rotational (D_R) diffusion coefficients on bending angle after normalizing by those properties characteristic of the most compact trimer, D_To = 0.088 µm²/s and D_Ro = 208 deg²/s. (a) Normalized D_T (right ordinate) and D_R (left ordinate) are plotted against θ. (b) Ratio of the quantities plotted in panel (a), referred to here as K, is plotted against θ. In both panels, dashed lines are the ratio predicted using the Stokes–Einstein relations for hard spheres, taking the radius of gyration of the isomers as an effective radius and normalizing by values for the most compact trimer.

It was also interesting to consider the ratio of rotational to translational diffusion coefficients, taking the radius of gyration as an effective radius, as is traditional to do in modelling complex shapes.¹ In Fig. 2b, this ratio is plotted against bending angle and one observes that the radius of gyration description systematically overpredicts the data, even though it might seem at first glance a natural approximation of complex shape. The common model of a prolate spheroid^7,8 also predicts poorly the motion of these “pearl necklace” isomers, as seen by the comparison in Fig. 3c. This is because of the curvature where colloidal particles meet. It causes nonlinear hydrodynamic drag, which is very different from the smooth surface of the shapes modelled in classical theory regarding this problem.⁹ For this same reason, classical models based on cigar shapes⁷ are not quantitative either if one seeks to apply them to these geometries. We have not encountered an analytic solution for a circular cylinder whose length along the long axis is comparable to width of the short axis.

Fig. 3 The more linear the isomeric shape, the more anisotropic its diffusion. To quantify this, parallel (D_//) and perpendicular (D_⊥) directions are defined as shown in Fig. 1a. (a) D_//(filled symbols) and D_⊥ (open symbols) are plotted against θ. (b) The ratio, D_///D_⊥ is plotted against θ. For reference, D_///D_⊥ = 2 for an infinitely long slender rod and D_///D_⊥ = 1 for a sphere. (c). The ratio D_///D_⊥ of linear clusters with 2, 3 and 4 constituent particles. For 2 particles the analytical result, D_///D_⊥ = 1.123, is known.⁷ The solid line is the expectation for a prolate spheroid with the same ratio of linear clusters. The dash dot line is the expectation for an infinitely long slender rod. The line drawn through the data points is just a guide to the eye.

Furthermore, the more linear the isomeric shape, the more anisotropic is the mobility—diffusion is faster parallel to the long axis (D_//) and slower perpendicular to it (D_⊥). In Fig. 3a, D_// and D_⊥ are plotted against bending angle. Their ratio was also considered (Fig. 3b). As the shape deviates increasingly from linear, there is more speeding up of perpendicular motion than slowing down of parallel motion. Notice also, in Fig. 3a and 3b, that D_//, D_⊥ and their ratio show the most rapid change when 0°< θ < 20—this contrasts with minimal change of the overall translational diffusion coefficient, which is the mean of D_// and D_⊥. The minimal overall change is actually the result of rapid increase and decrease of two constituent directional motions; it is a cancellation of effects.

The capability shown here to discriminate cluster shape by contrasting translational and rotational mobility also suggests the possibility that one may seek to deduce particle shape by measuring the mobility of an unknown structure, though at present this approach will apply only to particles that sediment to a fairly well-defined distance from the wall. In the future, with the development of methods to acquire large statistics of single-particle level for unbounded diffusion, this restriction may be relaxed, but this would require elaborate feedback to maintain the diffusing particle with an imaging microscope's plane of focus. This would be exciting because in fact, anisotropic shape is also typical of proteins, which also often exist as oligomeric structures with distinct subunits, but a quantitative connection is not offered at this time. The poor predictive capability of the prolate spheroid model, shown in Fig. 3(c), also provides support for recent approaches to include atomistic structures into the theory of liquid crystals,¹⁰ whose mobility has traditionally been modelled using models of ellipsoids, which are shown here for colloidal clusters to fail on the quantitative side. Similarly, the mobility of “banana-shaped” liquid crystals¹¹ ought by analogy also to depend on the bending effects demonstrated here, after extending these findings to three-dimensional diffusion.

The results presented here for small colloidal isomers apply by rational extension to larger assemblies also. A limitation of the current experiments is that the diffusion studied here is parallel to a planar surface, but this is not considered fundamental because we do not consider diffusion in the constrained vertical dimension anyway, while diffusion parallel to the surface is unbounded.

Acknowledgements

This work was supported by the National Science Foundation, NSF-DMR-06-05947. SA acknowledges the Donors of the Petroleum Research Fund, administered by the American Chemical Society, #45523-AC7, and also the NSF for financial support in the form of a Graduate Research Fellowship.

References

1. T. F. Tadros, Colloid Stability and Application in Pharmacy, Wiley-VCH, Weinheim, Germany, 1st edn, 2007.
2. (a) J. G. de la Torre, G. D. Echenique and A. Ortega, J. Phys. Chem. B, 2007, 111, 955–961; (b) M. L. Mansfield, J. F. Douglas, S. Irfan and E. H. Kang, Macromolecules, 2007, 40, 2575–2589.
3. L. P. Faucheux and A. J. Libchaber, Phys. Rev. E., 1994, 49, 5158–5164.
4. S. Anthony, L. Hong, M. Kim and S. Granick, Langmuir, 2006, 22, 9812–9815.
5. (a) H. Takei and N. Shimizu, Langmuir, 1997, 13, 1865–1868; (b) J. C. Love, B. D. Gates, D. B. Wolfe, K. E. Paul and G. M. Whitesides, Nano Lett., 2002, 2, 891–894; (c) A. V. Whitney, J. W. Elam, P. C. Stair and R. P. Van Duyne, J. Phys. Chem., 2007, 111, 16827–16832; (d) L. Hong, S. M. Anthony and S. Granick, Langmuir, 2006, 22, 7128–7131.
6. S. Anthony, L. Zhang and S. Granick, Langmuir, 2006, 22, 5266–5272.
7. H. Brenner, Int. J. Multiphase Flow, 1974, 1, 195–341.
8. Y. Han, A. M. Alsayed, M. Nobili, J. Zhang, T. C. Lubensky and A. G. Yodh, Science, 2006, 314, 626–630.
9. D. Mukhija and M. J. Solomon, J. Colloid Interface Sci., 2007, 314, 98–106.
10. R. M. Wilson, Int. Rev. Phys. Chem., 2005, 24, 421–455.
11. M. B. Ros, J. L. Serrano, M. R. de la Fuente and C. L. Folcia, J. Mater. Chem., 2005, 15, 5093–5098.

---