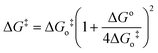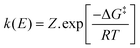DOI:
10.1039/B814895C
(Paper)
New J. Chem., 2009,
33, 207-210
Received (in Montpellier, France) 27th August 2008, Accepted 9th October 2008
First published on 18th November 2008
Abstract
Voltammetric investigations of mechanistic aspects and estimation of thermo-chemical parameters of nitrate ion reduction at silver electrode, in alkaline medium are reported. The activation barrier determined from cyclic voltammetry fits a quadratic relation rather than the expected Butler-Volmer kinetics. Intrinsic barrier calculations show that the reduction of nitrate ion on silver follows a concerted mechanism, involving electron transfer initiated bond cleavage, followed by chemical reaction. The bond dissociation energy for the O–NO2− bond was estimated to be 48.40 kcal mol−1, which matches well with the reported value of 47.5 kcal mol−1, determined from photodissociation experiments.
1. Introduction
The high water solubility of nitrate ions is responsible for its virtual presence everywhere. Serious clinical symptoms have been reported to be caused by their ingestion,1–3 which necessitates effective monitoring and development of sensing tools for this ion. For its detection and estimation, a series of methods have been proposed in refs. 4–8. Among them, the electrochemical methods have proved to be advantageous in terms of reproducibility, accuracy, time response and durability.9 The voltammetric detection is based on the irreversible two-electron transfer process shown in eqn (1):10| | | O–NO2− + 2e + H2O → NO2− + 2OH− | (1) |
Using conventional voltammetry,11,12 in combination with electrochemical scanning tunneling microscopy, surface enhanced Raman spectroscopy,13 and differential electrochemical mass spectrometry,14 it is reported that the nitrate ion reduction is very sensitive to the solution conditions, pH and the nature of the electrode material. For example, on polycrystalline platinum electrode, it proceeds through a dissociative adsorption pathway,15 albeit with slow kinetics. Similar results have been also reported for palladium electrodes,16 while on Cu, the reduction is found to be very facile and proceeds through the formation of NO2− in alkaline medium.13 Dima et al.14 have reported varying activity of transition and coinage metals and proposed a probable general scheme for the nitrate ion reduction process. In general, nitrate reduction is understood to be a multistep process with the first electron transfer as the rate determining step.12–14 Among all the metals studied, silver shows highest sensitivity for nitrate ion reduction, and is thus strongly advocated for their electrochemical sensing.10,17,18 For better understanding and development of Ag as a nitrate ion sensor, it is of utmost importance to have knowledge about the mechanism of this reduction—especially with respect to the rate determining step. To our knowledge, these aspects have not been considered so far. Thus, it was of our immense interest to study the mechanism of this reaction on Ag-electrode, voltammetrically. With this aim, the kinetic investigations of nitrate ion reduction in alkaline media were undertaken through cyclic voltammetry. Our analysis for the first time revealed that the nitrate ion reduction on Ag follows a dissociative electron transfer mechanism. Besides, the related calculations led to the quantification of thermo-chemical parameters, such as bond dissociation energy of the O–NO2− bond, which is otherwise estimated through thermal- and photo-dissociation measurements.192. Experimental
Potassium nitrate and sodium hydroxide were purchased from Merck. Ag-bulk electrode was prepared by sealing a 2 mm diameter Ag (99.9%) wire in a glass tube, with the help of epoxy adhesive. The electrode surface was exposed by grinding it on emery paper. It was polished with commercially available silver cleaner, followed by 0.2 μm alumina powder. Ag/AgCl, KCl (3.0 M), and a Pt rod from Metrohm devices were used as reference and counter electrodes, respectively. Cyclic voltammetric (CV) investigations were performed using Metrohm PGSTAT 100 POTENTIOSTAT/GALVANOSTAT in a three-electrode setup. All the measurements were performed under an argon atmosphere. Prior to measurements, the Ag electrode was electrochemically activated by cycling the potential twenty times (scan rate 1 V s−1) in the potential range −1.3 to 1.0 V, followed by ten potential steps (of 1 s duration) in increasing order of potential, ranging from −0.25 to 0.9 V in 2.0 M NaOH. CVs used for analysis were background corrected for the charging current. In view of the reported complications observed during nitrate ion reduction at Ag-electrode,17 every scan used for the analysis was recorded on a freshly polished and electrochemically cleaned electrode surface. All the measurements were carried out in thermostatted condition at 298 ± 0.1 K.3. Results and discussion
A typical CV recorded using the Ag electrode in 10 mM KNO3 and 2 M NaOH (pH = 12) at the scan rate of 10 mV s−1 is shown in Fig. 1. High pH helps to shift hydrogen evolution towards more negative potential in comparison to the nitrate ion reduction. A cathodic peak at −0.94 V is assigned to the reduction of nitrate ions. The linear relationship between ip and the square root of scan rate (ν1/2) (Fig. 1, inset) indicates that the process is diffusion controlled.20 The scan rate dependent shift in peak potential (Ep), as shown in Fig. 2, is attributed to the irreversibility in the electron transfer process. The magnitude of Ep−Ep/2 was in the range 47 to 96 mV, which is an indication of electron transfer being the rate determining step.21 Interestingly, ip/ν1/2 (Fig. 3) and Ep−Ep/2 (Table 1) were found to be scan rate dependent. Additionally, peak broadening with increase in scan rate is observed (Fig. 2). Prima facie, both these observations could be attributed to the uncompensated iR drop and charging current contributions. However, the electrolyte used was highly conducting and moreover, we had subtracted background charging current. Therefore, the contributions of iR drop and the capacitance are ruled out. Thus, the shift in the potential and Ep−Ep/2 with the scan rate are attributed to the potential dependent electron transfer coefficient (α) for the reaction22 and nitrate ion reduction does not follow a normal Butler–Volmer kinetics. Since the ipvs. ν1/2 plot shows that the process is diffusion controlled, it also suggests that the potential dependent free energy of activation for the reaction is a quadratic function of electrode potential, as per eqn (2):23| | 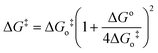 | (2) |
where,in which Eo′ is the formal potential for overall reaction and has a value of 0.01 V24 and ΔGo‡, is the intrinsic energy barrier for the reduction reaction.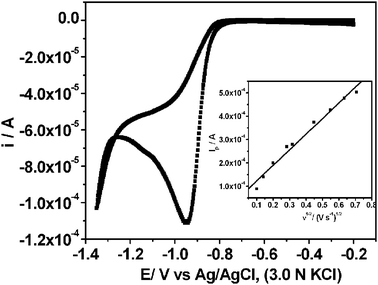 |
| | Fig. 1 Typical cyclic voltammogram recorded on Ag electrode in 10 mM KNO3 and 2 M NaOH, at a scan rate of 10 mV s−1. Inset shows a linear fit of the peak current (ip) vs. square root of scan rate (ν1/2), which indicates diffusion controlled reaction. | |
 |
| | Fig. 2 Cyclic voltammograms recorded on Ag electrode in 10 mM KNO3 and 2 M NaOH, at varying scan rates from 10 to 500 mV s−1. Inset shows peak potential vs. scan rate, which indicates that the reduction is irreversible. | |
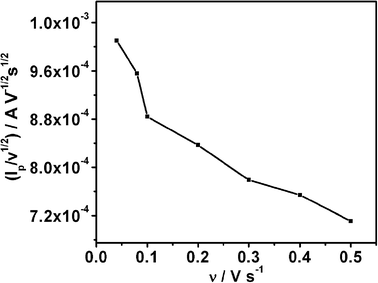 |
| | Fig. 3 ip/ν1/2vs. scan rate for NO3 reduction on Ag electrode in alkaline medium, indicating a deviation from Butler-Volmer kinetics. | |
Table 1 Analysis of cyclic voltammetric (CV) data obtained for nitrate ion reduction (10 mM) at an Ag electrode in 2 M NaOH at 298 K
| Scan rate/V s−1 | 104Ip/A | Ep/V | (Ep−Ep/2)/V | ΔGo‡/kcal mol−1 |
|---|
| 0.01 | 0.891 | −0.944 | 0.060 | 19.97 |
| 0.02 | 1.40 | −0.920 | 0.065 | 19.56 |
| 0.04 | 2.01 | −0.926 | 0.072 | 19.66 |
| 0.08 | 2.70 | −0.932 | 0.078 | 19.77 |
| 0.1 | 2.80 | −0.934 | 0.083 | 19.80 |
| 0.2 | 3.74 | −0.944 | 0.085 | 19.97 |
| 0.3 | 4.27 | −0.948 | 0.087 | 20.04 |
| 0.4 | 4.77 | −0.958 | 0.089 | 20.22 |
| 0.5 | 5.03 | −0.962 | 0.094 | 20.28 |
The potential dependent rate constant (k(E)) is given by eqn (4):
| | 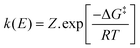 | (4) |
where,
Z (= (
RT/2π
M)
1/2,
M is the molecular mass of NO
3−) = 2521.79 cm s
−1.
Such dissociative redox reactions initiated with electron transfer can occur through two plausible mechanisms, namely stepwise (eqn (5) and (6)) and concerted (eqn (7)):
Products formed through both these mechanisms can undergo further electron transfer or chemical reactions, which affect the thermodynamic and kinetic aspects of the overall process. Theory as well as experimental predictions associated with these mechanisms for alkyl halides,25 peroxides22,26 and other analytes27,28 have been well documented in the literature. The two mechanisms can be differentiated on the basis of difference in the value of intrinsic energy barrier, as given below (eqn (8) and (9)):
| |  | (8) |
| |  | (9) |
where, BDFE is the bond dissociation free energy, and
λ0, the
solvent reorganization energy, which is calculated through the Marcus equation
(10):
| |  | (10) |
Here,
εo and
εs are the optical and static dielectric constants of the
solvent, respectively and
ao, the effective radius of the
analyte, which is calculated using
eqn (11):
| |  | (11) |
where
aAB =
aNO3− = 2.64 Å and
aB =
aO− = 1.76 Å are as reported previously.
29λi is regarded as the internal reorganization energy and can be neglected due to its comparatively small magnitude.
λ0 was calculated using reported values for optical and static dielectric constants for
water.
30 Use of convolutive analysis of CVs has been reported for the calculation of intrinsic barriers and other mechanistic details of such
electron transfer reactions. Though, the method has many advantages, its use is limited due to the requirement of information regarding the double layer structure. Except for
mercury, such information is not available for other metal
electrodes. We used another simple approach for calculation of the barrier using
cyclic voltammetry, without any convolution analysis, which is as follows.
The free energy of activation at peak potentials obtained in cyclic voltammograms is given by eqn (12):31
| |  | (12) |
Knowing the value of α calculated from Ep−Ep/2, where Ep is the peak potential and Ep/2 is the potential where the current is at half the peak value (Table 1), through eqn (13):20
| |  | (13) |
and
D (1.9 × 10
−5 cm
2 s
−1), Δ
GP‡ values for the various scan rates were calculated. These values were substituted in
eqn (2) and the resulting quadratic equation was solved for Δ
Go‡ with the help of the FORTRAN program, written specifically for this purpose. Among the two roots obtained, the negative root was not considered as the value emerged out to be less than that obtained from
eqn (8), which is the bare minimum value expected for the overall reaction. The positive root, gives a value of Δ
Go‡ much greater than that expected for a stepwise mechanism (
eqn (5) and (6)) and hence negating the possibility that the
reduction follows a stepwise mechanism. Therefore, the reaction occurring through the concerted mechanism as shown in
eqn (7) is inferred. Preference of a concerted mechanism over a stepwise one is also realized by considering the resonance structure of
nitrate ion and the
nitrite ion as against the open shell structure of NO
3˙
2−—an intermediate which would be formed in a stepwise mechanism.
The bond dissociation energy was calculated by substituting the value of ΔGo‡ (from the above procedure) and λo (from eqn (10)) in eqn (9) and found to be ca. 48.4 kcal mol−1, which matches well with the value of 47.5 kcal mol−1, reported from photodissociation measurements.19 The small difference is attributed to the neglecting the value of λi in the calculations as a first approximation.
Based on our experimental findings and earlier reports,13,14,32,33 we conclude that, electron transfer to the nitrate ion is the rate determining step, similar to the process reported for Cu, and following the overall reaction scheme given by eqn (14) and (15):
| | | NO3− + e−→ NO2− + O˙− (rate determining step) | (14) |
| | | O˙− + e− + H2O → 2OH− | (15) |
Results published recently by Broder et al.34 also suggest the formation of O˙− as an intermediate in reduction of nitrate ion at Pt electrode in room-temperature ionic liquids.
4. Conclusion
For the first time, we have used a simple procedure for analyzing the cyclic voltammetric data for nitrate ion reduction at a silver electrode. Data fits very well in the dissociative electron transfer concerted mechanism. Besides, the value of the bond dissociation energy, ca. 48.4 kcal mol−1, calculated from these investigations, matches with 47.5 kcal mol−1 the value obtained from photodissociation measurements. This knowledge of mechanistic and thermo-chemical parameters is believed to be useful in designing Ag electrodes as nitrate ion sensors.
Acknowledgements
M. A. B. would like to thank the University authorities, especially Vice Chancellor, University of Kashmir, and Head, Department of Chemistry, University of Kashmir, for sanction of study leave. P. P. I. thanks CSIR—India, for a fellowship. V. R. C. thanks the BARC–Pune University collaborative PhD program for financial support. The authors would like to thank CNQS, University of Pune, for financial support.References
- G. Ellis, I. Adatia, M. Yazdanpanah and S. K. Makela, Clin. Biochem., 1998, 31, 195 CrossRef CAS.
- C. S. Bruning-Fann and J. B. Kaneene, Vet. Hum. Toxicol., 1993, 35, 237 CAS.
- National Research Council, Ground Water Vulnerability Assessment, Predicting relative contamination potential under conditions of uncertainty, National Academy Press, Washington DC, 1993, p. 14 Search PubMed.
- M. A. Ferree and R. D. Shannon, Water Res., 2001, 35, 327 CrossRef CAS.
- S. Kage, K. Kudo and N. Ikeda, J. Chromatogr. B: Biomed. Appl., 2000, 742, 363 CrossRef CAS.
- J. A. Morales, L. S. de Graterol and J. Mesa, J. Chromatogr. A, 2000, 884, 185 CrossRef CAS.
- V. Jedlickova, Z. Paluch and S. Alusik, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2002, 780, 193 CrossRef CAS.
- T. Miyado, Y. Tanaka, H. Nagai, S. Takeda, K. Saito, K. Fukushi, Y. Yoshida, S. Wakida and E. Niki, J. Chromatogr. A, 2004, 1051, 185 CrossRef CAS.
- M. J. Moorcroft, J. Davis and R. G. Compton, Talanta, 2001, 54, 785 CrossRef CAS.
- J. Krista, M. Kopanica and L. Novotny, Electroanalysis, 2000, 12, 199 CrossRef CAS.
- K. Bouzek, M. Paidar, A. Sadilkova and H. Bergmann, J. Appl. Electrochem., 2001, 31, 1185 CrossRef CAS.
- J. Davis, M. J. Moorcroft, S. J. Wilkins, R. G. Compton and M. F. Cardosi, Analyst, 2000, 125, 737 RSC.
- S.-E. Bae, K. L. Stewart and A. A. Gewirth, J. Am. Chem. Soc., 2007, 129, 10171 CrossRef CAS.
- G. E. Dima, A. C. A. de Vooys and M. T. M. Koper, J. Electroanal. Chem., 2003, 554, 15 CrossRef.
- M. C. P. M. da cunha, M. Weber and F. C. Nart, J. Electroanal. Chem., 1996, 414, 163 CrossRef.
- M. Wasberg and G. Horanyi, Electrochim. Acta, 1995, 40, 615 CrossRef CAS.
- D. Kim, I. B. Goldberg and J. W. Judy, Analyst, 2007, 132, 350 RSC.
- M. Fedurco, P. Kedzierzawski and J. Augustynski, J. Electrochem. Soc., 1999, 146, 2569 CrossRef CAS.
- B. Kim, PhD Thesis, University of California, USA, 1991.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2nd edn, 2001 Search PubMed.
- C. P. Andrieux and J. M. Saveant, in Investigations of Rates and Mechanisms of Reactions, ed. C. F. Bernasconi, Wiley, New York, 1986, part 2, vol. VI/4E Search PubMed.
- S. Antonello, M. Musumeci, D. D. M. Wayney and F. Maran, J. Am. Chem. Soc., 1997, 119, 9541 CrossRef CAS.
- J. M. Saveant, in Advances in Electrontransfer Reactions, ed. P. S. Mariano, JAI Press, Greenwich, 1994, vol. 4, p. 53 Search PubMed.
- Handbook of Electrochemistry, ed. C. G. Zoski, Elsevier, Amsterdam, 1st edn, 2007 Search PubMed.
- J. M. Saveant, J. Am. Chem. Soc., 1987, 109, 6788 CrossRef CAS.
- S. Antonello and F. Maran, J. Am. Chem. Soc., 1999, 121, 9668 CrossRef CAS.
- A. Cardinale, A. A. Isse, A. Gennaro, M. Robert and J. M. Saveant, J. Am. Chem. Soc., 2002, 124, 13533 CrossRef CAS.
- R. L. Donkers and M. S. Workentin, J. Phys. Chem. B, 1998, 102, 4061 CrossRef CAS.
- Handbook of Chemistry and Physics, CRC Press, New York, 80th edn, 1999–2000 Search PubMed.
- J. A. Riddick and W. B. Bunger, in Organic Solvents: Physical Properties and Methods of Purification, John Wiley and Sons, New York, 3rd edn, 1970, vol. II Search PubMed.
- L. Pause, M. Robert and J. M. Saveant, J. Am. Chem. Soc., 2000, 122, 9829 CrossRef CAS.
- O. M. Magnussen, Chem. Rev., 2002, 102, 679 CrossRef CAS.
- M. Kleinert, A. Cuesta, L. A. Kibler and D. M. Kolb, Surf. Sci., 1999, 430, L521 CrossRef CAS.
- T. L. Broder, D. S. Silvester, L. Aldous, C. Hardacre, A. Crossley and R. G. Compton, New J. Chem., 2007, 31, 966 RSC.
Footnote |
| † Permanent address: Department of Chemistry, University of Kashmir, Srinagar-190006, India. |
|
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2009 |
Click here to see how this site uses Cookies. View our privacy policy here.