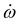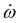N-Inversion in 2-azabicyclopentane derivatives: model simulations for a laser controlled molecular switch
Bastian
Klaumünzer
* and
Dominik
Kröner
Universität Potsdam, Institut für Chemie, Karl-Liebknecht-Str. 24-25, D-14476, Potsdam, Germany. E-mail: bastian.klaumuenzer@uni-potsdam.de
First published on 5th November 2008
Abstract
We report model quantum simulations for the nitrogen inversion in 2-azabicyclo[1.1.1]pentane derivates controlled by laser pulses proposing to use this class of molecules as molecular switches. The derivatives trans-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane and cis-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane are investigated by means of density functional theory and quantum wave packet dynamics. The molecules have two stable, i.e. energetically well-separated, conformers along the N-inversion coordinate. In 1D model simulations the transformation from one conformer to the other is accomplished in the electronic ground state by using two overlapping chirped linearly polarized IR laser pulses for the trans- and cis-isomer or alternatively via an electronic excited state employing a pump-dump sequence of ultrashort UV laser pulses.
1. Introduction
Currently molecular switches are of interest in the field of nanotechnology, e.g. for application in molecular electronics.1,2 In addition, they are also important in biology since many biological functions are based on them, for instance, allosteric regulation and vision. In general, theoretical and experimental research on photo-switchable compounds has mainly focused on cis-trans isomerization or photocyclic reactions.3–5 Examples are chiroptical switches based on sterically overcrowded alkenes,6 azobenzenes used as surface mounted molecular switches7,8 or the laser controlled reversible ring-opening of cyclohexadiene.9Conformational transformations in molecules without affecting the bond order have been, however, of rather less interest for the design of molecular switches. The reason is obvious since the barrier separating conformers is often in the order of 1–10 kJ mol−1 making differentiation and, hence, detection of the switchable molecular property, at room temperature difficult if not impossible. Nevertheless, energy barriers between conformers can be increased by sterically demanding substituents making those molecules more attractive for controlled conformational switching. For instance, Umeda et al. presented quantum simulations for the optical isomerization of helical difluorobenzo[c]phenanthrene10 and Hoki et al. performed quantum simulations for the change of axial chiral 1,1′-binaphthyl from its P- to M-form by laser induced torsion around a single bond.11 Recently, we reported a laser controlled axial chiral molecular switch, which allows for the selective transformation between the achiral and either the left- or right-handed form of an F-substituted styrene derivative by torsion around a C–C single bond.12
A particular type of conformational change is the nitrogen inversion (N-inversion).13,14 A nitrogen compound like ammonia in a trigonal pyramid geometry (tertiary amine) undergoes rapid nitrogen inversion. This interconversion is very fast at room temperature because the energy barrier (24.2 kJ mol−1) is relatively small.15 However, if the nitrogen has sterically demanding substituents or is part of a rigid ring system, it cannot easily invert around the lone electron pair making the two conformers separable at room temperature.
Here we report quantum dynamical simulations of laser controlled N-inversion of two 2-azabicycles. This class of azabicyclic molecules has a particularly high inversion barrier due the bicyclic effect, which has been of great experimental and theoretical interest.13,16,17 We propose that derivatives of 5-X/Y-2-azabicyclo[1.1.1]pentane could serve as laser pulse controlled molecular switches, which change according to their conformation the size and direction of their dipole moment mainly originating from an electronegative substituent X/Y, see Fig. 1. For a defined setup of the molecular switch this system could be immobilized by chemi- or physisorption on a surface via an adequate linking group R, see Fig. 1.
![Model for a laser controlled molecular switch: N-inversion of 5-X/Y-2-R-2-azabicyclo[1.1.1]pentane with X/Y being an electronegative substituent (here: cis X = F/Y = H and trans X = H/Y = F) and R being e.g. a linker for a surface (here R = methyl).](/image/article/2009/NJ/b812319e/b812319e-f1.gif) | ||
| Fig. 1 Model for a laser controlled molecular switch: N-inversion of 5-X/Y-2-R-2-azabicyclo[1.1.1]pentane with X/Y being an electronegative substituent (here: cis X = F/Y = H and trans X = H/Y = F) and R being e.g. a linker for a surface (here R = methyl). | ||
In this paper we investigate cis-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane (X = F, Y = H and R = CH3 in Fig. 1) and trans-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane (X = H, Y = F and R = CH3 in Fig. 1). These molecules possess two conformers of different dipole moments separated by a high N-inversion barrier. In the following we will demonstrate how these molecular systems can be switched via vibrational or vibronic states. For these purposes control mechanisms employing ultrafast laser pulses have been developed.
The remainder of the paper is organized as follows: The model and the applied theoretical methods are explained in section 2, the results of the quantum chemical and quantum dynamical calculations including the laser control are presented in section 3. Section 4 provides a summary.
2. Model and methods
2.1 Quantum chemistry
The geometries of the two N-inversion conformers of both isomers, namely the trans- and cis-isomer, were optimized with density functional theory (DFT) employing the B3LYP18,19 functional and the ANO-L-DZ20 basis set as implemented in the Molcas 6.4 program package.21 The obtained geometries are denoted trans-Min1 and trans-Min2 for the trans-molecule or cis-Min1 and cis-Min2 for the cis-molecule, see section 3.1 and Fig. 2 and 4. The transition states, called trans-TS and cis-TS, were also calculated at the same level of theory.![Optimized geometries of trans-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane obtained from B3LYP/ANO-L-DZ: trans-Min1 is the global minimum with angle α set to 90.0° in the space fixed coordinate system. trans-Min2 is the optimized geometry of the second N-inversion conformer at α≈189°. trans-TS is the transition state geometry at α≈165°. trans-Min3 is the unrelaxed minimum along α with α≈193° using trans-Min1 as reference.](/image/article/2009/NJ/b812319e/b812319e-f2.gif) | ||
| Fig. 2 Optimized geometries of trans-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane obtained from B3LYP/ANO-L-DZ: trans-Min1 is the global minimum with angle α set to 90.0° in the space fixed coordinate system. trans-Min2 is the optimized geometry of the second N-inversion conformer at α≈189°. trans-TS is the transition state geometry at α≈165°. trans-Min3 is the unrelaxed minimum along α with α≈193° using trans-Min1 as reference. | ||
To simulate the change of conformation the molecules are assumed to be oriented with their N–C1-bond along the space fixed z-axis, as shown in Fig. 2. Then, the N-inversion is approximated by a partial rotation of the methyl group around the y-axis while keeping the rest of the molecule fixed in space. The angle α between the N–C1-bond and the x-axis is used as reaction coordinate. In addition, for the trans-isomer the free rotation of the methyl group around the N–C1-bond is simulated by a rotation of the hydrogen atoms of the methyl group around the N–C1-bond. Here the dihedral β, measured between the H1–C1-bond and the x-axis, is used as reaction coordinate, see Fig. 2. (In practice, first, the hydrogen atoms of the methyl group are rotated clockwise around z-axis by β and afterwards the whole methyl group is rotated around the y-axis by α.)
For the laser control via the ground state N-inversion states, see section 3.3, the unrelaxed potential energy surface (PES) of the electronic ground state along α is calculated by B3LYP/ANO-L-DZ while keeping the rest of the geometrical parameters frozen to the minimum energy geometry trans-Min1 or cis-Min1. For the trans-switch the calculations are also performed along β obtaining a two-dimensional PES. Accordingly, the permanent dipole moment along α is obtained on the same level of theory as the PES.
For the control scenario using UV laser pulses for the cis-isomer, see section 3.4, the first ten singlet electronic excited states along α are calculated by time-dependent DFT (TDDFT) with B3LYP and 6-31G(d,p) as implemented in the GAUSSIAN0322 package. Transition dipole moments between ground and any of the electronic excited states are obtained on the same level of theory. As previously cis-Min1 is used as reference geometry.
2.2 Model Hamiltonian
As the moment of inertia of the methyl group with respect to the space fixed y-axis is about 100-times smaller than that of the rest of the molecule, we assume the F-azabicyclo group being fixed in space with only the methyl group moving,23 see Fig. 2. To obtain the N-inversion eigenenergies εiv and eigenfunctions ϕiv of the ith electronic state the time-independent Schrödinger equation| Ĥimol(α)ϕiv(α) = εivϕiv(α) | (1) |
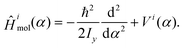 | (2) |
| αi = α0 + iΔα, i = 0, …, N− 1, | (3) |
2.3 Quantum dynamics
To describe the laser-driven quantum dynamics the time-dependent Schrödinger equation is solved numerically: | (4) |
 | (5) |
 | (6) |
 | (7) |
 | (8) |
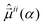 are the permanent dipole moments of the ith electronic state and
are the permanent dipole moments of the ith electronic state and  are the electronic transition dipole moments. For the dynamical simulations we set the permanent dipole moments of the ith excited state equal to that of the electronic ground state
are the electronic transition dipole moments. For the dynamical simulations we set the permanent dipole moments of the ith excited state equal to that of the electronic ground state  , the transition dipole moments are set
, the transition dipole moments are set  and the transition dipole moments between all other electronic excited states are set zero
and the transition dipole moments between all other electronic excited states are set zero  .
.
The electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) of the laser pulses used here is given by:
(t) of the laser pulses used here is given by:
 | (9) |
![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) φ =
φ = ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) xcos(φ) +
xcos(φ) + ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) zsin(φ) with polarization angle φ, where
zsin(φ) with polarization angle φ, where ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) x/z is the unit vector along the x/z-axis. Hence, the laser is chosen to propagate in y-direction. E0 is the electric field amplitude and tc the pulse center, i.e. the time when the sin2 shape-function reaches its maximum. The laser pulse frequency ω can be linearly chirped by
x/z is the unit vector along the x/z-axis. Hence, the laser is chosen to propagate in y-direction. E0 is the electric field amplitude and tc the pulse center, i.e. the time when the sin2 shape-function reaches its maximum. The laser pulse frequency ω can be linearly chirped by  :
: | (10) |
3. Results and discussion
3.1 Geometries and PESs
The geometry optimization of the trans-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane with B3LYP/ANO-L-DZ resulted in two stable minima trans-Min1 and trans-Min2, shown in Fig. 2, where trans-Min1 is the global minimum. In terms of the angle α the two minima are at 90° (trans-Min1) and at 189.4° (trans-Min2) according to the space fixed coordinate system. Thus, the transformation between them is achieved by a rotation of the methyl group around the y-axis by about 100°. At the transition state trans-TS of the nitrogen inversion the angle α≈140.2°. The molecule has CS-symmetry with respect to the xz-plane in all conformations. The energy difference between the transition state trans-TS and the absolute minimum trans-Min1 is 6397.9 cm−1 corresponding to 76.5 kJ mol−1 which is more than three times higher than the inversion barrier of ammonia (24.2 kJ mol−1).15 As one can see from Fig. 2 the methyl group is rotated around the C1–N bond by about 180° while going from trans-Min1 to trans-Min2. Therefore a two-dimensional PES (Fig. 3) along α and β was calculated.![Unrelaxed potential energy surface along α and β for trans-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane (B3LYP/ANO-L-DZ). trans-Min1 denotes the minimum energy geometry which was used as reference geometry.](/image/article/2009/NJ/b812319e/b812319e-f3.gif) | ||
| Fig. 3 Unrelaxed potential energy surface along α and β for trans-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane (B3LYP/ANO-L-DZ). trans-Min1 denotes the minimum energy geometry which was used as reference geometry. | ||
The PES shows three minima belonging to three different molecular structures. We find minima at α = 90°/β = 0° (trans-Min1), at α = 190°/β = 0° (trans-Min3) and at α = 190°/β = 180° (trans-Min4), while the latter corresponds to the unrelaxed geometry of trans-Min2. Additionally there are three distinct maxima: trans-Max1 at α = 90°/β = 180°, trans-Max2 at α = 150°/β = 0°, which belongs to the unrelaxed geometry of trans-TS, and trans-Max3 at α = 150°/β = 180°. The energy differences between trans-Min1 and trans-Max1 and the barrier height between trans-Min4 and trans-Min3 are approximately of the same size, namely 1000 cm−1 (12 kJ mol−1). This barrier, resulting from the free rotation of the methyl group around the C1–N bond, is, as expected, of the same height as the rotational barrier of ethane (12 kJ mol−1).27 The PES shows that the N-inversion should not significantly be affected by the free rotation of the methyl group, see Fig. 3. Yet, the methyl group used here represents merely a placeholder for an arbitrary substituent R, for instance, a linker to a surface. The free rotation of the methyl group around the C1–N bond is neglected in the following, i.e. the unrelaxed PES only along α with trans-Min1 as reference geometry is used for all dynamical simulations.
It should be noted, as an aside, that a normal mode analysis of the relaxed minimum geometry trans-Min1 employing B3LYP/6-31G(d,p) reveals three modes that should be considered important for the dynamical simulations: (i) The rotation of the methyl group around the C1–N bond (β) at 245 cm−1, (ii) the bending of the C1–N-bicylo-angle describing the rotation of the methyl group around the y-axis at 251 cm−1 (α), and (iii) the torsion of the C1–N-bicylo-dihedral describing the rotation of the methyl group around the x-axis at 286 cm−1 (all frequencies scaled according to ref. 29). Hence, a coupling of mode (ii), which characterizes our model reaction coordinate α, to modes (i) and (iii) cannot completely be ruled out for higher excited states, because their energies lie within the range of the inversion excitation energies, see section 3.2.
Due to the unrelaxed geometry the inversion barrier is approx. 1600 cm−1 higher compared to the relaxed one. To get an idea whether the barrier can be crossed thermally we calculated N-inversion rates according to the theory of Eyring.28 The necessary thermodynamic quantities were obtained with the GAUSSIAN03 program package employing B3LYP/6-31G(d,p). At 298 K we obtain an inversion rate from trans-Min1 to trans-Min2 of 2.20 s−1. So at room temperature we find a rather small rate for spontaneous N-inversion compared to ammonia (about 109 s−1 without tunneling). As the backward reaction rate is also fairly small at room temperature (3.54 s−1) the here investigated conformers are considered thermally sufficiently stable to monitor the change of the dipole moment, see discussion below. For a more detailed discussion the reader is referred to ref. 23.
The geometry optimization of the cis-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane with B3LYP/ANO-L-DZ resulted in two stable minima, denoted cis-Min1 and cis-Min2. The corresponding structures are shown in Fig. 4. Cis-Min1 is the global minimum, however, the energy difference between the two minima is only 7 cm−1. In terms of the inversion angle α the two minima are found at 90° (cis-Min1) by definition and at 179.8° (cis-Min2), i.e. the transformation between them is achieved by flipping the methyl group by about 90°. As the steric interactions of the X-substituent (X = F) with the methyl group (R) is stronger than for the trans-isomer (X = H), the change in α going from one conformer to the other (≈90°) is smaller than for the trans-isomer (≈100°).
![Optimized geometries of cis-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane obtained from B3LYP/ANO-L-DZ: cis-Min1 is the global minimum with angle α set to 90.0° in the space fixed coordinate system. cis-Min2 is the optimized geometry of the second N-inversion conformer at α≈179°. cis-TS is the transition state geometry at α≈165°. cis-Min3 is the unrelaxed minimum along α with α≈191° using cis-Min1 as reference.](/image/article/2009/NJ/b812319e/b812319e-f4.gif) | ||
| Fig. 4 Optimized geometries of cis-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane obtained from B3LYP/ANO-L-DZ: cis-Min1 is the global minimum with angle α set to 90.0° in the space fixed coordinate system. cis-Min2 is the optimized geometry of the second N-inversion conformer at α≈179°. cis-TS is the transition state geometry at α≈165°. cis-Min3 is the unrelaxed minimum along α with α≈191° using cis-Min1 as reference. | ||
At the transition state cis-TS of the nitrogen inversion the angle α≈164.7°. The molecule has a mirror plane in the xz-plane in all conformations. The energetic difference between the transition state cis-TS and the absolute minimum cis-Min1 is now 6358.6 cm−1 corresponding to 76.1 kJ mol−1. Hence, the barrier height is similar to the one of the trans-isomer (76.5 kJ mol−1).
For the cis-isomer we also observe that the methyl group is rotated around the C1–N bond by about 180° while going from cis-Min1 to cis-Min2. As the coupling of the N-inversion to the rotation of the methyl group is, as discussed above, rather weak, only the one-dimensional PES along α starting from cis-Min1 is considered. The unrelaxed electronic ground state potential along α (B3LYP/ANO-L-DZ) is shown in Fig. 5. The inversion barrier height is 8000 cm−1 and due to the unrelaxed geometry approx. 1600 cm−1 higher than in the relaxed case (cis-TS). As noted previously, due to the frozen geometry the inversion angles at the top of the inversion barrier (cis-Max2) and for cis-Min3 differ from those of the optimized geometries, i.e. α(cis-Max2) ≈148° and α(cis-Min3) ≈191°. Here we can denote that the 1D cut of the potential energy surface of the trans- and cis-isomer, Fig. 5, are quantitatively similar, so that the curves overlap in the figure.
![Potential energy surface of 5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane along α for the electronic ground state S0 (B3LYP/ANO-L-DZ) (fitted from 33 single point calculations with a cubic spline) and first three electronic excited states, S1 to S3 (TD-B3LYP/6-31G(d,p)). Min1 denotes cis- and trans-Min1, Min3 cis- and trans-Min1 and Max2 denotes cis- and trans-Max2, since the potentials for the cis- and trans-isomers overlap on the scale of the picture.](/image/article/2009/NJ/b812319e/b812319e-f5.gif) | ||
| Fig. 5 Potential energy surface of 5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane along α for the electronic ground state S0 (B3LYP/ANO-L-DZ) (fitted from 33 single point calculations with a cubic spline) and first three electronic excited states, S1 to S3 (TD-B3LYP/6-31G(d,p)). Min1 denotes cis- and trans-Min1, Min3 cis- and trans-Min1 and Max2 denotes cis- and trans-Max2, since the potentials for the cis- and trans-isomers overlap on the scale of the picture. | ||
For the UV laser pulse control of the cis-isomer electronic excited states were calculated as explained in section 2.1. The first three excited states S1, S2 and S3 (TD-B3LYP/6-31G(d,p)) of the cis-isomer are depicted in Fig. 5. The shape of the excited state potentials are similar to those of other aliphatic tertiary amines calculated by Solling et al. with TD-B3LYP/6-31++G(2df).30 We observe a vertical excitation energy from S0 to S1 at α = 90° of approx. 7.2 eV (58071.9 cm−1). Compared to the amines in ref. 30 the here computed excitation energies are similar, so that we consider the level of theory used for the calculation of the electronic excited states to be sufficient for our needs, although Rydberg states might not be described precisely due to the restrictions of the basis set used here, i.e. the lack of diffuse functions. An orbital analysis shows that the transitions are predominantly of n →π and n →σ character in accordance to the amines in ref. 30.
The topology of the excited states differ from the ground state. Instead of two minima along α there is only one single minimum. The topology of the S1 potential is suited well for switching the molecule via this excited state since no barrier has to be crossed on V1 by switching from one conformer to the other, see section 3.4.
The components of the permanent dipole moment 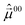 along α are shown in Fig. 6(a) for the trans-isomer. Because of the Cs-symmetry in the xz-plane the permanent dipole moment along y is zero at all α. The laser will, therefore, be chosen to propagate in y-direction, see eqn (9). The major change in μ00x occurs in range of 150–210°, while μ00z has its major change in the range of 70–150°.
along α are shown in Fig. 6(a) for the trans-isomer. Because of the Cs-symmetry in the xz-plane the permanent dipole moment along y is zero at all α. The laser will, therefore, be chosen to propagate in y-direction, see eqn (9). The major change in μ00x occurs in range of 150–210°, while μ00z has its major change in the range of 70–150°.
![x-, y- and z-component along α for the permanent dipole moment 00 (B3LYP/ANO-L-DZ) of (a) trans- and (b) cis-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane, and (c) the transition dipole moments to S1 (TD-B3LYP/6-31G(d,p)) for the cis-isomer.](/image/article/2009/NJ/b812319e/b812319e-f6.gif) | ||
Fig. 6
x-, y- and z-component along α for the permanent dipole moment ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) 00 (B3LYP/ANO-L-DZ) of (a) trans- and (b) cis-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane, and (c) the transition dipole moments 00 (B3LYP/ANO-L-DZ) of (a) trans- and (b) cis-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane, and (c) the transition dipole moments  to S1 (TD-B3LYP/6-31G(d,p)) for the cis-isomer. to S1 (TD-B3LYP/6-31G(d,p)) for the cis-isomer. | ||
For the cis-isomer the components of the permanent dipole moment,  , and of the transition dipole moments from S0 to S1,
, and of the transition dipole moments from S0 to S1, 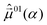 , are plotted in Fig. 6(b) and (c). For reasons of symmetry again μ00y = 0 for all α. In contrast to the trans-isomer the major change in μ00x is in range of 70–120°, while for μ00z the major change occurs in the range of 120–210° now. For an efficient pump–dump mechanism31,32 for both the trans- and the cis-isomer the laser pulses will be polarized in accordance to the regions of largest change in the dipole components, see section 3.3. For the electronic transition to the S1 state of the cis-isomer, UV laser pulses will be xz-polarized as well, as transitions in y polarization are forbidden by symmetry.
, are plotted in Fig. 6(b) and (c). For reasons of symmetry again μ00y = 0 for all α. In contrast to the trans-isomer the major change in μ00x is in range of 70–120°, while for μ00z the major change occurs in the range of 120–210° now. For an efficient pump–dump mechanism31,32 for both the trans- and the cis-isomer the laser pulses will be polarized in accordance to the regions of largest change in the dipole components, see section 3.3. For the electronic transition to the S1 state of the cis-isomer, UV laser pulses will be xz-polarized as well, as transitions in y polarization are forbidden by symmetry.
3.2 Inversion eigenstates
The inversion eigenstates of the ground state were calculated as described in section 2.2. There are 36 eigenstates (trans-isomer)/35 eigenstates (cis-isomer) below the barrier whose eigenfunctions ϕ0v are localized in the left and 21 eigenstates (both isomers) whose eigenfunctions ϕ0v are localized in the right potential well. All eigenfunctions ϕ0v which satisfy ∑K−1i=1|ϕ0v(αi)|2Δα≥ 0.999 are called “left localized” eigenfunctions. Correspondingly, an eigenfunction is called “right localized” if ∑NK+1|ϕ0v(αi)|2Δα≥ 0.999 is fulfilled, where αK is the grid point defined by the maximum of the inversion barrier V0(αK) (trans-Max2/cis-Max2). All states in the left quantum well are termed “L” and those in the right quantum well are termed “R”. The associated wave functions ϕ0v are denoted ϕuL with ϕ0L to ϕ35L/ϕ34L (trans/cis) for the left well and ϕuR with ϕ0R to ϕ20R for the right well. (The superscript 0 is omitted for the “localized” eigenfunctions since the concept applies only for the ground state.) In addition, there are two more eigenstates below the barrier (both isomers) which are considered “delocalized” in these terms. Table 1 lists the two lowest N-inversion eigenenergies ε0v in each ground state minimum, their energy difference Δε = ε0v′−ε0v and the corresponding dipole matrix elements 〈ϕ0v′|μ00x/z|ϕ0v〉 = 〈μx/z〉 for trans- and cis-isomer.| Isomer | trans | cis | ||||||
|---|---|---|---|---|---|---|---|---|
| ϕ 0L | ϕ 1L | ϕ 0R | ϕ 1R | ϕ 0L | ϕ 1L | ϕ 0R | ϕ 1R | |
| ε 0 v | 126.2 | 379.0 | 3397.2 | 3649.3 | 124.5 | 389.7 | 3383.9 | 3642.0 |
| Δε | 252.8 | 252.1 | 265.2 | 258.1 | ||||
| 〈μx〉 | −0.0095 | −0.029 | −0.078 | −0.019 | ||||
| 〈μz〉 | −0.044 | −0.0082 | 0.013 | 0.051 | ||||
3.3 Switching via ladder climbing
For the quantum dynamical simulations the system is initially assumed to be in the inversion ground state 0L, i.e.Ψ(t = 0) = ϕ0L. The goal of the laser control is, to transfer the population to the R states. This is achieved, first, by climbing up the vibrational ladder until the wave packet is above the barrier. Then, a dump laser pulse will be used to induce a downward ladder climbing in the right potential well to trap the wave packet there. To achieve a most efficient ladder climbing the laser pulses will be linearly chirped33–35 according to eqn (10) to compensate for the anharmonicity of the potential at higher energies.Fig. 7(a)/(d) show the time evolution of the electric field of the laser pulse sequences for switching the trans- (a) or cis-isomer (d). The resulting time evolution of the expectation value of the angle α and the population of the L (PL) and R (PR) states are shown in Fig. 7(b)/(e) and (c)/(f) for trans (b, c) or cis (e, f), respectively. The populations in the L and R states and the population in all other states (PD) are calculated as follows:
 | (11) |
 | (12) |
| PD(t) = 1 −PL(t) −PR(t). | (13) |
 36 for the transition between 0L and 1L (77.80°) and 1R and 0R (15.80°). Further optimization of the pulse parameter resulted in almost the same values for the pump (77.80°) and dump pulse (15.95°), see Table 2. A non-overlapping sequence of pump and dump pulse sequence was found less efficient. At first, the overall pulse is more z-polarized and has a negative chirp; after 450–500 fs it changes its polarization towards x-direction and the chirp becomes positive. One can see the change in polarization direction as well as the frequency chirp more clearly in the Husimi probability distributions in Fig. 8. The Husimi distribution37 is obtained from:
36 for the transition between 0L and 1L (77.80°) and 1R and 0R (15.80°). Further optimization of the pulse parameter resulted in almost the same values for the pump (77.80°) and dump pulse (15.95°), see Table 2. A non-overlapping sequence of pump and dump pulse sequence was found less efficient. At first, the overall pulse is more z-polarized and has a negative chirp; after 450–500 fs it changes its polarization towards x-direction and the chirp becomes positive. One can see the change in polarization direction as well as the frequency chirp more clearly in the Husimi probability distributions in Fig. 8. The Husimi distribution37 is obtained from: | (14) |
 | (15) |
 , ε the energy, and t the time.
, ε the energy, and t the time.
 | ||
| Fig. 7 Laser pulse sequence for the N-inversion via IR ladder climbing from trans-Min1 to trans-Min3 (a)–(c) and cis-Min1 to cis-Min3 (d)–(f); for the laser pulse parameters see Table 2. Time evolution of (a)/(d) the x- and z- component of the electric field, (b)/(e) the expectation value of the inversion angle 〈α〉, and (c)/(f) the population of the L, R and D-states according to eqns (11)–(13). | ||
 | ||
| Fig. 8 Husimi probability distributions of the (a) z- and (b) x-component of the electric field of the IR switching pulse sequence for the trans-isomer. | ||
| Isomer | Pulse type | φ (°) | fwhm/fs | t c /fs | E 0/GV m−1 | ω 0/cm−1 |
|
η/rad |
|---|---|---|---|---|---|---|---|---|
| trans | Pump | 77.80 | 640 | 640 | 16.5 | 243.25 | −0.365 | −3.25 |
| Dump | 15.95 | 955 | 1060 | 16.5 | 202.00 | 0.178 | 0.125 | |
| cis | Pump | −10.00 | 400 | 400 | 8.0 | 252.25 | 0.036 | −0.25 |
| Dump | −75.00 | 550 | 650 | 11.5 | 220.25 | 0.180 | 0.75 |
From Fig. 7(b) one can see that once the propagation is started the wave packet begins to oscillate in the left quantum well until it crosses the barrier after 500 fs and is dumped into the right quantum well (α = 185°). The final population is spread over several R states such that the expectation value of α still oscillates around 185° as the mainly R-localized wave packet evolves in time. Nevertheless, the switching of the molecule was successful as at final time 92.5% of the population has been transferred from the left potential well (α = 90°) to the right potential well (α = 191°). States 0R to 6R are the most populated eigenstates after the laser pulse sequence. The missing 7.5% of population remains in the D-states, i.e. mainly above the barrier.
It should be noted that the mean peak intensity (Ī = 0.5ε0c|E0|2) of the IR pulse is rather high: Ī = 16.5 TW cm−2 due to the high N-inversion barrier and the comparatively small change of the dipole moment components along α. The high laser amplitudes could be decreased by using longer pulses. But longer pulses could cause a decrease of efficiency in transferring population from L to R for effects as wave packet broadening. For very long times even intramolecular vibrational redistribution (IVR) cannot be neglected any more. Therefore, we considered the cis-isomer in the next section which has greater transition dipole matrix elements, cf.Table 1, between the eigenstates and such should lead to a decrease of the laser pulse intensities.
For getting the wave packet above the barrier a pump pulse with a slight positive chirp was found beneficial. The second pulse, then, has a notable positive chirp and dumps the wave packet into the right potential well. The wave packet propagation shows almost the same behaviour as for the trans-isomer concerning the expectation value of α and the population dynamics, see Fig. 7(d–f). The pulse sequence is found with 90% PR at final time almost as efficient as what we achieved for the trans-isomer. The population is mostly transferred to the states 3R–9R. As expected the intensity of the laser pulse (Ī = 11.5 TW cm−2) was lowered by 5 TW cm−2, however, it is still high. For that reason a switching mechanism via the electronic excited states will be investigated in the following section.
3.4 Switching the cis-isomer via S1
For the transformation of the cis-isomer of the azabicycle via the excited state S1 the initial state is the inversion ground state 0L as in the previous case. Now the wave packet is to be excited to S1 employing a UV pump laser pulse, and after some short time the wave packet is dumped into the right potential well of the electronic ground state. The criterion for a successful propagation is again that a large part of population is transferred to the twenty R states below the central barrier of the ground state potential. Higher states are omitted at this point, see discussion below.
Fig. 9 shows (a) the electric field of the UV pump dump pulse sequence, (b) the expectation value of angle α, (c) and the population (P) of S0 (P(S0)), S1 (P(S1)) and of the R states (PR). We obtain a sequence of pulses where the pump and dump pulse do not overlap at all. The UV pulse sequence is polarized in the xz-direction. The pulse parameters for the initial guess were obtained in analogy to the procedure discussed above: We set the frequency ω0 to the energy difference V1–V0 at α = 90° for the pump pulse and at α = 190° for the dump pulse. From the transition dipole moments  and
and  we computed the initial polarization angles φ of the pump pulse (−83.1°) and of the dump pulse (7.4°), see 3.2. For the pump pulse we obtained φ = −83.2° and for the dump pulse φ = 10.5° after further manual optimization.
we computed the initial polarization angles φ of the pump pulse (−83.1°) and of the dump pulse (7.4°), see 3.2. For the pump pulse we obtained φ = −83.2° and for the dump pulse φ = 10.5° after further manual optimization.
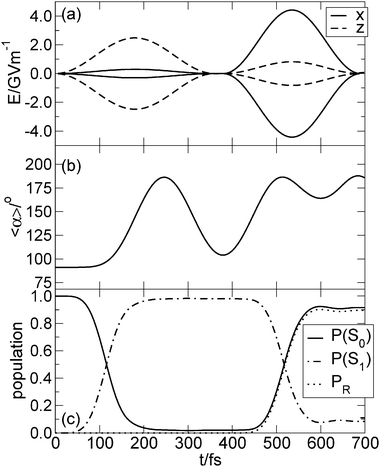 | ||
| Fig. 9 Laser pulse sequence for the transformation of the cis-isomer via the excited state S1 from cis-Min1 to cis-Min3; for the laser pulse parameters see Table 3. Time evolution of (a) the x- and z-component of the envelope function of the electric field, (b) the expectation value of the inversion angle 〈α〉, and (c) the population in S0, S1 and R-states. | ||
| Pulse type | φ (°) | fwhm/fs | t c/fs | E 0/GV m−1 | ω 0/cm−1 |
|
η/rad |
|---|---|---|---|---|---|---|---|
| Pump | −83.20 | 180 | 180 | 2.5 | 58170.0 | 0.0 | 0.0 |
| Dump | 10.50 | 155 | 535 | 4.5 | 51387.0 | 0.86 | 0.0 |
During the control sequence the pump pulse transfers 99% of the population from S0 to S1 (t = 360 fs), see Fig. 9(c). The center of the wave packet then travels on S1 back and forth until the dump pulse transfers 91.5% of the population back to the ground state (t = 600 fs) where the wave packet is then mostly trapped in the right potential well of the ground state (89.5%), see Fig. 9(c). All the population transferred from S1 to the R-states of S0 is found in the inversion states 14R to 17R; so the wave packet is still highly vibrationally excited and it is therefore oscillating between α = 163° and α = 188°, see Fig. 9(b). The missing 2% of the ground state population remains above the barrier (Max2). 8.5% of the electronically excited population remains in S1.
The goal of reducing the laser pulse intensity is reached. The intensity was brought down to 0.83 TW cm−2 for the pump pulse and 2.3 TW cm−2 for the dump pulse. As the population is transferred to high N-inversion states of S1, namely eigenstates 67–72, whereas 70 is the most populated, the wave packet is not in a compact form any more on the excited state and hence it turned out to be very difficult to dump the population effectively to the ground state. The transition frequency of the pump pulse ω0 = 58170 cm−1 is close to the energy difference of the eigenenergies of the eigenstates ϕ170 and ϕ0L (58169.65 cm−1). Neither shortening or prolonging the laser pulse durations nor lowering or increasing their intensity increased the population of the R states.
Comparing the ladder climbing mechanism to the excited state mechanism one can say that almost the same amount of the population is transferred to the twenty R states below the barrier. But in the ladder climbing case lower vibrational R states have been populated, which leads to smaller oscillations in α. In the UV case the laser pulse durations are much shorter (690 fs) than in the IR case (1200 fs). However, upon including the excited state S2 in the calculations the population transferred back to S0 is excited to S2 by the dump pulse such that at the end of the propagation only 50% of the population is transferred to the R states of S0 (not shown). Hence, we have a loss of efficiency, when S2 is included. When including more states up to S10 there is only additional population transfer to S6 by 2%. There will be, however, no population transfer to S3, S4, S7 and S8 as the transitions from S0 are symmetry forbidden in x and z direction. For energetic reasons there is also no population transfer to S9 or S10. Furthermore, due to the different sign of the transition dipole moment of S5 in the z direction the coupling to the x–z polarized dump pulse is rather weak due to the improper polarization. Therefore, no significant population transfer to S5 takes place. Here we also note, that a more precise description of the electronic excited state potentials might be necessary in order to correctly account for avoided crossings in the regions of α = 165° to 215° which might lead to nonadiabatic transitions. In summary, while the laser induced switching via electronic excited states is faster and allows for more realistic laser parameters—at least within the framework of our model—the efficiency is reduced due to undesired electronic excitations mainly to S2.
4. Summary and conclusions
Quantum simulations for a laser driven model system were presented based on the approximate description of the nitrogen inversion in two azabicycles. Each of the two proposed molecules, cis- and trans-5-X-2-R-2-azabicyclo[1.1.1]pentane, possesses two stable conformers due to the sterically hindered N-inversion. The molecules change the size and direction of their dipole moment upon N-inversion where the electronegative substituent X/Y mainly determines this property. The substituent R can be used to immobilize the system, for instance, by mounting it via a linker group R on a surface. To investigate the possibilities of laser control we chose here for a toy model X/Y = F and R = CH3. For trans-5-fluoro-2-methyl-2-azabicyclo[1.1.1]pentane a two-dimensional potential along α and β was calculated, where α models the N-inversion and β describes the free rotation of the methyl group around its single bond to N. For the cis-isomer the potential energy curve only along the nitrogen inversion coordinate (α) was computed. In addition, the potential energy curve was evaluated along α for several electronic excited states. The designed laser pulse sequences allow to transfer the molecules from their energetically more stable conformer (Min1) to the less stable conformer (Min3) along the model reaction coordinate (N-inversion). Linearly polarized laser pulses were used to switch the molecule by either IR induced ladder climbing or alternatively using the electronic excited state (S1) as intermediate state in case of the cis-isomer.In the case of vibrational ladder climbing two overlapping laser pulses with chirped frequencies in the IR range were used to switch the molecules. Thereby excitation and de-excitation were mainly controlled by changing the chirp and the polarization of the laser pulse. But the obtained laser intensities are rather high.
Hence, we applied a control mechanism for the cis-isomer via the first electronic excited S1. In this case the molecule is initially excited by a UV pump laser pulse to a highly vibrational state of S1. Afterwards a second UV laser pulse brings it down to the electronic ground state in the right potential well.
In all cases the molecule was switched effectively as at least 90% of population was found in the target potential well. However, if the second excited state S2 is considered as well there is only population transfer of 50% to the R states in case of UV pulses.
The efficiency of the population transfer could be diminished due to dissipative effects as intramolecular vibrational redistribution (IVR). However, due to the overlapped pump-dump control scheme the system will most probably return to its thermal equilibrium geometry from where it can be switched again, cf.ref. 14. The inversion mode may also couple to other bending modes of the methyl group making the proposed control strategy more complicated. Here, simulations including more degrees of freedom could help to quantify the effect. In this sense the mechanism via electronic excited states could be more efficient as the switching process is faster than in the case of vibrational ladder climbing. The switching process via electronic excited states contains, however, the possible risk of undesired photochemical pathways which could lead to a diminution of the desired control.
The degree of orientation of the molecule with respect to the polarization vector of the laser field determines the efficiency of the control mechanism. There are, however, theoretical and experimental methods for orienting or aligning molecules, e.g. in strong electric fields,39,40 using elliptically polarized lasers41 or applying optimal control theory.42
For the molecular system to be used in electronic devices, it should be immobilized e.g. by adsorption to a surface. For this one has to find a suitable linking group. By immobilizing the molecule on a surface the switching mechanism will be different from those presented here since the azabicycle will flip instead of the R-group. Investigations along this thread are on the way. Still, different fixed molecular orientations (with potentially restricted rotations with respect to the surface normal) are possible upon chemisorption depending on the symmetry of the surface and the linker group. For surface mounted molecules with different orientation along the surface normal stochastically optimized elliptically polarized laser pulses were found efficient for control of molecular isomerization.43 Note that the coupling of the vibrational and electronic degrees of freedom of the molecule to the surface degrees of freedom (phonons, electron-hole pairs) may intensify energy dissipation depending on the nature of the solid and the linking groups. Nevertheless, the model molecules presented here could be a good supplement to the model molecular switches which are based on cis–trans isomerization or photocyclization reaction.
Acknowledgements
We thank P. Saalfrank for stimulating discussions. Financial support by the Deutsche Forschungsgemeinschaft, project KR 2942/1 is gratefully acknowledged.References
- B. L. Feringa, R. A. van Delden and M. K. J. ter Wiel, Pure Appl. Chem., 2003, 75, 563 CrossRef CAS.
- A. H. Flood, J. F. Stoddart, D. W. Steuerman and J. R. Heath, Science, 2004, 306, 2055 CrossRef CAS.
- M. Irie, Chem. Rev., 2000, 100, 1685 CrossRef CAS.
- C. Ciminelli, G. Granucci and M. Persico, Chem. Phys., 2008, 349, 325 CrossRef CAS.
- N. Tamai and H. Miyasaka, Chem. Rev., 2000, 100, 1875 CrossRef CAS.
- R. A. van Delden, M. K. J. ter Wiel and B. L. Feringa, Chem. Commun., 2005, 200 Search PubMed.
- G. Füchsel, T. Klamroth, J. Dokic and P. Saalfrank, J. Phys. Chem. B, 2006, 110, 16337 CrossRef.
- S. Hagen, F. Leyßner, D. Nandi, M. Wolf and P. Tegeder, Chem. Phys. Lett., 2007, 444, 850.
- D. Geppert, L. Seyfarth and R. de Vivie-Riedle, Appl. Phys. B: Lasers Opt., 2004, 79, 987 CrossRef CAS.
- H. Umeda, M. Takagi, S. Yamada, S. Koseki and Y. Fujimura, J. Am. Chem. Soc., 2002, 124, 9265 CrossRef CAS.
- K. Hoki, S. Koseki, T. Matsushita, R. Sahnoun and Y. Fujimura, J. Photochem. Photobiol., A, 2006, 178, 258 CrossRef CAS.
- D. Kröner and B. Klaumünzer, Phys. Chem. Chem. Phys., 2007, 9, 5009 RSC.
- J. M. Lehn, Fortschr. Chem. Forsch., 1970, 311 Search PubMed.
- G. K. Paramonov and P. Saalfrank, Chem. Phys. Lett., 1999, 301, 509 CrossRef CAS.
- J. D. Swalen and J. A. Ibers, J. Chem. Phys., 1962, 36, 1914 CrossRef.
- S. F. Nelsen, J. T. Ippoliti, T. B. Frigo and P. A. Petillo, J. Am. Chem. Soc., 1989, 111, 1776 CrossRef CAS.
- A. M. Belostotskii, H. G. Gottlieb and M. Shakhen, J. Org. Chem., 2002, 67, 9257 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. O. Widmark, P. Å. Malmqvist and B. O. Ross, Theor. Chim. Acta, 1990, 77, 291 CAS.
- G. Karlström, R. Lindh, P. Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P. O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 (Revision C.02), Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- B. Klaumünzer, Diplomarbeit, Universität Potsdam, 2008, URL: http://opus.kobv.de/ubp/volltexte/2008/1748/ (URN: urn:nbn:de:kobv:517-opus-17482) Search PubMed.
- C. C. Marston and G. G. Balint-Kurti, J. Chem. Phys., 1989, 91, 3571 CrossRef CAS.
- B. Schmidt, Wavepacket: A program package for quantum-mechanic wave packet propagation, 1999 Search PubMed.
- M. D. Feit and J. A. Fleck, Jr, J. Chem. Phys., 1983, 78, 301 CrossRef CAS.
- J. D. Kemp and K. S. Pitzer, J. Chem. Phys., 1936, 4, 749 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS.
- K. Irikura, R. Johnson and R. Kacker, J. Phys. Chem. A, 2005, 109, 8430 CrossRef CAS.
- T. I. Solling, C. Kotting and A. H. Zewail, J. Phys. Chem. A, 2003, 107, 10872 CrossRef CAS.
- D. J. Tannor and S. A. Rice, J. Chem. Phys., 1985, 83, 5013 CrossRef CAS.
- D. J. Tannor, R. Kosloff and S. A. Rice, J. Chem. Phys., 1986, 85, 5805 CrossRef CAS.
- S. Chelkowski, A. D. Bandrauk and P. B. Corkum, Phys. Rev. Lett., 1990, 65, 2355 CrossRef CAS.
- D. J. Maas, D. I. Duncan, R. B. Vrijen, W. J. van der Zande and L. D. Noordam, Chem. Phys. Lett., 1998, 290, 75 CrossRef CAS.
- T. Witte, T. Hornung, L. Windhorn, D. Proch, R. de Vivie-Riedle, M. Motzkus and K. L. Kompa, J. Chem. Phys., 2003, 118, 2021 CrossRef CAS.
- D. Kröner and B. Klaumünzer, Chem. Phys., 2007, 338, 268 CrossRef.
- K. Husimi, Proc. Phys.-Math. Soc. Jpn., 1940, 4, 264 Search PubMed.
- E. Wigner, Phys. Rev., 1932, 40, 749 CrossRef CAS.
- H. J. Loesch and A. Remscheid, J. Chem. Phys., 1990, 93, 4779 CrossRef CAS.
- B. Friedrich and D. R. Herschbach, Nature, 1991, 353, 412 CAS.
- J. J. Larsen, K. Hald, N. Bjerre, H. Stapelfeldt and T. Seideman, Phys. Rev. Lett., 2000, 85, 2470 CrossRef CAS.
- K. Hoki and Y. Fujimura, Chem. Phys., 2001, 267, 187 CrossRef CAS.
- D. Kröner, B. Klaumünzer and T. Klamroth, J. Phys. Chem. A, 2008, 112, 9924 CrossRef.
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2009 |