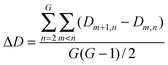The powerful law of the power law and other myths in network biology

Abstract

For almost 10 years, topological analysis of different large-scale biological networks (metabolic reactions, protein interactions, transcriptional regulation) has been highlighting some recurrent properties: power law distribution of degree, scale-freeness, small world, which have been proposed to confer functional advantages such as robustness to environmental changes and tolerance to random mutations. Stochastic generative models inspired different scenarios to explain the growth of interaction networks during evolution. The power law and the associated properties appeared so ubiquitous in complex networks that they were qualified as “universal laws”. However, these properties are no longer observed when the data are subjected to statistical tests: in most cases, the data do not fit the expected theoretical models, and the cases of good fitting merely result from sampling artefacts or improper data representation. The field of network biology seems to be founded on a series of myths, i.e. widely believed but false ideas. The weaknesses of these foundations should however not be considered as a failure for the entire domain. Network analysis provides a powerful frame for understanding the function and evolution of biological processes, provided it is brought to an appropriate level of description, by focussing on smaller functional modules and establishing the link between their topological properties and their dynamical behaviour.

---

Gipsi Lima-Mendez

Gipsi Lima-Mendez earned her BS degree in biochemistry at the University of Havana in Cuba. During those years she fell in love with the evolution of biological systems at the molecular level. With the advent of genomics, she decided bioinformatics would be her ‘lab tools' to address general questions in biology. She gained her PhD in Bioinformatics at the Université Libre de Bruxelles in Belgium. As a graduate student, she joined the lab of Professor Jacques van Helden and dedicated her doctoral research to the study of bacteriophage evolution. Bacteriophages (phages) are genetic mosaics resulting from homologous and illegitimate recombination with other phages and with the bacterial genomes. Because classical phylogenetic approaches do not apply to these systems, she used graph-analysis to model the evolutionary relationships between bacteriophages and designed a reticulate system for their classification. She also developed an algorithm to predict phage sequences in bacterial genomes (prophages). Currently, she is interested in the impact of bacteriophages on bacterial genome evolution, at the protein and regulatory levels.

Jacques van Helden

Jacques van Helden is currently Chargé de cours at the Université Libre de Bruxelles (Belgium) and head of the group “Genome and Network Bioinformatics”. He trained as a bioengineer with a PhD in developmental genetics. The main research activities of his group consist in implementing, evaluating and applying bioinformatics approaches to analyze regulatory sequences and molecular networks. They have developed software tools to detect cis-regulatory elements in genomic sequences (Regulatory Sequence Analysis Tools, http://rsat.ulb.ac.be/rsat/), to infer metabolic pathways using weighted path finding in metabolic networks, and to analyze molecular interaction networks (Network Analysis Tools http://rsat.ulb.ac.be/neat/).

---

Introduction

During the last 10 years, topological analyses have been applied to a variety of “real-world” networks such as World-Wide Web connections, scientist co-authoring, actor collaborations,^1,2 metabolic reactions,^3–6protein interactions,⁷ regulatory networks,^8–11 leading to seminal publications in the most reputed scientific journals. Typically, some statistical properties (node degree, inter-node distances, cliquishness, etc.) are computed on a given network and compared with their expected values according to a few theoretical models considered as the only possible alternatives. Interestingly, these networks were all found to bear a set of properties that distinguish them from random networks: power law degree distribution,² scale-freeness, and small world¹ (see Box 1 for definitions). These properties were reported for a wide variety of biological networks (metabolism, protein interactions, gene regulation), leading to the idea that “cellular networks are governed by universal laws”.¹²

Box 1. Network topology semantics

Node degree: number of edges linked to a node. The count can be restricted to incoming edges (in-degree), outgoing edges (out-degree) or include both (total degree).

Hub: highly connected node.

Distance: the distance between two nodes is the number of edges in the shortest path between them.

Node eccentricity: length of the longest of all shortest paths between a given node and any other node.⁶⁷

Characteristic path length: number of edges of the shortest paths between two nodes averaged over all pairs of nodes.¹

Network diameter: length of the longest among all shortest paths between node pairs. This is equal to the maximal eccentricity over all nodes of the network. Note that the term “diameter” has mistakenly been used to denote the average length of the shortest paths between all the pairs of nodes,⁵i.e. the characteristic path length.

Network radius: minimum value of eccentricity over all nodes.⁶⁷

Power law: a polynomial relationship between two quantities:

y = ax^k

where a and k are constants. The constant k is often referred to as the “power law exponent” or “scaling index”.¹⁷

Poisson distribution: discrete distribution defined by a single parameter λ (lambda), indicating its mean value.

Erdös–Renyi (ER): stochastic model generating graphs where each pair of nodes has the same probability of being linked by an edge. The degree distribution of ER graphs typically follows a Poisson distribution, as exemplified in Fig. 1C–F.

Scale-freeness: a probability function p(x) of a variable x is scale-free if, for any value of b, it satisfies the condition:

p(bx) = g(b)p(x)

where g(b) is a multiplicative constant depending on b. In words, the scaled and the original functions have the same shape. The only distribution satisfying that condition is the power-law (reviewed by ref. 68).

Clustering coefficient: the clustering coefficient of a node is the fraction of connections among all possible connections between its neighbours. In a non-directed graph without self-loops, a node has N neighbours, the number of possible connections between them is N(N − 1)/2.

Small world network: the term, coined by Watts and Strogatz, refers to networks that are highly clustered (high average clustering coefficient), like regular lattices, yet with small average shortest path length, like random networks.¹ The shortest distance between two vertices increases logarithmically with the number of nodes n (as for random graphs).⁶⁹ Humphries defines a parameter S to measure the small-worldness of a network.⁷⁰

S = C_g/C_r × L_r/L_g

Where C denotes the clustering coefficient and L the average path length of a graph, g is the graph of interest, and r is an ER-random graph of the same size as g. The graph g is qualified of “small-world network” if S > 1.

Interaction density and interaction density gradient: These measures were introduced recently¹⁹ to compare different proposed models of PPI network growth. Depending on the model attachment rule, a different pattern of connections will be observed between groups of nodes of different ages. For example, under the preferential attachment model, new nodes connect more likely to older nodes, since the latter have higher connectivity.

The interaction density D_m,n between two (age) groups m and n is the ratio of observed interconnecting edges between the groups (l_m,n) out of all possible edges between them (E_m,n), normalized according to the total number of edges (L) and nodes (N) in the network:

The average interaction density gradient (ΔD) of the network is calculated as the average of the differences in the number of connections of a group n to the consecutive groups m and m + 1, where 1 ≤ m < n ≤ G (G is the newest group and 1 the oldest):

Network modules: “Patterns of interconnections that recur in many different parts of a network at frequencies much higher than those found in randomized networks”⁴¹

Surprisingly, most initial claims about topological properties were proposed on the simple basis of graphical representations, but were contradicted as soon as the models were challenged by actual statistical tests.^13,14 Would the “universal laws” merely be myths according to the sensu lato definition, i.e. “widely held but false beliefs”?¹⁵

Furthermore, several hypotheses about the functional and evolutionary implications of those network properties are based on analyses led at a high abstraction level, but their relevance rapidly fades out as soon as the nodes (genes, proteins, metabolites) and their interactions are inspected with more details. Despite their elegance, the evolutionary scenarios derived by transposing theoretical generative models onto biological networks are reminiscent of the sensu stricto definition of myth, i.e. “a traditional story, esp. one concerning the early history of people or explaining some natural or social phenomenon”.¹⁵

Despite the lack of consistency between theoretical models and data, new papers are steadily published, suffering from the same flaws, in apparent ignorance of the serious concerns raised by several authors.^13,16–19 To justify the observed discrepancies between theoretical models and biological networks, some authors invoke the incompleteness of network annotations. When the “universal laws” are contradicted by the facts, the first reflex is to question the quality of the data rather than the validity of the models. We are thus in the typical situation of a dogma: “a principle or a set of principles laid down by an authority as incontrovertibly true”.¹⁵

In this article, we review the main concepts having emerged from topological analysis of biological networks, and discuss the controversial issues about their statistical validity, as well as their functional and evolutionary interpretation.

Myth 1: the degree distribution of biological networks follows a power law

In the literature on biological network topology, the power law is usually opposed to Poisson distribution, which would be expected from random graphs generated following the Erdös–Renyi (ER) model (Box 1). Surprisingly, the classical publications reporting the alleged power laws were only based on a visual inspection of degree distribution plots, without any attempt to actually fit a straight line over the observed data, and to test the goodness of the fit. It was only in 2006 that such a test was finally applied to 10 networks previously reported to follow a power law:¹³ this analysis revealed that none of them fits the theoretical distribution.

The illusion of the power law partly came from several representation issues. Firstly, in seminal articles,^5,12 the power law is illustrated by plotting the degrees (k) and their probabilities P(k) on logarithmic scales (inset of Fig. 1B), whereas the Poisson is illustrated with linear scale (inset of Fig. 1C). This way to oppose two models is obviously misleading: alternative distributions should be displayed consistently with the same scale, either linear (Fig. 1Aversus C or E) or logarithmic (Fig. 1Bversus D or F).

Fig. 1 Power law versus Poisson distributions. Random simulations based on various models (power law, Poisson) fitted with their respective theoretical distributions. A, B: power law function y = ax^γ with γ = −2.5 and a = 1, displayed with linear (A) and logarithmic (B) scales, respectively. C, D: Poisson fit on the degree distribution of a random ER graph with an average of 20 connections per node with linear (C) and logarithmic (D) scales. E, F: Poisson fit on a random ER graph with an average of 1 connection per node displayed with linear (E) and logarithmic (F) scales, respectively. On each graph, the dotted line represents the number N(k) of nodes having degree k, and the plain line the inverse cumulative distribution, i.e. number of nodes (iCumN) with degree greater than or equal to k. Insets B and C: in the seminal paper on the topology of metabolic networks,⁵ the power law was illustrated with logarithmic scales, whereas the Poisson law was depicted with linear scales, and with a high mean value.

Secondly, the illustration of the ER model is usually based on a Poisson distribution with a high expected mean (λ parameter), irrespective of the mean degree of the networks to be analyzed. However, this parameter has an important effect on the shape of the distribution: symmetrical bell shape for high λ values (Fig. 1C and D), but strongly asymmetrical for lower values (Fig. 1E and F). When contrasting the two a priori models, the λ parameter of the Poisson should thus be adapted to the mean degree of the observed network.

Another representation issue is that the degree values are sometimes regrouped by class intervals,⁵ thereby enforcing the apparent linearity on the log–log plot (inset of Fig. 2A), whereas displaying the raw distribution highlights the wide dispersion of the right tails (Fig. 2A), denoting the fact that the hubs are statistical outliers of the alleged power law. Indeed, when a straight line is fitted on the non-binned distribution (Fig. 2A, dotted line), the fit appears very poor, because its slope is strongly affected by the hubs. Strikingly, a better fit is obtained when we discard the 30 most connected nodes from the network (Fig. 2A, dashed line). The same trend is observed when the power law is fitted onto the inverse cumulative distribution rather than on the density function (Fig. 2B). Considering that the power law property of the metabolic networks has always been attributed to the presence of “hub compounds”, it is somewhat paradoxical that the fit looks valid only if those hubs are removed from the graph.

Fig. 2 Fitting of power law on the degree distributions of various biological networks. The abscissa represents node degrees (k), the ordinate the frequency of nodes having that degree (P(k)). Squares: density function; plain curve: inverted cumulative distribution function (iCDF); dotted: power law fitted onto the data; dashed: Poisson distribution fitted onto the data. A: metabolic network from the KEGG database, where nodes correspond to compounds, and their degree is the number of reactions in which they participate. Theoretical distributions fitted onto the density function. Note the discontinuity between the core of the distribution and its right tail, appearing as a bump on iCDF. Inset A: reproduction of the figure published to support for the power law character of metabolic networks.⁵ Note that the fact to regroup degrees into classes (“binning”) masks the discontinuity between the core of the distribution and its right tail. B: the same metabolic network with theoretical distributions fitted onto the iCDF. C, D: distributions of outgoing (C) and incoming (D) degrees in the regulatory network built from RegulonDB. Outgoing degrees (C) indicate the number of target genes per transcription factor. Incoming degrees (D) indicate the number of regulators per regulated gene. E, F: protein interaction networks from the high-throughput experiment of Gavin et al. (E)⁷³ and Krogan et al. (F),⁷⁴ respectively.

The fitting of a power law onto other types of networks is even less convincing. The analysis of the regulatory network of Escherichia coli reflects the presence of many specific transcription factors (having between 1 and 15 target genes) and some global factors involved in the regulation of many genes (Fig. 2C). The incoming degree distribution (Fig. 2D), which indicates the number of regulating factors per gene, shows an asymmetric bell-shaped distribution (square) which is reminiscent of Poisson law. It however shows a poor fit with the Poisson distribution (dashes-dots). Protein interaction networks obtained from high-throughput experiments display a curved shape (Fig. 2E and F), which can hardly be confused with the straight line expected from a power law.

In summary, careful analyses fail to confirm the power law distribution of degrees in biological networks. Even more, the variability between the degree distributions observed in different networks (metabolic, regulatory, protein interactions) rules out the hope to discover any universal law that would describe them altogether.

Myth 2: Biological networks are scale-free

Since the beginning of the above-mentioned wave of literature, some confusion has been maintained between the concepts of “power law” and “scale-freeness”, so that in many papers these two expressions are used in an almost interchangeable way. As pointed out in some reviews,^16,17,20 the concepts are generally not even defined.

A first remark is that scale-freeness does not apply to a network as a whole, but to some of its properties. In fact, to speak about “scale-free networks” is completely misleading since it would imply that a subset of the network would have an identical structure as the whole network (fractal images are the typical illustration of this concept).

It is thus important to specify which property of a network is supposed to be scale-free, and this is frequently not clear in the papers speaking about scale-freeness. The topological property that is generally claimed to be scale-free is the power law character of the degree distribution, and, in some articles, the scaling exponent (which corresponds to the slope of the regression line on the log–log graph). The scale-freeness of the power law has been tested by selecting random sub-networks from artificial networks whose degree distribution follows a power law. It has been shown that the degree distribution of such sub-networks retains the power law shape, but not the scaling exponent.²¹

Han and co-workers performed an extensive study of the effect of sampling on artificial networks generated with various degree distributions: Poisson (Erdös–Renyi model), exponential, power law, or truncated normal. Interestingly, they showed that sub-networks tend to exhibit a power law distribution, irrespective of the topological property of the larger network they were sampled from. They conclude that the apparent power law property observed in some biological networks might result from a sampling artefact, rather than reflecting some property of the complete network. The distribution of the complete network can thus not be estimated from the distribution of sub-networks, preventing to draw general conclusions about parameters estimated from incomplete datasets. This confirms that the concepts of “power law” and “scale-freeness” should not be considered as synonymous.

Myth 3: the metabolic network is a small world

Two independent studies^5,4 reported that metabolic networks display the small-world property (Box 1). Despite the large size of the network (regrouping a few thousands of compounds and reactions), both studies revealed that the distance between any pair of compounds averages around 3, with a very narrow range of variations (typically between 1 and 4 reactions), suggesting that metabolites could be inter-converted into each other in a very small number of steps. However, in the first study,⁵ shortest paths were searched in the raw metabolic network, where any compound is allowed to serve as intermediate to link two reactions. Consequently, most reported paths contain irrelevant shortcuts where pairs of reactions are linked via pool metabolites such as H₂O, O₂, H⁺, etc. (Table 1). Basically, this procedure predicts the single-step conversion of water into ethanol, thereby violating the mass conservation law (actually a law). Pool metabolites thus create irrelevant shortcuts that artificially confer a small-world property to metabolic networks.^22,23

Table 1 Example of paths using irrelevant shortcuts in the metabolic network. The table shows the 10 first paths from D-glucose to ethanol obtained by path finding algorithm^23,71 in the raw metabolic network. Note that all these paths are biochemically meaningless, because they use irrelevant shortcuts to link reactions via pool metabolites (H₂O, NADH)

Path number	Path
1	D-Glucose → R04094 → H2O → R02682 → ethanol
2	D-Glucose → R00300 → NADH → R00754 → ethanol
3	D-Glucose → R00534 → H2O → R02359 → ethanol
4	D-Glucose → R02558 → H2O → R02682 → ethanol
5	D-Glucose → R00304 → H2O → R02359 → ethanol
6	D-Glucose → R02558 → H2O → R02359 → ethanol
7	D-Glucose → R05142 → H2O → R02682 → ethanol
8	D-Glucose → R00534 → H2O → R02682 → ethanol
9	D-Glucose → R01444 → H2O → R02682 → ethanol
10	D-Glucose → R04006 → H2O → R02359 → ethanol

---

In another study,⁴ the obvious trap of the pool metabolites was avoided by suppressing a selection of “hub compounds” from the network. Path finding in such a filtered graph returns slightly more relevant pathways, but only when they comprise a small number of steps.^22,23

Alternative methods were designed to increase the relevance of the pathways inferred by path finding, by tracing the transfers of atomic groups between reactions,¹⁸ by weighting the graphs in order to penalize highly connected compounds,²³ or by restricting path finding to valid reactant pairs.^24,25 When path finding is adapted in such ways to better correspond to biochemical pathways, distances between compounds show a significant increase, indicating that the metabolic world is not so small.¹⁸

Myth 4: small worlds are tolerant to random deletions, but vulnerable to targeted attacks

Another common belief is that the small world character confers two properties to biological networks: robustness to random node deletions (also denoted as “error tolerance”) and sensitivity to hub removal (denoted as “attack vulnerability”).²⁶

The small diameter of metabolic networks was proposed to reflect the capability of cells to convert compounds into each other within a few reactions, thereby ensuring their robust response to environment variations.⁵ Error tolerance was related to the capability of living cells to survive random deletions of metabolic enzymes, whereas “attacks” targeted towards the hub compounds would “disintegrate [the network] into isolated clusters that are no longer functional”. As soon as we consider the nature of the nodes in the metabolic network, this rough transposition of computer network-derived properties onto metabolic networks is devoid of sense. Firstly, the tolerance to random deletions is far from trivial: the classical approach used by biochemists to discover enzyme-coding genes was to perform a random mutagenesis and to select mutants showing an auxotrophic phenotype . Such mutants lose their ability to synthesize a given compound, because the only path leading to this compound has been disrupted by the deletion of a single enzyme. Although the missing compound has generally very few links in the metabolic network, auxotrophy often results in lethality, unless the missing compound is provided in the culture medium. Metabolic networks are thus not so robust to random deletions.

The concept of “attacks” targeted to the hubs is even more questionable, because mutations affect genes (and thus the enzymes they code for), but cannot directly target metabolites. Pool metabolites appear as “hubs” in the metabolic network because they can be produced and consumed by several hundreds of different reactions, which are catalyzed by distinct enzymes. The suppression of a single hub like H₂O from the metabolic network would thus require deleting or inactivating several hundred enzyme-coding genes. After a handful of such mutations, the cell would already suffer from the depletion of its main enzymatic products (which are generally poorly connected compounds) and die, so that it is unconceivable to suppress, by natural or even directed mutations, a pool metabolite from the network. Thus, the concepts of error tolerance and vulnerability to attacks simply do not apply to metabolic networks.

In protein networks, the correspondence between mutations and node deletions is more straightforward than in metabolic networks. Jeong and co-workers showed that the hubs of PPIs correspond to essential proteins.⁷ By combining an analysis of network topology and temporal profiles of gene expression, Han and co-workers distinguish two subtypes among the highly connected proteins:²⁷ “party hubs interact with most of their partners simultaneously, whereas date hubs bind different partners at different times or locations”. The distinction between those subtypes is supported by an independent analysis of structural interfaces between proteins,²⁸ revealing that the relation between high degree and essentiality is stronger for proteins having multiple interaction interfaces (consistent with the concept of party hubs) than for those with only one interface (consistent with date hubs). It is not surprising that deletions of proteins involved in many interactions, either because they form large protein complexes or are involved in multiple processes, are likely to be deleterious. The apparent vulnerability of PPI networks to hub removal obviously results from the particular functions of each of these proteins and the biological processes in which they participate rather than to some general small world character they would confer to the network. In particular, it has to be noted that PPI networks integrate various types of interactions, going from stable protein complexes to transient interactions intervening in signal transduction pathways. Distance-related concepts such as pathway distance and “small worldness” may be relevant for signal transduction pathways, but these only represent a subset of the data. A deeper insight into the mechanisms underlying the relationship between topology and essentiality will thus require a case-by-case analysis of protein functions in the context of the processes in which they participate.

Myth 5: biological networks grow by preferential attachment

One way to generate artificial networks that follow a power law is to apply an algorithm where nodes and arcs are progressively added, with new nodes being preferentially attached to highly connected nodes (“rich gets richer”).^2,29 This generative model creates networks where initial differences are progressively amplified so that the first created nodes are more likely to become hubs (“older gets rich”).

Based on this generative model, several authors hypothesized that the power law structure of biological networks results from a tendency of new nodes (metabolites, proteins, genes) to establish interactions with more ancient nodes. Evelyn Fox Keller questions the general validity of this reasoning, since other models would as well generate networks with power law degree distributions, albeit their underlying topologies might be very different.¹⁶ There is thus a trivial logical fallacy under the reasoning: the fact that preferential attachment generates power law does not mean that power law implies preferential attachment (A → B ≠ B → A). The claim that a given biological network evolves by preferential attachment must thus be supported by other arguments than simply the shape of the degree distribution.

If we examine the raw metabolic network, preferential attachment can certainly not be considered as a general explanation for the top-ranking metabolites. The identity of the “hubs” (Table 2) provides a direct explanation for their high degree: they are either inorganic compounds (e.g.water, oxygen, CO₂, H₂O₂), or cofactors (ATP, NAD, SAM). Each of these molecules is involved in a specific type of chemical modification applied to a large diversity of substrates: H₂O is involved in hydrolysis and (de)hydration, ATP is the main currency for energy transfer, SAM is the methyl carrier, etc. Fell and Wagner proposed the preferential attachment model to metabolic networks from which pool metabolites had been filtered out: If, early in the evolution of life, metabolic networks grew by adding new metabolites, then the most highly connected metabolites should also be the phylogenetically oldest.^4,30 Indeed, this scenario seems reasonable for some of the highly connected compounds involved in intermediary metabolism, e.g.oxaloacetate, pyruvate, glutamate, as well as some amino acids pointed by the authors. A strict application of this model would however lead to impossibilities, since it would imply that ATP appeared before adenosine, S-adenosyl-L-homocysteine before cysteine, etc. The preferential attachment model may thus partly explain some relationships between central and peripheral metabolism, but should certainly not be considered as the reason for the topological properties of the network (hubs, degree distribution).

Table 2 Highly connected compounds and their metabolic function. In-degree and out-degree represent the number of reactions that produce or consume a given compound, respectively (data from KEGG/LIGAND http://www.genome.jp/ligand/)

Rank	ID	Name	In-degree	Out-degree	Total degree	Metabolic function (from ref. 72)
1	C00001	H2O	769	1444	2213	Hydrolysis, hydration
2	C00080	H+	809	460	1269	Proton pumps (e.g.respiratory chain, photosynthesis) and other redox reactions
3	C00007	Oxygen	43	817	860	Electron acceptor
4	C00006	NADP+	318	406	724	Coenzyme: electron acceptor
5	C00005	NADPH	405	316	721	Coenzyme: electron donor in anabolism
6	C00003	NAD+	160	503	663	Coenzyme: electron acceptor in catabolism
7	C00004	NADH	497	158	655	Coenzyme: electron donor
8	C00002	ATP	17	449	466	Coenzyme: energy donor
9	C00011	CO2	378	49	427	Last product of oxidation, precursor of photosynthesis
10	C00009	Orthophosphate	315	78	393	Product of ATP, ADP and AMP hydrolysis.
11	C00010	CoA	242	127	369	Coenzyme: universal acyl donnor
12	C00008	ADP	313	20	333	Product of ATP hydrolysis and substrate for ATP synthesis
13	C00014	NH3	253	43	296	Source of N for all organisms incapable of fixating N2. Product of aa and nucleotide catabolism, urea cycle.
14	C00013	Pyrophosphate	256	30	286	Product of ATP hydrolysis
15	C00019	S-Adenosyl-L-methionine (SAM)	6	239	245	Coenzyme: methyl donor
16	C00021	S-Adenosyl-L-homocysteine	227	9	236	Subproduct of methylation by SAM
17	C00015	UDP	216	6	222	Coenzyme: carrier of hexose groups
18	C00027	H2O2	142	21	163	Redox reactions
19	C00026	2-Oxoglutarate	33	125	158	Participates in the citric acid cycle. Transfer of amino groups in aa and nucleotide catabolism.
20	C00020	AMP	144	14	158	Product of ATP/ADP hydrolysis and substrate for ATP/ADP synthesis
21	C00022	Pyruvate	101	50	151	Final product of glycolysis and some aa metabolism, e.g., Ala, Cys, Ser. Gluconeogenesis.
22	C00024	Acetyl-CoA	35	101	136	Coenzyme: acetyl donor
23	C00025	L-Glutamate	83	46	129	Transfer of amino groups in reactions of aa and nucleotide metabolism, intermediate in Pro, Arg, Gln, His, degradation/biosynthesis, precursor of glutathione, ornithine, GABA, Ser and Gly biosynthesis (NH3 donor)
24	C00036	Oxaloacetate	29	14	43	Participates in the citric acid cycle and gluconeogenesis. Precursor of Asp. Produced by several anaplerotic reactions.

---

The preferential attachment model has also been proposed for protein interaction networks. Eisenberg and Levanon³¹ tested the validity of this model by partitioning all the proteins of the yeast Saccharomyces cerevisiae into 4 age groups, estimated from the taxonomical range in which they were found: Saccharomyces only, all fungi, fungi + plants, or fungi + plants + bacteria, respectively. Their study clearly shows that the average degree is higher for older than for newer proteins. A first concern should be raised about the design of this test. Even though the mean differences may differ between age classes, this is not a proof for the preferential attachment model. Indeed, since power law distributions are intrinsically characterized by the presence of statistical outliers (the “hubs”), the arithmetic mean is a poor estimator of the central tendency of the degree distribution. In other words, the fact that the mean degree is higher for proteins of older groups might result from the very high degree of a few ancient proteins (“hubs”) involved in primordial functions having evolved during early forms of life,^32,33 and would thus not support a general rule of preferential attachment.

Rather than comparing the means, the test should thus rely on the medians (which are robust to outliers and thus better suitable for highly skewed distributions), or, even better, on the whole distribution. Under the preferential attachment model, nodes would progressively acquire links during evolution, and the entire distribution would thus be shifted towards higher degrees for older proteins, as compared with newer proteins. As a matter of illustration, we analyzed the degree distributions per age group using a literature-curated (LC) and a high-throughput (HTP) PPI from a more recent study.¹⁹ The inverse cumulative distributions (Fig. 3) indeed reveal differences between age groups, but the relationship is not as simple as expected from a preferential attachment to the most ancient proteins. In the literature-curated network (Fig. 3B), the most recent proteins (found in fungi only) present the same distribution as the most ancient ones (those found in archaea, bacteria and eukaryotes), whereas a right-hand side shift is observed for proteins found in eukaryotes only, and in eukaryotes + archaea, respectively. The same trend is perceptible in the high-throughput network (Fig. 3C), even though the most ancient proteins show a slight increase in degree compared to the most recent ones. The fact that proteins found specifically in eukaryotes and/or archaea have more connections might result from an over-representation, in these datasets, of proteins involved in processes involving many protein interactions (e.g.cell cycle, transcription machinery, etc.).

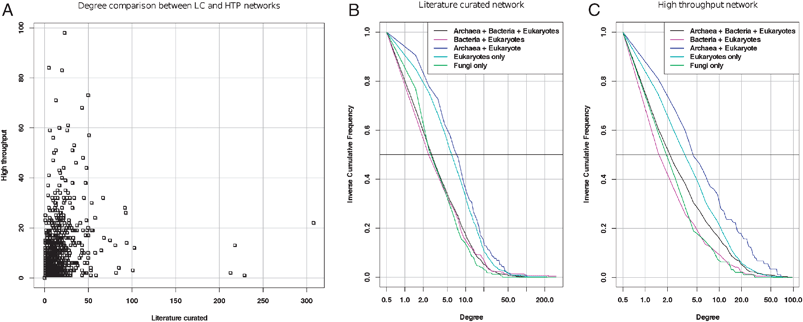Fig. 3 Degree distributions in the interactome for proteins of different classes of age (data from ref. 19). A: degree per protein in the literature-curated (abscissa) versus high-throughput (ordinate) networks. Note that the hubs are completely different between these two networks. B, C: inverse cumulative distributions (iCDF) of degrees of proteins partitioned into different age groups for the literature-curated (B) and high-throughput (C) network, respectively. The horizontal bar (Freq = 0.5) indicates the median degree of each age class (the abscissa of its intersect with each iCDF). The horizontal dotted line indicates the third quartile, which separates the 25% most connected from the 75% less connected nodes.

The duplication–divergence model (or families of models) explains the topology of protein interaction networks based on genetic mechanisms underlying genome evolution.^30,34–37 The hypothesis is that partial and/or whole genome duplications must have a direct impact on the evolution of protein interaction networks. Under this model, immediately after gene duplication, both duplicates interact with all the former neighbours of the parent gene. Later mutations in one of the redundant copies provoke a loss of some or all of its interactions. The model is supported by several observations: paralogous proteins are more likely to share partners than randomly chosen proteins,³⁴proteins sharing partners are more likely to be paralogs²⁸ and a proportion of protein complexes have similarities to other complexes.³⁸ However, the partners acquired by this mechanism alone would compete for the same (duplicated) interface.²⁸ Network rewiring is necessary to introduce novel interactions (rather than merely duplicate existing ones)³⁷ and is thought to occur mainly by exon shuffling of genes encoding for multimeric proteins.³⁴

Despite the popularity of the duplication–divergence model, no consensus exists yet on how the protein network evolves. Recently, four alternative generative models (preferential attachment, duplication–divergence, anti-preferential attachment and crystal growth) were compared in their capability to reproduce the topology and age-dependence of interaction patterns observed in the yeast protein interaction network.¹⁹ Age-dependence of interaction patterns of the real and simulated networks was evaluated using a measure of the interaction density (D) between different age groups and the network-wise propensity for a new node to connect with older nodes (average interaction density gradient, ΔD) (see Box 1 for definitions). The duplication–divergence model seems to reproduce the topology of the yeast PPI network but not its age-dependence interaction pattern. In the yeast PPI network, most links are made between proteins belonging to close age groups (ΔD > 0). This feature is only observed in the network generated following the crystal growth model (which is the only other reproducing the PPI network topology), although the pattern of interaction density between the different age groups does not reproduce that of the yeast network.

In summary, it seems that each of the generative models proposed so far captures a subset of the topological properties of protein interaction networks, but none of them is able to account for all topological aspects.

Outlook: beyond myths and dogmas

Given the numerous discrepancies between the theoretical models and the actual properties of biological networks, should we conclude that the domain of network biology has to be reconsidered as a whole? Despite our criticism in the previous sections, we believe that graph theory offers powerful methods for handling and analyzing the vast amounts of biological data resulting both from the accumulation of detailed studies as well as from high-throughput experiments. However, in order to gain insight into the way biological systems are organized and function, networks have to be considered under a different angle: (1) developing dedicated models for representing and analyzing biological processes; (2) focusing on local modules rather than on global distributions; (3) bridging the gap between static descriptions and dynamic behaviour of biological systems.

Developing dedicated models

Graph-based representations of molecular and chemical interactions undoubtedly provide synthetic views enabling computational analyses, which may eventually lead to increase our biological knowledge. However, knowledge will not emerge from the simple representation of biological data as dots and lines. A relevant interpretation requires a case-by-case adaptation of representations to the biological object under study.

This can for example be done by incorporating biochemical knowledge into metabolic networks: the relevant pathways can be inferred by tracing the exchanges of atom groups between compounds,³⁹ or by decomposing reactions into reactant pairs.^24,40 In PPI networks, the incorporation of structural analysis has already improved our understanding of the network evolution.²⁸

Ultimately, understanding the wiring of biochemical networks will sooner or later require us to integrate the different layers of biological processes (genetic, protein–protein, metabolic), and to map them onto the specific cellular compartment and tissues where they take place.

Focusing on local modules

Topological analysis of biological networks has been quite fertile if we consider the number of generative models that it inspired: preferential attachment, duplication–divergence, anti-preferential attachment, crystal growth, etc. Despite all these efforts, none of these models is able to capture all parameters of the topology, probably because this topology results from billions of years of interplay between organisms and their environments, which will never be captured by any stochastic model. The topology of current networks can probably better be explained as resulting from the integration of many distinct functional modules, whose individual topologies are anchored in functional constraints related to a particular biological process. Rather than spending our energy inventing ever more complex statistical models in order to reach the holy grail of the perfect fit with all the topological parameters, it would thus be more productive to analyze biological networks at a closer detail, and to understand the links between molecules at the level of functional modules, as well as the relationship between multiple modules on a network-wide scale. Networks become interpretable as soon as one makes the effort to zoom into their local structures, and inspect the molecular structures, interactions and reaction kinetics of the actor molecules.

Transcription regulatory networks were the first to be targeted from a module perspective. A systematic study of the transcription network of E. coli led to the identification of recurrent motifs⁴¹ (see Box 1 for the definition) that were further found in regulatory networks of other organisms (yeasts, plants and animals) and in other types of biological networks.⁴² The recurrent presence of these motifs in a variety of biological networks has been proposed to be due not only to conservation but also to convergent evolution under the effect of functional selection.^42,43 The criterion for considering that a motif is over-represented or not is itself debatable, and the significance of some recurrent motifs may have been over-estimated due to inappropriate null models for network randomization.^44,45 Nevertheless, such studies are of interest because they bring back the focus from global networks to local structures that can be related to specific information-processing units.

From static representation to dynamical modelling

Beyond the detection of recurrent modules, understanding the relationship between network architecture and function will imply to push the analysis to dynamical models, incorporating temporal and spatial dimensions.⁴⁶ Strangely enough, the network topology community seems to completely ignore the insights gained from several decades of mathematical biology, and barely cite any pre-2000 article.

Actually, the relationship between network motifs and their dynamical behaviour has been tackled by geneticists since half a century: the first network motifs to be discovered were the feedback loops, whose effect was characterized by experimental and theoretical analyses of small genetic networks. In their historical article on the Lac operon,⁴⁷ Jacobs and Monod not only demonstrated the existence of genetic regulation (repression), but also pointed out the essential role of the positive feedback to ensure multistationarity, i.e. the existence of two alternative cellular states (induced or repressed, respectively). In the early 70’s, Kauffman^48,49 and Thomas⁵⁰ modelled genetic networks with Boolean approaches. Thomas further defined a logical formalism based on multi-value variables that allowed him to systematically analyze the role of feedback loops in regulatory networks,^51,52 and demonstrated that the presence of positive feedback loops (i.e. a loop containing an even number of negative interactions) is a necessary condition to generate multistationarity (differentiation, cell memory), whereas negative feedback loops (odd number of negative interactions) ensure sustained oscillations and homeostasis (see ref. 53 for a recent review). The respective roles of positive and negative feedback loops are confirmed by innumerable examples of regulatory circuits involved in controlling metabolism, development, immune system, etc.

On the way back from theory to wet biology, mathematical modelling can also be the starting point to pinpoint a set of molecules and interactions that will be further studied using classical molecular genetics methods. Synthetic biology applies the theoretical concepts to design artificial genetic systems that can be empirically tested in living cells. Small circuits that we designed following this approach include a positive loop acting as a genetic toggle between two alternative stable states,⁵⁴ or a negative loop generating an oscillating behaviour.⁵⁵ Artificial regulatory interactions can also be inserted into existing biological systems in order to decipher their function and evolution, by engineering small circuits⁵⁶ or even rewiring the entire regulatory network.⁵⁷

Albeit the action of individual motifs on small genetic systems has been well described, much remains to be done before we understand the rules underlying the combination of multiple such motifs in large networks. A great challenge for the future will be to bridge the gap between mathematical modelling of small circuits and integrative analysis of large networks. Instead of considering network biology as a new and thus separate field, combination of graph theory with other established approaches in mathematical biology, and their confrontation with prior biological knowledge are critical elements if we aim to fully understand, model and design biological systems.⁵⁸

Abbreviations

ER	Erdös–Renyi
PPIs	Protein–protein Interactions
LC	Literature-curated PPI network
HTP	High-throughput PPI network

Acknowledgements

This work was supported by the Belgian Program on Inter-University Attraction Poles, initiated by the Belgian Federal Science Policy Office, project P6/25 (BioMaGNet), who funded the postdoc grant of Gipsi Lima-Mendez. The BiGRe laboratory is a member of the BioSapiens Network of Excellence funded under the sixth Framework program of the European Communities (LSHG-CT-2003-503265). We are grateful to Alejandra Medina-Rivera and Nicolas Simonis for discussions, comments and corrections on the manuscript, to Heladia Salgado-Osorio for providing the RegulonDB network, and to Karoline Faust for providing the metabolic network.

References and notes

1. D. J. Watts and S. H. Strogatz, Nature, 1998, 393, 440–442.
2. A. L. Barabási and R. Albert, Science, 1999, 286, 509–512.
3. D. Fell and A. Wagner, Structural properties of metabolic networks: implications for evolution and modelling of metabolism, in Animating the cellular map, ed. J. Hofmeyr, J. Rohwer and J. L. Snoep, Stellenbosch Univ. Press, Stellenbosch, 2000, pp. 79–85.
4. D. A. Fell and A. Wagner, Nat. Biotechnol., 2000, 18, 1121–1122.
5. H. Jeong, B. Tombor, R. Albert, Z. N. Oltvai and A. L. Barabasi, Nature, 2000, 407, 651–654.
6. E. Ravasz, A. L. Somera, D. A. Mongru, Z. N. Oltvai and A. L. Barabasi, Science, 2002, 297, 1551–1555.
7. H. Jeong, S. P. Mason, A. L. Barabasi and Z. N. Oltvai, Nature, 2001, 411, 41–42.
8. A. Bhan, D. J. Galas and T. G. Dewey, Bioinformatics, 2002, 18, 1486–1493.
9. M. M. Babu, N. M. Luscombe, L. Aravind, M. Gerstein and S. A. Teichmann, Curr. Opin. Struct. Biol., 2004, 14, 283–291.
10. N. M. Luscombe, M. M. Babu, H. Yu, M. Snyder, S. A. Teichmann and M. Gerstein, Nature, 2004, 431, 308–312.
11. S. H. Yook, F. Radicchi and H. Meyer-Ortmanns, Phys. Rev. E, 2005, 72, 045105.
12. A. L. Barabási and Z. N. Oltvai, Nat. Rev. Genet., 2004, 5, 101–113.
13. R. Khanin and E. Wit, J. Comput. Biol., 2006, 13, 810–818.
14. J. J. Daudin, F. Picard and S. Robin, Stat. Comput, 2008, 18, 173–183.
15. http://www.askoxford.com, Oxford University Press, 2005.
16. E. F. Keller, BioEssays, 2005, 27, 1060–1068.
17. L. Li, D. Alderson, J. C. Doyle and W. Willinger, Internet Math., 2005, 2, 431–523.
18. M. Arita, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 1543–1547.
19. W. K. Kim and E. M. Marcotte, PLoS Comput. Biol., 2008, 4, e1000232.
20. M. Arita, J. Biochem. (Tokyo), 2005, 138, 1–4.
21. M. P. Stumpf, C. Wiuf and R. M. May, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4221–4224.
22. J. van Helden, L. Wernisch, D. Gilbert and S. J. Wodak, Ernst Schering Res. Found. Workshop, 2002, 245–274.
23. D. Croes, F. Couche, S. J. Wodak and J. van Helden, J. Mol. Biol., 2006, 356, 222–236.
24. M. Kotera, M. Hattori, M.-A. Oh, R. Yamamoto, T. Komeno, J. Yabuzaki, K. Tonomura, S. Goto and M. Kanehisa, Genome Informatics, presented at the 15th International Conference on Genome Informatics, Yokohama Pacifico, Japan, 2004,.
25. M. Kotera, Y. Okuno, M. Hattori, S. Goto and M. Kanehisa, J. Am. Chem. Soc., 2004, 126, 16487–16498.
26. R. Albert, H. Jeong and A. L. Barabasi, Nature, 2000, 406, 378–382.
27. J. D. Han, N. Bertin, T. Hao, D. S. Goldberg, G. F. Berriz, L. V. Zhang, D. Dupuy, A. J. Walhout, M. E. Cusick, F. P. Roth and M. Vidal, Nature, 2004, 430, 88–93.
28. P. M. Kim, L. J. Lu, Y. Xia and M. B. Gerstein, Science, 2006, 314, 1938–1941.
29. E. Ravasz and A. L. Barabasi, Phys. Rev. E, 2003, 67, 026112.
30. A. Wagner, Mol. Biol. Evol., 2001, 18, 1283–1292.
31. E. Eisenberg and E. Y. Levanon, Phys. Rev. Lett., 2003, 91, 138701.
32. K. S. Makarova, L. Aravind, M. Y. Galperin, N. V. Grishin, R. L. Tatusov, Y. I. Wolf and E. V. Koonin, Genome Res., 1999, 9, 608–628.
33. N. Kyrpides, R. Overbeek and C. Ouzounis, J. Mol. Evol., 1999, 49, 413–423.
34. K. Evlampiev and H. Isambert, BMC Syst. Biol., 2007, 1, 49.
35. K. Evlampiev and H. Isambert, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9863–9868.
36. I. Ispolatov, P. L. Krapivsky and A. Yuryev, Phys. Rev. E, 2005, 71, 061911.
37. R. Pastor-Satorras, E. Smith and R. V. Solé, J. Theor. Biol., 2003, 222, 199–210.
38. J. B. Pereira-Leal and S. A. Teichmann, Genome Res., 2005, 15, 552–559.
39. M. Arita, Genome Res., 2003, 13, 2455–2466.
40. K. Faust, D. Croes and J. van Helden, J. Mol. Biol., 2009, 388, 390–414.
41. S. S. Shen-Orr, R. Milo, S. Mangan and U. Alon, Nat. Genet., 2002, 31, 64–68.
42. R. Milo, S. Shen-Orr, S. Itzkovitz, N. Kashtan, D. Chklovskii and U. Alon, Science, 2002, 298, 824–827.
43. R. Milo, S. Itzkovitz, N. Kashtan, R. Levitt, S. Shen-Orr, I. Ayzenshtat, M. Sheffer and U. Alon, Science, 2004, 303, 1538–1542.
44. Y. Artzy-Randrup, S. J. Fleishman, N. Ben-Tal and L. Stone, Science, 2004, 305, 1107; R. Milo, S. Itzkovitz, N. Kashtan, R. Levitt and U. Alon, Science, 2004, 305, 1107.
45. R. Milo, S. Itzkovitz, N. Kashtan, R. Levitt and U. Alon, Science, 2004, 305, 1107d,  DOI:10.1126/science.1100519.
46. R. P. Alexander, P. M. Kim, T. Emonet and M. B. Gerstein, Sci. Signaling, 2009, 2, pe44.
47. F. Jacob and J. Monod, J. Mol. Biol., 1961, 3, 318–356.
48. S. A. Kauffman, Science, 1973, 181, 310–318.
49. L. Glass and S. A. Kauffman, J. Theor. Biol., 1973, 39, 103–129.
50. R. Thomas, J. Theor. Biol., 1973, 42, 563–585.
51. R. Thomas and R. D'Ari, Biological feedback, CRC Press, Boca Raton, 1990.
52. R. Thomas, J. Theor. Biol., 1978, 73, 631–656.
53. D. Thieffry, Briefings Bioinf., 2007, 8, 220–225.
54. T. S. Gardner, C. R. Cantor and J. J. Collins, Nature, 2000, 403, 339–342.
55. M. B. Elowitz and S. Leibler, Nature, 2000, 403, 335–338.
56. S. Atsumi and J. W. Little, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19045–19050.
57. M. Isalan, C. Lemerle, K. Michalodimitrakis, C. Horn, P. Beltrao, E. Raineri, M. Garriga-Canut and L. Serrano, Nature, 2008, 452, 840–845.
58. Note: At the last moment of the revision of this article, the journal Science dedicated a special issue to Complex Systems and Networks, emphasizing a wide diversity of applications of network topology in biology,⁵⁹ ecology,⁶⁰ socio-ecology,⁶¹ economy,⁶² sociology⁶³ or counterterrorism^64,65 and warning over the importance of choosing the right network representation for the problem being addressed.⁶⁶.
59. A. L. Barabasi, Science, 2009, 325, 412–413.
60. J. Bascompte, Science, 2009, 325, 416–419.
61. E. Ostrom, Science, 2009, 325, 419–422.
62. F. Schweitzer, G. Fagiolo, D. Sornette, F. Vega-Redondo, A. Vespignani and D. R. White, Science, 2009, 325, 422–425.
63. A. Vespignani, Science, 2009, 325, 425–428.
64. J. Bohannon, Science, 2009, 325, 409–411.
65. J. Bohannon, Science, 2009, 325, 410–411.
66. C. T. Butts, Science, 2009, 325, 414–416.
67. L. Hakes, J. W. Pinney, D. L. Robertson and S. C. Lovell, Nat. Biotechnol., 2008, 26, 69–72.
68. M. E. J. Newman, Contemp. Phys., 2005, 46, 323–351.
69. L. A. Amaral, A. Scala, M. Barthelemy and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 11149–11152.
70. M. D. Humphries and K. Gurney, PLoS One, 2008, 3, e0002051.
71. S. Brohee, K. Faust, G. Lima-Mendez, O. Sand, R. Janky, G. Vanderstocken, Y. Deville and J. van Helden, Nucleic Acids Res., 2008, 36, W444–W451.
72. A. L. Lehninger, D. L. Nelson and M. M. Cox, Lehninger Principles of Biochemistry, W. H. Freeman, New York, 4th edn., 2005.
73. A. C. Gavin, P. Aloy, P. Grandi, R. Krause, M. Boesche, M. Marzioch, C. Rau, L. J. Jensen, S. Bastuck, B. Dumpelfeld, A. Edelmann, M. A. Heurtier, V. Hoffman, C. Hoefert, K. Klein, M. Hudak, A. M. Michon, M. Schelder, M. Schirle, M. Remor, T. Rudi, S. Hooper, A. Bauer, T. Bouwmeester, G. Casari, G. Drewes, G. Neubauer, J. M. Rick, B. Kuster, P. Bork, R. B. Russell and G. Superti-Furga, Nature, 2006, 440, 631–636.
74. N. J. Krogan, G. Cagney, H. Yu, G. Zhong, X. Guo, A. Ignatchenko, J. Li, S. Pu, N. Datta, A. P. Tikuisis, T. Punna, J. M. Peregrin-Alvarez, M. Shales, X. Zhang, M. Davey, M. D. Robinson, A. Paccanaro, J. E. Bray, A. Sheung, B. Beattie, D. P. Richards, V. Canadien, A. Lalev, F. Mena, P. Wong, A. Starostine, M. M. Canete, J. Vlasblom, S. Wu, C. Orsi, S. R. Collins, S. Chandran, R. Haw, J. J. Rilstone, K. Gandi, N. J. Thompson, G. Musso, P. St Onge, S. Ghanny, M. H. Lam, G. Butland, A. M. Altaf-Ul, S. Kanaya, A. Shilatifard, E. O'Shea, J. S. Weissman, C. J. Ingles, T. R. Hughes, J. Parkinson, M. Gerstein, S. J. Wodak, A. Emili and J. F. Greenblatt, Nature, 2006, 440, 637–643.

---

Footnote

† This article is part of a Molecular BioSystems themed issue on Computational and Systems Biology.

---