Computation of transient flow rates in passive pumping micro-fluidic systems†
I-Jane
Chen
,
Eugene C.
Eckstein
and
Ernő
Lindner
Department of Biomedical Engineering, The University of Memphis, Memphis, TN 38152, USA. E-mail: ijchen@memphis.edu; eckstein@memphis.edu; elindner@memphis.edu
First published on 20th October 2008
Abstract
Motion in micro-channels of passive flow micro-fluidic systems can be controlled by proper design and estimated by careful modeling. We report on methods to describe the flow rate as function of time in a passive pump driven micro-fluidic system. The model considers the surface energy present in small droplets, which prompts their shrinkage and induces flow. The droplet geometries are controlled by the micro-fluidic system geometry and hydrophilicity of the droplet channel contact area so that the chord of the droplet's cross section is restrained as the fluid is pumped. The model uses interfacial thermodynamics and the Hagen–Poiseuille equation for calculating the flow rate in micro-channels. Existing analyses consider the theoretical relationships among sample volume and induced flow rate, surface energy of the drops at the entrance and exit ports, and the resistance to flow. This model provides more specific information on the influence of the experimental conditions in computations of the flow rate. The model was validated in four sets of experiments. Passive pumps with 1.8 mm diameter, hydrophobic or hydrophilic entry ports, 5.0 or 10.0 mm channel length, and 2.5 or 3.3 mm diameter reservoir ports provided initial flow rates between 85 nL s−1 and 196 nL s−1.
Introduction
Various pumping methods have been developed for use with micro-fluidic systems.1–7 Although these methods can provide stable flow in a wide flow-rate range, they generally require bulky equipment, which is inconsistent with the simplicity of micro-fluidic systems. Burns et al. showed that it is possible to manipulate discrete drops inside microchannels8,9 for metering nanoliter volumes precisely and accurately. The integrated nanoliter DNA analysis device described by the authors worked without a conventional mechanical pump. Walker et al.10 proposed the use of the interfacial energy in small droplets to pump liquids through micro-channels. By placing a small liquid droplet over the hydrophobic sample port of a micro-channel, fluids could be pumped semi-autonomously and semi-continuously. The mathematical model established by the authors considered the contraction of spherical droplets (pumping droplets) in a concentric pattern and utilized the Young–Laplace equation to estimate the driving force of the flow. More recently Berthier et al.11 provided an analytical solution to describe the flow in passive pump driven micro-fluidic devices. The applicability of the analytical solution however is limited by restrictive model assumptions.To provide a generally applicable description of the passive pump driven flow in micro-channels, we report on numerical modeling of volume flow rate as function of time for different experimental conditions, i.e. system geometry, and the hydropobicity of the droplet-channel contact area. The model considers the surface energy present in small droplets, the hydrostatic pressure difference between input and output ports of the micro-fluidic device, and the hydrodynamic resistance of the liquid flow in a micro-fluidic channel of specified geometry. The surface energies are calculated by the original or a modified Young–Laplace equation while the hydrodynamic resistance is assessed by the Hagen–Poiseuille equation. The model provides the induced flow rate (sample volume change over time) as a function of the driving force (overall pressure difference generated by interfacial and hydrostatic energies), hydrodynamic resistance, and time.
Passive pump
A solution-filled micro-channel with liquid droplets on its entry (sample) and exit (reservoir) ports is considered a passive pumping device when the sample fluid is spontaneously driven from the entry port to the reservoir port (Fig. 1). During the pumping process potential and interfacial energies in the sample droplet are converted into kinetic energy and heat, which are dissipated to the environment.12 Simultaneously, the potential and interfacial energies in the reservoir droplet increase slightly. | ||
| Fig. 1 Front and end cross sectional views of the polydimethylsiloxane (PDMS)-based micro-fluidic system used in passive pumping experiments. | ||
Theory
| Ri = (hi2 + a2)/2hi | (1) |
| Vi = πhi (3a2 + hi2)/6 | (2) |
| Ai = π(a2 + hi2) | (3) |
 | ||
| Fig. 2 Schematic view of a droplet placed over a cylindrical entry port of a micro-fluidic device (a) and cross sectional snapshots of droplets sinking into cylindrical entry ports with different descent patterns: (b) concentric with decreasing cord length, (c) pseudo-concentric with fixed cord length, decreasing R, and descending center, (d) pseudo-concentric with fixed cord length, increasing R, and descending center. Consecutive time instances are labeled as ti, ti + 1, and ti + 2, r is the radius of the cylindrical entry port, a is the half chord length of the droplet, h is the height of the droplet above the surface of the micro-fluidic manifold, R is the radius of the droplet, O is the center of the droplet, Θ is the half-angle of the arc, ΔPi is the pressure difference measured from inside to outside, dhi, and dhi,j are distances the individual points of the air/water interface descent in a time interval Δt. The subscripts of O, R, and Θ correspond to the time instances ti, ti + 1 and ti + 2. | ||
If the contact ring (Fig. 2a) of the sample droplet remains constant as the droplet descends into the cylindrical entry port of the device, it is adequate to consider only the energy changes at the air/water interface and neglect the energy changes at the water/PDMS and air/PDMS interfaces since the areas of latter interfaces remain constant. The pseudo-concentric shapes of sample droplets, as shown during descent in Fig. 2c and d, are relevant examples. However, neglect of energy changes at the water/PDMS and air/PDMS interfaces cannot be justified when the area of the contact ring gradually decreases during the pumping process. The energy changes at the water/PDMS and air/PDMS interfaces can be important, during a concentric descent as shown in Fig. 2b. The patterns of sample droplet shape changes (e.g., concentric vs. pseudo-concentric or fixed cord vs. decreasing cord) are controlled by the experimental conditions (e.g., by the a/r ratio), and can merge into each other during the pumping process.11 For example, in the passive pumping device described in this paper the descent pattern of the droplet is the combination of the pseudo-concentric descents with decreasing and increasing radii. The descent starts in a pseudo-concentric fashion with gradually decreasing radius and continues in a pseudo-concentric fashion with increasing radius. In this paper we evaluate the validity of two models for calculating the passive pump driven flow rates in micro-channels. Both models are applied to experimental conditions in which the cord length of the sample droplet remains constant during the entire pumping process. These conditions are labeled as pseudo-concentric descents with decreasing or increasing radii (Fig. 2c and d).
Several pressure differences must be considered to compute the flow in a microfluidic channel. The one of primary concern is the pressure difference across the length of the channel, which occurs in response to the flow. This flow is induced by the shrinking sample droplet. The pressure in a droplet shrinking in concentric fashion (Fig. 2b) can be calculated with the Young–Laplace equation:
| ΔPi = 2γ/Ri | (4a) |
However, droplets in passive pumping experiments most commonly do not shrink in a strictly concentric fashion, i.e., their centers descend while their cord length remains fixed as shown in Figs. 2c and d. To apply the Young–Laplace equation for these conditions, the Ri values in eqn (4a) are calculated from the decreasing droplet volumes using eqn. (1) and (2).
Conversely, the formula for the pressure difference for droplets is no longer a simple expression if the conversion of interfacial energy Ei is calculated numerically from the changing shape of the descending droplet. The derivation of an appropriate expression (eqn (4b)) is provided in the ESI†:
 | (4b) |
Eqn (4b) can be considered as a modified Young–Laplace equation with rather complicated, specific expression for the radius of the droplet as a consequence of the sinking pattern. The radius of the droplet is used to calculate its surface area and volume. During the pseudo-concentric descent with decreasing and than increasing radii, the shape of the droplet above the entry port is continuously changing because as the center of the droplet sinks, the angle θ decreases concomitantly (Fig. 2c and d).
The overall pressure gradient (ΔPtotal) in the micro-fluidic system shown in Fig. 1 is governed by the pressure differences generated at the interfaces of the sample and reservoir droplets, ΔPs andΔPR, respectively, and the hydrostatic pressure difference, (ΔPH), due to the height difference of the liquid on the sample and reservoir sides of the micro-channel:
| ΔPtot = ΔPS − ΔPR + ΔPH | (5) |
Both ΔPS and ΔPR can be assessed with eqn (4a) or (4b) using the appropriate droplet geometries. The ΔPH hydrostatic pressure difference is a function of the height difference between the pumping (sample) and reservoir droplets. ΔPH changes simultaneously with the decrease of the sample and increase of the reservoir droplet volumes. At time instant ti the hydrostatic pressure difference can be expressed as:
| ΔPH = ρg(hS − hR) | (6) |
The flow rate (Qi) in a passive flow driven micro-fluidic device, can be calculated from the overall pressure gradient (ΔPtotal) across the flow path and the hydrodynamic resistance (Ω) of the micro-channel:
 | (7) |
where ΔVi = Vi–Vi + 1 is the volume change in a Δti = ti + 1 − ti time interval. The hydrodynamic resistance of a rectangular channel with close to unity width to height ratio (w/ĥ ≅ 1) under laminar flow conditions is:13
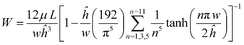 | (8) |
The changes in the sample volume and flow rate with time have been calculated by using a Matlab program. The volume of the droplet sinking into the entry port of the micro-channel has been computed for its initial value (ti = t0 and hi = hi,max) and following each 2 μm incremental change in the height of its apex (hi). The value of n in eqn. (8) was set to 11. With n = 11 the calculated hydrodynamic resistance has less than 0.001% error compared to its actual value (n = ∞).
Experimental
The micro-fluidic systems for this study were made with conventional techniques for soft lithography by casting Sylgard 184 (Dow Corning, MI) poly-dimethylsiloxane (PDMS) on a silicon master.14 After curing the PDMS replica of the master, its surface was treated in a 300 mTorr air plasma using PDC-32G plasma cleaner (Harrick Scientific, Pleasantville, NY) in combination with a Robinair model 15600 vacuum pump (SPX Corp. Montpelier, OH) and then bound to a flat, simultaneously treated PDMS surface to form the channel. This plasma treatment procedure increases the hydrophilicity of the PDMS-based micro-channels. However, this induced hydrophilicity is gradually lost. The rate at which the loss occurs depends on the environment in which the plasma-treated PDMS is stored. An air plasma treated PDMS retains its hydrophilic properties over a one month period when kept in contact with deionized water.15The passive flow micro-fluidic system shown in Fig. 1 has been tested in horizontal position. It has cylindrical entry and exit ports that are connected by a rectangular micro-channel. The nominal dimensions of the micro-channels were 5.0 or 10.0 mm long; 192 μm wide; and 96 μm high. The actual dimensions were measured with a Nikon Eclipse E600 (Nikon, Japan) optical microscope. The approximately 1 mm deep, cylindrical entry and exit ports (wells), perpendicular to the rectangular micro-channel, were created by punching the PDMS slab with a sharpened glass pipette. Inspection with a microscope showed that the punched edges were free of burrs. The diameter of the entry port was 1.8 mm; 2.5 and 3.3 mm diameter exit ports were utilized in the different experiments.
Air bubbles in the micro-channel induce unexpected resistance in the flow-through system.16 To prevent the appearance of trapped air bubbles in the micro-channel and the connected wells the micro-fluidic manifolds were first filled with methanol, which was subsequently replaced with deionized water. Deionized water (18.2 Mohm resistivity) provided by a Milli Q Gradient A-10 water purification system (Millipore, MA) was used in all experiments.
Once filled with deionized water the micro-channel is ready for passive pumping. In our protocol, first the volume of the reservoir droplet is set by adjusting its height to the required value (approximately 0.4 mm, representing ∼1.1 or ∼2.3 μL reservoir volumes for wells with 2.5 or 3.3 mm diameter, respectively). Next, a 2.5 μL sample droplet is placed onto the entry port of the device. With placing the sample droplet onto the entry port of the device the flow begins and the droplet's image is captured. Then images of the sample droplet are captured every second for a minimum of 60 s. The pumped sample volume is calculated from the acquired images. A VCA Optima Surface Analysis System (Advanced Surface Technology, Billerica, MA) with 7.3 μm pixel−1 resolution has been used for imaging the sample and reservoir droplets.
Parameters in our model calculations were the volumes of the sample and reservoir droplets, the channel geometry, and the viscosity (1 cP), density (0.998 g cm−3), and surface tension (72.88 dyn cm−1) of pure water.12 The validity of our model, especially its assumptions, has been tested in four sets of experiments (A, B, C, and D) that were designed to study the effect of the (i) hydrodynamic resistance, (ii) reservoir diameter and (iii) material properties of the channel on the induced flow rate. The volumes, heights and radii of the sample and reservoir droplets utilized in these four sets of experiments are summarized in Table 1, which also contains the pressure differences of eqn (5) that reflect the experimental conditions at time zero, the time instant when passive pumping process was initiated. In the first set of experiments, (row A), a 1.8 mm diameter sample port was connected to a 2.5 mm diameter reservoir port via a 5.0 mm long rectangular channel. In the second set of experiments, (row B), the dimensions of the sample and reservoir ports were the same as in experiments shown in row (A) of Table 1 but the channel length has been doubled from 5.0 to 10.0 mm to show the effect of the hydrodynamic resistance on the induced flow rate. In the third set of experiments, (row C), a 1.8 mm diameter sample port was connected to a 3.3 mm diameter reservoir port via a 5.0 mm long rectangular channel. So, by comparing the results of experiments shown in rows (A) and (C) the effect of increased reservoir port diameter on ΔPR and the induced flow rate could be demonstrated. Finally, in the fourth set of experiments, (row D), the dimensions of the micro-fluidic channel were the same as in experiments shown in row (A) of Table 1 but the entry port of the device was made somewhat hydrophilic through air plasma treatment. The differences in the induced flow rates in experiments summarized by data in rows (A) and (D) are related to the differences in the surface properties and geometries of the two micro-fluidic devices.
| Experiment | Channel length/mm | Droplet volume/μL | Droplet height/mm | Droplet radius/mm | Pressure differences derived from eqn (4a)a and (4b)b/dyn cm−2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Printed italic. b Printed bold. | |||||||||||
| V S | V R | h S | h R | R S | R R | ΔPs | ΔPR | ΔPH | ΔPtotal | ||
| A | 5.0 | 2.26 | 1.64 | 1.2 | 0.6 | 0.91 | 1.82 | 1602 | 801 | 59 | 860 |
| 1493 | 832 | 720 | |||||||||
| B | 10 | 2.49 | 1.12 | 1.3 | 0.4 | 0.92 | 2.13 | 1584 | 684 | 88 | 988 |
| 1513 | 700 | 901 | |||||||||
| C | 5.0 | 2.60 | 2.34 | 1.2 | 0.5 | 0.97 | 3.01 | 1503 | 454 | 69 | 1118 |
| 1457 | 503 | 1023 | |||||||||
| D | 5.0 | 2.97 | 1.09 | 1.1 | 0.4 | 1.17 | 2.21 | 1246 | 660 | 69 | 655 |
| 1259 | 671 | 657 | |||||||||
The pressure differences in Table 1 were calculated to show the different results by using the classical (eqn (4a)) or the modified (eqn (4b)) Young–Laplace equation for estimating the passive pump induced flow rate in micro-fluidic channels. The hydrodynamic resistances of a 5.0 and a 10.0 mm long channel, used in this work, were determined as 5.15 × 106 and 10.3 × 106 dyn s cm−5, respectively. The hydrodynamic resistances of the wells are six orders of magnitude less than that of the micro-channels, hence their contributions were neglected.
Results and discussion
On hydrophobic surfaces, water molecules tend to aggregate, the contact angle φ is larger than 90°, and a < h. In contrast, on hydrophilic surfaces water droplets tend to spread, φ is smaller than 90°, and a > h. The contact angles measured on the surfaces of the micro-fluidic devices used in this work were 112 ± 4° (hydrophobic) and 86 ± 1° (somewhat hydrophilic). The half chord lengths of 2.5 μL volume water droplets, placed over the entry ports of the hydrophobic devices (a = 1.0 mm), were about the same size as the radii of the wells (r = 0.95 mm). In contrast, on the slightly hydrophilic surfaces the sample droplets spread outside the wells, i.e., the half chord lengths of 2.5 μL volume water droplets (a = 1.16 mm), were larger than the radii of the wells (r = 0.98 mm). However, the cord length of the droplets on both the hydrophobic and hydrophilic PDMS surfaces remained nearly constant during the entire pumping process.The flow rate in a passive flow driven micro-fluidic device depends on the overall pressure difference (ΔPtotal) between the sample and reservoir ports of the micro-channel and the hydrodynamic resistance (Ω) of the micro-channel (eqn. (7)). The total pressure difference (eqn (5)) is governed by the pressure differences generated at the interfaces of the sample (ΔPS) and reservoir (ΔPR) droplets and the hydrostatic pressure difference (ΔPH). All three pressure differences change in time. The magnitude (Table 1) and time dependence (Fig. 3) of the individual pressure differences determine the time dependence of the passive pump driven flow rate in the micro-channel. The terms in eqn (5) can be calculated by eqn (4a) or (4b) (ΔPS and ΔPR) and eqn (6) (ΔPH). In this work, the advantages of using modified Young–Laplace equation (eqn (4b)) instead of its classical form (eqn (4a)) for calculating ΔPS and ΔPR and evaluating the passive pump induced flow rate in micro-fluidic channels is assessed in four sets of experiments. As we show in Table 1, the relative contribution of the individual pressure differences to ΔPtotal and the absolute values of ΔPtotal are strongly influenced by the experimental conditions, i.e., the volume of the sample and reservoir droplets and the dimensions of the sample and reservoir wells. Similarly, the difference in the ΔPtotal values calculated with eqn (4a) and (4b) depend on the experimental conditions. The differences between the values calculated with eqn (4a) or (4b) were the largest (around 20%) in the row (A) experiments in Table 1. The time dependences of the individual pressure differences and ΔPtotal are shown in Fig. 3 for the experimental conditions summarized in row (A) in Table 1. From the data in Table 1 and Fig. 3 it is obvious that the pressure difference generated by the surface tension at the reservoir droplet (ΔPR) and the hydrostatic pressure difference (ΔPH) are significant and cannot be neglected when the overall pressure difference (ΔPtot) is determined. The error in ΔPtotal can be greater than 50% when the contributions of ΔPR and ΔPH are disregarded in the calculations. Likewise, ΔPR and ΔPH should not be assumed constant. As shown in Fig. 3, the time dependent changes in ΔPR and ΔPH significantly influence the time course of ΔPtotal.
 | ||
| Fig. 3 The time dependence of the individual pressure differences (eqn (4b) and (6)) and the total pressure difference (eqn (5)) in a passive flow driven micro-fluidic system. The experimental conditions are in row (A) in Table 1. ΔPS and ΔPR are pressure differences generated at the interfaces of the sample and reservoir droplets, ΔPH is the hydrostatic pressure difference related to differences in the height of the sample and reservoir droplets and ΔPtot is the total pressure difference calculated by eqn (5). The images of the droplets correspond to time instances marked on the top of the figure. | ||
In Fig. 4(a) through 4(d) the sample droplet volumes assessed from captured images and calculated by using different models are compared as a function of time. The experimental conditions utilized in recording the data of Fig. 4a through 4d correspond to the experimental conditions in rows (A) through (D) in Table 1. In the figures the circles represent the volumes calculated from the captured images of the sinking droplets. The solid lines represent droplet volumes calculated with our computational model by utilizing eqn (4a) or eqn (4b) in combination with eqn (5). Finally, the diamonds (labelled as B & B) represent computed volumes based on the model of Berthier's et. al.11 The images in Fig. 4e are shown to prove the validity of the assumption of constant chord lengths for the sample droplet in our computational model. These images were captured at t= 0, 8 and 35 s after the passive flow in the micro-fluidic device has been initiated. Similar to Fig. 4(e), in all of our experiments the half chord lengths of the sample droplets remained practically constant during the entire pumping process or its decrease remained always below 1%.
 | ||
| Fig. 4 Comparison of the experimentally measured (circles) and computed sample droplet volumes in four sets of experiments. The solid lines were calculated by utilizing the traditional Young–Laplace equation (eqn (4a), labeled as YL) or its more complex form (eqn (4b) labeled as m-YL) in combination with eqn (5), respectively. The diamonds (labelled as B & B) represent the computed results based on the model Berthier and Beebe.11 (a) 5.0 mm hydrophobic PDMS channel with 2.5 mm diameter reservoir port (b) 10.0 mm hydrophobic PDMS channel with 2.5 mm diameter reservoir port. (c) 5.0 mm hydrophobic PDMS channel with 3.3 mm reservoir port (d) 5.0 mm hydrophilic PDMS channel with 2.5 mm diameter reservoir port. (e) Images of sample droplets captured during the experiment shown in eqn (4a). | ||
A striking aspect of Fig. 4 is the difference between the quality of the description of the experimental data with the computational models and with the analytical description obtained by Berthier et al.11 This difference is assumed to be related to differences in the experimental conditions. In the work of Berthier et al. the radii of sample and reservoir ports were much smaller than the half chord length of the droplets and the volume of the reservoir droplet was much larger than that of the sample droplet. Due to the large difference in the volumes of the sample and reservoir droplets Berthier assumed that changes in ΔPR can be neglected. For the same reason, changes in the hydrostatic pressure differences (ΔPH) caused by the height difference between sample and reservoir droplets were ignored. These assumptions are not met for the experimental conditions used in this work (see Table 1 and Fig. 4), but the conditions of the experiments are suited to practical lab-on-a-chip devices. Indeed, neglecting changes in ΔPR and ignoring changes in ΔPH could have a significant influence on ΔPtot and the calculated flow rates even in systems with large reservoir droplet volumes (e.g. VS = 2.5 μL and VR = 20.0 μL). Large reservoir droplets were avoided in this work because above 10 μL the shapes notably diverged from the ideal spherical shape, and this shape could not be taken into account in our computational model.
In contrast to Berthier's model11 our computational approach provides a reasonable match between measured and calculated volumes. However, in three of the four examples discussed in this paper (Figs. 4(a), (b) and (c) corresponding to rows (A), (B) and (C) in Table 1) the computed volumes decreased somewhat faster than the experimentally measured ones, i.e., the actual flow rates were smaller than predicted by the model. The reasons for the differences between the computed and measured rate of change in the sample volume (Figs. 4(a) ,(b) and (c)) are not clear. The inaccuracies in estimating the dhi,j values (Fig. 2(d)) with a cosine function as discussed in the ESI† (eqn S1) could be an explanation. Hardly visible air bubbles trapped in the micro-channel may have increased the hydrodynamic resistance of the system, which is a factor that was not considered in our model. Similarly, a slight slope of the channel was not considered in our model although the perfect horizontal placement of the channel could not be unambiguously assured in our protocol. Small slopes can slow or enhance the experimentally recorded flow rates. Finally, evaporation related losses in the sample and reservoir droplet volumes can play a role in the measured flow rates. This factor was neglected in this work because in control experiments the mass losses from 2.5 μL volume deionized water droplets were always below 5% in the time frame of our experiments.
As shown in Table 1 the various experimental conditions generate different pressure differences which in turn produce different flow rates in the micro-fluidic manifolds (Fig. 4 and 5). For example, a 2.5 μL volume sample droplet generated 150 nL s−1 initial flow rate (Fig. 5(a)) in a 5.0 mm long micro-channel channel with a 2.5 mm diameter reservoir port. The influence of the channel resistance on the generated flow rate can be seen by comparing the flow rates generated in 5.0 and 10.0 mm long flow channels (Figs. 5(a) and (b)). In agreement with the expectations, the same 2.5 μL volume sample droplet generated about half of the initial flow rate in the 10.0 mm long (85 nL s−1) channel than in the 5.0 mm (150 nL s−1) long one. The influence of the reservoir diameter on the induced flow rate can be assessed by comparing Fig. 5(a) and (c). Increasing the diameter of the reservoir well decreases ΔPR and increases ΔPtot. When the diameter of the reservoir well was increased from 2.5 to 3.3 mm a 2.5 μL sample droplet generated 196 nL s−1 initial flow rate (Fig. 5(c)) instead of 150 nL s−1 (Fig. 5a) in the same length of channel. The effect of the surface properties of the micro-fluidic manifold on the generated flow rate can be evaluated by comparing the Fig. 5(a) and (d). Over hydrophilic entry ports, the sample droplets have bigger radii which mean decreased ΔPS compared to hydrophobic entry ports. Consequently the induced flow rates in such systems are expected to be smaller. Indeed, when 2.5 μL sample droplets were placed over the hydrophilic entry port of a 5.0 mm long channel they induced only 121 nL s−1 initial flow rate (Fig. 5(d)).
 | ||
| Fig. 5 Experimentally measured (circles) and computed volumetric flow rates in four sets of experiments. The solid lines were computed by utilizing eqn (4a) and (4b) in combination with eqn (5) and (7), and are marked as (YL) or (m-YL), respectively. Where the lines ran on the same path they are labeled as (YL and m-YL). The experimental conditions were the same as in Fig. 4 and are summarized in Table 1. | ||
Similar to the ΔPtotvs. time curve (Fig. 3), the computed flow rate vs. time curves in Fig. 5(a), (b) and (c) have three well defined phases with transition times that are strongly correlated with the shape changes in the “pumping” (sample) droplet (pseudo-concentric descent). These shape changes can be characterized as changes in the radius of the droplet. The first transition time appears at the curves when the pumping droplet has a minimum radius and ΔPS peaks (around 8 s in Fig. 3). After the first transition phase, the radius of the droplet gradually increases, with simultaneous gradual decrease in ΔPS, ΔPtot and induced flow rate. The flow stops when ΔPtot drops to zero (second transition time around 25 s in Fig. 3), i.e., when the system reaches equilibrium. On the surface of a hydrophilic channel (Fig. 5(d)) the radius of the sample droplet continuously increases as the droplet sinks into the sample well (pseudo-concentric descent with increasing radius as shown in Fig. 2(d)). Consequently, ΔPS, ΔPtot and the induced flow rate continuously decreases without an apparent transition time.
Based on the data summarized in Table 1 and Figs. 4 and 5, it is clear that the use of the more complex computational approach (eqn (4b) instead of eqn (4a)) is not essential for all experimental conditions. Indeed, in two of the four sets of experiments (Figs. 4(c) and (d)), the curves calculated with the different models were indistinguishable. The differences between the two computational approaches (eqn (4a) and (4b)) become more noticeable by plotting the calculated flow rates vs. time (Fig. 5). Although the more complex computational model seems to provide somewhat better fits, its advantages could not be proved unambiguously due to the relatively large standard deviation of the experimental data. The large standard deviations of the experimental data points in Fig. 5 are the consequences of the limited resolution of the digital camera utilized to capture images of the sample droplets sinking into the input port of the device, and the non-linear equation (eqn (2)) used to calculate the droplet volumes from the captured images. A single pixel difference in the digital camera reading can easily change the calculated flow rate by 50%. For example, the calculated flow rate of the data point marked with the filled circle (5.5 s, 46 nL s−1) in Fig. 5(b) would increase from 46 nL s−1 to 69 nL s−1 when the reading of the height of the sinking droplet was changed from 155 to 156 pixels.
Conclusion
Passive pumps can provide low flow rates with good reproducibility. The induced flow rates can be controlled by the material (hydrophobic vs. hydrophilic) and geometrical properties of the channel (shape, height, length and slant), the sample and reservoir wells (diameter) and the sample and reservoir droplets (volume, surface tension, density and viscosity). A computational model has been derived to describe the time dependent flow rate in a passive pump driven micro-fluidic system. The effects of the experimental parameters on the calculated flow are demonstrated. The results from the computational model are consistent with experimental results measured in micro-fluidic systems with different channel length (5.0 and 10.0 mm), reservoir well diameter (2.5 and 3.3 mm) and surface properties (hydrophobic or hydrophilic). The mathematical model is expected to help in designing passive flow driven micro-fluidic systems with required flow conditions.Acknowledgements
This work has been supported by the NIH/NHLBI grant # 1 RO1 HL079147-01.References
- H. Andersson, W. von der Wijngaart, P. Nilsson, P. Enoksson and G. Stemme, Sens. Actuators, B, 2001, 72, 259–265 CrossRef.
- S. Bohm, W. Olthuis and P. Bergveld, Sens. Actuators, A, 1999, 77, 223–228 CrossRef.
- B. S. Gallardo, V. K. Gupta, F. D. Eagerton, L. I. Jong, V. S. Craig, R. R. Shah and N. L. Abbott, Science, 1999, 283, 57–60 CrossRef CAS.
- B. Good, C. Bowman and R. Davis, J. Colloid Interface Sci., 2004, 14, 239–249.
- M. Khoo and C. Liu, Sens. Actuators, A, 2001, 89, 259–266 CrossRef.
- B. J. Kirby and E. F. Hasselbrink, Electrophoresis, 2004, 25, 187–202 CrossRef CAS.
- T. Vestad, D. W. M. Marr and J. Oakey, J. Micromech. Microeng., 2004, 14, 1503–1506 CrossRef.
- K. Handique, D. T. Burke, C. H. Mastrangelo and M. A. Burns, Anal. Chem., 2000, 72, 4100–4109 CrossRef CAS.
- M. A. Burns, B. N. Johnson, S. N. Brahmasandra, K. Handique, J. R. Webster, M. Krishnan, T. S. Sammarco, P. M. Man, D. Jones, D. Heldsinger, C. H. Mastrangelo and D. T. Burke, Science, 1998, 282, 484–487 CrossRef CAS.
- G. M. Walker and D. J. Beebe, Lab Chip, 2002, 2, 131–134 RSC.
- E. Berthier and D. Beebe, Lab Chip, 2007, 7, 1475–1478 RSC.
- A. W. Adamson, A Textbook of Physical Chemistry, Academic Press, New York, 1979 Search PubMed.
- F. White, Viscous Fluid Flow, McGraw-Hill, Rhode Island, 2006 Search PubMed.
- S. K. Sia and G. M. Whitesides, Electrophoresis, 2003, 24, 3563–3576 CrossRef CAS.
- I. J. Chen and E. Lindner, Langmuir, 2007, 23, 3118–3122 CrossRef CAS.
- H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381–411 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Derivation of modified Young–Laplace equation and calculation of geometrical parameters of sample and reservoir droplets. See DOI: 10.1039/b808660e |
| This journal is © The Royal Society of Chemistry 2009 |
