Comprehensive analysis of particle motion under non-uniform AC electric fields in a microchannel†
Jonghyun
Oh
*a,
Robert
Hart
*b,
Jorge
Capurro
a and
Hongseok (Moses)
Noh
c
aDepartment of Mechanical Engineering and Mechanics, Drexel University, 3141 Chestnut St., Philadelphia, PA 19104, USA. E-mail: jo72@drexel.edu; Tel: +1 215 895 2174
bDepartment of Biomedical Engineering, Science & Health Systems, Drexel University, 3141 Chestnut St., Philadelphia, PA 19104, USA. E-mail: rw58@drexel.edu; Tel: +1 215 895 2261
cDepartment of Mechanical Engineering and Mechanics, Drexel University, 3141 Chestnut St., Philadelphia, PA 19104, USA. E-mail: mosesnoh@coe.drexel.edu; Tel: +1 215 895 2273
First published on 21st October 2008
Abstract
AC electrokinetics is rapidly becoming a foundational tool for lab-on-a-chip systems due to its versatility and the simplicity of the components capable of generating them. Predicting the behavior of fluids and particles under non-uniform AC electric fields is important for the design of next generation devices. Though there are several important phenomena that contribute to the overall behavior of particles and fluids, current predictive techniques consider special conditions where only a single phenomenon may be considered. We report a 2D numerical simulation, using COMSOL Multiphysics, which incorporates the three major AC electrokinetic phenomena (dielectrophoresis, AC electroosmosis and electrothermal effect) and is valid for a wide range of operational conditions. Corroboration has been performed using experimental conditions that mimic those of the simulation and shows good qualitative agreement. Furthermore, a broad range of experiments has been performed using four of the most widely reported devices under varying conditions in order to show their behavior as it relates to the simulation. The large number of experimental conditions reported, together with the comprehensive numerical simulation, will help provide guidelines for scientists and engineers interested in incorporating AC electrokinetics into their lab-on-a-chip systems.
Introduction
AC electrokinetic phenomena such as dielectrophoresis (DEP), AC electroosmosis (ACEO), and electrothermal effect (ETE) are rapidly becoming an indispensable technology for microfluidic devices and lab-on-a-chip systems. Since Pohl discovered the phenomena in the 1970’s,1 DEP has been explored for the manipulation of micro- and nanoscale particles such as polymer micro/nanospheres,2–4cells,5–9 bacteria,10 viruses,11DNA,12 and carbon nanotubes.13ACEO is a relatively newly discovered phenomenon14–16 and it has been applied mainly for fluid and chemical species mixing applications in low Reynolds number flows in microchannels.17–19 It has also been shown capable of generating bulk flow in microchannels using assymetric electrode arrays.20,21ETE has also been applied for mixing applications in a microfluidic device.19AC electrokinetic particle manipulation is readily achieved in a microchannel via non-uniform electric fields generated by microfabricated planar electrodes. (Though the use of dielectric material to cause electric field perturbations has been shown as well.)22 High electric fields required for particle motion (104–106 V m−1) can be easily achieved with only a few volts since the electrode gap is micro- or nanoscale. The electrolysis of water is avoided since AC power is applied. Moreover, each of the electrokinetic and electrohydrodynamic (EHD) forces has fairly distinct characteristics and as a result various types of particle motion can be achieved by simply varying operational conditions.23 This convenience and versatility make AC electrokinetics the most suitable particle manipulation technique for microfluidic devices compared with other techniques such as optical tweezers,24,25 ultrasonic techniques,26 and magnetic techniques.27–29
In order to fully leverage the capabilities of devices which use AC electrokinetics a comprehensive understanding of the varied and competing forces is required. So far, most studies have only analyzed and simulated a single phenomenon alone. However, it is only under certain circumstances that one phenomenon predominates and all others may be ignored. It is therefore necessary to consider several of the AC electrokinetic phenomena together since they often compete with each other under a wide range of conditions. This paper presents numerical studies that consider all major relevant forces and compares the simulation results with experimental data. The experimental study includes the use of several different device designs and considers the major operational parameters to show the numerous particle behaviors possible. In this way, a comprehensive analysis of particle motion under non-uniform electric fields in a microchannel has been performed. The analysis reported in this article will help further the efforts of scientists and engineers who wish to control the behavior of micro- and nanoparticles in microfluidic environments using AC electrokinetics. It is our hope that this presentation may provide insight and design guidelines to the lab-on-a-chip community.
AC electrokinetics phenomena
The wide range of particle behavior under non-uniform AC electric fields is a result of the numerous physical processes (interfacial polarization, electric double layer formation, fluid heating, etc.) that occur at both the electrode and particle surface. The three predominant AC electrokinetic phenomena that result are DEP, ACEO and ETE. This section provides a brief introduction to these forces.DEP occurs when a particle is subject to a non-uniform electric field. The particle will experience a net force either in the direction of higher electric field strength (positive DEP) or lower electric field strength (negative DEP) due to the relative polarizability between the particle and the surrounding media. Both the magnitude and direction of the force is determined by factors such as the electrical conductivities and permittivities of media and particle, particle size, and both the frequency and strength of the electric field. In the case of microfabricated planar electrodes, particles will accumulate at the edges of the electrode under positive DEP, or they will be repelled from this region and travel towards low electric field strength under negative DEP (Fig. 1(a)).
 | ||
| Fig. 1 Predominant AC electrokinetic behaviors. (a) Dielectrophoresis (DEP), (b) AC electroosmosis (ACEO), and (c) Electrothermal effect (ETE). | ||
Unlike DEP, both ACEO and ETE are hydrodynamic phenomena and cause fluid motion, which brings suspended particles along with it. ACEO is the motion of fluid due to an interaction between an electric field and the electrical double layer (EDL) induced at the electrode surface. If the electric field at this surface contains a tangential component (Et), the ions in EDL will traverse laterally and drag the fluid along (Fig. 1(b)). In the case of planar electrodes, a continuous and easily recognizable rotational fluid pattern emerges. This pattern, which can be described as a set of counter rotating vortexes, may cause particles to orbit out of plane near the electrodes or cause them to collect on the electrode itself.
ETE is caused by temperature gradients induced by joule heating. These temperature gradients create fluctuations in the electrical conductivity and permittivity of the fluid. These fluctuations, in turn, induce fluid motion through their interaction with the electric field (Fig. 1(c)). Like ACEO, electrothermally driven fluid flow can be rotational in nature.
Each of the AC electrokinetic phenomena causes dramatic, organized and often rapid particle motion. With larger particles (greater than 1 μm), collection may occur within seconds and particles may move at hundreds of microns per second. Typically, DEP and ACEO are both used for particle collection and active mixing applications can be performed using ACEO and ETE. An important factor that has great control over the application and the possible AC electrokinetic phenomena that may be used is media conductivity. High conductivity media that is physiologically relevant prohibits positive DEP and ACEO. (This will be further discussed in the Theory section.)
Besides AC electrokinetics, there are several other well studied phenomena that are known to act upon particles suspended in microfluidic environment. Brownian motion, buoyancy, gravity, and natural convection all play roles to some extent.
Theory
Dielectrophoresis
The dielectrophoretic force acting on a particle is caused by the interfacial polarization between the particle and the media in a non-uniform electric field. For the case of a solid sphere, the effective dipole moment (p) is expressed as | (1) |
 | (2) |
| 〈FDEP〉 = (p·∇)E = 2πr3εmRe[CM]∇|Erms|2 | (3) |
The CM factor is determined by the three dimensional particle geometry (interior as well as exterior) and by the properties of its constituent materials. In many cases it is difficult to determine an exact expression for an object (for example a Eukaryotic cell, which is composed of many layers of different materials of varying thickness) and the function must be ascertained experimentally.
Fig. 2 shows how the CM factor varies as a function of frequency and media conductivity for both a solid sphere and for a shell structure. For a given particle, the Clausius–Mossotti factor is a function of frequency of the applied electrical signal and the conductivity of the media in which the particle is suspended. For a solid polystyrene sphere with a diameter of 2 μm (Fig. 2(a)), the three different media conductivities shown dramatically change the shape of the CM factor. At low conductivity, it is possible to induce positive DEP (Re[CM] values greater than 0), where particles are attracted to an electrode edge or other high density electric field areas. This occurs at low frequencies and transitions to negative DEP at high frequencies, where particles will be forced into regions of low electric field strength. For example, particles may accumulate where electric field minima exist, such as on the center of the electrode, between electrodes or may even levitate above the electrodes. As the conductivity is raised, the strength of positive DEP becomes diminished and will eventually disappear completely, to be replaced with negative DEP for any applied frequency.
 | ||
| Fig. 2 Clausius–Mossotti factor as a function of frequency and media conductivity for (a) a solid 2 μm diameter polystyrene sphere (particle permittivity = 2.5ε0), (b) a solid 200 nm diameter polystyrene sphere (particle permittivity = 2.5ε0), and (c) a shell structure modeled on Chlorella sp. (surface capacitance = 12.4 × 10−3 S, radius = 3.29 × 10−6 m, inside conductivity = 8 × 10−3 S m−1, inside permittivity = 150ε0).9 For all cases, a media permittivity of 80.2ε0 was used. | ||
Since the conductivity of a solid particle is the sum of the bulk and surface conductivities, changing the size of a particle changes its overall conductivity. A solid polystyrene sphere with a diameter of 200 nm (Fig. 2(b)) therefore has a different CM factor. The surface conductivity is as follows:
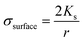 | (4) |
The CM factor for a shell structure (Fig. 2(c)) is more complicated. All three conuctivities shown exhibit negative DEP at low freuqncies and transition into positive DEP as the frequency increases. A peak DEP plateau is seen at mid-range frequencies for lower media conductivities compared to the shell conductivity. For higher media conductivities a transition to positive DEP occurs at high frequencies. CM factor at low frequency goes to −0.5 depending on the conductivities of shell and media, but this factor at high frequency depends on the surface capacitance, the permittivities of shell and media, as well as the shell radius.
It should be noted that particle separation, one of the most promising applications of DEP, can be easily accomplished by comparing the CM factors of two different particles and choosing an appropriate frequency and conductivity. The solid spheres and shell particles, for example, may be separated with high frequency at any conductivity. The solid particles will experience negative DEP and be repulsed from the electrode edges while the shell particles will experience positive DEP and be attracted to the electrode edges. Furthermore, since the CM factor is a function of particle conductivity, which, in turn is a function of the particle size, two particles of different sizes will have different CM plots. They may then be separated in the same way, by chosing an appropriate media conductivity and frequency of electric signal.
| DEP | ACEO | ETE |
|---|---|---|
| ✦ Electrokinetic force; positive or negative | ✦ Electrohydrodynamic force | |
| ✦ High dependency on particle size and property (selective manipulation) | ✦ Does not depend on particle size and property (non-selective manipulation) | |
| ✦ Long-range flow (circular motion) | ||
| ✦ Has strong effects near electrode with exponential decrease in force with increasing distance | ✦ Constant flow direction from edge to center of electrode: | ✦ Flow direction varies depending on medium conductivity and frequency |
| ✦ Frequency-dependence from relative polarizability of the particle and the medium | ✦ Frequency-dependence from surface charge and Et | ✦ Frequency-dependence from coulomb and dielectric body force |
| ✦ Conductivity increase leads to lesser ACEO | ✦ Conductivity increase leads to greater ETE | |
AC electroosmosis
ACEO occurs when mobile counter ions in the diffuse electric layer, which is induced by electrode polarization, interact with the electric field. In the case of parallel planar electrodes, the field contains a tangential component that induces counter ion movement towards the center of the electrode (Fig. 1(b)). The direction of the movement does not change with a potential switch because the counter ions are switched as well. The motion of the ions drags the bulk fluid along the surface, generating a rotational motion of bulk the fluid in the microchannel.The time-averaged AC electroosmotic velocity on two parallel electrodes is derived by Ramos et al.2 assuming a linear relationship between the surface charge and the potential and neglecting the stern layer. The ACEO velocity expression is as follows:
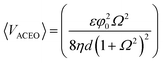 | (5) |
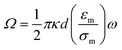 | (6) |
Fig. 3 shows the AC electroosmotic velocity as a function of frequency and position on an electrode. The velocity is always greatest at the edge and decreases as the center is approached. The velocity also is zero at low and high frequencies and reaches a maximum at mid-range frequencies.
 | ||
| Fig. 3 Using eqn (5), AC electroosmotic velocity is plotted as a function of (a) Ω at different locations ‘x’ from the electrode edge and (b) frequency and distance ‘x’ from the electrode edge at 0.0002 S m−1, 1 V, and 20 μm gap between electrodes. (Note that ‘x’ has a different coordinate system than ‘d’ in eqn (5)). | ||
Electrothermal effects
Like ACEO, ETE is a hydrodynamic phenomena and acts on a suspended particle only through fluid drag. The passage of current through the bulk fluid causes Joule heating according to the expression:| k∇2T + σE2 = 0 | (7) |
 | (8) |
 | (9) |
Next, the electrohydrodynamic force (FETE) caused by the conductivity and permittivity gradients is calculated according to the time-averaged electrothermal force equation per unit volume.2 This neglects the resulting fluid convection, which is slower than the charge organization. This force is as follows:
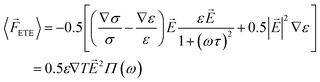 | (10) |
 | (11) |
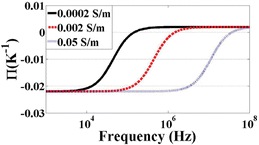 | ||
| Fig. 4 Π of ETE as a function of frequency with three different conductivities. | ||
The fluid velocity can be calculated using FETE as a body force on the liquid once the temperature gradient and electric field are known. It is important to note that both gradient of temperature and electric field are functions of amplitude. Though temperature gradient depends on the geometry of the system, analyitical approximations for similar geometries estimate this temperature gradient to be poportional to voltage squared.2 Together, gradient of temperature and electric field squared makes the total force proportional to voltage to the fourth power. Generally, when frequency or conductivity are high and ACEO ceases to play an important role, ETE can predominate, especially if the applied voltage is large. For an approximation of this force for two planar electrodes seperated by a small gap, we refer the reader to Ramos et al.2 For this geometry, at 10 V applied signal, they predict velocity values ranging from 0.7 to 5 μm s−1 at a radial distance of 20 μm from the center of the gap.
Another source of temperature gradient in the media can be due to external heating of electrodes such as from a microscope light. The presence of this heat source causes fluid motion in much the same way as from joule heating except that the direction is reversed. This is due to the reversal of the temperature gradient. For ETE, the fluid is heated from the electric fields and the electrodes (nearly) maintain their temperature and act as heat sinks. In the case of external heating, the electrodes become the heat source as they are heated by the light which passes through the transparent electrode gaps. This effect has been reported before but did not seem to play a significant role in experiments. With no applied electrical signal, particles were not observed to move (except by Brownian motion) under the presence of microscope lights. These temperature gradients also give rise to natural convection. However, these effects were also eliminated from the simulations because its effect is known to be much less than ETE as considered above.2
Materials and methods (experiments)
Microfabricated devices and materials
Each device used for experimental studies consists of a glass substrate (Pyrex 7740) containing planar gold electrodes of various designs. A PDMS membrane, containing a recessed chamber was then placed on top of the glass to form a completed channel.All of the thin-film electrodes were fabricated using the well known lift-off process. Photolithography was performed on 3 inch Pyrex glass wafers. Negative photoresist (Futurrex NR-7 1500PY) was spincoated onto the substrate followed by exposure and development to create a negative mask pattern prior to metal deposition. Next, 30 nm of titanium and 200 nm of gold were evaporated on top using an electron beam evaporator, followed by lift-off using acetone.
The microchannels were fabricated using PDMS replica molding. The microchannel molds were created on a 2 × 2 in2 Pyrex glass plate using negative photoresist (SU-8 2035). A PDMS mixture (10 : 1 of Sylgard 184 base resin to curing agent) was then poured onto the negative mold pattern. A 30 min degassing step in a vacuum dessicator, followed by baking at 80 °C for 2 h took place. After baking, the fully cured PDMS was peeled off and cut into individual devices. Holes with approximately 1 mm in diameter were punched into either side of the channel to form an inlet and outlet. The completed microchannels were 100 μm high, 1 mm wide and 1.1 cm long.
Assembly of the device consists of placing a PDMS channel on top of the electrode pattern and applying gentle pressure to ensure adhesion. Electrical connections were made by attaching wires to the planar electrodes with an electrically conductive adhesive. Fig. 5(a) shows an assembled device and electrodes with different patterns used in the experiments. The four electrode types used are the parallel interdigitated, castellated interdigitated, quadropole and pocket well designs. To understand the distribution of the electric field and the locations of the minima and maxima of the ∇|E|2, Fig. 6 shows 3D simulation results for each electrode geometry as well as dimension information.
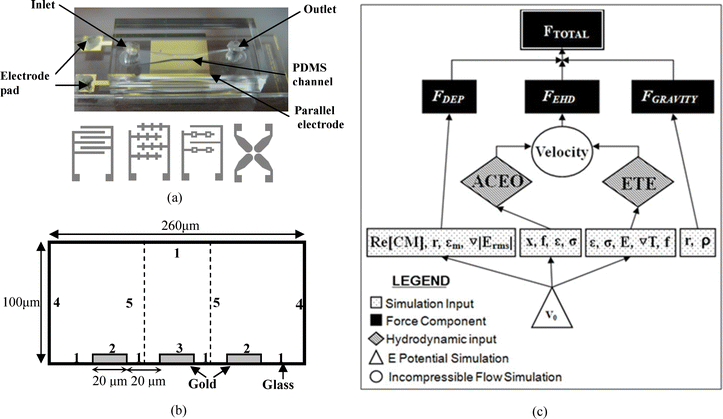 | ||
| Fig. 5 (a) An image of an assembled device. Conceptual drawings of the four electrode types, (from left to right) parallel interdigitated (20 μm width and 20 μm gap), castellated (20 μm width and 20 μm gap from main arm to main arm), potential well (20 μm width solid electrode, 10 μm width potential well electrodes. The pocket is a 20 μm square and the interelectrode gap is 60 μm at its closest) and quadrupole (adjacent electrodes are separated by a 50 μm gap and opposite electrodes are 200 μm apart) are shown. (b) Geometry (cross-sectional view of the microchannel) and boundary conditions for numerical simulation. For the electrostatics simulation: Zero charge on 1, and 4; V0 = Vrms/2 on 2; V0 = −Vrms/2 on 3; continuity for 5. For the convection and conduction simulation: Continuity on 1; zero heat flux on 4 and 5; and fixed temperature on 2 and 3. PDMS above the channel and glass below the channel have a thermal conductance of 0.15 W m−1K−1 and 0.6 W m−1K−1 respectively. For the incompressible Navier–Stokes simulation: 0 pressure on 4; No slip on 1; slip velocity (electroosmotic velocity) on 2 and 3; and symmetry conditions on 5. (c) Simulation strategy flow chart. | ||
![3D simulation for (a) Parallel interdigitated, (b) castellated, (c) pocket well and (d) quadrupole electrodes at 0.354 Vrms. (Surface plot: log10(∇|Erms|2) [V2 m−3], Arrow: Electric field [V m−1].) In the castellated electrode plot, a small normalized arrow plot at the corner shows the electric field direction 1 μm off the surface of the substrate. Black areas are the electrodes and the white area is the inter-electrode space.](/image/article/2009/LC/b801594e/b801594e-f6.gif) | ||
| Fig. 6 3D simulation for (a) Parallel interdigitated, (b) castellated, (c) pocket well and (d) quadrupole electrodes at 0.354 Vrms. (Surface plot: log10(∇|Erms|2) [V2 m−3], Arrow: Electric field [V m−1].) In the castellated electrode plot, a small normalized arrow plot at the corner shows the electric field direction 1 μm off the surface of the substrate. Black areas are the electrodes and the white area is the inter-electrode space. | ||
Particles and solution preparation
Polystyrene microbeads (Polysciences, Inc.) were added to aqueous solutions to make a colloidal mixture for the experiments (0.05 g ml−1). Microbeads with diameters of 2 μm and 200 nm were used. KCl was added to deionized water to control the media conductivity. Two different colloidal mixtures were prepared for the experiments: a low conductivity mixture (0.0002 S m−1) and a high conductivity (0.05 S m−1) mixture. The conductivity of each solution was measured by a conductivity meter (Orion Model 105A+).Experiment procedure
The experimental setup consists of a microscope (Nikon Eclipse ME600) equipped with a CCD camera and a function generator (HP 33120A 15 MHz), which connects to an assembled device placed on the microscope stage. In order to better visualize particles on electrodes, an external, through-objective light source was used.There were four electrode types and two conductivities used for each experiment. This makes for a total of 8 experimental conditions. For each condition, the selected electrode device was assembled and the appropriate solution (high or low conductivity) was injected into the chamber. Then, a time course of different frequency and voltage settings was supplied by the function generator while the CCD camera recorded the behavior of the particles.
Methods (simulation)
The overall aim of the simulation is to predict the behavior of particles under non-uniform AC electric fields. The simulation, therefore, should be able to produce a force vector field for each given experimental condition. This is done by calculating the total force (Ftot) at each position as: | (12) |
Simulation process
The simulation strategy is diagrammed in Fig. 5(c). Using COMSOL's multiphysics capabilities, three simulations were used to generate the final solution: An electrostatic simulation, a conduction heat transfer simulation and an incompressible Navier–Stokes simulation. The geometry and details of each simulation are described below.![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) = ∇V. The maximum norm value of the electric field is 2.24 × 105 V m−1 at both edges of the middle electrode.
= ∇V. The maximum norm value of the electric field is 2.24 × 105 V m−1 at both edges of the middle electrode.
The time-averaged dielectrophoretic force is calculated according to eqn (3) and uses the CM function for that of a sphere. The CM factor is simulated externally with Matlab using the material properties of the media and a polystyrene sphere (see Fig. 2(a)). The imported function describes the CM factor for both media conductivities as a function of frequency.
The thin layer of liquid that experiences the ACEO force extends less than a few nanometers away from the surface.5 Since this is much smaller than the channel height, ACEO may be modeled as a slip velocity boundary condition. To determine the velocity at the electrode, the time-averaged equation for electroosmotic velocity is used (eqn (5)). This function is used as the slip velocity boundary condition for the surface of each electrode. Since the equation is intended to be centered on an electrode gap, it may easily be applied to a pair of electrodes. However, since three electrodes are used in this simulation, eqn (5) must be used twice—once centered on the right gap and once centered on the left gap.
The ETE force is calculated using the thermal field as an input and using eqn (10) to act as a body force for the incompressible Navier–Stokes simulation.
The drag force acting on the particle due to both EHD effects is calculated in the postprocessing mode of COMSOL. The drag force for a sphere, FEHD is
| FEHD = 6πηr(vf − vp) | (13) |
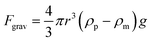 | (14) |
Ramos et al.2 showed that natural convection is insignificant when dealing with micro-electrode structures when compared to AC electrokinetic forces.2 The change in density of water with temperature is about 10−4 kg m−3°C−1. Even with a change of 10 °C a 1 μm particle will experience a buoyancy force of 10−17N, far less than AC electrokinetic forces, as will be shown.
Results and discussion
Experimental results
Using a microscope to observe the motion of particles under non-uniform AC electric fields shows the versatility and dramatic capabilities of AC electrokinetics. By simply adjusting the frequency, a wide range of distinct, directed and highly organized particle behaviors can be perceived. The immediate and rapid nature of this movement is striking, as particles become assembled or repelled within a few seconds to a few minutes, though this depends highly on the size of the particles and other experimental conditions. In general, higher voltages increase the magnitude of each phenomenon but sometimes different effects are observed at different voltages even while maintaining the same frequency. Different conductivities can adjust the prevalence or strength of some phenomena, restrict them completely or bring about entirely new phenomena altogether. In general, five distinct behaviors can be identified and will be discussed in brief. | ||
| Fig. 7 Parallel interdigitated electrodes with 2 μm diameter polystyrene microbeads at 1 kHz and 1 V suspended in 0.0002 S m−1 media with (a) low concentration of particles and (b) high concentration of particles. | ||
In the parallel electrode case, the aligned particles are sometimes referred to as an “assembly line.” If the particle concentration is low (Fig. 7(a)), the particles are collected in the center of the electrode as a linear pattern with a constant interval. The interesting nature of this constant interval may be explained by the repulsion of two similar particles when they are aligned perpendicularly to the direction of the electric field. In this low frequency and low conductivity case, where particles are more polarizable then the media, a region of low electric field strength exists between the particles and is intensified when such particles approach. Since the particles experience positive DEP, they will move away from this region and thus be repulsed. The EHD flow keeps the particles from forming the particle chains that this phenomenon would otherwise create.
When the particle concentration is high (Fig. 7(b), the collected particles form a zig-zag or close-packed assembly. As will be discussed in the particle chains section, depending on their orientation within the electric field, two nearby particles may experience either repulsive DEP forces or attractive DEP forces. It is hypothesized that the particles form such organized patterns in order to find a stable arrangement where the repulsive forces of DEP are minimized and the attractive forces of DEP forces are maximized as they are forced towards the center of the electrode due to the EHD forces. In the castellated electrode case, this behavior results in particles collecting at each electrode intersection in a remarkably clear “diamond” shape (Fig. 8 E1, E2, F1, F2).
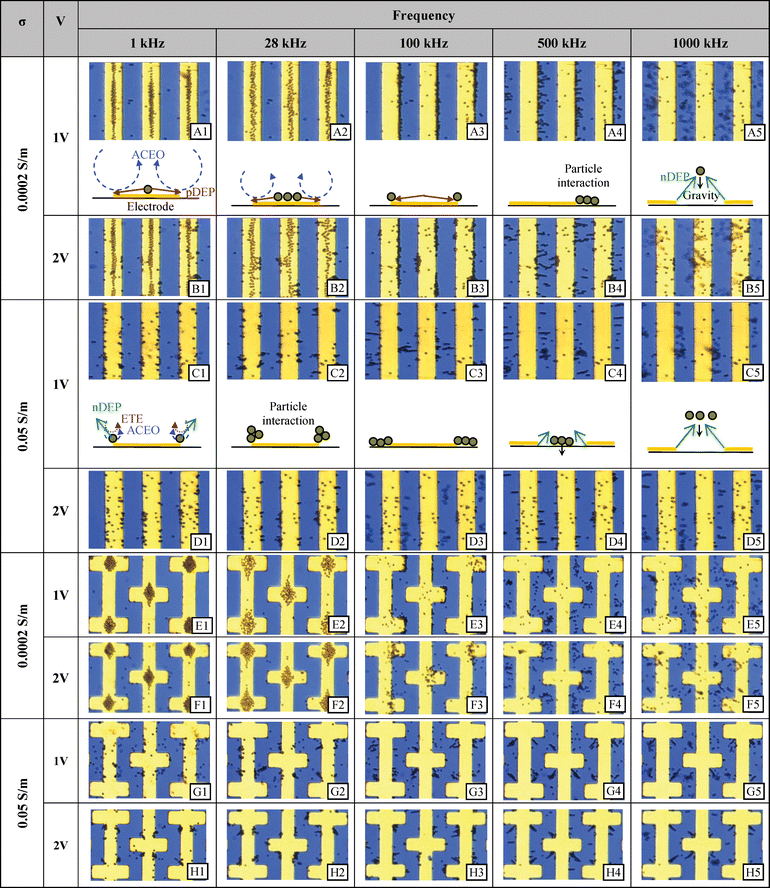 | ||
| Fig. 8 Experimental results at selected frequencies and voltages for the parallel and castellated interdigitated electrodes using two different conductivities. 2 μm diameter polystyrene microspheres were randomly dispersed before a signal was supplied. | ||
Fig. 8 shows the changes in particle motion as a function of frequency. As the frequency is increased, the balance between the two major competing phenomena starts to shift. Particles spread out on the electrodes as the effect of ACEO is diminished and thus positive DEP begins to play a stronger role (Fig. 8 A2, B2, and E2).
Parallel and castellated. Electric field minima can occur in-between electrodes and at the center of the electrode (Fig. 6(a and b)). If the particles have been previously collected at the edge of the electrode and formed particle chains due to positive DEP, they will move to the gap between electrodes. However, if the initial condition was random distribution of the particles, they may either be pushed towards the gap between electrodes or the center of the electrodes, depending on their starting position. At frequencies of approximately 1 MHz and above, most of the particles levitate up into the media to the point where the negative DEP force is balanced with the gravitational force.
Potential well and quadrupole. The quadrupole electrode type and potential well electrode type are designed to be particle traps through negative DEP. With the use of high frequency in either low or high conductivity, the particles are repelled from the edges of the electrodes and move either in between the four electrodes in the quadrupole case or congregate within the geometrical pocket within the potential well electrode (see the electric field minima shown in 3D Fig. 6(c and d). They have been used as such and the images may be seen in Fig. 9. Note that the higher the voltage, the more tightly focused the particles become. Furthermore, not only are the particles collected within the gap between the electrodes, but in the quadrupole case, they are also moved toward the center of the electrode itself, where another electric field minimum exists.
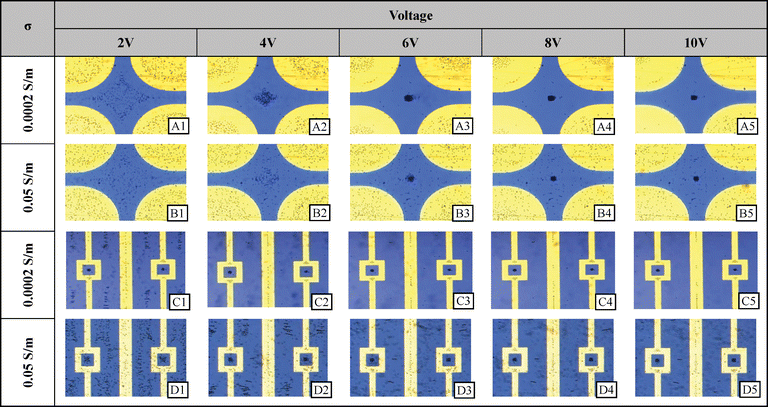 | ||
| Fig. 9 Experimental results at selected voltages and solution conductivities for the quadrupole and pocket well electrodes. 2 μm diameter polystyrene microspheres were randomly dispersed before a signal was supplied. | ||
In some cases, positive DEP between particles and the electrode is still present with enough strength to keep the pearl chains rooted at the electrode edge. However, the strength of the particle–particle attraction is greater than that of the DEP between particles and the electrode and so particles align. This behavior may be clearly seen in the parallel electrode case in Fig. 8 (A4 and B4). A similar case may be seen at high conductivity in Fig. 8 (C3). However, unlike the low conductivity cases, the particles are not as stable and stationary as they are not firmly “rooted” to the electrode by positive DEP. Instead, a close inspection of a video reveals that in most cases, the root particles are undergoing slight orbital movement, which indicates ACEO or ETE is in effect. (The simulation study shows that the ACEO effect is much stronger than ETE for the given conditions.) It is likely that these situations show a force balance between ACEO and negative DEP and the particles are free to form pearl chains in this equilibrium. When the frequency is raised, negative DEP overcomes the ACEO and the pearl chains become uprooted, as shown in Fig. 8 (C4). The particles are then levitated as the frequency further increases and the chains are decomposed into individual particles as they move away from the electrode and the DEP forces decrease.
For the castellated electrodes, an interesting particle organization occurs. Pearl chains form with particles streatching from the inside corner of one electrode towards the outside corner of an adjacent electrode as can be seen in Fig. 8 (G4 and H4). Since the induced dipoles of each microsphere form along the electric field lines, so too do the pearl chains. In the case of the castellated electrode type, the direction of the electric field lines can be determined from a 3D simulation (see Fig. 6). From this figure, it is apparent that a pearl chain starting from the inside corner of a castellated electrode will extend along the field lines in the manner demonstrated in the experiment.
Note, however that these pearl chains do not form in the same ‘X’ pattern for the low conductivity case in Fig. 8 (E4 and F4) as one might expect from the predominance of negative DEP among all of the major forces. The reason for this is that the particle starting positions are different. In the high conductivity case particles have migrated to the inside corners whereas in the low conductivity case particles have collected on the outside corners (most clearely shown in Fig. 8 G3 compared to E3). This difference in starting position has two important effects. (1) The outside corners have a greater electric field strength than the inner corners (Fig. 6(b)) which can have the effect of forcing particles more strongly away from the edge (Fig. 8E4). (2) The electric field lines converge as they stretch away from the inside corner and across the gap (Fig. 6 (b) vector plot) causing a stable arrangement of particles along the converged field lines. On the outside corner the electric field lines diverge as they cross the gap creating an unstable situation for aligned particles. A close look at Fig. 8 (F4) shows that, in fact, there are particle–particle interactions stemming from the outside corner but they are not collected as neatly as they are in the converging electric field case of its high conductivity analog (H4)
Additional experimental results (200 nm particles)
Fig. 10 shows the experimental results for 200 nm fluorescent polystyrene spheres with a castellated electrode. Because Brownian motion becomes much more dominant with a decrease in particle size (particle displacement after a given time is approximately proportional to r−½), collection is much more challenging for these particles. | ||
| Fig. 10 Experimental results at selected frequencies and voltages for the quadruple and pocket well electrodes using two different conductivities. 200 nm diameter polystyrene microspheres were randomly dispersed before a signal was supplied. | ||
For 2 μm particles, positive DEP collection occurs readily at 1 V. Under the same conditions, 200 nm particles show no DEP collection. When the signal amplitude is increaset to 2 V, however, 200 nm particles collect readily at the electrode edges. Furthermore, the particles remain collected at the edges for the entire frequency range. As can be seen in Fig. 2(b), the transition from positive to negative DEP occurs much later than for 2 μm particles (∼8 MHz for 200 nm particles).
At lower frequencies and conductivities, particles are seen to be collected in the center of the electrode. Interestingly, the greatest particle collection at 1 V occurs near or below 1 kHz where there is no corresponding collection at 2 V. The greatest particle collection for 2 V instead occurs at 4 kHz, where the collection for 1 V appears to be waning. It is hypothesized that the greatest particle concentration does not necessarily occur when the ACEO velocity is maximum. An increase in ACEO velocity may, in fact, have a dispersing effect on already collected particles as they are swept up in the flow stream and are mixed with the bulk solution. This might explain how 2 V particle collection has become more effective with an increase in frequency from 1 kHz to 4 kHz–the velocity at 1 kHz may be too fast for particle collection.
For the high conductivity case, there is less apparent organized particle behavior. Clearly, at 1 V (Fig. 10, Row C) there is no particle concentration either due to DEP or ACEO. Since the particles will not sediment except over very long time scales, and the CM factor indicates that the particles are in the negative DEP regime, this is expected. Particles may simply be levitating above the electrodes or are slowly moving within in the fluid field which is not strong enough to cause particle concentration.
At high conductivity and 2 V, ACEO and negative DEP become more significant and particles at 1 kHz and 4 kHz (Fig. 10 D1 and D2) are being concentrated at the concave corners of the electrodes synanimous to the 2 μm particle case (Fig. 8 G2–4, H2–4). It seems that the particles become trapped in the counter vortexes generated by ACEO. The presence of negative DEP will keep particles from reaching the center of the electrode or from getting too close to the actual electrode edge.
Simulation results
 | ||
| Fig. 11 Mapping of each force isolated from the others at 1 kHz at 1 V. The surface plot uses a logarithmic scale with force streamlines. | ||
 | ||
| Fig. 12 Total force simulation results at 1 V. Each surface plot represents the log of the force acting on a 2 μm particle at rest. Force streamlines are shown as well as normalized arrows which show the direction of the force at each location. Corresponding experimental results are showed inlaid on each simulation plot. | ||
Distance. The relationship between the magnitude of each force and distance to the electrode is shown in Fig. 13. With DEP, the force is known to die off exponentially with distance from the electrode. However, ACEO and ETE forces are hydrodynamic and will depend on the properties of the liquid as well as the geometry of the chamber. Furthermore, since these phenomena generate non-trivial flow patterns which are spatially dependant in x and y positions (z as well for more complicated geometry electrodes) the force distance relationship is most easily shown graphically. In order to remove the dependence on the x coordinate, the average force for each distance above the center electrode is computed.
 | ||
| Fig. 13 The relationship between the strength of each phenomena and the height off the center electrode is shown for several frequencies and conductivities. Since the force varies as a function of x as well, an average was taken across all x for each given y point so that only general relationships can be understood. Exact spatial values therefore cannot be obtained. | ||
The DEP force does not vary greatly with frequency except during the transition between positive and negative DEP. This transition starts around 100 kHz, crosses zero at ∼300 kHz and reaches a steady negative value near 1 MHz (see Fig. 2(a)). The frequencies shown in Fig. 13 are outside the transition phase, and therefore look identical in all images. Note that the hydrodynamic forces are much more penetrating than the DEP forces which die off far more rapidly with distance.
Frequency. The ascendance and subsidence of different phenomena as the frequency of the applied signal changes are one of the most important and compelling aspects of AC electrokinetics. This relationship was investigated and is shown in Fig. 14, which shows the relationship between force and frequency for several different heights above the electrode and for two conductivities.
 | ||
| Fig. 14 The magnitude of each force is shown as a function of frequency for four distances (displayed on each graph) above the electrode surface. As before, in order to eliminate x spatial variations, the x component is averaged across the entire electrode so that only general relationships can be understood and exact spatial values cannot be obtained. | ||
One important feature shown in the figure is the way in which conductivity affects the hydrodynamic and DEP forces. Since the hydrodynamic forces are predominantly caused by ACEO (rather than ETE) at these conductivities and voltages, increasing the conductivity will result in a frequency shift in the peak hydrodynamic force. In ETE dominated conditions, an increase in conductivity will result in an increase in hydrodynamic force and the dependence on frequency is much less exaggerated.
The transition point between positive DEP and negative DEP at low conductivities can be clearly seen in the figure. DEP, which remains at a constant value for most frequencies undergoes a transition and reaches a minimum magnitude at ∼300kHz (at which the actual value changes from positive to negative). At high conductivities, only negative DEP is present and does not undergo a transition.
Particle radius. A reduction in particle radius greatly increases the difficulty of manipulation due to an increase in the randomization effects of thermal motion. Reliable manipulation of submicron particles requires careful device design and control of environmental conditions as well as a valid method for predicting behavior. Fig. 15 shows the relationship between particle velocity and radius and considers several voltage and frequency settings for two conductivities. The values in the y-axis indicate instantaneous velocity one micron off the surface of the electrode, since the forces acting on particles are highly spatially dependant. This analysis also assumes that DEP force is in constant equilibrium with drag forces (a valid assumption since initial acceleration of such small particles will be quite large—hundreds to thousands of m s−2). The instantaneous velocity of the particles due solely to DEP can therefore be estimated by balancing drag force with DEP force and solving for v:
 | (15) |
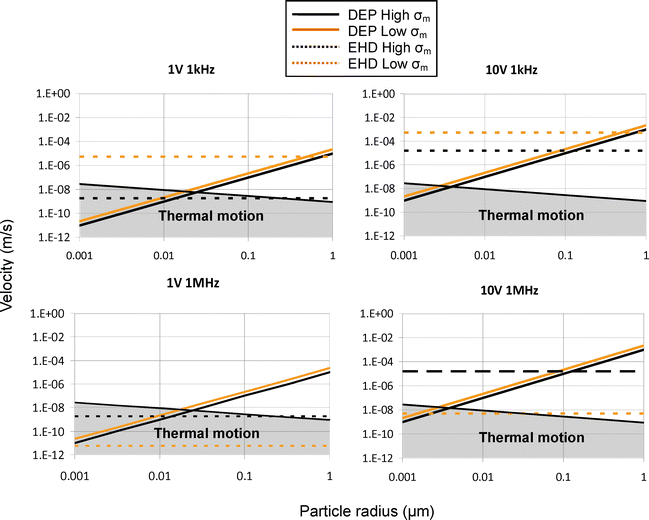 | ||
| Fig. 15 The magnitude of velocity for particles experiencing DEP and drag is shown as a function of particle radius for four frequency and voltage settings (displayed on each graph). The force is averaged (as before) for all x, 1 μm above the electrode surface. It must be stressed that only general relationships can be learned from such analysis. Velocity caused by DEP was found by equating drag force and DEP force and solving for velocity. The region in grey shows the area where deterministic particle organization by AC electrokinetics is overcome by thermal motion. | ||
It is also important to note that even though the conductivity and frequency have little effect on the magnitude of the DEP (except during the transition from positive to negative DEP), the direction can change according to the CM factor as mentioned previously.
An inspection of Fig. 15 shows that at low conductivity (shown in grey), an increase in voltage does not greatly change the point at which DEP force overcomes the EHD force. This is because at this conductivity, ACEO is the predominant EHD force and both DEP and ACEO forces have the same relationship with amplitude of the applied signal (proportional to V2). In fact, the relationship between DEP and ACEO can change slightly since the fluid pattern caused by ACEO is not perfectly constant with voltage. At higher conductivities, however, the balance of forces can change since ETE, which is proportional to V4, becomes more important to the hydrodynamic force.
Media conductivity. Media conductivity plays an important role in all three of the AC electrokinetic forces (as can be seen in each of the equations describing them) and its affects may be seen in all three of the Fig. 13–15 previously mentioned. Since the figures display the magnitude of the force, and not its direction, it is difficult to be understood from these figures alone. A much better understanding can be gained from CM (Fig. 2) and Π (Fig. 4) figures. For low frequencies, an increase in conductivity will change the direction of DEP force. Like DEP, the direction of the ETE force can be switched by changing the conductivity. Also, an increase in conductivity will increase the magnitude of ETE force but this is also not clear from the figures since the conductivity and voltage ranges used in the simulations cause ACEO to be predominant. The effects of the conductivity change on ACEO is most dramatically seen in Fig. 14. The low conductivity EHD force has a peak around 200 Hz. The higher conductivity peak is around 3 kHz and has a lower peak magnitude.
Amplitude. The relationship between the force of each phenomena and amplitude of applied signal is straightforward. DEP and ACEO are increased according to the square of amplitude (eqn (3) and (5)) and ETE according to amplitude to the fourth power (eqn (10)—note that both E2 and gradient of T depend on voltage). Fig. 15 shows some of the ramifications of the fourth power dependance on conductivity for ETE. For both frequency cases at low conductivity, an increase in voltage does not significantly change the point at which DEP overcomes the EHD force and the DEP force. This is because ACEO is the dominant EHD force at low conductivity and both ACEO and DEP have a similar amplitude relationship. At high conductivity, this changes due to the increased influence of ETE. An increase of the voltage by 10 times has increased the ETE force by ∼4 orders of magnitude and has increased its relative importance compared to the other two forces. For example, at 50 nm particles at high conductivity are predominantly under the influence of DEP at 1 V but at 10 V, EHD flow predominates.
Conclusions
A new method for simulating the three major AC electrokinetic forces has been demonstrated and this numerical simulation shows good qualitative agreement with the experimental part. The wide range of additional experiments using varied device designs and operational conditions along with this simulation should provide scientists and engineers with an invaluable tool for future lab-on-a-chip designs.Future improvements to the numerical simulation will include incorporation of particle–particle interactions as well as making the ACEO boundary conditions more generic so as to apply to more complicated electrode geometries.
This, and future numerical simulations will continue to play a critical role in the design of AC electrokinetic components of lab-on-a-chip devices. Specifically, this simulation will be used to improve micro-mixer, particle separation and cell manipulation devices in the authors' laboratory.
Acknowledgements
The authors would like to thank the Drexel University Department of Mechanical Engineering and Mechanics for their support.Notes and references
- H. A. Pohl, Dielectrophoresis, Cambridge University Press, Cambridge, 1978 Search PubMed.
- A. Ramos, H. Morgan, N. G. Green and A. Castellanos, J. Phys. D: Appl. Phys., 1998, 31, 2338–2353 CrossRef CAS.
- N. G. Green and H. Morgan, J. Phys. D: Appl. Phys., 1998, 31, L25–30 CrossRef CAS.
- N. G. Green and H. Morgan, J. Phys. D: Appl. Phys., 1997, 30, L41–L84 CrossRef CAS.
- H. Morgan and N. G. Green, AC Electrokinetics: colloids and nanoparticles, SRP Ltd, UK, 2002 Search PubMed.
- R. C. Peter, X. X. Gascoyne and J. Vykoukal, Electrophoresis, 2002, 23, 1973–1983 CrossRef CAS.
- N. G. Green and H. Morgan, J. Phys. D: Appl. Phys., 1997, 30, 2626 CrossRef CAS.
- A. Rosenthal and J. Voldman, Biophys. J., 2005, 88, 2193–2205 CAS.
- P. Wanichapichart and S. Bunthawin, ScienceAsia, 2002, 28, 113–119 CrossRef.
- M. Riegelman, H. Liu and H. H. Bau, J. Fluids Eng., 2006, 128, 6–13 CrossRef CAS.
- T. B. Jones, Electromechanics of Particles, Cambridge University Press, New York, 1995 Search PubMed.
- A. Rosenthal, B. M. Taff and J. Voldman, Lab Chip, 2006, 6, 508–515 RSC.
- Y. Liu, J. -H. Chung, W. K. Liu and S. Rodney, J. Phys. Chem. B, 2006, 110, 14098–14106 CrossRef CAS.
- N. G. Green, A. Ramos, A. Gonzalez, H. Morgan and A. Castellanos, Phys. Rev. E, 2000, 61, 4011–4018 Search PubMed.
- A. Castellanos, A. Ramos, A. Gonzalez, N. G. Green and H. Morgan, J. Phys. D: Appl. Phys., 2003, 36, 2584–2597 CrossRef CAS.
- A. Belisle, M. Brown, T. Hubbard and M. Kujath, J. Vac. Sci. Technol., A, 2006, 24, 737–741 CrossRef CAS.
- S. Huang, S. Wang, H. S. Khoo and F. Tseng, Sens. Actuators, B, 2007, 125, 326–336 CrossRef.
- S. Jacobson, T. McKnight and J. Ramsey, Anal. Chem., 1999, 71, 4455–4459 CrossRef CAS.
- M. Sigurdson, D. Wang and C. D. Meinhart, Lab Chip, 2005, 5, 1366–1373 RSC.
- A. Ajdari, Phys. Rev. E, 2000, 61, 45–48 Search PubMed.
- M. Mpholo, C. G. Smith and A. B. D. Brown, Sens. Actuators, B, 2003, B92, 262–268 CrossRef CAS.
- B. H. Lapizco-Encinas, B. A. Simmons, E. B. Cummings and Y. Fintschenko, Anal. Chem., 2004, 76, 1571–1579 CrossRef.
- D. Wang, M. Sigurdson and C. D. Meinhart, Exp. Fluids, 2005, 38, 1–10 CrossRef.
- P. Li, K. Shi and Z. Liu, Opt. Lett., 2005, 30, 156–158 Search PubMed.
- A. Ashkin, IEEE J. Quantum Electron., 2000, 6, 841–856 CrossRef CAS.
- M. M. Blideran, G. Bertsche, W. Henschel and D. P. Kern, Microelectron. Eng., 2006, 83, 1382–1385 CrossRef CAS.
- C. Thelander and L. Samuelson, Nanotechnology, 2002, 13, 108–113 CrossRef CAS.
- T. R. Ramachandran, C. Baur, A. Bugacov, A. Madhukar, B. E. Koel, A. Requicha and C. Gazen, Nanotechnology, 1998, 9, 237–245 CrossRef CAS.
- T. Takekawa, K. Nakagawa and G. Hashiguchi, in Transducers, 2005 Search PubMed.
- N. G. G. Hywel Morgan, AC Electrokinetics: colloids and nanoparticles, SRP Ltd, UK, 2002 Search PubMed.
- J. P. Urbanski, T. Thorsen, J. A. Levitan and M. Z. Bazant, Appl. Phys. Lett., 2006, 89, 143508 CrossRef.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, New York, 2000 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Castellated labeled sequence and parallel labeled sequence videos. See DOI: 10.1039/b801594e |
| This journal is © The Royal Society of Chemistry 2009 |
