Formation, microstructures and crystallization of anodic titanium oxide tubular arrays
Zixue
Su
and
Wuzong
Zhou
*
EaStChem, School of Chemistry, University of St. Andrews, St. Andrews, Fife, KY16 9ST, United Kingdom. E-mail: wzhou@st-andrews.ac.uk; Fax: +44 (0)1334![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463808; Tel: +44 (0)1334
463808; Tel: +44 (0)1334![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467276
467276
First published on 16th March 2009
Abstract
Formation of highly ordered TiO2 nanotubular arrays during anodization of titanium can be elucidated by using the equifield strength model and a double-layer structure. The two characteristic microstructural features of anodic titanium oxide (ATO) in comparison with anodic aluminium oxide (AAO), a thin titanium hydroxide layer and an O-ring like surface pattern, were investigated using scanning electron microscopy and high resolution transmission electron microscopy (HRTEM). Field-enhanced dissociation of water is extremely important in the formation of the nanotubes with a double-layer wall and an O-ring-like pattern, and in the determination of porosity. The relations between porosity of the ATO films and the anodization conditions, such as current density and electric field strength, have been established. Crystallization of the anodic TiO2 nanotubular arrays was also achieved and the microstructures were studied by using HRTEM.
1. Introduction
Although fabrication of porous aluminium oxide layer viaanodization of aluminium has a long history,1 only in recent years was this process also achieved for other metals such as Hf,2Zr,3Nb,4Ta5 and Ti,6et al. Since the formation of the pores is a competition between dissolution of oxide at the oxide/electrolyte interface and oxidation of metal at the oxide/metal interface, selection of suitable electrolyte is critically important. For construction of uniformly sized and self-arranged honeycomb pores, the anodization conditions are even more restricted. For example, ordered anodic aluminium oxide pore arrays do not form in a near-neutral electrolyte or using a very low anodization voltage. Anodization of Ti using a NH4F non-aqueous solution as electrolyte may lead to hexagonally ordered nanotubular arrays. Compared to the metal substrates, these nanoarchitectured porous oxide films are expected to have specific functional properties, which may be promising in applications in catalysis, optics and electronics, etc. Among the known porous anodic metal oxides, anodic aluminium oxide (AAO) and anodic titanium oxide (ATO) are the two most extensively investigated materials. The former is often used as template for fabrication of other low-dimensional nanomaterials, e.g.nanowires and nanotubes.7 It is well known that polycrystalline titanium dioxide has great gas-sensing capabilities,8 self-cleaning ability9 and very promising photocatalytic activities.10 Porous ATO has been used as photoanodes in dye-sensitized solar cells,11 in the photocleavage of water12 and for applications in biology.13The most significant difference between ATO and AAO is that the former contains separated nanotubes and the latter is a continuous film with a pore array (Fig. 1). The mechanism of this difference has not been well established. The microstructures of ATO are obviously more complicated than those in AAO. Even for AAO, the formation mechanism is still not fully understood. A widely accepted model for the hexagonally ordering in AAO is based on mechanical stress associated with volume expansion during the oxidation of aluminium.14 However, it is difficult to use this model to elucidate the self-ordering process in ATO since the nanotubes are separated by at least a few nanometers. Recently, we proposed an equifield strength model for explaining the formation of parallel pores and geometry of the pores in AAO.15 We believe this model can also be used in ATO and other porous metal oxides. We also found that the relative dissociation rate of water during anodization is a very important factor in governing the porosity of the anodic oxide films.
 | ||
| Fig. 1 Typical top-view SEM images of (a) AAO and (b) ATO films. | ||
In the present work, the equifield strength model was used to elucidate the formation of the pores in ATO, the self-ordering and the geometry (e.g. hemispherical pore bottom) of the pores. Transmission electron microscopy (TEM) and scanning electron microscopy (SEM) were applied to reveal the microstructures of ATO nanotubes, including a double-layer wall and the periodically appearing O-ring-like pattern on the outer surface of the nanotubes, therefore understanding the reason of the separation of the nanotubes. In addition, the porosity of ATO films was found to be governed by the relative dissociation rate of water which is dependent on anodization conditions, such as electrolyte, applied voltage, current density and electric field strength. With these achievements, the fabrication of ATO films can now be controlled more precisely. Finally, crystallization of the ATO films has been achieved, widening the potential application of the materials.
2. Experimental
High purity titanium foil (0.25 mm, 99.5%) was sonicated in acetone and then rinsed in deionized water. The anodization was performed in a home-made cell with typical conditions: anodization voltage range from DC 10 V to 60 V, ethylene glycol containing 0.3 wt% NH4F and 2 wt% water as electrolyte, and working temperature of 15 °C. TiO2 specimens were collected with different anodization times from 20 min to 17 h in order to investigate the tube formation at different stages.Observation of the morphology of the produced ATO films was carried out using SEM on a JEOL JSM-5600 microscope. TEM and high resolution TEM (HRTEM) characterizations of individual TiO2nanotubes were performed on JEOL JEM-2011 electron microscope operated at 200 kV, equipped with an Oxford Link ISIS energy dispersive X-ray spectroscopy (EDX) system and a Gatan 794 camera. Images were recorded at magnifications of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 600
000 to 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×. Crystallization of the ATO films, by annealing from 285 °C to 600 °C in air, was monitored by X-ray powder diffraction (XRD) method on a Philips-1 diffractometer. Infrared spectra in a range of 400–4000 cm−1 were collected on a Perkin Elmer Spectrum GX IR spectrometer.
000×. Crystallization of the ATO films, by annealing from 285 °C to 600 °C in air, was monitored by X-ray powder diffraction (XRD) method on a Philips-1 diffractometer. Infrared spectra in a range of 400–4000 cm−1 were collected on a Perkin Elmer Spectrum GX IR spectrometer.
3. Results and discussion
3.1 Microstructures of ATO
With a long time of anodization (15 h), an ATO film with a thickness of about 40 µm has been produced (Fig. 2a). A top view on the opened ends of the nanotubes (Fig. 1b) and a bottom view on the closed ends of the nanotubes (top part of Fig. 2b) show that these nanotubes are almost hexagonally ordered. The morphology of the bottom of nanotubes seems to be hemispherical. However, some distortions and non-uniform wall thicknesses of the nanotubes can be seen from the top-view images. The enlarged SEM image along the profile direction shows the outer surface of the nanotubes with an O-ring like pattern. In fact, these O-rings are the remains of some two-dimensional sheets supporting the nanotubes. These porous sheets can be revealed when the nanotubes are partially removed by an ultrasonic treatment. To achieve this, a relatively thinner ATO film was prepared and the corresponding SEM image is shown in Fig. 2(c). When all the nanotubes were removed, the porous sheets can be collected. This discovery is important for future application of the materials. If these sheets can be maintained after crystallization, they play a role of support to the nanotubes and can significantly increase the mechanical strength of the ATO films. The typical morphology of the as-prepared ATO film is like test-tubes stored in a tube stand as we often see on the laboratory benches (Fig. 2d). | ||
| Fig. 2 SEM images of the produced ATO films with (a) a profile view at a low magnification showing the film thickness, (b) a profile view at a larger magnification showing O-ring pattern as indicated by the arrow, (c) a top view of a film with nanotubes being partially removed. (d) Schematic drawing of the microstructure of ATO. | ||
Unlike AAO where the wall of the pores is monophasic aluminium oxide, the nanotubes in ATO have a double-layer wall as revealed by TEM images. Fig. 3a is a TEM image of two parallel nanotubes of 130 nm in diameter, 30 nm thickness of the inner layer, 8 nm thickness of the outer layer and about a 3 nm the space between the nanotubes. After electron beam irradiation for a few minutes, the outer layer was separated from the inner layer due to the different thermal expansion coefficients (Fig. 3b), confirming that these two layers have different compositions and an obvious boundary. Infrared spectrum of the as-prepared ATO shows a peak at ∼1630 cm−1 and a broad band between 3000 cm−1 and 3700 cm−1, both corresponding to structural OH−.15,16 The intensities of these peaks drop when the sample was heated at a high temperature. Bearing in mind that Taveira, et al. identified the existence of Ti(OH)4 by XPS in the compact layer formed at the early stage of anodization of titanium,17 the infrared information together with the volume shrinkage behavior indicate that the outer layer is more likely to be some type of titanium hydroxide with a relatively lower density, while the inner layer is titanium oxide.
 | ||
| Fig. 3 (a) TEM image of two nanotubes dropped from an ATO film, showing a double-layer wall. The arrows indicate the outer layers. After electron beam irradiation for a few minutes, the inner layer and outer layer are separated (b). | ||
3.2 Chemical reactions
Chemical reactions during the anodization of titanium are complicated and have been investigated by several groups.18–20 It is commonly accepted that the process includes field assisted oxidation of Ti metal to form TiO2, field assisted dissolution of Ti metal ions in the electrolyte and chemical dissolution of Ti and TiO2 due to etching by fluoride ions.18 Unfortunately, no quantitative investigation was reported and the role of dissociation of water is often ignored. We try to propose more detailed reactions based on our microstructural investigation.When titanium is anodized, a barrier layer of titanium oxide forms on the metal surface. The initiation of pore formation should be the same as that in AAO, which is due to defects and a rough surface in the barrier layer.15 We now consider chemical reactions when a pore is developed from a surface pit. At the electrolyte/oxide interface, titanium oxide is dissolved in the fluoride-anion-containing electrolyte. This process will reduce the thickness of the oxide layer. Suppose all the oxide anions created from this dissolution migrate from the electrolyte/oxide interface to the oxide/Ti interface to form Ti oxide or Ti hydroxide, the amount of oxide anions is just enough to form a new layer at the pore bottom and the thickness of the oxide layer in the hemispherical bottom is maintained. On the other hand, a large amount of oxide anions are still needed to build the wall of the pores with a volume corresponding to ΔL during anodization time Δt (Fig. 4a). These oxide anions are from dissociation of water on the oxide surface. Consequently, the overall reaction at the electrolyte/oxide interface can be written as
| TiO2 + nH2O + 6F− → [TiF6]2− + (n + 2 − x) O2− + xOH− + (2n − x)H+ | (1) |
| 2Ti + 2O2− + 4OH− → TiO2 + Ti(OH)4 + 8e− | (2) |
 | ||
| Fig. 4 Schematic drawing of nanotube formation in ATO. (a) Two neighbouring nanotubes with Ti metal in between would move closer to each other by expanding their diameter. (b) The expansion stops when they touch each other. (c) The hydroxide layer in between two nanotubes shrinks along the side surfaces when it decomposes. (d) The corresponding TEM image of such twin nanotubes. | ||
Reaction (2) leads to an increase of the thickness of the oxide layer. When titanium is oxidized into Ti4+ cations, part of them stays in the oxide/hydroxide layer and other part moves directly from the hydroxide/metal interface towards the electrolyte without forming oxide or hydroxide.
3.3 Equifield strength model
When a constant voltage U is applied to the oxide layer, the electric-field strength E in the oxide layer is inversely proportional to the oxide layer thickness d, E = U/d. When titanium is anodized in a fluorine-containing electrolyte, the dissolution rate of TiO2 is fast, resulting in a reduction of thickness (d) of the oxide layer and therefore an increase of the field strength. The dissociation rate of water will then be increased and the growth of oxide layer be enhanced. Finally, an equilibrium state between the oxidation and the dissolution processes will be approached with a constant barrier thickness (dB) corresponding to a constant field strength (EB) in the whole anodization area.Since the whole electrolyte/oxide interface has a uniform potential, so does the hydroxide/metal interface, the field direction is always perpendicular to the interfaces. Hemispherical morphology of the bottoms of the ATO nanotubes is the only shape which can meet the above mentioned equifield strength requirement. On the other hand, it was previously reported that the hemispherical pore bottom cannot be achieved when a very strong Cl−-containing acidic solution is used in anodization of titanium, when chemical etch dominates the process and no stable oxide layer forms.21 In this case, the equifield strength model cannot be applied and a square shape or other non-spherical shape could appear. The HF-based electrolyte is also too strong an acid for anodization of titanium and chemical etching is so significant that the nanotubes formed at earlier stage would be dissolved during the process and it is difficult to increase the thickness of the nanotubular arrays.6 This is the reason why HF-based electrolytes have been recently replaced by NH4F-based electrolytes22 or a non-aqueous organic electrolyte.18
Another important characteristic of the equifield strength model is that a single nanotube can not only grow at the bottom (downwards) but also expand its pore diameter as indicated by the arrows in Fig. 4a. Only when two nanotubes touch each other, as shown in Fig. 4b, does the expansion stop. The hydroxide layer can shrink along the directions perpendicular to the side surfaces of the nanotubes, forming separated nanotubes with double layer walls (Fig. 4c). In this case, the bottoms of the nanotubes are still connected each other. The experimental observation for this microstructure is shown in Fig. 4(d).
Since the thickness of the wall is determined by the anodization conditions, mainly the field strength, and the porosity of the ATO film is governed by the relative dissociation rate of water, as we discuss later, the diameter of the nanotubes tends to be constant. The movement of the nanotube walls towards each other, driven by the self-enlargement potential, eventually results in a shift of the nanotubes. This is the principal driving force of the self-organization of the nanotubes in ATO to form a honeycomb pattern.
3.4 Formation of O-rings
The O-rings on the outer surface of the nanotubes are actually part of two-dimensional porous sheets as shown by SEM images in Fig. 2(c). TEM images from multi-tube clusters and separated nanotubes also show this characteristic (Fig. 5a,b). It is obvious that the inter-O-ring distance is almost constant as seen in Fig. 5(b). Macak, et al. attributed the formation of the O-rings to a variation of nanotube diameter.20 This was not in agreement with our TEM observation, since there is no variation of the nanotube diameters observed from inner surface of the nanotubes, and the O-rings are extra parts connected only to the outer surface of the nanotubes. | ||
| Fig. 5 TEM images of (a) a cluster of ATO nanotubes and (b) a single nanotube, showing an O-ring pattern on the outer surface of the nanotubes. (c) and (d) Schematic drawings of the O-ring formation in ATO films. Arrows in (c) indicate the directions of volume contraction of the hydroxide layer. | ||
Since the hydroxide layer is revealed, the formation mechanism of these O-rings can be understood by considering the directions of volume contraction. Due to the electric field and local-heating-enhanced dehydration, the ATO nanotubes could separate from each other as elucidated in Fig. 4, where the directions of volume contraction of the hydroxide layer are normal to the walls. However, the direction of the field-induced contraction can also be parallel to the growth direction of the nanotubes (field direction), leaving some small bridges of more condensed oxide in between nanotubes. As shown in Fig. 5(c), the electric field at the pore base between two neighbouring tubes could be divided into the parallel and normal directions, leading to a volume contraction along and perpendicular to the wall. It is expected that the intervals of the O-rings (bridges), like the thickness of the barrier layer, is also a function of the applied voltage. For example, an increase of the intervals of the O-rings was observed, from ∼36.2 nm at 25 V to ∼62.0 nm at 60 V as measured from the TEM images, and the corresponding barrier thickness were ∼40.0 nm and 70.2 nm, respectively.
3.5 Porosity of anodic titanium oxide
In the same way as the formation of AAO, in the formation process of ATO we assume all the oxide anions from dissolution of titanium oxide will contribute to the oxidation of titanium at the bottom of the film, and that all the oxide anions needed for building the wall (corresponding to a net change of ΔL during the anodization time of Δt) are from the dissociation of water (Fig. 6a). The total moles (No) of the oxide anions from water dissociation during the time of Δt are those in the volume of the newly formed part of the wall corresponding to ΔL,| No = (SC − SP) × ΔL × Do | (3) |
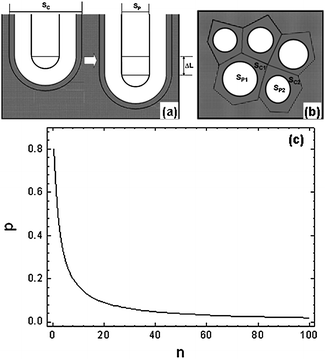 | ||
| Fig. 6 Schematic drawings of a single pore growth for a length increase of ΔL (a) and the compact pore array on top view (b). (c) Porosity of ATO (P) as a function of the relative rate of water dissociation (n) at the oxide/electrolyte interface. | ||
On the other hand, the total moles of dissolution of TiO2 in the oxide/electrolyte interface following the eqn (1) is (1/n)No. The total moles of titanium dissolved during the time of Δt are SP × ΔL × DTi, where DTi is the mole density of Ti cations in TiO2. If all the oxygen-containing anions migrate across the oxide layer to contribute to the formation of TiO2, we have
| No = (SC − SP) × ΔL × Do = n × SP × ΔL × DTi | (4) |
 | (5) |
Since the value of n describes moles of water dissociated when one mole of TiO2 dissolved, which should be constant at a certain anodization condition, n should be constant in all cells where the field strength across the barrier layer has a constant value. Therefore, the total porosity of the whole pore array is
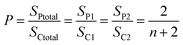 | (6) |
The P–n plot for ATO is shown in Fig. 6(c), which is similar to that for AAO. Directly measured from the TEM images of the ATO specimen prepared at 30 V in the present work, the ratio of the pore diameter to the cell diameter is about 0.348. Assuming the film has a perfect hexagonal pore array, the porosity could be written as
Thus the porosity of the TiO2 nanotubular array anodized under the given conditions is about 11.0% (Table 1), corresponding to n = 16.2. It is necessary to point out that the porosity of ATO mentioned here could only be measured near the pore base as the severe chemical etching by the electrolyte could widen the pores significantly especially at the pore mouth.
The anionic current across the oxide layer can be divided into two parts, joxide from the electric field enhanced dissolution of titanium oxide at the oxide/electrolyte interface and jwater from the dissociation of water, i.e. j = joxide + jwater, where jwater/joxide = n/2 derived from eqn (1), since the current density is proportional to the moles of anions created from the surface reactions. The porosity of the ATO film then have a relation with these current densities,
 | (7) |
According to Tafel's Law, j = j0exp(βU/d) = j0exp(βE), where j0 and β can be estimated from experiments. For example, when anodization was carried out in ethylene glycol containing 0.3 wt% NH4F and 2 wt% H2O, an empirical estimation of j0 and β could be derived by fitting the experimental data for the current density (j) and effective field strength (E) in Table 1. Then we have j0 = 4.50 × 10−4 mA and β = 10.09 nm V−1, therefore,
| j = 4.50 × 10−4 exp(10.09E) | (8) |
Analogy to the AAO case, the electric current contributed by dissolution of the barrier oxide at the pore base of ATO should have an exponential relation with the electric field strength. Therefore we can write joxide = A exp(kE), where A is the pre-exponential factor for dissolution reactions and the coefficient k depends on the working temperature and material property. Neglecting the current induced local heating of the barrier layer at the pore base, for fixed anodization conditions, A and k can be treated as constants. To fit the experimental data for the current density from dissolution of the barrier layer (joxide) and effective field strength (E) in Table 1, the empirical relationship could be derived by
| joxide = 2.50 × 10−4 exp(7.66E) | (9) |
The porosity can be written as
 | (10) |
From eqn (8) and (10), the relationship between the porosity and the ionic current density (j) can also be deduced as follows
 | (11) |
The corresponding P–E and P–j plots, together with experimental data, are shown in Fig. 7, demonstrating a good matching between the experimental data and the calculated curves.
 | ||
| Fig. 7 Porosity of ATO produced in ethylene glycol containing 0.3 wt% NH4F and 2 wt% H2O as a function of the electric field strength (a) and current density (b) across the oxide layer at the pore base. The inset of (b) shows P–j plots in a larger range of current density. The solid curves are plotted viaeqn (9) and (10), while the circles represent the experimental data. | ||
As the applied voltage is directly known from the experiments, the relationship between the porosity and the applied voltage is practically more useful than that between the porosity and the field strength. In Tafel's Law, j = j0exp(βU/d), where U/d = E and j is a function of both U and d. We assume the current density increases exponentially with the applied voltage in a steady state in the working range for anodization as implied by the observed data, then
| j = j0′exp(αU) | (12) |
Used the current density and applied voltage listed in Table 1, j0′ = 0.057 mA and α = 0.063 V−1.
A combination of eqn (8) and (12) enables us to derive a relationship between the thickness of the oxide layer and the applied voltage:
 | (13) |
 | (14) |
In another consideration, we know that the thickness of the barrier layer will be finite even at a very low voltage. We can model a relation between the thickness of the barrier layer and the voltage according to the following equation,
| d = dmax(1 − exp(−γU)) + d0 | (15) |
 | (16) |
Figs. 8(a) and (b) show the plots of porosity of ATOversus applied voltage when we regard either the current density or the barrier thickness as having an exponential relation with the applied voltage, respectively. A good agreement with the experimental results was observed in range of the working conditions for the anodization of titanium.
 | ||
| Fig. 8 Porosity of ATOversus applied voltage in ethylene glycol containing 0.3 wt% NH4F and 2 wt% H2O as a function of applied voltage, assuming that (a) the current density or (b) the barrier thickness has an exponential relation with the applied voltage. The circles represent experimental data from the present work. | ||
Eqn (13) predicts a zero thickness of oxide layer if no voltage is applied, which is not quite true as a thin native oxide layer could still form. The P–U relation described in eqn (14) would encounter certain errors while fitting the experiments, which could be much more significant in the low voltage range. Taking this into account, we are much more confident with the exponential relationship of the barrier thickness with the applied voltage.
Since both the barrier layer at pore bottom and the wall thickness are governed by the applied voltage, the established relationship of P–U implies that the pore size in ATO is also governed by the applied voltage. Although a single nanotube has an intention of increasing its pore size according to the equifield strength model (as we mentioned above and experimental observation confirmed this mechanism, e.g. the diameter of the single nanotube in Fig. 5b continuously increases from top to bottom), this self-adjustment can only be allowed in a small range since both the overall porosity and pore size are determined by the field strength. This is why a uniform pore size can be achieved in a whole ATO film (Fig. 9). When a single nanotube increases its pore size, beyond the limit determined by the porosity requirement, the nanotube may split into two or more nanotubes as shown in the inset of Fig. 9. This phenomenon was also often observed from AAO films.
 | ||
| Fig. 9 SEM image of a top view of an ATO film showing uniform pore size in a large area. The inset shows when the pore size of a single nanotube increases beyond the value restricted by the applied voltage; where there are no neighbouring nanotubes to stop its growth, it may split to two or more nanotubes. | ||
3.6 Dissolved Ti4+ cations from two interfaces
The proposed model also allows us to estimate the molar ratio of the titanium cations dissolved from TiO2 barrier layer (Tidiss) to the total titanium cations (Tilost) lost into the bulk solution during the film growth. The latter is the sum of Tidiss and the moles of titanium cations directly ejected from the hydroxide/metal interface into the electrolyte (Tieject). Using the hexagonal model, | (17) |
then,
 | (18) |
When anodization takes place at 30 V, the porosity is about 11.0% and the corresponding n is about 16.2. Consequently, only 12.4% of the total titanium cations lost during the anodization are from the dissolution of TiO2 in the oxide/electrolyte interface, while 87.6% of the titanium cations leave the hydroxide/metal interface, migrate across the barrier layer and are ejected into the electrolyte without forming oxide.
3.7. Crystallization of anodic titanium oxide
As-synthesized ATO nanotubular arrays are normally non-crystalline in both oxide and hydroxide layers. This property limits the application of the materials, since both the conductivity and the mechanical strength of these materials are low. It has been established that, compared to the amorphous and the rutile form of TiO2, the anatase phase of titanium dioxide is a preferred electrode material in dye sensitized solar cells,23 and has a higher catalytic activity.24 Furthermore, as we discussed above, due to the dehydration of titanium hydroxide, the fabricated ATO nanotubes are separated from each other, leading to a relative loose linkage of the nanotubes. The only conjunctions between the nanotubes are the so-called O-rings (Fig. 2) and a connection at the nanotube base (Fig. 4d). A weak mechanical vibration could peel off the nanotubes from an ATO film easily or even cause a collapse of the whole array structure. To overcome this problem, crystallization of the as-synthesized ATO is of interest. It has been noted that under some conditions, as-anodized ATO can be partially crystalline and polycrystalline anatase ATO can be achieved via a heat treatment at 300 °C or above, as reported by Grimes and other groups.25,26 However, microstructures of these ATO have not been extensively investigated.Based on the HRTEM studies, it was found the hydroxide layer can be partially crystallized into a polycrystalline state during dehydration enhanced by the electric field without any heat treatment.15 A large number of d-spacings measured from lattice fringes on HRTEM images indicated that these nanocrystallites are β-TiO2, monoclinic with a = 1.216, b = 0.374, c = 0.651 and β = 107.29°. In the present work, it was found that the whole hydroxide layer including the small bridges connecting the nanotubes can be crystallized after annealing at 285 °C for 24 h into a single crystal shell on the nanotubes, when some nanocrystallites were developed in the inner oxide layer. Annealing in air at 600 °C for 5 h, the sizes of monocrystalline domains increased remarkably. It is interesting to see that the crystal phase after high temperature treatment is pure anatase, as all the XRD peaks can be indexed onto this tetragonal phase with the unit cell parameters of a = 0.378 and c = 0.951 nm. Importantly, the original morphology of nanotubular array is almost intact (Fig. 10).
 | ||
| Fig. 10 (a) SEM image of an ATO nanotubular array after annealing at 600 °C. (b) Corresponding XRD pattern indexed onto the tetragonal anatase structure. | ||
Fig. 11(a) is a HRTEM image of a sample after annealing at 300 °C for 2 h, showing a small bridge connecting two nanotubes with its structure approaching a single crystal, but many oriented-domains can still be identified. This is an intermediate state of recrystallization process from polycrystalline to monocrystalline phases. Fig. 11(b) is a typical HRTEM image of recrystallized shells of nanotubes after annealing at 285 °C for 24 h. The image contrast pattern and the corresponding diffraction pattern, projected along the [13-1] zone axis of anatase, show that the whole area including bridges overlapped along the view direction as indicated by an arrow is monocrystalline. The HRTEM images from the same sample also suggested that polycrystallites were developed in the original oxide layer, leading to a smart material with polycrystalline titanium oxide nanotubes coated by a single crystal layer on the outer surface and connected by some small bridges with the same anatase phase. It is expected that further annealing may allow recrystallization expanding from the outer surface to the inner surface via an Ostwald ripening process and eventually form a connected single crystal nanotubular array. This crystallization process is similar to the recently established NARS route of crystal growth,27i.e. crystal growth can follow a reversed route: nanoparticles, aggregation, surface recrystallization and single crystals.
![HRTEM images of small bridges connecting nanotubes after recrystallization by annealing, showing (a) an intermediate state with oriented domains at 300 °C 2 h, and (b) single crystal shell viewed down the [13-1] zone axis of anatase structure at 285 °C 24 h. The arrow points two bridges overlapped along the view direction. The inset is the corresponding FFT diffraction pattern.](/image/article/2009/JM/b820504c/b820504c-f11.gif) | ||
| Fig. 11 HRTEM images of small bridges connecting nanotubes after recrystallization by annealing, showing (a) an intermediate state with oriented domains at 300 °C 2 h, and (b) single crystal shell viewed down the [13-1] zone axis of anatase structure at 285 °C 24 h. The arrow points two bridges overlapped along the view direction. The inset is the corresponding FFT diffraction pattern. | ||
4. Conclusion
The newly established equifield model can be used to interpret the formation of anodic TiO2 nanotubular arrays with a hemispherical tube bottom and a self-ordering potential. It has also been revealed that the electric field enhanced dissociation of water followed by anion migration play an important role in the formation of ATO films, i.e. governing the porosity and geometry of nanotubular arrays. The establishments of the relations between porosity and anodization conditions enable the production of ATO films to be more controllable and predictable. Crystallization of the as-synthesized amorphous ATO into anatase phase has been successfully achieved. On the other hand, as observed in experiments, O2 bubbles were often produced at the electrolyte/oxide interface during the anodization, the ionic current density thus should be slightly smaller than the measured current density. In addition, local current heating could increase the dissolution rate of titanium oxide, which might induce further deviation. Further investigations about these effects and the physico-chemical properties of the crystalline ATO films are currently being carried out in this laboratory.Acknowledgements
WZ thanks EPSRC and EaStChem for financial support.References
- F. Keller, M. S. Hunter and D. L. Robinson, J. Electrochem. Soc., 1953, 100, 411 CrossRef CAS.
- H. Tsuchiya and P. Schmuki, Electrochem. Commun, 2005, 7, 49 CrossRef CAS.
- H. Tsuchiya, J. M. Macak, I. Sieber and P. Schmuki, Small, 2005, 7, 722 CrossRef.
- I. Sieber, H. Hildebrand, A. Friedrich and P. Schmuki, Electrochem. Commun, 2005, 7, 97 CrossRef CAS.
- I. Sieber, B. Kannan and P. Schmuki, Electrochem. Solid-State Lett, 2005, 8, J10 CrossRef CAS.
- D. W. Gong, C. A. Grimes, O. K. Varghese, W. C. Hu, R. S. Singh, Z. Chen and E. C. Dickey, J. Mater. Res., 2001, 16, 3331 CrossRef CAS.
- C. R. Martin, Chem. Mater., 1996, 8, 1739 CrossRef CAS; Z. X. Su, J. Sha, G. W. Pan, J. X. Liu, D. R. Yang, C. Dickinson and W. Z. Zhou, J. Phys. Chem. B, 2006, 110, 1229 CrossRef CAS.
- O. K. Varghese, D. W. Gong, M. Paulose, K. G. Ong, E. C. Dickey and C. A. Grimes, Adv. Mater, 2003, 15, 624 CrossRef.
- G. K. Mor, M. Paulose, O. K. Varghese and C. A. Grimes, Sensor Lett., 2003, 1, 42 Search PubMed; G. K. Mor, M. A. Carvalho, O. K. Varghese, M. V. Pishko and C. A. Grimes, J. Mater. Res, 2004, 19, 628 CrossRef CAS.
- R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269 CrossRef CAS.
- G. K. Mor, K. Shankar, M. Paulose, O. K. Varghese and C. A. Grimes, Nano Lett., 2006, 6, 215 CrossRef CAS.
- G. K. Mor, K. Shankar, M. Paulose, O. K. Varghese and C. A. Grimes, Nano Lett., 2005, 5, 191 CrossRef CAS.
- B. C. Yang, M. Uchida, H. M. Kim, X. D. Zhang and T. Kokubo, Biomaterials, 2004, 25, 1003 CrossRef CAS.
- O. Jessensky, F. Müller and U. Gösele, Appl. Phys. Lett, 1998, 72, 1173 CrossRef CAS.
- Z. X. Su and W. Z. Zhou, Adv. Mater., 2008, 20, 3663 CrossRef CAS; Z. X. Su, G. Hahner and W. Z. Zhou, J. Mater. Chem., 2008, 18, 5787 RSC.
- P. A. Connor, K. D. Dobson and A. J. McQuillan, Langmuir, 1999, 15, 2402 CrossRef CAS.
- L. V. Taveira, J. M. Macak, H. Tsuchiya, L. F. P. Dick and P. Schmuki, J. Electrochem. Soc., 2005, 152, B405 CrossRef CAS.
- M. Paulose, K. Shankar, S. Yoriya, H. E. Prakasam, O. K. Varghese, G. K. Mor, T. A. Latempa, A. Fitzgerald and C. A. Grimes, J. Phys. Chem. B, 2006, 110, 16179 CrossRef CAS.
- G. K. Mor, O. K. Varghese, M. Paulose, N. Mukherjee and C. A. Grimes, J. Mater. Res., 2003, 18, 2588 CrossRef CAS.
- J. M. Macak, H. Tsuchiya and P. Schmuki, Angew. Chem., Int. Ed., 2005, 44, 2100 CrossRef CAS.
- J. Choi, R. B. Wehrspohn, J. Lee and U. Gosele, Electrochim Acta., 2004, 49, 2645 CrossRef CAS.
- J. M. Macak, H. Tsuchiya, L. Taveira, S. Aldabergerova and P. Schmuki, Angew. Chem., Int. Ed, 2005, 44, 7463 CrossRef CAS.
- N. G. Park, J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2000, 104, 8989 CrossRef CAS.
- Z. Ma, Y. H. Yue, X. Y. Deng and Z. Gao, J. Mol. Catal. A: Chem, 2002, 178, 97 CrossRef CAS; A. Wold, Chem. Mater, 1993, 5, 280 CrossRef CAS.
- S. Yoriya, G. K. Mor, S. Sharma and C. A. Grimes, J. Mater. Chem., 2008, 18, 3332 RSC.
- W. J. Lee, M. Alhoshan and W. H. Smyrl, J. Electrochem. Soc., 2006, 153, B499 CrossRef CAS.
- S. H. Xie, W. Z. Zhou and Y. Q. Zhu, J. Phys. Chem. B, 2004, 108, 11561 CrossRef CAS; X. Y. Chen, M. H. Qiao, S. H. Xie, K. N. Fan, W. Z. Zhou and H. Y. He, J. Am. Chem. Soc., 2007, 129, 13305 CrossRef CAS; J. F. Yao, D. Li, X. Y. Zhang, C. H. Kong, W. B. Yue, W. Z. Zhou and H. T. Wang, Angew. Chem., Int. Ed., 2008, 47, 8397 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2009 |


