DOI:
10.1039/B803716G
(Paper)
Faraday Discuss., 2009,
140, 81-92
Nanoparticle
catalysts with high energy surfaces and enhanced activity synthesized by electrochemical method†
Received
4th March 2008
, Accepted 9th May 2008
First published on 14th August 2008
Abstract
Electrochemical shape-controlled synthesis of metal nanocrystal (NC) catalysts bounded by high-index facets with high surface energy was achieved by developing a square-wave potential route. Tetrahexahedral Pt NCs with 24 {hk0} facets, concave hexoctahedral Pt NCs with 48 {hkl} facets, and multiple twinned Pt nanorods with {hk0} facets were produced. The method was employed also to synthesize successfully trapezohedral Pd NCs with 24 {hkk} facets, and concave hexoctahedral Pd NCs with 48 {hkl} facets. It has been tested that, thanks to the high-index facets with high density of atomic steps and dangling bonds, the tetrahexahedral Pt NCs exhibit much enhanced catalytic activity for equivalent Pt surface areas for electrooxidation of small organic fuels such as ethanol. These results demonstrate that the developed square-wave potential method has surmounted the limit of conventional chemical methods that could synthesize merely metal nanocrystals with low surface energy, and opened a new prospect avenue in shape-controlled synthesis of nanoparticle catalysts with high surface energy and enhanced activity.
1. Introduction
Metal nanoparticles display often novel properties thanks to their nanosize effects, surface effects, and other unique effects.1,2 In particular, nanoparticles of platinum group metals (PGM: Pt, Pd, Rh, Ir, Ru and Os) play a vital role as catalysts for many important reactions applied in industrial chemical processing, in petroleum reform, in motor vehicle catalytic converters that reduce exhaust pollution, in fuel cells and in sensors.3–6 Since the price of PGM is extremely high due to the rare reserve of the PGM on the earth and the continuing increase in demand, to find and design new type PGM catalysts with higher activity and stability are therefore key issues in development of the above momentous fields.7 At present, the commercially available Pt nanocrystal (NC) catalysts exist often as cubes, cuboctahedra, tetrahedra and octahedra, which are enclosed with low energy surfaces characterized by “low-index” facets such as {100} and {111}.8 From the knowledge gained in studies of model catalysis using single crystal planes, it is known that the “low-index” planes do not present, in general, good catalytic properties; and instead, the “high-index” planes with high densities of atomic steps, ledges, and kinks display often higher catalytic activity and stability.9–11 Unfortunately, it is rather challenging to synthesize metal nanoparticles enclosed by high-index facets. The surface energy of different crystal planes of face-centered cubic (fcc) metals such as Pt is increased in the order of γ{111} < γ{100} < γ{110} < γ{hkl}.12 As a consequence, the growth rate in the direction perpendicular to a high-index facet with high surface energy is much faster than that along the normal direction of a low-index facet, which results in a rapid disappearance of high-index facets during the formation of nanoparticles,13 and yields NCs with shapes of cube, cuboctahedron, tetrahedron and octahedron, as those produced in shape-controlled synthesis through conventional chemical ways.14–16
We have developed, recently, an electrochemical square-wave potential method to control the growth and the surface structure of metal nanoparticles, and synthesized successfully tetrahexahedral (THH) Pt NCs.17,18 This new Pt NC is enclosed by 24 high-index facets of {730} and vicinal planes, and exhibits a superior catalytic activity and stability; its electrocatalytic activity per unit area can be as much as four times of the existing commercial Pt catalysts.
In the current paper, we will present our new results concerning synthesis of nanoparticle catalysts of PGM enclosed by high energy surfaces, including (1) single crystalline nanoparticles of different shapes, such as tetrahexahedron (THH) enclosed by {hk0} facets, trapezohedron by {hkk}, and concave hexoctahedron by {hkl}; (2) multiple twinned crystals. The successful synthesis of nanoparticle catalysts enclosed by high-index facets has promoted effectively the study that bridges the fundamental gained from model catalysts of single crystal planes with the design and fabrication of real catalysts of high performances.
2. Correlation between crystal planes and nanocrystal shape
For fcc metals, such as Pt, a unit stereographic triangle (Fig. 1) is usually employed to illustrate the coordinates of different crystal planes.19 The three low-index or basal planes, i.e. (111), (100), and (110) locate at three vertexes. Among them, the (111) and (100) planes are flat with closely packed surface atoms, whereas the (110) plane is rough with step atoms. The coordination numbers (CNs) of top-layer atoms on (111), (100), and (110) are 9, 8, and 7, respectively. Other planes located at the sidelines and inside of the triangle are high-index planes. The three sidelines represent [01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], [1
], [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0], and [001] crystallographic zones, the planes lying in these zones exhibit terrace-step structure.20 The CNs of step atoms on the planes belonging to the [001] zone is 6, and 7 for planes lying in the other two zones. In the [001] zone, the Pt(210) plane possesses the highest density of step atoms (5.81 × 1014 cm−2). Along with decreasing the width of (100) terraces, the density of step atoms decreases to 4.11 × 1014 cm−2 on Pt(310), and to 2.55 × 1014 cm−2 on Pt(510). The planes inside the triangle are distinguished by their chirality and kink atoms with CNs of 6. These low-coordinated step and kink atoms (CNs = 6–7) intrinsically exhibit very high chemical activity.21
0], and [001] crystallographic zones, the planes lying in these zones exhibit terrace-step structure.20 The CNs of step atoms on the planes belonging to the [001] zone is 6, and 7 for planes lying in the other two zones. In the [001] zone, the Pt(210) plane possesses the highest density of step atoms (5.81 × 1014 cm−2). Along with decreasing the width of (100) terraces, the density of step atoms decreases to 4.11 × 1014 cm−2 on Pt(310), and to 2.55 × 1014 cm−2 on Pt(510). The planes inside the triangle are distinguished by their chirality and kink atoms with CNs of 6. These low-coordinated step and kink atoms (CNs = 6–7) intrinsically exhibit very high chemical activity.21
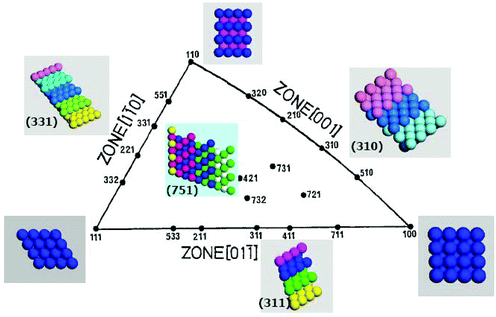 |
| | Fig. 1 Unit stereographic triangle of fcc single-crystal and models of surface atomic arrangement. | |
In analogue with the unit stereographic triangle, there is also an intrinsic triangle that coordinates the crystal surface index and the shape of metal NCs,22 as shown in Fig. 2. Three vertexes represent the coordinates of polyhedral nanocrystals bounded by basal facets, i.e. cube covered by {100}, octahedron by {111}, and rhombic dodecahedron by {110}. The polyhedral NCs lying in the sidelines of the triangle are THH bounded by {hk0} facets, trapezohedra by {hkk} facets, and trisoctahedra by {hhl} facets. They all have 24 facets. The polyhedra situated inside the triangle are hexoctahedra bounded by 48 {hkl} (h > k > l > 0) facets. These polyhedra belong to Catalan solids or Archimedean duals,22 and their shapes are complex and unconventional. To identify them quickly, the THH can be considered as a cube with each face capped by a square pyramid; the trisoctahedron can be considered as an octahedron with each face capped by a pyramid. It is worthwhile to note that along with variation of the geometric parameters of NCs, their surface structure can be changed following those planes as illustrated in the unit stereographic triangle shown in Fig. 1. Taking the THH as an example, the relationship between the facet index (hk0) and the nanocrystal parameters, i.e. the height of the square pyramid, b, and the side length of the cube, a, is expressed as follows:
| | 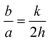 | (1) |
 |
| | Fig. 2 Unit stereographic triangle of polyhedral nanocrystals bounded by different crystal planes. | |
3. Electrochemically shape-controlled synthesis of Pt, Pd nanocrystals with high-index facets
We have developed an electrochemical route for synthesis of PGM nanocrystals bounded by high-index facets.17 In brief, the electrochemical synthesis was carried out in a standard three-electrode cell at room temperature (about 25 °C). The working electrode was glassy carbon (GC, ϕ = 6 mm), the counter and reference electrodes were a Pt foil and a saturated calomel electrode (SCE), respectively. Electrode potential was controlled by a PAR 263A potentiostat/galvanostat (EG&G) via home-developed software that can generate arbitrary potential waveform. The electrochemical synthesis procedures include: (1) Pt nanospheres of ∼750 nm in diameter were deposited on the GC substrate by pulse electrodeposition in 2 mM K2PtCl6 + 0.5 M H2SO4 solution; (2) the Pt nanospheres were then subjected to a treatment of square-wave potential at 10 Hz, with upper potential of 1.20 V and lower potential between −0.10 to −0.20 V, in a solution of 0.1 M H2SO4 + 30 mM ascorbic acid for 5–60 min. The Pt NCs bounded by high-index facets were grown exclusively on GC surface at the expense of Pt nanospheres.
Fig. 3 shows the scanning electron microscopy (SEM) images of THH Pt NCs with different sizes by controlling the growth time. Three perfect square pyramids can be seen clearly, which is fully consistent with the THH model. The size distribution of THH Pt NCs is relatively narrow with relative standard deviation ranging from 10% to 15%, and the yield in the final products is over 90%.
 |
| | Fig. 3 Model of a tetrahexahedron (THH) and atomic arrangement structure of {hk0} high-index planes (above). SEM images of THH Pt NCs of different sizes prepared by an electrochemical square-wave potential method and supported on GC. | |
The surface structure (Miller indices) of THH Pt NCs was identified to be mainly {730} facets by high-resolution transmission electron microscopy (HRTEM) and selected-area electron diffraction (SAED). Besides, some THH Pt NCs bounded by {210}, {310}, or {520} were also observed. The atomic arrangements of these surfaces are also illustrated in Fig. 3. The density of step atoms on Pt(730) is as high as 5.1 × 1014 cm−2, that is, 43% of the total number of atoms on the surface. Therefore, the THH Pt NCs exhibit high electrocatalytic activity. As for the electrooxidation of ethanol, the steady-state current density recorded at 0.25 V is 0.39 mA cm−2 on the THH Pt NCs of 81 nm, 0.16 mA cm−2 on Pt nanospheres of 115 nm, and 0.12 mA cm−2 on commercial 3.2 nm Pt/C catalyst, as demonstrated in Fig. 4. In addition, at a fixed current density of technical interest, such as 0.20 mA cm−2, the oxidation potential on the THH Pt NCs was shifted negatively about 80 mV in comparison with that of the Pt nanospheres and the commercial Pt/C catalyst.
 |
| | Fig. 4 Comparison of electrocatalytic activity (current density) towards ethanol oxidation at 0.25 V on THH Pt NCs (81 nm), Pt nanospheres (115 nm, the sphere is composed of primary Pt nanoparticles of ~3–5 nm), and commercial Pt/C (3.2 nm) catalysts. | |
It was found that the formation of THH Pt NCs with high-index facts is related to the oxygen adsorption/desorption generated by square-wave potential. Under this condition, low-index facets with high coordinated surface atoms, such as Pt(111) and Pt(100), are disturbed through site exchange between Pt and oxygen, whereas, high-index facets of {hk0} with low coordinated surface atoms, such as {730} and {210} are retained.
Our recent progresses confirmed that the electrochemical square-wave potential route can be further extended to synthesize NCs of other shapes with high-index facets besides the THH Pt NCs.
3.2 Concave hexoctahedral Pt nanocrystals
In the square-wave potential route, when the 30 mM ascorbic acid is replaced by 50 mM sodium citrate, complex concave polyhedral Pt NCs were obtained. As shown in Fig. 5, on this concave polyhedral Pt nanocrystal, six facets intersect on a point in a three-fold axis, and four facets intersect on a point in a four-fold axis. This symmetry is identical to that of the convex hexoctahedron illustrated in Fig. 2. The bottom left inset to Fig. 5 is a model of concave hexoctahedron bounded by {321} facets, whose shape is similar to the Pt NCs seen from an SEM image. The result indicates that the Pt NCs are of concave hexoctahedral shape and bounded by 48 {hkl} high-index facets. In geometry, the THH can be easily transformed into concave hexoctahedron just by shrinking along the 〈110〉 direction. As a result, one {h′k′0} facet will be split into two {hkl} facets in the transformation of a THH to concave hexoctahedron.
 |
| | Fig. 5
SEM images of concave hexoctahedral Pt NCs with {hkl} facets prepared by electrochemical square-wave potential method. The inset illustrates a model of concave hexoctahedron bounded by {321} facets. | |
3.3 Trapezohedral and concave hexoctahedral Pd nanocrystals
Pd
nanoparticles are also very important electrocatalysts, especially for the electrooxidation of formic acid. The electrochemical square-wave potential route can also be applied to synthesize Pd NCs with high-index facets. SEM images of as-prepared Pd NCs on indium-tin-oxide (ITO) glass substrate are illustrated in Fig. 6. We can observe Pd NCs of trapezohedral shape bounded by 24 {hkk} high-index facets in Fig. 6a and b, and Pd NCs with concave hexoctahedral shape bounded by 48 {hkl} high-index facets in Fig. 6c. Although the exact surface structure, i.e., Miller indices of these Pd NCs are yet unknown due to the complexity of their shape, these preliminary results demonstrate that the square-wave potential route is a powerful method to synthesize metal nanoparticles bounded by high-index facets.
 |
| | Fig. 6
SEM images of trapezohedral Pd NCs with {hkk} facets (a and b), and concave hexoctahedral Pd NCs with {hkl} facets (c) prepared by electrochemical square-wave potential method and supported on ITO substrate. | |
4. Multiple twinned crystalline Pt nanorods with high-index facets
Great efforts have been devoted to the synthesis of metal nanorods and nanowires due to their unique physical and chemical properties, and important applications in the fabrication of nanoscale devices.23,24 The properties of nanorods can be tuned by controlling their aspect ratio and size.25,26 Recent studies have shown that the surface structure of nanorods can also significantly affect their properties including thermal stability, chemical reactivity and surface functionalization.24,27–29 Despite a variety of methods having been developed to synthesize metal nanorods in the last decade,30–34 only limited cases have shown the control of surface structure. Metal nanorods grown in rigid templates usually expose a polycrystalline surface with irregular atom arrangement.35 Although rod-shaped micelles or localized oxidative etching can be used to synthesize several kinds of metal single crystalline nanorods enclosed by a mixture of {100}, {111} and {110} facets, they are generally limited in Au and Pd nanorods.36–39 The growth of metal nanorods with fivefold twinned structure is relatively easy, since the growth along lateral direction is greatly inhibited due to the stress originated from structure mismatch.40 The fivefold twinned metal nanorods exhibit highly faceted structure: five {100} facets as side surfaces, and five {111} facets as end surfaces.40 They are frequently observed in Au, Ag, Cu, and even in Pd,41–45 but rarely in Pt.46
Recently, we extended the electrochemical square-wave potential route to synthesize fivefold twinned Pt nanorods with {hk0} high-index facets. Interestingly, the indices of the facets, i.e. the value of h and k, vary along the geometry of Pt nanorods.
4.1 Synthesis of Pt nanorods
The synthesis processes of the Pt nanorods are similar to those of the THH Pt NCs, except that the GC electrode loading Pt nanospheres was exposed in air for 3–5 h prior to the treatment of square-wave potential. It was found that the exposure could decrease the activity of the GC surface, on which new Pt nanocrystals could barely grow during the treatment of square-wave potential. Instead, Pt nanorods grew on the Pt nanospheres. It has confirmed that this step is crucial for the synthesis of the Pt nanorods. If the procedure of exposure to air was skipped, only THH Pt NCs grown on GC were obtained, as shown in Fig. 3.17 If the exposure time was shortened to 1 h, both THH Pt NCs on GC and Pt nanorods on the Pt nanospheres were produced.
4.2 Characterization of Pt nanorods
Fig. 7a illustrates a typical SEM image of the as-prepared Pt nanorods with growth time of 30 min. The yield of Pt nanorods is about 30%. Other irregular nanostructures are the residua of Pt nanospheres. The nanorods are not uniform in diameter along the longitudinal axis; broadest at the middle and gradually tapering to both ends. The average diameter of the nanorods measured at the middle is 124 nm. The length varies from 0.7 to 1.4 μm, and the aspect ratio of Pt nanorods is about 8. Fig. 7b shows a high-magnification SEM image of a Pt nanorod. Zigzag-arranged facets can be observed on the surface of the middle part. Also, there are several ridges along the nanorod. Very interestingly, on both ends of the nanorod, five facets can be discerned clearly from the SEM image, which indicates that the ends are enclosed by ten facets, i.e. the ends are decagonal pyramids.
 |
| | Fig. 7
SEM images of Pt nanorods. (a) Low magnification. (b) High magnification, showing fine surface facets. | |
The structure of the Pt nanorod was analyzed by SAED and HRTEM. A TEM image of the Pt nanorod is presented in Fig. 8a. The wriggling border of the nanorod is related to the zigzag pattern on the surface. Fig. 8b and c demonstrate two typical SAED patterns obtained from the Pt nanorod. Each diffraction pattern contains two sets of diffraction from the face-centered cubic Pt. The growth direction of the Pt nanorod was determined to be along [110], according to the (220) diffraction. In Fig. 8b, the square (solid line) and rectangular (dashed line) symmetrical diffractions correspond to [001] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 12] zone axes, respectively. The SAED pattern in Fig. 8c was obtained after rotating the nanorod by 18° along the longitudinal axis. The rectangular (solid line) and rhombic (dashed line) symmetrical diffractions correspond to [ 1
12] zone axes, respectively. The SAED pattern in Fig. 8c was obtained after rotating the nanorod by 18° along the longitudinal axis. The rectangular (solid line) and rhombic (dashed line) symmetrical diffractions correspond to [ 1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and [1
0] and [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] zone axes, respectively. These results are well consistent with those obtained from fivefold twinned nanorods of Au, Ag and Cu,41,47,48 demonstrating that the as-prepared Pt nanorod is of fivefold twinned structure.
] zone axes, respectively. These results are well consistent with those obtained from fivefold twinned nanorods of Au, Ag and Cu,41,47,48 demonstrating that the as-prepared Pt nanorod is of fivefold twinned structure.
 |
| | Fig. 8 (a) TEM image of a Pt nanorod. (b), (c) Two typical SAED patterns obtained from the Pt nanorod, demonstrating that the Pt nanorod is of fivefold twinned structure. (d) A model of typical fivefold twinned nanorod. | |
4.3 Surface structure of the Pt nanorods
The structure of the fivefold twinned nanorod has been well documented.41–44,47,48 It consists of five sub-crystals twinned at (111) planes, with side surfaces bounded by five {100} facets and end surfaces by five {111} facets, as illustrated in Fig. 8d. Besides, the diameter of nanorods is uniform. Clearly, although the Pt nanorod is of fivefold twinned structure, its morphology, especially the zigzag pattern on side surfaces and the sharp ends, is quite different from that of the typical fivefold twinned nanorod (Fig. 8d). The fine facets on side surfaces of the Pt nanorod are not likely to be {100} facets, since the {100} facets should be parallel to the longitudinal [110] axis, whereas the fine facets of the Pt nanorod obviously do not satisfy this criterion. Moreover, the end surfaces of the Pt nanorod are not {111} facets, because the end of the typical fivefold twinned nanorod is a pentagonal pyramid, while the end of the as-prepared Pt nanorod is an elongated decagonal pyramid. Since the growth of the Pt nanorods are under similar conditions to those of producing the THH Pt NCs, the surface facets of Pt nanorods are very likely to be {hk0} high-index facets. We then carefully analyzed the surface structure of the ends and the middle part of the Pt nanorods, respectively.
Based on the structure characteristic of fivefold twinned nanorod, one {111} facet will evolve into two {hk0} facets if the end of nanorod is bounded by {hk0} facets. Correspondingly, the shape of the end will change from pentagonal pyramid to decagonal pyramid, as demonstrated in Fig. 9a. The enlarged SEM image of the end of the Pt nanorod is shown in Fig. 9b, from which five facets can be discerned clearly, confirming the shape of decagonal pyramid. The good consistency between the model and experimental result demonstrates that the end of the Pt nanorod is bounded by {hk0} high-index facets. The value of h and k can be determined by measuring the geometrical parameters, i.e. the ratio of height to width (H/L) and the cone angle (θ) of the decagonal pyramid:
| |  | (2) |
| | 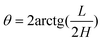 | (3) |
 |
| | Fig. 9 (a) Schematic model of decagonal pyramid bounded by ten {hk0} facets with fivefold twinned structure. (b) SEM image of the sharp end of a Pt nanorod. Both the cone angles (θ) and H/L indicate the sharp end is enclosed by a {410} facet. | |
Table 1 lists the theoretical values of H/L and θ for decagonal pyramids bounded by different {hk0} facets. The H/L values of the as-prepared Pt nanorods were measured between 2.7 and 2.9 for the sharp ends, and between 1.2 and 1.7 for the obtuse ends. By comparing these measured values with the theoretical ones listed in Table 1, we can identify that the sharp ends of the Pt nanorods are practically enclosed by {410} facets, and the obtuse ends are enclosed by {320}, {210} or {730} facets.
Table 1 Theoretical ratio of height to width (H/L) and cone angle (θ) of decagonal pyramids bounded by {hk0} facets
| {hk0} |
{320} |
{210} |
{730} |
{520} |
{310} |
{410} |
{510} |
|
H
/L |
1.21 |
1.52 |
1.72 |
1.82 |
2.12 |
2.73 |
3.34 |
|
θ
|
44.77° |
36.47° |
32.42° |
30.70° |
26.48° |
20.74° |
17.03° |
Fig. 10a depicts the magnified SEM image of the middle part of the Pt nanorod, from which the fine facets and ridges along the nanorod can be seen more clearly. To identify the indices of the fine facets, we should first determine twin boundaries. Two kinds of ridges appearing alternatively on the nanorod can be distinguished, denoted as I and II in Fig. 10a. It can be observed that the fine facets at the two sides of the ridge I are essentially symmetrical to each other, while those at the two sides of the ridge II are asymmetrical. According to the crystal symmetry, the symmetrical facets are more likely on the same sub-crystal, so ridge II should be the boundary of two sub-crystals. Four fine facets in the boxed area marked in Fig. 10a can be considered as a surface unit. This kind of arrangement of the fine facets can be observed on a THH bouned by {hk0} facets. Every four {hk0} facets, i.e. (k0h), (0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) h), (0kh), (
h), (0kh), (![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 0h), situated in different directions, form a surface unit of the Pt nanorod, which repeatedly arranges along the growth direction of the Pt nanorod and results in the zigzag pattern on the crystal surface. The indices of these {hk0} facets can be determined by measuring the slope angle (ϕ) between the border line and the longitudinal axis in the TEM image, as illustrated in Fig. 10c. The angle of ϕ was measured to be 15.2 ± 0.5°, so the corresponding θ is about 30° as θ = 2ϕ. By comparing these values of θ with the theoretical values listed in Table 1, the surface of the middle part of the nanorod is mainly composed of {520} facets.
0h), situated in different directions, form a surface unit of the Pt nanorod, which repeatedly arranges along the growth direction of the Pt nanorod and results in the zigzag pattern on the crystal surface. The indices of these {hk0} facets can be determined by measuring the slope angle (ϕ) between the border line and the longitudinal axis in the TEM image, as illustrated in Fig. 10c. The angle of ϕ was measured to be 15.2 ± 0.5°, so the corresponding θ is about 30° as θ = 2ϕ. By comparing these values of θ with the theoretical values listed in Table 1, the surface of the middle part of the nanorod is mainly composed of {520} facets.
 |
| | Fig. 10 (a) Magnified SEM image of the middle part of a Pt nanorod; (b) schematic illustration of the surface unit bounded by {hk0} facets. (c) Magnified TEM image of the middle part of another nanorod, showing that the surfaces are mainly {520} facets. | |
The surface structures of the Pt nanorod are summarized in Fig. 11, i.e. the sharp end is enclosed by {410} facets, the obtuse end by {320}, {210} or {730} facets, the middle part mainly by the zigzag-arranged {520} facets. The densities of stepped atoms on these facets are significantly different, among which the {320} facet has the highest density and the {410} facet holds the lowest one. The difference in density of stepped atoms on different parts of the Pt nanorod may correlate with the different growth rate. During the growth, the sharp end grows outward, so it can receive more Pt ions from solution, i.e. the sharp end has the highest growth rate. In contrast, the other end rooted on the Pt nanosphere has the lowest growth rate due to the interparticle diffusion coupling between the nanorod and the Pt nanosphere.49 In this study, the {hk0} facets were formed through the repetitive oxygen adsorption/desorption generated by square-wave potential.17 So, slower growth rate of the obtuse end implies an intensive surface reconstruction by oxygen, resulting in {hk0} facets with higher density of stepped atoms, such as {320} and {210} facets. On the other hand, the faster growth rate of the sharp end leads to the formation of a surface with a lower density of stepped atoms, such as {410}. These results demonstrate that the indices of {hk0} facets of Pt NCs can be tuned by changing the growth rate during the square-wave potential treatment.
 |
| | Fig. 11 The Miller indices and the densities of stepped atom of {hk0} facets at different parts of the Pt nanorod. | |
Furthermore, we have also synthesized fivefold twinned Pd nanorods with {hk0} and {hkk} type high-index facets, and found that the catalytic activity of Pd nanorods with {hkk} facets (near {15 1 1} facet) for the electrooxidation of ethanol in alkaline solution was about 2.5 times larger than that of a commercial Pd black catalyst.
5. Conclusions
In the current paper, we report the development of a novel square-wave potential route that has successfully overcome the difficulties in synthesis of Pt nanocrystals (NCs) bounded by high-index facets with high surface energy. It has revealed that the dynamic oxygen adsorption/desorption mediated by square-wave potential and the difficulty of site-exchange between oxygen and surface atoms of open-structure planes play key roles in the electrochemically shape-controlled synthesis of metal nanoparticle catalysts with high-index facets. By this method, tetrahexahedral (THH) Pt NCs bounded by 24 {hk0} high-index facets, concave hexoctahedral Pt NCs by 48 {hkl} facets, trapezohedral Pd NCs by 24 {hkk} facets, and concave hexoctahedral Pd NCs by 48 {hkl} facets have been successfully synthesized. Besides single crystalline nanoparticle catalysts, fivefold twinned Pt nanorods by high-index facets are also obtained by controlling the nucleation mode. It was determined that the sharp end of the Pt nanorods was enclosed by ten {410} facets, the obtuse end by {320}, {210} or {730} facets, and the middle part mainly by the zigzag-arranged {520} facets. Owing to the high density of atomic steps and dangling bonds on the high-index facets, the nanoparticle catalysts bounded by high-index facets display in general high catalytic reactivity and stability. Such excellent catalytic properties were confirmed on the THH Pt NCs with {hk0} facets and also on the Pd nanorods with {hkk} facets towards electrooxidation of small organic fuels. These results demonstrate that square-wave potential is a versatile method to synthesize metal NCs bounded by high-index facets. The study has opened a new prospect avenue in shape-controlled synthesis of nanoparticle catalysts with high performances.
Acknowledgements
This study was supported by NSFC (grant Nos. 20673091, 20503023, 2043060) and Ministry of Science and Technology of China (2002CB211804 and 2007DFA40890) and by the Natural Science Foundation of Fujian Province of China (No.2008I0025). The authors are grateful to Prof. Z. X. Xie for helpful discussion on the studies of Pt nanorods.
References
- A. Roucoux, J. Schulz and H. Patin, Chem. Rev., 2002, 102, 3757 CrossRef CAS.
- C. Burda, X. B. Chen, R. Narayanan and M. A. El-Sayed, Chem. Rev., 2005, 105, 1025 CrossRef CAS.
- A. T. Bell, Science, 2003, 299, 1688 CrossRef CAS.
- R. M. Heck and R. J. Farrauto, Appl. Catal., A, 2001, 221, 443 CrossRef CAS.
-
J. Larminie, A. Dicks, Fuel Cell Systems Explained, John Wiley & Sons, Chichester, West Sussex, 2nd edn, 2003 Search PubMed.
- F. Favier, E. C. Walter, M. P. Zach, T. Benter and R. M. Penner, Science, 2001, 293, 2227 CrossRef CAS.
- D. J. Berger, Science, 1999, 286, 49 CrossRef CAS.
- L. C. Gontard, L. Y. Chang, C. J. D. Hetherington, A. I. Kirkland, D. Ozkaya and R. E. Dunin-Borkowski, Angew. Chem., Int. Ed., 2007, 46, 3683 CrossRef CAS.
-
G. A. Somorjai, Chemistry in Two Dimensions: Surfaces, Cornell University Press, Ithaca, 1981 Search PubMed.
- S. G. Sun, A. C. Chen, T. S. Huang, J. B. Li and Z. W. Tian, J. Electroanal. Chem., 1992, 340, 213 CrossRef CAS.
- G. A. Attard, J. Phys. Chem. B, 2001, 105, 3158 CrossRef CAS.
- Z. L. Wang, J. Phys. Chem. B, 2000, 104, 1153 CrossRef CAS.
-
H. E. Buckley, Crystal growth, Wiley, New York, 1951 Search PubMed.
- T. S. Ahmadi, Z. L. Wang, T. G. Green, A. Henglein and M. A. El-Sayed, Science, 1996, 272, 1924 CrossRef CAS.
- H. Song, F. Kim, S. Connor, G. A. Somorjai and P. D. Yang, J. Phys. Chem. B, 2005, 109, 188 CrossRef CAS.
- J. T. Ren and R. D. Tilley, J. Am. Chem. Soc., 2007, 129, 3287 CrossRef CAS.
- N. Tian, Z. Y. Zhou, S. G. Sun, Y. Ding and Z. L. Wang, Science, 2007, 316, 732 CrossRef CAS.
- Y. Ding, Y. Gao, Z. L. Wang, N. Tian, Z. Y. Zhou and S. G. Sun, Appl. Phys. Lett., 2007, 91, 121901 CrossRef.
-
J. F. Nicholas, An Atlas of Models of Crystal Surfaces, Gordon & Breach, New York, 1965 Search PubMed.
- M. A. Van Hove and G. A. Somorjai, Surf. Sci., 1980, 92, 489 CrossRef CAS.
- G. A. Somorjai and D. W. Blakely, Nature, 1975, 258, 580 CrossRef CAS.
- A. A. Proussevitch and D. L. Sahagian, Comput. Geosci., 2001, 27, 441 CrossRef.
- Y. N. Xia, P. D. Yang, Y. G. Sun, Y. Y. Wu, B. Mayers, B. Gates, Y. D. Yin, F. Kim and Y. Q. Yan, Adv. Mater., 2003, 15, 353 CrossRef CAS.
- C. J. Murphy, T. K. San, A. M. Gole, C. J. Orendorff, J. X. Gao, L. Gou, S. E. Hunyadi and T. Li, J. Phys. Chem. B, 2005, 109, 13857 CrossRef CAS.
- M. A. El-Sayed, Acc. Chem. Res., 2001, 34, 257 CrossRef CAS.
- C. J. Murphy and N. R. Jana, Adv. Mater., 2002, 14, 80 CrossRef CAS.
- Y. Wang, S. Teitel and C. Dellago, Nano Lett., 2005, 5, 2174 CrossRef CAS.
- J. H. Song, F. Kim, D. Kim and P. D. Yang, Chem.–Eur. J., 2005, 11, 910 CrossRef CAS.
- J. K. Diao, K. Gall and M. L. Dunn, Nat. Mater., 2003, 2, 656 CrossRef CAS.
- Y. G. Sun, B. Gates, B. Mayers and Y. N. Xia, Nano Lett., 2002, 2, 165 CrossRef CAS.
- H. J. Choi, H. K. Seong, J. Chang, K. I. Lee, Y. J. Park, J. J. Kim, S. K. Lee, R. R. He, T. Kuykendall and P. D. Yang, Adv. Mater., 2005, 17, 1351 CrossRef CAS.
- J. C. Hulteen and C. R. Martin, J. Mater. Chem., 1997, 7, 1075 RSC.
- J. Y. Chen, T. Herricks, M. Geissler and Y. N. Xia, J. Am. Chem. Soc., 2004, 126, 10854 CrossRef CAS.
- M. P. Zach, K. H. Ng and R. M. Penner, Science, 2000, 290, 2120 CrossRef CAS.
- M. Tian, J. Wang, J. Kurta, T. E. Mallouk and M. H. W. Chan, Nano Lett., 2003, 3, 919 CrossRef CAS.
- Y. Y. Yu, S. S. Chang, C. L. Lee and C. R. C. Wang, J. Phys. Chem. B, 1997, 101, 6661 CrossRef CAS.
- Z. L. Wang, M. B. Mohamed, S. Link and M. A. El-Sayed, Surf. Sci., 1999, 440, L809 CrossRef CAS.
- H. A. Keul, M. Möller and M. R. Bockstaller, Langmuir, 2007, 23, 10307 CrossRef CAS.
- Y. J. Xiong, H. G. Cai, B. J. Wiley, J. G. Wang, M. J. Kim and Y. N. Xia, J. Am. Chem. Soc., 2007, 129, 3665 CrossRef CAS.
- V. G. Gryaznov, J. Heydenreich, A. M. Kaprelov, S. Nepijko, A., A. E. Romanov and J. Urban, Cryst. Res. Technol., 1999, 34, 1091 CrossRef CAS.
- I. Lisiecki, A. Filankembo, H. Sack-Kongehl, K. Weiss, M. P. Pileni and J. Urban, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 4968 CrossRef CAS.
- C. J. Johnson, E. Dujardin, S. A. Davis, C. J. Murphy and S. Mann, J. Mater. Chem., 2002, 12, 1765 RSC.
- Y. G. Sun, B. Mayers, T. Herricks and Y. N. Xia, Nano Lett., 2003, 3, 955 CrossRef CAS.
- S. H. Zhang, Z. Y. Jiang, Z. X. Xie, X. Xu, R. B. Huang and L. S. Zheng, J. Phys. Chem. B, 2005, 109, 9416 CrossRef CAS.
- Y. Xiong, H. Cai, Y. Yin and Y. N. Xia, Chem. Phys. Lett., 2007, 440, 273 CrossRef CAS.
- A. J. Melmed and D. O. Hayward, J. Chem. Phys., 1959, 31, 545 CrossRef CAS.
- C. Lofton and W. Sigmund, Adv. Funct. Mater., 2005, 15, 1197 CrossRef CAS.
- H. Y. Chen, Y. Gao, H. C. Yu, H. R. Zhang, L. B. Liu, Y. G. Shi, H. F. Tian, S. S. Xie and J. Q. Li, Micro, 2004, 35, 4694 Search PubMed.
- M. Z. Liu and P. Guyot-Sionnest, J. Phys. Chem. B, 2005, 109, 22192 CrossRef CAS.
Footnote |
| † The HTML version of this article has been enhanced with colour images. |
|
| This journal is © The Royal Society of Chemistry 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], [1
], [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0], and [001] crystallographic zones, the planes lying in these zones exhibit terrace-step structure.20 The CNs of step atoms on the planes belonging to the [001] zone is 6, and 7 for planes lying in the other two zones. In the [001] zone, the Pt(210) plane possesses the highest density of step atoms (5.81 × 1014 cm−2). Along with decreasing the width of (100) terraces, the density of step atoms decreases to 4.11 × 1014 cm−2 on Pt(310), and to 2.55 × 1014 cm−2 on Pt(510). The planes inside the triangle are distinguished by their chirality and kink atoms with CNs of 6. These low-coordinated step and kink atoms (CNs = 6–7) intrinsically exhibit very high chemical activity.21
0], and [001] crystallographic zones, the planes lying in these zones exhibit terrace-step structure.20 The CNs of step atoms on the planes belonging to the [001] zone is 6, and 7 for planes lying in the other two zones. In the [001] zone, the Pt(210) plane possesses the highest density of step atoms (5.81 × 1014 cm−2). Along with decreasing the width of (100) terraces, the density of step atoms decreases to 4.11 × 1014 cm−2 on Pt(310), and to 2.55 × 1014 cm−2 on Pt(510). The planes inside the triangle are distinguished by their chirality and kink atoms with CNs of 6. These low-coordinated step and kink atoms (CNs = 6–7) intrinsically exhibit very high chemical activity.21







![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 12] zone axes, respectively. The SAED pattern in Fig. 8c was obtained after rotating the nanorod by 18° along the longitudinal axis. The rectangular (solid line) and rhombic (dashed line) symmetrical diffractions correspond to [ 1
12] zone axes, respectively. The SAED pattern in Fig. 8c was obtained after rotating the nanorod by 18° along the longitudinal axis. The rectangular (solid line) and rhombic (dashed line) symmetrical diffractions correspond to [ 1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and [1
0] and [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] zone axes, respectively. These results are well consistent with those obtained from fivefold twinned nanorods of Au, Ag and Cu,41,47,48 demonstrating that the as-prepared Pt nanorod is of fivefold twinned structure.
] zone axes, respectively. These results are well consistent with those obtained from fivefold twinned nanorods of Au, Ag and Cu,41,47,48 demonstrating that the as-prepared Pt nanorod is of fivefold twinned structure.

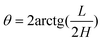

![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) h), (0kh), (
h), (0kh), (![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 0h), situated in different directions, form a surface unit of the Pt nanorod, which repeatedly arranges along the growth direction of the Pt nanorod and results in the zigzag pattern on the crystal surface. The indices of these {hk0} facets can be determined by measuring the slope angle (ϕ) between the border line and the longitudinal axis in the TEM image, as illustrated in Fig. 10c. The angle of ϕ was measured to be 15.2 ± 0.5°, so the corresponding θ is about 30° as θ = 2ϕ. By comparing these values of θ with the theoretical values listed in Table 1, the surface of the middle part of the nanorod is mainly composed of {520} facets.
0h), situated in different directions, form a surface unit of the Pt nanorod, which repeatedly arranges along the growth direction of the Pt nanorod and results in the zigzag pattern on the crystal surface. The indices of these {hk0} facets can be determined by measuring the slope angle (ϕ) between the border line and the longitudinal axis in the TEM image, as illustrated in Fig. 10c. The angle of ϕ was measured to be 15.2 ± 0.5°, so the corresponding θ is about 30° as θ = 2ϕ. By comparing these values of θ with the theoretical values listed in Table 1, the surface of the middle part of the nanorod is mainly composed of {520} facets.

