Bridging the gap between nanoparticles and single crystal surfaces
Payam
Kaghazchi
a,
Felice C.
Simeone
b,
Khaled A.
Soliman
b,
Ludwig A.
Kibler
b and
Timo
Jacob
*ab
aFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, D-14195, Berlin, Germany. E-mail: jacob@fhi-berlin.mpg.de; Fax: +49-(0)30-8413-4701; Tel: +49-(0)30-8413-4816
bInstitut für Elektrochemie, Universität Ulm, Ulm, D-89081, Germany
First published on 7th August 2008
Abstract
Using density functional theory calculations and the extended ab initio atomistic thermodynamics approach, we studied the adsorption of oxygen on the different surface faces, which are involved in the faceting of Ir(210). Constructing the (p,T)-surface phase diagrams of the corresponding surfaces in contact with an oxygen atmosphere, we find that at high temperatures the planar surfaces are stable, while lowering the temperature stabilizes those nano-facets found experimentally. Afterwards, we constructed the (a,T,Δϕ)-phase diagram for Ir(210) in contact with an aqueous electrolyte and found that the same nano-facets should be stable under electrochemical conditions. Motivated by this prediction from theory, experiments were performed using cyclic voltammetry and in-situ scanning tunneling microscopy. The presence of nanofacets for Ir(210) gives rise to a characteristic current-peak in the hydrogen adsorption region for sulfuric acid solution. Furthermore, first results on the electrocatalytic behavior of nano-faceted Ir(210) are presented.
Introduction
Highly-disperse nanoparticles are often used to catalyze (electro-)chemical reactions. Unfortunately, not all nanoparticles have the same size and shape, but show a relatively large distribution. Since the electronic properties of the nanoparticles are correlated with their morphology, experimental measurements usually represent the averaged behavior of (almost) the entire ensemble of particles. This limits our understanding of the ongoing processes and makes direct comparison with theoretical studies difficult.One way out of this dilemma is the formation of well-defined nanostructures or facets on single-crystal surfaces, which provide a reproducible basis and model systems for studying structural sensitivity in (electro-)catalytic reactions. Surface faceting can be understood as a morphology change from a flat bulk-truncated surface to a hill-and-valley structure. While clean surfaces rarely facet, adsorbate-induced faceting of surfaces, driven by the anisotropy of surface free energy, is a general phenomenon observed in many systems.1–3 Usually the facets have more close-packed surface structures than the original surface, resulting in a minimized surface free energy although the total surface area may be increased. Therefore, in order to actively select and control a desired surface morphology, it is necessary to deepen our understanding of adsorbate-induced faceting. Furthermore, this would provide model systems to study structural sensitivity in catalytic reactions4–6 and may be used as templates to grow nanostructures.7,8
So far experimental studies of adsorbate-induced faceting of metal surfaces focused mainly on body-centered cubic or face-centered cubic metals, such as W(111),1,2Mo(111),9,10Ni(210),11,12Pt(210),13Ir(210),14Rh(553),15 and vicinal Cu surfaces.16–19 Although the enhancement of the anisotropy in surface free energy is the thermodynamic driving force for facet formation, in most cases this process is hindered by kinetic limitations. Therefore, not only is a critical adsorbate coverage required but also a minimum annealing temperature, allowing the system to overcome all kinetic barriers in the process of facet formation.
Recently the group of Madey found that on particular rough surfaces certain adsorbates are able to induce the formation of well-defined nanostructures after annealing the system to elevated temperatures.14,20 Using scanning tunnelling microscopy (STM) and low-energy electron diffraction (LEED) under ultra-high vacuum (UHV) they could demonstrate that an initially planar Ir(210) surface becomes faceted when being covered with more than 0.5 ML oxygen and annealed to temperatures above 600 K. The facets that form were characterized as an array of three-sided pyramidal nanostructures having Ir(311), Ir(31−1) and Ir(110) faces. Furthermore, higher resolution STM images showed that while the (311) and (31−1) faces are always unreconstructed, some (110) faces are partially reconstructed. This superstructure was proposed to be a “stepped double-missing-row”-(110) surface.21
After facet formation, oxygen that still remains on the surface can be removed by reaction with H2 at T < 400 K. During this reaction the nanopyramidal surface structure is not affected, since the kinetic barrier of facet destruction is not reached at these low temperatures. The clean nanofacets remain stable up to ∼600 K, and for higher temperatures the initial planar Ir(210) surface becomes stable again.
Similar behavior could also be observed in the case of Re(11−21), where by adsorption of oxygen pyramid-like facets having each two (01−11) and (10−11) faces could be generated. However, changing the adsorbate to ammonia and annealing to 900 K, led to the formation of two-sided ridges with (13−42) and (31−42) faces.22
It has also been demonstrated that planar and nano-faceted Ir(210) surfaces can be prepared outside an UHV chamber by inductive heating in a N2 + H2 mixture and a nitrogen atmosphere, respectively.23 Cooling the sample in a reducing gas atmosphere yields a planar surface according to the preparation of unreconstructed low-index planes of iridium.24–27 The presence of trace amounts of oxygen in nitrogen gas was found to be crucial for facet formation on Ir(210).23 Nano-faceted Ir(210) in contact with aqueous sulfuric acid is easily characterised by a sharp voltammetric current peak around −0.2 V vs.SCE.23 The similarity of the nano-pyramids obtained outside an UHV chamber with those reported by Madey et al.14,21 has been verified by in-situscanning tunnelling microscopy (STM).23
By the combination of theory and experiments we will demonstrate that choosing appropriate adsorbate and potential conditions it should be possible to electrochemically generate a reproducible and well-defined basis for studying catalytic reactions on unsupported monometallic nanostructures with controllable size and shape.
In the following, we will first describe the theoretical and experimental methods that were used to investigate the faceting of Ir(210). Afterwards, a brief description on calculations for oxygen-induced facet-formation on Ir(210) is given, which provides the basis for generating the electrochemical phase diagram. The theoretical prediction that facet formation should also be possible electrochemically was then studied experimentally. In this context, cyclic voltammetry and in-situSTM studies on the electrochemical behaviour of Ir(210) in contact with perchloric acid solution are described, followed by electrocatalytic investigations for different simple reactions.
Methods
Theoretical calculations
The energy required to form facets can be expressed as a sum of changes in the Gibbs free energies mainly related to surface, edge, kink and strain contributions:| ΔGform = ΔGsurface + ΔGedge + ΔGkink + ΔGstrain + … | (1) |
As long as the facets are large enough, such that contributions from step-edges, kinks, and strain are negligible compared to surface contributions, the overall formation energy can be approximated by the surface contribution only. This condition, usually referred as Herring-condition, is comparable to the so-called Wulff-construction. On the basis of this condition, facet formation should occur when
 | (2) |
 | (3) |
Here S311 and S110 specify the partial contributions of the different faces to each pyramidal-shaped facet, while θ311 and θ110 are the tilt angles of the faces with respect to the initial substrate, T is the temperature, a the water activity, and Δϕ the electrode potential. Experimentally and geometrically obtained values for Sf and θf are summarized in Table 1. It should be noted that since Ir(311) and Ir(31−1) show the same surface morphology, both have been combined.
The interfacial free energies γ, which are relevant for eqn (3), give the stability of the corresponding electrode/electrolyte-interfaces. As described in ref. 28 and 29, an exact evaluation of the interfacial free energies is in principle possible, but requires a self-consistent modeling of the entire interfacial region, which might range up to several 100 Å. Since this is currently beyond capabilities of ab initio approaches, we reduce our model to the electrode and the adlayer only and assume a constant influence of the electrolyte, allowing us to neglect its presence when studying relative stabilities only. Consequently, the interfacial free energy reduces to
 | (4) |
 | (5) |
With eqn (4) we now can evaluate (approximate) the interfacial free energies of the different surface faces of the facets, since all relevant quantities can be deduced from first principles, here density functional theory calculations. These can then be used together with eqn (3) to finally obtain the electrochemical phase diagram.
In order to calculate the total energies of different surface structures, which are required for eqn (4), we performed DFT slab calculations using the CASTEP code31 with Vanderbilt-type ultrasoft pseudopotentials32 and the generalized gradient approximation (GGA) exchange–correlation functional proposed by Perdew, Burke and Ernzerhof (PBE).33 Layer-converged supercells consisting of 16-layer slabs for Ir(210), 11-layer slabs for Ir(311), 12-layer slabs for Ir(110), and 7-layer slabs for Ir(110)-superstructure were used to model oxygen adsorption with different coverages and adlayer structures. To decouple the interactions between neighboring slabs in the supercell geometry, repeated slabs were separated by a ∼12 Å vacuum. For Ir(210), Ir(311) and Ir(110)-superstructure, the bottom three layers, and for Ir(110) the bottom four layers, were fixed at the calculated bulk structure, while the geometry of the remaining layers plus adsorbates were fully optimized (to <0.03 eV Å−1). The Brillouin zones of the (1 × 1)-surface unitcells of Ir(210), Ir(311), Ir(110), and the superstructure were sampled with 10 × 8, 14 × 8, 14 × 10, and 4 × 4 Monkhorst-Pack k-point meshes, respectively. Finally, a plane-wave basis set with an energy cutoff 340 eV was used.
Investigating the error sources related to slab thickness, vacuum size, plane-wave cutoff and k-point mesh, we found the maximum overall error bar in the surface free energy to be <5 meV Å−2, when using optimized values for each parameter.
Throughout this section oxygen binding energies are with respect to half an gas-phase oxygen molecule.
Experimental
The Ir(210) single crystal (MaTecK, Jülich, Germany) was a cylinder of 4 mm height and 4 mm diameter. The surface had been polished down to 0.03 μm and oriented to better than 1°. The electrode was heated up to 1000 °C for about 30 s by an induction coil in presence of inert (nitrogen) or reducing gas (nitrogen + hydrogen), cooled down slowly in the same atmosphere and immersed into 0.1 M H2SO4 solution under potential control. A conventional three electrode glass cell was used for electrochemical measurements. A platinum wire and a saturated calomel electrode (SCE) were used as counter and reference electrode, respectively. The solution was prepared from suprapure chemicals and ultrapure water (18.2 MΩ cm at 25 °C, total organic carbon < 1 ppb). After voltammetric experiments, the electrode was eventually transferred directly to an STM cell without further surface preparation. Pt wires were used in the STM cell as counter and reference electrodes. The STM images were recorded with a Digital Instruments Nanoscope III (Santa Barbara, California). For the preparation of the STM tips, a Pt/Ir wire (80/20) was etched in 4.5 M NaCN and coated with an electrophoretic paint to reduce the Faraday current at the tip to below 50 pA.Results and discussion
Electrochemical surface phase diagram
UHV-experiments on faceting of Ir(210) performed in the group of Madey14,21 showed that adsorption of oxygen is capable of stabilizing the faceted surface morphology. Motivated by these observations, in a previous work we described theoretical studies on facet formation on Ir(210) in contact with a gaseous atmosphere by first studying the oxygen adsorption on each relevant Ir-surface (see Fig. 1) separately and then combining the obtained energetics to an overall (pO2,T)-phase diagram.34 There we had seen that the presence of surface oxygen enhances the anisotropy in surface free energy for the different orientations, which finally causes the faceted surface to become thermodynamically favorable. Since even for the smallest experimentally prepared nanopyramids with 4 nm base-length we obtained good agreement between theory and experiment, this can be used as upper limit nanostructure size at which the Herring-condition is applicable. However, further investigations will aim on evaluating step-edge, kink and strain contributions. | ||
| Fig. 1 Hard-sphere models of Ir(210), Ir(311), Ir(110), and Ir(110)-superstructure, which are the surfaces relevant for faceting of Ir(210). | ||
Besides the external parameters temperature and pressure, it is well-known that under electrochemical conditions even the electrode potential is able to cause surface oxidation. Therefore, in the following we will combine both concepts, the oxygen-induced surface faceting and the potential-induced electrooxidation. We will show that under electrochemical conditions, potential-induced surface faceting should be possible.
In order to generate the electrochemical phase diagram shown in Fig. 2, we made use of the assumption that oxygen binding energies as well as the electrolyte structure and properties should be potential-independent, which in turn allowed us to directly use the DFT-energies that were obtained when investigating the gas-phase system.34 This is certainly a strong assumption and different theoretical studies have been performed on the role of surrounding water on binding energies and reaction barriers.35–40 But in previous studies on Pt-oxide formation we were able to reproduce the experimental CV-curve on the basis of this approximation. However, so far it is not clear how the surrounding water might influence the nanostructured surface that shows a variety of lower coordinated sites (e.g. step-edges or kinks).
 | ||
| Fig. 2 (a,T,Δϕ)-phase diagram for the electrochemical faceting of Ir(210) in an aqueous electrolyte. The left figure shows the interfacial free energy γ as function of the water chemical potential and electrode potential (referenced to RHE), while the right figure shows the view to the bottom. In addition, the temperature scale, which corresponds to a = 1, is given on the right side of the phase diagram. The structure-labeling corresponds to the models shown in Fig. 3. | ||
 | ||
| Fig. 3 Models of the different surface structures that are present on Ir(210) at specific electrode potentials (see Table 2). For all surfaces 1 ML is defined as one oxygen atom per surface unit cell. | ||
| Phase | Potential range/V |
|---|---|
| a | Δϕ < 0.10 |
| b | 0.10 < Δϕ < 0.18 |
| c | 0.18 < Δϕ < 0.26 |
| d | 0.26 < Δϕ < 0.57 |
| e | 0.57 < Δϕ < 0.65 |
| f | 0.65 < Δϕ < 0.85 |
| oxide | 0.85 < Δϕ |
On the basis of this approach, we distinguish between clean and oxygen-covered surfaces of:
• planar Ir(210),
• nanopyramids with (311), (31−1) and (110)-regular faces,
• and nanopyramids with (311), (31−1) and (110)-superstructure faces.
The surface free energies of the faceted surfaces were calculated using the left side of eqn (3) with the parameters for the partial surface areas and facet tilt angles summarized in Table 1. Each summand of this equation was evaluated by eqn (4), where the main temperature- and pressure-dependence is assumed to be dominated by the water chemical potential eqn (5). As already mentioned above, this approach is based on the Herring-condition, in which contributions from step-edges, kinks and surface stress or strain are considered to be small.
Although experimentally the coexistence of (110)-regular and (110)-superstructure was observed on most nanopyramids, we only consider the extremes in which the entire (110)-faces of all pyramids have one of both structures at the same time. However, in the following we will also discuss the consequences of having a mixture (coexistence).
Since all binding energies were calculated for oxygen adsorption on pure Ir, the following discussion is restricted to the part of the phase diagram where the IrO2 bulk-oxide is not stable yet. Equivalent to eqn (4), this can be translated to the following stability condition, which restricts the electrode potential range of interest
| +1.29 eV − 2eΔϕ < μH2O < 0 eV. | (6) |
Fig. 2 shows the final phase diagram, where on the left side γ is plotted against the water chemical potential and the electrode potential referenced to half an oxygen molecule
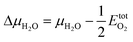 | (7) |
Above 0.1 V adsorption of oxygen takes place, causing the formation or stabilization of the nanofaceted surface. While at lower electrode potentials (0.1 V > Δϕ > 0.26 V) nanopyramids of the type (311)/(31−1)/(110)-superstructure are most stable, at more positive potentials (0.26 V > Δϕ > 0.85 V) the (110)-superstructure face is replaced by regular (110)-(1 × 1). In this range, increasing the potential does not change the structure, but causes the coverage of oxygen on the facets to increase. Finally the IrO2 bulk-oxide appears as stable phase for electrode potentials above 0.85 V. Overall, we find the surfaces phases summarized in Table 2. Interestingly, the overall phase transition behavior is qualitatively comparable to the temperature decrease in the gas-phase UHV system.
Finally, regarding the phase diagram, two aspects should be mentioned. While clean planar Ir(210) is most probably the stable phase at low electrode potentials (phase a), oxygen coverages of around or above 0.5 ML are required in order to stabilize the nanofacets. If one would only concentrate on coverages below this value, oxygen-covered planar Ir(210) would become stable at potentials above 0.13 V. This coverage-dependence is in agreement with experimental observations.14,21
Moreover, the presence of the (110)-superstructure face at potentials of 0.1 V > Δϕ > 0.26 V is rather remarkable. On a planar Ir(110) surface this superstructure is always less favorable than regular (110), but this is different for the faceted Ir(210) surface. There, the superstructure forms on the (110)-side of the nanopyramids at lower potential, which is a consequence of the nonlinear dependency of the surface free energy on the tilt angle [see prefactors on the left side of eqn (3)] and the fact that the (110)-faces of the nanopyramids are already tilted with respect to the (210)-substrate. Again, this behavior is also confirmed experimentally.21
In order to evaluate the influences coming from choosing the PBE exchange–correlation functional, we recalculated the most relevant surface structures with the LDA functional and generated the equivalent surface phase diagram. Comparison shows that with the LDA functional all phase transitions are shifted toward lower potentials, without causing any changes in the ordering of the stable phases. Furthermore, the stability ranges, respectively chemical potential ranges, of the different phases are almost the same with both xc-functionals. Therefore, it is reasonable to assume that the conclusions drawn above are qualitatively independent of the xc-functional.
Electrochemical behaviour
Differences in the electrochemical behaviour of planar and faceted Ir(210) in acidic solutions are obviously manifested in the hydrogen adsorption region. While voltammograms for planar Ir(210) are almost featureless, the faceted surface is characterized by narrow peaks, the position and shape of which are strongly dependent on electrolyte anions. In the case of 0.1 M H2SO4, a sharp voltammetric peak located around −0.2 V can be taken as indicator for the presence of nano-facets, as proven by STM measurements.23 While the Ir(210) surface structure was found to be unchanged in 0.1 M H2SO4, the stability has been tested with other electrolytes. In Fig. 4, voltammograms for planar and faceted Ir(210) in 0.1 M HClO4 are shown. | ||
| Fig. 4 Cyclic voltammograms for planar (dashed line) and nano-faceted (solid line) Ir(210) in 0.1 M HClO4. Scan rate: 50 mV s−1. | ||
It is well-known that the perchlorate anion can easily be reduced by iridium to chloride. Therefore, stable curves representing stationary behaviour show slightly smaller peaks as the curves in Fig. 4 for the 1st cycles. A variety of peaks can be discerned in the hydrogen adsorption region, i.e., at potentials between −0.3 and +0.1 V. These might be attributed to well-ordered domains of unreconstructed Ir(210) in the case of the planar surface or to the (110) and (311) faces for the faceted surface. However, since details on the electrochemical behaviour of Ir(110) and Ir(311) are not available yet, a direct assignment of the peaks in Fig. 4 is not possible. When going towards the faceted surface, three peaks are emerging between −0.2 and 0 V, while the peak at −0.25 V is slightly decreasing. Even more evidently, a relatively sharp reversible peak at 0.22 V is related to the presence of nano-facets on the surface (Fig. 4). This peak is probably related to the initial stages of OH or O adsorption from water and absent in the case of planar Ir(210). Restricting the positive potential limit to 0.4 V did not give rise to significant changes in the voltammograms. Thus, we conclude that simple potential variation does not lead to an electrochemical faceting of planar Ir(210) at room temperature.
The STM image shown in Fig. 5 was recorded for nano-faceted Ir(210) in 0.1 M HClO4 after measuring the respective voltammogram in the electrochemical cell (see Fig. 4). The electrode was contacted with the solution in the STM cell at 0.4 V. The surface consists of pyramids with facets of different orientation corresponding to slightly different size. It can be seen in Fig. 5 that the pyramids are uniformly distributed. Moreover, there are no planar zones alternating with the pyramids. The vertical distance between two consecutive pyramidal-extremes (apex/valley) never exceeds 3 nm and the average width at the base of the pyramids is 30 nm. It should be mentioned that the size of the pyramids changes slightly for various measurements, pointing out that subtle differences in the preparation procedure (e.g., different annealing times and/or temperatures) may influence the faceting process. By carefully watching the disposition of the pyramids, some order can be seen. The pyramids seem to share one edge along which they align. This could be a consequence of the faceting mechanism.
 | ||
| Fig. 5 STM-image for nano-faceted Ir(210) in 0.1 M HClO4 at 0.4 V. | ||
The STM measurements give also the opportunity to estimate the tilt angle that the different facets form with the horizontal plane of the STM images. The (311) facet forms a tilt angle of 18 ± 2°, a value already obtained with different techniques by Madey and co-workers.14 For the other facet, the angle is 9 ± 2° and indicates the presence of a superstructure formed by the Ir atoms of the top most plane of a reconstructed (110) facet.21 The model proposed by Madey and co-workers,21 which identifies the geometry of the pyramids as made by two (311) and one (110), describes correctly the experimental results reported here.
Since the adsorption of oxygen was seen to provoke facet formation, an attempt was made to apply more positive potential values, where surface oxidation is expected to take place. Such experiments were also performed with 0.1 M H2SO4 to rule out any disturbance by perchlorate reduction. In addition, the differences in the voltammograms for planar and faceted Ir(210) are much more pronounced for sulfuric acid compared with perchloric acid solution. Although slight changes in the voltammetric profile could be discerned after potential excursions to 0.8 V, a straightforward electrochemical method for nanofacet formation on Ir(210) as function of electrode potential has still to be explored.
Electrocatalytic behaviour
Since both the planar and the faceted Ir(210) surface represent stable and well-ordered systems of distinct structure, they are predestined for model studies in electrocatalysis. Furthermore, the faceted structure of Ir(210) constitutes a highly ordered array of (110) and (311) oriented nano-pyramids of narrow size distribution for a single component, i.e., without foreign substrate as it is common for metal nanostrucures. Not comprehending the mechanistic details, for both planar and faceted Ir(210) the onset of oxidation or reduction was tested for a series of rather simple electrocatalytic reactions. The latter involved (i) adlayer oxidation of carbon monoxide, (ii) formic acid oxidation, (iii) hydrogen evolution reaction, (iv) oxygen reduction, and (v) nitrous oxide reduction. Without going into details, the main result for all of these reactions is that the reaction overpotential is larger for the faceted Ir(210) surfaces compared with the planar one in all cases. The adlayer oxidation of CO for the two types of Ir(210) is shown in Fig. 6 as representative example. The difference in the onset potential is more than 0.1 V. CO adlayer oxidation on the planar Ir(210) surface starts around 0.2 V. The presence of two distinct oxidation peaks at 0.25 V and 0.4 V suggests that diffusion of reaction partners may be involved in the mechanism. It is likely that surface defects, such as monoatomic-high steps, act as active centres for CO oxidation. These sites are absent for the faceted Ir(210) surface, which explains the higher overpotential. In essence, it can be concluded that the planar surface is, in general, more active than the faceted surface. Changes in the local geometry of the Ir surfaces thus have significant impact on the interaction with adsorbates and therefore on reaction rates, which is in agreement with the findings for oxidation of CO under UHV conditions.4 | ||
| Fig. 6 Current–potential curves for CO adlayer oxidation on planar (dashed line) and on nano-faceted (solid line) Ir(210) in 0.1 M H2SO4. Scan rate: 10 mV s−1. | ||
It should be mentioned that higher overpotentials have also been reported for CO monolayer oxidation on Pt nanoparticles supported on glassy carbon electrodes.41 Spatially confined formation of oxygen containing species at active sites and slow diffusion of CO molecules to the active sites were given as main reasons for slower kinetics compared to extended Pt surfaces.41 While size effects have been addressed for the latter Pt systems,42 it still remains to be a challenge to significantly vary the size of the nano-facets on Ir(210). However, the faceted Ir(210) surface can ideally serve as a model system to study structure sensitivity of electrocatalytic reactions.
Conclusion
In this paper we have shown that surface faceting of Ir(210) should not only be a phenomenon observable under gas-phase or UHV-conditions, respectively, but should also be possible under electrochemical conditions. There, the important parameter to tune the surface morphology is the electrode potential. Focusing on the former parameter, our theoretical studies showed that although the process itself might be kinetically hindered at room temperature, nanofacets become thermodynamically stable above +0.1 V. Since this potential range is easily accessible by experiments, we afterwards presented first cyclic voltammetry and in-situSTM measurements on planar and nanofaceted Ir(210). After the morphological characterization, we further investigated the electrocatalytic behavior of both surface structures with different simple reactions, finding an increased overpotential for faceted Ir(210). Future studies will aim to develop suitable methods, so that facet formation can be induced electrochemically by the electrode potential.Acknowledgements
P.K. and T.J. gratefully acknowledge support by the “Fonds der Chemischen Industrie” (FCI), the “Deutscher Akademischer Austauschdienst” (DAAD), and the “Deutsche Forschungsgemeinschaft” (DFG) within the Emmy-Noether-Program.References
- T. E. Madey, J. Guan, C.-H. Nien, C.-Z. Dong, H.-S. Tao and R. A. Campbell, Surf. Rev. Lett., 1996, 3, 1315 CrossRef CAS.
- T. E. Madey, C.-H. Nien, K. Pelhos, J. J. Kolodziej, I. M. Abdelrehim and H.-S. Tao, Surf. Sci., 1999, 438, 191 CrossRef CAS.
- Q. Chen and N. V. Richardson, Prog. Surf. Sci., 2003, 73, 59 CrossRef CAS.
- W. Chen, I. Ermanoski, T. Jacob and T. E. Madey, Langmuir, 2006, 22, 3166 CrossRef CAS.
- W. Chen, I. Ermanoski, Q. Wu, T. E. Madey, H. H. Hwu and J. G. Chen, J. Phys. Chem. B, 2003, 107, 5231 CrossRef CAS.
- W. Chen, I. Ermanoski and T. E. Madey, J. Am. Chem. Soc., 2005, 127, 5014 CrossRef CAS.
- R. Bachelet, S. Cottrino, G. Nahélou, V. Coudert, A. Boulle, B. Soulestin, F. Rossignol, R. Guinebretière and A. Dauger, Nanotechnology, 2007, 18, 015301 CrossRef.
- H. Wang, M. Reyhan, T. E. Madey, unpublished data.
- K.-J. Song, J. C. Lin, M. Y. Lai and Y. L. Wang, Surf. Sci., 1995, 327, 17 CrossRef CAS.
- D. B. Danko, M. Kuchowicz and J. Kolacziewicz, Surf. Sci., 2004, 552, 111 CrossRef CAS.
- R. E. Kirby, C. S. McKee and M. W. Roberts, Surf. Sci., 1976, 55, 725 CrossRef CAS.
- R. E. Kirby, C. S. McKee and L. V. Renny, Surf. Sci., 1980, 97, 457 CrossRef CAS.
- M. Sander, R. Imbihl, R. Schuster, J. V. Barth and G. Ertl, Surf. Sci., 1992, 271, 159 CrossRef CAS.
- I. Ermanoski, K. Pelhos, W. Chen, J. S. Quinton and T. E. Madey, Surf. Sci., 2004, 549, 1 CrossRef CAS.
- J. Gustafson, A. Resta, A. Mikkelsen, R. Westerström, J. N. Andersen, E. Lundgren, J. Weissenrieder, M. Schmid, P. Varga and N. Kasper, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035401 CrossRef.
- P. J. Knight, S. M. Driver and D. P. Woodruff, Surf. Sci., 1997, 376, 374 CrossRef CAS.
- S. Vollmer, A. Birkner, S. Lucas, G. Witte and C. Wöll, Appl. Phys. Lett., 2000, 76, 2686 CrossRef CAS.
- N. Reinecke and E. Taglauer, Surf. Sci., 2000, 454, 94 CrossRef.
- D. A. Walko and I. K. Robinson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 045412 CrossRef.
- I. Ermanoski, W. Swiech and T. E. Madey, Surf. Sci., 2005, 592, L299 CrossRef CAS.
- I. Ermanoski, C. Kim, S. P. Kelty and T. E. Madey, Surf. Sci., 2005, 596, 89 CrossRef CAS.
- H. Wang, A. S. Y. Chan, P. Kaghazchi, T. Jacob and T. E. Madey, ACS Nano, 2007, 1(5), 449 CrossRef CAS.
- K. A. Soliman, F. C. Simeone, L. A. Kibler, in preparation.
- S. Motoo and N. Furuya, J. Electroanal. Chem., 1984, 167, 309 CrossRef CAS.
- S. Motoo and N. Furuya, J. Electroanal. Chem., 1984, 172, 339 CrossRef CAS.
- T. Pajkossy, L. A. Kibler and D. M. Kolb, J. Electroanal. Chem., 2005, 582, 69 CrossRef CAS.
- T. Pajkossy, L. A. Kibler and D. M. Kolb, J. Electroanal. Chem., 2007, 600, 113 CrossRef CAS.
- T. Jacob, J. Electroanal. Chem., 2007, 607, 158 CrossRef CAS.
- T. Jacob, M. Scheffler, to be submitted.
- JANAF Thermochemical Tables, ed. D. R. Stull and H. Prophet, U.S. National Bureau of Standards, U.S. EPO, Washinghton, DC, 2nd edn, 1971 Search PubMed.
- M. D. Segall, P. L. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 88, 3865 CrossRef.
- P. Kaghazchi, W. Chen, H. Wang, I. Ermanoski, T. E. Madey and T. Jacob, ACS Nano, 2008, 2, 1280 CrossRef CAS.
- C. Hartnig, P. Vassilev and M. T. M. Koper, Electrochim. Acta, 2003, 48, 3751 CrossRef CAS.
- P. Vassilev and M. T. M. Koper, J. Phys. Chem. C, 2007, 111, 2607 CrossRef CAS.
- C. D. Taylor and M. Neurock, Curr. Opin. Solid State and Mater. Sci., 2005, 9, 49 Search PubMed.
- Z. Gu and P. B. Balbuena, J. Phys. Chem. A, 2006, 110, 9783 CrossRef CAS.
- G. S. Karlberg, T. F. Jaramillo, E. Skúlason, J. Rossmeisl, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 126101 CrossRef CAS.
- A. Roudgar and A. Gross, Chem. Phys. Lett., 2005, 409, 157 CrossRef CAS.
- O. V. Cherstiouk, P. A. Simonov, V. I. Zaikovskii and E. R. Savinova, J. Electroanal. Chem., 2003, 554/555, 241 CrossRef.
- F. Maillard, E. R. Savinova and U. Stimming, J. Electroanal. Chem., 2007, 599, 221 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2009 |
