From ultra-high vacuum to the electrochemical interface: X-ray scattering studies of model electrocatalysts

Abstract

In-situ surface X-ray scattering (SXS) has become a powerful probe of the atomic structure at the metal–electrolyte interface. In this paper we describe an experiment in which a Pt(111) sample is prepared under ultra-high vacuum (UHV) conditions to have a p(2 × 2) oxygen layer adsorbed on the surface. The surface is then studied using SXS under UHV conditions before successive transfer to a bulk water environment and then to the electrochemical environment (0.1 M KOH solution) under an applied electrode potential. The Pt surface structure is examined in detail using crystal truncation rod (CTR) measurements under these different conditions. Finally, some suggestions for future experiments on alloy materials, using the same methodology, are proposed and discussed in relation to previous results.

---

1. Introduction

Since the early days of modern surface science, the main goal in the electrochemical community has been to find correlations between the microscopic structures formed by surface atoms and adsorbates and the macroscopic kinetic rates of a particular electrochemical reaction. The establishment of such relationships, previously only developed for catalysts under ultra-high vacuum (UHV) conditions, has been broadened to embrace electrochemical interfaces. In early work, determination of the surface structures in an electrochemical environment was derived from ex situ UHV analysis of emersed surfaces. Although such ex situ tactics remain important, the relationship between the structure of the interface in electrolyte and that observed in UHV was always problematic and had to be carefully examined on a case-by-case basis. The application of in situ surface sensitive probes, most notably synchrotron based surface X-ray scattering (SXS)^1–6 and scanning tunneling microscopy (STM)^7,8 has overcome this “emersion gap” and provided information on potential-dependent surface structures at a level of sophistication that is on a par with (or, even, in advance of) that obtained for surfaces in UHV.⁹

Central to all electrochemical reactions in water-based electrolytes and, indeed, to a wide range of physical phenomena in nature, is the structure and bonding of water at a surface. The interaction of water with solid surfaces plays a crucial role in many areas of science. The water structure at well-defined metal surfaces is of particular importance in catalysis and electrochemistry, as the activation of water is the crucial step in many surface reactions. Despite this importance, at the electrified interface numerous experimental and theoretical studies have yet to provide a detailed picture of the atomic-scale structure of water and its behavior remains poorly understood. In traditional surface science experiments, there has recently been a leap forward in understanding the structure and bonding of water on transition metal surfaces.¹⁰ Using density-functional theory (DFT) calculations, Feibelman postulated that the stable configuration for water on Ru(0001) was a partially dissociated overlayer containing a hexagonal network and that the partial dissociation was a necessary prerequisite for wetting, at least for Ru(0001).¹¹Vibrational spectroscopy results¹² suggest that a similar layer is present on Pt(111) but consisting of intact water molecules, although low energy electron diffraction (LEED) analysis is consistent with a layer consisting of dissociated OH.¹³ The issue of dissociation was addressed recently by Clay et al.,¹⁴ who studied a mixed OH/H₂O (“OH_x”) layer on Pt(111) as a function of its composition to determine the role of hydrogen bonding in stabilizing the overlayer. They found that the optimal structure is a mixed (OH + H₂O) phase forming a hexagonal (√3 x √3)R30° lattice with a weak (3 × 3) superstructure caused by ordering of the hydrogen bonds. The mixed overlayer can accommodate a range of H₂O/OH compositions but becomes less stable as the H₂O content is reduced.

Although water structures can be observed by LEED on metal surfaces under ultra-high vacuum (UHV) conditions, the electrochemical interface is much harder to study due to the presence of the bulk electrolyte. In order to understand the role of hydration water molecules on the electrochemical double layer, it is imperative to reveal the structure under control of the electrode potential. In electrolyte solutions free of strongly adsorbing anions, e.g.KOH, the electrochemical interface offers the opportunity of controlling the surface coverage by hydrogen, H₂O and OH species simply by controlling the applied electrode potential. To probe, in situ, the structure of the water layer at the metal/electrolyte interface is a technically challenging experiment as the scattering signal from the ordered oxygen atoms is relatively small compared to the diffuse scattering from the bulk of the electrolyte solution.

In this paper, we describe preliminary results obtained using a UHV transfer system to provide unprecedented control over the electrode surface structure during transfer from UHV to the electrochemical environment. To illustrate the experimental possibilities, in section 3 we describe a single experiment in which a Pt(111) surface was prepared in UHV, dosed with oxygen to form a p(2 × 2) oxygen adlayer and then studied with SXS, initially under UHV conditions, then in a N₂ atmosphere before a droplet of water was contacted with the surface. Measurements of the surface structure were then performed on the surface modified by the bulk water overlayer before the water was exchanged with 0.1 M KOH electrolyte and the Pt(111) electrode put under potential control to allow potential-dependent studies of the interface structure. In section 4, results for the Pt₃Ni alloy system obtained by UHV preparation followed by external transfer to the X-ray electrochemical cell are described. In this case, it is found that the (111) surface of Pt₃Ni is extremely stable both during the transfer and under potential control in the electrochemical environment. Variations in the compositional profile at the surface are probed by resonant surface X-ray diffraction techniques. Results for the other low-index Pt₃Ni surfaces, (100) and (110), are less conclusive and indicate that the UHV-transfer system would offer a more controlled way in which to probe the surface structure and electrochemistry of these model electrocatalysts.

2. Experimental methods

Surface X-ray scattering (SXS) is now a well-established technique for probing the atomic structure at the electrochemical interface and, since the first in situsynchrotron X-ray study in 1988,¹ several groups have used the technique to probe a variety of electrochemical systems.^1,2,9,15 As in the UHV environment, the extraction of structural information, such as surface coverage, surface roughness and layer spacing (both adsorbate–substrate distances and the expansion/contraction of the substrate surface atoms themselves), at the electrified solid–liquid interface relies on measurement of the crystal truncation rods (CTR's).^16,17 By combining measurements of several symmetry-independent CTR's it is possible to build up a 3-dimensional picture of the atomic structure at the electrode surface. If the surface or adlayer adopts a different symmetry from that of the underlying bulk crystal lattice then the scattering from the surface becomes separate from that of the bulk in reciprocal space and it is possible to measure the surface scattering independently.

In this paper, we describe SXS studies of electrode surfaces that are prepared in the ultra-high vacuum (UHV) environment. This methodology has the advantage that the surface quality can be checked during preparation by standard surface science techniques such as low energy electron diffraction (LEED) and auger electron spectroscopy (AES). UHV preparation is also vital for bimetallic surfaces for which precise surface compositions are dependent on annealing temperatures. The Pt(111) electrode was prepared by cycles of sputtering and annealing in the UHV system in the surface characterization laboratory (SCL) at the ESRF.¹⁸ After a sharp (1 × 1) LEED pattern was obtained, the sample was exposed to molecular oxygen at room temperature until a sharp p(2 × 2) LEED pattern, characteristic of the stable Pt(111)–O structure with a saturation coverage of 0.25 monolayers of atomic oxygen, was observed.¹⁹ The sample was then transferred to a portable chamber (called TRECXI) connected with a CF38 UHV valve to a docking port of the main UHV chamber. The TRECXI chamber²⁰ (which has portable UHV ion pumps to maintain the UHV conditions and a large cylindrical Be window to allow the incident and scattered X-ray beams to pass through the chamber) was then detached from the main chamber and mounted on the ID32 diffractometer at the ESRF. Full details of the TRECXI chamber describing the transfer process and operation can be found in ref. 20.

SXS measurements were performed on the 6-circle surface diffractometer at the ID32 beamline at the ESRF. The horizontal sample surface was aligned with the X-ray beam for a fixed incidence angle of 0.2° and the orientation of the crystal lattice was then determined. The close-packed (111) surface has a hexagonal unit cell that is defined such that the surface normal is along the (0, 0, L)_hex direction and the (H, 0, 0)_hex and (0, K, 0)_hex vectors lie in the plane of the surface and subtend 60°. The units for H, K and L are a* = b* = 4π/√3a_NN and c* = 2π/√6a_NN where a_NN is the nearest-neighbor distance in the crystal (a_NN = 2.78 Å). Due to the ABC stacking along the surface normal direction, the unit cell contains three monolayers and the Bragg reflections are spaced apart by multiples of three in L. The incident X-ray beam (energy = 22.2 keV) was collimated to a spot size of 40 μm (vertically) by 0.3 mm (horizontally) and the scattered X-ray beam was detected after reflection from a graphite analyzer crystal. CTR data were obtained by performing rocking scans around the surface normal at successive L values to obtain background-subtracted integrated intensities at each L position.

Following the experiments performed under UHV conditions (section 3.1), the TRECXI chamber was filled with inert gas and selected X-ray measurements were performed to verify the stability of the Pt(111)–O surface. The electrochemical cell was then mounted above a UHV valve on top of the Be cylinder and can be lowered toward the sample once the chamber is filled with inert gas at ambient temperature and the UHV valve is open. The electrochemical cell in this setup consists of a glass tube (about 25 cm long) that has an open end for forming a droplet of electrolyte on one side and is connected to a glass cross on the other side. The glass cross contains connectors for the electrochemical inlet and outlet tubings, the counter-electrode (Pt wire) and a reference electrode (a commercial Ag/AgCl microelectrode). The cell is part of a complete electrolyte handling system including a computer-controlled pumping system and potentiostat (full details are given in ref. 20). Initially pure water was used in place of electrolyte (without potential control) and a droplet was contacted with the Pt(111)–O surface (measurements described in section 3.2). During the experiment the droplet is monitored by an endoscope and can be regularly adjusted in volume to replace evaporated liquid. Following the measurements in pure water, 0.1 M KOH was used as the electrolyte and potential contact to the sample was made at −1 V (relative to Ag/AgCl). The measurements performed in the electrolyte solution are described in section 3.3.

The Pt₃Ni samples were mechanically cut and polished into 6 mm diameter disks (2 mm thick), with the surface orientated to within 0.5° of the low index crystal planes and then prepared and characterized in a UHV system with a base pressure of 1 × 10⁻¹⁰ Torr. In addition, the surface was examined in a separate UHV system using synchrotron-based high resolution ultraviolet photoemission spectroscopy (UPS). After UHV characterization the sample was transferred into an electrochemical cell where cyclic voltammetry (CV) measurements were performed. Low energy ion scattering (LEIS) showed that, after a final anneal, the surface atomic layer was composed of pure Pt, the so called ‘Pt-skin’ surface. This is in agreement with previous LEED studies of a Pt_0.78Ni₂₂(111) sample where a Pt-rich surface atomic layer accompanied by a damped oscillation in the Pt occupation over the next two atomic layers was observed.^21,22 Full details of the sample preparation and UHV characterization can be found in ref. 23.

Following the UHV measurements the sample was transferred to the X-ray electrochemical cell with a drop of pure water protecting the surface.²⁴ In all of the Pt₃Ni experiments presented, the electrolyte was 0.1 M HClO₄, the reference electrode was a saturated calomel electrode (SCE) and after immersion into the electrolyte the electrode potential was contacted at 0.05 V (versus the reversible hydrogen electrode (RHE)). The SXS measurements were carried out on beamline 7–2 at the Stanford Synchrotron Radiation Laboratory (SSRL) and beamline BM12-BESSRC at the Advanced Photon Source (APS), Argonne National Laboratory. The Pt₃Ni(111) surface was indexed using the standard hexagonal unit cell notation described above, whereas the regular fcc unit cell was used for the Pt₃Ni(100) surface with the L direction along [1 0 0]. The Pt₃Ni lattice parameter was measured to be 3.841 Å during the X-ray diffraction experiment, which is close to a 75 : 25 combination of the Pt and Ni fcc lattice constants. Measurement of the bulk Bragg reflections revealed that the crystal had a well-defined mosaic spread with a rocking scan showing several distinct peaks over an angular range of ∼1 degree. This mosaic spread was found for all three low-index single crystals that were cut from the as-grown Pt₃Ni crystal and reflects the difficulty in preparing single crystals of this material.

3. Results and discussion

3.1 Pt(111)–p(2 × 2)-O

The first experiment after preparation and transfer of the Pt(111)–O surface in the baby chamber to the beamline was to characterize the surface under UHV conditions. Due to the increased size of the p(2 × 2)-O unit cell, scattering is expected at the half integer positions in the surface plane (H, K) of the reciprocal lattice.¹⁹Fig. 1 shows a radial scan (along the 〈H, K〉 direction) and a rocking scan measured at (½, ½, 0.1). The count time in this measurement was 10 seconds per point, which illustrates the weakness of the scattering signal. This is expected if the structure consists of only 0.25 monolayers of O (which is a weak scatterer due to the low atomic number). Fits of a Lorentzian lineshape to the data (shown by the solid lines in Fig. 1) give a coherent domain size in the range 90–130 Å. Due to the weakness of the scattering it was impossible to collect a full set of structure factors that could then be used for structural refinement. In fact the intensity distribution implied that there was no significant Pt contribution to the scattering from the p(2 × 2) unit cell in contrast to previous SXS measurements of the structure in which relaxation of multiple Pt layers was proposed.²⁵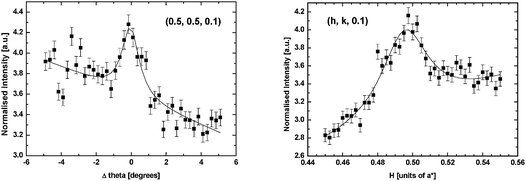

Fig. 1 A rocking scan (left) and a radial scan (right) through the (0.5, 0.5, 0.1) reciprocal lattice position from the Pt(111)–p(2 × 2)-O surface in UHV.

In order to fully characterize the Pt surface, we measured 7 symmetry-independent CTR's and representative results (6 of the measured CTR's) are shown in Fig. 2. The data has been corrected for the instrumental resolution according to the formalization developed by Vlieg.²⁶ Errors due to counting statistics are relatively small, but in fitting the data a 10% systematic error was associated with each data point. This error is typical of that obtained by comparison of data measured at symmetry-equivalent CTR positions.²⁷ The lack of any significant features in the CTR data is consistent with the weakness of the p(2 × 2) scattering (Fig. 1) which implies that there is no substantial relaxation in the surface Pt layers. The data was fitted using the simple structural model shown in Fig. 3. Inclusion of the p(2 × 2)-O unit cell made a slight improvement to the calculated fit (χ² improved from 4.0 to 3.5) which was obtained by least squares refinement of the structural parameters shown in Fig. 3 with the O atom adsorbed in the 3-fold hollow Pt surface site (as previously determined in UHV experiments).¹⁹ The best fit parameters are listed in Table 1. Including buckling of the surface and sub-surface Pt atoms in the p(2 × 2) unit cell (as found in the LEED-IV study of the Pt(111)–O surface) did not improve the fit to the data. The data was therefore modelled with a Pt-(1 × 1) unit cell allowing for relaxation, according to the parameters ε₁ and ε₂, and an asymmetric static Debye–Waller factor of the form 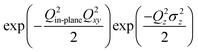to account for small distortions of the Pt lattice. This same model was then used to fit all of the CTR measurements made for the different states of the Pt surface, as described in the subsequent sections of this paper. The structural parameters imply that there is outward relaxation of the surface Pt atomic layer by 0.05 Å (compared with the previous LEED-IV study¹⁹ that found an outward relaxation of 0.01 Å with an additional bucking of the adlayer so that 3 of the 4 Pt atoms in the unit cell were additionally expanded by 0.04 Å). The Pt–O vertical spacing was found to be 1.5 ± 0.2 Å compared to 1.24 Å found in the LEED-IV study and 1.46 Å in density functional theory (DFT) calculations.²⁸ The SXS results are thus generally in good agreement with the previous LEED-IV study and theoretical results. As described above, buckling of the Pt surface layers in the p(2 × 2) unit cell did not improve the fit to the data and so was not included in the structural model.

Table 1 Structural parameters for the fits to the Pt(111) CTR data. f indicates a parameter that was fixed. Uncertainties are indicated in brackets. ε₁ is also quoted as a percentage of the Pt(111) atomic layer spacing.

System	θ O , θOH	d Pt-O /Å	ε 1/Å	ε 2/Å	σ xy/Å	σ z/Å
Pt(111)–O	0.25f	1.5 (0.2)	+0.05 (0.005) (2.2%)	0.005 (0.005)	0.06 (0.01)	0.0
Pt(111)–H2O	0.7 (0.3)	1.9 (0.4)	+0.03 (1.3%)	0.01	0.10	0.0
Pt(111)–KOH (E = −1.0 V)	0	—	+0.05 (2.2%)	0.005	0.06	0.0
Pt(111)–KOH (E = −0.1 V)	0.55 (0.2)	2.1 (0.4)	+0.04 (1.8%)	0.0	0.06	0.0

---

Fig. 2 Crystal truncation rod (CTR) data of the Pt(111)-p(2 × 2)-O surface measured in UHV. The circles correspond to background-subtracted integrated intensities that are corrected for the instrumental resolution. The (H, K) values for each CTR are indicated. The solid line is a fit to the data using the structural model shown in Fig. 3 according to the parameters listed in Table 1.

Fig. 3 A schematic of the structural model used to fit the CTR data in Fig. 2, 3, 6 and 7. The structural parameters to the fit are indicated in the Figure and the values obtained are listed in Table 1.

Following the measurements under UHV conditions, the chamber was brought up to an N₂ atmosphere and the measurements shown in Fig. 1 and some of the CTR measurements shown in Fig. 2 were repeated. These results were identical indicating that the Pt(111)–p(2 × 2)-O surface was stable in the inert atmosphere. A droplet of water was then contacted with the surface according to the experimental procedures described in section 2.

3.2 Pt(111)–H₂O interface

One of the key aims of this experiment was to search for the existence of ordered water structures at the Pt(111)–bulk water interface. Adsorption of water onto the Pt(111)–p(2 × 2)-O surface was chosen as this helps to pin the water molecules into an ordered phase when such surfaces are prepared under UHV conditions at low temperatures.^14,29 Following contact with the water droplet, a search for scattering due to ordered structures was made in the surface plane (H,K) of reciprocal space by scans along the high symmetry directions (〈H, 0〉, 〈0, K〉 and 〈H, K〉 at fixed L values, 0.1, 0.8). Additionally, rocking scans were performed at key reciprocal lattice positions, i.e. half-integer and 1/3 integer, where scattering from the p(2 × 2)-O structure,¹⁹ the (√3 × √3)-R30° and (3 × 3) structures of water that are formed in the UHV experiments^14,29 at monolayer coverage of water would be expected. In all cases no scattering above the background level was observed. It should be noted that the background scattering due to the presence of the liquid droplet was significant and it cannot be ruled out that the background signal is too high to observe the weak scattering that would be expected from such an ordered structure (particularly given the weakness of the scattering from the p(2 × 2)-O layer shown in Fig. 1). At this stage it is impossible to determine if an ordered water adlayer is present at the interface. A future experiment would be to prepare an ordered (√3 × √3)-R30° water monolayer on Pt(111) under UHV conditions and contact this surface with the water droplet. This would require a development of the TRECXI chamber to facilitate cold transfer of the sample.

In order to characterize changes to the surface atomic structure, measurements of the CTR data (as shown in Fig. 2) were repeated. The CTR data measured with the surface exposed to the bulk water environment was then normalized to the data shown in Fig. 2 to obtain a ratio data set and the results are shown in Fig. 4. The ratio data set shows a clear systematic change in the intensities of the CTR's which corresponds to a change in the interface structure due to the presence of the water overlayer. The data was modeled using the same structural model shown in Fig. 3. Adsorption of the X-ray beam by the electrolyte essentially leads to a constant attenuation (compared to the UHV data) as the pathlength of the X-ray beam does not change significantly as a function of L. This was accounted for by allowing the scale factor multiplying the CTR data to vary in fitting the ratio data set. The best fit of the ratio data set is shown by the solid lines in Fig. 4 according to the structural parameters listed in Table 1. A constant error of ±0.1 was assumed for each ratio data point as indicated by the error bars in Fig. 4.

Fig. 4 Ratios of CTR data (Pt(111)–H₂O divided by Pt(111)–p(2 × 2)-O, i.e. data in Fig. 1). The circles correspond to the measured ratios (a constant error of ±0.1 is estimated). The (H, K) values for each CTR are indicated. The solid line is a fit to the data using the structural model shown in Fig. 3 according to the parameters listed in Table 1 as described in the text.

Given that no in-plane ordering at the Pt(111)–H₂O interface was detected, it is impossible to build detailed structural models in order to reproduce the CTR ratio data. However, the systematic changes observed in Fig. 4 are consistent with a structural rearrangement at the interface and so it is intuitive to explore the origin of the changes. The calculated curves (shown by the solid lines in Fig. 4) used a very simple (1 × 1) unit cell allowing only for changes in the relaxation parameters. A fit to the data without the presence of a θ_O adlayer gave a χ² of 1.9. The principal structural changes are a reduction in the Pt surface expansion accompanied by an increase in the in-plane component of the Debye–Waller factor consistent with some in-plane distortion of the Pt lattice. This result would be expected for an increased surface coverage by oxygenated species. Including an oxygen layer in the model gave the fit to the data shown in Fig. 4 (χ² = 1.3). Different adsorption sites in the (1 × 1) unit cell were tried but there was a clear preference for the 3-fold hollow site. Models based on the (√3 × √3)R30° and (3 × 3) structures, previously observed for the mixed OH–H₂O layer in UHV,²⁹ did not improve the fit to the data obtained without an adsorbed O layer. In particular, it was found that a good fit could not be obtained with O adsorbed at a Pt on-top site. In UHV studies the sharpest LEED patterns are observed when water is adsorbed onto a disordered oxygen adlayer with a reduced coverage of θ_O ∼ 0.15^14,30 compared to the p(2 × 2) phase (θ_O = 0.25). It is possible, therefore, that in our experiment the oxygen was stabilized in the 3-fold hollow site although it is clear that a reaction with bulk H₂O has occurred. At present it is thus difficult to reconcile the results with the UHV studies of water adsorption at low temperature. As noted in the following section, the inclusion of the oxygen adlayer to fit the data in Fig. 4 is statistically significant, as fits to the CTR data in 0.1 M KOH at −1 V, where atomic hydrogen is adsorbed onto the surface,³¹ are consistent with the removal of the oxygen adlayer (see below). At this stage, however, we cannot rule out that the CTR data could be reproduced with more complex surface models.

3.3 Pt(111)–0.1 M KOH

Following the measurements performed with the water droplet, the water was replaced by 0.1 M KOH electrolyte and potential contact was established at −1 V (versusAg/AgCl). A cyclic voltammogram and X-ray voltammogram (at (1, 0, 3.6), a position that is sensitive to the Pt surface expansion) were then recorded and the results are shown in Fig. 5 (sweep rate 2 mV s⁻¹). Starting at −1.0 V and scanning anodically it is clear that the desorption of hydrogen from the surface leads to an inward relaxation reaching a minimum at ∼−0.6 V. Adsorption of OH anions then causes an outward relaxation which is stable during the cathodic sweep until the OH desorbs. Adsorption of hydrogen then again results in the outward expansion of the surface Pt layer and the XRV is seen to be fully reversible.

Fig. 5 (Top) The cyclic voltammogram measured in the droplet cell for the Pt(111) electrode in 0.1 M KOH. (Bottom) The simultaneously measured X-ray voltammetry (XRV) measured at (1, 0, 3.6), a reciprocal lattice position sensitive to the Pt surface expansion (the sweep rate was 2 mV s⁻¹).

Characterization of the surface structure was again obtained by measuring and modeling of the CTR data. Fig. 6 shows the CTR data measured at E = −1.0 V. At this potential there is adsorption of ∼0.66 monolayers of hydrogen on the surface^31,32 and so the data was modeled without any adsorbed oxygenated species, i.e.θ_OH = 0. The results indicate that there is an outward relaxation of the topmost Pt layer by ∼2.2% of the bulk layer spacing which is in excellent agreement with previous measurements on this system.³³ Interestingly, this surface expansion in the presence of adsorbed hydrogen is also in excellent agreement with the local-density-functional (LDF) calculations by Feibelman for hydrogen adsorbed onto Pt(111).³⁴ As noted above, fits to a CTR ratio data set (not shown) for I_KOH/I_H2O indicated that the oxygen adlayer is not present in 0.1 M KOH at −1 V, and so its presence at the Pt(111)–H₂O interface is statistically significant.

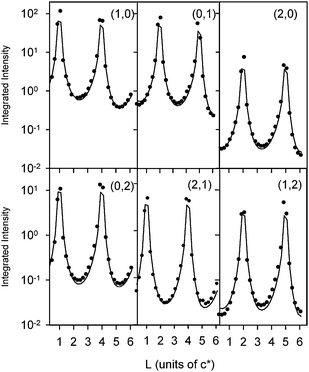Fig. 6 CTR data of Pt(111) in 0.1 M KOH measured at an electrode potential of −1 V (versusAg/AgCl). The circles correspond to background-subtracted integrated intensities that are corrected for the instrumental resolution. The (H, K) values for each CTR are indicated. The solid line is a fit to the data using the structural model shown in Fig. 3 according to the parameters listed in Table 1.

After potential cycles over the range shown in Fig. 5, the potential was held at −0.1 V and the SXS measurements were repeated. As for the Pt(111)–H₂O interface, searches in the (H, K) surface plane for scattering due to an ordered OH adlayer were unsuccessful. The data in Fig. 7 is the ratio CTR data set obtained by dividing the CTR data measured at −0.1 V by the data measured at −1 V (Fig. 6). Systematic changes in the measured intensities are again observed, although it should be noted that the changes are significantly smaller than those observed in Fig. 4. The same (1 × 1) structural model was used to fit the data in Fig. 7 giving the structural parameters listed in Table 1. As for Pt(111)–H₂O, the best fit was obtained with OH species adsorbed into the Pt 3-fold hollow sites although the Pt–O spacing seems rather large in this case. The fact that there are features in the ratio data set that are not reproduced in the calculation implies that the model is too simple. Further analysis and measurement is required to get more insight into the Pt(111)–OH_ad interface.

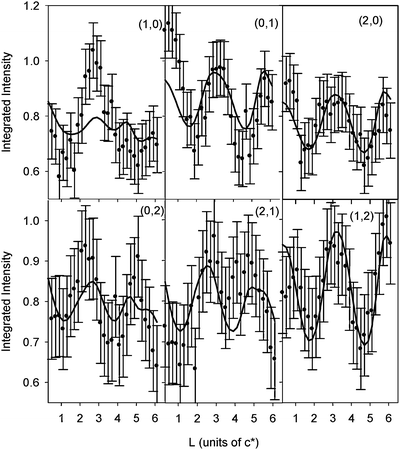Fig. 7 Ratios of CTR data for Pt(111) in 0.1 M KOH (data measured at E = −0.1 V divided by data measured at E = −1.0 V, i.e. data in Fig. 6). The circles correspond to the measured ratios (a constant error of ±0.1 is estimated). The (H, K) values for each CTR are indicated. The solid line is a fit to the data using the structural model shown in Fig. 3 according to the parameters listed in Table 1 as described in the text.

4. Future directions: alloy surfaces

As with all PtNi alloys, Pt₃Ni forms an fcc solid solution with random occupation of the lattice sites by Pt and Ni. An important initial step is the preparation and characterization of Pt₃Ni(hkl) alloy surfaces in ultra-high vacuum (UHV) (Fig. 8). The surface sensitive techniques employed included LEED, AES, low energy ion scattering (LEIS) and synchrotron based high-resolution ultraviolet photoemission spectroscopy (UPS). Each of these methods has certain unique advantages, and they yield complementary information. For example, the atomic structure of the surface is obtained from LEED analysis, which shows that whereas the Pt₃Ni(111) surface exhibits a (1 × 1) pattern (Fig. 8), the atomically less dense Pt₃Ni(100) surface shows a clear (1 × 5) reconstruction pattern (the so-called “hex” phase) in both the [011] and [0-11] directions (Fig. 8). Analysis of the Pt₃Ni(110) LEED data (Fig. 8) indicates that this surface may exhibit a mixture of (1 × 1) and (1 × 2) periodicities, the latter being known as the (1 × 2) missing row structure.³⁵ The exact surface composition of the outermost atomic layer is obtained by utilizing LEIS, as previously shown for Pt₃Ni polycrystalline alloys.^36,37 The LEIS spectra showed that, after a final anneal, the surface atomic layer of all three Pt₃Ni(hkl) crystals is pure Pt, i.e. they all form the so-called Pt-skin structure.^38,39 Earlier reports from similar studies suggested that this surface enrichment of Pt in the first layer is counterbalanced by its depletion in the next two to three atomic layers, resulting in a concentration profile that oscillates around the bulk value.^40,41 These types of near-surface compositional changes account for the unique electronic properties of alloys.

Fig. 8 Surface characterization of the Pt₃Ni single crystals in UHV. LEED patterns and the corresponding ball and stick models for the three low-index surfaces.

While the phenomenon of surface segregation at bimetallic surfaces has been well studied under UHV conditions, the stability of such surfaces in the electrochemical environment is relatively unknown, and yet this is crucially important to their potential application as electrocatalysts. After immersion of the crystal at 0.05 V into the electrolyte the Pt₃Ni(111) surface structure was determined by measurement and analysis of the crystal truncation rods (CTR's).¹⁷Fig. 9a shows the (0, 0, L) and (0, 1, L) CTR data measured at 0.05 V. The data points, indicated by the error bars, represent background-subtracted integrated intensities obtained from rocking scans over the full mosaic range which were taken at sequential L values along the CTR. The CTR data can be modeled using kinematical scattering theory. The model assumes the crystal to be a perfectly random alloy with an fcc lattice, each atom having an average atomic form factor of 0.75f_Pt + 0.25f_Ni.⁴² In order to provide uniqueness in the modeling of the CTR data, energy dependent measurements at two reciprocal lattice positions were performed. The data points in Fig. 9b correspond to background-subtracted integrated intensities obtained from rocking scans at (0, 0, 3.3) and (0, 0, 1.5) as a function of the incident X-ray energy. The energy range of the measurement was 200 eV either side of the Ni K adsorption edge at 8333 eV. The resultant spectra were approximately corrected for detector efficiency and adsorption by normalizing to a linear change in the background signal. Gaussian line shapes with a fixed centre at 8333 eV were fitted to both of the normalized spectra and are shown as the solid lines in Fig. 9b. From this data, an intensity ratio at each CTR position, I_8323eV/I_8133eV, was calculated and the results are plotted in the inset to Fig. 9a. Over the energy range 8133–8323 eV, i.e. below the Ni K adsorption edge, the change in the anomalous dispersion corrections to the Ni form factor is due to only to the real part, f′, and can be calculated exactly.⁴³ By simultaneously fitting this ratio data, which constrains the fit to the full CTR data, sensitivity to the elemental concentration profile at the surface, i.e. separation from surface roughness effects in the modeling of the CTR data, is obtained.

Fig. 9 CTR data of the Pt₃Ni(111) crystal surface in 0.1 M HClO₄ with an applied potential of 0.05 V (vs. RHE). (a) The error bars are the data points and the solid line is the best fit to the data. (Inset) Energy ratio data as described in the text. The data points are denoted by circles and the best fit to the data is a solid line. (b) Measurements at the (0, 0, 1.5) and (0, 0, 3.3) reciprocal lattice positions as a function of the incident X-ray energy. The vertical dashed line is at 8333 eV, the Ni K adsorption edge. The segregation profile obtained from the SXS measurements is shown in the center of the figure.

In order to fit the model to the data, a least squares minimization was performed in which the variable structural parameters of the three outermost atomic layers were; the fractional Pt occupation assuming fully occupied atomic layers (θ_Pt), relaxation of the surface layer (ε) and a static enhanced Debye–Waller factor (σ). A β factor according to the model developed by Robinson^16,17 was used to model surface roughness effects. The best fit to both CTR data and the ratio data is shown by the solid line in Fig. 9a. A list of the structural fit parameters is given in Table 2. The surface atomic layer is thus determined to be 100% Pt, the second atomic layer to be 48% Pt, the third to be 87% and beyond that the bulk value of 75%. It is clear from these results that the Pt-rich segregated surface (as determined by LEIS in the UHV chamber) is stable both during transfer from UHV and, subsequently, in the electrochemical environment. Furthermore, the CTR measurements also provide the composition of the sub-surface atomic layers and indicate that the second atomic layer is Ni-rich compared to the bulk alloy composition. This is key to understanding the modified electronic properties of the surface Pt layer [compared to bulk Pt(111)] which determines the surface reactivity.²³

Table 2 Structural parameters for the calculated fits to the Pt₃Ni(111) data in Fig. 9

θ Pt1 = 1.00 ± 0.11	ε 1 = −0.003 ± 0.008 Å	σ 1 = 0.288 ± 0.035 Å
θ Pt2 = 0.48 ± 0.11	ε 2 = 0.012 ± 0.005 Å	σ 2 = 0
θ Pt3 = 0.87 ± 0.11	ε 3 = 0	σ 3 = 0
Bulk D-W = 0.13 ± 0.04Å		β = 0.20 ± 0.06

---

Following the determination of the surface atomic structure, the potential dependence of the surface was investigated using X-ray voltammetry (XRV) and cyclic voltammetry (CV). Results were obtained for both the Pt₃Ni(111) sample and a Pt(111) electrode for comparison, and representative results are shown in Fig. 10. The potential response of the two surfaces (Fig. 10b) can be separated into three regions; the first corresponds to the underpotential deposition of atomic hydrogen on the surface (H_upd), the intermediate region to the charging of the double layer and the positive potential region to the reversible adsorption of OH (OH_ad). Integration of the charge in the CV gives the surface coverages by H_upd and OH_ad and these are shown in Fig. 10b. There is a negative potential shift of ∼0.15 V in H_upd and a positive potential shift of ∼0.1 V in OH_ad on the Pt-skin surface relative to the Pt(111) surface. Fig. 10a shows the XRV's for the Pt₃Ni(111) surface measured at (0, 0, 2.7) and for the Pt(111) surface at (1, 0, 3.6). Both of these reciprocal lattice positions, at l values just below a bulk Bragg reflection, are sensitive to surface relaxation as confirmed by the corresponding measurements at l values above the Bragg reflections, (0, 0, 3.3) and (1, 0, 4.4), which showed ‘mirror-like’ behavior. For this reason the intensities are converted to surface expansion (by model calculations after fits to the full CTR data sets in each case) normalized to the values obtained at 0.05 V. It is important to note that at 0.05 V the Pt(111) surface is expanded by ∼2% of the lattice spacing whereas the Pt₃Ni(111) surface is essentially unrelaxed. Fig. 10a shows the change in expansion relative to the value measured at 0.0 V, i.e. the pure Pt(111) surface is expanded by ∼2% at 0.0 V and this is reduced to ∼1.5% expansion at 0.8 V, whereas the Pt₃Ni(111) surface is unrelaxed at 0.0 V and undergoes a ∼1.5% contraction at 1.0 V. Surface expansion is dependent on the substrate-adsorbate bondstrength, i.e. the chemisorption properties that depend on the surface electronic structure (the d-band center).⁴⁴ On both surfaces the adsorption of OH_ad causes surface contraction (the shift in the potential for OH_ad is clearly seen in Fig. 10) and this is the precursor to oxide formation via place exchange with the Pt surface atoms.⁴⁵ The hysteresis observed for Pt(111) is large and is presumably due to the fact that the relaxation not only depends on the coverage but also the ordering of the adlayer species. The structural changes are thus dependent on the kinetics of ordering on the surface, a process that can have a timescale of several minutes. The reduced hysteresis on the Pt₃Ni(111) surface is likely due to the weaker metal-adsorbate interaction. The stability of the Pt-skin surface is a consequence of the electronic structure (d-band center) that decreases the amount of OH_ad (Fig. 10b) so that there is less tendency for place exchange and irreversible roughening. This mechanism is also responsible for the increased activity for the ORR.

Fig. 10 Potential-dependent measurements of the Pt₃Ni(111) and Pt(111) crystal surfaces. (a) XRV measurements for Pt₃Ni(111) at the (0, 0, 2.7) (red line) and Pt(111) at (1, 0, 3.6) (blue line) with 2 mV s⁻¹ sweep rate. (b) Cyclic voltammetry recorded in 0.1 M HClO₄ with 50 mV s⁻¹ sweep rate. (c) Surface coverage by underpotentially deposited hydrogen (H_upd) and hydroxyl species (OH_ad) calculated from the cyclic voltammograms of Pt₃Ni(111) (red curve) and Pt(111) (blue curve).

The Pt₃Ni(100) electrode surface was also transferred into the X-ray electrochemical cell using the same methodology as for Pt₃Ni(111). As shown in Fig. 8, the LEED pattern from this surface was consistent with the presence of a hexagonal surface reconstruction, analogous to the reconstruction of Au(100) found in both UHV³⁵ and electrolyte.^2,15 A search of the (H, K) surface plane of reciprocal space, however, was inconclusive as to the presence of such a hexagonal reconstruction. This may be due to a loss of ordering during the transfer to, or inherent to, the electrochemical environment. The (0, 0, L) CTR was then measured at a potential of 0.05 V, i.e. at the same potential as the data for Pt₃Ni(111) shown in Fig. 9. The (0, 0, L) CTR is only sensitive to the electron density profile perpendicular to the sample surface and doesn't require registry of the surface atoms with the underlying bulk crystal. Attempts were made to fit the data with different structural models; (i) bulk termination of the Pt₃Ni lattice and (ii) variation in the Pt surface concentration (as used for the Pt₃Ni(111) surface) but it was not possible to get a good fit to the data. The data in Fig. 11 shows that the secondary maxima in the CTR data occur at values of L ∼ √3 and L ∼ 2√3, and this implies that there is a (111) stacking at the surface that goes beyond a single atomic layer. The solid line in Fig. 11 includes two surface atomic Pt layers that a have a density corresponding to that of a hexagonal plane, i.e. 1.2 times greater than the cubic (100) plane, and are separated by the (111) plane spacing. These results imply that considerable Pt enrichment has occurred at the Pt₃Ni(100) surface leading to the formation of hexagonal Pt overlayers. This in turn may explain the reduced activity for the oxygen reduction reaction (ORR) on Pt₃Ni(100) compared to Pt₃Ni(111).²³

Fig. 11 Specular CTR data (0, 0, L) of the Pt₃Ni(100) crystal surface in 0.1 M HClO₄ with an applied potential of 0.05 V (vs. RHE). The solid line is a fit to the data described in the text.

For both Pt₃Ni(100) and Pt₃Ni(110), it was not possible using SXS to observe any scattering due to the ordered surface structures that were observed by LEED (Fig. 8). Furthermore, it was not possible to obtain any reliable XRV measurements (as shown for Pt₃Ni(111) in Fig. 10) from these surfaces, i.e. follow structural changes as a function of the applied potential. This implies either that the surfaces are unstable during the transfer from UHV or that they are unstable in the electrochemical environment. Gaining more insight into these more open surfaces would be feasible using the UHV-transfer system described in section 3, as it would then be possible to characterize the surfaces under UHV conditions before adding the electrolyte droplet.

5. Conclusions

In this paper we have described a new experimental methodology for the study of model electrocatalyst materials using surface X-ray scattering (SXS). As a test case we have performed a systematic study of a Pt(111) surface. Initially this was prepared in UHV to have a p(2 × 2)-O layer adsorbed onto the surface. This was characterized by SXS, principally by measurement and modeling of the CTR data. The sample was then contacted with a droplet of pure water and the SXS measurements were repeated. Unfortunately, it was not possible to observe any ordering in the water layers at the Pt–water interface, although it cannot be ruled out that this is due to the weakness of the expected signal compared to the background scattering from the liquid droplet. Analysis of the CTR data showed systematic changes in the measured intensities associated with restructuring at the interface. The data was reproduced with a simple structural model showing reduced outward relaxation in the Pt surface accompanied by increased in-plane distortion of the surface Pt layer and an increased coverage by oxygenated species. Measurements performed in 0.1 M KOH were consistent with previous SXS results and give some insight into the adsorption of hydrogen and oxygenated species.

The experiment on Pt(111) indicates the possibility of studying a range of model electrocatalysts using this methodology. For example, experiments on the low index surfaces of Pt₃Ni, using a less direct transfer method from UHV to the electrochemical environment, were only fully successful for the (111) surface, whereas results on Pt₃Ni(100) and Pt₃Ni(110) were more ambiguous. These systems would be ideal future experiments using the direct transfer system. It is also envisaged that the UHV characterization methods could be developed to include direct imaging techniques, such as STM. A transfer system which enabled both transfer to and from the electrochemical environment would then offer unique opportunities to further probe the link between atomic structure and reactions at the electrochemical interface.

Acknowledgements

Tien-Lin Lee is acknowledged for his assistance with the ID32 beamline and discussion of the correction factors that are applied to the CTR data. The work at the Argonne National Laboratory was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract DE-AC02-06CH11357 and by a travel grant from the EPSRC. Research was carried out in part at SSRL, which is funded by the Division of Chemical Sciences (DCS), U.S. DOE.

References

1. M. G. Samant, M. F. Toney, G. L. Borges, K. F. Blurton and L. M. O. R. Blum, J. Phys. Chem., 1988, 92, 220.
2. B. M. Ocko, J. Wang, A. Davenport and H. Isaacs, Phys. Rev. Lett., 1990, 65, 1466.
3. M. F. Toney and B. M. Ocko, Synchrotron Radiat. News, 1993, 6, 28.
4. I. M. Tidswell, N. M. Markovic and P. N. Ross, Phys. Rev. Lett., 1993, 71, 1601.
5. C. A. Lucas, N. M. Markovic and P. N. Ross, Surf. Sci., 1996, 340, L949.
6. C. A. Lucas, N. M. Markovic and P. N. Ross, Phys. Rev. Lett., 1996, 77, 4922.
7. D. M. Kolb, Prog. Surf. Sci., 1996, 51, 109.
8. K. Itaya, Prog. Surf. Sci., 1998, 58, 121.
9. C. A. Lucas and N. M. Markovic, in 9th Volume of Advances in Electrochemical Science and Engineering, ed. R. Alkire, D. M. Kolb, P. N. Ross and J. Lipkowski, Wiley-VCH, 2006, Chapter 1.
10. D. Menzel, Science, 2002, 295, 58.
11. P. J. Feibelman, Science, 2002, 295, 99.
12. A. Glebov, A. P. Graham, A. Menzel and J. P. Toennies, J. Chem. Phys., 1997, 106, 9382.
13. A. P. Seitsonen, Y. J. Zhu, K. Bedürftig and H. Over, J. Am. Chem. Soc., 2001, 123, 7347.
14. C. Clay, S. Haq and A. Hodgson, Phys. Rev. Lett., 2004, 92, 046102.
15. I. M. Tidswell, N. M. Markovic, C. A. Lucas and P. N. Ross, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 16542.
16. I. K. Robinson and D. J. Tweet, Rep. Prog. Phys., 1992, 55, 599.
17. I. K. Robinson, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 3830.
18. http://www.esrf.eu/UsersAndScience/Experiments/SurfaceScience/ID32/SurfaceLab .
19. N. Materer, U. Starke, A. Barbieri, R. Doll, K. Heinz, M. A. Van Hove and G. A. Somorjai, Surf. Sci., 1995, 325, 207.
20. F. U. Renner, Y. Grunder and J. Zegenhagen, Rev. Sci. Instrum., 2007, 78, 033903.
21. Y. Gauthier, Y. Joly, R. Baudoing and J. Rundgren, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6216.
22. Y. Gauthier, R. Baudoing, Y. Joly, J. Rundgren, J. C. Bertolini and J. Massardier, Surf. Sci., 1985, 162, 342.
23. V. R. Stamenković, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Marković, Science, 2007, 315, 493.
24. C. A. Lucas and N. M. Marković, in Encyclopedia of electrochemistry, ed. E. J. Calvo, Wiley-VCH, 2003, vol. 2, section 4.1.2.1.2.
25. M. Nakamura, K. Sumitani, M. Ito, T. Takahashi and O. Sakata, Surf. Sci., 2004, 563, 199.
26. E. Vlieg, J. Appl. Crystallogr., 1997, 30, 532.
27. R. Feidenhans'l, Surf. Sci. Rep., 1989, 10, 105.
28. M. T. M. Koper and R. A. van Santen, J. Electroanal. Chem., 1999, 472, 126.
29. G. Held, C. Clay, S. D. Barrett, S. Haq and A. Hodgson, J. Chem. Phys., 2005, 123, 064711.
30. K. Bedurftig, S. Volkening, Y. Wang, J. Wintterlin, K. Jacobi and G. Ertl, J. Chem. Phys., 1999, 111, 11147.
31. N. M. Markovic and P. N. Ross, Surf. Sci. Rep., 2002, 45, 117.
32. N. Marinkovic, N. M. Markovic and R. R. Adzic, J. Electroanal. Chem., 1992, 330, 433.
33. C. A. Lucas, Electrochim. Acta, 2002, 47, 3065.
34. P. J. Feibelman, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 2175.
35. P. A. Thiel and P. J. Estrup, in The Handbook of Surface Imaging and Visualization, ed. A. T. Hubbard, CRC Press, Boca Raton, FL, USA, 1995.
36. V. Stamenkovic, T. J. Schmidt, N. M. Markovic and P. N. Ross, J. Phys. Chem. B, 2002, 106, 11970.
37. V. Stamenkovic, T. J. Schmidt, P. N. Ross and N. M. Markovic, J. Electroanal. Chem., 2003, 554–555, 191.
38. V. R. Stamenković, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Marković, J. Rossmeisl, J. Greeley and J. K. Nørskov, Angew. Chem., Int. Ed., 2006, 45, 2897.
39. V. R. Stamenković, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, P. N. Ross, C. A. Lucas and N. M. Marković, Nat. Mater., 2007, 6, 241.
40. Y. Gauthier, R. Baudoing and J. Rundgren, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6216.
41. Y. Gauthier, Surf. Rev. Lett., 1996, 3, 1663.
42. B. E. Warren, X-Ray Diffraction, Dover Publications Inc., 1990.
43. f′ changes from −4.04 electrons to −6.50 electrons, calculated from: S. Brennan and P. L. Cowen, Rev. Sci. Instrum., 1992, 63, 850.
44. B. Hammer and J. K. Norskov, in Chemisorption and Reactivity on Supported Clusters and Thin Films, ed. R. M. Lambert and G. Pacchioni, Kluwer Academic, 1997.
45. H. You, D. J. Zurawski, Z. Nagy and R. M. Yonco, J. Chem. Phys., 1994, 100, 4699.

---