The roles of the first and second coordination spheres in the design of molecular catalysts for H2 production and oxidation†
M. Rakowski DuBois* and Daniel L. DuBois*
Chemical and Materials Sciences Division, Pacific Northwest National Laboratory, Richland, WA 99352, USA
First published on 6th November 2008
Abstract
This tutorial review describes the development of discrete transition metal complexes as electrocatalysts for H2 formation and oxidation. The approach involves the study of thermodynamic properties of metal hydride intermediates and the design of ligands that incorporate proton relays. The work is inspired by structural features of the H2ase enzymes and should be of interest to researchers in the areas of biomimetic chemistry as well as catalyst design and hydrogen utilization.
 M. Rakowski DuBois | Mary Rakowski DuBois joined the faculty of the University of Colorado in 1976, after completion of her PhD at Ohio State University and postdoctoral work at Cornell University. In 2007 she moved to the Pacific Northwest National Laboratory at Richland, Washington. Her research interests have included the syntheses and studies of organometallic and metallosulfur complexes that function as catalysts or models for heterogeneous catalysts. |
 Daniel L. DuBois | Daniel L. DuBois is a Senior Scientist at Pacific Northwest National Laboratory. He received his PhD from the Ohio State University and did postdoctoral work at Cornell University. His research interests include the catalytic interconversion of fuels and electricity, synthetic organometallic and inorganic chemistry, and thermodynamic studies relevant to catalysis. |
1. Introduction
Catalysts for the conversion of electrical energy to fuels and for the reverse process, the conversion of fuels to electricity, will have a significant impact on future renewable energy systems. The intermittent nature of renewable energy sources such as photovoltaics and wind energy makes efficient energy storage a requirement. Because of the large amount of energy that needs to be stored, an inexpensive and abundant material such as H2O is an attractive substrate for energy storage. The simplest fuel is H2, and its production from electricity and water requires the reduction of two protons by two electrons. Both platinum metal and hydrogenase enzymes efficiently catalyze this reaction. In addition to inexpensive substrates for fuel generation, it is also important that catalysts for fuel production be based on inexpensive and relatively abundant metals. The presence of iron or a combination of iron and nickel in the active sites of hydrogenase enzymes1–8 demonstrates that expensive precious metals such as platinum are not required for this reaction. However, those structural features of the enzyme active site that are required to achieve high activity are not necessarily obvious.Our approach to the development of catalysts for H2 production and oxidation is based on an understanding of those factors controlling the energies of potential intermediates and transition states in the catalytic cycle. Three hypothetical energy profiles for the formation of hydrogen are shown in Fig. 1. For an uncatalyzed reduction of two protons to H2 (shown by the solid black curve in Fig. 1), there will be a large activation barrier for H2 production. As a result, rates of H2 production for uncatalyzed processes will involve large overpotentials and/or very slow catalytic rates. For a moderately active catalyst (green curve in Fig. 1), the large energy barrier(s) associated with an uncatalyzed reaction are avoided, but the high and low energy intermediates shown are associated with significant activation barriers that result in overpotentials and less than optimal catalytic rates. However, the overall performance will clearly be better than for the uncatalyzed reaction. For an ideal catalytic process (shown by the blue curve), the energies of the catalytic intermediates decrease in a monotonic fashion from the energy of the reactants (two protons and two electrons provided at a sufficient potential) to the energy of the products. The high and low energy intermediates observed for a reaction profile corresponding to a moderate catalyst are avoided. Similarly, the intrinsic activation barriers between the catalytic intermediates for the ideal catalytic cycle will be much lower than those for the moderately catalyzed or uncatalyzed reaction.
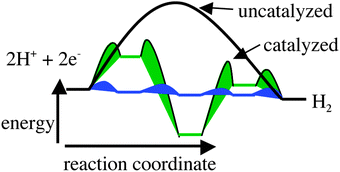 | ||
| Fig. 1 Reaction profiles for the formation of H2 (proceeding from left to right) for an uncatalyzed reaction (solid black curve), a moderate catalyst (green curve), and an ideal catalyst (blue curve). | ||
How can the relative energies of catalytic intermediates and the activation barriers between these intermediates be controlled? To answer the first part of this question, our laboratories have studied how the first coordination sphere of metal complexes can be used to determine the relative energies of potential catalytic intermediates. This will be the topic of the first half of the following discussion. To answer the second part of the question, we have studied the roles that pendant bases incorporated into the second coordination sphere can play in processes such as the intramolecular heterolytic cleavage of H2 and the transfer of the resulting proton to solution. This topic and how these two general tools can be applied to the design of highly active catalysts for H2 oxidation and production is the subject of the second section.
2. Factors controlling the thermodynamic properties of transition metal hydrides
The activation of H2 by the active site of [FeFe]–H2ase has been proposed to occur as shown in reaction (1).1,9,10 In this reaction, H2 binds to the distal iron atom (Fed) in the first step to form a dihydrogen complex. This is followed by heterolytic cleavage of hydrogen in step 2 to produce an iron hydride and a protonated amine. In this overall reaction, the hydride acceptor ability of the distal iron and the proton acceptor ability of the pendant base must be precisely matched so that the overall free energy change for this reaction is nearly 0 kcal mol−1. This is required for reversibility and to avoid high or low energy intermediates.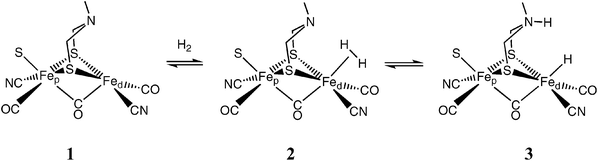 | (1) |
As a result, we wanted to understand what factors control the hydride acceptor ability of metal complexes. This led to the development of several different methods for measuring the free energy associated with the reverse reaction, MH → M+ + H−, using a variety of thermodynamic cycles.11–14 One of these cycles is shown in Scheme 1. Reaction (2) in this cycle is the deprotonation of the metal hydride represented by [HMLn]+. The free energy associated with this reaction is simply –RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka or 1.37 pKa at 25 °C. Reaction (3) is the oxidation of the metal complex formed in the first reaction by two electrons. The standard free energy associated with this reaction is nFEo when the reaction involved is an oxidation. Reaction (4) is the reduction of a proton by two electrons to form a hydride ion in acetonitrile, and the free energy value associated with this reaction is of course a constant.15 The sum of reactions (2)–(4) is the heterolytic cleavage of the M–H bond to form H− (reaction (5)) and the associated metal fragment, and the free energy associated with this heterolytic bond cleavage reaction, ΔG°H−, is the sum of the free energies for reactions (2)–(4). Smaller values of ΔG°H− correspond to better hydride donor abilities of the corresponding metal hydride, [HMLn]+, and larger values of ΔG°H− correspond to better hydride acceptor abilities of the corresponding [MLn]2+ complex.
Ka or 1.37 pKa at 25 °C. Reaction (3) is the oxidation of the metal complex formed in the first reaction by two electrons. The standard free energy associated with this reaction is nFEo when the reaction involved is an oxidation. Reaction (4) is the reduction of a proton by two electrons to form a hydride ion in acetonitrile, and the free energy value associated with this reaction is of course a constant.15 The sum of reactions (2)–(4) is the heterolytic cleavage of the M–H bond to form H− (reaction (5)) and the associated metal fragment, and the free energy associated with this heterolytic bond cleavage reaction, ΔG°H−, is the sum of the free energies for reactions (2)–(4). Smaller values of ΔG°H− correspond to better hydride donor abilities of the corresponding metal hydride, [HMLn]+, and larger values of ΔG°H− correspond to better hydride acceptor abilities of the corresponding [MLn]2+ complex.
 | ||
| Scheme 1 | ||
Using thermodynamic cycles of this type, the hydride donor/acceptor abilities of a large range of compounds have been determined using acetonitrile as the solvent. These include a diverse array of compounds such as NADH analogues (a biological hydride donor),16–18 hydroquinone derivatives,19 transition metal hydrides of various types,16,20–22 bridging hydroxides in bimetallic complexes,23 and aromatic hydrocarbons.24,25 Of these different classes of compounds, those containing transition metals were of interest because of their ability to bind and activate H2 to form either dihydrogen or dihydride complexes. In particular, we were interested in transition metal complexes containing two diphosphine ligands, because in addition to their ability to activate H2, they frequently exhibit two reversible one-electron reductions or a single reversible two-electron reduction26,27 so that ΔG°H− could be determined using Scheme 1 for these complexes.
2.1 Ligand electronic effects and hydride donor/acceptor abilities
[HM(diphosphine)2]+, 4, (where M = Ni, Pd, and Pt) and HM(diphosphine)2 (where M = Co and Rh) complexes were studied to determine the influence of ligand substituents (R), natural bite angles (β) or dihedral angle (α), and the metal (M) on the hydride donor ability of these complexes, as shown in reaction (6).11,21,22,28,29Fig. 2 shows a plot of the hydride donor ability for a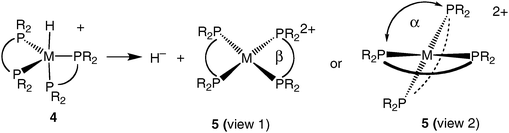 | (6) |
![Plots of ΔG°H− (top) and pKa (bottom) values of [HNi(diphosphine)2]+ complexes vs. the sum of substituent inductive and resonance parameters.](/image/article/2009/CS/b801197b/b801197b-f2.gif) | ||
| Fig. 2 Plots of ΔG°H− (top) and pKa (bottom) values of [HNi(diphosphine)2]+ complexes vs. the sum of substituent inductive and resonance parameters. | ||
2.2 Relationships between natural bite angles, dihedral angles, and hydride donor/acceptor abilities
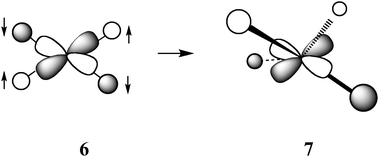
Studies of the influence of the steric properties of the diphosphine ligand on reaction (6) have shown that the geometry of the four-coordinate, sixteen-electron product, 5, plays a major role in determining the hydride donor ability of [HM(diphosphine)2]+ complexes. One geometric parameter is the natural bite angle (NBA) of the diphosphine ligand, which is the P–M–P angle the ligand would prefer to impose on the metal (β in view 1 of structure 5). NBA parameters for many diphosphine ligands are readily available from several reviews.33,34 There is also the P–M–P bond angle that the metal complex prefers to adopt for a particular electronic configuration and environment. The observed P–M–P bond angles in metal complexes are of course a compromise between the NBA preferred by the ligand and the bite angle preferred by the metal. A second geometrical parameter is the crystallographically determined dihedral angle between the two planes formed by M and the phosphorus atoms of each diphosphine ligand in [M(diphosphine)2]2+ complexes (α in view 2 of structure 5).As can be seen from the bottom graph in Fig. 3, there is a reasonable correlation of ΔG°H− of [HPd(diphosphine)2]+ complexes with the NBA of the diphosphine ligands. A significantly better correlation (as indicated by a higher r2 value) is observed when ΔG°H− is plotted vs. the dihedral angles of the corresponding [Pd(diphosphine)2]2+ complexes, as shown in the top graph of Fig. 3.29 The origin of the correlations shown in Fig. 3 can be understood in terms of a simple molecular orbital treatment.35 The lowest unoccupied molecular orbital (LUMO) for sixteen-electron ‘square-planar’ [M(diphosphine)2]2+ complexes is an orbital that is antibonding between the d(x2–y2) orbital of nickel and the sigma orbitals of the four phosphine donors as shown by molecular orbital 6. A tetrahedral distortion arising from a twisting of the two diphosphine ligands (as shown in view 2 of structure 5) results in a decrease in the antibonding interaction between the ligands and the metal (molecular orbital 7) and a lower energy for the LUMO.
Because this orbital is the acceptor orbital for the two electrons upon addition of a hydride ligand, there is a strong correlation between the energy of this orbital and the hydride acceptor ability of the metal complex. As the NBA of the diphosphine ligands increases, this tetrahedral distortion also increases, and this leads to the correlation shown in the bottom graph of Fig. 3. However, the steric bulk of the phosphine substituents also contributes to this tetrahedral distortion. In fact, substituent size alone can be used to vary the dihedral angle and the hydride acceptor ability of [M(diphosphine)2]2+ complexes.36 Because the dihedral angle accounts for increased distortions from both substituent size and the NBA, this parameter correlates more strongly with the hydride donor ability than does the NBA alone as seen in the top graph of Fig. 3. In contrast, the pKa values and homolytic solution bond dissociation free energies are unaffected by the NBAs of the diphosphine ligands or the dihedral angles of the complexes. In summary, the two ligand parameters that effectively control the hydride donor/acceptor abilities of [HM(diphosphine)2]+/[M(diphosphine)2]2+ complexes are the dihedral angle between the two diphosphine ligands and the electron donor/acceptor ability of the ligand substituents.
![Plot of ΔG°H− for [HPd(diphosphine)2]+ complexes vs. the NBA (natural bite angle) of the diphosphine ligands (bottom) and vs. the dihedral angle between the two diphosphine ligands of the corresponding [Pd(diphosphine)2]2+ complexes (top).](/image/article/2009/CS/b801197b/b801197b-f3.gif) | ||
| Fig. 3 Plot of ΔG°H− for [HPd(diphosphine)2]+ complexes vs. the NBA (natural bite angle) of the diphosphine ligands (bottom) and vs. the dihedral angle between the two diphosphine ligands of the corresponding [Pd(diphosphine)2]2+ complexes (top). | ||
2.3 The role of the metal and hydride donor/acceptor abilities
The final factor affecting the hydride acceptor/donor properties of transition metal complexes is the nature of the metal. Fig. 4 is a graph of ΔG°H− for [HM(diphosphine)2]+ complexes where M = Ni, Pd and Pt for seven different ligands.11,22,28,29 On average, nickel complexes are approximately 10 and 13 kcal mol−1 poorer hydride donors than the corresponding platinum and palladium complexes, respectively. Conversely, [Ni(diphosphine)2]2+ complexes are significantly better hydride acceptors than their palladium and platinum analogs. Comparison of [HNi(diphosphine)2]+ complexes with HCo(diphosphine)2 derivatives indicate that cobalt hydrides with the same ligand set are better hydride donors their nickel analogues by about 14 kcal mol−1.11,20 Theoretical calculations suggest similar differences.31![Plot of ΔG°H− for [HM(diphosphine)2]+ complexes where M = Ni, Pd, and Pt for the following ligands: (1) bis(diethylphosphinomethyl)methylamine, (2) bis(diethylphosphino)ethane, (3) bis(dimethylphosphino)propane, (4) bis(dimethylphosphino)ethane, (5) bis(diphenylphosphino)ethane, (6) bis(diethylphosphino)propane, (7) 9,9-dimethyl-4,5-bis(diethylphosphino)xanthene.](/image/article/2009/CS/b801197b/b801197b-f4.gif) | ||
| Fig. 4 Plot of ΔG°H− for [HM(diphosphine)2]+ complexes where M = Ni, Pd, and Pt for the following ligands: (1) bis(diethylphosphinomethyl)methylamine, (2) bis(diethylphosphino)ethane, (3) bis(dimethylphosphino)propane, (4) bis(dimethylphosphino)ethane, (5) bis(diphenylphosphino)ethane, (6) bis(diethylphosphino)propane, (7) 9,9-dimethyl-4,5-bis(diethylphosphino)xanthene. | ||
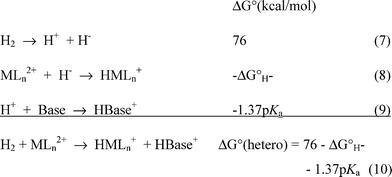
As discussed above, the heterolytic cleavage of H2 by a metal complex requires a matching of the hydride acceptor ability of a transition metal complex with the proton acceptor ability of a base. Scheme 2 shows the fundamental reactions involved in this overall process. Reaction (7) is the heterolytic cleavage of H2 in acetonitrile, which requires 76 kcal mol−1.15,16 The ΔG°H− values for [HNi(diphosphine)2]+ complexes in acetonitrile (reaction (8)) have been determined, as discussed in the preceding section, and the pKa values of protonated amines in acetonitrile (reaction (9)) are also known.37,38 The sum of these three reactions is the heterolytic cleavage of H2 by a metal complex in the presence of a base (reaction (10)), and the free energy of this reaction is the sum of the free energies associated with reactions (7), (8) and (9). It is possible to choose a protonated amine with an appropriate pKa for energy matching with a given metal hydride so that ΔG° for reaction (9) is close to 0. A number of heterolytic hydrogen cleavage reactions have been designed and carried out for nickel complexes, confirming that such an energy matching approach is viable.12,28,36
 | ||
| Scheme 2 | ||
2.4 Generalization to other reaction intermediates
The discussion above focuses on matching the hydride acceptor ability of the transition metal complex (which can be controlled by varying the metal, the dihedral angle of the complex, and the ligand substituents) to the proton acceptor ability of the base so that the energy for the heterolytic cleavage of H2 is close to 0. In a complete catalytic cycle, a number of elementary reactions need to occur, and the energies of all of these reactions would ideally require the same energy matching described for the heterolytic cleavage of H2. A more general approach to this problem is to determine all three bond dissociation free energies for the transition metal hydride complexes of interest. The metal–hydrogen bond can be cleaved in three ways as shown by Scheme 3: the heterolytic cleavage of the M–H bond to form H+ and the corresponding LxM fragment, the homolytic cleavage of the M–H bond to form the hydrogen radical and LxM+, and a second heterolytic cleavage of the M–H bond to form H− and LxM2+. Associated with each of these bond cleavage reactions is a free energy that determines the relative free energies of the four metal species shown.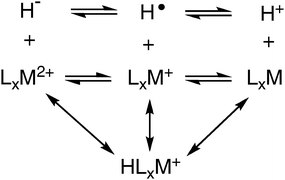 | ||
| Scheme 3 | ||
This same approach can be extended to include dihydride complexes, for which all three bond dissociation free energies can be determined, and the free energies of the corresponding monohydride derivatives as well.20,39,40 An example of this is shown by the thermodynamic diagram on the left side of Fig. 5 for the [Ni(depp)2]2+ system (where depp is bis(diethylphosphino)propane).12
![Relationships between thermodynamic diagrams (top left diagram), a free energy landscape showing the relative energies of all species derived from M–H bond cleavage reactions (top right bar graph, acetonitrile solutions, 1 atm H2, and pH = 8.5), and the reaction profile for the electrocatalytic oxidation of H2 using [Ni(depp)2]2+ as the catalyst under the same conditions.](/image/article/2009/CS/b801197b/b801197b-f5.gif) | ||
| Fig. 5 Relationships between thermodynamic diagrams (top left diagram), a free energy landscape showing the relative energies of all species derived from M–H bond cleavage reactions (top right bar graph, acetonitrile solutions, 1 atm H2, and pH = 8.5), and the reaction profile for the electrocatalytic oxidation of H2 using [Ni(depp)2]2+ as the catalyst under the same conditions. | ||
In this diagram, the columns specify the charge on the individual species, in this case 2+, 1+ and 0, and the rows specify the number of hydrogens bound to the metal, 0 for the first row, 1 for the second row, and two for the third row. The bond energies (in kcal mol−1) have been calculated using appropriate thermodynamic cycles such as that shown in Scheme 1. This data can be used to construct three dimensional free energy landscapes that show the relative free energies of the different complexes under specified conditions as shown by the right bar graph in Fig. 5. In this bar graph, the six different bars represent the six different complexes shown in the thermodynamic diagram with the number of hydrogen atoms for each species plotted along the y axis and the charge plotted along the x axis. The free energies of these species, relative to the most stable complex for the specified conditions, are indicated by the height of the bars. This transformation from a thermodynamic diagram to a three dimensional free energy map requires the use of thermodynamic cycles such as those shown in Schemes 1 and 2.
The free energy landscape in Fig. 5 can in turn be used to construct the reaction profile shown at the bottom of the figure for the electrocatalytic oxidation of H2 using [Ni(depp)2]2+ as the catalyst. In this reaction profile, the relative free energies of the intermediates indicated in the catalytic cycle are determined by the thermodynamic parameters shown in the thermodynamic diagram and the energy map shown in Fig. 5. However, the barriers between these intermediates are arbitrary, and are shown only for purposes of illustration. Comprehensive studies of the thermodynamic properties of transition metal hydrides and dihydrides thus provide a method for determining the free energies of the reaction intermediates involved in the catalytic oxidation of H2. As a result, knowledge of the factors that determine the free energies of the various bond cleavage reactions (such as ligand substituents, dihedral angles, and the metal) provide an approach to controlling the relative energies of the intermediates in the catalytic cycle. These thermodynamic considerations provide an extremely useful tool for designing H2 oxidation/production catalysts as well as catalysts for other reactions. From the reaction profile shown in Fig. 5 for [Ni(depp)2]2+, it can be seen that the Ni(III) hydride complex, [HNi(depp)2]2+, is a high energy intermediate, but the remaining intermediates have similar energies as desired for a catalytic process. The oxidation of [HNi(depp)2]+to [HNi(depp)2]2+ is followed by an energetically favorable proton transfer reaction, and this suggests that introducing structural features that would couple the electron and proton transfer events may help to avoid this high energy intermediate. This leads naturally to the incorporation of proton relays.
3. The role of pendant bases in the second coordination sphere
3.1 Structural considerations
The preceding sections focus on the energies of reaction intermediates, which are largely controlled by the metal and the electronic and steric properties of the ligands in the first coordination sphere. In this section, emphasis is placed on the roles played by pendant bases incorporated into the second coordination sphere, as suggested by proposed structures of the active site of the [FeFe]-H2ase enzyme (structures 1–3). Studies in our laboratories of octahedral iron complexes containing pendant amines in the second coordination sphere have shown that such bases can promote heterolytic cleavage of coordinated dihydrogen, exchange of protons in solution with the hydride ligand, and proton-coupled electron-transfer reactions.41–44A series of nickel complexes with structures 8–10 were prepared in an effort to incorporate these features of the second coordination sphere into complexes for which an understanding of the thermodynamic properties existed. Complex 8, [Ni(depp)2]2+, is the nickel complex discussed above for which the reaction profile for H2 oxidation is shown in Fig. 5. Complex 9, [Ni(PNP)2]2+, differs from 8 by replacement of the central methylene group of the trimethylene link of depp with an NMe group.45 The direct coordination of the pendant nitrogen base to the metal is disfavored by formation of two strained four-membered rings when both phosphorus atoms are coordinated. The incorporation of this base was intended to provide a flexible relay for moving protons between the metal and the solution during the catalytic cycle. Structural features of this PNP ligand are similar to the structure proposed for the bridging dithiolate ligand in the active site of [FeFe]-H2ase.
Further examination of the structure of the [FeFe]-H2ase active site indicates that the six-membered ring formed by the dithiolate ligand and the distal iron adopts a boat conformation as a result of steric interactions between the ligand and substituents on the proximal iron atom. This positions the amine of the ligand backbone in close proximity to the incoming H2 ligand during the catalytic cycle. In an attempt to incorporate this feature into potential catalysts, nickel complexes of three different cyclic 1,5-diaza-3,7-diphosphacyclooctane ligands were prepared.36,46 Structure 10 was observed for the ligand with R = cyclohexyl and R′ = benzyl, 10c, while five coordinate structures with a coordinated acetonitrile ligand were characterized for R = phenyl, R′ = phenyl, 10a, and R = phenyl, R′ = benzyl, 10b. The presence of two six-membered rings within each diphosphine ligand is expected to result in one ring always adopting a boat conformation. X-Ray diffraction studies have confirmed that at least one boat conformation is present in each coordinated cyclic ligand. Each of the [Ni(PR2NR′2)2]2+ complexes displays two non-bonding Ni–N distances of 3.2–3.4 Å. Complexes 9 and 10, and derivatives of them, can be used to probe how structural modifications involving a pendant amine can influence catalytic properties and proton transfer reactions for these complexes.
3.2 Catalytic studies of [Ni(depp)2]2+ and [Ni(PNP)2]2+ complexes
Thermodynamic studies in our laboratories demonstrated that [Ni(diphosphine)2]2+ complexes are capable of heterolytically cleaving H2 in the presence of appropriate bases. In particular, [N(depp)2]2+ rapidly cleaves H2 (within seconds) to form [HNi(depp)2]+.45 In the absence of added base, the depp ligand from a second equivalent of [Ni(depp)2]2+ is protonated and serves as a source of base. In the presence of an additional base, such as triethylamine or anisidine, the formation of [HNi(depp)2]+ is quantitative, and no depp ligand is consumed during the heterolytic activation of H2. [Ni(depp)2]2+ serves as an electrocatalyst for the oxidation of H2 in the presence of a base (confirmed by product characterization), but this reaction is slow. No measurable current enhancement is observed by cyclic voltammetry in the presence of H2 and added base, indicating a turnover frequency of less than 0.5 s−1 under the conditions studied. The oxidation of [HNi(depp)2]+ occurs at approximately +0.1 V vs. the ferrocenium/ferrocene couple in the presence of base. Even though this complex rapidly cleaves H2 by synthetic standards, it is a poor catalyst for H2 oxidation with a slow catalytic rate and a large overpotential.[Ni(PNP)2]2+, 9, also heterolytically cleaves H2, and the pendant nitrogen atom of one PNP ligand serves as the base.45 In the presence of an excess of an external base, this process becomes catalytic. The overpotential for the reaction is significantly decreased; oxidation now occurs at −0.62 V, or 0.7 volts more negative than observed for [Ni(depp)2]2+. Although, the presence of a pendant base has a large effect on the catalytic potential, the catalytic rate still remains slow, with a turnover frequency less than 0.5 s−1. Detailed spectroscopic and electrochemical studies of the [Ni(PNP)2]2+ system resulted in the proposed mechanism shown in Scheme 4.
 | ||
| Scheme 4 | ||
The slow overall rate for H2 oxidation is attributed to a rate-determining addition of H2 to [Ni(PNP)2]2+ to form [(H2)Ni(PNP)2]2+, 9b (step 1). This putative intermediate has not been observed spectroscopically, but it is inferred from DFT calculations. Based on these calculations, a conformational change of one of the six-membered rings from the more stable chair form to a boat form occurs and an attractive interaction between the pendant base and coordinated H2 occurs. Step 2 involves the heterolytic cleavage of H2 to form [HNi(PNP)(PNHP)]2+, 9c, the first observable intermediate in the catalytic cycle, which is 6 kcal mol−1 more stable than [Ni(PNP)2]2+ under 1 atm of H2. The energy profile for H2 addition to [Ni(PNP)2]2+ can be compared to that of [Ni(depp)2]2+ and is shown by the dashed green line of Fig. 6. Variable temperature NMR experiments on [HNi(PNP)(PNHP)]2+, 9c, demonstrate that intramolecular NH/NiH exchange occurs with a rate of approximately 104 s−1 at 25 °C. Since the exchange is proposed to proceed through a dihydrogen intermediate, the high exchange rate indicates that the actual intramolecular heterolytic cleavage of H2 is fast, consistent with step 1 of Scheme 4 being the rate-determining reaction.
![Comparison of free energy reaction profiles for the electrocatalyic oxidation of H2 using [Ni(depp)2]2+, discussed previously (solid lines), and [Ni(PNP)2]2+ (dashed lines) as catalysts under the same conditions.](/image/article/2009/CS/b801197b/b801197b-f6.gif) | ||
| Fig. 6 Comparison of free energy reaction profiles for the electrocatalyic oxidation of H2 using [Ni(depp)2]2+, discussed previously (solid lines), and [Ni(PNP)2]2+ (dashed lines) as catalysts under the same conditions. | ||
NOESY NMR data showed that intermolecular exchange between D2O and the hydride ligand of [HNi(PNP)2]+ , 9d, was also fast (>10 s−1).45 In contrast, when D2O was added to [HNi(depp)2]+ under the same conditions, less than 10% deuterium incorporation was observed after 48 h. These results demonstrate two important roles for the pendant base: (1) facilitating intramolecular heterolytic cleavage of H2, and (2) facilitating intermolecular exchange between the hydride ligand and protons in solution (steps 2 and 3 of Scheme 4). The fast intermolecular exchange of a proton between two nitrogen bases is not surprising. However, it is important that this intermolecular exchange be coupled with an intramolecular exchange process if the pendant base is to function as a proton relay and provide a new pathway for transferring a proton from the metal to a base in solution.
The pendant base in the PNP ligand also couples the electron and proton transfer events shown in steps 4 and 5. As discussed above, cyclic voltammograms of acetonitrile solutions of [HNi(depp)2]+ and [HNi(PNP)2]+ were compared in the presence of triethylamine as a proton acceptor. In each case a two-electron oxidation is observed, but for [HNi(PNP)2]2+, this oxidation wave occurs at the same potential as the Ni(II/I) couple of [Ni(PNP)2]2+, or 0.7 V more negative than observed for [HNi(depp)2]+. The large shift in potential (−0.7 V) for the oxidation wave of [HNi(PNP)2]+ indicates an extremely fast (or coupled) intramolecular proton transfer from nickel to the amine of the PNP ligand upon oxidation of the metal from Ni(II)–H to Ni(III)–H. This coupling of the proton and electron transfer events permits the large energy barrier associated with the formation of a N(III)–H complex to be avoided. The dashed purple line in the reaction profile of Fig. 6 qualitatively illustrates the effect of the relay on this energy barrier. A second intermolecular proton transfer event occurs in step 6 of Scheme 4, and the catalytic cycle is completed by a second electron transfer resulting in the oxidation of Ni(I) to Ni(II) (step 7).
3.3 Studies of nickel complexes containing cyclic PR2NR′2 ligands
In Scheme 4, a conformational change of one PNP ligand from a chair to a boat form is required for the pendant amine to interact with the coordinated H2 molecule in the rate-determining step. The series of nickel complexes [Ni(PR2NR′2)2]2+ , 10, were prepared to investigate whether positioning a pendant base in close proximity to nickel stabilizes the formation of dihydrogen or dihydride complexes resulting from reaction with H2.36,46,47 This could lead to faster catalysts for H2 oxidation and production.The substituents on the cyclic PR2NR′2 ligands can be tuned to provide different thermodynamic driving forces for the addition of H2 to these complexes (reaction (11)). A
| [Ni (PR2NR′2)2]2+ + H2→ [Ni(PR2NR′2H)2]2+ | (11) |
Both complexes 10a and 10b exhibit a thermodynamic bias for the reverse of reaction (11), hydrogen elimination, and both of these complexes are found to function as electrocatalysts for hydrogen formation.36,46,47 Kinetic studies of the reaction of 10a established that the catalytic rate is first order in catalyst and second order in acid at low acid concentrations, and it becomes independent of acid at high concentrations. In the high [acid] regime (where protonated dimethylformamide is the acid in acetonitrile), a turnover frequency for H2 production of 350 s−1 at 22 °C has been observed with an overpotential of approximately 0.35 V.47 This catalytic rate is similar to that reported for NiFe–H2ase (700 s−1 at 30 °C),48 although the overpotential is larger. In contrast when 10b is the electrocatalyst, the rate of hydrogen formation decreases by about two orders of magnitude, with a turnover frequency of 5 s−1 and an overpotential of ca. 0.2 V at 22 °C and high acid (bromoanilinium) concentrations.36 The lower catalytic rate for 10b is consistent with the smaller thermodynamic driving force associated with release of hydrogen from this complex.
A comparison of the reactions of [Ni(PPh2NBz2)2]2+, 10b, and [Ni(PCy2NBz2)2]2+, 10c, with hydrogen illustrates the effect of changing the substituent on the phosphine donors. More bulky substituents on the phosphorus atoms should result in larger tetrahedral distortions and a greater hydride affinity at nickel, as discussed under the section on thermodynamic studies. In agreement with this prediction, 10c reacts with one atm of hydrogen with an equilibrium constant of 190 ± 20 atm−1 at 22 °C,46 corresponding to a free energy of −3.1 kcal mol−1 for 10c in reaction (11). As a result of this bias for hydrogen addition, 10c is found to be an electrocatalyst for hydrogen oxidation. Kinetic studies established that the reaction is first order in catalyst and first order in hydrogen and a turnover frequency of 10 s−1 was determined in the presence of 1 atm of H2 and excess base (triethylamine).46
These results clearly demonstrate that electronic and steric properties of substituents on both phosphorus and nitrogen can be used to tune these catalysts. The balance of the hydride donor/acceptor properties of the complex and the proton donor/acceptor properties of the pendant base can be biased to favor either catalytic production or oxidation of H2. Although the rates of H2 oxidation and production in these catalytic reactions are controlled by transition state energies, a knowledge of the factors controlling the thermodynamics of the intermediates can greatly assist in understanding their bias toward H2 production or oxidation.
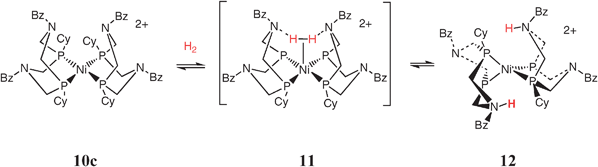
Because the addition of H2 to [Ni(PCy2NBz2)]2+, 10c, is favorable by 3 kcal mol−1, this reaction provided the opportunity to obtain detailed information about the nature of the products formed upon H2 addition to complexes containing positioned pendant bases. Surprisingly, the first complex observed at low temperature upon adding H2 to [Ni (PCy2NBz2)2]2+ is the hydrogen oxidation product [Ni(PR2NR′2H)2]2+, 12, in which one amine in each ligand of the tetrahedral Ni(0) complex has been protonated, as shown in reaction (12). The structure of 12 has been established by extensive variable-temperature 1H, 2D, 31P, and 15N NMR studies of isotopically labeled species.47 Our spectroscopic
 | (12) |
The heterolytic cleavage of hydrogen in this system appears to involve a novel mechanism that relies on the presence of two positioned pendant bases. Polarization of the H2 molecule is proposed to occur by the removal of two electrons by nickel from a symmetric transition state in which both of the hydrogen atoms gradually develop a more positive charge. This mode of activating H2 is very different from that observed for the intramolecular heterolytic cleavage of H2 by [Ni(PNP)2]2+, shown in steps 1 and 2 of Scheme 4. In that system the heterolytic activation of hydrogen involves an asymmetric polarization of H2 to form protonic and hydridic species and the oxidation state of nickel remains unchanged. As discussed above, 10c is an electrocatalyst for the oxidation of H2 in acetonitrile solutions with a turnover frequency of 10 s−1 in the presence of excess triethylamine and 1 atm of H2. This rate is significantly higher than that observed for [Ni(PNP)2]2+ (<0.5 s−1), although the latter complex has a larger driving force for H2 addition (6 kcal mol−1).45 On the basis of our kinetic, theoretical and structural studies, the larger catalytic rate observed for [Ni(PCy2NBz2)2]2+ compared to [Ni(PNP)2]2+ is attributed to the stabilization of the dihydrogen intermediate, 11, by interaction of the H2 ligand with two positioned nitrogen bases. The stabilization of dihydrogen binding is another function of one or two bases incorporated into the second coordination sphere of a metal catalyst-in addition to promoting heterolytic cleavage, proton transfer, and proton-coupled electron transfer reactions.
Subsequent to H2 addition and H–H bond cleavage in eqn (12), reaction of 12 with an external base deprotonates one of the cyclic ligands. This results in increased electron density on Ni(0) and promotes proton transfer from the second protonated ligand to the metal ion, with formation of [HNi(PCy2NBz2)2]+, 13, (step 1 of reaction (13)). In this reaction the protonation/deprotonation of a base in the second coordination sphere results in a two-electron change in oxidation state at the metal center. Subsequent steps in the electrocatalytic cycle are similar to those shown previously in Scheme 4 for [Ni(PNP)2]2+. The oxidation of [HNi(PCy2NBz2)2]+ to [HNi(PCy2NBz2)2]2+ is coupled to an intramolecular proton transfer step, followed by an intermolecular proton transfer and oxidation of the resulting Ni(I) complex, [Ni(PCy2NBz2)2]+, to regenerate the original Ni(II) species, 10c. For H2 production by [Ni(PPh2NPh2)2]2+, the cycle discussed here for H2 oxidation proceeds in the opposite direction.
 | (13) |
3.4 Additional ligand stabilizations by pendant bases
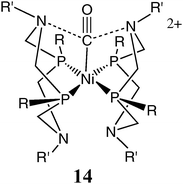
A novel feature of the complexes of structure 10 is the proposed role of the two amines positioned near the nickel ion in the stabilization of the dihydrogen ligand. A similar type of interaction between the positioned bases and an additional ligand in the coordination sphere has been observed for other ligand types. Complex 10c, the hydrogen oxidation catalyst, reacts reversibly with carbon monoxide, and provides a rare example of a dicationic Ni(II) complex that binds CO.49 Other [Ni(diphosphine)2]2+ derivatives do not bind CO under similar conditions. The structure of [Ni(CO)(PCy2NBz2)]2+, 14, was determined by an X-ray diffraction study. It was found that all four chelate rings of the cyclic ligands are arranged in boat conformations, bringing two of the pendant bases within 3.4 Å of the carbonyl carbon, close to the sum of the van der Waals radii for carbon and nitrogen. Structural studies of an analogous isonitrile complex, [Ni(CyNC)(PCy2NBz2)]2+ (where CyNC is cyclohexylisonitrile) also exhibited close contacts of 3.4 Å between the isonitrile carbon atom and two of the N atoms of the pendant bases despite the increased steric bulk of the isonitrile ligand relative to CO.49 The structural results suggest that stabilizing ion–dipole interactions between the positively charged carbon and the pendant amines contribute to the stability of the carbonyl and isonitrile adducts. These complexes illustrate that the two positioned pendant bases in the second coordination sphere can stabilize ligands other than dihydrogen or hydrides and that such stabilization can involve interactions other than hydrogen bonds.Trace amounts of carbon monoxide are known to rapidly deactivate platinum catalysts currently used in fuel cells, and hydrogenase enzymes are also inhibited by CO.50–54 Thermodynamic studies of the reversible CO binding to [Ni(PCy2NBz2)]2+ compared to H2 binding to this complex indicate that the equilibrium constant for H2 binding is 20 times larger than that for CO. As a result, CO concentrations as high as 5% have no measurable inhibiting effect on the catalytic response of this nickel complex for hydrogen oxidation.49
3.5 Summary of the roles of the pendant bases for nickel systems
Comparison of [Ni(depp)2]2+, [Ni(PNP)2]2+, and [Ni(PR2NR′2)]2+ systems indicate that the pendant bases can facilitate intermolecular exchange of protons between the protons in solution, protons on the pendant base, and the hydride ligand. In addition, the pendant base provides the necessary structural component for the coupling of proton- and electron-transfer processes. For the nickel systems containing cyclic diphosphine ligands with two positioned pendant bases, relatively rapid electrocatalytic rates have been observed, and the catalysts can be tuned for either hydrogen oxidation or production by changing the substituents of the diphosphine ligands. Finally, H2 binding appears to be stabilized by interaction with two positioned pendant bases, and this is an important factor in achieving high catalytic rates for the [Ni(PR2NR′2)]2+ derivatives.4. Studies of cobalt complexes containing cyclic PR2NR′2 ligands
The study of the role of pendant bases in developing electrocatalysts for H2 production and oxidation has recently been extended to cobalt complexes.55 The complex with two cyclic ligands [Co(PPh2NPh2)2(CH3CN)](BF4)2 is very similar in composition and structure to the nickel analogue, 10a, but this cobalt derivative was not catalytically active for the electrochemical formation of H2. However the complex with a single cyclic diphosphine ligand, [Co(PPh2NPh2)(CH3CN)3](BF4)2, has been shown to be an electrocatalyst for H2 production using bromoanilinium tetrafluoroborate as the proton source with a catalytic turnover frequency of 90 s−1 and an estimated overpotential of 285 mV. In contrast to the nickel complex 10a, the positioning of two amine bases near the metal ion is not required for high activity. Although a detailed mechanistic understanding of the catalytic cycle involving the cobalt complex is not yet available, a comparison of the catalytic behavior of [Co(PPh2NPh2)(CH3CN)3](BF4)2 with that of [Co(dppp)(CH3CN)3](BF4)2 (where dppp is bis(diphenylphosphino)propane), for which no catalytic activity is observed, suggests that the pendant amine is playing an important role in the catalysis of H2 production. Similarly, [Co(PNP)(CH3CN)3](BF4)2 is also a catalyst for the reduction of protons to H2 in the presence of a weak acid. These cobalt complexes exhibit catalytic rates for hydrogen production comparable to those of 10a and 10b, and the amine base in the second coordination sphere plays a crucial role in these catalytic processes. However, for cobalt complexes this high catalytic activity is obtained with only one pendant base rather than two positioned bases as required in the active nickel complexes.5. Summary
Efforts in our laboratories to develop simple molecular catalysts based on inexpensive first row transition metal complexes have focused on two aspects of this problem. First we have studied the thermodynamic properties of a number of transition metal hydrides with particular emphasis on [HM(diphosphine)2]+ complexes. These studies have provided an understanding of those structural and electronic features of both the ligands and the metal that control the relative energies of potential catalytic intermediates. From this thermodynamic information, reaction profiles indicating the relative energies of intermediates in potential catalytic cycles can be constructed. How these reaction profiles change as a function of the ligand and metal are used to guide catalyst development. In an effort to lower the activation barriers between these intermediates, pendant bases were incorporated into the second coordination sphere to facilitate H2 binding, intramolecular heterolytic cleavage of H2 and proton-coupled electron-transfer reactions. This dual approach has led to the development of highly active H2 production and oxidation catalysts based on both nickel and cobalt. It is hoped that in the future some of the insights developed in these studies will contribute to the design and discovery of molecular catalysts based on inexpensive metals that can ultimately replace platinum with superior performance characteristics.In a broader sense, the tools developed in the course of these studies may find applications in a range of multiproton and multielectron transfer processes. The understanding of free energy landscapes and how they are controlled by the first coordination sphere of the metal provides a rational basis for initial catalyst design by providing the information needed to avoid high energy intermediates. The incorporation of proton relays into the second coordination sphere provides low energy pathways for controlling the movement of protons between the metal and solution. Energy matching of the proton relays in the second coordination sphere with substrates coordinated in the first coordination sphere comprises the third stage of catalyst design. This simple modular approach can be useful in catalyst development and provide insights into more complex biological systems.
Acknowledgements
We are grateful to the many students, postdoctoral coworkers, and colleagues who have participated in this project and whose names are listed in the referenced papers from our laboratories. This work was supported by Grant CHE-0240106 from the National Science Foundation. The support of the Office of Basic Energy Sciences of the Department of Energy, by the Chemical Sciences program is also acknowledged. The Pacific Northwest National Laboratory is operated by Battelle for the US Department of Energy.References
- Y. Nicolet, A. L. de Lacey, X. Vernède, V. M. Fernandez, E. C. Hatchikian and J. C. Fontecilla-Camps, J. Am. Chem. Soc., 2001, 123, 1596 CrossRef CAS.
- J. W. Peters, W. N. Lanzilotta, B. J. Lemon and L. C. Seefeldt, Science, 1998, 282, 1853 CrossRef CAS.
- A. S. Pereira, P. Tavares, I. Moura, J. J. G. Moura and B. H. Huynh, J. Am. Chem. Soc., 2001, 123, 2771 CrossRef CAS.
- J. W. Peters, Curr. Opin. Struct. Biol., 1999, 9, 670 CrossRef CAS.
- A. Volbeda, E. Garcin, C. Piras, A. L. de Lacey, V. M. Fernandez, E. C. Hatchikian, M. Frey and J. C. Fontecilla-Camps, J. Am. Chem. Soc., 1996, 118, 12989 CrossRef CAS.
- Y. Higuchi, H. Ogata, K. Miki, N. Yasuoka and T. Yagi, Structure, 1999, 7, 549 CrossRef CAS.
- E. Garcin, X. Vernede, E. C. Hatchikian, A. Volbeda, M. Frey and J. C. Fontecilla-Camps, Structure, 1999, 7, 557 CrossRef CAS.
- A. Volbeda and J. C. Fontecilla-Camps, Dalton Trans., 2003, 4030 RSC.
- C. Greco. M. Bruschi, L. De Gioia and U. Ryde, Inorg. Chem., 2007, 46, 5911 CrossRef CAS.
- H.-J. Fan and M. B. Hall, J. Am. Chem. Soc., 2001, 123, 3828 CrossRef CAS.
- D. Berning, B. Noll and D. DuBois, J. Am. Chem. Soc., 1999, 121, 11432 CrossRef CAS.
- C. J. Curtis, A. Miedaner, W. W. Ellis and D. L. DuBois, J. Am. Chem. Soc., 2002, 124, 1918 CrossRef CAS.
- W. W. Ellis, R. Ciancanelli, S. M. Miller, J. W. Raebiger, M. Rakowski DuBois and D. L. DuBois, J. Am. Chem. Soc., 2003, 125, 12230 CrossRef CAS.
- D. L. DuBois, D. M. Blake, A. Miedaner, C. J. Curtis, M. Rakowski DuBois, J. A. Franz and J. C. Linehan, Organometallics, 2006, 25, 4414 CrossRef CAS.
- D. D. M. Wayner and V. D. Parker, Acc. Chem. Res., 1993, 26, 287 CrossRef CAS.
- W. W. Ellis, J. W. Raebiger, C. J. Curtis, J. W. Bruno and D. L. DuBois, J. Am. Chem. Soc., 2004, 126, 2738 CrossRef CAS.
- A. Anne and J. Moiroux, J. Org. Chem., 1990, 55, 4608–4614 CrossRef CAS.
- D. Ostovic, I. S. H. Lee, R. M. G. Roberts and M. M. Kreevoy, J. Org. Chem., 1985, 50, 4206 CrossRef CAS.
- J.-P. Cheng, K. L. Handoo, J. Xue and V. D. Parker, J. Org. Chem., 1993, 58, 5050–5054 CrossRef CAS.
- R. Ciancanelli, B. C. Noll, D. L. DuBois and M. Rakowski DuBois, J. Am. Chem. Soc., 2002, 124, 1926 CrossRef CAS.
- A. Price, R. Ciancanelli, B. C. Noll, C. J. Curtis, D. L. DuBois and M. Rakowski DuBois, Organometallics, 2002, 21, 4833 CrossRef CAS.
- C. J. Curtis, A. Miedaner, J. W. Raebiger and D. L. DuBois, Organometallics, 2004, 23, 511 CrossRef CAS.
- A. S. Larsen, K. Wang, M. A. Lockwood, G. L. Rice, T.-J. Won, S. Lovell, M. Sadílek, F. Turcek and J. M. Mayer, J. Am. Chem. Soc., 2002, 124, 10112 CrossRef CAS.
- K. L. Handoo, J.-P. Cheng and V. D. Parker, J. Am. Chem. Soc., 1993, 115, 5067 CrossRef CAS.
- X.-M. Zhang, J. W. Bruno and E. Ennyinnaya, J. Org. Chem., 1998, 63, 4671 CrossRef CAS.
- G. Zotti, S. Zecchini and G. J. Pilloni, J. Organomet. Chem., 1983, 246, 61 CrossRef CAS.
- B. Longato, L. Riello, G. Bandoli and G. Pilloni, Inorg. Chem., 1999, 37, 2818 CrossRef.
- D. E. Berning, A. Miedaner, C. J. Curtis, B. C. Noll, M. Rakowski DuBois and D. L. DuBois, Organometallics, 2001, 20, 1832 CrossRef CAS.
- J. W. Raebiger, A. Miedaner, C. J. Curtis, S. M. Miller and D. L. DuBois, J. Am. Chem. Soc., 2004, 126, 5502 CrossRef CAS.
- J. March, Advanced Organic Chemistry: Reactions, Mechanism, Structure, McGraw-Hill, New York, 1968, p. 243 Search PubMed.
- X.-J. Qi, Y. Fu, L. Liu and Q.-X. Guo, Organometallics, 2007, 26, 4197 CrossRef CAS.
- X.-J. Qi, L. Liu, Y. Fu and Q.-X. Guo, Organometallics, 2006, 25, 5879 CrossRef CAS.
- P. W. N. M. Van Leeuwen, P. C. J. Kamer, J. N. H. Reek and P. Dierkes, Chem. Rev., 2000, 100, 2741 CrossRef CAS.
- C. P. Casey and G. T. Whiteker, Isr. J. Chem., 1990, 30, 299 CAS.
- M. R. Nimlos, C. H. Chang, C. J. Curtis, A. Miedaner, H. M. Pilath and D. L. DuBois, Organometallics, 2008, 27, 2715 CrossRef CAS and references therein.
- K. Fraze, A. D. Wilson, A. M. Appel, M. Rakowski DuBois and D. L. DuBois, Organometallics, 2007, 26, 3918 CrossRef CAS.
- I. Kaljurand, A. Kutt, L. Soovali, T. Rodima, V. Maemets, I. Leito and I. A. Koppel, J. Org. Chem., 2005, 70, 1019 CrossRef CAS.
- K. Izutsu, Acid–Base Dissociation Constants in Dipolar Aprotic Solvents, IUPAC Chemical Data Series, No. 35, Blackwell Scientific Publications, Oxford, 1990 Search PubMed.
- J. W. Raebiger and D. L. DuBois, Organometallics, 2005, 24, 110 CrossRef CAS.
- A. Miedaner, J. W. Raebiger, C. J. Curtis, C. S. M. Miller and D. L. DuBois, Organometallics, 2004, 23, 2670 CrossRef CAS.
- G. M. Jacobsen, R. K. Shoemaker, M. J. McNevin, M. Rakowski DuBois and D. L. DuBois, Organometallics, 2007, 26, 5003 CrossRef CAS.
- G. M. Jacobsen, R. K. Shoemaker, M. Rakowski DuBois and D. L. DuBois, Organometallics, 2007, 26, 4964 CrossRef CAS.
- R. M. Henry, R. K. Shoemaker, R. H. Newell, G. M. Jacobsen, D. L. DuBois and M. Rakowski DuBois, Organometallics, 2005, 24, 2481 CrossRef CAS.
- R. M. Henry, R. K. Shoemaker, D. L. DuBois and M. Rakowski DuBois, J. Am. Chem. Soc., 2006, 128, 3002 CrossRef CAS.
- C. J. Curtis, A. Miedaner, R. Ciancanelli, W. Ellis, B. Noll, M. Rakowski DuBois and D. DuBois, Inorg. Chem., 2003, 42, 216 CrossRef CAS.
- A. D. Wilson, R. H. Newell, M. J. McNevin, J. T. Muckerman, M. Rakowski DuBois and D. L. DuBois, J. Am. Chem. Soc., 2006, 128, 358 CrossRef CAS.
- A. D. Wilson, R. Shoemaker, A. Miedaner, J. T. Muckerman, D. L. DuBois and M. Rakowski DuBois, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6951 CrossRef CAS.
- M. Frey, ChemBioChem, 2002, 3, 153 CrossRef CAS.
- A. D. Wilson, K. Fraze, B. Twamley, S. M. Miller, D. L. DuBois and M. Rakowski DuBois, J. Am. Chem. Soc., 2008, 130, 1061 CrossRef CAS.
- S. E. Lamle, K. A. Vincent, M. L. Halliwell, S. P. J. Albracht and F. A. Armstrong, Dalton Trans., 2003, 4152 RSC.
- S. E. Lamle, S. P. J. Albracht and F. A. Armstrong, J. Am. Chem. Soc., 2004, 126, 14899 CrossRef CAS.
- J. W. Van der Zwaan, J. M. C. C. Coremane, E. C. V. M. Bouwens and S. P. J. Albracht, Biochim. Biophys. Acta, 1990, 1041, 101 CAS.
- C. Greco, M. Bruschi, J. Heimdal, P. Fantucci, L. De Gioia and U. Ryde, Inorg. Chem., 2007, 46, 7256 CrossRef CAS.
- A. L. De Lacey, C. Stadler, C. Cavazza, E. C. Hatchikian and V. M. Fernandez, J. Am. Chem. Soc., 2000, 122, 11232 CrossRef CAS.
- G. M. Jacobsen, J. Y. Yang, B. Twamley, A. D. Wilson, R. M. Bullock, M. Rakowski DuBois and D. L. DuBois, Energy Environ. Sci., 2008, 1, 167–174 RSC.
Footnote |
| † Part of the renewable energy theme issue. |
| This journal is © The Royal Society of Chemistry 2009 |