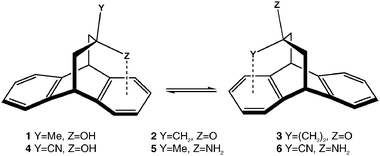
Probing weak non-covalent interactions in solution and solid states with designed molecules

Abstract

Selective examples of OH⋯arene, NH₂⋯arene and C–H⋯N≡C weak interactions are presented using a flexible dibenzobicyclo[3.2.2]nonane scaffold for detection and comparative characterisation of non-covalent interactions in solution and solid states.

---

Introduction

The key role of non-covalent interactions in proteins, DNA and other biologically important systems is well recognised.^1,2Hydrogen bonds, being one of the strongest amongst the non-covalent interactions, have attracted most attention, whilst considerably less is known about non-covalent interactions of aromatic rings and other systems with π-orbitals, especially in the solution state. A generally accepted view is that many non-covalent interactions while present in the solid state are often too weak to compete with thermal motions in solution. In fact, crystallisation itself can be considered as an energy preserving process accomplished via a large number of cumulative non-covalent interactions between molecules: on cooling the destructive effect of thermal motions decreases and at certain orientational proximities (“self-recognitions”) molecules can form an optimum set of non-covalent interactions, leading to close packing in the solid state, in accordance with Kitaygorodsky’s “no waste of space” principle.^2a A fair question then arises: do weak interactions seen in the solid state have any relevance in solutions? Another related question is how to detect weak non-covalent interactions in solutions?

With these considerations in mind we chose to study weak O(N)–H⋯π interactions, the existence of which in the solid state is well established.^1d,e,3 In particular, a comprehensive structural analysis of 592 published high-resolution crystal structures were undertaken, which demonstrated the importance of O(N,S)–H⋯π(Ar) interactions in proteins.^3b Detailed theoretical studies have revealed that the potential energy surface of the X–H⋯π(Ph) interaction is flat, allowing some freedom of movement for a proton over the phenyl surface.⁴ This conclusion is further supported by experimental data in the solid state, which suggest that the O–H direction does not always coincide with the midpoint normal of the phenyl ring and may be oriented towards one of the aromatic carbons.^1d A π-type intramolecular hydrogen bonding in aryl alcohols and amines in the gas phase has also been reported using IR/UV data.⁵ We have recently described our preliminary studies showing that a dibenzobicyclo[3.2.2]nonane scaffold provides a sensitive tool for investigation of non-covalent arene interactions with C≡CH, OH, F and S functionalities.⁶ Here we use dibenzobicyclo[3.2.2]nonanes 1–6 for the identification of OH⋯π interactions with an emphasis on their spectroscopic detection in the solution state, followed by their comparison with π-interactions of other functionalities. In addition, single crystal structure determinations were undertaken for the comparison of weak non-covalent interactions in solution and solid states. Such condensed phase studies are in principle better suited for assessing the importance of non-covalent interactions of aromatic π-electrons in biologically important systems than theoretical in vacuo calculations or experimental gas phase measurements.

Results and discussion

Non-covalent OH⋯arene interactions

The advantage of dibenzobicyclo[3.2.2]nonane, as compared to the torsional balance of Wilcox⁷ or 3-phenylpropanol,⁵ is that the degree of conformational freedom for the carbon chain is considerably restricted, thus creating an opportunity for the formation of π-hydrogen bonds. There is nevertheless sufficient freedom retained. For example, the hydroxyl group in alcohol 1 can adopt a gauche or trans orientation relative to the methyl group or an endo- or exo-orientation relative to the aromatic ring (Fig. 1).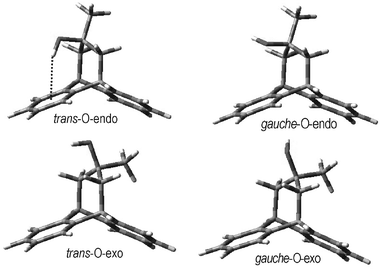

Fig. 1 Conformations of 1 from calculations using density functional theory (DFT). The dotted line highlights the O–H⋯π interaction.

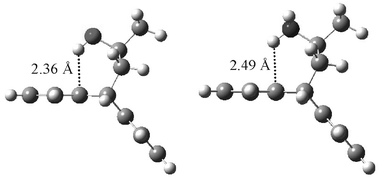
From our gas phase DFT calculations for the O-endo conformer of 1 with the trans-rotameric hydroxyl proton (ω = 180°, where ω denotes the torsional angle between the methyl carbon and the OH proton), the optimised geometry is such that the hydroxyl proton is symmetrically positioned just above the two quaternary aromatic carbons at a short distance of 2.36 Å. For comparison, in amine 5 the corresponding distance is 2.49 Å:

Initially, it was expected that the intramolecular OH⋯π interaction would be present in the solid state. However, the single crystal X-ray measurements⁶ revealed that alcohol 1 crystallises in a most unexpected way with a 1 : 1 ratio of trans-O-endo (ω = 177°) and gauche-O-exo (ω = 78°) conformers stabilised via two different intermolecular close contacts of the OH protons (Fig. 2).

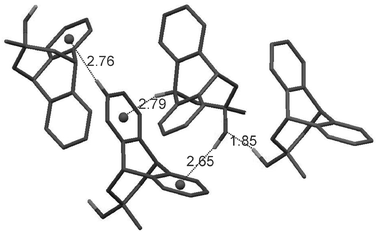Fig. 2 Non-covalent interactions involving OH and CH hydrogen atoms in the single crystal of 1. The distances shown are in Å.

Detailed NMR measurements were undertaken in order to verify the existence of O–H⋯π hydrogen bonding in solution. First, the population x^endo of the O-endo conformer was measured from the ³J-couplings of the aliphatic protons in various solvents (Table 1). The results revealed predominance of the O-endo conformer in non-polar solvents. The temperature dependence of ³J_HH-couplings was also studied in toluene-d₈. The observed linear dependence of ln K vs. T⁻¹ (K = x^endo/x^exo, Fig. S1 in ESI†) revealed a negative sign of entropy, confirming further stabilisation of the major conformer on cooling. In addition, a relatively weak temperature dependence of −0.3 ppb K⁻¹ for the OH peak of 1 was found in CCl₄.

Table 1 Population (in %) of the O(N)-endo conformer (x^endo) in different solvents at 298 K determined using ³J_HH couplings (x^exo = 100 −x^endo)^a

	C6D12	CCl4	C6D6	C6H5CH3-d8	CDCl3	C5D5N	CD3OD	CD3CN	DMSO-d6
a Estimated error is ±5%.
1	93	93	89	89	94	55	51	74	50
2			25	24			38	39	35
3			5		12			14
4	31	24	24	21	27		4	7	5
5	78	78	73	74	78	68	75	70	59
6		4	5	5	4		0	0	0

---

How can we identify the O–H⋯π interactions in the O-endo conformer in solutions? Structurally, this question reduces to whether the trans- or gauche-rotamer about the C–O bond is preferred, as only the trans-rotamer provides the required geometry for π-hydrogen bonds. In the following we identify various NMR parameters which are sensitive to the rotameric changes of the hydroxyl group in various solvents.

The above mentioned weak temperature dependence of the hydroxyl proton chemical shift, together with its actual value in inert solvents (0.67 ppm in CCl₄ and 0.79 ppm in C₆D₁₂) are in favour of an intramolecular type of OH⋯π bonding. For comparison, the calculated chemical shifts of the hydroxyl proton using B3LYP/6-311+G(2d,p) were −0.56 and 0.71 ppm in the gauche- and trans-rotamers in C₆D₁₂, respectively (Table S2 in ESI†).

From various selectively decoupled ¹³C and selective 2D J-resolved measurements in toluene-d₈, the ³J_CH-coupling for the (¹³CH₃, O¹H) pair was 6.3 Hz. Based on the Karplus type relationship for ³J_CH,⁸ the presence of ³J_CH of this magnitude suggests that the trans-rotamer about the C–O bond is the major rotamer. In addition, long-range ⁴J_HH coupling for the (CH₃, OH) pair was 0.8 Hz at 298 K and 1.0 Hz at 193 K. The ⁴J_HH coupling of 1.1 Hz for the (CH₃,OH) protons and the ³J_CH coupling of 7.5 Hz for the (CH₃, OH) pair was measured in cyclohexane-d₁₂ at 298 K. Both of these values approximate their maximum possible values in the trans-rotamer, which suggests that the population of the gauche-rotamer is negligibly small in cyclohexane-d₁₂.

Various selective ¹³C{¹H} and HMBC experiments in CDCl₃ in the range 256–298 K showed no ³J_CH coupling for the (¹³CH₃, O¹H) pair, which was associated with the intermolecular proton exchange of hydroxyl protons, leading to self-decoupling from other spins due to short T₂-effects. The presence of such exchange with residual water (possibly catalysed by acidic chloroform) was apparent from the field dependent linewidths of the OH peak, as well as from negative enhancements in the NOE experiments. In a specially dried solution, using distillation of chloroform-d₁ directly into an NMR tube under nitrogen, a ⁴J_HH coupling of 1.0 Hz for the (CH₃, OH) protons was measured, in agreement with the trans-orientation of the hydroxyl proton in chloroform-d₁.

Amongst polar solvents, only the acetonitrile-d₃ solution showed ⁴J_OH,H coupling of 0.6 Hz. In this solvent, however, there is a substantial population of the O-exo conformer (Table 1).

A detailed analysis of IR data was also undertaken. For conventional hydrogen bonds, the O–H bond is elongated and the shift of the hydroxyl stretching vibration to lower frequencies is observed (red shift). For the C–H⋯π hydrogen bonds, however, high-frequency (blue) shifts are common and this has been attributed to the contraction of the C–H bond on forming a π-hydrogen bond.^1b A small high-frequency shift of ca. 20 cm⁻¹ was also predicted for O–H⋯π hydrogen bonds for 3-phenylpropanol based on the HF/6-31G calculations.⁹ Solid 1 showed two peaks at 3441 and 3562 cm⁻¹ due to O–H⋯O and O–H⋯π, respectively (Fig. 2), whereas one sharp peak at 3595 cm⁻¹ was observed in the CCl₄ solution of 1. The predicted peak positions for trans- and gauche-O-endo-conformers by B3LYP/6-31G(d)/IEFPCM¹⁰ were 3605 and 3557 cm⁻¹ in CCl₄, respectively, where the value for the trans-rotamer agrees better with the experimentally measured value of 3595 cm⁻¹. Regarding the elongation or contraction of O–H bonds on forming π-hydrogen bonds,^1b the predicted distances were 96.97 and 97.05 pm in the trans- and gauche-O-endo conformers, respectively.

Further estimates of conformational stability in the O-endo conformer were also undertaken using computational techniques. In particular, various force fields estimate the gauche-rotamer as the more stable form in the gas phase, while DFT, which provides a significantly better account of electronic interactions, favours the trans-rotamer. The change of the population of the trans-rotamer on solvent variation was in qualitative agreement with the calculations using B3LYP/6-31G(d)/IEFPCM, as the predicted energies of the gauche-rotamer relative to the trans-rotamer were 8.9, 5.4, 4.6, −1.7, −2.0 kJ mol⁻¹ in the gas phase, C₆H₁₂, CCl₄, CH₃CN and DMSO, respectively. In addition, a quantum mechanical molecular dynamics simulation was found to reproduce well the observed populations of conformers (see ESI† for details). The success of these initial computational studies may be attributed to the fact that the OH⋯arene separation in the O-endo conformer of 1 is relatively short and that dispersion interactions in dielectric media are weaker than in vacuum.^2b Further higher level calculations are currently underway in order to verify the significance of various terms contributing to the stability of the OH⋯π interaction in 1 in different solvents.

Non-covalent interactions of NH and CH hydrogen atoms

Selective functional group variation provides a powerful means for better understanding of weak interactions via comparative analysis, and, in the following we consider a few examples related to 1. In particular, apart from the OH⋯π stabilisation in 1, interactions of oxygen lone pairs (LP) with aromatic rings are of interest.¹¹ Here we first consider epoxide 2 and oxetane 3 which compared to 1 have no hydrogen atom attached to oxygen. From our analysis, 2 shows only the O-exo conformation in the solid state and does not exhibit any obvious π intractions, except for some C–H⋯π contacts (Fig. 3).‡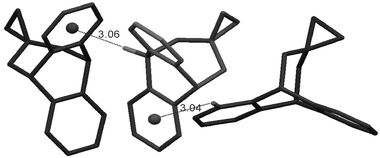

Fig. 3 The arrangement of the O-exo conformers of epoxide 2 in the single crystalline phase. The distances shown are in Å.

Similarly, in the solution state the preferred conformer of 2 is the O-exo form with relatively weak dependence of the conformational populations on solvent properties (Table 1) compared to 1. Thus, the stabilisation of this conformer may be caused by the intramolecular repulsion of oxygen lone pairs and aromatic π-orbitals in the O-endo form. This explanation is in agreement with the fact that increasing the size of the spiro cyclic unit from epoxide in 2 to oxetane in 3 brings the oxygen atom closer to the aromatic ring in the O-endo conformer, thus leading to a significant decrease of x^endo in C₆D₆: from 25% in 2 to 5% in 3. Alternatively, the stabilising role of the attraction between the aromatic ring and the cyclic methylene hydrogens may be important in the corresponding O-exo conformers.

Another important comparison is the relative strength of the O–H⋯π and N–H⋯π interactions, both occurring widely in proteins and other biologically important species. Here we use two pairs of methyl ( 1 and 5) and cyano ( 4 and 6) derivatives for comparison. These showed considerably different populations of the O(N)-endo conformers in benzene-d₆ and chloroform-d₁ solutions (Table 1). From the data obtained, the O–H⋯π interaction can be estimated to be stronger than the N–H⋯π interaction by 4 ± 1 kJ mol⁻¹.

Finally, a C–H⋯N≡C close contact of 2.64 Å was found in the single crystal of 6 (Fig. 4).‡ For comparison, in the case of a C–H⋯O bond, the H⋯O distance is 2.59 Å.¹² The distance between heavy atoms C and N is 3.590(3) Å in 6 which is comparable to that reported for the C(aromatic)⋯N(nitrile) distance of 3.47 Å.¹³ If we regard the given geometry as a frozen state of a proton transfer reaction, then the CN⋯H contact can be considered as significant provided its orientation coincides with that in the product of the proton transfer reaction.^1d,14 The measured angle for the C≡N⋯H fragment is 118°, which is similar to the C=N–H bond angle expected in the product of the proton transfer reaction. This consideration together with geometric characteristics, as well as a 4 ppm high-frequency shift of the cyano carbon in the ¹³C CPMAS spectrum compared to the solution spectrum (Table S1 in ESI†), supports the presence of the C(sp³)–H⋯N=C interaction in solid 6.

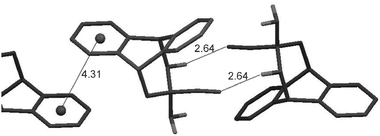Fig. 4 The single crystalline arrangement of 6, showing only the N-exo conformer. The molecules shown are related by inversion centre operations. The distances shown are in Å. The C–H⋯N angle is 168°.

Conclusions

In summary, the trans-O-endo conformer of 1 was detected in solvents of low polarity. The better stability of the trans-rotamer relative to the gauche-rotamer is attributed to the non-covalent O–H⋯π interaction. In polar solvents the ability of solvent molecules to form hydrogen bonds with the hydroxyl group of 1 interferes with the O–H⋯π interaction, thus leading to higher population of the gauche-rotamer and O-exo conformer. From the results obtained for epoxide 2 and oxetane 3, the interaction between an aromatic ring and methylene hydrogen atoms may also have a stabilising effect. Comparison of the O–H⋯π and N–H⋯π interactions showed that the O–H⋯π interaction is stronger than the N–H⋯π interaction by ca. 4 kJ mol⁻¹. Weak C(sp³)–H⋯N≡C interactions were detected in the sold state. Overall, the results revealed significant conformational variations on going from solution to the solid state. In addition to close contacts involving central functionalities, various intermolecular C–H⋯π and π⋯π pairings were also detected in solid dibenzobicyclo[3.2.2]nonanes (Fig. 2–4).

Acknowledgements

We are grateful for the provision of studentships from Organon (J.M.) and Dr Alfred Bader (MN). We thank Prof. W. Clegg (EPSRC National Crystallographic Service, University of Newcastle) for crystallographic measurements of 2.

References

1. (a) C. A. Hunter, Angew. Chem., Int. Ed. Engl., 1993, 32, 1584; (b) K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143; (c) W. B. Jennings, B. M. Farrell and J. F. Malone, Acc. Chem. Res., 2001, 34, 885; (d) T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48; (e) E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210; (f) S. Tsuzuki, Struct. Bonding, 2005, 115, 149; (g) J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2007, 9, 5291.
2. (a) A. I. Kitaygorodsky, Molecular Crystals and Molecules, Academic Press, New York, 1973; (b) J. N. Israelachvili, Intermolecular and surface forces, Academic Press, San Diego, 1992; (c) C. Branden and J. Tooze, Introduction to Protein Structure, Garland Publishing, New York, 1999.
3. (a) T. Steiner, A. M. M. Schreurs, M. Lutz and J. Kroon, New J. Chem., 2001, 25, 174; (b) T. Steiner and G. Koellner, J. Mol. Biol., 2001, 305, 535.
4. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2000, 122, 11450.
5. M. Mons, E. G. Robertson and J. P. Simons, J. Phys. Chem. A, 2000, 104, 1430.
6. W. B. Motherwell, J. Moïse, A. E. Aliev, M. Nič, S. J. Coles, P. N. Horton, M. B. Hursthouse, G. Chessari, C. A. Hunter and J. G. Vinter, Angew. Chem., Int. Ed., 2007, 46, 7823.
7. S. Paliwal, S. Geib and C. S. Wilcox, J. Am. Chem. Soc., 1994, 116, 4497.
8. R. H. Contreras and J. E. Peralta, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 37, 321.
9. N. Guchhait, T. Ebata and N. Mikami, J. Am. Chem. Soc., 1999, 121, 5705.
10. E. Cances and B. Mennucci, J. Math. Chem., 1998, 23, 309.
11. (a) T. Korenaga, H. Tanaka, T. Ema and T. Sakai, J. Fluorine Chem., 2003, 122, 201; (b) M. Egli and S. Sarkhel, Acc. Chem. Res., 2007, 40, 197.
12. G. R. Desiraju, J. Chem. Soc., Dalton Trans., 2000, 3745.
13. P. Betchmann, S. Sahli, F. Diederich, U. Obst and V. Gramlich, Helv. Chim. Acta, 2002, 85, 1210.
14. H.-B. Bürgi and J. D. Dunitz, Acc. Chem. Res., 1983, 16, 153.

---

Footnotes

† Electronic supplementary information (ESI) available: Descriptions of calculations, further details of NMR and X-ray diffraction analyses and MD calculations. CCDC reference numbers 701931 and 701932. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/b815906h

‡ Crystal data for compound2: C₁₈H₁₆O, M = 248.31, monoclinic, a = 16.312(8), b = 7.247(3), c = 16.383(8) Å, β= 90.243(7)°, V = 1936.7(16) ų, T = 120(2) K, space groupP2₁, Z = 6, 10 797 reflections measured, 2577 independent reflections (R_int = 0.0736). Final R indices [F² > 2σ] wR2 = 0.1699 and R1 = 0.0678; R indices (all data) wR₂ = 0.1837 and R₁ = 0.0791. Crystal data for compound6: C₁₈H₁₆N₂, M = 260.33, monoclinic, a = 13.8169(18), b = 11.8799(15), c = 8.5789(11) Å, β = 100.271(2)°, V = 1385.6(3) ų. T = 293(2) K, space groupP2₁/c, Z = 4, 12  052 reflections measured, 3318 independent reflections (R_int = 0.0325). Final R indices [F² > 2σ] wR2 = 0.1391 and R1 = 0.0594; R indices (all data) wR₂ = 0.1536 and R₁ = 0.0847.

---