Cyclohexadiene ring opening observed with 13 fs resolution: coherent oscillations confirm the reaction path

Abstract

The third harmonic (270 nm, 11 fs), produced in a short argon cell from Ti-sapphire laser pulses (810 nm, 12 fs), was used to excite 1,3-cyclohexadiene to its lowest ππ* state (1B). Probing was done by transient ionization by the 810 nm pulses, measuring the yields of the parent and a fragment ion. As previously found with 10 times longer pulses, the molecule leaves in two steps (time constants τ₁, τ₂) from the spectroscopic (1B) to a dark (2A) state and from there (within τ₃) to the ground-state surface. In addition to slightly improved values for τ₁–τ₃, we found in all three locations (L₁–L₃) on the potentials coherent oscillations, which can be assigned to vibrations. They are stimulated by slopes (driving forces) of the potentials, and the vibrational coordinates indicate the slope directions. From them we can infer the path following the initial excitation: the molecule is first not only accelerated towards CC stretching in the π system but also along a symmetric C=C twist. The latter motion—after some excursion—also erects and stretches the CH₂–CH₂ bond, so that Woodward–Hoffmann interactions are activated after this delay (in L₂). On leaving L₂ (the 1B minimum) around the lower cone of the 1B/2A conical intersection, the wave packet is rapidly accelerated along an antisymmetric coordinate, which breaks the C₂ symmetry of the molecule and eventually leads in a ballistic path to (and through) the last (2A/1A) conical intersection. The ring opening begins already on the 1B surface; near the 2A minimum it is already far advanced, but is only completed on the ground-state surface.

---

1. Introduction

Photochemical ring opening of 1,3-cyclohexadiene (CHD) to Z-hexatriene (HT) and its reverse is a prototype of pericyclic reactions.¹ The stereochemistry of such reactions with steroid derivatives has played an important role in the derivation of the Woodward–Hoffmann (WH) rules.^2,3Cyclohexadiene/hexatriene interconversion is also the basis of many photochromic dyes.^4,5 The reaction was therefore much investigated over the last two decades by quantum-chemical calculations,^6–21 by resonance-Raman spectroscopy,^22,23 in part with time resolution,^24–28 by transient absorption in solution,^29–31 in the gas phase by transient ionization (time-resolved mass spectroscopy),^11,32–34 transient photoelectron spectroscopy³⁵ and time-resolved electron diffraction.^36–39 It may be the system, for which most details are now known on the reaction path over the different surfaces (see, in particular, ref. 11). This is probably also the reason, why the system has been studied for application of shaped pulses for controlling the reaction, both theoretically^12,15,40,41 and experimentally.^42,43

As is typical for photoinduced pericyclic reactions^1,44 (see Fig. 3 and 6 below), the molecule is first excited to a “spectroscopic” state (1B₂ in C_2v, 1B in C₂), from where it is initially accelerated along Franck–Condon active coordinates (stretches and twists of the π system¹¹). Then also the CH₂–CH₂ σ bond is stretched and the WH rules are “turned on”.¹¹ From there the wave packet falls into a dark (2A₁ or 2A) state; in doing so, it circumvents the 1B/2A conical intersection (CI) along an antisymmetric (b₂ or b, C₂-symmetry breaking) coordinate, as previously suggested.¹¹ Under C₂-constraint, the 2A potential has a “pericyclic minimum” half-way between the reactant and product. From there, the same b₂ distortion slightly lowers the 2A energy and further leads to a CI, the minimum of the 2A/1A intersection space.¹¹ From this CI the path branches to the product HT and the reactant CHD. On the 1B surface the wave packet travels ≈55 fs (a time consisting of two phases^11,33,34), and its departure from 2A takes ≈80 fs.^11,33–35 The early work^24–28 and electron diffraction^36–39 did not have sufficient time resolution and only detected the ground-state products or those resulting from reactions in the hot ground state.^38,39 The investigations in solution^29–31 found the correct total time (≈200 fs) for the process, but could not monitor the individual steps.

Also in our previous transient-ionization work^11,33,34 and the time-resolved photoelectron spectroscopy³⁵ deconvolution was necessary, because in particular the UV pump pulses had durations of 130–150 fs. Recently we developed a simple source of UV pulses with duration ≤10 fs⁴⁵ and demonstrated its use for time-resolved spectroscopy of metal carbonyl dissociation.⁴⁶ It seemed suggestive to measure also the times of the different phases of CHD ring opening directly. Even more interesting is the possibility to resolve coherent oscillations. They cannot be revealed by deconvolution. We previously demonstrated, how much information of the reaction path can be deduced from them, if the corresponding vibrational coordinate can be identified.^46–52 For their observation a certain degree of coherence is necessary in the molecule. A coherence seems to survive over a long time in CHD, as we concluded from the compactness of the wave packet, when it arrives at the ground state surface.³⁴ The main goal of the present work was therefore to detect coherent oscillations, in the hope that the corresponding vibrations indicate the (varying) directions of the path on the excited-state surfaces. In fact, we detect such oscillations. They also provide evidence of the details (e.g. symmetry breaking), for which there have only been suggestions before, and support the idea of describing the process by driving forces.

2. Experimental

As in our previous work,³⁴CHD was excited by the third harmonic (270 nm) of a 1-kHz Ti-sapphire laser, and the fundamental (810 nm) was used to probe the molecules by ionizing them at high intensity (≈10¹³W cm⁻²). The ion yield was detected mass-selectively in a time-of-flight mass spectrometer. As compared to ref. 34, the pulse duration of the laser system was shorter (45 fs) and was further shortened to 12 fs by self-phase modulation of the radiation focused (f = 2 m) into argon (500 mbar) and reflection from chirped mirrors.^45,53,54 For third-harmonic generation, most (up to ≈0.7 mJ) of this radiation was then refocused (f = 1 m) into a small steel cell (length 18 mm) with pinholes, filled with Ar (≈250 mbar) and embedded in vacuum (<4 mbar). The beam further propagated in vacuum through apertures (for differential pumping), via two dielectric mirrors (to isolate the 270 nm, collimate and focus the beam to the mass spectrometer) and through the hole of a mirror, serving to merge it with the probe beam (≈0.03 mJ). The duration (11 fs) of the 270-nm pulses was determined by cross correlation with the fundamental in the mass spectrometer by ionizing Xe.⁴⁵ The detailed setup is described in ref. 45, 54 and 55.

3. Results

The yields of the parent ion (mass 80 u, Fig. 1) and one fragment (79 u, Fig. 2) were recorded versus the pump–probe delay. According to ref. 34, these two masses are sufficient to monitor the wave-packet motion on the excited-state surfaces: the mass spectrum from 1B contains both, although in different ratio from an earlier (L₁, Franck–Condon region) and a later location (L₂, near the 1B minimum). From 2A (location L₃) only mass 79 is observed,³⁴ so that the parent ion does not provide any information on this state. (The assignment to 1B and 2A has recently been confirmed by time-resolved photoelectron spectroscopy by Kuthirummal et al., who found the same time constants.³⁵)

Fig. 1 Time dependence of the parent ion signal. (a) Full signal (symbols) and its decomposition into contributions from L₁ and L₂ (without and with modulation, curves without symbols). The sum of these contributions is the simulation curve for the full signal. (b) L₁ contribution to the parent ion signal (symbols) with exponential and modulated simulations. Division of these two curves (diminished by 1) results in the modulation function at the bottom, whose Fourier transform is shown in the inset. (c) The corresponding L₂ contribution.

Fig. 2 Time dependence of the fragment ion signal. (a) Full signal (symbols) and its decomposition into contributions from L₁–L₃. The sum of these contributions is the simulation curve for the full signal. (b) L₃ contribution to the fragment ion signal (symbols) with exponential and modulated simulations. The division of these two curves (and subtracting 1) results in the modulation function at the bottom, whose Fourier transform is shown in the inset.

In a first step the signals are analysed by a sum of exponentials (convoluted with the laser pulse shapes, if necessary; i.e., for the shortest times), whose time constants τ_i correspond to the lifetimes of the population in the locations L_i. This is a description of the population flow by rate equations. In the present case, all signals showed also a periodic modulation. It is interpreted as a modulation of the ionization probability, caused by a vibration of the wave packet in location Li. The modulating function has the form

f_osc = 1 + A cos(2πνct − ϕ) (1)

where the amplitude A, wavenumber ν (frequency νc) and phase ϕ are fit parameters. To extract the frequencies, we divide the signals (or the contributions to them from the different L_i, see below) by their exponential simulations; the result (diminished by 1) is then Fourier-transformed. As it turned out, all three L_i required the product of two factors of the type (1), because each L_i exhibits two modulation frequencies. Details of the procedure are described in ref. 46 and 49.

It should be noted that, in contrast to previous cases (e.g., in ref. 46 and 49), eqn (1) does not contain a dephasing term (exponential decay) before the cosine; introduction of such a factor resulted in an only marginal improvement, so that we neglected it. That is, all detected oscillations practically decay with the lifetime of the population at the corresponding location. It seems that there is not much opportunity for dephasing of the oscillations within the short lifetimes.

Table 1 summarizes the wavenumbers and time constants resulting from the evaluation of the two time-dependent signals. The error limits are estimated to be near ±5%, as determined in our previous experiments. Near the end of section 5 we also discuss why it is justified to use rate equations and time constants for part of the analysis, although there are clear signatures of wave packet motion such as oscillations or the ballistic motion introduced below.

Table 1 Lifetimes (τ_i) and oscillation wavenumbers (ν_ia and ν_ib) found for the locations L₁–L₃ in the excited states. The estimated error limits are ±5%

i	1	2	3
τ i /fs	21	35	80
ν ia, νib/cm^−1	950, 1430	310, 630	140, 270

---

The parent-ion signal is shown in Fig. 1a. Its decay is obviously doubly exponential (τ₁ = 21 fs, τ₂ = 35 fs), both parts showing some modulation. Looking first to the later time (70–150 fs) and dividing by the exponential simulation, we extract from it two modulation functions of type (1) with wavenumbers ν_2a = 310 cm⁻¹ and ν_2b = 630 cm⁻¹ (these numbers result from the second iteration step, using Fig. 1c), which represent vibrations in L₂. The modulated signal part (i.e., an exponential with time constant τ₂, multiplied by the modulation functions, the flatter pair of curves in Fig. 1a) is extrapolated back to time 0 (with convolution) and subtracted from the signal. The result is the signal contribution from L₁ (Franck–Condon region) shown in Fig. 1b. It also shows a modulation (lower curve in Fig. 1b), whose Fourier transform (inset) has two maxima (ν_1a = 950 cm⁻¹, ν_1b = 1430 cm⁻¹). Using these frequencies, the modulation of the L₁ part of the parent-ion signal can be well simulated (Fig. 1b). Subtracting the thus obtained L₁ contribution from the full signal (Fig. 1a) yields the L₂ contribution, which is shown in Fig. 1c, including its oscillatory part (with its simulation) and its Fourier transform (inset).

Fig. 2 shows the corresponding fragment-ion signal. It not only contains contributions from L₃ (in contrast to the parent ion) but also from L₁ and L₂. The latter time dependence (time constants and parameters of the modulation functions) are known from the parent ion and are subtracted. The result (Fig. 2b) shows a decay (τ₃ = 80 fs) with a modulation showing two frequencies in the Fourier transform (ν_3a = 140 cm⁻¹, ν_3b = 270 cm⁻¹). At early times (<60 fs) this curve also exhibits a weak high-frequency modulation with the two frequencies observed in L₁; the structure also disappears within about τ₁. Therefore we ascribe it to a residue from L₁, which is obviously not perfectly eliminated from the signal by our subtraction procedure.

4. Discussion

4.1 Assignment of time constants and oscillations

In Fig. 3 we assign the measured time constants to three locations on the excited-state surfaces. These surfaces are schematic cuts of the potential along a C₂-preserving coordinate. (Calculated potentials along the minimum-energy path, that also includes antisymmetric deformation, are shown in ref. 11) The assignment is taken over from our previous work.^11,33,34 It is based on the idea that the change of the electronic energy can be roughly estimated from the ionization probability and degree of fragmentation: a lower-lying state is harder to ionize at the long wavelength used; on the other hand, it has vibrational excess energy (because the total energy is conserved), and such a hot molecule will give rise to a hot ion, which can then dissociate in the long time (nanoseconds) before acceleration in the ion source. As already mentioned, the assignment was recently confirmed by time-resolved photoelectron spectroscopy: the spectra showed the 2B state, which is left within 55 fs (which is very near to our τ₁ + τ₂ = 56 fs) towards a lower-lying state (2A) with a lifetime of 84 fs (which agrees well with our τ₃ = 80 fs);³⁵ only one step on the 1B surface was resolved with the long pulses in ref. 35.

Fig. 3 Potentials for CHD ring opening with assignment of the excited-state time constants and motion directions. The second conical intersection (CI) is out of the drawing plane, as is also the path around the first CI.

Also our previously determined time constants^33,34 (τ_1old = 10 fs, τ_2old = 43 fs, τ_3old = 77 fs) agree well, if we compare the sum τ₁ + τ₂ instead of the individual lifetimes. In fact, as said in ref. 33 and 34, the deconvolution method is more accurate for the sum than for the individual constants; but also if we compare the latter, the agreement is still satisfactory within the standard deviation (±5 fs) quoted in ref. 33 and 34. On the other hand, there might also be a physical reason behind the small deviation: the limit between the detection windows L₁ and L₂ will occur in a region, where the ionization energy (and hence the ionization probability) changes sufficiently; if this change is not very sudden (i.e., if the ion potential rises only gradually), it may be that our shorter pulses with their 10 times broader coherent bandwidth require a larger change, so that τ₁ is lengthened at the expense of τ₂.

From the fluorescence quantum yield a lifetime of the emitting state of 10 fs was inferred in ref. 23 and 28, and it was suggested that emission is stopped by depletion from the spectroscopic 1B to the dark 2A state.^23,28 This would not be compatible with our τ₁ + τ₂. We suggest that fluorescence fades much earlier, already on the 1B surface, by a strong long-wavelength shift along the path. (The radiative rate depends on the emission wavelength λ as λ⁻³.⁵⁶) In fact, the S₀ potential is expected to rise steeply along the path in L₂, that involves CH₂–CH₂ stretching (see below). One can conclude that the detection windows are not defined by the molecule alone but also by the probing process, so that the observation window for fluorescence can be narrower than our L₁, and the width of L₁ can depend on the duration of the probe pulse.

The coherent oscillations in L₁ are expected to be Franck–Condon active vibrations, caused by the changed bond properties in the π system after excitation. An obvious assignment is the symmetric C=C stretch and the C–C stretch vibration for ν_1a = 1430 cm⁻¹ and ν_1b = 950 cm⁻¹, respectively (ground-state values 1579 and 945 cm⁻¹, the latter strongly mixed with other vibrations^57,58). They should also be apparent in the UV absorption spectrum of CHD. In fact, a weak modulation with four distinguishable peaks is detected in the spectrum (Fig. 4), converging from 1540 to 1360 cm⁻¹ (average 1440 cm⁻¹). The convergence is too rapid to be due to anharmonicity, but is characteristic of superposition of two or more progressions in the way as demonstrated in ref. 59. The UV spectrum is much less well resolved than our Fourier transform. Hence the broadening in the former (see the simulations in ref. 59) is not only caused by the short lifetime (10 or 21 fs would give rise to a width of only 500 or 250 cm⁻¹) but also by activity of additional vibrations that are not active in ionization probing. A Franck–Condon activity of the C=C vibration on ionization from the 1B state was also found in the time-resolved photoelectron spectrum (1350 cm⁻¹ in the ion).³⁵

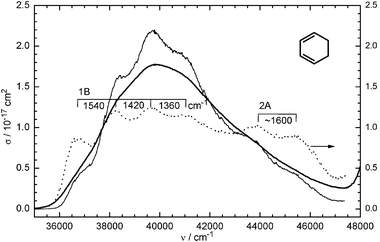Fig. 4 Gas-phase UV spectrum (absorption cross-section σ(ν) versus wavenumber ν) of CHD (bold line), measured with 50 mbar in a 10 cm cell. For enhancing the vibrational structure and showing the 2A band, the spectrumσ was multiplied (result shown by the thin line) by a factor F⁴ (dotted line), where F = σ/〈σ〉 and 〈σ〉 is the spectrum after applying a Fourier low-pass filter. The pump laser is near 37 000 cm⁻¹ and has a half-width of ≈2100 cm⁻¹.

In L₂, we observed oscillations with ν_2a = 310 cm⁻¹ and ν_2b = 630 cm⁻¹; the latter probably an overtone of the first. Such low wavenumbers can only be due to ring puckering (ring twisting); in the ground state they have wavenumbers of 199 (ν₁₉) and 506 cm⁻¹ (ν₁₈),^57,58 ignoring antisymmetric (b in C₂) vibrations (which would appear only as overtones, if active at all). They are outlined on the left of Scheme 1.

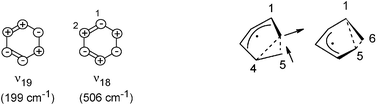Scheme 1 Vibrations in L₂ and L₃, as discussed in the text. The vibration observed in L₂ (ν₂) is identified as ν₁₈. The right-hand side shows the two symmetry-equivalent structures in the 2A minima; the arrows indicate the coordinate (“p*–CI” in the text) connecting them, which is also the coordinate of the 140-cm⁻¹ vibration (ν_3a).

The lower-frequency vibration represents a twist of the CH₂–CH₂group against the rest of the molecule, whereas ν₁₈ can be described as a conrotatory twist of the two C=C bonds. If our observed ν₂ corresponded to ν₁₉, it would imply that the ν₁₉ frequency was raised by 56% in 1B. This seems unlikely; frequency lowering would be expected. In particular, also because resonance Raman spectra^22,23 indicate an early acceleration to the ν₁₈ direction but not to ν₁₉, we compare our ν₂ in 1B (L₂) with the 506 cm⁻¹ in the ground state. The smaller wavenumber in 1B indicates that the restoring force in this state is already strongly reduced along this coordinate. In fact the calculation of ref. 11 for this vibration in the 1B minimum (point “MEP(6)”, which we identify with a point in our L₂) reports a value of 245 cm⁻¹, not too far from our experimental ν₂.

As said above, the location L₃ is assigned to the 2A state. According to the calculations (e.g.ref. 11, 17 and 18), the 2A potential has two symmetry-equivalent very flat minima, in which the C₂ symmetry is broken. The structures are shown on the right in Scheme 1: in one, C-atom 6 forms a weak three-electron three-center bond with atoms 4 and 5, whereas in the other the three-center bond connects atoms 1, 5 and 6. The arrows indicate the coordinate connecting the two minima via the flat C₂-symmetric saddle point (the traditional “pericyclic minimum” p*, i.e., the 2A minimum in the cut shown in Fig. 3); it is hence the symmetry-breaking coordinate (b in C₂). Proceeding further along this direction beyond the minima leads to the 2A/1A CI. Therefore this coordinate is called p*–CI.

The main oscillation observed in L₃ has a very small wavenumber (ν_3a = 140 cm⁻¹). The corresponding vibration must again have a small restoring force and (or) must move large masses. Hence also in this case one should consider some ring deformations. An obvious candidate is a vibration along the symmetry-breaking coordinate (p*–CI) above, because the potential is very flat in this direction. In fact, its wavenumber has been calculated in the 2A minimum: Celani et al. report 135 cm⁻¹ (Fig. 5 of ref. 6), whereas 204 cm⁻¹ was found more recently⁶⁰ (for the method of ref. 60, see ref. 15 and 16); in both cases it is the lowest frequency in this state. The small restoring force (flatness of the potential) is unique for the p*–CI coordinate and would be higher for other directions. Therefore we assign our ν_3a = 140 cm⁻¹ oscillation to a vibration in the p*–CI direction.

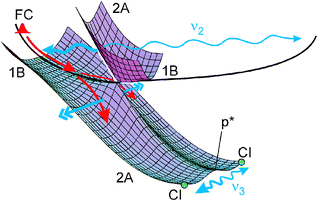Fig. 5 Surfaces and illustrations of acceleration forces (double arrows) and directions of vibrations (wavy lines; actually the indicated ranges only comprise a single period). For a calculated surface, see ref. 11. Most of the wave packet falls down from the 1B to the lower 2A surface near the first CI; a small fraction remains, however, on the 1B surface and completes an oscillation (thin wavy line). For the final CI, only the two (symmetry-equivalent) positions are indicated. Vibrations in the Franck–Condon (FC) region follow different coordinates (C=C and C–C stretch) and therefore cannot be indicated in this figure.

However, this coordinate is antisymmetric (b) in C₂. The molecule has enough excess energy to vibrate above the small barrier between the minima, so that the effective symmetry is C₂. One should then only observe overtones (Δv = 2, 4,⋯…,^48–51 because the ion is probably also C₂ symmetric. The lowest calculated frequency seems thus too large by a factor of 2–3 compared to observation. However, the calculated frequency is derived from the curvature in the minimum (harmonic approximation), whereas above the barrier of a double-minimum potential a vibrational frequency usually drops by a factor of two. The discrepancy is thus eliminated: the observed 140 cm⁻¹ then corresponds to a Δv = 2 overtone of the calculated vibration, whose frequency is lowered by the anharmonicity above the barrier. The higher wavenumber (ν_3b = 270 cm⁻¹) observed in the C₆H₇⁺ fragment may then be the next higher overtone (Δv = 4). It would be unlikely that ν_3b is just the same ring puckering as in L₂ (wavenumber ν_2a = 310 cm⁻¹), since the geometric structure and bonding at the two locations are very different.

It may be worth noting that a frequency very similar to our ν_3a was observed in optimal-control experiments: Carroll et al. excited CHD by shaped 800 nm pulses, which implies three-photon excitation of the 1B or 2A state.^42,43 The hexatriene yield was highest with a pulse having a modulation with a period of ≈250 fs (or a pulse train with this period), corresponding to a wavenumber of ≈135 cm⁻¹, very similar to our ν_3a. Such pulses, which have side bands with a distance of 135 cm⁻¹, efficiently excite via a Raman process vibrations of such a frequency in the ground and/or excited state and in such a way displace the molecule along the corresponding direction.⁶¹ The ground-state frequencies are higher (and would not be resolved by the long pulses in ref. 42 and 43). However it is an open question whether the 135 cm⁻¹ in the control experiment can belong to a vibration in 2A far from the Franck–Condon region.

4.2 Conclusions on the potentials and the reaction path

It was already mentioned that many features of the potentials and the path were only deduced from calculations, some from interpretation of experiments. More evidence can now be deduced from the observed oscillations. As pointed out, e.g., in ref. 44, after excitation the molecules are guided by the slopes on the potential, even if after some advance on its path the wave packet may deviate from the minimum-energy path due to accumulated momentum. Down-slopes are the driving forces. Typically, their direction changes repeatedly along the path, as also in the case of CHD ring opening.^11,34 Acceleration on a slope can also cause oscillations of the wave packet, if it is reflected back by a rising slope. (A common description is based on the superposition of stationary vibrational states in the Franck–Condon region by the coherent width (≈1400 cm⁻¹) of a pump laser, which gives rise to oscillating wave packets. This is just an alternative description to the acceleration mechanism.) It may happen that such an oscillation is stimulated in an early location and is only (or still) observed later. This is another momentum effect. Examples are discussed below. If the vibrational coordinate can be identified, it provides information on the direction of the slope.

As pointed out in ref. 11, the initial slope of every photochemical reaction is towards Franck–Condon (FC) active coordinates, as is already implied by their definition. They involve only the π system. Only later, when the molecule is enough distorted to allow also interaction of σ bonds with the π system, the Woodward–Hoffmann (WH) rules are turned on and the direction of motion changes (by modifying the σ bond length, for instance).¹¹ This rule is relatively general, too: it was also found in H migration in cycloheptatriene,⁶² for example, and plays an important role in cyclobutene ring opening, where it can explain the deviations from the WH rules.⁶³

It was argued in ref. 11, and substantiated by calculation and by substituent effects, that the FC active modes not only involve bond stretching in the π system but also double-bond torsion. The latter distorts all the backbone of the molecule, erecting also the CH₂–CH₂ bond, so that after some excursion the WH (σ–π) interactions can in fact set in (Fig. 3). A more recent calculation by Tamura et al. finds the same path.¹⁸ The initial motion and acceleration directions are now confirmed by the oscillations: two CC stretch vibrations are found in L₁ (the FC region) and a C=C torsion (ν₁₈, Scheme 1) in L₂. The latter (period 110 fs) cannot be observed in the short-lived (21 fs) L₁, but is certainly stimulated already there (in the FC region), because according to calculation the lower part of the 1B surface before the intersection with 2A (i.e., location L₂) is energetically very flat, so that there is also no slope towards ν₁₈. The fact that ν₁₈ is actually FC active is confirmed by the resonance Raman spectrum.^22,23

It is worth noting that distortion in ν₁₈ direction conserves the C₂ symmetry; i.e., it is conrotatory. This does not mean that the WH rules are active already in the FC region. Instead, the conrotatory initial acceleration follows from the fact that ν₁₈ is totally symmetric in C₂ and thus can be FC active, whereas the corresponding disrotatory combination of the C=C torsions (ν₃₆, b symmetry⁵⁸) is antisymmetric and FC inactive. (If CHD were planar, symmetry groupC_2v, also ν₁₈ would by antisymmetric, symmetry type a₂. On the other hand, disrotatory distortion as in some CHD derivatives would render ν₃₆FC active. In fact, the importance of predistortion for the choice e.g. between con- and disrotatory reactions was pointed out in ref. 64). The conrotatory twist (ν₁₈) of the C=C bonds also implies a torsion of the C–C bond between them; this is just the coordinate ϕ, identified in the calculations of de Vivie–Riedle et al. as the direction of initial motion.^12–16,40

The low-frequency oscillation (140 cm⁻¹ and its overtone 270 cm⁻¹) in L₃ (2A state) was assigned above to an (overtone) vibration along the minimum-energy path; i.e., along the line p*–CI (antisymmetric in C₂) connecting the C₂-symmetric stationary point of 2A (“pericyclic minimum” p*) with the 2A minima and 2A/1A CIs (Scheme 1). Since this region of the potential is very flat,^11,18 the vibration must again have been stimulated before. It is not excited in the FC region, because it is antisymmetric (also because it very much involves the former CH₂–CH₂ bond—see Scheme 1, which should not initially be affected by the excitation). However, it was pointed out¹¹ that 1B → 2A relaxation requires an antisymmetric (b type) distortion, so that the wave packet circumvents the 1B/2A CI around its lower cone; thereafter, the wave function even has a node along the symmetry line connecting this first CI with p* (Fig. 5), a consequence of the Berry phase.¹⁸ The calculations say that this deflection is just in the p*–CI direction.^11,17,18 (The background of this theoretical result is the fact that the 1B/2A and 2A/1A conical intersections have very similar branching spaces, also in other examples.⁶⁴) The observation of an oscillation in the p*–CI direction now provides a neat experimental confirmation of this antisymmetric deflection near the first CI.

With Fig. 5 we try to illustrate how the oscillations ν₂ and ν₃ are stimulated: The symmetric C=C torsion ν₂ (ν₁₈) is already excited in the FC region, but only a small part of the wave packet completes a full period, whereas the dominant part immediately falls down to the 2A surface. (Only the division through the exponential decay, exp(–t/τ₂), in the evaluation brings the small part to light. A full period of 110 fs corresponds to 3.2τ₂, so that only exp(–3.2) = 4% of the molecules are expected to have survived without decay.) Around the 1B/2A CI, the wave packet is accelerated to an antisymmetric direction (the partial wave packets always being in symmetry-equivalent positions). This eventually leads to the ν₃ vibration along the p*–CI direction over the double minimum. Also in this case, only a small part of the wave packet (again revealed through division by the exponential decay) performs a full period, whereas most of it immediately passes through the CI region down to the ground-state surface.

An early acceleration (near the first CI) towards the last CI was also invoked in ref. 11 to rationalize the short τ₃. The argument can now be quantified. In fact, on a flat potential such as from p* to the CI, i.e., in the absence of a strong acceleration, the wave packet would normally find the outlet (the 2A/1A CI) only by a kind of a diffusive process (as assumed in ref. 6), which would be slow.⁶ By contrast, the fastest conceivable process would be a ballistic motion from the initial symmetric structure to the antisymmetrically distorted turning point; starting from p*, the wave packet could then reach the CI region (which is near the turning point) in a quarter of the period of the corresponding vibration. This time would be 120 fs for the 140 cm⁻¹ vibration (which we assign to an overtone, see above), longer than τ₃ = 80 fs. However, the acceleration in this direction is much faster near the first CI, because the negative curvature on the lower cone of this CI is very much larger than at the stationary point p*. (Values are given in terms of imaginary frequencies in Fig. 9 of ref. 10.) Hence in this interpretation a ballistic path of the wave packet in an antisymmetric direction, leading eventually to the outlet to the ground state, already begins in the surrounding of the first CI.

An alternative or supplementary mechanism to explain the short τ₃ was also offered in ref. 11: “The 2A/1A CI” actually means the energy minimum of the 2A/1A intersection space (IS). The IS extends also to molecular structures closer to C₂-symmetric geometries. (A point in the IS with C₂-symmetry lies, however, higher than our excitation energy,^11,18 which is in the long-wavelength wing of the UV spectrum (Fig. 4). By contrast, quantum-dynamical calculations with higher initial energy predict a preferential passage through the C₂-symmetric CI.^{12–14,16,40}) If energetically reachable parts of the IS are, e.g., by 30% closer to a C₂-symmetric structure, a ballistic trajectory could arrive at it in about 30% less time than in 120 fs, i.e., in about the measured τ₃. However, even in this case an early and rapid acceleration is necessary to trigger a ballistic motion. The observation of the antisymmetric vibration makes it most likely that this acceleration leads to a region of the IS, which involves asymmetric distortion of the molecule and is energetically easily accessible, although not the very minimum of the IS, as already suggested in ref. 11. The time for departure from the 2A surface was calculated by quantum dynamics to 130–180 fs after leaving the FC region (the path leading through the asymmetric CI region).¹⁸ This is in the range of our τ₁ + τ₂ + τ₃ = 136 fs.

The region of the outlet from 2A (the 2A/1A IS), where the wave packet actually passes through, cannot be very extended. Otherwise the arrival time at S₀ would be spread over a certain range. This would be in conflict with the finding³⁴ that the wave packet is still very compact, when it arrives at a location (L₅ in ref. 34) on the S₀ surface, characterized by a narrow resonance in the ion at this geometry. Hence the wave packet seems to leave the 2A surface in a narrow region near the minimum of the IS (usually called “the CI”), which is near the turning point of the antisymmetric vibration. In this case we can expect that the 2A population drops in a stepwise manner. Indeed a first such step can be recognized from the data of Fig. 2 (near 110–130 fs); a second step is probably washed out by interference between the vibrational frequencies.

A more or less ballistic path is, of course, only conceivable, if any barriers are negligible compared with the available excess energy. This is practically consistent with the calculations (an energy difference of ≈0.09 eV was found between 2A minimum and the last CI¹⁸) but can primarily be inferred from the short time constants and the fact that they are the same in a cold supersonic beam.³⁵ This result should not be generalized to all derivatives of CHD. Thus, the steroid derivatives 7-dehydrocholesterol and ergosterol fluoresce (quantum yield 0.19⁶⁵) in a matrix at 80 K,^65,66 probably because the initial conrotatory twist is hindered by the substituents, giving rise to a minor barrier. (This is another confirmation that a ring twist such as ν₁₈ is FC active and is required to reach the 1B outlet, i.e., the first CI: stretching of CC bonds alone could not be hindered by bulky substituents or the matrix.) Also the departure from the 2A state is slower (0.95 ps),⁶⁷ certainly also due to hindering of ring twisting (along the antisymmetric coordinate in this case). Similar (though smaller) substituent effects on the individual L_i lifetimes have been found for two dialkyl derivatives of CHD and have been interpreted by mass effects (i.e., not by activation energies).¹¹ A barrier before the last CI may also arise, if extension of the π system (such as in photochromic substances) lowers the spectroscopic state very much, but does much less so with the 2A state and hence the 2A/1A CI; activation energies were in fact calculated for such systems²¹ and relatively slow ring-opening and closing times were found.^68,69

An instructive correlation of the observed wavenumbers of the low-frequency vibrations with the calculated¹¹ distances d of the two CH₂groups is possible, even without detailed knowledge of the nature of ν₃. It is shown in Fig. 6. The low frequencies indicate that these vibrations must be delocalized over the ring and have a small restoring force such as twisting or bending. The lowered wavenumber of ν_2a (310 cm⁻¹, 61% of the ground-state value of ν₁₈ = 506 cm⁻¹) indicates that the ring is already weakened (restoring force 37% of that in S₀), consistent with the calculated beginning of d lengthening near the first CI (i.e., in L₂). A more drastic decrease of the wavenumber and force constant occurs on arrival at the 2A minimum. This is consistent with the very long calculated d and the only weak interaction of one CH₂group with the other end of the ring. The wavenumbers hence demonstrate (in agreement with theory) that the ring begins to be opened near the 1B/2A CI (near the 1B minimum) but advances very much more on the 2A surface. On the other hand, the reaction is not completed in the excited state; otherwise a ring vibration would not exist anymore.

Fig. 6 Correlation of wavenumbers of ring vibrations with the calculated¹¹ CH₂–CH₂ distance d.

For completeness, we should also consider here the possibility that—despite the calculations—the ring would already be fully open in the 2A state and the 140 cm⁻¹ would be a hexatriene vibration. Indeed, in the ground state, Z-hexatriene has vibrations of such low wavenumbers.⁷⁰ They correspond to hindered free rotation around the C–C bonds and to CCC bending. However, they would both not be Franck–Condon active in the probing transition, since the respective angles in the ion would not (or not much) differ from those in the neutral molecule. Hence these hexatriene vibrations would not be observed, and the observed oscillation must be due to the intermediate structure discussed above. Furthermore, it was shown in ref. 34 by means of an ionic resonance that a structure corresponding to Z-hexatriene is only reached after arrival on the S₀ surface.

5. Concluding remarks

For photochemical reactions, Woodward and Hoffmann^2,3 primarily considered the orbitals and the spectroscopic state (1B), i.e., the state resulting from excitation of one electron from the highest occupied (HOMO) to the lowest unoccupied (LUMO) molecular orbital. Whereas in this way one could rationalize, for instance, the ring opening of cyclobutene to a diene, the backward reaction would be very endothermic (>2 eV) in this excited state. This problem was solved when van der Lugt and Oosterhoff^71,72 found that the dark state 2A can have a low-lying minimum, the pericyclic minimum (p*), resulting from an avoided crossing of the potentials correlating the reactant ground state and a two-electron excited product state and the corresponding pair for the backward reaction. (Two recent calculations with time-dependent density-functional theory for technical reasons also considered the 1B state alone and found a CI with S₀ on the hexatriene side.^19,20 However the present and previous^11,32–35 time-resolved spectroscopy shows clear evidence that the path passes via the 2A state.) However, the calculations usually show two 2A minima, a lower one in the WH-allowed and a higher one in the WH-forbidden direction, both easily accessible (see, e.g., ref. 72 for cyclobutene or Fig. 3 of ref. 73 for butadiene); continuing in anti-WH direction, the exit of the latter has a barrier. According to our results, the molecules in the “wrong” minimum cannot simply go back and then find the allowed minimum in the second attempt; this path would imply an activation energy, and therefore this process would be too slow to be compatible with our observed short times.

The problem is solved by considering more than one reaction, taking also into account that the initial acceleration is towards the FC-active coordinates, whereas the WH rules are turned on only later. In CHD, most molecules (those excited from the lower-energy chair-like conformer with C₂ symmetry) initially follow a conrotatory path; thereafter, the WH-type interactions facilitate its continuation via the first CI to the 2A minimum and the last CI towards the allowed ring opening. But a small fraction of the molecule (those excited from a higher-energy boat-like conformer with C_s symmetry) are accelerated towards a disrotatory direction.⁶⁴ However, then (probably only in the 2A state, if the calculations for butadiene⁷³ can be generalized) a barrier resulting from WH interactions hinders continuation towards disrotatory ring opening. Instead, from there the molecules (such as many dienes) can follow a nearly barrierless WH-allowed path to the disrotatory ring closure to a cyclobutene derivative (bicyclo[2,2,0]hexene-2). (The fact that the diene → cyclobutene path is nearly barrierless and ultrafast, was found for cycloheptadiene and cyclooctadiene in ref. 74.) It was pointed out in ref. 64 that CHD derivatives favoring the C_s-symmetric conformer in fact prefer this disrotatory path. Hence in these (and probably more) examples, the acceleration direction in the FC region controls, which of several WH-allowed reactions are initiated later on.

On the basis of the calculated lengthening of the CH₂–CH₂ distance (Fig. 6), it was suggested that the ring opening is already more or less complete before leaving the 1B surface.^7,10 The ring vibrations observed by us, however, demonstrate that the ring is still intact, though weakened, even in the dark state. In principle, in the latter case most of the restoring force could be located in the rest of the backbone, not in the weak three-electron three-center bond (Scheme 1). However our previous investigation shows that the geometrical structure of hexatriene is only reached on arrival on the S₀ surface, some distance after the last CI (location L₅ in ref. 34). This is probably characteristic of all nonadiabatic photochemical processes: the reaction already begins on the excited surface(s) but is only half completed near the location of the radiationless transition (through a CI) to the ground-state surface.

The observed coherent oscillations also confirm the previous (e.g.ref. 11) ideas on the reaction path: initial motion along FC-active coordinates (CC stretch and conrotatory CC torsion), which after some excursion still on the 1B surface activates WH interactions (because the CH₂–CH₂ bond is now more parallel to the π orbitals); then on surrounding the 1B/2A CI, acceleration to a symmetry-breaking direction that leads directly to a part (probably not the minimum) of the 2A/1A IS. The wave packet moves in “record time”, i.e., within a small fraction of the periods of the torsional vibrations along the local reaction coordinates; this is ascribed to early acceleration in regions of the potential, where it is still steeper. The largest part of the wave packet is transmitted through the two CIs at the first attempt; only a smaller part (revealed in the evaluation by division by the exponential decay) passes by, oscillates and returns to the CI. This part is small enough, so that on arrival at the ground-state surface, the wave packet is still compact.

In view of this more or less ballistic motion, one may ask whether the analysis by rate equations (modified by periodic modulation functions, eqn. (1)) is justified. If the observation windows, associated with the probing technique, were very narrow, then the signal would reflect the shape of the wave packet passing by the window; it would not be exponential. However, these windows are broad (symbolized by the lengths of the arrows in the figures), and the ionization probability continuously varies within them. This may contribute to wash out in the signals some signatures of a coherent or ballistic motion. A similar suggestion, applied to dissociation reactions, is due to Møller, Hendriksen and Zewail.^75,76 A closer theoretical analysis would be desirable, however. It is a related idea that we write the time constants besides the arrows, not to localized points (“states”): if these times are as short as in CHD, they mostly reflect the travelling times of the wave packet, not any time for transmission through a bottleneck.

As already pointed out, breaking of the molecular symmetry is necessary to render the radiationless (symmetry nonconserving) 1B → 2A transition possible. The calculations^10,11,18 find substantial down-slopes in such a direction near the 1B/2A CI, which are now confirmed by the observation of the antisymmetric vibration (ν_3a) after the radiationless transition. It is worth mentioning that the loss of molecular symmetry also withdraws the basis for the “conservation of orbital symmetry”, which was the initial interpretation of the WH rules.^2,3 The crucial property of the orbitals is the relative sign on surrounding a full perimeter, i.e., the corresponding bonding or antibonding properties.

Acknowledgements

This work was supported by the Deutsche Forschungsgemeinschaft (project FU 363/1). We thank Regina de Vivie-Riedle for providing the unpublished information on the lowest-frequency vibration in 2A.

References

1. M. Klessinger and J. Michl, Excited states and photochemistry of organic molecules, VCH, New York, 1995.
2. R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 8, 781–853.
3. R. B. Woodward and R. Hoffmann, The Conservation of Orbital Symmetry, VCH, Weinheim, 1970.
4. H. Dürr and H. Bouas-Laurent, Photochromism—Molecules and systems, Elsevier, Amsterdam, 1990.
5. M. Irie, Chem. Rev., 2000, 100, 1685–1716.
6. P. Celani, S. Ottani, M. Olivucci, F. Bernardi and M. A. Robb, J. Am. Chem. Soc., 1994, 116, 10141–10151.
7. P. Celani, F. Bernardi, M. A. Robb and M. Olivucci, J. Phys. Chem., 1996, 100, 19364–19366.
8. M. Garavelli, P. Celani, M. J. Bearpark, B. R. Smith, M. Olivucci and M. A. Robb, J. Phys. Chem. A, 1997, 101, 2023–2032.
9. M. Garavelli, P. Celani, F. Bernardi, M. A. Robb and M. Olivucci, J. Am. Chem. Soc., 1997, 119, 11487–11494.
10. M. Garavelli, F. Bernardi, M. Olivucci, T. Vreven, S. Klein, P. Celani and M. A. Robb, Faraday Discuss., 1998, 110, 51–70.
11. M. Garavelli, C. S. Page, P. Celani, M. Olivucci, W. E. Schmid, S. A. Trushin and W. Fuß, J. Phys. Chem. A, 2001, 105, 4458–4469.
12. A. Hofmann and R. de Vivie-Riedle, J. Chem. Phys., 2000, 112, 5054–5059.
13. A. Hofmann and R. de Vivie-Riedle, Chem. Phys. Lett., 2001, 346, 299–304.
14. A. Hofmann and R. de Vivie-Riedle, J. Information Recording, 2000, 25, 397–403.
15. L. Kurtz, A. Hofmann and R. de Vivie-Riedle, J. Chem. Phys., 2001, 114, 6151–6159.
16. A. Hofmann, L. Kurtz and R. de Vivie-Riedle, Appl. Phys. B, 2000, 71, 391–396.
17. H. Tamura, N. Shinkoh, H. Nakamura and T. Ishida, Chem. Phys. Lett., 2005, 401, 487–491.
18. H. Tamura, S. Nanbu, T. Ishida and H. Nakamura, J. Chem. Phys., 2006, 124 , 084313/1–13.
19. Y. Dou, S. Yuan and G. V. Lo, Appl. Surf. Sci., 2007, 253, 6494–6408.
20. C. Nonnenberg, S. Grimm and I. Frank, J. Chem. Phys., 2003, 119, 11585–11590.
21. M. Boggio-Pasqua, M. Ravaglia, M. J. Bearpark, M. Garavelli and M. A. Robb, J. Phys. Chem. A, 2003, 107, 11139–11152.
22. M. O. Trulson, G. D. Dollinger and R. A. Mathies, J. Am. Chem. Soc., 1987, 109, 586–587.
23. M. O. Trulson, G. D. Dollinger and R. A. Mathies, J. Chem. Phys., 1989, 90, 4274–4281.
24. P. J. Reid, S. J. Doig and R. A. Mathies, Chem. Phys. Lett., 1989, 156, 163–169.
25. P. J. Reid, S. J. Doig and R. A. Mathies, J. Phys. Chem., 1990, 94, 8396–8399.
26. P. J. Reid, S. J. Doig, S. D. Wickham and R. A. Mathies, J. Am. Chem. Soc., 1993, 115, 4754–4763.
27. P. J. Reid, S. D. Wickham and R. A. Mathies, J. Phys. Chem., 1992, 96, 5720–5724.
28. M. K. Lawless, S. D. Wickham and R. A. Mathies, Acc. Chem. Res., 1995, 28, 493–502.
29. S. Pullen, L. A. Walker II, B. Donovan and R. J. Sension, Chem. Phys. Lett., 1995, 242, 415–420.
30. S. H. Pullen, N. A. Anderson, L. A. Walker II and R. J. Sension, J. Chem. Phys., 1998, 108, 556–563.
31. S. Lochbrunner, W. Fuß, W. E. Schmid and K. L. Kompa, J. Phys. Chem. A, 1998, 102, 9334–9344.
32. W. Fuß, T. Schikarski, W. E. Schmid, S. A. Trushin and K. L. Kompa, Chem. Phys. Lett., 1996, 262, 675–682.
33. S. A. Trushin, W. Fuß, T. Schikarski, W. E. Schmid and K. L. Kompa, J. Chem. Phys., 1997, 106, 9386–9389.
34. W. Fuß, W. E. Schmid and S. A. Trushin, J. Chem. Phys., 2000, 112, 8347–8362.
35. N. Kuthirummal, F. M. Rudakov, C. L. Evans and P. M. Weber, J. Chem. Phys., 2006, 125 , 133307/1–8.
36. R. C. Dudek and P. M. Weber, J. Phys. Chem. A, 2001, 105, 4167–4171.
37. J. D. Cardoza, R. C. Dudek, R. J. Mawhorter and P. M. Weber, Chem. Phys., 2004, 299, 307–312.
38. C.-Y. Ruan, V. A. Lobastov, R. Srinivasan, B. M. Goodson, H. Ihee and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 7117–7122.
39. H. Ihee, V. A. Lobastov, U. M. Gomez, B. M. Goodson, R. Srinivasan, C.-Y. Ruan and A. H. Zewail, Science, 2001, 291, 458–462.
40. D. Geppert and R. de Vivie-Riedle, Chem. Phys. Lett., 2005, 404, 289–295.
41. H. Tamura, S. Nanbu, T. Ishida and H. Nakamura, J. Chem. Phys., 2006, 125 , 034307/1–10.
42. E. C. Carroll, B. J. Pearson, A. C. Florean, P. H. Bucksbaum and R. J. Sension, J. Chem. Phys., 2006, 124 , 114506/1–10.
43. E. C. Carroll, J. L. White, A. C. Florean, P. H. Bucksbaum and R. J. Sension, J. Phys. Chem. A, 2008, 112, 6811–6822.
44. W. Fuß, S. Lochbrunner, A. M. Müller, T. Schikarski, W. E. Schmid and S. A. Trushin, Chem. Phys., 1998, 232, 161–174.
45. S. A. Trushin, K. Kosma, W. Fuß and W. E. Schmid, Opt. Lett., 2007, 32, 2432–2434.
46. S. A. Trushin, K. Kosma, W. Fuß and W. E. Schmid, Chem. Phys., 2008, 347, 309–323.
47. S. A. Trushin, W. Fuß and W. E. Schmid, Chem. Phys., 2000, 259, 313–330.
48. S. A. Trushin, T. Yatsuhashi, W. Fuß and W. E. Schmid, Chem. Phys. Lett., 2003, 376, 282–291.
49. T. Yatsuhashi, S. A. Trushin, W. Fuß, W. Rettig, W. E. Schmid and S. Zilberg, Chem. Phys., 2004, 296, 1–12.
50. W. Fuß, W. Rettig, W. E. Schmid, S. A. Trushin and T. Yatsuhashi, Faraday Discuss., 2004, 127, 23–33.
51. W. Fuß, W. E. Schmid, K. K. Pushpa, S. A. Trushin and T. Yatsuhashi, Phys. Chem. Chem. Phys., 2007, 9, 1151–1169.
52. S. A. Trushin, S. Sorgues, W. Fuß and W. E. Schmid, ChemPhysChem, 2004, 5, 1389–1397.
53. S. A. Trushin, S. Panja, K. Kosma, W. E. Schmid and W. Fuß, Appl. Phys. B, 2005, 80, 399–403.
54. K. Kosma, S. A. Trushin, W. Fuß and W. E. Schmid, J. Mod. Opt., 2008, 55, 2141–2177.
55. K. Kosma, S. A. Trushin, W. E. Schmid and W. Fuß, Opt. Lett., 2008, 33, 723–725.
56. A. P. Thorne, U. Litzén and S. Johansson, Spectrophysics, Springer, Heidelberg, 1999.
57. C. Di Lauro and N. Neto, J. Mol. Struct., 1972, 3, 219–226.
58. D. Autrey, J. Choo and J. Laane, J. Phys. Chem. A, 2001, 105, 10230–10236.
59. A. M. Warshel and M. Karplus, Chem. Phys. Lett., 1972, 17, 7–14.
60. R. de Vivie-Riedle, personal communication.
61. A. M. Weiner, D. E. Leaird, G. P. Wiederrecht and K. A. Nelson, J. Opt. Soc. Am. B, 1991, 8, 1264–1275.
62. S. A. Trushin, S. Diemer, W. Fuß, K. L. Kompa and W. E. Schmid, Phys. Chem. Chem. Phys., 1999, 1, 1431–1440.
63. W. Fuß, W. E. Schmid, S. A. Trushin, P. S. Billone and W. J. Leigh, ChemPhysChem, 2007, 8, 592–598.
64. W. Fuß, Branching and momentum effects in photochemistry. in International Conference on Computational Methods in Science and Engineering, ed. T. E. Simos and G. Maroulis, American Institute of Physics, Corfu, Greece, 2007, vol. 963_2A, p. 627–630.
65. N. Nakashima, S. R. Meech, A. R. Auty, A. C. Jones and D. Phillips, J. Photochem., 1985, 30, 207–214.
66. E. Havinga, R. J. De Kock and M. P. Rappoldt, Tetrahedron, 1960, 11, 276–284.
67. N. A. Anderson, J. J. Shiang and R. J. Sension, J. Phys. Chem. A, 1999, 103, 10730–10736.
68. B. Heinz, S. Malkmus, S. Laimgruber, S. Dietrich, C. Schulz, K. Rück-Braun, M. Braun, W. Zinth and P. Gilch, J. Am. Chem. Soc., 2007, 129, 8577–8584.
69. J. Ern, A. T. Bens, H. D. Martin, S. Mukamel, D. Schmid, S. Tretiak, E. Tsiper and C. Kryschi, Chem. Phys., 1999, 246, 115–125.
70. H. Torii and M. Tasumi, Vib. Spectrosc., 1995, 8, 205–214.
71. W. T. A. M. van der Lugt and L. J. Oosterhoff, Chem. Commun. (London), 1968, 1235–1236.
72. W. T. A. M. van der Lugt and L. J. Oosterhoff, J. Am. Chem. Soc., 1969, 91, 6042–6049.
73. F. Bernardi, M. Olivucci and M. A. Robb, J. Photochem. Photobiol., A, 1997, 105, 365–371.
74. W. Fuß, S. Panja, W. E. Schmid and S. A. Trushin, Mol. Phys., 2006, 104, 1133–1143.
75. K. B. Møller and A. H. Zewail, Chem. Phys. Lett., 2002, 351, 281–288.
76. K. B. Møller, N. E. Hendriksen and A. H. Zewail, J. Chem. Phys., 2000, 113, 10477–10485.

---