Theoretical analysis of specific evolution of some faces of plant COM crystals
Jolanta
Prywer
*
Institute of Physics, Technical University of Łódź, Wólczańska 219, 93-005, Łódź, Poland. E-mail: jolanta.prywer@p.lodz.pl; Fax: +48 42 6313639; Tel: +48 42 6313653
First published on 13th October 2008
Abstract
Calcium oxalate is the most frequently found crystal in plants. Its crystals have been reported in more than 200 plant families. Calcium oxalate crystals observed in the Solanacea family form unique pseudotetrahedral and chiral morphology, although the molecular structure is achiral. Additionally, the crystals extracted from some plants of this family possess some extra faces. The present paper concerns the theoretical analysis of the evolution of these extra faces which demonstrate a very specific behaviour. In particular, they may exist and develop, growing much faster (three times) than the neighbouring faces. Despite the very high growth rates, these faces remain morphologically stable.
1. Introduction
The crystals of calcium oxalate are prevalent in nature and can be found in more than 200 plant families.1,2Calcium oxalate crystals are found in most organs and tissues of many plant species. They occur in leaves,3 stems,4 roots,5 seeds6 or floral organs.7 The shape of calcium oxalate crystals in plants is described as: (1) prisms - simple regular prismatic shapes, (2) druses - spherical aggregates of crystals, (3) styloids - single needle-shaped crystals often with sharply pointed ends, (4) raphides - needle-shaped crystals formed in bundles and (5) crystal sand - small usually tetrahedral crystals.7,8 In spite of the common occurrence of calcium oxalate among plants, the functions of these crystals are not fully known and understood. However, it seems that the crystals play multiple roles. Calcium oxalate could serve as a means of regulating internal calcium stores,9,10 or as a way to maintain ionic balance, e.g.sodium and potassium.1Calcium oxalate crystals are also formed to maintain low soluble levels of potentially toxic substances like oxalic acid.1,8,11 The possible role of calcium oxalate crystals is defence against insects2 or foraging animals.12 This function is implicated by the size, shape and placement of crystals in some tissues and organs.12 For example, needle-shaped crystals are believed to play a defence function against grazing animals.13–15 The needles can have grooves, which may probably be responsible for channelling the toxins in wounds.It is a very interesting feature that individual plant species produce crystals of specific morphology. Crystal morphology and distribution are usually similar within specific taxa and differ among divergent taxa. Therefore, the distribution and morphologies of these crystals are often used as taxonomic characters for plant families.3,16,17,18 These observations indicate that calcium oxalate crystals do not result from random processes, but preferably these specific crystal morphologies seem to reflect genetic regulation of crystal formation.1,8,11,19 For example, in plants of Helianthus annuus L. and Helianthus tuberosus L. (the Asteraceae family) styloid and prismatic types of crystals were observed.7 The styloid crystals are also characteristic for some families of Asparagales, where raphid crystals are not observed.8 Some plants from Solanacea produce in their leaves crystals with tetrahedral morphology.
Calcium oxalate exists in plants in two forms: (1) calcium oxalate monohydrate (COM), CaC2O4·H2O (whewellite) belonging to the monoclinic system and (2) calcium oxalate dihydrate (COD), CaC2O4·2H2O (weddellite) belonging to the tetragonal system.20,21COD crystals are less stable and less commonly observed in plants.
The studies of the calcium oxalate in plants may give more comprehensive understanding of the plant growth process and physiology of many plant species. The studies of calcium oxalate in plants are also important because of human health. Plant foods are the main source of dietary oxalate. Spinach, rhubarb or dry beans are examples of plant foods with a substantial amount of oxalate, which may have negative influence on human health. For example, an intake of oxalate-rich plants may lead to COM formation, which is the most frequent crystalline phase of human kidney stones.22,23
In this paper we focus on the morphology of crystal sand most frequently found in the leaves of the plants of the Solanacea19,24 or Rosaceae family.8 These crystals demonstrate some unique features such as chirality or pseudotetrahedral morphology, which are described in detail in the next section. The aim of the present study is to analyse this unique morphology and unique evolution of some faces of these crystals.
2. Morphology characterization of calcium oxalate crystals extracted from plants of the Solanacea family
As we stated above, the shapes of calcium oxalate crystals are characteristic of a given plant species. In literature, there are crystals extracted from a few plants from the Solanacea family such as: tomato19 (Lycopersicon esculentum), tobacco19 (Nicotiana tabacum), potato24 (Solanum tuberosum L.), hot pepper24 (Capsicum annum L.) and one species of wild Solanum24 (Solanum villosum M.). Calcium oxalate occurs in these plants is a monohydrate form24 (COM). In literature the shapes of these crystals are described as pseudotetrahedral and chiral.19 Both these features are surprising because of the space groupP21/n of these crystals, which is incompatible with chirality. A chiral object is one which cannot be superimposed on its mirror image by rotations or translations. Objects, which occur as both mirror-related versions, are called enantiomorphs. An achiral object can be superimposed on its mirror image and its space group must contain some operations, which invert its geometry, for example glide plane. Therefore, the pseudotetrahedral morphology observed in the crystal sand under considerations is incompatible with the space group, and the symmetry of the crystal structure is not reflected in the crystal morphology. These pseudotetrahedral crystals demonstrate lower symmetry than it results from its space group. Such a decrease in the morphological symmetry is known as hypomorphism.25,26 This phenomenon is observed, for example, for gibbsite,27Al(OH)3, potassium dichromate,28 K2Cr2O7 (KBC) or ammonium phosphate,29 NH4H2PO4. However, the reduction in symmetry in these crystals is very small and related to the molecular scale. For example, in ref. 28 the authors described the KBC crystal and the differences in the molecular structure in the (001) and (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces, which should be symmetry-related by inversion (space group: P
) faces, which should be symmetry-related by inversion (space group: P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ). This observation suggests hypomorphism on a molecular scale, not visible in the macroscopic crystal.
). This observation suggests hypomorphism on a molecular scale, not visible in the macroscopic crystal.
We stated above that biogenic COM crystals in the Solanacea family adopt a very unique pseudotetrahedral morphology. The question arises: what is the difference in morphology between these biogenic crystals and the crystals obtained in vitro? In vitroCOM crystal morphology is centrosymmetric (in agreement with the P21/n space group) with symmetry-related forms: {![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01}, {010} and either the {110} or {120} form;24,30,31Fig. 1a. In contrast, COM crystals in plants from the Solanacea family adopt a pseudotetrahedral morphology19,24 delimited by the (
01}, {010} and either the {110} or {120} form;24,30,31Fig. 1a. In contrast, COM crystals in plants from the Solanacea family adopt a pseudotetrahedral morphology19,24 delimited by the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10), (101), (
10), (101), (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) and (10
0) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces; Fig. 1b. The (101) face is the only face that has never been observed in crystals grown synthetically from solutions of calcium oxalate. As shown in literature,24 some crystals extracted from pepper leaves possess also the (
) faces; Fig. 1b. The (101) face is the only face that has never been observed in crystals grown synthetically from solutions of calcium oxalate. As shown in literature,24 some crystals extracted from pepper leaves possess also the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face and some extracted from wild Solanum possess also the (
32) face and some extracted from wild Solanum possess also the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face. The aim of the present study is the analysis of the existence and evolution of these two extra faces in COM plant crystals, which demonstrate unique behaviour.
01) face. The aim of the present study is the analysis of the existence and evolution of these two extra faces in COM plant crystals, which demonstrate unique behaviour.
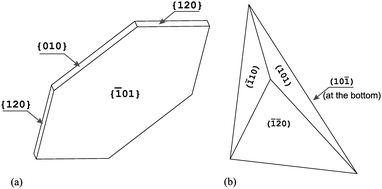 | ||
| Fig. 1 Schematic representation showing the morphology of COM crystals, (a) centrosymmetric non-biogenic; (b) pseudotetrahedral biogenic. | ||
3. Method of analysis
To analyse the existence and evolution of these faces in the crystal habit we use the idea of the critical growth rate Rcrithkl, which is defined as the normal growth rate of the (hkl) face at which a given size of this face is preserved.32 As it is more convenient to use the relative growth rates rather than the absolute ones, we use the critical relative growth rate Rhkl/Rcrithkl, which is given in the form:32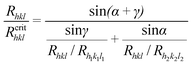 | (1) |
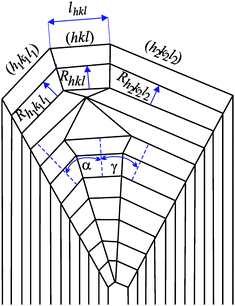 | ||
| Fig. 2 Schematic representation of cross-section of hypothetical crystal illustrating the (hkl), (h1k1l1) and (h2k2l2) faces and their normal growth rates Rhkl, Rh1k1l1, Rh2k2l2, respectively. lhkl represents the cross-section size of the (hkl) face, α and γ are the interfacial angles. | ||
The physical meaning of the ratio Rhkl/Rcrithkl is as follows: (i) for Rhkl/Rcrithkl < 1, the size lhkl of the (hkl) face increases; (ii) for Rhkl/Rcrithkl = 1, the size lhkl of the (hkl) face is preserved and (iii) for Rhkl/Rcrithkl > 1, the (hkl) does not appear in crystal habit or if it exists, the size lhkl of the (hkl) face decreases. From this it follows that the presence, absence, decrease or increase in size of crystal face depends on the value of the critical relative growth rate Rhkl/Rcrithkl.
4. Evolution of extra faces in COM plant crystals—theoretical analysis
In order to analyse the morphology and evolution of particular faces of the COM crystals we use unit cell parameters proposed by Deganello and Piro:33 space groupP21/n, a = 9.976 Å, b = 14.588 Å, c = 6.291 Å, β = 107.05°. Such parameters have been used by other researchers19 in their investigations related to COM crystallization in plants.First, we focus on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face, which takes a rectangle shape; Fig. 3a. In order to apply the method of the critical relative growth rate to the (
32) face, which takes a rectangle shape; Fig. 3a. In order to apply the method of the critical relative growth rate to the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face we must cut our 3D crystal along the cross-section line shown in Fig. 3a, as eqn (1) concerns the 2D case. In this way we obtain a 2D cross-section of a crystal (Fig. 3d,e) and the analysis of the evolution of the (
32) face we must cut our 3D crystal along the cross-section line shown in Fig. 3a, as eqn (1) concerns the 2D case. In this way we obtain a 2D cross-section of a crystal (Fig. 3d,e) and the analysis of the evolution of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face reduces to the analysis of the cross-section size l(
32) face reduces to the analysis of the cross-section size l(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) of the face (Fig. 3d). Applying eqn (1) to the l(
32) of the face (Fig. 3d). Applying eqn (1) to the l(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) cross-section size of the (
32) cross-section size of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face we should remember that the (hkl), (h1k1l1) and (h2k2l2) faces correspond to the (
32) face we should remember that the (hkl), (h1k1l1) and (h2k2l2) faces correspond to the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32), (
32), (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and (101) faces, respectively, and α and γ are equal to 71.74° and 53.84°, respectively. After substituting these values of angles into eqn (1) we obtain the dependence of the critical relative growth rate R(
10) and (101) faces, respectively, and α and γ are equal to 71.74° and 53.84°, respectively. After substituting these values of angles into eqn (1) we obtain the dependence of the critical relative growth rate R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) on the relative growth rates R(
32) on the relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(
32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) presented in Fig. 3b. Additionally, in this figure the R(
32)/R(101) presented in Fig. 3b. Additionally, in this figure the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) = 1 plane is visible. Fig. 3c presents the same dependence but in 2D graph. Here, the presented curve represents the intersection of the R(
32) = 1 plane is visible. Fig. 3c presents the same dependence but in 2D graph. Here, the presented curve represents the intersection of the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) ratio with the R(
32) ratio with the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) = 1 plane. Now, it is easier to notice that below the curve, the R(
32) = 1 plane. Now, it is easier to notice that below the curve, the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) ratio takes values smaller than unity and, therefore, in this region of relative growth rates R(
32) ratio takes values smaller than unity and, therefore, in this region of relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(
32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) the (
32)/R(101) the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face appears and develops its size in crystal habit. Above the curve, the R(
32) face appears and develops its size in crystal habit. Above the curve, the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) ratio is greater than unity and this corresponds to the decreasing the size of the (
32) ratio is greater than unity and this corresponds to the decreasing the size of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face in crystal habit or its disappearance. Based on this 2D graph we are able to notice a very interesting phenomenon: the (
32) face in crystal habit or its disappearance. Based on this 2D graph we are able to notice a very interesting phenomenon: the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face may appear in a crystal habit and develop its size growing much faster than both neighbouring (
32) face may appear in a crystal habit and develop its size growing much faster than both neighbouring (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and (101) faces. The region of relative growth rates R(
10) and (101) faces. The region of relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(
32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) for which such a phenomenon is possible, is marked as dashed region in Fig. 3c. It is easy to notice that the (
32)/R(101) for which such a phenomenon is possible, is marked as dashed region in Fig. 3c. It is easy to notice that the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face may appear in the crystal habit growing even 2 times faster than both neighbouring faces. The existence of the (
32) face may appear in the crystal habit growing even 2 times faster than both neighbouring faces. The existence of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face is also possible when it grows 3 or 4 times faster than one of the neighbouring face and, at the same time, only a little faster than the other neighbouring face. We may follow such behaviour of the (
32) face is also possible when it grows 3 or 4 times faster than one of the neighbouring face and, at the same time, only a little faster than the other neighbouring face. We may follow such behaviour of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face based in Fig. 3d, which presents the exemplary growth history obtained by computer simulation with the aid of Shape software.34
32) face based in Fig. 3d, which presents the exemplary growth history obtained by computer simulation with the aid of Shape software.34
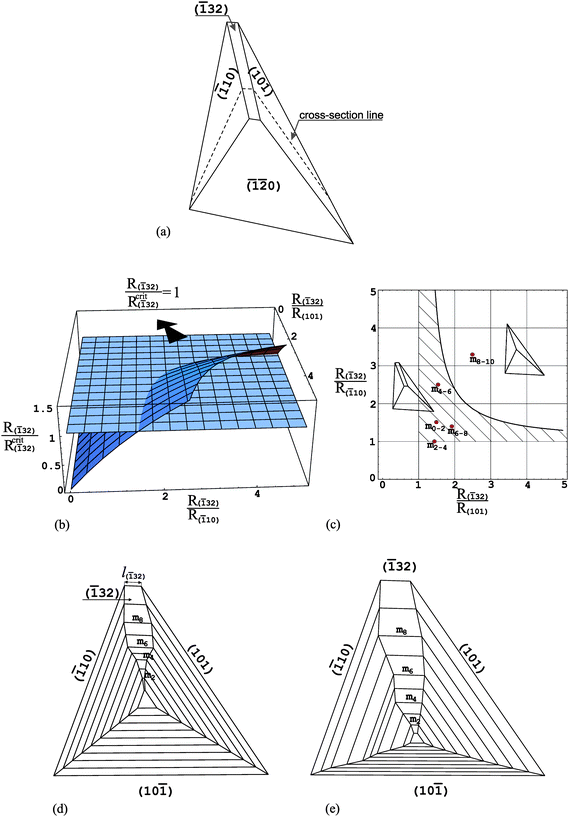 | ||
Fig. 3 (a) COM crystal morphology with the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face; (b) dependence of the critical relative growth rate R( 32) face; (b) dependence of the critical relative growth rate R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit( 32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) on the relative growth rates R( 32) on the relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R( 32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R( 10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101); (c) 2D graph of the same dependence; (e) and (f) cross-sections along cross-section line shown in (a) revealing two different evolutions of crystal morphology. mi in (d) and (e) denote consecutive growth bands. Points mi in (c) correspond to growth bands in (e) and relative growth rates R( 32)/R(101); (c) 2D graph of the same dependence; (e) and (f) cross-sections along cross-section line shown in (a) revealing two different evolutions of crystal morphology. mi in (d) and (e) denote consecutive growth bands. Points mi in (c) correspond to growth bands in (e) and relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R( 32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R( 10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) (Table 1) for which the growth history in (e) is obtained. 32)/R(101) (Table 1) for which the growth history in (e) is obtained. | ||
The relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(
32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) applied here are equal to each other and they are collected in Table 1. We may notice that at the beginning, up to the m2 growth band the (
32)/R(101) applied here are equal to each other and they are collected in Table 1. We may notice that at the beginning, up to the m2 growth band the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face grows 2 times faster than both neighbouring faces and it appears and increases in size. Then, it grows more slowly (R(
32) face grows 2 times faster than both neighbouring faces and it appears and increases in size. Then, it grows more slowly (R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(
32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) = R(
10) = R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) = 1.5 and 1.0 between m2–m4 and m4–m6growth bands, respectively) and the growth sector of this face is very wide. The (
32)/R(101) = 1.5 and 1.0 between m2–m4 and m4–m6growth bands, respectively) and the growth sector of this face is very wide. The (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face starts to decrease its growth sector, only beginning from the m8 growth band, when its growth rate is 3 times higher than the growth rates of both neighbouring faces.
32) face starts to decrease its growth sector, only beginning from the m8 growth band, when its growth rate is 3 times higher than the growth rates of both neighbouring faces.
| (hkl) | Growth bands mi | R (hkl)/R(h1k1l1) | R (hkl)/R(h2k2l2) | R (hkl)/R(h3k3l3) |
|---|---|---|---|---|
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R( 32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) 10) |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) 32)/R(101) |
— | ||
| m0–m2 | 2.0 | 2.0 | — | |
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face 32) face |
m2–m4 | 1.5 | 1.5 | — |
| m4–m6 | 1.0 | 1.0 | — | |
| Fig. 3d | m6–m8 | 2.0 | 2.0 | — |
| m8–m10 | 3.0 | 3.0 | — | |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R( 32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) 10) |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) 32)/R(101) |
— | ||
| m0–m2 | 1.5 | 1.5 | — | |
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face 32) face |
m2–m4 | 1.0 | 1.43 | — |
| m4–m6 | 2.5 | 1.56 | — | |
| Fig. 3e | m6–m8 | 1.4 | 1.94 | — |
| m8–m10 | 3.33 | 2.5 | — | |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R( 01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) 10) |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(101) 01)/R(101) |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R( 01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20) 20) |
||
| m0–m2 | 1.5 | 1.5 | 1.5 | |
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face 01) face |
m2–m4 | 2.0 | 2.0 | 2.0 |
| m4–m6 | 2.5 | 2.5 | 2.5 | |
| Fig. 4d | m6–m8 | 3.0 | 3.0 | 3.0 |
| m8–m10 | 2.0 | 2.0 | 2.0 | |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R( 01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) 10) |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(101) 01)/R(101) |
R
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R( 01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20) 20) |
||
| m0–m2 | 1.0 | 1.0 | 1.0 | |
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face 01) face |
m2–m4 | 1.5 | 1.5 | 1.5 |
| m4–m6 | 2.0 | 2.0 | 2.0 | |
| Fig. 4e | m6–m8 | 5.0 | 5.0 | 5.0 |
| m8–m10 | 2.0 | 2.0 | 2.0 |
Fig. 3e presents a little different growth history. Here, the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face grows with a constant growth rate only and the growth rates of the other faces change during the growth process (they are constant between single growth bands). In addition, the (10
) face grows with a constant growth rate only and the growth rates of the other faces change during the growth process (they are constant between single growth bands). In addition, the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face is the most slowly growing face in this case. It is assumed so because, as described in paper 24 the crystal lies on this face. In such a case it happens very frequently that the “bottom” face grows very slowly. The relative growth rates R(
) face is the most slowly growing face in this case. It is assumed so because, as described in paper 24 the crystal lies on this face. In such a case it happens very frequently that the “bottom” face grows very slowly. The relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(
32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) used here are collected in Table 1 and they are also marked in Fig. 3c as red circles. These circles correspond to the appropriate growth bands mi shown in Fig. 3e.
32)/R(101) used here are collected in Table 1 and they are also marked in Fig. 3c as red circles. These circles correspond to the appropriate growth bands mi shown in Fig. 3e.
It is worth noticing also that the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face seems to be very morphologically stable in the crystal habit. This conclusion ensues from the slope of the surface given by the R(
32) face seems to be very morphologically stable in the crystal habit. This conclusion ensues from the slope of the surface given by the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) ratio (Fig. 3b). The slope of this surface in relation to the R(
32) ratio (Fig. 3b). The slope of this surface in relation to the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) = 1 plane is small.35 This means that even big changes in relative growth rates R(
32) = 1 plane is small.35 This means that even big changes in relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(
32)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/R(101) induce only small changes in the critical relative growth rate R(
32)/R(101) induce only small changes in the critical relative growth rate R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32). In other words, the changes in the R(
32). In other words, the changes in the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32)/Rcrit(
32)/Rcrit(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) ratio are too small to change the way of evolution of the (
32) ratio are too small to change the way of evolution of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face.
32) face.
Similar analysis is performed for the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face, which was observed in crystals extracted from wild Solanum. The (
01) face, which was observed in crystals extracted from wild Solanum. The (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face takes a triangular shape (Fig. 4a) and, therefore, we cannot apply eqn (1), which is valid only for faces with parallel edges.32 In this case we apply the derived in paper 36 equation for triangular faces which, in the case of the (
01) face takes a triangular shape (Fig. 4a) and, therefore, we cannot apply eqn (1), which is valid only for faces with parallel edges.32 In this case we apply the derived in paper 36 equation for triangular faces which, in the case of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face, takes the form:
01) face, takes the form:
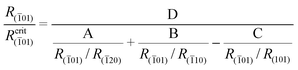 | (2) |
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face. These constants are equal to: 0.49, 0.71, −0.94 and 0.72, respectively. The details of these derivations are given in the Appendix. The dependence of the R(
01) face. These constants are equal to: 0.49, 0.71, −0.94 and 0.72, respectively. The details of these derivations are given in the Appendix. The dependence of the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)crit ratio on the relative growth rates R(
01)crit ratio on the relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(101) is given in Fig. 4b. Here, there are four surfaces 1, 2, 3 and 4 obtained for different values of the relative growth rate R(
01)/R(101) is given in Fig. 4b. Here, there are four surfaces 1, 2, 3 and 4 obtained for different values of the relative growth rate R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20), which is a parameter here. The relative growth rate R(
20), which is a parameter here. The relative growth rate R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20) is equal to 1.0, 1.5, 3.0 and 5.0 for the 1, 2, 3 and 4 surfaces, respectively. The curves being the intersections lines of these surfaces with the R(
20) is equal to 1.0, 1.5, 3.0 and 5.0 for the 1, 2, 3 and 4 surfaces, respectively. The curves being the intersections lines of these surfaces with the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)crit = 1 plane are presented in Fig. 4c. It should be noticed that in the range of relative growth rates R(
01)crit = 1 plane are presented in Fig. 4c. It should be noticed that in the range of relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(101) shown in Fig. 4b, the surface 1 does not intersect the R(
01)/R(101) shown in Fig. 4b, the surface 1 does not intersect the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)crit = 1 plane. Therefore, we have only 3 intersection curves (for surfaces 2, 3 and 4) in Fig. 4c. Similarly, as for the case of the (
01)crit = 1 plane. Therefore, we have only 3 intersection curves (for surfaces 2, 3 and 4) in Fig. 4c. Similarly, as for the case of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) face, the (
32) face, the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face can appear and develop its size for the growth rates much greater than the growth rates of the neighbouring faces. We also present two exemplary growth histories (Fig. 4d,e) revealing the evolution of the (
01) face can appear and develop its size for the growth rates much greater than the growth rates of the neighbouring faces. We also present two exemplary growth histories (Fig. 4d,e) revealing the evolution of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face. The relative growth rates R(
01) face. The relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R(
10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(101) applied to obtain these cross-sections are collected in Table 1. In the case of the cross-section presented in Fig. 4e the appropriate relative growth rates are also marked in Fig. 4c. The considered (
01)/R(101) applied to obtain these cross-sections are collected in Table 1. In the case of the cross-section presented in Fig. 4e the appropriate relative growth rates are also marked in Fig. 4c. The considered (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face is also morphologically stable because of the slight slope of the surface given by the R(
01) face is also morphologically stable because of the slight slope of the surface given by the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)crit ratio in relation to the R(
01)crit ratio in relation to the R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(
01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)crit = 1 plane.
01)crit = 1 plane.
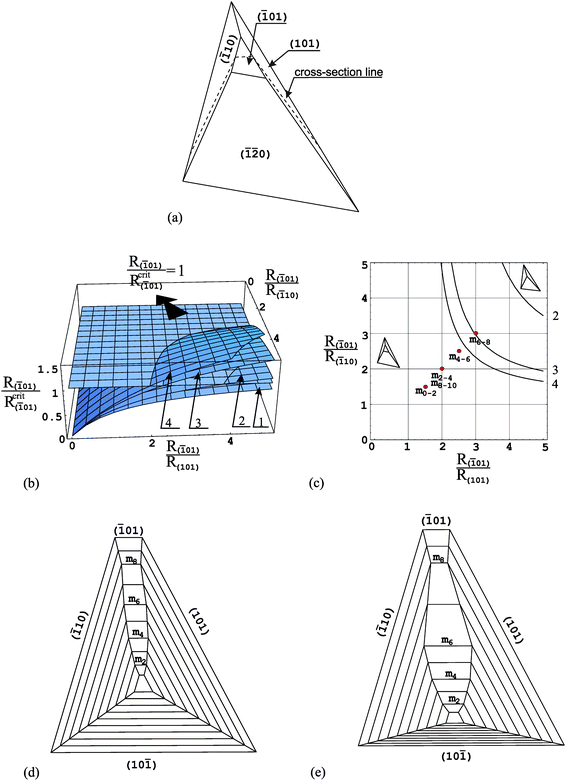 | ||
Fig. 4 (a) COM crystal morphology with the triangular (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face; (b) dependence of the critical relative growth rate R( 01) face; (b) dependence of the critical relative growth rate R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R( 01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)crit on the relative growth rates R( 01)crit on the relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R( 01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R( 10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(101); (c) 2D graph of the same dependence; (e) and (f) cross-sections along cross-section line shown in (a) revealing two different evolutions of crystal morphology. mi in (d) and (e) denotes consecutive growth bands. The points mi in (c) correspond to the growth bands in (e) and the relative growth rates R( 01)/R(101); (c) 2D graph of the same dependence; (e) and (f) cross-sections along cross-section line shown in (a) revealing two different evolutions of crystal morphology. mi in (d) and (e) denotes consecutive growth bands. The points mi in (c) correspond to the growth bands in (e) and the relative growth rates R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R( 01)/R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) and R( 10) and R(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)/R(101) (Table 1) for which the growth history in (e) is obtained. 01)/R(101) (Table 1) for which the growth history in (e) is obtained. | ||
Summarizing, both the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) and (
32) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) faces may appear and exist in the crystal habit for a very wide range of growth rates in relation to the growth rates of the neighbouring faces. The faces exist in the crystal habit, even growing much faster than the neighbouring faces. The range of relative growth rates for which both these faces grow faster than the neighbouring faces and appear in the crystal habit is surprisingly wide. The existence of fast-growing faces in crystal habits is quite rare and even if it occurs, the range of relative growth rates, for which such a phenomenon is observed, is very narrow.37 Therefore, the evolution of both the (
01) faces may appear and exist in the crystal habit for a very wide range of growth rates in relation to the growth rates of the neighbouring faces. The faces exist in the crystal habit, even growing much faster than the neighbouring faces. The range of relative growth rates for which both these faces grow faster than the neighbouring faces and appear in the crystal habit is surprisingly wide. The existence of fast-growing faces in crystal habits is quite rare and even if it occurs, the range of relative growth rates, for which such a phenomenon is observed, is very narrow.37 Therefore, the evolution of both the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) and (
32) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) faces is very uncommon. We noticed also that both the (
01) faces is very uncommon. We noticed also that both the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) and (
32) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) faces are morphologically stable, i.e. even big changes in their growth rates in relation to the neighbouring faces do not induce the disappearance of these faces.
01) faces are morphologically stable, i.e. even big changes in their growth rates in relation to the neighbouring faces do not induce the disappearance of these faces.
These findings arise questions about the mechanisms used by plants to stabilize these fast-growing faces and about the mechanisms of plant cells to control crystal morphology. The answer to such questions is not easy, because the biomineralization is not consistent with our physico-chemical knowledge of crystal growth. This is because the crystals in plants are formed in an unique environment of the membrane-bound chamber within the vacuole. This biological membrane separates the crystallization space (chamber) from the vacuole sap and allows regulation of the pH or the ion concentration (e.g.Ca2+). Additionally, the chamber may enclose macromolecules which have a profound effect on the course of the growth process. In particular, they may inhibit or promote the crystal nucleation and growth process. To macromolecules that affect the plant crystal growth we may include proteins, particularly acidic proteins and glycoproteins,38,39polysaccharides40 or lipids.41 Some of these macromolecules have been found to be incorporated into plant crystals. From this it follows that the chemical features of the chamber may directly affect the crystallization process and thus crystal morphology. Therefore, knowledge about crystal chambers is crucial to understanding cell-mediated crystallization. Besides, understanding the interconnection between the macromolecules and the growing crystalline phase is very important. The molecular structure of all faces delimiting the tetrahedral morphology which is under consideration in the present study is presented in ref. 24. Based on the molecular structure some ideas are given concerning this tetrahedral morphology. For example, the authors suggest that the macromolecules, using a very sophisticated mechanism, distinguish the (101) face from the opposite (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face. Additionally, there are indications that the macromolecules play a key role during nucleation and this role may be variable. When the macromolecule is adsorbed on the crystal surface, it acts as a promoter, when it is present in the growth solution it acts as an inhibitor. In spite of many attempts and efforts, the interaction mechanisms between macromolecular additives and calcium oxalate crystals are still poorly understood and many questions about the promoting and inhibiting factors still remain unanswered. Therefore, the explanation of the very unique features of plant COM crystals is still an open challenge for theory.
) face. Additionally, there are indications that the macromolecules play a key role during nucleation and this role may be variable. When the macromolecule is adsorbed on the crystal surface, it acts as a promoter, when it is present in the growth solution it acts as an inhibitor. In spite of many attempts and efforts, the interaction mechanisms between macromolecular additives and calcium oxalate crystals are still poorly understood and many questions about the promoting and inhibiting factors still remain unanswered. Therefore, the explanation of the very unique features of plant COM crystals is still an open challenge for theory.
5. Conclusions
In this paper we have highlighted the unique features of COM plant crystals in the Solanacea family such as: (1) pseudotetrahedral morphology, (2) chirality, (3) hypomorphism. Additionally, a new unique feature—the evolution of some extra faces in pseudotetrahedral morphology—is analysed. The present theoretical analysis demonstrates that faces such as (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 32) and (
32) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) observed in crystals extracted from pepper and wild Solanum leaves can appear in crystal morphology for a very wide range of relative growth rates. They can appear and develop growing even two or three times faster than the neighbouring faces, and at the same time they remain morphologically stable. Although the phenomenon of development of fast-growing faces in crystal morphology is known, in the case of these COM plant crystals such a phenomenon occurs for surprisingly high growth rates.
01) observed in crystals extracted from pepper and wild Solanum leaves can appear in crystal morphology for a very wide range of relative growth rates. They can appear and develop growing even two or three times faster than the neighbouring faces, and at the same time they remain morphologically stable. Although the phenomenon of development of fast-growing faces in crystal morphology is known, in the case of these COM plant crystals such a phenomenon occurs for surprisingly high growth rates.
These findings may suggest that the crystallisation process in plants differs from such a process in the case of synthetically grown crystals. Therefore, crystallisation in plants still requires investigation to clearly understand the crystal formation in plants.
Appendix
In the case of triangular-shaped face we are not able to use eqn (1), which is derived for faces with at least two parallel edges. The appropriate formula, which we may use in our case, is derived in ref. 36. We may analyse one edge of the triangular face only because the appearance (disappearance) of one edge is equivalent to the existence (absence) of the whole face. For our analysis we chose the edge created by the (hkl) and (h2k2l2) faces; Fig. A1. The critical growth rate Rcrithkl is now defined in the form:36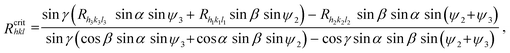 | (A1) |
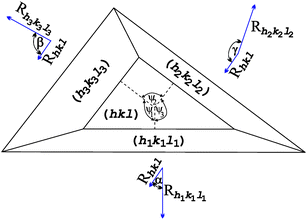 | ||
| Fig. 5 Schematic representation of triangular-shaped face (hkl), normal growth rates RhklRh1k1l1, Rh2k2l2 and Rh3k3l3 of the (hkl), (h1k1l1), (h2k2l2) and (h3k3l3) faces, respectively; interfacial angles α, β, γ and appropriate angles ψ1, ψ2 and ψ3. | ||
Now, we transform the above equation in order to obtain the critical relative growth rate:
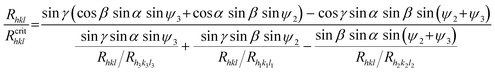 | (A2) |
The physical meaning of the Rhkl/Rcrithkl ratio remains the same as for the previous case (Section 3: Method of analysis). In eqn (A2), besides the relative growth rates there are four geometrical expressions which we denoted by: A = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ sin
γ sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α sin
α sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ3, B = sin
ψ3, B = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ sin
γ sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β sin
β sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ2, C = sin
ψ2, C = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β sin
β sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αsin(ψ2+ψ3) and the whole numerator we denote by D. For a given face, the expressions A, B, C and D are constant. In this way we derived eqn (2) for the triangular (
αsin(ψ2+ψ3) and the whole numerator we denote by D. For a given face, the expressions A, B, C and D are constant. In this way we derived eqn (2) for the triangular (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face of the COM crystal which is under considerations. We used the following values for the angles: α = 73.83°, β = 78.33°, γ = 63.46°, ψ1 = 88.94°, ψ2 = 125.80° and ψ3 = 145.27°.
01) face of the COM crystal which is under considerations. We used the following values for the angles: α = 73.83°, β = 78.33°, γ = 63.46°, ψ1 = 88.94°, ψ2 = 125.80° and ψ3 = 145.27°.
References
- P. A. Nakata, Plant Sci., 2003, 164, 901–909 CrossRef CAS.
- K. L. Korth, S. J. Doege, S. H. Park, F. L. Goggin, Q. Wang, S. K. Gomez, G. Liu, L. Jia and P. A. Nakata, Plant Physiol., 2006, 141, 188–195 CrossRef CAS.
- N. R. Lersten and H. T. Horner, Plant Syst. Evol., 2000, 224, 83–96 CrossRef CAS.
- M. J. Grimson and H. J. Arnott, Scan Electron Microsc. IV, 1983, 1771–1778 Search PubMed.
- H. T. Horner, A. P. Kausch and B. L. Wagner, Int. J. Plant Sci., 2000, 161, 861–868 CrossRef CAS.
- H. Ilarslan, R. G. Palmer, J. Imsande and H. T. Horner, Am. J. Bot., 1997, 84, 1042–1046 CrossRef CAS.
- C. Meric and F. Dane, Acta Biol. Szegediensis, 2004, 48, 19–23 Search PubMed.
- H. Demiray, Biologia, Bratislava, 2007, 62, 46–50 Search PubMed.
- E. Zindler-Frank, R. Honow and A. Hesse, J. Plant Physiol., 2001, 158, 139–144 CrossRef CAS.
- P. V. Monje and E. J. Baran, Plant Physiol., 2002, 128, 707–713 CrossRef CAS.
- V. R. Franceschi and P. A. Nakata, Annu. Rev. Plant Biol, 2005, 56, 41–71 CrossRef CAS.
- V. R. Franceschi, Trends Plant Sci., 2001, 6, 331 CrossRef CAS.
- W. S. Sakai, S. S. Sherona and M. A. Nagao, Scan. Electron Microsc., 1984, 2, 979–986.
- B. Kuballa, A. J. Lugnier and R. Anton, Toxicol. Appl. Pharmacol., 1981, 58, 444–449 CrossRef CAS.
- A. Doaigey, Am. J. Bot., 1991, 78, 1608–1616 CrossRef CAS.
- S. V. Pennisi and D. B. McConnell, Hort. Sci., 2001, 36, 1033–1036 Search PubMed.
- C. J. Prychid, C. A. Furness and P. J. Rudall, Ann. Bot., 2003, 92, 571–580 CrossRef.
- S. Zona, Ann. Bot., 2004, 93, 415–421 CrossRef.
- N. Bouropoulos, S. Weiner and L. Addadi, Chem.–Eur. J., 2001, 7, 1881–1888 CrossRef CAS.
- D. Jáuregui-Zúñiga, J. P. Reyes-Grajeda, J. D. Sepúlveda-Sánchez, J. R. Whitaker and A. Moreno, J. Plant Physiol., 2003, 160, 239–245 CrossRef CAS.
- A. Frey-Wyssling, Am. J. Bot., 1981, 68, 130–141 CrossRef CAS.
- R. P. Holmes, H. O. Goodman and D. G. Assimos, Kidney Int., 2001, 59, 270–276 CrossRef CAS.
- S. Lewandowski and A. L. Rodgers, Clin. Chim. Acta, 2004, 345, 17–34 CrossRef CAS.
- A. Levy-Lior, S. Weiner and L. Addadi, Helv. Chim. Acta, 2003, 86, 4007–4017 CrossRef CAS.
- O. G. Kozlova, Y. A. Kharitonov and N. Belov, Sov. Phys. Dokl., 1979, 24, 509 Search PubMed.
- A. Shubnikov, Z. Kristallogr., 1912, 50, 19–23 CAS.
- C. Sweegers, M. Plomp, H. C. de Coninck, H. Meekes, W. J. P. van Enckevort, I. D. K. Hiralal and A. Rijkboer, Appl. Surf. Sci., 2002, 187, 218–234 CrossRef CAS.
- M. Plomp, W. J. P. van Enckevort and E. Vlieg, J. Cryst. Growth, 2000, 216, 413–427 CrossRef CAS.
- M. A. Verheijen, L. J. P. Vogels and H. Meekes, J. Cryst. Growth, 1996, 160, 337–345 CrossRef CAS.
- A. Millan, Cryst. Growth Des., 2001, 1, 245–254 CrossRef CAS.
- Jian-Ming Ouyang and Sui-Ping Deng, Dalton Trans., 2003, 2846–2851 RSC.
- J. Prywer, Prog. Cryst. Growth Charact. Mater., 2005, 50, 1–38 CrossRef CAS.
- S. Deganello and O. E. Piro, Neues Jb. Miner. Monat., 1981, 2, 81–88 Search PubMed.
- SHAPE ver. 4.1.1 professional, Copyright 1994-Eric Dowty, Shape Software, 521 Hidden Valley Road, Kingsport, TN 37663 USA; http://www.shapesoftware.com.
- J. Prywer, Cryst. Growth Des., 2003, 3, 593–598 CrossRef CAS.
- J. Prywer, J. Cryst. Growth, 1996, 165, 335–340 CrossRef CAS.
- J. Prywer, J. Phys. Chem. Solids, 2002, 63, 491–499 CrossRef CAS.
- L. Addadi and S. Weiner, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 4110–4114 CAS.
- D. A. Walters, B. L. Smith, A. M. Belcher, G. T. Paloczi, G. D. Stucky, D. E. Morse and P. K. Hansma, Biophys. J., 1997, 72, 1425–1433 CAS.
- D. J. Kok, L. J. Blomen, P. Westbroek and O. L. Bijvoet, Eur. J. Biochem., 1986, 158, 167–172 CAS.
- S. R. Letellier, M. J. Lochhead, A. A. Campbell and V. Vogel, Biochim. Biophys. Acta, 1998, 1380, 31–45 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2009 |
