Single injection microarray-based biosensor kinetics

Abstract

Binding affinity of biomolecular interactions can be directly extracted from measured surface plasmon resonance biosensor sensorgrams by fitting the data to the appropriate model equations. The conventional method for affinity estimation uses a series of analytes and buffers that are injected serially to a single immobilized ligand on the sensing surface, including a regeneration step between each injection, to generate information about the binding behavior. We present an alternative method to estimate the affinity using a single analyte concentration injected to multiple ligand densities in a microarray format. This parameter estimation method eliminates the need for multiple analyte injections and surface regeneration steps, which can be important for applications where there is limited analyte serum, fragile ligand-surface attachment, or the detection of multiple biomolecule interactions. The single analyte injection approach for binding affinity estimation has been demonstrated for two different interactant pairs, β2 microglobulin/anti-β2 microglobulin (β2M) and human IgG/Fab fragments of anti-human IgG (hIgG), where the ligands are printed in a microarray format. Quantitative comparisons between the estimated binding affinities measured with the conventional method are β2M: K_D = 1.48 ± 0.28 nM and hIgG: K_D = 12.6 ± 0.2 nM and for the single injection method are β2M: K_D = 1.52 ± 0.22 nM and hIgG: K_D = 12.5 ± 0.6 nM, which are in good agreement in both cases.

---

Introduction

A microarray is a two-dimensional array of biomolecular capture probe spots immobilized on a surface with predetermined spatial order that is an assay used for gene expression and discovery, disease diagnostics, drug discovery, biomarker discovery and toxicology. The microarray was first described in literature in the late 1970's¹ and formally defined as a microarray in the late 1980's.² Since the initial application of high-throughput genomics, microarrays are now being applied in different fields, including proteomics,³ cellomics⁴ and drug discovery,⁷ as well as to many different types of biomaterials, including antibodies,⁵ chemicals,⁶ tissues,⁸ carbohydrates⁹ and peptides.¹⁰

Since the first report of the surface plasmon resonance imaging (iSPR) biosensor system in the late 1980's,¹¹ the iSPR technique is now commonly accepted as being suitable for the label-free measurement of multiple simultaneous biomolecular interactions, compared to other established methods, such as the quartz crystal microbalance,¹² Suprex MALDI mass spectroscopy¹³ and kinetic capillary electrophoresis,¹⁴ due to its compatibility with microarray substrates. Currently, there are many commercially available iSPR systems, including the Biacore Flexchip,¹⁵GWC SPRimagerII,¹⁶IBIS-iSPR,^17,53 Genoptics SPRi-Lab+,¹⁸ and also many custom-made iSPR systems.^19,20

Biomolecular interactions measured with iSPR,^21–23 can provide binding information, such as binding quantitation and specificity, and rate and affinity constants²⁴ of two or more interactants, which can lead to further understanding of interactant binding. For example, in the development process of new drugs, kinetic experiments provide insights into potential drug candidates as well as the definition of lead targets.²⁵ Kinetic parameter estimation of biomolecular interactions from integrated microarray-iSPR is increasingly being utilized for multi-analyte or multi-ligand studies.^24–36Table 1 shows a compilation of SPR-microarray studies from literature for various application areas, including protein–DNA interactions,^26,27epitope mapping,^28,32antibody screening,^29,31 demonstration of new imaging systems,^30,34,36protein–carbohydrate interactions,³³ allergen–antibody interactions,³⁵ affinity ranking,³⁷ and small molecules analysis.³⁸

Table 1 Reported integrated microarray-SPR measurements for various application areas using multiple analyte and ligand densities as well as multiple ligand types (Spots: regions of immobilized ligands; Ligands: target molecules immobilized on the sensor surface). The microarray arrangement of ligand spots is represented as a · b where a is the number of ligands and b is the number of times the ligand is repeated

Ref.	No. spots	Spot conc.	No. ligands	No. analytes	Analyte conc.	Application
26	20	Same	5 · 4	1	Same	Protein–DNA interaction
27	36	Same	6 · 6	1	Same	Protein–DNA interaction
28	54	Same	18 · 3	18 (1/ligand type)	Different	Epitope mapping
29	96	Same	2 · 36; 1 · 4; 1 · 20	4	Multiple	Antibody screening
30	900	Same	30 · 30	30 (1/ligand type)	Different	New iSPR system demonstration
31	8	—	1 · 8	386 (1/ligand type)	Different	Antibody screening
31	16	—	16 · 1	80 (5/ligand type)	Different and multiple	Antibody screening
32	12	—	12 · 1	1	Same	Epitope mapping
32	9	—	9 · 1	1	Same	Epitope mapping
33	8	Multiple	2 · 4	2 (1/ligand type)	Different	Protein–carbohydrate interaction
34	156	Same	12 · 13 Matrix + 156 (ref.)	5	Multiple	New iSPR system demonstration
35	24	—	24 · 1	24 × (8/10/12)	Multiple	Allergen–antibody interactions
36	110	Same	1 sample shown	6	Multiple	New iSPR system demonstration
37	302	Same	2 · 151	191	Different	Affinity ranking
37	288	Same	3 · 96	191	Different	Affinity ranking
38	36	Same	1 · 6	6	Multiple	Small molecules analysis
38	36	Same	1 · 6 (8 comp.)	40 (5/ligand type)	Different and multiple	Small molecules analysis

---

Conventional kinetic parameter estimation is done by measuring sensor responses in a serial way by introducing a range of analyte concentrations to a fixed ligand density on the sensing surface where between each analyte injection step, dissociation and surface regeneration steps are performed each requiring a different buffer solution. Although the conventional procedure is important for general ligand–ligate binding parameter estimation, there are certain applications that can benefit from alternative parameter estimation methods. We present an alternative binding affinity estimation method that uses a single analyte injection and multiple ligand densities in a microarray format; different than the conventional estimation method used to extract the binding affinity. This parameter estimation method eliminates the need for multiple analyte injections and surface regeneration steps, which can be important for applications where there is limited analyte serum, fragile ligand–surface attachment, or the detection of multiple biomolecule interactions. This approach was briefly described in our previous article, which describes a new lab-on-a-chip device integrated with iSPR system.³⁹ In this article we demonstrate the effectiveness of the new method by comparing the estimated binding affinity of two well-known interactant pairs along with the conventional method. Differences between various measurement scenarios in this combination (microarray-iSPR) are discussed, as well as advantages and disadvantages of the single injection method.

Measurement scenarios

Three general iSPR-microarray measurement scenarios, shown in Fig. 1, can be defined as: i) single ligand type and density with multiple analyte concentrations (Fig. 1a and 1b) referred to as the conventional measurement, ii) multiple ligand densities with multiple analyte concentrations (Fig. 1c and 1d), and iii) multiple ligand densities and types with multiple analyte concentrations and types (Fig. 1e–1h).

Fig. 1 Measurement scenarios (a) Conventional method with single ligand [B] and multiple analyte concentrations [A_p] (b) Single ligand density microarray [B_m·n] and multiple analyte concentrations [A_p] (c) Multiple ligand densities and multiple analyte concentrations (d) Multiple ligand density and single analyte concentration (e) Multiple ligand types [B₁]-[B_q] and multiple analyte concentrations [A_p]₁-[A_p]_q (f) Multiple ligand types [B₁]-[B_q] and multiple analyte concentrations of [A]₁-[A]_q (g) Multiple ligand densities and types [B_m·n]₁-[B_m·n]_q and multiple analyte concentrations [A_p]₁-[A_p]_q (h) Multiple ligand densities and types [B_m·n]₁-[B_m·n]_q and multiple analyte concentrations [A]₁-[A]_q. (m · n is multiplication of the number of row m and the number of columns n of the microarray).

The most commonly reported SPR binding kinetics measurement, or conventional measurement, uses panalytes [A]_p serially injected to a single ligand density [B], where each of the p injections is separated by a surface regeneration step (Fig. 1a) and measurement responses are recorded over the entire experimental time. The responses are recorded as R̲_t = [R̄_1t,R̄_2t,…,R̄_pt], where R̲_t is a matrix of p response vectors R̄_it for each analyte concentration i sampled over the experimental time t_e. Kinetic model parameters are extracted from the measured responses by finding the global-minimum of an error function, such as the “chi-square” function , where σ_it is the standard deviation of each data point, such that the chosen model function f_t(a_j), best matches the measured responses R̲_t with an optimal set of model parameters a_j. This type of parameter extraction is referred to as a “global” fitting procedure since the model parameters a_j are estimated over all measured responses, which is considered a more accurate method for parameter estimation.⁴⁰ The scenario where a constant ligand density is printed in a microarray (Fig. 1b) is similar to the single spot ligand density (Fig. 1a).

The second experimental scenario consists of multiple ligand densities of the same type printed in a microarray format (Fig. 1c and 1d). For the case where both the analyte and ligand densities are varied (Fig. 1c), the measured responses form a three-dimensional matrix consisting of p response vectors for all m · n ligands R̲_t = [R̄_1t,R̄_2t,…,R̄_m·nt]_p. The model parameters are extracted with a global fitting procedure as previously described. An interesting alternative, and the topic of this article, is the injection of a single analyte concentration, referred to as “single injection”, and using multiple ligand densities (Fig. 1d) to extract the model parameters. In this case, the measured response matrix contains m · n response vectors R̄_t = [R_1t,R_2t,…,R_m·nt]. Compared to the conventional method (Fig. 1a and 1b), this method offers some clear advantages such as a reduction in analyte sample and the elimination of regeneration steps. For example, five different analyte concentrations used in a conventional kinetics experiment, each 100 µl, requires about 500 µl of sample; a five-fold reduction in sample volume. We expect a reduction in ligand consumption using a microarray-based approach. The main disadvantage with the single analyte injection approach is that ligand surface density cannot be well controlled with conventional spotting techniques, which can be problematic if each spot requires calibration, which is usually the case when screening for binding interaction parameters, however, this limitation will diminish with improvements in spotting techniques. From a model parameter extraction perspective, the accuracy of the fitting procedure favors the former method (Fig. 1c) where m · n response vectors are typically larger than p response vectors from multiple analyte concentrations, however, this requires the greatest experimental effort and requires surface regeneration.

The third experimental scenario consists of four possibilities, shown in Fig. 1e–h, consisting of multi-analyte and multi-ligand measurement scenarios. In this case, multiple ligand types (Fig. 1e and 1f) with duplicates as well as multiple ligand densities (Fig. 1g and 1h) are immobilized on the surface. This approach is mainly useful in the screening of drug targets where hundreds to thousands of molecules are to be screened. These scenarios are not described in detail in this article and have been included for sake of completeness.

In this article we evaluate the single injection kinetics method (Fig. 1d) and compare results from two different ligand–analyte systems with measurements from the conventional method (Fig. 1a/1b) and assess its use for actual experimental applications described in Fig. 1c and 1d.

Biomolecular interaction model functions

Different biomolecular interaction models have been reported for describing SPR data including 1:1 interaction models,^40–42 1:1 interaction model with mass transport effects,^43–45 heterogeneous ligand model,⁴⁶ decaying surface model,⁴⁷ heterogeneous analyte model,⁴⁸ avidity effects,⁴⁹ and conformation change model.⁴⁸ The most commonly used model is the 1:1 interaction model represented by , where i is the number of analytes and j is the number of ligands and k_a and k_d are the association and dissociation rates, respectively. The affinity constant is defined as K_D = k_d/k_a.⁴⁰ The observed SPR response signal R_t is proportional to the formation of ‘AB’ complexes at the surface with respect to the ligand density. Accordingly, the maximum signal R_m represents the maximum ligand capacity that can bind with analytes without any dissociation of the AB complex and is proportional to the active ligand density at the surface.

From the rate equation, assuming [A]≫[B] and initial conditions f (t = 0) = 0, the model response function is f = α(1 − e^−βt) = f(k_a,k_d,R_m), where α = k_a[A]R_m/k_a[A] + k_d and β = −k_a[A] + k_d.⁴⁰ The dissociation rate constant can be evaluated using the initial condition f_d(t = t_d) = R₀ resulting in f_d(t) = R₀e^−k_dt, where R₀ is the response at time t_d, the onset of the dissociation phase.⁴⁰ The simple 1:1 interaction model is used for parameter extraction in this article.

Experiments

Experiments have been performed to quantitatively compare extracted kinetic parameters K_D and R_m between the scenarios described in Fig. 1a, 1b, 1c and 1d. A single ligand density, which is obtained when a ligand concentration of 250 µg/ml is exposed to the surface, was used for the conventional measurement. Additionally, the measurement scenario in Fig. 1c provides information about the reproducibility of the extracted affinity constants with respect to the varying ligand densities for the ligand–analyte pairs.

β2 microglobulin–monoclonal anti-β2 microglobulin

Experiments are performed with the interactant pair β2 microglobulin (β2M) (Sigma, The Netherlands)/monoclonal anti-β2M (a-β2M) (Abcam, Cambridge, United Kingdom), which follows the 1:1 interaction model function.⁵⁰ Twenty-four β2M ligand spots were spotted (TopSpot, Biofluidics, Germany) on a sensor disk with varying ligand densities: [B₁] = 0, [B₂] = 250, [B₃] = 125, [B₄] = 62.5, [B₅] = 31.2, and [B₆] = 15.6 µg/ml.^17,51,54 The immobilization buffer consisted of 10 mM sodium acetate buffer (pH 5.4) and the binding/running buffer was HBS-EP buffer (GE Healthcare/Biacore, Sweden) with pH 7.2. Prior to ligand spotting, the functionalized hydroxy gel sensor disk (HC-80m, XanTec, Germany) was activated with 400 mM EDC (Sigma, The Netherlands) and 100 mM NHS (Sigma, The Netherlands) for 20 minutes followed by rinsing with 0.25v/v% acetic acid. The activated disk was dried for 30 minutes under continuous dry nitrogen flow. The β2M ligand was spotted on the sensor disk and incubated in a humidity chamber for one hour. Following protein immobilization, the sensor surface was blocked with 1M ethanolamine (Sigma, The Netherlands). The sensor containing the protein microarray was mounted in the IBIS-iSPR (IBIS Technologies BV, Hengelo, The Netherlands) with a drop of refractive index matching oil (n_oil = 1.518 from Cargille Lab, USA). The system was equilibrated using 1 mL binding buffer in the flow-cell at a flow-speed of 2 µL/sec at 25 °C. After defining the ROIs each 30 × 30 pixels, corresponding to 225 × 225 µm², the SPR-dip was measured automatically by the IBIS-iSPR software (IBIS Technologies BV, Hengelo, The Netherlands). A baseline measurement was made by injecting the binding buffer.

Different analyte concentrations: [A₁] = 72, [A₂] = 36, [A₃] = 18, [A₄] = 9, [A₅] = 4.5, [A₆] = 2.25, [A₇] = 1.1 and [A₈] = 0.5 nM, were prepared in the binding buffer. An iSPR image of the fabricated microarray is shown in Fig. 2a. The SPR dips were measured for all the 24 spots (Fig. 2b). Regeneration was done with 10 mM Glycine-HCl (pH 1.6) between each analyte injections in the case of multiple analyte injections. In this case, the association and dissociation profiles were measured for 900 and 600 seconds respectively.

Fig. 2 (a) Real-time image of the microarray with multiple ligand densities of β2M (b) SPR measurement dips for twenty-four ligand spots (c) Conventional kinetics estimation for ligand density 125 µg/ml and 250 µg/ml and different analyte concentrations [A₁]-[A₈]. The point plots represents the residual plots obtained from the results of 1:1 model fit function to the recorded iSPR data.

Human IgG–Fab fragments of anti-human IgG

Experiments were also performed with Human IgG (Sigma, The Netherlands)–Fab fragments of anti-human IgG (a-IgG) (Jacksons, UK), which follows the 1:1 interaction model function.⁵² Human IgG was spotted as previously described, ([B₁] = 500, [B₂] = 250, [B₃] = 125, [B₄] = 62.5, [B₅] = 31.2 and [B₆] = 0 µg/ml). An iSPR image is shown in Fig. 4a. Fig. 4b shows the measured SPR dips for all the 24 spots. The analyte (a-IgG) concentrations were [A₁] = 200, [A₂] = 100, [A₃] = 50, [A₄] = 25, [A₅] = 12.5, [A₆] = 6.25, [A₇] = 3.1 and [A₈] = 1.5 nM. Both association and dissociation profiles were measured for 1800 seconds in this case.

Data analysis

Data analysis was performed with the SPRint software (IBIS Technologies BV, Hengelo, The Netherlands) and kinetic parameter extraction was performed using Scrubber 2 (Biologic software, Australia).⁴⁶ All model functions are plotted in orange. The 1:1 interaction model was considered here for both the interactant pairs used in this paper. Global fit analyses were carried out for the conventional experiments whereas global fit analyses were carried out with the exception that R_m is estimated as a local fit for the single injection experiments is because of the varying ligand densities.

Results and discussions

Experiments of scenarios in Fig. 1b, 1c and 1d have been performed and model parameters representing binding affinity K_D and maximum response R_m were extracted using the 1:1 interaction model.

β2 microglobulin–monoclonal anti-β2 microglobulin

The conventional measurement profiles were observed for the ligand spot with concentration 250 µg/ml. The affinity K_D and R_m were extracted and listed in the first column of Table 2. The results of various β2M density spots were recorded simultaneously for the whole array. Representative sensorgrams from ligand spots 14 and 15 are shown in Fig. 2c. Since the ligand density varies from spot to spot, the measured responses can also vary with different analyte concentrations.

Table 2 Extracted K_D and R_m for different scenarios for β2M/Anti-β2M interactions. The K_D unit nM in all cases

Multi-analyte/Single-ligand (Fig. 1a/1b)	Multi-analyte/Multi-ligand (Fig. 1c)	Single-analyte/Multi-ligand (Fig. 1d)
	[B2]: KD = 1.48 ± 0.28
	R m = 66.4 ± 5.4 m°	[A1]: KD = 1.50 ± 0.60
	[B3]: KD = 1.21 ± 0.18	[A2]: KD = 1.57 ± 0.67
	R m = 52.6 ± 3.7 m°	[A3]: KD = 1.50 ± 0.66
K D = 1.48 ± 0.28	[B4]: KD = 1.37 ± 0.29	[A4]: KD = 1.61 ± 0.58
R m = 66.4 m°	R m = 12.8 ± 3.6 m°	[A5]: KD = 1.57 ± 0.53
	[B5]: KD = 1.43 ± 0.28	[A6]: KD = 1.29 ± 0.55
	R m = 5.9 ± 1.0 m°	[A7]: KD = 1.60 ± 0.64
	[B6]: KD = 1.49 ± 0.27	[A8]: KD = 1.57 ± 0.82
	R m = 1.6 ± 0.9 m°
Weighted average	K D = 1.36 ± 0.11	K D = 1.52 ± 0.22

---

Fig. 3 Single injection kinetics estimation of β2M/a-β2M: Sensorgram obtained for the injection single analyte concentration over five different ligand densities for creating the spots ((a) a-β2M: [A] = 36 nM (b) a-β2M: [A] = 72 nM). Residual plots are shown for the respective analyte concentrations.

The single injection measurement (Fig. 1d) was performed and example images and sensorgrams are shown in Fig. 3a and 3b, respectively. The affinity for each analyte concentration is listed in the third column of Table 2 (see Supporting information for more details†). The R_m values are not listed in the tables for the single injection kinetics approach as the different analyte concentrations have five different R_m values due to the five different ligand densities. It is also due to the well known fact that R_m is directly proportional to ligand densities and is an indirect way to quantify the ligand spots. The varying spacing between measured responses from ligand densities [B₂] and [B₃] in Fig. 3 is due to the lack of precise control of the spot concentration as recently described.⁵³ A certain ligand density is achieved by a timed exposure of the ligand with the surface; we use the term density rather than concentration to describe the final amount of ligand. The ligand densities are directly proportional to the extracted R_m values (see Supporting information for more details†). In Fig. 2 the values of the ligand density for creating the spots are given. The extracted affinities K_D are in good agreement among all three measurements shown here, as well as another recent report.⁵⁰

For the single injection measurement, it is important that the analyte concentration is large enough to ensure that the response signal-to-noise ratio is large enough to avoid measurement errors. Another important consideration for the single injection approach is that at least one injection of a known analyte concentration has to be done to calibrate the analyte/ligand behavior. If the affinity constant is known, then one can easily prepare the analyte close to the affinity constant. The obtained rate constants are shown in Table 4.

Human IgG–Fab fragments of anti-human IgG

The experiment with the second interactant pair (human IgG/a-IgG) was performed for the three measurement scenerios. Fig. 4c shows the recorded sensorgrams with ligand concentrations 250 and 500 µg/ml. The affinity K_D and R_m extracted with the conventional measurement are listed in the first column of Table 3.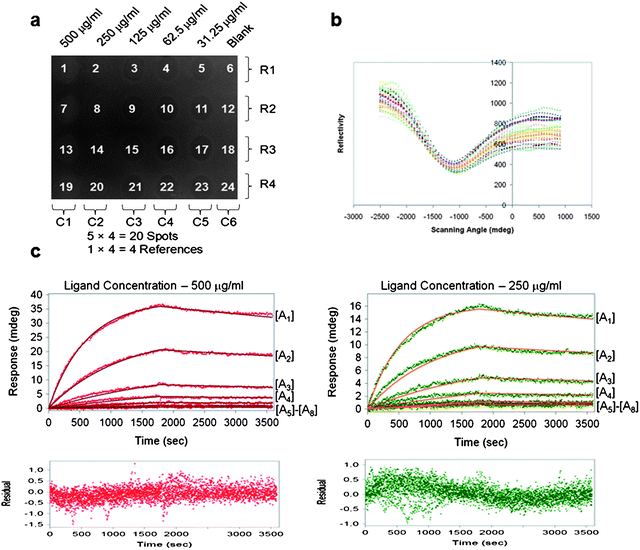

Fig. 4 (a) Real-time SPR image of multiple concentration hIgG ligand spots (b) SPR measurement dips for twenty-four ligand spots (c) Conventional kinetics estimation (1:1 model) of 500 µg/ml and 250 µg/ml ligand spots and multiple analyte concentrations. Residual plots shown for the respective ligand concentrations.

Table 3 Extracted K_D and R_m for different scenarios for hIgG/a-IgG interactions. The K_D unit is nM in all cases

Multi-analyte/Single-ligand (Fig. 1a/1b)	Multi-analyte/Multi-ligand (Fig. 1c)	Single-analyte/Multi-ligand (Fig. 1d)
	[B1]: KD = 12.6 ± 0.2
	R m = 43.8 m°	[A1]: -
	[B2]: KD = 12.0 ± 1.3	[A2]: -
	R m = 41.0 m°	[A3]: KD = 11.1 ± 3.2
K D = 12.0 ± 1.3	[B3]: KD = 13.0 ± 1.7	[A4]: KD = 10.0 ± 3.0
R m = 41.0 m°	R m = 2.6 m°	[A5]: KD = 12.6 ± 4.7
	[B4]: KD = 12.8 ± 3.8	[A6]: KD = 12.1 ± 1.7
	R m = 1.9 m°	[A7]: KD = 12.9 ± 0.8
	[B5]: KD = 12.3 ± 3.96	[A8]: KD = 12.3 ± 1.6
	R m = 0.8 m°
Weighted average	K D = 12.6 ± 0.2	K D = 12.5 ± 0.6

---

Since the affinity is approximately 12 nM, the lower analyte concentrations can be neglected. Also mass transport affected the high concentration ligand spots when the analyte concentration is very low, as well as the low concentration spots with a high analyte concentration (results not shown). The single injection measurement was performed and example images and sensorgrams are shown in Fig. 5a and 5b, respectively.

Fig. 5 Single injection kinetics estimation of hIgG/a-IgG interaction. Sensorgrams obtained for the injection single analyte concentration over five different ligand concentrations ((a) a-IgG: [A] = 100 nM (b) a-IgG: [A] = 200 nM). Residual plots shown for the respective analyte concentrations.

The affinity for each analyte concentration is listed in the third column of Table 3. The extracted affinities K_D are in good agreement among all three measurements. The estimated maximum response R_m shows a systematic decrease that is proportional to the reduced ligand densities (see Supporting information for more details†). The advantage of experimental time reduction and elimination of regeneration steps must be balanced with larger measurement errors when using the single injection approach as shown in Table 2 and 3 for the second scenario (Fig 1d). This is due to the fact that ligand immobilization is not well controlled with our present spotting technique, which is done offline and the immobilization is completely due to the diffusion of molecules from liquid droplets to the sensor surface over an incubation time. The obtained rate constants are shown in Table 4.

Table 4 Estimated kinetic parameters for both the model systems (β2M/Anti-β2M and hIgG/a-IgG) using conventional kinetics and single injection kinetics approaches. The number of sample points for the estimation of standard deviation is five (n = 8) for conventional approach and eight (n = 5) for single injection approach

Interactant pairs	Conventional kinetics		Single injection kinetics
	k a (M^−1 s^−1)	k d (s^−1)	k a (M^−1 s^−1)	k d (s^−1)
β2M/Anti-β2M	(1.31 ± 2.77) × 10^6	(2.47 ± 5.32) × 10^−3	(2.77 ± 4.36) × 10^6	(3.52 ± 5.64) × 10^−3
HIgG/a-IgG	(1.42 ± 0.69) × 10^4	(1.78 ± 0.88) × 10^−5	(1.88 ± 0.89) × 10^4	(1.72 ± 1.31) × 10^−4

---

For the conventional measurement, the analyte concentrations are highly controllable as demonstrated by the near equidistant sensor response curves (Fig. 2c). The number of sample points for each scenario is also different. In general, larger sample sizes (number of samples) result in higher accuracy parameter extraction compared to smaller sample sizes. Single injection kinetic estimations of multiple interactant pairs can reduce the time for kinetic experiments, as well as measurement costs as only a single sensor chip and single analyte injection are required.

The single injection approach can be extended to any number of target biological systems. As long as the ligand density is small and the analyte concentration is close to the real affinity of the biomolecules, this approach can be used. Considerations to mass transport limitations, rebinding effects, steric hindrance in hydrogels and other factors that may complicate the 1:1 binding model should be taken into account and low ligand densities are always the best to determine kinetic rate constants. The application of single injection kinetics over a microarray with multiple ligand densities can lead to fast kinetic parameter estimation of many samples from the same sensor surface. Certain aspects should be considered when designing such experiments, one of which is sample cross reactivity that can lead to inaccurate kinetic estimation.

Conclusion

The single injection kinetics estimation method was successfully demonstrated for two well known interactant pairs with the major advantage that a reduced amount of sample is used and that the binding affinities were extracted in a couple of minutes rather than in a couple of hours compared to the conventional method. Quantitative comparisons between the estimated binding affinities measured with the conventional method are β2M: K_D = 1.48 ± 0.28 nM and HIgG: K_D = 12.6 ± 0.2 nM and for the single injection method are β2M: K_D = 1.52 ± 0.22 nM and HIgG: K_D = 12.5 ± 0.6 nM, which are in good agreement in both cases. The extracted affinity constants in both cases were in good agreement with parameters described in literature as well as with the conventional measurement method. Since the demonstrated approach and extracted results are very promising, the general method could be very well implemented to other biomolecular systems without any method modifications.

Acknowledgements

The authors thank the Dutch Technology Foundation STW for financial support of the project titled “Multi-analyte food screening with microfluidic biochips.” The authors thank Hans de Boer for his extensive technical support.

References

1. E. M. Southern, J. Mol. Biol., 1975, 98, 503–517.
2. D. A. Kulesh, D. R. Clive, D. S. Zarlenga and J. J. Greene, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 8453–8457.
3. G. Macbeath and S. L. Schreiber, Science, 2000, 289, 1760–1763.
4. F. Yamauchi, K. Kato and H. Iwata, Biochim. Biophys. Acta, 2004, 1672, 138–147.
5. R. P. Ekins, Clin. Chem., 1998, 44, 2015–2030.
6. D. N. Gosalia and S. L. Diamond, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8721–8726.
7. M. Hoever and P. Zbinden, Drug Discovery Today, 2004, 9, 358–365.
8. J. Kononen, L. Bubendorf, A. Kallionimeni, M. Baerlund, P. Schrami, S. Leighton, J. Torhorst, M. J. Mihatsch, G. Sauter and O.-P. Kallionimeni, Nat. Med., 1998, 4, 844–847.
9. B. T. Houseman and M. Mrksich, Chem. Biol., 2002, 9, 443–454.
10. Y. Inoue, T. Mori, G. Yomanouchi, X. Han, T. Sonoda, T. Niidome and Y. Katayama, Anal. Biochem., 2008, 375, 147–149.
11. B. Rothenhaeusler and W. Knoll, Nature, 1988, 332, 615–617.
12. K. A. Marx, Biomacromolecules, 2003, 4, 1099–1120.
13. S. Ghaemmaghami, M. C. Fitzgerald and T. G. Oas, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8296–8301.
14. A. Petrov, V. Okhonin, M. Berezovski and S. N. Krylov, J. Am. Chem. Soc., 2005, 127, 17104–17110.
15. D. G. Myszka and R. L. Rich, Pharm. Sci. Technol. Today, 2000, 3, 310–317.
16. B. P. Nelson, T. E. Grimsrud, M. R. Liles, R. M. Goodman and R. M. Corn, Anal. Chem., 2001, 73, 1–7.
17. A. M. C. Lokate, J. B. Beusink, G. A. J. Besselink, G. J. M. Pruijn and R. B. M. Schasfoort, J. Am. Chem. Soc., 2007, 129, 14013–14018.
18. B. Cherif, A. Roget, C. L. Villiers, R. Calemczuk, V. Leroy, P. N. Marche, T. Livache and M. B. Villiers, Clin. Chem., 2006, 52, 255–262.
19. N. Bassil, E. Maillart, M. Canva, Y. Levy, M. C. Millot, S. Pissard, R. Narwa and M. Goossens, Sens. Actuators, B, 2003, 94, 313–323.
20. I. Mannelli, V. Courtois, P. Lecaruyer, G. Roger, M. C. Millot, M. Goossens and M. Canva, Sens. Actuators, B, 2006, 119, 583–591.
21. D. J. O'Shannessy, M. B. Burke, K. K. Soneson and P. Hensley, Anal. Biochem., 1993, 212, 457–468.
22. R. Karlsson and R. Stahlberg, Anal. Biochem., 1995, 228, 274–280.
23. P. Schuck, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 541–566.
24. R. Karlson, A. Michaelsson and L. Mattsson, J. Immunol. Methods, 1991, 145, 229–240.
25. A. J. T. George, J. L. Gallop and M. Rashid, Expert Opin. Ther. Pat., 1997, 7, 947–963.
26. E. Maillart, K. Brengel-Pesce, D. Capela, A. Roget, T. Livache, M. Canva, Y. Levy and T. Soussi, Oncogene, 2004, 23, 5543–5550.
27. M. Kyo, T. Yamamoto, H. Motohashi, T. Kamiya, T. Kuroita, T. Tanaka, J. D. Engel, B. Kawakami and M. Yamamoto, Genes Cells, 2004, 9, 153–164.
28. R. Baggio, G. J. Carven, A. Chiulli, M. Palmer, L. J. Stern and J. E. Arenas, J. Biol. Chem., 2005, 280, 4188–4194.
29. R. V. Olkhov, J. D. Fowke and A. M. Shaw, Anal. Biochem., 2009, 385, 234–241.
30. C. Boozer, G. Kim, S. Conh, H. W. Guan and T. Londergan, Curr. Opin. Biotechnol., 2006, 17, 400–405.
31. P. Saefsten, S. L. Klakamp, A. W. Drake, R. Karlsson and D. G. Myszka, Anal. Biochem., 2006, 353, 181–190.
32. G. J. Wegner, H. J. Lee and R. M. Corn, Anal. Chem., 2002, 74, 5161–5168.
33. E. A. Smith, W. D. Thomas, L. L. Kiessling and R. M. Corn, J. Am. Chem. Soc., 2003, 125, 6140–6148.
34. R. L. Rich, M. J. Cannon, J. Jenkins, P. Pandian, S. Sundaram, R. Magyar, J. Brockman, J. Lambert and D. G. Myszka, Anal. Biochem., 2008, 373, 112–120.
35. B. Hantusch, I. Schoell, C. Harwanegg, S. Krieger, W. M. Becker, S. Spitzauer, G. Boltz-Nitulescu and E. Jensen-Jarolim, Immunol. Lett., 2005, 97, 81–89.
36. G. D. Van Wiggeren, M. A. Bynum, J. P. Ertel, S. Jefferson, K. M. Robotti, E. P. Thrush, D. M. Baney and K. P. Killeen, Sens. Actuators, B, 2007, 127, 341–349.
37. D. Wassaf, G. Kuang, K. Kopacz, Q. L. Wu, Q. Nguyen, M. Toews, J. Cosic, J. Jacques, S. Wiltshire, J. Lambert, C. C. Pazmany, S. Hogan, R. C. Ladner, A. E. Nixon and D. J. Sexton, Anal. Biochem., 2006, 351, 241–253.
38. T. Bravman, V. Bronner, K. Lavie, A. Notcovich, G. A. Papalia and D. G. Myszka, Anal. Biochem., 2006, 358, 281–288.
39. G. Krishnamoorthy, E. T. Carlen, D. Kohlheyer, R. B. M. Schasfoort and A. van den Berg, Anal. Chem., 2009, 81, 1957–1963.
40. I. M. Chaiken, S. Rose and R. Karlsson, Anal. Biochem., 1992, 201, 197–210.
41. D. G. Myszka, Curr. Opin. Biotechnol., 1997, 8, 50–57.
42. M. B. Khalifa, L. Choulier, H. L. Jacob, D. Altschuh and T. Vernet, Anal. Biochem., 2001, 293, 194–203.
43. P. Schuck, Biophys. J., 1996, 70, 1230–1249.
44. D. G. Myszka, T. A. Morton, M. Doyle and I. M. Chaiken, Biophys. Chem., 1997, 64, 127–137.
45. R. W. Glaser, Anal. Biochem., 1993, 213, 152–161.
46. T. A. Morton, D. G. Myszka and I. M. Chaiken, Anal. Biochem., 1995, 227, 176–185.
47. L. Joss, T. A. Morton, M. L. Doyle and D. G. Myszka, Anal. Biochem., 1998, 261, 203–210.
48. R. Karlsson and A. Faelt, J. Immunol. Methods, 1997, 200, 121–133.
49. S. Baumann, P. Grob, F. Stuart, D. Pertlik, M. Ackermann and M. Suter, J. Immunol. Methods, 1998, 221, 95–106.
50. J. Svitel, H. Boukari, D. Van Ryk, R. C. Willson and P. Schuck, Biophys. J., 2007, 92, 1742–1758.
51. B. de Heij, M. Daub, O. Gutmann, R. Niekrawietz, H. Sandmaier and R. Zengerle, Anal. Bioanal. Chem., 2004, 378, 119–122.
52. G. A. Papalia, M. Baer, K. Luehrsen, H. Nordin, P. Flynn and D. G. Myszka, Anal. Biochem., 2006, 359, 112–119.
53. J. B. Beusink; Label-free biomolecular interaction sensing on microarrays using surface plasmon resonance imaging; PhD dissertation, University of Twente, 2009.
54. J. B. Beusink, A. M. C. Lokate, G. A. J. Besselink, G. J. M. Pruijn and R. B. M. Schasfoort, Biosens. Bioelectron., 2008, 23, 839–844.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary material showing detailed data analysis including Fig. S1, Fig. S2, Fig. S3 and Table S1. See DOI: 10.1039/b9ay00176j

---