Net analyte signal-based simultaneous determination of dyes in environmental samples using moving window partial least squares regression with UV-vis spectroscopy

Abstract

The multivariate calibration methods—moving window selection partial least squares regression (MWPLSR) and net analyte signal (NAS)—were employed for simultaneous determination of a mixture of C.I. Disperse Blue 183, C.I. Disperse Blue 79, C.I. Disperse Red 82, C.I. Disperse Red 65, C.I. Disperse Yellow 211 and C.I. Disperse Orange 25 by UV-vis spectrophotometry. The absorption spectra of the six disperse dyes were recorded between 320 and 680 nm. A modified changeable size moving window partial least squares (CSMWPLS) and searching combination moving window partial least squares (SCMWPLS) were proposed to search for an optimized spectral interval and an optimized combination of spectral regions from informative regions obtained by MWPLSR. Different wavelength regions were selected by taking into account different spectral parameters including the starting wavelength, the ending wavelength and wavelength interval. It was found that wavelength selection improved the performance of the corresponding net analyte signal-partial least squares (NAS-PLS) model, in terms of root mean square error (RMSE), compared with the results obtained using whole spectra or direct combination of informative regions for each dye. The importance of calibration design was also investigated by calculating the prediction and validation errors. The influence of using independent validation sets were emphasized. The proposed calibration method gave better results in combination and informative spectral regions for determination of the six disperse dyes without prior separation.

---

1. Introduction

Large quantities of azodyes have been widely used in a variety of products, such as textiles, paper, foodstuffs and leather.^1–3 The release of azodyes into the environment is a major problem for life and a threat to the environment. Many azodyes and their breakdown products are toxic and/or mutagenic to life.^4,5

Disperse azodyes have been continuously used in the textile industry.⁶ These dyes can be applied to synthetic fibres such as polyester, nylon, acetate, cellulose and acrylic.⁷ The concentration of disperse dyes could be in the µg/L level in waste water.² Therefore, a pre-concentration step will be necessary for better detection and quantification limits of disperse dyes.

Recently, determination of dyes in waste water has been performed successfully by high performance liquid chromatography (HPLC), liquid chromatography and mass spectrometry (LC-MS), capillary electrophoresis (CE), and gas chromatography and mass spectrometry (GC-MS).² However, chromatographic determination of dyes in a mixture takes much more time and also a prior separation is needed because of spectral and chromatographic overlapping with matrix components. Therefore, UV-vis spectrophotometric determination is preferred to chromatographic techniques since it is possible to obtain high accuracy and reproducibility in complex matrices.

Multivariate calibration methods such as principal component regression (PCR) and partial least squares (PLS) have been applied to overlapping spectra and chromatograms successfully.^8–11 These methods offer an advantage of speed in the determination of components of matrices, because sample preparation is eliminated or minimized and a preliminary separation step in complex matrices is avoided.^12,13 PLS and PCR cover a full spectral region for calculating a calibration model and the use of the whole spectral region does not yield optimal results. Thus, a wavelength selection method is still important and necessary for quantifying highly complicated samples. A new method of spectral interval selection called moving window partial least squares regression (MWPLSR) has been proposed for solving problems to improve quality of model.^14–16 The advantage of applying MWPLSR is to search for informative spectral regions for the multi-component overlapped spectral analysis. MWPLSR develops PLS calibration models in every window that moves over the whole spectral region and then informative regions, in terms of the least complexity of PLS models reaching the calculated lowest sum of residuals, are located. Although MWPLSR is a powerful method in selecting informative regions, each informative region obtained by MWPLSR does not supply the best predictive results and these regions may be unsatisfactory for obtaining the optimum results. When complicated samples such as environmental matrices were analyzed, one informative region may contain several other regions because of the significant interferences. A combination of informative regions can be used to overcome interference problems to collect more useful information from the spectra for improving the prediction ability of a PLS model. Each informative region is optimized with the combination of separate best windows in the whole spectral region. Searching for an optimized sub-region for each selected informative region and the optimized combination of informative regions by changeable size moving window partial least squares (CSMWPLS) and searching combination moving window partial least squares (SCMWPLS) methods have been applied in literature.^14,17,18 The CSMWPLS procedure changes the window size and moves the window over a selected informative region with each window size. The SCMWPLS aims at looking for an optimized combination of informative regions by performing the CSMWPLS procedure for every informative region step by step.

Recently, comparative studies about advantages and limitations of net-analyte signal (NAS) based methods and PLS calibration in mixture analysis have been performed.^19,20 The use of signal filtering algorithms such as NAS may help simplify calibration models and construct models with an adequate predictive ability. NAS calibration method, previously described by Lorber,²¹ has been used for the reduction of noise (i.e., to isolate the analyte signal) and describing the part of a spectrum that the model relates to the predicted quantity. A part of mixture spectra is directly related to the concentration of analyte. The NAS vector was calculated and used in the corresponding PLS model to predict the unknown concentration for informative and combination spectral regions in our data.

In the present work, MWPLSR and NAS multivariate calibration methods were applied to the simultaneous determination of C.I. Disperse Blue 183, C.I. Disperse Blue 79, C.I. Disperse Red 82, C.I. Disperse Red 65, C.I. Disperse Yellow 211, and C.I. Disperse Orange 25 by UV-vis spectrophotometry. The absorption spectra of the six disperse dyes were recorded between 320 and 680 nm and the best informative wavelength regions were selected by MWPLSR for each dye separately. A modified changeable size moving window and searching combination moving window wavelength selection strategies were employed to enhance the predictions of multivariate calibration methods, and to investigate the effect of wavelength selection on the performance of the NAS-PLS method. Root means square errors were calculated for each dye as comparison criteria. To see how well the calibration set predicts the concentration of six dyes; two independent validation sets were generated. It was found out that NAS-PLS, MWPLSR and the known validation set results were compatible. The results also demonstrate that MWPLSR and NAS multivariate calibration methods can be applied successfully to a highly complex mixture of samples.

2. Theoretical background

2.1 Moving window partial least squares regression (MWPLSR)

MWPLSR is a wavelength interval selection method to search for informative spectral regions for the multi-component overlapped spectral analysis. MWPLSR is applied to these informative regions through spectra for optimizing and exploring the best optimized informative regions as either an individual region or combination of the informative regions.^16,22

PLS is an extension of the multiple linear regression model. In its simplest form, a linear model specifies the relationship between the spectra in the window (X), and the concentrations of an analyte (c), so that;

c = Xb + e (1)

where X is an m × n matrix collecting mspectra in rows; including n spectral points, c is an m × 1 vector of concentration of analytes (m: the number of analytes, n: wavelength points), e is the error vector associated with c, b is the regression coefficient.

In this study, an informative spectral window starting at the ith spectral channel and ending at the (i + h− 1)th spectral channel was constructed. The fixed window size, h, is selected as 7 through the spectral region (Fig. 1). The window was moved over the whole spectral region between 320 and 680 nm. For every window, a PLS model with a selected PLS component using cross-validation was constructed and the model was evaluated by the root mean square error (RMSE). Through this process, the informative regions having peak-like shapes with a low value of the RMSE can easily be found.

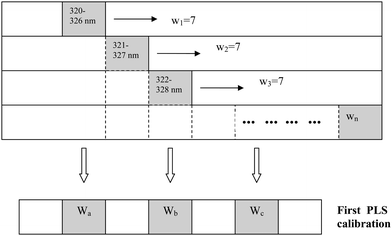Fig. 1 Scheme for explanation of MWPLSR.

2.2 Searching combination moving window partial least squares (SCMWPLS)

SCMWPLS was used for searching the optimized combinations of informative regions based on the optimized informative regions.^15,18 The first informative region obtained by MWPLSR was optimized by changing the moving window size from 1 to p for a given informative region with p spectral points. For every sub-region the window was moved from the first spectral point to the (p − w + 1)th point over the region. The sub-region with the smallest value of RMSE was considered as the optimized spectral interval which can be found by CSMWPLS.¹⁴ Although these sub-regions are optimum in their corresponding region, they cannot show an optimum performance. Therefore it is necessary to develop a method to search for the optimized combination of informative regions. The sub-regions with the same number of PLS components in successive windows were combined to search second optimum sub-regions at different wavelength intervals. The window was moved step by step in these first combined spectral regions to search for the second optimum region as illustrated in Fig. 2. Finally, the optimum spectral regions were obtained by combining each window with the smallest RMSE (W_a, W_b, W_c…) of second optimum informative regions. A new PLS model with a selected PLS component was constructed, and RMSE was calculated for every window and combination. The region with the smallest value of RMSE was considered as the final optimized spectral interval.

Fig. 2 Scheme for explanation of SCMWPLS.

In SCMWPLS, the region with the smallest RMSE was always selected as the base-region. A rational base-region selected should construct such a PLS model that the RMSE of the model is expected to reach an acceptable error level with a relatively small number of PLS components. Therefore, a maximum number of PLS component is constrained in this algorithm to avoid selecting the smallest RMSE with a relatively high number of PLS components; i.e., the selected number of PLS components by cross validation must not be larger than the maximum number of PLS components. The number of PLS components was determined to be the number where the RMSE begins to decrease insignificantly with the increase of PLS components. This number of PLS components was considered to be the maximum PLS component number.

2.3 Net analyte signal calculations (NAS)

The NAS was described by Lorber²¹ for an analyte, k, in a given mixture as part of its spectrum, which is related to the analyte and orthogonal to the interferents. The NAS in the most general scenario is then calculated by projecting spectrumr onto the space defined by the interferents (X_-k), the NAS being the orthogonal resultant (r*), which is defined as

r* = [I − X^T_−k (X^T_−k) ⁺ ]r (2)

X data matrix is split into two containing spectral information pertaining to the analyte k, X_k, and to all other variability sources, X_−k, including the contribution of the interferents (X = X_k + X_−k) by the NAS algorithm.

Different algorithms have been proposed for NAS calculations.^13,23–31 In this work, we used the NAS algorithm in order to obtain the NAS for multivariate calibration. The methodology for NAS calculation proposed was depicted in Fig. 3. In the proposed procedure, first matrix X_A was calculated by reconstructing from A principal components with standardizing of the original data. Second, the NAS vectors were calculated according to Lorber et al.²¹ Then the calculated NAS vectors and concentration values (Y) were used for the PLS calibration. The spectra for the prediction samples were centered by subtracting the average spectrum for the calibration samples and reconstructed from A principal components. Later, the NAS vectors of prediction samples were calculated and used in the PLS model for prediction of unknown concentration.

Fig. 3 Scheme of the methodology for NAS calculation.

3. Experimental

3.1 Reagents and sample preparation

Six disperse dyes including C.I. Disperse Blue 183, C.I. Disperse Blue 79, C.I. Disperse Red 82, C.I. Disperse Red 65, C.I. Disperse Yellow 211 and C.I. Disperse Orange 25 obtained from Setas Company (Turkey) were used in this study. The dye solutions were prepared in double distilled water (Millipore Waters Milli Q distillation unit). Aliquots of the stock solutions were added into 25 mL calibrated flasks to obtain concentrations between 1.806 and 9.03 mg L⁻¹ of C.I. Disperse Blue 183, 1.526 and 7.63 mg L⁻¹ of C.I. Disperse Blue 79, 1.674 and 8.37 mg L⁻¹ of C.I. Disperse Red 82, 0.884 and 4.42 mg L⁻¹ of C.I. Disperse Red 65, 1.075 and 5.375 mg L⁻¹ of C.I. Disperse Orange 25 and 1.092 and 5.46 mg L⁻¹ of C.I. Disperse Yellow 211 for the calibration design matrix.

3.2 UV-vis spectroscopy

The absorption spectra were recorded between 200 and 800 nm, employing a double beam UV-vis spectrometer (Shimadzu, model UV-1601) equipped with 10 mm quartz cuvettes. The digital resolution of the spectra was in 1 nm. The spectral region between 320 and 680 nm was selected for the calculations of MWPLSR and NAS. MWPLSR and NAS analysis were calculated with programs written in MATLAB (v. 6.5 for windows).

3.3 Calibration set

A calibration design set for 25 samples was used based on five levels, which was coded between −2 and +2 for each compound in the mixture. The levels relate to the concentrations of compounds. The same calibration design was used with our previous study.² Concentration of the calibration set solutions was prepared within the linear range of the calibration graph. The design has a value of r₁₂ = 0.0, so the two concentration vectors are orthogonal to one another.³² The difference vector [1320] and cyclical generator −2, −1, 2, 1 were used in the calibration design matrix. The construction of multilevel calibration designs has been described in other literature.³³

3.4 Validation set

To see how well the calibration set predicts the concentrations of six dyes, two independent validation sets were generated containing surfactant agent to obtain the same matrix components with real sample. The validation set 1 has a value of r₁₂ = 1.0 and the validation set 2 has a value of r₁₂ = 0.0.² The two validation sets consist of 25 spectra. The spectral region between 320 and 680 nm was selected as optimum for the analysis, which implies it will work for 361 experimental points for each spectrum.

3.5 Real sample

The real samples in this study were collected from waste water of a dyeing process containing six disperse dyes. The disperse dyeing procedure was applied in a lab-scale LabDye HT (High Temperature) dyeing machine. The dye-bath (150 ml) contains disperse dye and anionic-nonionic surfactant (Bestol 11A) as the dye-leveling agent. A 10:1 liquid ratio using 15 g polyester fabric was used and 1 ml of surfactant agent was added to each dye-bath. Polyester fabric was immersed in the dye-bath at 60 °C, the temperature was raised from 60 °C to 130 °C. Dyeing was continued for 50 min at 130 °C, the temperature was then reduced to 70 °C. The dyes in waste water were measured spectrophotometrically over the range of 320–680 nm. The concentrations of each dye were determined by a univariate calibration method as 10.91 mg L⁻¹ for C.I. Disperse Blue 183, 16.15 mg L⁻¹ for C.I. Disperse Blue 79, 191.90 mg L⁻¹ for C.I. Disperse Red 82, 21.2 mg L⁻¹ for C.I. Disperse Red 65, 207.67 mg L⁻¹ for C.I. Disperse Orange 25, and 23.5 mg L⁻¹ for C.I. Disperse Yellow 211. Real samples were prepared from those waste waters between 0.5 and 2.5 mg L⁻¹ of C.I. Disperse Blue 183, C.I. Disperse Blue 79, C.I. Disperse Red 65, C.I. Disperse Yellow 211, 2 and 6 mg L⁻¹ of C.I. Disperse Red 82 and C.I. Disperse Orange 25 for NAS analysis as the validation set 1 which has a value of r₁₂ = 1.0.

4. Results and discussion

4.1 MWPLSR analysis

UV-vis spectra for the standard dyes shown in Fig. 4 were recorded in the range 320–680 nm. The spectra are dominated by two broad absorption bands when the UV-vis spectra of six disperse dyes with various concentrations were recorded. In those spectra, concentration-dependent absorbance variations are very small. Therefore, the whole spectral region from 320 to 680 nm was used to find the informative regions by MWPLSR. In the first step, the informative regions that show the smallest error were selected by MWPLSR (Fig. 1). In the second step, another new sub region was selected to search second informative and combination regions from each window in the first step (Fig. 2).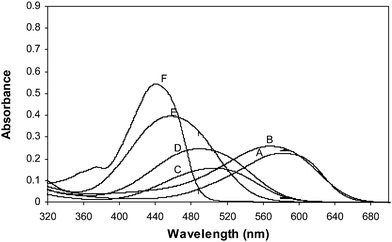

Fig. 4 UV-vis spectra of six disperse dyes (A; C.I. Disperse Blue 183 (10 mg L⁻¹), B; C.I. Disperse Blue 79 (10 mg L⁻¹), C; C.I. Disperse Red 82 (5 mg L⁻¹), D; C.I. Disperse Red 65 (5 mg L⁻¹), E; C.I. Disperse Orange 25 (10 mg L⁻¹) and F; C.I. Disperse Yellow 211 (10 mg L⁻¹).

The informative regions by the first step obtained by MWPLSR for C.I. Disperse Blue 183, C.I. Disperse Blue 79, C.I. Disperse Red 82, C.I. Disperse Red 65, C.I. Disperse Yellow 211 and C.I. Disperse Orange 25 are shown in Fig. 5–6. Informative regions in the 455–468, 470–484 and 546–567 nm for C.I. Disperse Blue 183; 425–450, 542–557, 576–609 and 618–649 nm for C.I. Disperse Blue 79; 539–587 nm for C.I. Disperse Red 82; 491–515, 534–568 and 573–585 nm for C.I. Disperse Red 65; 320–436 and 431–451 nm for C.I. Disperse Orange 25; 494–517 nm for C.I. Disperse Yellow 211 regions can be provided by MWPLSR. It is clearly shown in Fig. 5–6 that informative regions obtained well as in C.I. Disperse Blue 79 are in accordance with absorption bands of each of the disperse dyes. The minimum RMSE values were obtained at the maximum absorbance regions of C.I. Disperse Blue 79. This indicates that informative regions have no interference by other dyes in the mixtures. A clear informative region of 576–609 nm (Fig. 5b) was observed for C.I. Disperse Blue 79, which can easily be attributed to the absorption band in the same region. The absorption band in the visible region located at 580 nm is due to the azo linkage of C.I. Disperse Blue 79.

Fig. 5 Selection of informative regions obtained by the first step of MWPLSR for (a) C.I. Disperse Blue 183, (b) C.I. Disperse Blue 79, (c) C.I. Disperse Red 82.

Fig. 6 Selection of informative regions obtained by the first step of MWPLSR for (a) C.I. Disperse Red 65, (b) C.I. Orange 25, (c) C.I. Disperse Yellow 211.

4.2 SCMWPLS analysis

The SCMWPLS algorithm was performed to search for the optimized combinations of the informative regions. All these informative regions by the second step and the whole region were used to obtain optimum informative regions for PLS models with the calibration set by increasing the window size step by step, and then two validation sets including 25 samples were used to validate the performance of the models. CSMWPLS finds the optimized sub-regions of informative regions, which can improve the predictions of the PLS models. The two independent validation sets were generated with values of r₁₂ at 0.0 and 1.0 to see how well the calibration set predicts the concentrations of the six dyes. Leave-one out cross-validation procedure was used to select the optimum number of PLS components for each dye and the number of factors that produced the least RMSE was selected as the optimum value.^14,17 The selected PLS components and optimum RMSEs of the predictions by PLS calibration methods for a calibration set and two validation sets are listed in Tables 1–6 (See ESI † ). The validation sets show similar results with small RMSEs. This indicates that any of the validation sets with r₁₂ = 0.0 and r₁₂ = 1.0 can be used to validate the calibration models built for the prediction of dyes in complex mixtures. Optimum spectral regions are different for each dye in terms of the number of spectral regions, RMSE and the number of PLS components.

C.I. Disperse Blue 183 has three optimum informative regions suggested by CSMWPLS, one direct combination of these regions selected by SCMWPLS and a whole region as listed in Table 1 (See ESI † ). It is clear that the best individual region with the lowest RMSE values are 0.095, 0.601 and 0.567 for calibration and validation sets respectively with six PLS components located in the combination region. The optimized combination improves the prediction results by using the SCMWPLS. In spectroscopic data, it is expected to get the same components as compounds present in the mixture in the case of non-highly overlapped spectra in reality when standards are used during the calibration step. The results confirm that the calibration was well modeled by the number of components selected during the validation. The optimum informative region in the 546–567 nm shows higher RMSE error than the other two regions in the calibration set with three PLS components due to the higher interference of C.I. Disperse Blue 79. However, better validation errors were obtained in this region and this indicates that the performance of the prediction was better even in the case of more overlapped spectra.

For the second disperse dye, C.I. Disperse Blue 79 (Table 2, See ESI † ), four optimum informative regions and one combination region were found by CSMWPLS and SCMWPLS. The optimum informative regions in the 542–557 and 576–589 nm show the smallest RMSE errors than other optimum informative regions for calibration set, and better prediction was obtained in the 542–557 nm for two validation sets. The lowest error was obtained for the combination region selected by SCMWPLS. On the other hand the number of PLS components is three for all four optimum informative regions, but for combination regions the number of PLS components is six. It is clear that the informative region in the 576–589 nm and combination region in the 320–648 nm are the most optimum informative regions selected by CSMWPLS and SCMWPLS for C.I. Disperse Blue 79. On the contrary to our previous study,² higher RMSE was obtained for C.I. Disperse Blue 79 by conventional PLS calibration due to the narrow spectral region used in this study. It is possible that information was spread on the whole spectral range and a variable selection per interval could automatically reduce the information and induce an increase of RMSE compared with full-spectrum PLS.³⁴

C.I. Disperse Red 82, C.I. Disperse Orange 25 and C.I. Disperse Yellow 211 exhibit different behavior to other dyes in that they have only one optimum informative region by the second step obtained by SCMWPLS (Tables 3, 5, 6, see ESI † ), and also each optimum informative region of these disperse dyes can provide better prediction errors than the whole spectral region. The number of PLS components for C.I. Disperse Orange 25 and C.I. Disperse Yellow 211 are five for optimum informative region, but it is seven for C.I. Disperse Red 82. The reason for this might be that the spectral points are highly overlapped. C.I. Disperse Orange 25 has the lowest RMSE in the informative region of 431–451 nm which can be attributed to the absorption bands in the same region (Fig. 6b). C.I. Disperse Red 82 and C.I. Disperse Yellow 211 have maximum absorption bands in the 476–523 nm (Fig. 5c) and 413–448 nm (Fig. 6c) regions respectively. However, these compounds are highly overlapped in these regions, so that the corresponding information regions show high RMSE values.

C.I. Disperse Red 65 also shows three optimum informative regions and one combination region as in C.I. Disperse Blue 183. Optimum informative, combination regions and the number of PLS components were illustrated in Table 4 (See ESI † ). The combination region suggested by SCMWPLS is the most optimum informative region because the model, including this individual region, provides the smallest RMSE errors and the number of PLS components was higher than the three regions. Models including the two individual regions in the 491–498 and 534–546 nm ranges, respectively, show high RMSE errors due to the more overlapping points between these wavelengths. The informative region in the 573–585 nm range demonstrates better PLS model building since better calibration and validation errors were obtained in this region. On the other hand the informative region in the 491–515 nm range show the maximum absorption bands in the same region which has the second lowest RMSE (Fig. 6a). It is clear that SCMWPLS can decrease the prediction error of the PLS model significantly (Table 4, see ESI † ). If more than one informative region is available, a combination of regions may be more important.

The comparisons of prediction and validation results of six dyes in environmental mixtures clearly demonstrates the potential of SCMWPLS. All these SCMWPLS results, as also proved in literature,^14,15 provide the best prediction results for the PLS calibrations of C.I. Disperse Blue 183, C.I. Disperse Blue 79, C.I. Disperse Red 82, C.I. Disperse Red 65, C.I. Disperse Yellow 211 and C.I. Disperse Orange 25 in highly overlapped spectra of mixtures.

4.3 NAS analysis

The NAS calibration method has been used for reduction of noise and describing the part of a spectrum that the model relates to the predicted quantity of the compounds in the mixture.¹⁶ The NAS pretreatment was applied to standardized data reconstructed from PCA. The calculated NAS vector for the validation samples following standardization and reconstruction of their spectra from principal components was used to estimate the corresponding analyte concentrations by PLS. Tables 1–6 (see ESI † ) show the RMSEs for the prediction of concentration of each dye after NAS treatment.

As can be seen from Tables 1–6 (see ESI † ), the prediction results of validation set 1 provided by the model were very similar to validation set 2 as obtained in CSMWPLS. The RMSEs calculated by CSMWPLS in the optimum informative regions 455–468, 470–481 and 546–567 nm were smaller than the RMSEs calculated by NAS-PLS for validation sets, whereas the RMSE calculated by SCMWPLS in the region of 320–567 nm was higher than the RMSE calculated by NAS-PLS for calibration and validation sets (Table 1, see ESI † ). It is clear that the optimum region was obtained by SCMWPLS for C.I. Disperse Blue 183 for NAS-PLS. However, only the RMSE error calculated by NAS-PLS in the informative region of 425–445 nm was higher than the RMSEs calculated by CSMWPLS for validation sets (Table 2, see ESI † ). The RMSEs of the other optimum informative regions by CSMWPLS for C.I. Disperse Blue 79 were higher than the RMSEs calculated by NAS-PLS. The results are as expected when NAS pretreatment was applied to informative regions.

The RMSEs results obtained by NAS-PLS for C.I. Disperse Red 82, C.I. Disperse Orange 25, C.I. Disperse Yellow 211 in informative regions and C.I. Disperse Red 65 including combination region were smaller than the RMSEs by CSMWPLS (Table 3,5,6, see ESI † ). C.I. Disperse Red 65 only has combination region among these dyes (Table 4, see ESI † ). The number of PLS components is 7, 5, 5 and 5 for C.I. Disperse Red 82, C.I. Disperse Orange 25, C.I. Disperse Yellow 211 and C.I. Disperse Red 65, respectively. Smaller RMSE was obtained for C.I. Disperse Red 82, which has 7 PLS components.

As a result, the combination regions for C.I. Disperse Blue 183, C.I. Disperse Blue 79 and C.I. Disperse Red 65, the informative regions in the 539–582 nm for C.I. Disperse Red 82, 320–390 nm for C.I. Disperse Orange 25 and 494–517 nm for C.I. Disperse Yellow 211 were found to be the most optimum informative region by NAS-PLS. The prediction capability of the NAS-PLS was proven when compared with PLS prediction in the case of whole spectral region. In order to evaluate whether there are significant differences between the concentrations found for each dye and each calibration method, the F-test (at the 95% confidence level) was employed to compare the RMSE values. The results showed no significant (F_0.95 < F_crit) differences with any of the calibration methods for C.I. Disperse Blue 183 and C.I. Disperse Red 65 determination. However, NAS-PLS method was much better for predicting the concentrations of C.I. Disperse Blue 183 and C.I. Disperse Red 65 in the calibration and validation sets. For the rest of the dyes, there were significant differences between NAS-PLS and conventional PLS calibration methods. Since the NAS-PLS method gave the lowest RMSE values, this was the method that adopted for predicting dye concentrations in real samples.

4.4. Determination of dyes in real samples

In order to test the applicability of the proposed method to the analysis of real samples, the method was applied to a waste water containing six disperse dyes obtained as described in Section 3.2. The determination of disperse dyes in textile waste water was investigated and the results were summarized in Table 7 (see ESI † ). In spite of the complexity of the sample matrix, the employed NAS-PLS method gave acceptable results except for C.I. Disperse Red 82. It must be emphasized that the high and low predictions obtained by NAS-PLS and univariate calibration for C.I. Disperse Red 82 in waste water are quite reasonable taking into account the high spectral overlap with other dyes and the lower multivariate sensitivity and selectivity. To validate the proposed NAS-PLS calibration method, the dyes that are present in the real sample were analyzed by univariate calibration methodology. The univariate calibration method gave similar results with NAS-PLS in combination with the spectral region. However, lower results were obtained for C.I. Disperse Red 82 and C.I. Disperse Orange 25 dyes which have only one informative region. The superiority of the NAS-PLS method is expected because the informative regions were used in multivariate calibration, while in the univariate method, dyes were determined using single wavelength. Therefore, the proposed method could be used for the quantification of dyes in waste water. The dyes that are present in waste water were analyzed by HPLC methodology to validate the conventional PLS method in our previous study.² The HPLC method has higher sensitivity and selectivity, while in UV-vis spectrophotometry the dyes were determined without separation from the sample matrix. Compared to HPLC method, the proposed NAS-PLS method was rapid, easy and of low cost for the quantification of disperse dyes in waste water using simple UV-vis spectrophotometry.

5. Conclusion

The importance of selecting informative and optimum spectral regions by MWPLSR and SCMWPLS in NAS-PLS calibrations using real samples was demonstrated. Different spectral ranges depending on the complexity of the spectra can be used to construct PLS calibration and validation models. The prediction ability of the calibration models using selective and whole spectral regions was evaluated. SCMWPLS significantly improved the NAS-PLS models compared to the models based on the whole spectral region.

Experimental design and the nature of the validation sets play an important role when assessing the quality of calibration models. Two experimental design sets with r₁₂ = 0.0 and r₁₂ = 1.0 in validation of the PLS model gave similar low errors as 0.429 and 0.414, respectively. It was shown that any of the validation sets can be used to see how well the calibration set predicts the concentrations of each of the compounds in the mixture. Comparing the results obtained by using the whole spectral region, optimum informative and combination regions for compounds, NAS improves the prediction ability in terms of corresponding PLS calibration. The PLS models yield better prediction results by using the NAS pretreated spectra in the combination region rather then informative and whole spectral regions. The present study has demonstrated that SCMWPLS can select optimum combination of informative regions successfully, even for highly overlapped spectra mixtures and NAS-PLS can improve the performance of PLS calibration models for quantitative determination of components in complicated environmental samples.

References

1. M. Fuh and K. Chia, Talanta, 2002, 56, 663–671.
2. S. Şahin, C. Demir and Ş. Güçer, Dyes Pigm., 2007, 73, 368–376.
3. S. Bilgi and C. Demir, Dyes Pigm., 2005, 66, 69–76.
4. R. L. Cisneros, A. G. Espinoza and M. I. Litter, Chemosphere, 2002, 48, 393–399.
5. A. Rehorek, K. Urbig, R. Meurer, C. Schäfer, A. Plum and G. Braun, J. Chromatogr., A, 2002, 949, 263–268.
6. M. Neamtu, A. Yediler, I. Siminiceanu, M. Macoveanu and A. Kettrup, Dyes Pigm., 2004, 60, 61–68.
7. A. Akbari, J. C. Remigy and P. Aptel, Chem. Eng. Process., 2002, 41, 601–609.
8. C. Demir and R. G. Brereton, Analyst, 1998, 123, 181–189.
9. P. Geladi and B. R. Kowalski, Anal. Chim. Acta, 1986, 185, 1–17.
10. R. G. Brereton, Analyst, 2000, 125, 2125–2154.
11. S. Wold, M. Sjöströma and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109–130.
12. A. Espinosa-Mansilla, I. Durán Merás, M. José Rodríguez Gómez, A. Muñoz de la Peña and F. Salinas, Talanta, 2002, 58, 255–263.
13. B. Hemmateenejad, R. Ghavami, R. Miri and M. Shamsipur, Talanta, 2006, 68, 1222–1229.
14. Y. P. Du, Y. Z. Liang, J. H. Jiang, R. J. Berry and Y. Ozaki, Anal. Chim. Acta, 2004, 501, 183–191.
15. S. Kasemsumran, Y. P. Du, K. Murayama, M. Huehne and Y. Ozaki, Anal. Chim. Acta, 2004, 512, 223–230.
16. J. Jiang, R. J. Berry, H. W. Siesler and Y. Ozaki, Anal. Chem., 2002, 74, 3555–3565.
17. B. Hemmateenejad, M. Akhond and F. Samari, Spectrochim. Acta, Part A, 2007, 67, 958–965.
18. S. Kasemsumran, Y. P. Du, K. Maruo and Y. Ozaki, Anal. Chim. Acta, 2004, 526, 193–202.
19. A. Muñoz de la Peña, A. E. Mansilla, M. I. A. A. Valenzuela, H. C. Goicoechea and A. C. Olivieri, Anal. Chim. Acta, 2002, 463, 75–88.
20. M. Blanco, M. Castillo, A. Peinado and R. Beneyto, Anal. Chim. Acta, 2007, 581, 318–323.
21. A. Lorber, Anal. Chem., 1986, 58, 1167–1172.
22. N. Kang, S. Kasemsumran, Y. Woo, H. Kim and Y. Ozaki, Chemom. Intell. Lab. Syst., 2006, 82, 90–96.
23. N. M. Faber, Anal. Chem., 1999, 71, 557–565.
24. N. M. Faber, J. Ferré, R. Boqué and J. H. Kalivas, TrAC, Trends Anal. Chem., 2003, 22, 352–361.
25. N. M. Faber, Anal. Chem., 1998, 70, 5108–5110.
26. A. Lorber, K. Faber and B. R. Kowalski, Anal. Chem., 1997, 69, 1620–1626.
27. K. Faber, A. Lorber and B. R. Kowalski, J. Chemom., 1997, 11, 419–461.
28. J. T. Olesberg, M. A. Arnold, B. Shih-Yao, B. Shih-Yao Hu and J. M. Wiencek, Anal. Chem., 2000, 72, 4985–4990.
29. L. Xu and I. Schechter, Anal. Chem., 1997, 69, 3722–3730.
30. H. C. Goicoechea and A. C. Olivieri, Chemom. Intell. Lab. Syst., 2001, 56, 73–81.
31. N. R. Marsili, M. S. Sobrero and H. C. Goicoechea, Anal. Bioanal. Chem., 2003, 376, 126–133.
32. K. D. Zissis, R. G. Brereton and R. Escott, Analyst, 1998, 123, 1165–1173.
33. R. G. Brereton, Analyst, 1997, 122, 1521–1529.
34. L. C. M. Pataca, W. B. Neto, M. C. Marcucci and R. J. Poppi, Talanta, 2007, 71, 1926–1931.

---

Footnote

† Electronic supplementary information (ESI) available: Tables 1–6 show the selected PLS components and optimum RMSEs of the predictions by PLS calibration methods for a calibration set and two validation sets for each of the six dyes. Table 7 summarizes the calibration results. See DOI: 10.1039/b9ay00009g

---