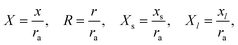DOI:
10.1039/B815256J
(Paper)
Analyst, 2009,
134, 148-158
Electrochemical ion transfer across liquid/liquid interfaces confined within solid-state micropore arrays – simulations and experiments
Received
2nd September 2008
, Accepted 17th October 2008
First published on 20th November 2008
Abstract
Miniaturised liquid/liquid interfaces provide benefits for bioanalytical detection with electrochemical methods. In this work, microporous silicon membranes which can be used for interface miniaturisation were characterized by simulations and experiments. The microporous membranes possessed hexagonal arrays of pores with radii between 10 and 25 µm, a pore depth of 100 µm and pore centre-to-centre separations between 99 and 986 µm. Cyclic voltammetry was used to monitor ion transfer across arrays of micro-interfaces between two immiscible electrolyte solutions (µITIES) formed at these membranes, with the organic phase present as an organogel. The results were compared to computational simulations taking into account mass transport by diffusion and encompassing diffusion to recessed interfaces and overlapped diffusion zones. The simulation and experimental data were both consistent with the situation where the location of the liquid/liquid (l/l) interface was on the aqueous side of the silicon membrane and the pores were filled with the organic phase. While the current for the forward potential scan (transfer of the ion from the aqueous phase to the organic phase) was strongly dependent on the location of the l/l interface, the current peak during the reverse scan (transfer of the ion from the organic phase to the aqueous phase) was influenced by the ratio of the transferring ion's diffusion coefficients in both phases. The diffusion coefficient of the transferring ion in the gelified organic phase was ca. nine times smaller than in the aqueous phase. Asymmetric cyclic voltammogram shapes were caused by the combined effect of non-symmetrical diffusion (spherical and linear) and by the inequality of the diffusion coefficient in both phases. Overlapping diffusion zones were responsible for the observation of current peaks instead of steady-state currents during the forward scan. The characterisation of the diffusion behaviour is an important requirement for application of these silicon membranes in electroanalytical chemistry.
Introduction
The application of electrochemical methods at the interface between two immiscible electrolyte solutions (ITIES) allows the detection and determination of various ion species, ranging from inorganic ions1,2 through organic compounds3 to biochemical substances.4–7 The main advantages of electrochemistry at the ITIES in analytical detection terms is that ionic substances may be detected in a label-free manner even if their oxidation/reduction is difficult.8
Just as the introduction of micron-sized solid electrodes (ultra-microelectrodes) led to major progress in electroanalytical chemistry9 important additional advantages for the ITIES may be obtained by replacing large interfaces with micron-scaled interfaces (µITIES). Decreasing the size of the ITIES results in smaller currents and therefore reduces the Ohmic potential drop in the resistive organic phase, which is important for reliable kinetic measurements. Furthermore, the enhanced mass transfer to micron-sized interfaces enables measurements of large interfacial transfer rates. For the development of analytical applications of electrochemistry at the ITIES, the availability of well-defined and reproducible steady-state currents at µITIES provides enhanced detection signals (current densities), as well as bringing about the miniaturisation of µITIES-based integrated electrochemical sensor devices. These are the main reasons for the effort to develop, characterize and apply electrochemical systems based on µITIES in recent years.10
Two approaches for establishing µITIES are available. One is based on the use of micropipettes, where the liquid/liquid (l/l) interface is formed at the tip of a pulled glass pipette.11–15 The other employs the placement of organic and aqueous phases on either sides of membranes possessing arrays of micron-sized holes. Girault and co-workers16,17 used laser ablation to drill holes through thin inert polymer films which were placed at the interface. Several subsequent studies employed this method for µITIES formation.18–22
Recently, silicon micropore array membranes for both stabilisation of the l/l interface and for exploring the enhanced mass transfer at µITIES for detection of biomolecules have been developed.23–25 These silicon membranes were prepared by a combination of wet and dry etching, established methods in microelectronic integrated circuit fabrication, and have been applied to investigate simple and facilitated ion transfer across ITIES25 and to the detection of dopamine23 and oligopeptides.24 Their hydrodynamic performance was also evaluated.26 For a quantitative interpretation of the interfacial charge transfer associated with analyte detection, the system consisting of the micropore array membrane in contact with the ITIES has to be characterized. The geometry of the array, i.e. the pore radius, the centre-to-centre separation of the pores and the membrane thickness (the depth of the pores), is defined by the fabrication procedure and can be confirmed by scanning electron microscopy (SEM). Features which are related to the properties of the two immiscible phases and to the transferring ion, such as the location of the l/l interface within the micropore and the diffusion coefficients of the transferring species in either phase, cannot be directly accessed. In this situation, comparison between simulated and experimental ion transfer voltammograms can be used to characterize the various properties of the microarray-based µITIES system.
Josserand et al.20 presented a finite element simulation of ion transfer reaction at a single micro-l/l interface supported on a thin polymer film. The simulations were compared to experimental cyclic voltammograms (CVs) of ion transfer for polymer membranes of 3 and 12 µm thickness. The maximal thickness of the hole taken into account in the simulation was 36 µm. The effect of different diffusion coefficients of the transferring ion in the two phases was also investigated. In the present case, the thickness of the silicon membrane is 100 µm. Furthermore, if the extension of the diffusion zones around neighbouring micropores during the time frame of the experiment exceeds half of the centre-to-centre separation of the pores, the current response cannot be treated as multiples of the signal of a single micropore. Instead, diffusion zone overlap (also known as shielding) has to be taken into account. This has been simulated for solid microelectrode arrays.27–35 The centre-to-centre distance of the different silicon micropore arrays used in the experiments presented here varied from ca. 100 µm to ca. 1000 µm and diffusion zone overlap was observed in some cases. To take this into account in the simulation we applied the so-called diffusion domain approach.27,30,34 This concept allows the reduction of the three-dimensional diffusion space to a two-dimensional axial symmetric region and its validity was investigated in detail by Davies and Compton.34
In this report, CVs for ion transfer reactions across l/l interfaces featuring regular arrays of cylindrical micro-holes are simulated by the finite element method. The influence of different geometrical and physical parameters was investigated. The results were compared to a series of measurements using different micropore array designs, varying in pore size, pore centre-to-centre separation and number of pores. The comparison of simulated and experimental CVs allowed parameters like the location of the l/l interface within the micropore and the ratio of diffusion coefficients of the transferring ion to be estimated. Knowledge of these parameters is essential for optimizing the array design for electroanalytical applications of the micropore arrays.
Experimental
Reagents
All reagents were purchased from Sigma-Aldrich Ireland Ltd. and used without further purification, with the exception of 1,6-dichlorohexane (1,6-DCH) which was purified as described elsewhere.36 The aqueous phase electrolyte of 10 mM LiCl was prepared in ultrapure water (resistivity: 18 MΩ cm) from an Elgastat Maxima – HPLC purifier (Elga, UK). The model analyte species studied was the tetraethylammonium cation (TEA+) prepared as the chloride salt (TEA+Cl−) in a 10 mM LiCl aqueous phase. The organic electrolyte salt was prepared by metathesis of bis-(triphenylphosphoranylidene)ammonium chloride (BTPPA+Cl−) and potassium tetrakis(4-chlorophenyl)borate (K+TPBCl−) to obtain BTPPATPBCl, following the published experimental procedure.37 The organic phase was prepared as a gel24 and was composed of the organic solvent (1,6-DCH), the organic electrolyte (BTPPATPBCl), and low molecular weight poly(vinyl chloride) (PVC, from Fluka Chemika).
Micropore array fabrication
The micropore arrays were fabricated from 525 µm thick silicon wafers using a combination of wet and dry silicon etching to thin the wafers and etch pores through the thinned portions, as described previously.25 Note that this fabrication process produces pores with fluorocarbon polymer-coated walls. Five micropore array designs were used in these studies and the geometries of the individual arrays (the number of pores, the pore radii and the centre-to-centre pore separation) are shown in Table 1. SEM images of the five designs are shown in Fig. 1.
 |
| | Fig. 1
SEM images of the five different micropore array designs. See Table 1 for details. | |
Table 1 Characteristics of the pores of the different solid-state membranes evaluated by SEM. Pore radius and centre-to-centre separation are values averaged over six pores (with the exception of design 1, where values were averaged over three pores)
| Design |
Pore radius, ra/µm |
Centre-to-centre separation, rc/µm |
Number of pores, Nh |
| 1 |
25.50 ± 0.09 |
985.73 ± 1.50 |
3 |
| 2 |
26.00 ± 0.01 |
491.27 ± 2.87 |
8 |
| 3 |
25.35 ± 0.02 |
246.15 ± 0.90 |
23 |
| 4 |
25.34 ± 0.11 |
99.06 ± 0.49 |
105 |
| 5 |
10.41 ± 0.04 |
99.38 ± 0.43 |
120 |
Apparatus
CV experiments at the µITIES array were performed using a CH Instruments 620B potentiostat (CH Instruments, Texas, USA). A microporous silicon membrane was sealed onto the lower orifice of a borosilicate glass cylinder (6 mm external diameter, 3 mm inner diameter) using silicone rubber (RS Components, stock number 555-588). The gel was inserted into the borosilicate glass cylinder, with the silicon micropore array chip attached, as a liquid at ca. 60 °C using a glass pipette. This procedure allows the gel to fill the hydrophobic pores of the micropore array rendering an interfacial geometry which is inlaid at the ITIES. The organogel was allowed to cure at room temperature for 1 h before use. A three-electrode experimental setup was implemented consisting of one Pt mesh counter electrode (in the aqueous phase) and two Ag|AgCl reference electrodes (one for each phase). The Ag|AgCl electrode on the organic side, in addition to serving as a reference electrode, also acts as a counter electrode and together with the Pt mesh counter electrode is used to monitor the current. This setup has been described previously in detail.24
Experimental procedure
Once the apparatus was set up repetitive blank CVs (i.e. no TEA+ present in the liquid phases) were run, five in total at intervals of 180 s. The starting potential, Δwoφst, for each of these CVs was set at 0.05 V and the switching potential, Δwoφsw, at 1.05 V. A quiet time of 10 s was set prior to each run and scan rates of 10 and 15 mV s−1 were applied. Subsequently an aliquot of TEA+ solution was injected into the aqueous phase using a calibrated micropipette to produce a TEA+ concentration of 100 µM and five repetitive CVs were run, as for the blank CVs. Background-subtracted CVs of 100 µM TEA+ were obtained using the CH Instruments software. This background subtraction procedure produced artefacts at higher potentials, as shown in the experimental CVs.
Theory
In the following we assume transport by diffusion only. The geometrical domain of a pore in a membrane separating two liquid phases is defined in cylindrical coordinates (Fig. 2A), where r and x are the coordinates in the direction parallel and normal to the l/l interface, respectively. The l/l interface is located at (0 ≤ r ≤ ra, x = xs), where ra is the pore radius and xs is an x-coordinate within the pore, xl ≤ xs ≤ 0, with l = |xl| being the depth of the pore. The computational domain is bounded at space variables rd, xm and xn.
 |
| | Fig. 2 (A) Computational domain for micropore array simulation. (B) Illustration of the diffusion domain approach for a hexagonal array of pores with a centre-to-centre separation of rc. The diffusion domain boundary rd is used as the maximum value of r in the computational domain shown in (A). | |
Diffusion in the domain shown in Fig. 2A is expressed by
| |  | (1) |
where
i = 1, 2. The diffusion coefficient
D2 and the local concentration
c2(
r,
x,
t) are associated with the transferring ionic species in the aqueous phase, whereas
D1 and
c1(
r,
x,
t) are associated with the same species but in the organic phase. The Laplace operator, ∇
2, is given by
| | 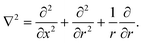 | (2) |
The initial condition for solving
eqn (1) is
c1(
r,
x,0) = 0 and
c2(
r,
x,0) =
cb, where
cb is the bulk concentration of the TEA
+ ions in the aqueous phase. The kinetics of ion transfer across the ITIES can be described by a Butler–Volmer type equation
38–40| | 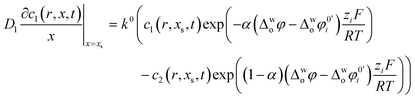 | (3) |
which, together with the equation for interfacial flux conservation,
| | 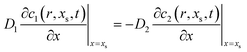 | (4) |
constitutes the boundary condition at the interface. In
eqn (3),
k0 is the standard rate constant for ion transfer,
α is the transfer coefficient, Δ
woφ is the Galvani potential between the aqueous and organic solutions, Δ
woφ0′i is the formal Galvani potential difference (or formal ion transfer potential) and
zi is the charge of the transferring ion (+1 in case of TEA
+). In the CV experiments reported here, the Galvani potential difference between the ITIES phases was changed with a constant scan rate
v from a starting potential Δ
woφst to a switching potential Δ
woφsw, where the potential scan direction was reversed back to the starting potential. The triangular potential wave can be expressed as an analytical formula for a Fourier series in the bounds of the starting and switching potential
11,41| |  | (5) |
The sgn() function in
eqn (5) returns an integer indicating the sign of the argument: sgn(Δ
woφsw − Δ
woφst) = +1 if Δ
woφsw > Δ
woφst (positive initial scan direction, transfer of a
cation from
water to the organic phase in the forward scan). For a negative initial scan direction Δ
woφsw < Δ
woφst and sgn(Δ
woφsw − Δ
woφst) = −1.
The far-field boundary conditions for t > 0 at (0 ≤ r ≤ rd, xm) and at (0 ≤ r ≤ rd, xn) are given by c1(r,x,t) = 0 and c2(r,x,t) = cb, respectively. The remaining boundary conditions along the surface lines of the membrane, the symmetry axis as well as the line (rd, 0 < x < xm) and (rd, xn < x < xl) are no-flux or symmetry conditions, expressed by vanishing of the directional derivative orthogonal to the line (normal derivative), ∂ci/∂n = 0, where n defines a vector normal to the line (normal vector).
The current, i, is evaluated by integration of the surface gradient for the transferring ion
| | 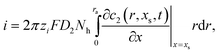 | (6) |
where
Nh is the number of pores in the membrane.
As a consequence of the change of concentration of the transferring ion at the interface between the two phases during the voltammetric experiment, a diffusion layer δ is formed around each individual pore in the array. If, on the time scale of the experiment, the diffusion layer does not exceed half of the centre-to-centre separation rc between the pores (0.5rc > δ), the voltammetric response of the system can be ascribed to the response of a single pore multiplied by the number of pores in the membrane. However, in the case of 0.5rc < δ, diffusion zones around pores overlap and vicinal pores deplete the same region in the solution, leading to a decrease of flux to an individual pore in comparison to an isolated pore, where spherical diffusion can evolve unhindered. This effect is taken into account by the concept of active and inactive regions or the diffusion domain approach, which was introduced by Matsuda and co-workers to model chronoamperometry and chronopotentiometry,27 linear and cyclic sweep voltammetry,28 and impedance measurements29 at hexagonal arrays of co-planar microdisk electrodes. The same concept was used by Amatore et al.30 to calculate CVs for hexagonal and cubic microelectrode arrays. Davies and Compton34 have also treated voltammetry at random arrays of co-planar microdisk electrodes within the diffusion domain framework. The diffusion domain approach allows the mapping of the three-dimensional multi-electrode array geometry onto a two-dimensional unit cell involving just one active area,27 as shown in Fig. 2. For simplicity, a circle whose area is equal to that of the hexagon is used (see Fig. 2B). The relation between the centre-to-centre separation rc of the closest neighbours in an hexagonal array and the radius rd of the diffusion domain taken into account in the simulation is then simply
| |  | (7) |
Because of the symmetry of the diffusion field between neighbouring unit cells, there is no flux of the reactant through the boundary of adjacent unit cells, (
rd, 0 <
x <
xm) and (
rd,
xl >
x >
xn).
All simulations of the diffusion problem were performed using dimensionless variables.11,42 Time t and potential scan rate v were normalised according to Aoki et al.43
Space was normalised by the pore radius
and
L = |
Xl|. Concentration was normalised with respect to bulk concentration of the transferring ion in the aqueous phase
The dimensionless forms of the interfacial standard rate constant and of the diffusion coefficient were
| |  | (8) |
and
| |  | (9) |
The current response from the normalised model yields a dimensionless current
I =
i/
ilim, where
i is given by
eqn (6) and
ilim is the limiting current at an array of
Nh non-interacting inlaid active micro-interfaces,
Therefore, the normalised steady-state limiting current for
Nh non-interacting micropores with an inlaid l/l interface was
Ilim = 1.
Computational details and mesh generation
Simulations were performed using the finite element method (FEM) program package COMSOL Multiphysics version 3.4 equipped with the chemical engineering module (COMSOL Ltd., Hertfordshire, UK). Meshes were generated from triangular elements, resulting in 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 15
000 to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mesh nodes. For mesh refinement, the maximum element size at the point of the orifice on both sides of the pore and along the boundary line of the l/l interface was set to 0.0002, since the highest concentration gradients are expected at these locations. The software package's built-in direct sparse matrix solver UMFPACK44 was used to solve the system of equations.
000 mesh nodes. For mesh refinement, the maximum element size at the point of the orifice on both sides of the pore and along the boundary line of the l/l interface was set to 0.0002, since the highest concentration gradients are expected at these locations. The software package's built-in direct sparse matrix solver UMFPACK44 was used to solve the system of equations.
The grid was tested by simulations for an infinitely thin membrane (xs = 0, xl → 0), resulting in a quasi ‘double sided’ microdisk electrode, co-planar with the surrounding insulating plane. Diffusion-limited current transients computed at both sides of the interface, i.e. at the organic and aqueous side, were compared to accurate finite difference calculations45 and to quasi-analytical functions for short and long time current transient behaviour.46 A maximum error of 0.8% for the current was found in a dimensionless time span of up to 50. Abercrombie and Denuault47 mentioned that an error of 2% as acceptable for microdisk electrode simulations, while Gavaghan48 gave a limit of 1%. Irrespective of those values, the simulation error values used here were smaller than experimental uncertainties.
Results and discussion
Before presenting the simulations, the effect of pore resistance on ion transfer through the pores of the membranes is briefly addressed. The diameter of the micropores defines the cross-sectional region in direct electrical contact with either the organic or the aqueous side. Reducing the pore radius ra and increasing the pore length l cause an increase in pore resistance. The first order approximation of the pore resistance is given by49| |  | (11) |
Here κ is the conductivity of the solution filling the pore, in the present case the organic phase (see experimental CVs later). Conductivity measurements of 1,6-DCH with tetraoctylammonium tetrakis(4-chlorophenyl)borate as an electrolyte by Katano and Senda50 resulted in a value of 49 µS cm−1 for κ. Conductivity measurements of Kontturi et al.51 and Sawada and Chigira52 for a series of electrolytes in 1,2-dichloroethane (DCE) showed that the conductivity is not substantially affected by the nature of the electrolyte. Therefore we assume that the conductivity measured by Katano and Senda50 is similar to the value of the BTPPATPBCl/organogel 1,6-DCH system. The resistance estimated from eqn (11) is 103 × 105 Ω per pore (radius 25 µm) and 650 × 105 Ω per pore (radius 10 µm). The pores of the array act like resistors in parallel. The total inverse resistance is therefore estimated by multiplying the inverse resistance of a single pore by the number of pores in the array. The total resistance of the different membrane designs lies between 9.8 × 104 Ω (ra = 25 µm, 105 pores, design 4, Table 1) and 3.4 × 106 Ω (ra = 25 µm, 3 pores, design 1, Table 1). These trans-membrane resistances are three-to-four orders of magnitude higher than values reported for PET track-etched membranes,53 which is due to a much smaller number of pores in the solid-state membrane used in the present study. However, the maximal current measured in the CV experiments was in the range 4–40 nA, which is relatively small compared to the currents measured at PET membranes.53 The resulting iR-drop across the membranes is about 4–10 mV. Although automatic positive feedback compensation was applied during the cyclic potential scans via the potentiostat, so as to minimize the effect of the resistance, Ohmic distortion of the voltammograms was observed for the three-hole design 1. This particular design possessed the highest trans-membrane resistance of the five designs studied, as shown by a slight increasing positive slope of the current in the limiting current region. Ohmic distortion increased with increasing scan rate, therefore an upper limit of v = 15 mV s−1 was set. In principle, the effect of Ohmic distortion is less pronounced and easier to recognize on steady-state currents then on transients involving current peaks. Therefore steady-state voltammograms for the ion transfer are desirable. On the one hand, to ensure steady-state behaviour, a bigger pore-to-pore separation is necessary to avoid overlap of diffusion zones which can result in linear diffusion and therefore in transient currents. On the other hand, an increased pore-to-pore distance implies a smaller number of pores in the membrane and therefore a higher trans-membrane resistance.
Simulations
In developing simulations of CV at the arrays of µITIES, several parameters which influence their general shape were taken into account. One set of parameters is related to the geometric properties of the membrane, such as the pore radius, ra, the centre-to-centre separation of the pores, rc, the thickness of the membrane, l, and the number of pores, Nh. Another set of parameters describes the interfacial ion transfer process, in this case following Butler–Volmer kinetics: the rate constant for the ion transfer, k0, the symmetry factor, α, the formal potential, Δwoφ0′, and the applied potential, Δwoφ, which itself is estimated by the scan rate and the initial and reverse potential. Finally, there are parameters which are related to the species in solution and the properties of the solvent, like the diffusion coefficients D1 and D2 of the transferring ion in the organic and aqueous phase, respectively, or the bulk concentration of the transferring ion. The location of the l/l interface, xs, depends mainly on the hydrophobicity and wetting properties of the membrane material.
The number of pores, their depth and radius and the centre-to-centre distance of the hexagonal array were determined by the design. SEM images, shown in Fig. 1, confirmed the quantities of ra, rc and Nh and these characteristics are summarised in Table 1.
Table 2 summarises the parameters used in the simulations. The TEA+ ion transfer across the ITIES was found to be reversible on the time scale of voltammetric experiments at macro-interfaces39,40 and micro-interfaces.11 A value of k0 = 0.5 cm s−1 was used in the simulations, which is within the range of the apparent standard rate constant for transfer of TEA+ across the water/nitrobenzene interface (no data were available for its transfer across the water/1,6-DCH interface), as studied by Kakiuchi and Teranishi.54 The resulting dimensionless rate constants are K = 127 and K = 51 for ra = 25 and 10 µm, respectively, which is within the reversible range of ion transfer. The formal potential Δwoφ0′ of 0.55 V for the TEA+ transfer was found by comparing half-wave potentials of simulated and experimental voltammograms. In all simulations, starting and switching potentials were the same as used in the experiments: Δwoφst = 0.05 V and Δwoφsw = 1.05 V. While the diffusion coefficient for TEA+ in the aqueous phase containing 10 mM LiCl was set to 9.8 × 10−6 cm2 s−1,13 a range of diffusion coefficients of the transferring ion in the gelified organic phase was used in the simulation to determine D1 by comparison with experimental voltammograms. The geometrical properties (ra, rc, l) employed in the simulations were taken from the SEM data of the array designs (Table 1).
Table 2 Parameters of the simulation model
|
Pore radius, ra/µm |
10, 25 |
|
Pore centre-to-centre distance rc/µm |
99.38 to 985.73 |
|
Pore depth, l/µm |
100 |
| Interface recess |xs|/µm |
0 to 100 |
| Potential sweep rate v/mV s−1 |
10, 15 |
| Starting and switching potential, Δwoφst and Δwoφsw/V |
0.05, 1.05 |
| Formal ion transfer potential, Δwoφ0′/V |
0.55 |
| Standard rate constant of transfer, k0/cm s−1 |
0.5 |
| Ion charge, zi |
+1 |
| Bulk ion concentration cb/mol l−1 |
10−4 |
| Ion diffusion coefficient in the aqueous phase, D2/cm2 s−1 |
9.8 × 10−6 |
|
γ = D1/D2 |
0.09 to 1.00 |
Effect of the interface recess and of the ratio of diffusion coefficients
The radius and centre-to-centre distance between pores was determined from SEM images. However, the location of the l/l interface cannot be determined this way. Interfacial transfer will depend on the supply of the transferring ion to the interface and this in turn depends on the location of the interface within the pore. For a given diffusion coefficient, a recessed interface will exhibit a lower current, since transport of transferring species to the interface is shielded by the surrounding pore walls, as first discussed for recessed solid electrodes.55–61 In comparison to a recessed solid microdisk electrode, the situation for a recessed l/l micro-interface is complicated by the fact that the recess for ion transfer from water to the organic phase can be different from the recess for the back transfer. If the interface is not in the middle of the micropore, the shielding effect of the surrounding wall will be different for the forward and backward transfer of the ions and transfer will be non-symmetric. Another non-symmetry of transfer is introduced by the fact that the diffusion coefficient of the TEA+ ion in the gelified organic phase, D1, is expected to be different from D2, the diffusion coefficient in the aqueous phase. The effect of both the ratio of diffusion coefficients, γ = D1/D2, and the location of the interface within the micropore, xs, on the shape of the cyclic voltammograms is shown in Fig. 3. For the simulations a pore radius of ra = 25 µm (normalised value Ra = 1) and a pore depth of 100 µm (L = 4) were used. The centre-to-centre pore separation was set to rc = 986 µm (Rc = 39.4). These parameters were taken from array design 1 (Table 1). Other parameters were as listed in Table 2. Owing to the large rc value, there was no interaction of diffusion zones of the individual pores in the time frame of the experiment (potential range 1.00 V, potential scan rate 10 mV s−1 (p = 0.062)). Fig. 3A shows the effect of interfaces recessed to depths of |xs| = 0, 25, 50, 75 and 100 µm for γ = 1. For xs = 0, the l/l interface is co-planar with the surrounding membrane at the aqueous side, resulting in an S-shaped current–potential curve, typical for inlaid microdisk interfaces, with a normalised limiting current of one. With increasing recess, the limiting current of the forward scan, i.e. the current for the ion transfer from the aqueous to the organic phase, decreased due to the shielding effect of the pore walls. Consequently, the current for the back transfer also decreased. The occurrence of a current peak for the reverse transfer of the ion is a consequence of the domination of linear diffusion, especially when the ions are still located within the pore on the organic side. For Fig. 3B, γ was set to 0.1, while the xs values are the same as in Fig. 3A. The limiting currents for the forward scan remain the same as in Fig. 3A, but a decrease in γ leads to a considerable increase of the current peak for the reverse transfer of the ion. The effect of γ on the CV shape can be better seen in Fig. 3C where γ values of 0.1, 0.25, 0.5, 0.75 and 1 were used and |xs| = 0 µm was kept constant. While in the forward scan a positive shift of the half-wave potential with decreasing γ was observed, the limiting current for the water-to-organic ion transfer was not affected and adopted the value of an inlaid microdisk interface. In contrast, the peak current for the reverse transfer of the ion increased with decreasing values of γ. If D1 < D2, the ion accumulates close to the interface within the pore on the organic side during the water-to-organic transfer. The reverse transfer is then dominated by linear diffusion and the diffusion layer is thinner for small γ values, hence an increase in the peak current occurs with a decrease of γ. The CVs shown in Fig. 3D were simulated using the same range of γ values as in Fig. 3C, but with |xs| = 100 µm (|Xs| = 4), i.e. the l/l interface is co-planar with the membrane surface on the organic side and the pore is filled with the aqueous phase. The appearance of current peaks during the forward scans is due to the fact that the current is controlled by the diffusion of ions confined within the pores, where linear diffusion pertains. As the diffusion layer expands beyond the depth of the pore, a spherical diffusion field is established rapidly in the aqueous phase and a steady state is attained at potentials higher than 0.75 V.
 |
| | Fig. 3 Simulated voltammograms showing the effect of the l/l interface recess Xs and diffusion coefficient ratio γ = D1/D2. (A) γ = 1 and |Xs| = 0 (a), 1 (b), 2 (c), 3 (d) and 4 (e). (B) γ = 0.1 and |Xs| = 0 (a), 1 (b), 2 (c), 3 (d) and 4 (e). (C) Xs = 0 and γ = 0.1 (a), 0.25 (b), 0.5 (c), 0.75 (d) and 1 (e). (C) Xs = 4 and γ = 0.1 (a), 0.25 (b), 0.5 (c), 0.75 (d) and 1 (e). The scan rate parameter p was 0.062. | |
The conclusion drawn from the above model simulation is that both the diffusion coefficient in the organic phase and the recess depth of the interface can in principle be estimated independently from one experimental CV. The location of the l/l interface can be evaluated by comparing measured limiting currents for the transfer of the TEA+ ion from the aqueous to the organic phase during the potential scan in a positive potential direction. For the present system, the aqueous TEA+ bulk concentration, the interfacial area and D2, the diffusion coefficient in the aqueous phase, are known and the experimental limiting current can therefore be used to estimate the recess depth of the interface. On the other hand, the effect of γ on the current–potential curve does not interfere with the limiting current on the forward scan, as shown in Fig. 3C and 3D. From the current behaviour of the negative-going potential scan, an estimation of γ or D1 can be made by comparison to simulated voltammograms.
Determination of interface location.
The question of the location of the l/l interface within the micropore is first addressed. The solid line in Fig. 4A shows simulated normalised limiting currents for an array of non-interacting micropores as a function of the dimensionless recess depth |Xs|. |Xs| varies from 0 (pore filled with organic phase, interface at the pore orifice on the aqueous side) to 4 (pore filled with the aqueous phase, interface at the pore orifice on the organic side). For a pore radius of 25 µm, |Xs| = 4 corresponds to 100 µm, which is the thickness of the solid-state membrane used in the experiments. The simulations were performed with a normalised scan rate p = 0.062 which corresponds to v = 10 mV s−1, considering ra = 25 µm and D2 = 9.8 × 10−5 cm2 s−1. The decrease of the curve with increasing recess is a consequence of the shielding of the interface. The experimental value, shown as the symbol × in Fig. 4A, is the limiting current (after background current subtraction) employing array design 2. The standard deviation of five measurements is indicated by the error bar. Taking the experimental uncertainty into account, the l/l interface can be located within a normalised distance of at maximum 0.1 to the aqueous side of the array. For a pore depth of 100 µm and a pore radius of 25 µm this implies a recess of maximal 2.5 µm. A recess length between 1 and 10 µm was previously estimated25 for the silicon-based porous membrane using an analytical equation for recessed electrodes.61 An inlaid l/l interface at the aqueous side of the membrane is well within the error limit, as can be seen in Fig. 4A. Considering the hydrophobic surface property of the silicon micropores,25 a situation where the organic phase forms a hemisphere located at the pore orifice at the aqueous side is also within the realm of possibility. However, the limited resolution and reproducibility of the CV experiment at the micro-l/l interfaces does not allow differentiation between these geometries. Within experimental error it is reasonable to consider the l/l interface as co-planar with the plane of the membrane at the aqueous side, i.e. the pore is filled with the organic phase.
 |
| | Fig. 4 (A) Dependence of the normalised limiting current of the forward scan (ion transfer w→o) on the recess depth |Xs| of the l/l interface. Solid line: simulation; symbol: measurement using array membrane design 2. (B) Dependence of the ratio of the peak current of the backward potential scan and the limiting current of the forward scan on γ. Solid and dashed lines: simulation for scan rate p = 0.062 (10 mV s−1) and 0.093 (15 mV s−1), respectively. Symbols are measurements using array design 2. | |
Determination of the ratio of diffusion coefficients.
For estimating the ratio of the diffusion coefficients of TEA+ in the gelified organic phase and aqueous phase, simulations were performed to evaluate the dependence of the current ratio, Ipeak,b/Ilim,f on γ, where Ilim,f is the (steady-state) limiting current observed during the forward potential scan and Ipeak,b is the peak current value of the backward scan. For the simulations we have Ilim,f = 1. The lines in Fig. 4B are simulations using xs = 0 for a γ range from 0.09 to 1, taking into account the rc value of 491 µm, which prevents diffusion zone interaction for both potential scan rates of 0.062 (10 mV s−1) and 0.092 (15 mV s−1). The two symbols in Fig. 4B are the results of measurements using array design 2 for scan rates of 10 and 15 mV s−1. By placing the measured values on the simulated curve, a γ value of 0.115 ± 0.03 is estimated for the experimental system. Using the diffusion coefficient D2 = 9.8 × 10−6 cm2 s−1 for TEA+ in the aqueous electrolyte solution, a diffusion coefficient of D1 = (1.13 ± 0.02)×10−6 cm2 s−1 is estimated for the TEA+ ion in the gelified organic phase. The decrease of the diffusion coefficient is a result of the higher viscosity of the gelified organic phase compared to the aqueous phase.
Comparison of simulated and experimental CVs.
Fig. 5 presents a direct comparison of simulated voltammograms (with the current given in nA) using the geometry of design 1 and 2 and experiments using array design 1 and 2. The potential scan rates were 10 mV s−1 for design 1 and 10 and 15 mV s−1 for design 2. The experimental CVs of design 1 were not used for evaluation because of the noticeable Ohmic resistance. (The tailing-off seen at higher potentials in Fig. 5 is an artefact associated with the background-subtraction procedure used.)
 |
| | Fig. 5 Experimental (right) and simulated (left) cyclic voltammograms using micropore array design 1 (A) and 2 (B). Scan rates are 10 mV s−1 for design 1 and 10 and 15 mV s−1 for design 2. The same scan rates and potential range as for the experiments were used for the simulations. The values for ra, rc and Nh were chosen according to the array design 1 and 2 (cf.Table 1). The pore depth for simulation was 100 µm, the location of the interace xs = 0 µm and γ = 0.115. | |
A consequence of the location of the l/l interface at xs = 0 is non-symmetrical diffusion, where the diffusion field at the aqueous side is spherical, while linear diffusion prevails inside the pore. This leads to a higher concentration of the transferring ion inside the pore. Non-symmetrical diffusion is also observed for ion transfer across l/l interfaces at the tip of micropipettes.14 However, in the present case the accumulation of the transferring species inside the pore is enhanced by the small diffusion coefficient in the organic phase. Fig. 6 presents a simulated concentration profile of the transferring ion in a single pore of array design 1, using γ = 0.115. The highest concentration is almost 50 times higher than the TEA+ bulk concentration and was observed at Δwoφ = 0.745 V during the reverse scan. This is the potential were the current starts to decrease from the limiting value on the reverse scan. For γ = 1, the maximum concentration of the transferring ion was only about six times higher than the bulk concentration. This higher concentration in the organogel phase within the pores may result in precipitation within the pores.
 |
| | Fig. 6 Simulated concentration profile in the region of the micropore for design 1 at Δwoφ = 0.745 V during the backscan. The l/l interface is at X = 0, 0 ≤ R ≤ 1. The highest concentration (about 50 times higher than the bulk concentration of the transferring ion) can be found within the micropore close to the l/l interface and the pore wall. | |
The effect of diffusion zone overlap
The effect of the diffusion zone overlap on the current response is now examined. The diffusion layer expands with t1/2 and for a potential step chronoamperometric experiment, the assignment of time during which the diffusion layer expands is obvious. However, in a CV experiment the time to consider is not so evident. For the extension of the diffusion zone under potential scanning conditions, the following equation was proposed62| |  | (12) |
where Δ(Δwoφ) is set to 0.3 V for microelectrodes,62 which approximately matches the potential interval between the onset of (Faradaic) current and the attainment of the steady-state current. Eqn (12) takes into account the effect of time on the diffusion layer thickness via the potential scan rate, but δ does not depend on the pore (or electrode) radius. This is because eqn (12) was derived with the assumption of one-dimensional diffusion.34 The condition to avoid diffusion zone overlap is then 0.5rc > δ. Using the diffusion coefficient of TEA+ in the aqueous phase, D2 = 9.8 × 10−6 cm s−1 in eqn (12), this condition is met by micropore array design 1 (rc = 985.73 µm) for scan rates v ≥ 2.5 mV s−1 and by design 2 (rc = 500 µm) for v ≥ 10 mV s−1. The current peaks occurring during the forward scans of the experimental voltammograms using micropore array designs 3, 4 and 5 (Fig. 7) are manifestations of the interaction of diffusion zones of neighbouring micropores. Fig. 8 shows simulated equiconcentration lines for design 1 and design 4 at Δwoφ = 0.75 V, which is the potential where the simulated current for design 1 has just reached its limiting value in the forward scan. The equiconcentration lines for design 1 do not reach to the right sided wall indicating no overlapping of diffusion zones. For the CV using design 4, the potential Δwoφ = 0.75 V is about 0.1 V past the current peak of the forward scan. In contrast to design 1, a strong overlap is perceivable, with equiconcentration lines running almost parallel to the R axis (Fig. 8). Only in the vicinity of the orifices of the pore is a slight bend of the contour line for C2 = 0.25 and C1 = 0.25 noticeable, indicating a contribution of radial diffusion to the diffusion field of TEA+ ions. If the diffusion field is linear (and semi-infinite), the peak current is expressed by the Randles–Sevcik equation| |  | (13) |
 |
| | Fig. 7 Experimental (right) and simulated (left) cyclic voltammograms using micropore array design 3 (A) and 4 (B) and 5 (C). Scan rate: 10 mV s−1. The same scan rate and potential range as for the experiments were used for the simulations. The values for ra, rc and Nh were chosen according to the array design 3, 4 and 5 (cf.Table 1). The pore depth for simulation was 100 µm, the location of the interface xs = 0 µm and γ = 0.115. | |
 |
| | Fig. 8 Equiconcentration lines for normalised concentrations of 0.04, 0.25, 0.5, 0.75 and 0.96 of the transferring ion at Δwoφ = 0.75 V (forward scan), p = 0.062, v = 10 mV s−1, γ = 0.115 and Xs = 0. Left: geometric parameter for design 1. Right: geometric parameter of design 4. | |
For a micropore array, the total cross-sectional area of the pores is A = Nhπra2, giving A = 1.96 × 10−5 cm2 for design 4 and a peak current of ip ≈ 20 nA. Comparison to the measured value of 47.2 ± 2.5 nA for background-subtracted voltammograms and to the simulated value of 55.0 nA shows that the diffusion field at potentials around the current peak is not strictly linear since diffusion is enhanced by a radial component.
Comparison of simulated and experimental CVs.
A direct comparison between measured and simulated CVs for designs 3–5 is shown in Fig. 7. These three micropore array designs have centre-to-centre pore separations, rc, of ca. 100 µm (designs 4 and 5) and ca. 250 µm (design 3), which lead to inter-acting diffusion zones within the time frame of the experiment (v = 10 mV s−1), as shown by the occurrence of a peak current during the positive-going forward potential scan. The values of rc for designs 4 and 5 are approximately identical, the difference is the pore radius which is 25 µm for design 4 and 10 µm for design 5. Both designs do not meet the criteria following from eqn (12) for non-interacting diffusion zones. Also the more frequently used condition rc > 12ra![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63 for non-overlapping diffusion zones is not fulfilled. However, the current peak is more pronounced for design 4, i.e. the array with larger pores, indicating a stronger overlap when design 4 is used. As mentioned by others,32,34 the conditions for diffusion zone interaction at arrays of micropores or electrodes can only provide a rough guideline for the design of systems based on arrays of micro-interfaces. An optimized design for a given membrane area would involve as high a number of pores as possible without having overlapping diffusion zones during experiments. This depends not only on rc but also on ra, on the diffusion coefficients of transferring species and on the time frame of the experiment. If ra is made smaller, as would be desirable in order to reduce the diffusion zone extension so as to fit more pores into the membrane, other effects like increasing trans-membrane resistance may have to be taken into consideration. Therefore for the individual application of arrays of µITIES, a simulation model is helpful to define optimal conditions. Note that the drop in current at the higher potentials of the experimental CVs is an artefact associated with the background subtraction procedure.
63 for non-overlapping diffusion zones is not fulfilled. However, the current peak is more pronounced for design 4, i.e. the array with larger pores, indicating a stronger overlap when design 4 is used. As mentioned by others,32,34 the conditions for diffusion zone interaction at arrays of micropores or electrodes can only provide a rough guideline for the design of systems based on arrays of micro-interfaces. An optimized design for a given membrane area would involve as high a number of pores as possible without having overlapping diffusion zones during experiments. This depends not only on rc but also on ra, on the diffusion coefficients of transferring species and on the time frame of the experiment. If ra is made smaller, as would be desirable in order to reduce the diffusion zone extension so as to fit more pores into the membrane, other effects like increasing trans-membrane resistance may have to be taken into consideration. Therefore for the individual application of arrays of µITIES, a simulation model is helpful to define optimal conditions. Note that the drop in current at the higher potentials of the experimental CVs is an artefact associated with the background subtraction procedure.
Conclusions
In this work, ion transfer voltammetry at micro-l/l interface (or µITIES) arrays has been studied by finite element modelling simulation with validation by comparison to experimental voltammograms. The arrays of µITIES were formed by placing a silicon membrane containing micron-sized pores at the interface between the immiscible electrolyte solutions. The simulations have shown that the l/l interface is at or in close proximity to the micropore orifices at the aqueous side, with the pores filled with the organic phase, in agreement with aqueous–organogel micro-interfaces, as well as with previously reported data for non-gelled organophase.23 Furthermore, the diffusion coefficient of the transferring TEA+ ion in the gelified organic electrolyte solution was determined to be 1.1 × 10−6 cm2 s−1, compared to 9.8 × 10−6 cm2 s−1 in the aqueous phase. It was found that both the location of the l/l interface and the difference of the diffusion coefficients contribute to an asymmetric diffusion field for interfacial transfer, which influenced the shape of the voltammograms. The observation of current peaks during the forward scan in experimental cyclic voltammetric experiments was found to be due to the overlap of the diffusion fields around the individual micropores. This effect was taken into account in the simulation model. The overlap of diffusion zones decreased the current density per pore, as quantified by the simulations.
From an electroanalytical point of view, a high (current) signal is desirable, which can be achieved by increasing the number of micropores in the solid-state membrane which is used to define the arrays of µITIES. However, if the micropores are packed too closely together in the membrane, the pore-to-pore distance may be too low and result in a decrease in current due to the overlap of diffusion zones. The simulation model presented here can be used to optimize electroanalytical devices based on µITIES confined in micropores of regular arrays. For such devices, the current response depends not only on the pore-to-pore distance, but also on the time scale of the experiment, diffusion coefficients in both phases, the pore radius and depth, as well as ion transfer kinetics. These features can be taken into account in the simulation model and employed in the design of new microporous membranes for applications in detection and bioanalytical science.
Acknowledgements
The support of Science Foundation Ireland (grant number 07/IN.1/B967), the Irish Research Council for Science Engineering and Technology (PhD scholarship to M. D. S., grant number RS/2005/122) and the European Commission's Framework Programme 6 (Marie Curie Transfer of Knowledge fellowship to J. S., Grant number MTKD-CT-2005-029568) are gratefully acknowledged. The authors are thankful to Dr N. Kehagias and Professor C. M. Sotomayor Torres for provision of the SEM images.
References
- Z. Samec, E. Samcova and H. H. Girault, Talanta, 2004, 63, 21–32 CrossRef CAS.
- P. Vanysek and L. B. Ramirez, J. Chil. Chem. Soc., 2008, 53, 1455–1463 Search PubMed.
- G. Herzog, V. Kam, A. Berduque and D. W. M. Arrigan, J. Agric. Food Chem., 2008, 56, 4304–4310 CrossRef CAS.
- S. Amemiya, X. T. Yang and T. L. Wazenegger, J. Am. Chem. Soc., 2003, 125, 11832–11833 CrossRef CAS.
- D. W. M. Arrigan, M. Ghita and V. Beni, Chem. Commun., 2004, 732–733 RSC.
- V. Beni, M. Ghita and D. W. M. Arrigan, Biosens. Bioelectron., 2005, 20, 2097–2103 CrossRef CAS.
- J. Langmaier, J. Olsak, E. Samcova, Z. Samec and A. Trojanek, Electroanalysis, 2006, 18, 115–120 CrossRef CAS.
- G. Herzog and D. W. M. Arrigan, Analyst, 2007, 132, 615–632 RSC.
- J. Heinze, Angew. Chem., Int. Ed. Engl., 1991, 30, 170–171 CrossRef.
- B. Liu and M. V. Mirkin, Electroanalysis, 2000, 12, 1433–1446 CrossRef CAS.
- P. J. Rodgers and S. Amemiya, Anal. Chem., 2007, 79, 9276–9285 CrossRef CAS.
- Y. Shao, M. D. Osborne and H. H. Girault, J. Electroanal. Chem., 1991, 318, 101–109 CrossRef CAS.
- Y. H. Shao and M. V. Mirkin, Anal. Chem., 1998, 70, 3155–3161 CrossRef CAS.
- A. A. Stewart, G. Taylor, H. H. Girault and J. McAleer, J. Electroanal. Chem., 1990, 296, 491–515 CrossRef CAS.
- N. Nishi, S. Imakura and T. Kakiuchi, J. Electroanal. Chem., 2008, 621, 297–303 CrossRef CAS.
- J. A. Campbell and H. H. Girault, J. Electroanal. Chem., 1989, 266, 465–469 CrossRef CAS.
- J. A. Campbell, A. A. Stewart and H. H. Girault, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 843–853 RSC.
- S. Wilke and T. Zerihun, Electrochim. Acta, 1998, 44, 15–22 CrossRef CAS.
- R. A. W. Dryfe, Phys. Chem. Chem. Phys., 2006, 8, 1869–1883 RSC.
- J. Josserand, J. Morandini, H. J. Lee, R. Ferrigno and H. H. Girault, J. Electroanal. Chem., 1999, 468, 42–52 CrossRef CAS.
- S. Peulon, V. Guillou and M. L'Her, J. Electroanal. Chem., 2001, 514, 94–102 CrossRef CAS.
- C. Beriet and H. H. Girault, J. Electroanal. Chem., 1998, 444, 219–229 CrossRef CAS.
- A. Berduque, R. Zazpe and D. W. M. Arrigan, Anal. Chim. Acta, 2008, 611, 156–162 CAS.
- M. D. Scanlon, G. Herzog and D. W. M. Arrigan, Anal. Chem., 2008, 80, 5743–5749 CrossRef CAS.
- R. Zazpe, C. Hibert, J. O'Brien, Y. H. Lanyon and D. W. M. Arrigan, Lab Chip, 2007, 7, 1732–1737 RSC.
-
M. D. Scanlon, A. Berduque, J. Strutwolf and D. W. M. Arrigan, submitted.
- T. Gueshi, K. Tokuda and H. Matsuda, J. Electroanal. Chem., 1978, 89, 247–260 CrossRef CAS.
- T. Gueshi, K. Tokuda and H. Matsuda, J. Electroanal. Chem., 1979, 101, 29–38 CrossRef CAS.
- K. Tokuda, T. Gueshi and H. Matsuda, J. Electroanal. Chem., 1979, 102, 41–48 CrossRef CAS.
- C. Amatore, J. M. Saveant and D. Tessier, J. Electroanal. Chem., 1983, 147, 39–51 CrossRef CAS.
- C. Beriet, R. Ferrigno and H. H. Girault, J. Electroanal. Chem., 2000, 486, 56–64 CrossRef CAS.
- H. J. Lee, C. Beriet, R. Ferrigno and H. H. Girault, J. Electroanal. Chem., 2001, 502, 138–145 CrossRef CAS.
- T. J. Davies, C. E. Banks and R. G. Compton, J. Solid State Electrochem., 2005, 9, 797–808 CrossRef CAS.
- T. J. Davies and R. G. Compton, J. Electroanal. Chem., 2005, 585, 63–82 CrossRef CAS.
- O. Ordeig, C. E. Banks, T. J. Davies, J. del Campo, F. X. Munoz and R. G. Compton, J. Electroanal. Chem., 2006, 592, 126–130 CrossRef CAS.
- H. Katano, H. Tatsumi and M. Senda, Talanta, 2004, 63, 185–193 CrossRef CAS.
- H. J. Lee, P. D. Beattie, B. J. Seddon, M. D. Osborne and H. H. Girault, J. Electroanal. Chem., 1997, 440, 73–82 CrossRef CAS.
- H. H. J. Girault and D. J. Schiffrin, J. Electroanal. Chem., 1985, 195, 213–227 CrossRef CAS.
- Z. Samec, J. Electroanal. Chem., 1979, 99, 197–205 CrossRef CAS.
- J. Strutwolf, J. A. Manzanares and D. E. Williams, Electrochem. Commun., 1999, 1, 139–144 CrossRef CAS.
-
E. W. Weisstein, Triangle Wave, MathWorld –A Wolfram Web Resource, http://mathworld.wolfram.com/TriangleWave.html (accessed 6 November 2008) Search PubMed.
-
D. Britz, Digital Simulation in Electrochemistry, Springer, Berlin, Heidelberg, 2005 Search PubMed.
- K. Aoki, K. Akimoto, K. Tokuda, H. Matsuda and J. Osteryoung, J. Electroanal. Chem., 1984, 171, 219–230 CrossRef CAS.
- T. A. Davis, ACM Transactions on Mathematical Software, 2004, 30, 196–199 Search PubMed.
- D. Britz, K. Poulsen and J. Strutwolf, Electrochim. Acta, 2004, 50, 107–113 CrossRef CAS.
- P. J. Mahon and K. B. Oldham, Electrochim. Acta, 2004, 49, 5041–5048 CrossRef CAS.
- S. C. B. Abercrombie and G. Denuault, Electrochem. Commun., 2003, 5, 647–656 CrossRef CAS.
- D. J. Gavaghan, J. Electroanal. Chem., 1998, 456, 1–12 CrossRef CAS.
- R. W. Deblois, C. P. Bean and R. K. A. Wesley, J. Colloid Interface Sci., 1977, 61, 323–335 CrossRef CAS.
- H. Katano and M. Senda, Anal. Sci., 2001, 17, 1027–1029 CrossRef CAS.
- A. K. Kontturi, K. Kontturi, J. A. Manzanares, S. Mafe and L. Murtomaki, Ber. Bunsen-Ges. Phys. Chem., 1995, 99, 1131–1136 CAS.
- K. Sawada and F. Chigira, J. Mol. Liq., 1995, 65–6, 265–268 CrossRef.
- B. Kralj and R. A. W. Dryfe, Phys. Chem. Chem. Phys., 2001, 3, 5274–5282 RSC.
- T. Kakiuchi and Y. Teranishi, J. Electroanal. Chem., 1995, 396, 401–406 CrossRef CAS.
- C. Amatore, A. I. Oleinick and I. Svir, J. Electroanal. Chem., 2006, 597, 77–85 CrossRef CAS.
- P. N. Bartlett and S. L. Taylor, J. Electroanal. Chem., 1998, 453, 49–60 CrossRef CAS.
- D. Britz and J. Strutwolf, Electrochim. Acta, 2006, 52, 33–41 CrossRef CAS.
- R. Ferrigno, P. F. Brevet and H. H. Girault, Electrochim. Acta, 1997, 42, 1895–1903 CrossRef CAS.
- J. Galceran, S. L. Taylor and P. N. Bartlett, J. Electroanal. Chem., 1999, 476, 132–147 CrossRef CAS.
- K. Harriman, D. J. Gavaghan, P. Houston and E. Suli, Electrochem. Commun., 2000, 2, 163–170 CrossRef CAS.
- A. M. Bond, D. Luscombe, K. B. Oldham and C. G. Zoski, J. Electroanal. Chem., 1988, 249, 1–14 CrossRef CAS.
- A. O. Simm, C. E. Banks, S. Ward-Jones, T. J. Davies, N. S. Lawrence, T. G. J. Jones, L. Jiang and R. G. Compton, Analyst, 2005, 130, 1303–1311 RSC.
- Y. Saito, Rev. Polarogr., 1968, 15, 177–187 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. 


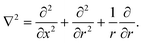
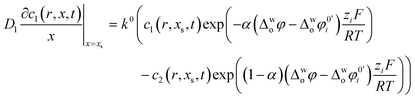
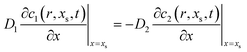

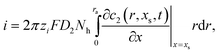



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 15
000 to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mesh nodes. For mesh refinement, the maximum element size at the point of the orifice on both sides of the pore and along the boundary line of the l/l interface was set to 0.0002, since the highest concentration gradients are expected at these locations. The software package's built-in direct sparse matrix solver UMFPACK44 was used to solve the system of equations.
000 mesh nodes. For mesh refinement, the maximum element size at the point of the orifice on both sides of the pore and along the boundary line of the l/l interface was set to 0.0002, since the highest concentration gradients are expected at these locations. The software package's built-in direct sparse matrix solver UMFPACK44 was used to solve the system of equations.









![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63 for non-overlapping diffusion zones is not fulfilled. However, the current peak is more pronounced for design 4, i.e. the array with larger pores, indicating a stronger overlap when design 4 is used. As mentioned by others,32,34 the conditions for diffusion zone interaction at arrays of micropores or electrodes can only provide a rough guideline for the design of systems based on arrays of micro-interfaces. An optimized design for a given membrane area would involve as high a number of pores as possible without having overlapping diffusion zones during experiments. This depends not only on rc but also on ra, on the diffusion coefficients of transferring species and on the time frame of the experiment. If ra is made smaller, as would be desirable in order to reduce the diffusion zone extension so as to fit more pores into the membrane, other effects like increasing trans-membrane resistance may have to be taken into consideration. Therefore for the individual application of arrays of µITIES, a simulation model is helpful to define optimal conditions. Note that the drop in current at the higher potentials of the experimental CVs is an artefact associated with the background subtraction procedure.
63 for non-overlapping diffusion zones is not fulfilled. However, the current peak is more pronounced for design 4, i.e. the array with larger pores, indicating a stronger overlap when design 4 is used. As mentioned by others,32,34 the conditions for diffusion zone interaction at arrays of micropores or electrodes can only provide a rough guideline for the design of systems based on arrays of micro-interfaces. An optimized design for a given membrane area would involve as high a number of pores as possible without having overlapping diffusion zones during experiments. This depends not only on rc but also on ra, on the diffusion coefficients of transferring species and on the time frame of the experiment. If ra is made smaller, as would be desirable in order to reduce the diffusion zone extension so as to fit more pores into the membrane, other effects like increasing trans-membrane resistance may have to be taken into consideration. Therefore for the individual application of arrays of µITIES, a simulation model is helpful to define optimal conditions. Note that the drop in current at the higher potentials of the experimental CVs is an artefact associated with the background subtraction procedure.