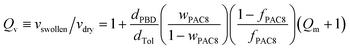A novel elastomer/liquid crystal polymer nanocomposite created in situ from controlled radical graft-polymerization

Abstract

We present the original design and properties of a novel, all-polymer hierarchical composite comprising an elastomer and a fluorinated liquid crystal polymer. The material follows from the phase separation between the two highly incompatible components, occuring in situ during the controlled radical graft-polymerization of the liquid crystal monomer onto functionalized elastomeric chains. We demonstrate that the composite remarkably combines the mechanical properties, static and dynamic, of both an elastomer and a semi-crystalline polymer. We thereby illustrate how the careful choice of a graft can provide a simple rubbery material with original and antonymic functionalities. Here, the temperature-sensitive liquid crystal polymeric domains act as hard particulate fillers under their fusion temperature and liquid softening inclusions above, with fast reversible transitions from one state to another. A variety of composites combining physico-chemical features difficult to marry otherwise may be designed following this simple method.

---

Introduction

Microphase separation of highly incompatible fluorinated liquid crystal polymer (LCP) hard inclusions occurs upon their in situ graft-polymerization onto functionalized elastomeric poly(butadiene) (PBd) chains.^1,2 The process leads to a novel composite comprising an elastomer and a liquid crystal polymer, organized at several length scales, from nano- to microscopic, as sketched in Fig. 1. The reaction is carried out via a nitroxyl-mediated controlled radical polymerization (NM-CRP).^3,4 The technique allows control of the grafting-from polymerization of the functional monomer, as well as the quality of phase separation in terms of domain size, homogeneity, etc, advantages that conventional free radical polymerization processes have never offered so far. High-impact poly(styrene) may be one of the most famous (if not, the unique) example in day-to-day life, of the use at an industrial level of a conventional free radical polymerization process effectively producing graft copolymers. However, the extent of control achieved over the microphase separation occuring upon polymerization, remains poor. In practise, conventional radical processes offer little control over the grafting reaction in terms of chain growth, molecular weight, polydispersity or overall grafted content. As a result, phase separation upon reaction is not well controlled and occurs over a wide range of domain sizes, from nano- to macroscopic, which often impacts the materials’ performance. Reactive coextrusion⁵ (which effectively produces graft-copolymers as well) recently showed a remarkable potential for designing complex phases with antonymic or complementary mechanical properties. The challenge of creating from the start and in situ at the synthesis step, a composite using graft copolymerization, was then renewed.

Fig. 1 Schematics of an elastomer-graft-LCP in situ composite at different length scales. (a) 1 μm: continuous PBd matrix filled with 10–100 nm sized strongly phase separated LCP domains. (b) 0.2 μm: a LCP inclusion chemically bound to PBd chains, with chemical/topological crosslinks in the elastomer. (c) 50 nm: a crystalline domain with lamellar order between neighbouring chains, separated by 32.8 Å, and a 5.7Å distance between consecutive fluorine pendant groups on a LCP chain.

The NM-CRP process is applied on a pure bulky material, in the present case, an elastomeric film simply immersed directly into the reactive monomer. In the end, a grafted composite film is recovered. In practise, as will be shown, the technique provides an apparent linearity between the reaction time and the amount of liquid crystal polymer grafted. The extent of modification achieved inside the film is thus very easy to tune. This reliable grafting process constitutes a convenient way to gain easy access to complex composites with remarkable properties, which we will focus on. We detail the hierarchical structure from nano- to microscopic scales, of this novel smectic-B LCP/elastomer composite. The mechanical properties of both an elastomer and a semi-crystalline polymer are successfully combined in the final composite material. Most importantly, we find that the composites show additional original features, unheard of, evidently resulting from the liquid crystal nature of the polymeric grafts. Indeed, we demonstrate that the temperature-sensitive LCP grafted domains can act either as hard particulate fillers under their fusion temperature, or as liquid softening inclusions above, with fast reversible transitions from one state to the other. The creation, inside a rubbery material, of regions with fast reversible transitions such as those displayed by the LCP domains is at the core of the design of artificial muscles based on alternating nematic-B/rubbery lamellae as proposed by de Gennes.⁶ Our smectic-B LCP/elastomer composites, or liquid crystal elastomer (LCE) may be regarded as a starting point, for a possible easy design of artificial muscles in the future, as considered by others.^7–9

Experimental

Grafting procedure

Elf-Atochem provided poly(butadiene)s, PBds, of number-average molecular weight M_n = 196 kg mol⁻¹ (size exclusion chromatography) functionalized with 2,2,6,6-tetramethyl-1-piperinyloxy (TEMPO) a well-known capping agent used for controlled radical polymerization, which were all used as received. Three PBds with number densities n = 0, 1, 10 and 20 of TEMPO functions per chain, corresponding to one TEMPO every 2000, 400 and 200 monomeric units, respectively, were investigated. The reacted specimens will often be named after the functionality n of their precursor poly(butadiene) (see Table 1 for examples).

Table 1 Characteristics of the homogeneous families synthesized

Series	Sample name	n ^a	t R ^b/min	w F ^c	w LCP ^d	f LCP ^e
a Number density of TEMPOs on the PBds. b Duration of the reaction. c Fluorine weight fraction from elemental analysis. d LCP weight fraction, as computed from the fluorine content. e LCP volume fraction, as computed from the weight content. f Specimens 20f and 20g derive from specimens 20d and 20e, respectively, after stopping and re-starting the synthesis in a new reactive bath for another 240 min.
	0a	0	180	0.084	0.133	0.077
(i)	1a	1	180	0.163	0.261	0.160
	10a	10	180	0.218	0.350	0.224
	20a	20	180	0.255	0.409	0.271
	20b	20	210	0.255	0.409	0.271
	20c	20	270	0.264	0.423	0.283
(ii)	20d	20	390	0.293	0.470	0.323
	20e	20	510	0.330	0.529	0.377
	20f ^f	20	630	0.372	0.596	0.443
	20g ^f	20	750	0.390	0.625	0.473

---

The PBds were dissolved in toluene at 5 wt%, filtered and poured into poly(tetrafluoroethylene) molds. The solutions were slowly evaporated at room temperature and the remaining traces of toluene were removed under vacuum for several days. This procedure led to 250 μm thick transparent, tacky films. In a 500 mL reactor, 5 × 5 cm² films were drowned directly into 250 mL of 3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10,10-heptadecafluorodecylacrylate, an acrylic monomer denoted AC8 liquid at room temperature, presenting a long fluorinated –(CF₂)₈–CF₃ pendant group. In specific cases, the reacting bath consisted of 250 mL of a 50/50 wt% mixture of toluene and AC8. At room temperature, the PBd films slightly swell with AC8 monomer due to an affinity between the elastomer and the monomer, yet the swelling is not extensive enough to alter the film, which retains its integrity and can be safely removed at the end. The medium was made inert by a bubbling of nitrogen N₂ for 30 min to one hour, and the temperature raised to 120 °C. The polymerization of AC8 was carried out for 2.5 to 8.5 h under a constant flux of N₂. The reactive bath was then slowly cooled down. All reacted films were washed 24 h in isopropanol, a good solvent for the AC8 monomer, marginal for PBd; the films swell enough to release trapped unreacted monomers. They were then dried for 3 h at room temperature and re-swollen for 72 h in toluene, a good solvent for PBd, miscible with AC8 yet a bad solvent for LCP, then dried again under vacuum at room temperature for several hours before mechanical experiments were carried out.

Chemical and structural characterizations

The reacted films were characterized using different techniques. Transmission infrared spectroscopy was first used on the films to verify that LCP is indeed formed in the reacted films, while the AC8 monomer is completely removed by the successive washes. However, for lack of absorbance coefficient values, this technique is not quantitative and not appropriate for measuring the amount of LCP created. Elemental analysis (EA) was thus used to determine the extent of grafting achieved. The fluorine weight fraction w_F was determined following the Schöniger combustion oxygen flask method, which involves the decomposition of the sample and the conversion of the halogen into a form which can be determined by manual titration. The fluorine weight content was readily converted to LCP weight fractions w_LCPviaw_PAC8 = M_AC8w_F/17M_F, where M_AC8 = 518 g mol⁻¹, M_F = 19 g mol⁻¹ and M_Bd = 54 g mol⁻¹ are the molar weights of, respectively, the AC8 monomer, fluorine and the butadiene monomer. The LCP volume fraction f_LCP on the other hand, reads f_LCP = 1/[1 + (1/w_LCP− 1)d_LCP/d_PBd], where d_LCP and d_PBd = 0.92 g cm⁻³ are the densities of LCP and PBd, respectively. The density of LCP was taken to be equal to that of the monomer, i.e. 1.62 g cm⁻³, for lack of experimental data. Table 1 shows the outcome of the chemical characterizations for several selected specimens.

Differential scanning calorimetry (DSC) was carried out from −110 °C to 90 °C at a constant heating rate of 10 °C min⁻¹, after a preliminary heating at high temperature and cooling. Transmission electron microscopy (TEM) was performed on thin cuts of selected reacted films after staining with OsO₄ which selectively stains PBd chains: stained PBd appears in dark grey in the pictures, while LCP appears in white.

Mechanical characterizations

Each dry washed composite film was placed in toluene to swell to equilibrium for several days. Its weight in the dry and swollen states was measured and, from these, we computed the weight- and volume-swelling ratios, respectively: Q_m≡m_swollen/m_dry and Q_v≡v_swollen/v_dry,¹⁰ using d_TOL = 0.87 g cm³ as the density of toluene.

Static deformations were carried out on an Instron apparatus on 25 × 5 × 0.25 mm³ cut-outs, cut into reacted films of thickness 0.25 mm. The nominal force f_N, from which the nominal and true stresses σ_N and σ were computed, was measured as a function of the percentage of deformation ε until breaking occurred. For small deformations, σ≈σ_N and the tensile modulus E = ∂σ/∂ε was simply derived from the slope at ε≪ 1 of the nominal curve, as will be fully justified experimentally in the Results and Discussion section. These experiments were carried out at a deformation rate chosen from 1 to 500 mm min⁻¹.

Finally, dynamic mechanical measurements were carried out on cut-outs at a 1 Hz frequency and a 1% deformation where these composites are still truly elastic. We used the torsional clamp set-up designed for solid materials on an Advanced Rheometric Expansion System (ARES) equipped with a forced convection oven and a liquid nitrogen cooling device. Storage (G′) and loss (G″) moduli were thus measured as a function of temperature, usually from +10 °C to +100 °C, varying heating and cooling rates, as detailed in the main text.

Results and discussion

The grafting mechanism: role of TEMPO functionalities

First, we point out that a non-negligible amount of LCP can effectively be grafted even when the precursor poly(butadiene) is not TEMPO-functionalized; after 180 min, the specimen denoted 0a was indeed found to contain a fraction f_LCP = 0.077 of LCP (cf. Table 1), even though n = 0 in this case. Polymerization may thus originate from thermal initiation inside PBd, whether the polymers bear TEMPOs or not. Consequently, one may challenge the role of TEMPO in the polymerization process itself and more specifically, in the extent of control achieved. We varied the reaction time t_R and the number density n of TEMPO reactive sites, through two different sets of experiments (cf. Table 1): series (i) consisted of four specimens of increasing TEMPO-functionalization, with n equal to 0, 1, 10 or 20, denoted 0a, 10a and 20a, reacted at T = 120 °C for t_R = 180 min; series (ii) consisted of six n = 20 specimens, of constant TEMPO-functionalization and reacted at the same temperature T = 120 °C but during an increasing reacting time t_R ranging from 210, 270, 390, 510, 630 to 750 min, denoted 20b to 20g; specimens 20b to 20e were reacted in pure AC8 monomer, while 20f and 20g were obtained by reacting 20d and 20e a second time, for an additional 4 h in a 50/50 mixture of toluene and AC8 monomer. In series (i), the fluorine content increases with the number density n (i.e.f_LCP = 0.160, 0.224 and 0.271 for n = 1, 10 and 20 respectively) and is in all cases larger than the fluorine content in the non TEMPO-functionalized specimen 0a (i.e.f_LCP = 0.077 for n = 0); TEMPO thus provides a way to incorporate more LCP material inside the PBd matrix.

However, the question of whether the synthesis of this extra material is controlled or not remains. From Table 1, one can verify that f_LCP increases linearly with t_R in series (ii). Such proportionality between the quantity of polymerized material and the reacting time is not characteristic of a CRP process,^1,2 the actual proof being a linear dependence with conversion of the degree of polymerization of the grafts in growth, which we cannot have access to for obvious practical reasons. However, specimens 20f and 20g, which were obtained by a second reaction performed during 4 additional hours on specimens 20d and 20e respectively, align very well with the other samples of series (ii). The polymerization can thus be stopped and re-started without affecting the apparent time-dependence. This feature is truly characteristic of a controlled polymerization and strongly suggests that the TEMPO sites are active as capping agents for the chains in growth.

To summarize, reactive sites may effectively originate either from thermally-induced radicals or from TEMPO-capped ones. Although thermal radicals seem to contribute non-negligibly to the amount of grafted LCP, they remain the minority source of polymerization compared to the TEMPO sites. Once reaction time t_R and TEMPO number density n are large enough, a controlled graft-polymerization is then achieved. For the design of our composite material, TEMPO plays a central and significant role in the success of the LCP grafting onto PBd. Since TEMPO brings an apparent linearity with t_R, the reaction time is a very simple and efficient way to control the degree of modification achieved on PBds.

The many-level structural organization of the composite

On the basis of their chemical structures,¹¹ we expected a rather high incompatibility between the elastomer and the fluorinated liquid crystal polymer used. Thus, microphase separation was expected to occur very early on during the polymerization process. The TEM micrographs (cf. Fig. 2) carried out on specimens of increasing LCP volume fraction, clearly show LCP domains of finite nanometric size, in white, in Fig. 2a–c, respectively. The nanometric LCP domains are rather polydisperse in shape and size, spherical to ovoidal, of average diameter ranging from 10 to 100 nm, approximately. Once the volume fraction f_LCP of grafted material becomes large enough (Fig. 2c), many domains become topologically connected on a larger micronic scale, leading to a connected, bicontinous morphology.

Fig. 2 Evolution of the multiscale structure of elastomer/ LCP composites with the extent of grafting. The figures show transmission electron micrographs on specimens of increasing LCP content: f_LCP = 0.185 (a); 0.250 (b); 0.380 (c) and 0.490 (d). Pictures a to c have the same length scale (scale bar 0.140 μm at the bottom left corner) and display individual microphase separated LCP domains dispersed in a homogeneous elastomeric matrix. When the amount grafted exceeds a critical value, the domains start connecting and a fractal-like, interpenetrated network appears on a larger scale (1.00 μm) in d.

On a larger scale (Fig. 2d) this connected phase does not appear to be regular, but rather fractal. The growth of LCP chains is thus accompanied by a microphase separation of LCP domains inside the elastomeric matrix to which they are topologically bound via true covalent bonds. The strength of the phase separation between LCP and PBd, as expected, is remarkable. From TEM, the LCP–PBd interface seems very sharp, a feature which was easily verified using differential scanning calorimetry (DSC) and small-angle X-ray scattering (SAXS),¹² not displayed here for obvious redundance with the TEM. DSC, in particular, showed that neither the glass transition temperature of the PBd matrix, nor the melting temperature of the LCP domains are affected by the grafting and microphase separation, since they have the values they would as separate homopolymers. Phase separation therefore has little impact on the crystallinity of the LCP inclusions. As is generally observed for diblock copolymers comprising a crystallizable block such as poly(ethylene) (PE) or poly(propylene) (PP), crystallization can be confined within a volume of finite size if the second block is soft (poly(isoprene) (PI), PBd) only in highly segregative conditions.¹³ Otherwise, spherulitic growth occurs at the expense of phase separation, and disrupts the phase (spherical, cylindrical, gyroid or lamellar) the diblock would otherwise adopt. On the contrary, when the second block is hard (polystyrene (PS)) and is the majority component, crystallization can be templated inside domains of finite size.¹⁴ It appears that, as long as the fraction of grafted LCP remains small enough, the crystallization of LCP remains confined within volumes of finite size 10–100 nm in spite of a soft PBd matrix, which seemed surprising at first.

To elucidate this feature, a pure elastomeric film was immersed and heated in perfluorononane (a non-reactive solvent) instead of the LC monomer. Consequently, no polymerization, hence no grafting, could ever take place in this film. In the end, the reacted film is not soluble in toluene anymore, as a slight thermal crosslinking has occured between PBd chains. Most probably, this crosslinking also occurs during the polymerization of the LC monomer, turning the PBd chains into a chemically crosslinked network, which may contribute to prevent the macrophase separation between LCP and PBd. Note also that as a result, these composites cannot be considered as thermoplastic materials anymore, as they will never flow, regardless how high the temperature of use might be. Fig. 1 schematically represents the typical PBd-graft-LCP composite material at different length scales, ranging from 1 μm down to a few tens of nanometres; the system consists of microphase separated, semi-crystalline LCP domains covalently bound to the PBd matrix and thus possibly acting as hard particulate fillers. Thermal crosslinking between PBd chains is represented in the outer matrix, as well as entanglements, occuring every 400 monomers in PBd.¹⁵ Microphase separated LCP inclusions, thermal crosslinks, and entanglements are all expected to play a role in the swelling and mechanical properties of the composites. Assessing these respective roles is the object of the next section. As the number density of trapped entanglements is identical in all PBd films, the specimen crosslinked in the non-reactive solvent, contains the topological crosslinks associated with entanglements. For these reasons, in the rest of the study, this crosslinked LCP-free specimen serves as a reference sample for the swelling and mechanical properties associated with the different crosslinks of the elastomeric matrix itself, whether chemical or topological.

The static swelling and mechanical behaviors

Swelling behavior: triaxial deformation. Fig. 3 shows the volume-swelling ratio Q_v as a function of the volume fraction f_LCP of LCP synthesized, for more than 30 grafted films. The crosslinked LCP-free reference was measured to swell in toluene up to Q_v,0≡Q_v(f_LCP = 0) = 42.5 cm³ cm⁻³, while all other composites were measured to swell less than this maximum value. It appears that LCP domains indeed act as physical crosslinks in the PBd matrix, they limit its swelling more than chemical and topological crosslinks do by themselves. More precisely, we find that the swelling follows two regimes: (i) regime (I) (i.e. 0 ≤f_LCP≤ 0.34), Q_v decreases sharply as f_LCP is increased; (ii) regime (II) (i.e. 0.34 ≤f_LCP≤ 1), Q_v decreases slowly as f_LCP is increased.

Fig. 3 Tri-axial network deformation and the extent of grafting: swelling. Volume-swelling ratio in toluene, as a function of the LCP volume fraction in the composite, defining two regimes, denoted (I) and (II). Insert: zoomed data, defining the critical LCP volume fraction f_LCP* and critical volume-swelling ratio Q_v* separating regime (I) from regime (II).

LCP domains do not only act as an excluded-volume in the matrix. If they did, the swelling behavior would follow the simple linear law Q_v = Q_v,0− (Q_v,0− 1)f_LCP plotted in Fig. 3 (thin line), which reaches unity only when f_LCP = 1, i.e. when the film is pure LCP, for which toluene is a bad solvent. Obviously, this behavior is not followed. LCP domains constrain the PBd matrix so that swelling is more limited than what excluded-volume effects could explain. Our understanding of this phenomenon is that a full swelling of the PBd matrix is highly hindered in the vicinity of the LCP/PBd interface, because of the covalent bonds between the two components. When percolation of LCP domains occurs for large enough amounts of grafted material (as evidenced by TEM), a continuous insoluble and undeformable LCP path exists, and the swelling of LCP-rich composites must be dramatically reduced. The swelling behavior in regime (I) may be best described by taking into account the percolation threshold of the LCP domains, which we conveniently chose as corresponding to the critical LCP content f_LCP* = 0.34 at which Q_v from regime (I) extrapolates to an asymptotic value of 1. The phenomenological equation:

Q_v = Q_v,0− (Q_v,0− 1)f_LCP/f_LCP*

including the effect of the percolation threshold, is plotted in Fig. 3 (thick line) and shows a good quantitative agreement with our experimental results in regime (I). We point out that our experimental data in regime (I) superimposes remarkably well with that presented by Berriot et al.¹⁶ on model filled elastomers. In regime (II), percolated LCP domains prevent the network deformation at the basis of isotropic swelling, for this reason it is difficult to quantitatively account for the observed behavior.

Static uniaxial deformation: reinforcement mechanisms. Let us first briefly detail the features of a stress–strain curve obtained with an elastomer, in the present case, a poly(butadiene) film simply thermally crosslinked in an oven at 90 °C overnight. Fig. 4a shows the nominal stress σ_N as well as the true stress σ, corrected for the cross-section evolution during the experiment. Once the correction has been applied, the true stress indeed shows a linear dependence with the percentage of deformation on the whole deformation range, when crosslinked enough, a poly(butadiene) network thus becomes a true elastic material. The insert of Fig. 4a shows little difference in the initial slopes of σ_N and σ, suggesting that the tensile modulus E can indeed be safely determined on the nominal stress curve. For this reason, from now on, we only present nominal stress–strain curves.

Fig. 4 Evolution of the static mechanical signatures of the composites with the extent of grafting. (a) Static deformation curves showing the nominal and true stresses as a function of deformation ε, on a thermally crosslinked poly(butadiene) melt deformed at a deformation rate of 500 mm min⁻¹. Once corrected for cross-section evolution, the true stress is perfectly proportional to deformation. Insert: zoom on the data between 0 and 10% deformation, showing the initial slopes coincide. (b) and (c) Nominal stress as a function of ε for: (b) specimen f_LCP = 0.377 at deformation rates 1, 10, 75 and 150 mm min⁻¹; (c) specimens f_LCP = 0.240 (A), 0.297 (B) and 0.365 (C), deformed at the same deformation rate. Both inserts are zooms on the data between 0 and 20% deformation.

We now review the main characteristics of stress–strain curves typically obtained with our composites. The LCP volume fraction, swelling ratios, rate of deformation, elastic modulus and maximum elongation at break of these specimens, are summarized in Table 2, together with those of the LCP-free specimen crosslinked in the non-reactive solvent and which serves as a reference. Note that the latter swells significantly more than all other specimens (Q_v = 42.4 cm³ cm⁻³), has a small tensile modulus (E = 0.45 MPa) and a very large deformation at break (ε_r = 1200%). The modulus measured is smaller than what one would expect from the “entanglement modulus” (roughly 3 times the shear plateau modulus) which should be about 3 MPa for PBd. As the crosslinked film was extracted in toluene prior to any investigation, the sol fraction removed was found to be rather large. This suggests that this reference network is in fact very lightly crosslinked and that dangling ends probably constitute a vast majority of the material.

Table 2 Tri-axial (swelling) and uniaxial (stretching) static deformation data on selected specimens

Sample name	f PAC8 ^a	Swelling ratio QV^b/cm^3 cm^−3	V ^c/mm s^−1	E ^d/MPa	Max. εr^e (%)
a PAC8 volume fraction. b Volume-swelling ratio in toluene. c Rate of deformation imposed. d Young modulus as derived from the nominal stress–strain curves at small deformation. e Maximum elongation at break, measured during a stress–strain experiment.
Reference	0	42.4	100	0.45	1200
S	0.376	5.35	1	4.3	380
			10	9.6	450
			75	10.0	540
			150	10.5	620
A	0.240	13.1	100	1.6	850
B	0.297	6.2	100	3.0	300
C	0.365	5.9	100	6.8	260

---

Fig. 4b shows nominal stress–strain curves obtained on a grafted specimen with f_LCP = 0.376 (denoted S) deformed at different rates. The tensile modulus E, as well as the maximum elongation at break ε_r obviously increase with the deformation rate (cf. Table 2 for values) which is generally not the case for semi-crystalline materials, but is characteristic of elastomers, a feature interpreted as originating from the relaxation in a viscoelastic material under strain. A large enough deformation rate was then adopted to get deformation rate-independent measures. In Fig. 4c, we plot the nominal stress–strain curves obtained on three grafted specimens denoted A, B and C, of increasing LCP content f_LCP = 0.240, 0.297 and 0.365 and deformed at the same rate of 100 mm min⁻¹. For small deformations, the composites are truly elastic and deformation is reversible. Moreover, the larger the LCP fraction, the larger the elastic modulus, i.e. from 1.6 to 6.8 MPa, and the smaller the deformation at break, i.e. from 850 to 260% (see Table 2). It is also interesting to note that the swelling ratio decreases at the same time, from 13.1 to 5.94 cm³ cm⁻³. As is usual for an elastic polymeric network, mechanical and swelling properties are related. This will be detailed further on.

Fig. 5 shows the outcome of stress–strain experiments carried out on more than 30 composites. Strikingly, two different behaviors are observed, which almost exactly correspond to the regimes (I) and (II), identified in the swelling behavior; the increase of E with f_LCP is much more pronounced in regime (II) than in regime (I). Note that beyond f_LCP≅ 0.06–0.08, the tensile modulus E, which ranges from approximately 0.5 to 100 Mpa, rapidly increases with f_LCP. Chemical and topological crosslinks, which control the mechanical properties of the elastomeric network, then become negligible compared to the reinforcement effect of the LCP inclusions. Almost three orders of magnitude separate the modulus of the LCP-free reference specimen (E₀ = 0.45 Mpa) from the most LCP-rich specimen obtained so far, i.e.f_LCP = 0.60. However, LCP/PBd composites still behave as elastomers, although not as deformable as a simply crosslinked and entangled network such as the crosslinked LCP-free reference which breaks at 1200% deformation. The composite can withstand large deformations of several hundred percents before breaking occurs. All these properties are those of a filled elastomer, and the LCP domains play the role of hard particulate fillers which mechanically reinforce the elastomeric PBd matrix.

Fig. 5 Uniaxial network deformation and the extent of grafting: stretching. Tensile modulus E of composite films as a function of f_LCP. For f_LCP≤ 0.34 and f_LCP≥ 0.34, the lines were respectively computed according to the Kerner's and Ball and Brown's models (see text for details). Insert: tensile modulus E as a function of the volume-swelling ratio Q_v. For f_LCP≤ 0.34 and f_LCP≥ 0.34, the two lines are power laws fitted to the experimental data, with exponents −1.4 and −4.0, respectively.

Depending on the strength of the adhesion between the matrix and the filler, and on the amount and structure of incorporated filler, different models have been developed to describe reinforcement. Graft polymerization, however, provides ad hoc adhesion between PBd and LCP; debonding of the matrix from the filler (i.e. the so-called “weak adhesion”) is unlikely. We thus introduce only models pertaining to strong adhesion, for non-percolated and percolated fillers, respectively:

(i) If filler particles remain well dispersed and separated, numerous models¹⁷ were designed to account for the evolution of E with the filler volume fraction ϕ. In particular, Kerner^18,19 predicts E = E₀(1 + ABϕ)/(1 −PBϕ), where E₀ and E₁ are, respectively, the elastomer and filler moduli, A = (7 − 5ν)/(8 − 10ν), ν = 0.5 being the Poisson ratio of an elastomer, B = (E₁/E₀− 1)/(E₁/E₀ + A) and P = 1 + (1 −ϕ)ϕ/ϕ*². The model explicitely takes into account the maximum packing ϕ* of the inclusions before close contact and percolation occur, a refinement never accounted for in the earliest models designed by Einstein,²⁰ Smallwood,²¹ Guth and Gold.²² The latter mainly consisting in Virial-like developments, they all fail when ϕ becomes too large. As ϕ approaches ϕ*, a marked increase of E is usually observed in filled elastomers, an event impossible to capture in Virial-like models, as the volume of the filler particle itself is omitted in the calculations.²³

(ii) When percolation of filler particles occurs, Witten et al.²⁴ described the tensile modulus of the material using the Ball and Brown equation: E = E₁×ϕ^β. Exponent β is related to the connectivity and fractal dimension of the filler agregates. Its use was confirmed by Heinrich and coworkers,^25,26 who showed β may adopt different values depending on the type of percolation occuring in the medium, namely β = +4.5 for a reaction-controlled percolation and +3.5 for the diffusion-controlled one.

While the value E₀ of the modulus of an equivalent crosslinked PBd matrix is set at 0.45 MPa as determined experimentally, and the percolation filler volume fraction ϕ* is simply taken equal to f_LCP* = 0.34, E₁ and β remain the only unknown parameters. Fitting procedures are launched on both domains, the experimental data in domains (I) and (II) are fitted to the Kerner and Ball and Brown models, respectively, to determine the values of E₁ and β which best satisfy a minimization procedure between experimental and predicted data. Note, however, that since both models explicitely take into account the modulus E₁ of the hard domains, they are not independent, the value of E₁ must be set the same for both. The two fitting procedures are thus linked and must be carried out accordingly. In Fig. 5, we superimpose onto the experimental data the best fits (in a least-square sense); the models very satisfactorily approach the experimental data for a modulus E₁ = 1.10 GPa of the LCP domains comparable to values found for semi-crystalline polymers like poly(propylene), poly(ethylene), poly(amide-6), and β = +4.5, which suggests a reaction-controlled percolation completely consistent with the method used to create the composites.

One may wonder of the relevance of a more molecular, Flory-like approach. Entropic elasticity being a common contribution to the free energies of a network either uniaxially stretched or triaxially deformed by swelling in a good solvent, the Flory descriptions of tensile modulus and swelling ratio can be explicitely related via^27,28E∝Q_v^−5/3. The Flory theory is accurate for polymer networks which are not extensively crosslinked, i.e. for volume-swelling ratios typically obeying Q_v≥ 10. The insert of Fig. 5 shows the tensile modulus E as a function of the volume-swelling ratio Q_v. In regime (I), which approximately satisfies Q_v≥ 10, we observe a scaling law whose exponent −1.4 is rather close to the value −5/3 = −1.7 predicted by Flory. On the other hand, an apparent scaling law of exponent −4.0, for which we have no theoretical explanation for now, is observed for regime (II) where swelling is hindered by percolation of the LCP domains.

The dynamic mechanical behavior in temperature

Figs. 6a and 6b show typical curves of respectively, the storage G′ and loss G″ moduli as a function of temperature, obtained on specimens with different LCP contents, namely f_LCP = 0, 0.165, 0.250, 0.363 and 0.521. For both sets of curves a sharp transition occurs around +78 °C, both moduli drop by up to two orders of magnitude and the larger the LCP content in the composite, the steeper the drop. The insert of Fig. 6b shows the corresponding portion of a DSC trace, the fusion peak associated with the transition exactly spreads from 60 to 82 °C, with a peak. The drops in the moduli thus correspond to the fusion of the LCP fraction of the composite. However, the composite displays a peculiar property:

Fig. 6 Evolution of the dynamic mechanical signatures of the composites in temperature. (a) Storage G′ and (b) loss G″ moduli as a function of temperature upon heating, for slowly cooled composites of increasing LCP volume fraction. Insert: the range 60–82 °C of the transition in a typical DSC curve. (c) Evolution of the storage G′ and loss G″ moduli upon heating, of composite f_LCP = 0.487, after different thermal treatments; three quenches from 100 °C down to +10, +30 and +50 °C and a reference slow cooling.

(i) For T≤T_f, the LCP domains are semi-crystalline and hard, and the larger the LCP content, the larger the value of the plateau storage modulus G′, an observation consistent with the static measurement of the tensile modulus E shown in the previous section. The crystalline LCP inclusions then reinforce the composite.

(ii) For T≥T_f, the LCP domains consist of a viscous liquid, the higher the LCP content, the lower the values of the plateau storage and loss moduli. Liquid LCP inclusions now soften the composite.

The LCP inclusions can therefore act as fillers or as softeners, depending on the temperature at which the material is used. It is now obvious that the crystallinity of the LCP domains in the PBd matrix must control the extent of reinforcement of the elastomer. Different cooling processes were applied to a composite with f_LCP = 0.487. After heating at a temperature, 100 °C, much larger than T_f, we either slowly cooled the specimen to room temperature or quenched it down to different temperatures T_quench smaller than T_f, namely 10, 30 and 50 °C. Fig. 6c shows G′ and G″versus temperature, measured as temperature was increased again. For G′ as well as G″, all four curves superimpose for T≥T_f; once the LCP domains are liquid, the composite mechanical properties no longer depend on thermal history. Similarly, for T≤T_quench, all curves superimpose onto the curve corresponding to a slow cooling, and only depart from this reference curve once the quenching temperature is reached. Indeed, for T_quench≤T≤T_f, each curve significantly deviates from the slow cooling reference curve, and the larger ΔT = T_f−T_quench, the larger the deviation. In the particular case of the quenching at 10 °C, G′ and G″ present a remarkable non-monotonic behavior, when T≥T_quench, the moduli first decrease until a minimim is reached, beyond which they increase and decrease again, as the smectic-B-to-isotropic transition is approached. In semi-crystalline polymers, it is well-known that the cooling process can greatly affect nucleation, spherulitic growth and the final degree of crystallinity. In particular, quenching sometimes results in a non-monotonic behavior of the degree of crystallinity, when the material is heated again. This phenomenon, known as “fusion-recrystallization”, results from relieved local mechanical constraints which unexpectedly allow for an increase in the degree of crystallization, although temperature is being increased. By analogy, the non-monotonic behavior observed for T_quench = +10 °C, is a direct consequence of a thermal history-dependent crystallinity in the LCP domains. LCP grafting onto poly(butadiene) therefore provides this elastomer with peculiar properties, which only belong to the field of semi-crystalline polymers.

Conclusions

As a conclusion, we successfully carried out the in situ graft-polymerization of a fluorinated liquid crystal polymer onto elastomeric chains functionalized with TEMPO from which polymerization was initiated. As such materials are highly incompatible, a natural, yet controlled microphase separation occurs, leading to a composite organized from a nano- to a microscopic level. The physical characteristics of each component are unaffected by the microphase separation and are retained in this final, original LCP/elastomer composite. The NM-CRP process can be stopped and re-started, and thus allows for an easy design of all-polymer hard/soft composites. A reliable control of the amount of LCP modification offers a panel of structured materials, from nanometric LCP inclusion embedded in an elastomer for small degrees of modification, to co-continuous (interpenetrated) LCP/elastomer networks at large degrees of modification.

The composites de facto combine physical properties of semi-crystalline and elastomeric materials, with unexpected, and unheard of, outcomes. Unlike inorganic fillers like fumed silica or glass beads, usually introduced in elastomers by a mechanical blending, LCP inclusions bring additional, very specific features to the elastomer, as the composite remains elastomeric, but is also thermosensitive because the LCP inclusions are. While LCP inclusions act as reinforcers at room temperature where they are harder than the elastomeric matrix, they act as tougheners at high temperature as they are liquid and then softer than the elastomer.

Interestingly, if deformed under the fusion temperature T_f, a co-continuous composite irreversibly retains its shape due to the hard LCP phase, while it quickly returns to its original shape once heated above T_f. By investigating the dynamic mechanical response of a composite subjected to a rapid change of the temperature inside the rheometric chamber (from above the fusion temperature to below and vice versa), we found that the composites in fact react very fast (within less than a second) to a temperature jump.²⁹ The fast transition kinetics of the LCP domains, from the molten state to the crystalline one, obviously provide the composite material with the ability to respond almost immediately and reversably, to an external stimulus like temperature. Artificial muscles based on alternating nematic-B/rubbery lamellae, as proposed by de Gennes,⁶ are one of many examples of systems relying on such fast relaxation and response times. In a more general way, a variety of novel composites could also be designed following the method, provided the graft is carefully chosen to impart the material with the desired physico-chemical properties and responses to different stimuli such as UV, and electric or magnetic fields.

Acknowledgements

The authors are indebted to B. Vuillemin and S. Régénet for providing the functionalized polymers, to D. Basset and P. Coupart for the TEM photographs and to S. Tencé-Girault for carrying out the SAXS/WAXS experiment. The present work was carried out in 1998 in the Elf-Atochen/CNRS joined laboratory (UMR 167) in the Levallois-Perret, France.

References

1. P. Nicol and M. Plechot, U. S. patent 5 919 871, 1999.
2. M. Abbasian, H. Namazi and A. A. Entezami, Polym. Adv. Technol., 2004, 15, 606–611.
3. D. Greszia and K. Matyjaszewski, Macromolecules, 1996, 29, 7661–7670.
4. K. Matyjaszewski, Controlled/living radical polymerization: progress in ATRP, NM, and RAFT, ACS, Washington, DC, 2000.
5. H. Pernot, M. Baumert, F. Court and L. Leibler, Nat. Mater., 2002, 1, 54–58.
6. P. G. de Gennes, C. R. Acad. Sci., Ser. IIb: Mec., Phys., Chim., Astron., 1997, 324, 343–348.
7. M.-H. Li and P. Keller, Philos. Trans. R. Soc. London, Ser. A, 2006, 364, 2763–2777.
8. B. R. Ratna, D. L. Thomsen and P. Keller, Proc. SPIE-Int. Soc. Opt. Eng., 2001, 4329, 233–237.
9. D. L. Thomsen, P. Keller, J. Nacirir, R. Pink, H. Jeon, D. Shenoy and B. R. Ratna, Macromolecules, 2001, 34, 5868–5875.
10. 
    .
11. See Fig. S1 entitled Chemical Structures in the ESI†.
12. See Fig. S2 and S3 for DSC and SAXS data, respectively and the section in the ESI entitled DSC and SAXS characterizations of the composites†.
13. Y.-L. Loo, R. A. Register and A. J. Ryan, Macromolecules, 2002, 35, 2365–2374.
14. Y.-L. Loo, R. A. Register, A. J. Ryan and G. T. Dee, Macromolecules, 2001, 34, 8968–8977.
15. S. M. Aharoni, Macromolecules, 1983, 16, 1722–1728.
16. J. Berriot, F. Lequeux, H. Montes and H. Pernot, Polymer, 2002, 43, 6131–6138.
17. D. J. Kohls and G. Beaucage, Curr. Opin. Solid State Mater. Sci., 2002, 6, 183–194.
18. S. N. Maiti and B. H. Lopez, J. Appl. Polym. Sci., 1992, 44, 353–360.
19. L. E. Nielsen and R. F. Landel, Mechanical Properties of Polymers and Composites, Marcel Dekker, New York, 1994, ch. 7.
20. A. Einstein, Ann. Phys., 1905, 17, 549–560.
21. H. M. Smallwood, J. Appl. Phys., 1944, 15, 758–766.
22. E. Guth and O. Gold, J. Appl. Phys., 1945, 16, 20–25.
23. Virial expansion of the Kerner model for small filler content, leads to E/E₀− 1 ≅ aϕ + bϕ² + …, where a = B(A + 1) and b = B[p + B(A + 1)]. For a filler of modulus infinitely larger than that of the elastomer, i.e.E₁≫E₀, generally the case for hard fillers in elastomers, we compute a = 2.5 and b = 14.2, Kerner extrapolates to the Guth and Smallwood if the filler content is small enough.
24. T. Witten, M. Rubenstein and R. Colby, J. Phys. II, 1993, 3, 367–383.
25. M. Klüppel and G. Heinrich, Rubber Chem. Technol., 1995, 68, 623–655.
26. M. Klüppel, R. Schuster and G. Heinrich, Rubber Chem. Technol., 1997, 70, 243–255.
27. P. J. Flory, Principles of polymer chemistry, Cornell University Press, Ithaca, New York, 7th edn, 1969.
28. P. J. Flory and J. Rehner, Jr., J. Chem. Phys., 1943, 11, 512–520; P. J. Flory and J. Rehner, Jr., J. Chem. Phys., 1943, 11, 521–526; P. J. Flory and B. Erman, Macromolecules, 1982, 15, 800–806.
29. See Fig. S4 and S5 for time-dependent responses of a composite to a temperature jump (decrease and increase) and the section in the ESI entitled Reactivity of a composite to an external stimulus : Response to a temperature jump†.

---

Footnote

† Electronic supplementary information (ESI) available: Differential scanning calorimetry and small-angle X-ray scattering data, as well as the reactivity of the composites to sudden temperature changes. See DOI: 10.1039/b711928c

---