Computer simulation of anisotropic polymer brushes
Alla I.
Tupitsyna
*ab,
Anatoly A.
Darinskii
b,
Igor
Emri
c and
Michael P.
Allen
d
aInstitute of Problems of Mechanical Engineering, Russian Academy of Sciences, St. Petersburg, Russia. E-mail: atupitsyna@mail.ru
bInstitute of Macromolecular Compounds, Russian Academy of Sciences, St. Petersburg, Russia
cCentre of Experimental Mechanics, University of Ljubljana, Slovenia
dDepartment of Physics, and Centre for Scientific Computing, University of Warwick, Coventry, UK CV4 7AL
First published on 5th November 2007
Abstract
A polymer brush with chains consisting of anisotropic monomers, in a liquid consisting of free spherical particles, is studied by the molecular dynamics method. It is shown that, at some value of the concentration of spheres, a liquid-crystal or oriented-domain transition occurs in the brush. A densely-grafted brush and a sparsely-grafted brush are studied; for this system, the transition point seems not to depend strongly upon the grafting density. In the case of the densely-grafted brush, a liquid-crystal transition proceeds via an intermediate microphase segregated state. One microphase, located near the grafting surface, is characterized by high density and high degree of ordering of monomers. This part of the brush contains only a small concentration of spheres. On the periphery of the brush, a disordered microphase with low monomer density is located. This part of the brush is enriched with spherical particles. The two microphases are separated by a well-defined boundary. On increasing the sphere concentration, the boundary between microphases shifts towards the periphery, and eventually the ordered microphase extends through the whole brush volume. The monomers of the densely-grafted brush in their ordered state form different structures, namely, a smectic structure at relatively low values of sphere concentration, and a structure of orientationally ordered domains at the higher sphere densities.
Introduction
Polymer brushes formed by long chains, end-grafted to an impenetrable surface, are well-known examples of nanostructures.1–6 They can be used for surface modification, for controlling the permeability of membranes, for regulating the particle interaction in colloids, etc.Polymer brushes consisting of chains composed of rigid mesogenic segments are of special interest. Such segments are characterized by orientational anisotropy of interactions or by a geometric anisotropy, determined by the elongation, p = ℓ/w, where ℓ is the length of a segment, and w is its width. In the following, we shall call these “anisotropic brushes”. Anisotropic brushes are capable of liquid crystal (LC) ordering at decreasing temperature (thermotropic LC-transition) or at increasing concentration of anisotropic mesogenic groups (lyotropic LC-transition).
Thermotropic phase transitions in anisotropic brushes are caused by an increase in the energy of orientational interactions compared with the energy of thermal motion. Such transitions have been studied during the last several years.7–10 It has been shown that three states characterized by different degrees of monomer ordering are possible for the anisotropic brush. They are a conventional brush (CB) state, a liquid crystal (LC) state and an intermediate microsegregated brush (MSB) state. The transition from the disordered CB-state to the highly ordered LC-state through the MSB-state is a first-order phase transition and takes place at a definite critical temperature.
Lyotropic LC-transitions in anisotropic brushes have been investigated to a much lesser extent. It is well known11–16 that solutions of chain molecules, which consist of geometrically anisotropic monomers, can form nematic and smectic LC phases with increasing chain concentration. The LC phases are formed via phase transitions. On the other hand the growth of chain concentration in the anisotropic brush induced by an increasing grafting density does not lead to a phase transition. (The grafting density is defined as the number of chains per unit grafting area.) In this case one can observe only a gradual development of the monomer ordering caused by increased chain stretching. A lyotropic phase transition in the anisotropic brush, as was shown theoretically,17,18 is possible under conditions which increase the monomer density and simultaneously decrease the brush height and the chain stretching. It may be caused by compression of the brush or solvent quality deterioration. In the latter case the depletion of the isotropic attraction between the monomers and the solvent particles in the brush leads to brush compression and, as a result, to the phase transition.9
It is interesting to consider the problem of lyotropic phase transitions in a brush with pure repulsive interactions between the particles. In this case, the state of the system will be determined only by geometric factors: the shapes and the sizes of the particles and the entropy associated with packing. An example is the study of liquid crystal anchoring by an anisotropic brush, where both the brush monomers and liquid particles consisted of identical repulsive ellipsoids.19–21 In that work, an anchoring transition was observed as a function of grafting density. In the current paper, we are interested in the behaviour of a conventional brush (CB), whose chains consist of geometrically anisotropic segments, when isotropic spherical particles are added to the system.
Several studies published during the last decade22,33 have focused on the problem of phase transitions in mixtures of different-shaped hard-core particles. Ref. 22 reports a molecular dynamics simulation of the phase transitions among isotropic, nematic and smectic phases in a binary mixture of rod-like molecules and hard spheres, where each rod-like molecule was composed of a linear chain of 7 hard spheres (elongation p = 8) connected with strong springs. It was shown that the addition of hard spheres shifts the region of existence of nematic and smectic phases to higher densities. Phase separation was observed in the smectic phase. The structure was observed to be composed of the ordered rod-rich layers separated by hard sphere layers. By further adding spheres, another new phase appeared, where domains of rods were dispersed randomly in the sphere-rich environment. An entropy theory of LC-phase transitions in binary mixtures of hard spherocylinders with different lengths has been developed.23–26 (A spherocylinder is a cylinder with two hemispherical end-caps, of the same diameter as the width of the cylinder.) A mixture of hard spherocylinders and hard spheres was studied26 as a special case. The phase diagram for a mixture of spheres with diameter D and spherocylinders with width equal to D and cylinder length 7D (overall elongation p = 8) was presented in the paper. When the pressure (total density) is large enough and the sphere concentration in the mixture is not too high (<60%) microseparation of the components occurs and the spherocylinders form nematic and smectic LC-phases in sequence. At larger values of the sphere concentration, an isotropic state and a two-phase state are observed at different pressures.
It is reasonable to assume that phase separation of anisotropic and isotropic particles is also possible in the case of an anisotropic brush when spherical particles are added. Such models have not previously been studied theoretically or experimentally, as far as we know.
Model and method
The anisotropic chain in our model is a sequence of nm = 20 identical spherocylinder monomers, connected to each other at the ends with elastic bonds. The cylinder length is L = 3D, where D is the diameter, so the monomer elongation is p = 4 and the overall contour length Lc = 80D. Anisotropic brushes are formed of a number, Nc, of such anisotropic chains, end-grafted to an impenetrable surface. The brush is in contact with a liquid of Ns spherical particles with diameter D (Fig. 1). We have also considered a brush formed of isotropic chains, composed of spheres identical to those of the liquid, connected to each other with bonds identical to the bonds in the anisotropic brushes. The contour length of the chain in the isotropic brush is made the same as in the anisotropic brush, i.e. the isotropic macromolecule consists of 80 spherical monomers. | ||
| Fig. 1 The model of the system formed by an anisotropic polymer brush in the presence of free isotropic particles. | ||
The simulations were carried out for systems placed in a cuboidal MD cell of dimensions X×Y×Z. Periodic boundary conditions were imposed along the x and y axes of a Cartesian coordinate system. The first monomer of each chain was connected to the plane z = 0 with an elastic bond. The condition of impermeability was imposed both on the planes z = 0 (grafting surface) and z = Z. Taking D as a unit of length, a dimensionless grafting density is defined as d = NcD2/XY.
Potentials
The spheres interact in accordance with a modified Lennard-Jones potential, corresponding to a pure repulsion: | (1) |
We have used a repulsive Kihara potential34,35 to describe pair interactions between spherocylindrical monomers. This takes a similar form Ur(cjk) where cjk is the closest distance between the line segments defining the long axes of cylinders j and k; cjk can be defined in terms of the unit vectors ej and ek, oriented along the long axes of the spherocylinders, and their centre–centre separation r. A graph of Ur(r), with sketches illustrating the relationship between r and cjk, corresponding to different orientation vectors  , ej and ek, is shown in Fig. 2. To describe the interaction between the sphere and the spherocylinder, a similar potential was used, where cjk is the closest distance between the centre of the sphere and the cylinder axis.
, ej and ek, is shown in Fig. 2. To describe the interaction between the sphere and the spherocylinder, a similar potential was used, where cjk is the closest distance between the centre of the sphere and the cylinder axis.
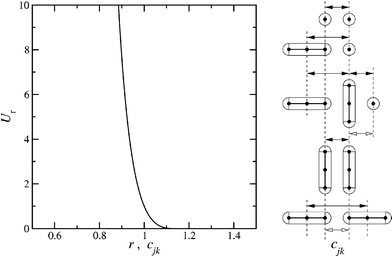 | ||
Fig. 2 (a) Pair interaction potential Urversus separation. (b) Sketches showing the relation between closest separation cjk (open arrowheads) and centre–centre separations r = rjk = |rjk| = |rj−rk| (filled arrowheads) for simple examples of relative orientations. Top to bottom: two spheres; spherocylinder–sphere with  ; two spherocylinders with (on the left) ; two spherocylinders with (on the left)  and (on the right) and (on the right)  ; two spherocylinders with ; two spherocylinders with  ; and finally two spherocylinders with ; and finally two spherocylinders with  . . | ||
The bonds between neighbouring monomers in the chains are described by an elastic potential:
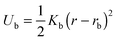 | (2) |
Molecular dynamics techniques
The translational and rotational equations of motion were numerically integrated according to the leapfrog algorithm for the constant-NVT ensemble, i.e. for constant number of particles, volume and temperature. In preparing some initial systems, the MD cell has been compressed at constant pressure P; in these cases a correspondingly modified form of the leapfrog algorithm was used. The presence of the upper and lower impenetrable surfaces was accounted for by an elastic collision rule applied whenever wall–particle overlaps were detected. The masses of all the particles in our model were taken equal to unity (M = 1). The characteristic time for the Lennard-Jones potential, , was used as the time unit. The integration step varied from 4 × 10−3τ to 6 × 10−3τ; its precise value depended upon the system and upon the stage of the simulation. The directions of the translational motion velocity vectors were initially defined randomly on the lattice and their magnitudes were taken equal to
, was used as the time unit. The integration step varied from 4 × 10−3τ to 6 × 10−3τ; its precise value depended upon the system and upon the stage of the simulation. The directions of the translational motion velocity vectors were initially defined randomly on the lattice and their magnitudes were taken equal to  for all the particles (Tin is the prescribed initial temperature of the system). The directions of the initial spherocylinder angular velocities were chosen randomly to lie along lattice vectors perpendicular to the corresponding axis vector ej and their magnitudes were taken equal to
for all the particles (Tin is the prescribed initial temperature of the system). The directions of the initial spherocylinder angular velocities were chosen randomly to lie along lattice vectors perpendicular to the corresponding axis vector ej and their magnitudes were taken equal to  where I is the moment of inertia.
where I is the moment of inertia.
Systems under investigation
We have performed simulations of a set of constant-NVT systems, characterized by different values of N and V. The box sizes for each system were determined by the chosen value of the brush grafting density d, number of chains Nc and the value of the brush height H. The description of systems studied in the paper and corresponding MD cell dimensions are presented in Table 1.| d | N c | X/D, Y/D | Z/D | |
|---|---|---|---|---|
| Anisotropic brush in empty cell (Ns = 0) | 0.02 | 4 | 14 | 65 |
| 16 | 28 | 65 | ||
| 36 | 42 | 65 | ||
| 0.12 | 16 | 11.5 | 65 | |
| 36 | 17.3 | 65 | ||
| 0.24 | 16 | 8.17 | 80.2 | |
| 36 | 12.25 | 80.2 | ||
| 0.37 | 16 | 6.57 | 80.2 | |
| Anisotropic brush plus spherical particles (Ns > 0) | 0.02 | 4 | 14 | 65 |
| 0.12 | 16 | 11.5 | 65 | |
| Isotropic brush (Ns≥ 0) | 0.12 | 16 | 11.5 | 65 |
| Anisotropic chain (Ns > 0) | 0.01 | 1 | 10 | 65 |
System preparation
The starting conformations of the anisotropic brushes were created on a simple cubic lattice with lattice constant equal to D. Grafting points were given coordinates (xg, yg, 0) = (7(i− 1)D, 7(j− 1)D, 0), with . Such arrangements of grafting points correspond to grafting density d≈ 0.02. Each chain configuration was constructed by a self-avoiding random walk method on the aforementioned cubic lattice, in the space delimited by a cuboid with height Z = 65D (usually, it exceeded the brush height by 10D− 12D). The base of the cuboid was a square around the grafting point with vertices at (xg± 3D, yg± 3D, 0). Each monomer occupied on the lattice four consecutive sites in a direction randomly chosen from the five possible Cartesian ones (excluding the negative z direction); if (x(4)m, y(4)m, z(4)m) represents the end (4th site) of monomer m, then the first site (the beginning) of monomer m + 1 satisfies (x(1)m+1, y(1)m+1, z(1)m+1) = (x(4)m, y(4)m, z(4)m + D). After the construction of all chains, the spherical particles were placed at the free sites of the lattice at regular intervals (determined by the desired concentration) along each of the axes. The starting conformations for the isotropic brush were constructed according to a similar algorithm.
. Such arrangements of grafting points correspond to grafting density d≈ 0.02. Each chain configuration was constructed by a self-avoiding random walk method on the aforementioned cubic lattice, in the space delimited by a cuboid with height Z = 65D (usually, it exceeded the brush height by 10D− 12D). The base of the cuboid was a square around the grafting point with vertices at (xg± 3D, yg± 3D, 0). Each monomer occupied on the lattice four consecutive sites in a direction randomly chosen from the five possible Cartesian ones (excluding the negative z direction); if (x(4)m, y(4)m, z(4)m) represents the end (4th site) of monomer m, then the first site (the beginning) of monomer m + 1 satisfies (x(1)m+1, y(1)m+1, z(1)m+1) = (x(4)m, y(4)m, z(4)m + D). After the construction of all chains, the spherical particles were placed at the free sites of the lattice at regular intervals (determined by the desired concentration) along each of the axes. The starting conformations for the isotropic brush were constructed according to a similar algorithm.
For the systems with values of grafting density d > 0.02, an initial system constructed as described above was compressed along the x and y axes at fixed pressure P using the Nosé–Hoover barostat. The periodicity of the distribution of grafting points during the deformation was preserved. Care was taken to compress at a rate that avoided unphysical bond stretching or ultra-high local densities. After the cell attained the desired sizes, the constant-NVT ensemble simulation began.
The full simulation time for each system was 40–45 × 103τ. The temperature for the majority of systems was set to T = 1.5ε/kB. In some cases, for ensembles with high density, it was necessary to raise the temperature to T = 1.8 − 2.0ε/kB because of the slowest speed of the process (“freezing” of the system) at lower T. This increase in temperature accelerates the kinetics, and does not greatly affect the structural and thermodynamic properties of the system, because all the interparticle interactions are strongly repulsive, and the spring potentials are also very strong.
Calculation of system properties
The overall packing fraction of free spherical particles ηs is defined as follows:| ηs = NsVs/V | (3) |
For the description of the structure of the brush, time-averaged profiles of the main characteristics were calculated. Local number densities of free spheres ρs(z) and brush monomers ρm(z) are defined by
 | (4) |
 | (5) |
The number density profile of chain ends ρe(z) is calculated as in eqn (5), except that the sum is restricted to the monomers at the ends of the chains:
 | (6) |
Here the sum is over all chains, and zce is the coordinate of the end-point of the terminal monomer of chain c. This number density is related to the chain-end probability density ge(z) through the grafting density d:
| ge(z) = ρe(z)D2/d = ρe(z)XY/Nc | (7) |
It is convenient to note the ideal forms of the brush profiles. For so-called “parabolic brushes”9 the density profile is well approximated by the equation
| ηm(z) = η(0)m (1 −z2/H2) | (8) |
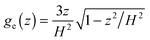 | (9) |
Expressions of type (8,9) are valid for isotropic brushes in a good solvent (CB brushes) at not-too-strong stretching of chains. It is known that isotropic brushes are parabolic over a reasonably wide range of values of d. So for the model of a brush on a simple cubic lattice, noticeable deviations from the above equations were observed only at d > 0.5.5–7
The profiles of nematic director (preferred alignment direction of monomers) and order parameter are obtained from the matrix Q(z) with elements
 | (10) |
Here α, β = x, y, z, emα, emβ are components of the axial unit vector of a spherocylinder, and δαβ is the Kronecker symbol. In practice, Qαβ(z) is estimated by dividing the system into layers as above, and computing the number-average of the quantity in square brackets over all monomers lying within a layer close to position z. The order parameter, s(z), is the largest eigenvalue of Q(z) and the nematic director n(z) is the corresponding eigenvector. For systems in which the director is oriented along the z axis, an equivalent definition of the order parameter profile is
 | (11) |
The equilibration of the system was monitored through the mean values of the brush packing fraction [ηm], and order parameter [s], calculated as follows:
 | (12) |
 | (13) |
Results and discussion
Anisotropic brushes in an empty box
The initial stage of our investigation was the simulation of a set of anisotropic brushes with different values of the grafting density d in an empty MD box (“empty brushes”). The data characterizing the behaviour of the “empty” 16-chain (Nc = 16) anisotropic brush with increase of grafting density are presented in Figs. 3, 4. On increasing d, the brush stretches along the z axis (Fig. 3a); thus a gradual growth of order parameter is observed (Figs. 3c–d, 4c), together with a displacement of the z-coordinates of chain free ends towards the periphery of the brush (Fig. 3b). | ||
| Fig. 3 Anisotropic brush in vacuum. Characteristics of the structure at the following values of grafting density d: 0.02; 0.12; 0.24; 0.37. (a) monomer density profiles ηm(z); (b) free-end distribution function ge(z); (c) order parameter profile s(z), where solid lines are calculated viaeqn (10) and dashed lines from eqn (11) of the text; (d) z-component of the director profile n(z). | ||
![Anisotropic brush in vacuum. Comparisons of (a) ηm(z) with eqn (8) and (b) ge(z) with eqn (9) at different values of brush height H arising from the following values of grafting density d: 0.02, 0.12, 0.24. Dashed lines correspond to analytical expressions. (c) Average value of order parameter [s] versus grafting density d. (d) Brush height Hversusd1/3.](/image/article/2008/SM/b711649g/b711649g-f4.gif) | ||
| Fig. 4 Anisotropic brush in vacuum. Comparisons of (a) ηm(z) with eqn (8) and (b) ge(z) with eqn (9) at different values of brush height H arising from the following values of grafting density d: 0.02, 0.12, 0.24. Dashed lines correspond to analytical expressions. (c) Average value of order parameter [s] versus grafting density d. (d) Brush height Hversusd1/3. | ||
The density profile and the chain free end distribution function ge(z) for the sparsely-grafted brush (d = 0.02) are well approximated by the formulae appropriate to a parabolic brush, eqns (8,9) (Figs. 4a,b). For brushes with higher values of grafting density, d≥ 0.12, expressions (8,9) are not accurate (Fig. 4a,b), and the brush height must be estimated from the density profile using ρm(H) = 0.001. As mentioned earlier, the parabolic brush profile is seen for isotropic brushes in a good solvent at not-too-strong stretching of chains.
For brushes consisting of macromolecules with rigid anisotropic segments, the anisotropy of monomers is an additional factor determining chain stretching; therefore it is not unexpected that the range of validity of expressions (8,9) for such brushes must be moved towards smaller values of d, as observed in our simulations.
The brush height is observed to vary with grafting density as H∝d1/3 (Fig. 4d), as is typical for CB brushes in the Gaussian regime of elasticity (i.e.E∝H2; where E is the free energy of stretching). Thus, in the examined interval of grafting density values 0.02 ≤d≤ 0.37, an anisotropic brush of this kind, with repulsive interactions between monomers in a vacuum, exists in the CB regime: a vacuum in this case is a good solvent.
To estimate the size effect on this system, we have also carried out simulations of “empty” brushes of grafting density d = 0.02, 0.12 and 0.24 consisting of Nc = 36 chains. Monomer density profiles for the systems of different sizes are shown in Fig. 5. One can see that the curves for Nc = 16 and Nc = 36 are practically identical at the same values of grafting densities (Fig. 5a,b,c). This indicates that the model of the 16-chain brush is appropriate for reflecting the features of larger systems. For the sparse-grafted brush (d = 0.02), in which interactions between chains are insignificant, the number of chains in the brush model may be reduced to Nc = 4 without greatly affecting the results (Fig. 5a).
 | ||
| Fig. 5 Monomer density profiles at the following values of grafting density d: (a) 0.02; (b) 0.12; (c) 0.24. Results are shown for different transverse box dimensions and corresponding numbers of chains: Nc = 4 (circles), Nc = 16 (solid line), Nc = 36 (dashed line). | ||
Densely-grafted anisotropic brushes plus spherical particles
The following stage was the simulation of the anisotropic brush formed by 16 chains in the presence of different numbers of free spherical particles. Here the grafting density was chosen to be d = 0.12. Such a value of d allows intercrossing of the macromolecules, so that the chains are rather stretched, but at the same time the degree of ordering of monomers due to chain stretching is not too high (Fig. 3).The data characterizing the dependence of averaged values of the brush parameters [ηm] and [s] on the density of free particles in the system ηs are presented in Fig. 6.
![Anisotropic brush with d = 0.12 in liquid. Averaged values of monomer density [ηm] and order parameter [s] for systems with different values of free-particle density ηs.](/image/article/2008/SM/b711649g/b711649g-f6.gif) | ||
| Fig. 6 Anisotropic brush with d = 0.12 in liquid. Averaged values of monomer density [ηm] and order parameter [s] for systems with different values of free-particle density ηs. | ||
In the range 0 ≤ηs≤ 0.27, [ηm] increases only insignificantly, while the order parameter of the brush, [s], remains practically unchanged. Drastic growth of [ηm] and [s] is observed over the range 0.27 ≤ηs≤ 0.34. In the range 0.34 ≤ηs≤ 0.38 the parameters [ηm] and [s] reach their maximum values; [ηm] changes non-monotonically, slightly diminishing in the interval 0.34–0.36 and increasing again from 0.36 to 0.38.
Further increasing the density of spherical particles to the value ηs = 0.42 results in a diminishing of the parameters [ηm] and [s]. These results show that in the range 0.27 ≤ηs≤ 0.34, a new structure of the brush is forming, characterized by high density and high degree of monomer ordering. This new structure is not stable against further increase of the density of free particles; apparently, further structural transformations take place.
A more detailed picture is given by the analysis of structural characteristics of the brush. In Figs. 7–10, the profiles of densities, order parameter, the director z-coordinate, density of free ends, and snapshots36 of instantaneous configurations of the brush in a state of equilibrium at different densities of spherical particles, are shown. From the sphere density profiles we can obtain the density of spherical particles far from the brush, ηbulks, and these values are summarized in Table 2. It can be seen that between ηs = 0.36 and ηs = 0.38 the liquid state point is essentially unchanged, ηbulks≈ 0.45, while the brush structure changes and it incorporates a significant proportion of spherical particles.
 | ||
| Fig. 7 Anisotropic brush with d = 0.12 in liquid. Profiles of monomer density ηm(z) (solid lines), free-particle density ηs(z) (dashed lines), and total density ηm(z) + ηs(z) (dashed–dot lines). The following values of free particle density ηs are shown: (a) 0.27; (b) 0.30; (c) 0.33; (d) 0.36; (e) 0.38; and (f) 0.42. | ||
 | ||
| Fig. 8 Anisotropic brush with d = 0.12 in liquid. Free-end distribution functions ge(z) at the following values of free-particle density ηs: (a) 0.27; (b) 0.30; (c) 0.33; (d) 0.36; (e) 0.38; and (f) 0.42. | ||
 | ||
| Fig. 9 Anisotropic brush with d = 0.12 in liquid. Order parameter profile s(z) (solid lines) and z-component of the director profile n(z) (dashed lines), at the following values of free-particle density ηs: (a) 0.27; (b) 0.30; (c) 0.33; (d) 0.36; (e) 0.38; and (f) 0.42. | ||
 | ||
| Fig. 10 Anisotropic brush with d = 0.12 in liquid. Instantaneous configurations of the brush in a state of equilibrium at the following values of free-particle density ηs: (a) 0.27; (b) 0.33; (c) 0.36; (d) 0.38; and (e) 0.42. Spheres (grey) are reduced to 30% of their true dimensions for clarity. The grafting points are represented in black. The brush monomers are colour-coded according to their orientation. 2×2 periodic box replicas are shown. Figure produced with visualization software QMGA.36 | ||
| η s | 0.27 | 0.30 | 0.33 | 0.36 | 0.38 | 0.42 |
| η bulks | 0.34 | 0.375 | 0.40 | 0.45 | 0.45 | 0.485 |
At ηs = 0.27 (Fig. 7a–10a) the brush mixes well with the spherical particles, and the monomer density profile (Fig. 7a) differs insignificantly from that of the empty brush at the same grafting density. The presence of free particles also has practically no effect on the degree of ordering of monomers: the order parameter does not exceed 0.4 in any part of the brush, except for the narrow layer near the grafting surface (Fig. 9a). (The maximum of the dependence s(z) in the range of small ηm(z) is an artefact.) The director is oriented mainly along the normal to the grafting surface. As for the empty brush, the terminal monomers of chains are distributed across the whole brush: the curve ge(z) has one broad maximum (Fig. 8a). The disordered structure of the chains is easily visible in the snapshot of Fig. 10a.
On increasing the free particle density to ηs = 0.30, the state of the system changes sharply (Figs. 7b–9b). Two microphases, separated by a well-defined boundary, appear in the brush. One microphase is located near the grafting surface and is characterized by a high density of monomers, high order parameter, and low density of isotropic particles; the other one spreads across the remaining, outer, brush volume, is disordered, and is characterized by low monomer density and, accordingly, a high density of spherical particles. On the distribution function ge(z) of terminal monomers, a few sharp maxima appear in the range of low z-values; thus the height of the maximum in the high-z range decreases. This means that a part of the chains is compressed.9
At an increase to ηs = 0.33, the ordered part of the brush noticeably extends (Figs. 7c–9c). The number of maxima of the ge(z) function increases. An instantaneous configuration of the brush at this state point is presented in Fig. 10b. The highly-ordered structure of the monomers is clear here, in the region where their density is high. Further detail can be obtained from the monomer number density function, defined by eqn (5) and shown in Fig. 11b. It is evident that centres of mass of monomers in the ordered part of the brush are located regularly along the z-axes, i.e. the microphase near the grafting surface has a layered or smectic-like structure.
 | ||
| Fig. 11 Anisotropic brush with d = 0.12 in liquid. Number density of monomer mass centres ρm(z) at the following values of free-particle density ηs: (a) 0.27; (b) 0.33; and (c) 0.38. | ||
At higher values of the density of free spherical particles, namely ηs = 0.36, 0.38 (Figs. 7d,e–9d,e) the macromolecules of the brush form a highly ordered liquid crystal structure which spreads over the whole brush volume. The order parameter reaches values s(z) ≈ 0.88–0.89. The terminal monomers are localized in a narrow region on the periphery of the brush. However the monomer density profile ηm(z) does not have a box-like form, characteristic of a simple LC-state: local maxima and minima are visible, and complementary minima and maxima appear in the local density of spherical particles (Fig. 7d,e). Similar structure is seen in the order parameter profiles s(z).
Figs. 10c,d explain the origin of these features. It can be seen that within the brush (z≤H) there are volumes inaccessible to penetration of monomers. In such micro-regions, spherical particles are concentrated. Thus, inside the brush, a separation of spherocylinders from spherical particles takes place. The result of such a separation is the formation of isolated micro-regions or domains filled by spherical particles. The domains are stable formations: their sizes practically do not vary during the entire simulation time of the equilibrium system. The presence of domains leads to distortions of the brush structure: redistribution of the local density, changes in the director orientation, and the appearance of local minima in s(z).
In this range of ηs = 0.36–0.38 (see Fig. 11b,c), corresponding to ηbulks≈ 0.45 (Table 2), the structural transition from the smectic to a “domain-phase” of the brush22 occurs. For the system with ηs = 0.36, the smectic structure of the brush is still observed, though it is strongly deformed owing to the formation of the micro-regions just discussed (Fig. 10c). On increasing the free particle density up to ηs = 0.38, the smectic phase practically disappears, the domain sizes decrease and the value of [ηm] grows (Figs. 11c, 10d, 6). The average value of the order parameter of the brush, [s], remains high. In some respects, the brush represents a nematic liquid crystal, but distinct domains of different alignment are observed, so we prefer the term “domain phase” for this state. The analogous transition from smectic to nematic structures in mixtures of low-molecular-weight geometrically anisotropic and spherical particles, on increasing the density of spheres, has been observed.22,26
On increasing the free particle density further to ηs = 0.42, the volume of the microphase formed by the spherical particles noticeably increases (Fig. 10e). There are several domains localized in various places. Therefore, the structure of the brush is broken into different ordered regions with various director orientations. This leads to some general disordering of the system, though the local order parameter inside each region remains high (Fig. 9f). The mean brush monomer density [ηm] also diminishes (Fig. 6).
It is possible to assume that a further increase in the density of spherical particles in the system will lead eventually to the destruction of the orientationally ordered domain structure. However the complexities connected with the simulation of brushes in systems with a high packing fraction (long relaxation times) have not allowed us to check this assumption.
Densely-grafted isotropic brushes plus spherical particles
As already noted, we also executed a simulation of a test system: the isotropic brush consisting of Nc = 16 chains, each monomer of which is a spherical particle identical to a free particle. The contour length of these chains was set equal to that of the anisotropic chains. The behaviour of an isotropic brush was investigated at the same grafting density d = 0.12, at different free particle densities ηs. Taking into account the fact that the total volume of anisotropic monomers exceeds that of the isotropic ones for the same contour length, we have increased the maximal density of free particles for the test system ηs = 0.54. The density profiles and the terminal monomer distribution functions for the isotropic brush at various values 0 ≤ηs≤ 0.54 are shown in Fig. 12. One can see from the plots that monomers of the isotropic brush chains mix with free particles; in the investigated interval of ηs, collapse of the brush does not occur, it is possible to note only an insignificant decrease of the brush height. | ||
| Fig. 12 Isotropic brush with d = 0.12 in liquid. Upper panel: profiles of monomer density ηm(z) (solid lines), free-particle density ηs(z) (dashed lines), and total density ηm(z) + ηs(z) (dashed–dot lines). Lower panel: free-end distribution function ge(z). We show results for the following values of free-particle density ηs: (a) 0; (b) 0.35; (c) 0.45; and (d) 0.54. | ||
Time evolution of the system
Figs. 13, 14 show the process of establishing equilibrium for the 16-chain anisotropic brush of d = 0.12 in the system with ηs = 0.36. In the equilibrium state such a brush has a smectic-like structure distorted by the presence of domains filled with spherical particles.![Time evolution of monomer density [ηm] and order parameter [s] for the 16-chain anisotropic brush of d = 0.12 in a liquid with ηs = 0.36 during the equilibration process. Time is measured in Lennard-Jones units τ and plotted on a log scale.](/image/article/2008/SM/b711649g/b711649g-f13.gif) | ||
| Fig. 13 Time evolution of monomer density [ηm] and order parameter [s] for the 16-chain anisotropic brush of d = 0.12 in a liquid with ηs = 0.36 during the equilibration process. Time is measured in Lennard-Jones units τ and plotted on a log scale. | ||
 | ||
| Fig. 14 Snapshots of the 16-chain anisotropic brush of d = 0.12 in a liquid with ηs = 0.36 during the equilibration process. Notation as for Fig. 10. 2 × 2 periodic box replicas are shown, at the following values of time t/τ: (a) 45; (b) 600; (c) 2000; (d) 4000. | ||
The early stage of simulation (0 < τ < 600) is characterized by drastic growth of the mean value of the order parameter [s], while the increase in [ηm] is not so pronounced. In this time interval the brush forms an ordered nematic structure (Fig. 14a,b). In the process of further evolution of the system, the gradual separation of brush monomers from spherical particles is observed (Fig. 14c); the separation takes place inside the brush and leads both to the domain formation and to the growth of the dense highly-ordered smectic-like structure of the monomers. This process lasted in general up to τ≈ 4000–5000. Further simulation leads to the gradual contracting of the brush structure.
To ensure that, during the time of the simulation, the “free” spheres have an opportunity to explore all of the space of the cell we have calculated the mean-square displacement 〈Δr2(t)〉 = 〈|rj(t) −rj(0)|2〉 (Fig. 15).
 | ||
| Fig. 15 Mean-square displacement of free particles 〈Δr2(t)〉: anisotropic brush with d 0.12, ηs = 0.36 (solid line); anisotropic brush with d = 0.12, ηs = 0.42 (dashed line); and isotropic brush with d = 0.12, ηs = 0.35 (dash–dot line). | ||
Estimates based on these data show that during the full time of the simulation (∼45 × 103τ) the free particles in the systems with high total density are displaced on the average  . Thus, the time of the simulation appears to be enough for mixing of spheres with the chain monomers, and in the case when monomers and free particles do not differ in size and form, such mixing is realized (Fig. 12).
. Thus, the time of the simulation appears to be enough for mixing of spheres with the chain monomers, and in the case when monomers and free particles do not differ in size and form, such mixing is realized (Fig. 12).
Sparsely-grafted brushes
The consideration of LC-transitions in anisotropic brushes usually includes a study of the dependence of the transition features upon the grafting density of the brush, d. In the present work, we have restricted ourselves to the cases of rather dense grafting (d = 0.12) and sparse grafting (d = 0.01, 0.02). The results of the simulation of the four-chain brush with d = 0.02 at values of ηs = 0, 0.40, 0.42, 0.43, 0.51 are presented in Figs. 16–18. The dependences of [ηm] and [s] on ηs (Fig. 16) show that the LC-transition for the sparsely-grafted chains is more drastic than for densely-grafted ones (Fig. 6) and occurs at similar values of ηbulks (which is very close to ηs here): these quantities increase suddenly between ηs = 0.42 and ηs = 0.43. It should be noted that at ηs = 0.43, [s] ≈ 1, meaning that the ordered structure extends throughout the brush. The structural analysis (Fig. 17) confirms that, unlike the case of dense grafting, the sparsely-grafted brush does not form an intermediate microsegregated brush (MSB) structure during the LC-transition, i.e. a disordered brush passes directly to the highly ordered folded state at a definite (critical) value of ηs. An instantaneous configuration of the brush in such a state is presented in Fig. 18c.![Anisotropic brush with d = 0.02. Averaged values of monomer density [ηm] and order parameter [s], for systems with different values of free-particle density ηs.](/image/article/2008/SM/b711649g/b711649g-f16.gif) | ||
| Fig. 16 Anisotropic brush with d = 0.02. Averaged values of monomer density [ηm] and order parameter [s], for systems with different values of free-particle density ηs. | ||
 | ||
| Fig. 17 Anisotropic brush with d = 0.02. Upper panel: profiles of monomer density ηm(z) (solid lines), free-particle density ηs(z) (dashed lines), and total density ηm(z) + ηs(z) (dashed–dot lines). Middle panel: free-end distribution function ge(z). Lower panel: order parameter profile s(z). The following values of free-particle density ηs are shown: (a) 0; (b) 0.42; (c) 0.43; and (d) 0.51. | ||
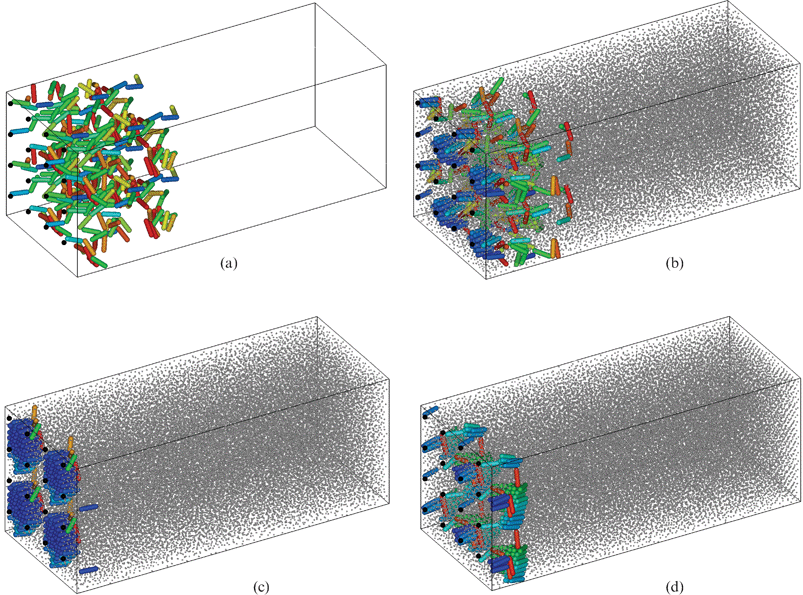 | ||
| Fig. 18 Anisotropic brush with d = 0.02 in liquid. Instantaneous configurations of the brush in a state of equilibrium. Notation as for Fig. 10. 2 × 2 periodic box replicas are shown, at the following values of free-particle density ηs: (a) 0; (b) 0.42; (c) 0.43; and (d) 0.51. Figure produced with visualization software QMGA.36 | ||
On increasing ηs from 0.43 to 0.51, [ηm] and [s] decrease, although the value of [s] remains rather high. More detailed examination shows that the highly ordered compact structure obtained for the brush at ηs = 0.43 distorts as the value of ηs reaches 0.51, due to the formation inside the brush of a domain filled with spherical particles (Figs. 17, 18). A similar effect was described above for the densely-anchored brush.
Single-chain system
In the last stage of our investigation, we have performed simulations of the behaviour of an isolated anisotropic macromolecule, anchored to the impenetrable surface, in the presence of different densities of spherical particles. A single chain in the MD box with horizontal dimensions X = Y = 10D may be considered as a special case of the brush with very low grafting density d = 0.01. The results of the single-chain simulation for ηs = 0.024, 0.40, 0.43, 0.45, 0.51 are depicted in Figs. 19–20 and snapshots are shown in Fig. 21. The transition to the ordered state in the chain occurs in the range 0.43 < ηs < 0.45 and corresponds to the sharply increasing values of [ηm] and [s] in Fig. 19. It is necessary to take into account that the abnormally large values of [s], determined viaeqn (10), for ηs≤ 0.43, are artefacts due to the low values of the monomer density. More realistic data in this interval are shown by the curve in Fig. 19 corresponding to eqn (11). For similar reasons, the order parameter profiles at the lowest free-particle densities exhibit significant artefacts and are therefore omitted from Fig. 20.![Single anisotropic chain with nominal d = 0.01. Averaged values of (a) monomer density [ηm], and (b) order parameter [s] for systems with different values of free particle density ηs. The solid line corresponds to the order parameter determined viaeqn (10), the dashed line to that defined by eqn (11).](/image/article/2008/SM/b711649g/b711649g-f19.gif) | ||
| Fig. 19 Single anisotropic chain with nominal d = 0.01. Averaged values of (a) monomer density [ηm], and (b) order parameter [s] for systems with different values of free particle density ηs. The solid line corresponds to the order parameter determined viaeqn (10), the dashed line to that defined by eqn (11). | ||
 | ||
| Fig. 20 Single anisotropic chain with nominal d = 0.01. Structural characteristics of the brush: Upper panel: profiles of monomer density ηm(z) (solid lines), free particle density ηs(z) (dashed lines), and total density ηm(z) + ηs(z) (dashed–dot lines). Middle panel: free-end distribution function ge(z). Lower panel: order parameter profile s(z) from eqn (10) (solid lines) and eqn (11) (dashed lines). Results for the following values of free particle density ηs are shown: (a) 0.024; (b) 0.43; (c) 0.45; and (d) 0.51. | ||
 | ||
| Fig. 21 Single anisotropic chain with nominal d = 0.01 in liquid. Instantaneous configurations of the brush in a state of equilibrium. Notation as for Fig. 10. 2 × 2 periodic box replicas are shown, at the following values of free particle density ηs: (a) 0.024; (b) 0.43; (c) 0.45; and (d) 0.51. Figure produced with visualization software QMGA.36 | ||
So the critical value of ηbulks (again practically identical with ηs) for the brush with nominal d = 0.01 is similar to that for the brushes with more dense grafting. Note that for LC-transitions in brushes induced by temperature (anisotropic interactions) or by solvent quality deterioration (isotropic interactions), a dependence of the transition point upon the grafting density is observed: higher critical values of the parameter of anisotropic or isotropic interactions correspond to lower values of grafting density.9,10,18
In the ordered state at ηs = 0.45, the macromolecule is practically folded and its monomers are aligned mainly along the normal to the grafting surface (Figs. 20, 21). The most unusual chain conformation is observed at ηs = 0.51. One can see from Fig. 19 that in the range 0.45 ≤ηs≤ 0.51 [ηm] increases, whereas [s] decreases. The value of [s] in Fig. 19 (dashed curve) at ηs = 0.51 is negative, meaning that the spherocylinders are arranged mainly in planes parallel to the grafting surface. The profile of the order parameter s(z) determined with respect to the z-direction (Fig. 20d, dashed curve) and the snapshot of the structure (Fig. 21d) also show the planar orientation of the spherocylinders at this state point. The increase in density of the monomers observed in Fig. 19 and in Fig. 20 at ηs = 0.51 can also be explained by the reorientation of spherocylinders: for planar orientation of monomers, the total height of the macromolecule decreases, so the volume occupied by monomers in each layer with unit height increases.
The possibility of the in-plane orientation of the monomers of the sparsely-grafted anisotropic brush was predicted for the case of the thermotropic LC-transition,37 and for the lyotropic case.18 Our simulation provides the experimental confirmation of the prediction of such structures.
Conclusion
The main result of this work is the demonstration of microphase separation and liquid crystal or oriented domain ordering in an anisotropic brush, driven by the addition of isotropic free particles to the system. This phenomenon was observed earlier for mixtures of low-molecular anisotropic and spherical particles; however for polymeric brushes it has been shown here for the first time. It should be noted that the effects discussed here for the brush are shown at a rather low monomer anisotropy (p = 4), while in the case of low-molecular mixtures, the phase separation was observed only at a degree of particle anisotropy no less than six.22–26 Lyotropic transitions in an anisotropic polymeric brush at p = 4 have been theoretically predicted18 on deterioration of the solvent quality, i.e. on strengthening of the isotropic attraction between monomers of a brush. As in our case only repulsive interactions between particles are possible, the observable effects have a purely entropic, rather than energetic, origin. It must be noted that the phase separation and ordering of the anisotropic component of low-molecular mixtures were observed in simulations of absolutely rigid (hard) particles. In our model, some “softness” was included in the potentials for reasons of computing convenience. This can lead to some numerical differences from hard models, but the qualitative results will be unaffected. In the present work, an anisotropic brush with only one value of the number of monomers in the chains (20), one value of monomer anisotropy (4) and one value of the spherical particle diameter (equal to unity) was studied. An investigation of the observed effects in a wider range of system parameters is of interest. The generalization of the theories developed for mixtures of anisotropic particles of different forms23–33 in an anisotropic polymeric brush mixed with isotropic spherical particles could be another direction of research.Acknowledgements
Part of this work was carried out during a visit of one of the authors (AT) to the Centre for Scientific Computing (CSC), University of Warwick funded by the ESF SUPERNET programme. Funding for the research was provided by RFBR grant 05-03-32450, and the programme of the section of Chemistry and Materials Science of the Russian Academy of Sciences. Computational resources were provided by CSC Warwick. Thanks are due to Adrian Gabriel for providing and supporting the QMGA visualization software.36References
- S. Alexander, J. Phys. (Paris), 1977, 38, 977 CAS.
- P.-G. De Gennes, Macromolecules, 1980, 13, 1069 CrossRef CAS.
- G. J. Fleer, S. M. A. Cohen, J. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at Interfaces, Chapman and Hall, London, 1993 Search PubMed.
- T. M. Birshtein and E. B. Zhulina, Vysokomol. Soedin., Ser. A, 1983, 25, 1862 Search PubMed ( Engl. Transl.: Polym. Sci., Ser. A, 1983, 25, 2165) Search PubMed.
- S. T. Milner, Science, 1991, 251, 905 CrossRef CAS.
- A. Halperin, M. Tirel and T. P. Lodge, Adv. Polym. Sci., 1992, 100, 31 CAS.
- V. M. Amoskov, T. M. Birshtein and V. A. Pryamitsyn, Macromolecules, 1996, 29, 7240 CrossRef CAS.
- T. M. Birshtein, V. M. Amoskov, A. A. Mercurieva and V. A. Pryamitsyn, Macromol. Symp., 1997, 113, 151 CAS.
- T. M. Birshtein and V. M. Amoskov, Polym. Sci., Ser. C, 2000, 42, 172 Search PubMed.
- A. A. Darinskii, A. I. Tupitsyna, T. M. Birshtein, M. G. Safyannikova, V. M. Amoskov and I. Emri, Polym. Sci., Ser. A, 2003, 45, 665 Search PubMed.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627 CrossRef CAS.
- D. Frenkel and B. M. Mulder, Mol. Phys., 1985, 55, 1171 CAS.
- A. Yu. Grosberg and A. R. Khokhlov, Sov. Sci. Rev., Sect. A, 1987, 8, 147 Search PubMed.
- M. P. Allen and M. R. Wilson, Mol. Phys., 1992, 80, 277.
- M. Dijkstra and D. Frenkel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 5891 CrossRef.
- A. Yethiraj and H. Fynewever, Mol. Phys., 1998, 93, 693 CrossRef CAS.
- T. M. Birshtein, A. A. Mercurieva, L. J. Klushin and A. Polotsky, Comput. Theor. Polym. Sci., 1998, 8, 179 CrossRef CAS.
- A. A. Polotsky, T. M. Birshtein and M. N. Chernyavsky, Polym. Sci., Ser. A, 2002, 44, 527 Search PubMed.
- H. Lange and F. Schmid, Eur. Phys. J. E, 2002, 7, 175 CrossRef CAS.
- H. Lange and F. Schmid, Comput. Phys. Commun., 2002, 147, 276 CrossRef.
- H. Lange and F. Schmid, J. Chem. Phys., 2002, 117, 362 CrossRef CAS.
- Y. Sakurai and I. Ono, Mol. Cryst. Liq. Cryst., 2000, 346, 137 CrossRef CAS.
- M. Dijkstra and R. Van Roij, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5594 CrossRef CAS.
- T. Koda, M. Numajiri and S. Ikeda, J. Phys. Soc. Jpn., 1996, 11, 3551 CrossRef.
- Z. Dogic, D. Frenkel and S. Fraden, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 3925 CrossRef CAS.
- G. Cinacchi, E. Velasco and L. Mederos, J. Phys.: Condens. Matter, 2004, 16, 2003 CrossRef.
- T. Schilling, S. Jungblut and M. A. Miller, Phys. Rev. Lett., 2007, 98, 108303 CrossRef CAS.
- L. Helden, R. Roth, G. H. Koenderink, P. Leiderer and C. Bechinger, Phys. Rev. Lett., 2003, 90, 048301 CrossRef CAS.
- A. Matsuyama and T. Kato, Eur. Phys. J. E, 2001, 6, 15 CrossRef CAS.
- P. van der Schoot, J. Chem. Phys., 2002, 117, 3537 CrossRef.
- Y. L. Chen and K. S. Schweizer, J. Chem. Phys., 2002, 117, 1351 CrossRef CAS.
- Y. L. Chen and K. S. Schweizer, J. Phys. Chem. B, 2004, 108, 6687 CrossRef CAS.
- P. G. Bolhuis, J. M. Brader and M. Schmidt, J. Phys.: Condens. Matter, 2003, 15, S3421 CrossRef CAS.
- T. Kihara, J. Phys. Soc. Jpn., 1951, 16, 289 Search PubMed.
- P. Bladon and D. Frenkel, J. Phys.: Condens. Matter, 1996, 8, 9445 CrossRef CAS.
- A. T. Gabriel, T. Meyer and G. Germano, submitted for publication, http://qmga.sourceforge.net/.
- T. M. Birshtein and V. M. Amoskov, Comput. Theor. Polym. Sci., 2000, 10, 159 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2008 |
