Intelligent behaviors of amoeboid movement based on complex dynamics of soft matter

Abstract

We review how soft matter is self-organized to perform information processing at the cell level by examining the model organism Physarum plasmodium. The amoeboid organism, Physarum polycephalum, in the class of true slime molds, exhibits the intelligent behavior of foraging in complex situations. When placed in a maze with food sources at two exits, the organism develops tubular structures with its body which connect the food sources along the shortest path so that the rates of nutrient absorption and intracellular communication are maximized. This intelligent behavior results from the organism's control of a dynamic network through which mechanical and chemical information is transmitted. We review experimental studies that explore the development and adaptation of structures that make up the network. Recently a model of the dynamic network has been developed, and we review the formulation of this model and present some key results. The model captures the dynamics of existing networks, but it does not answer the question of how such networks form initially. To address the development of cell shape, we review existing mechanochemical models of the protoplasm of Physarum, present more general models of motile cells, and discuss how to adapt existing models to explore the development of intelligent networks in Physarum.

---

Toshiyuki Nakagaki

Toshiyuki Nakagaki obtained his Ph.D. in Biophysics from Nagoya University. His research focuses on information processing at the cell level. He is an Associate Professor at the Research Institute for Electronic Science at Hokkaido University.

Robert Guy

Robert Guy received his Ph.D. in Mathematics from the University of Utah. His research interests include mathematical biology, complex fluids, and scientific computing. He is an Assistant Professor of Mathematics at the Univerisity of California Davis.

---

1. Introduction: intelligence at the cell level

The cell is the elementary unit of all organisms. Although cells are generally not described as ‘intelligent’, they have more ability to process information than one might think. The biologist S. H. Jennings discussed the psychology of the single cell organism (Paramecium) a hundred years ago. Understanding how cells perform high-level information processing remains an exciting challenge to modern scientists.

From a material science point of view, the cell is an exotic system in which nonliving materials act together to function as a living organism. That means intelligent biological functions can develop from properties of matter. Protoplasm, the contents of cells, is a complex viscoelastic material which is regarded as soft matter. The intelligent cellular behavior discussed in this review is closely related to the nonlinear dynamics of protoplasm. Recent advances in nonlinear dynamics, biochemistry, and computer simulation power have aided in understanding cellular behavior. The slime mold Physarum serves as a model organism in the study of cellular intelligence, and in this review we present recent experimental and theoretical results that address how the slime mold exhibits intelligence and the mechanisms behind it.

The plasmodium of Physarum polycephalum in the class of true slime molds is a large multinucleated amoeboid organism that resembles mustard spread on bread because of its bright yellow color and its uneven, slimy exterior (see Fig. 1a).¹ This slimy blob is well-organized and can behave in intelligent ways.² In fact, it is able to process environmental information to identify food and avoid risks.^3,4 Presented with multiple paths connecting food sources, it is able to select the shortest path (see Fig. 2 and 3), maximizing its chances for survival.^5–8

Fig. 1 Pictures of the plasmodium. (a) A true slime mold in the wild. (b) The plasmodium forms a network between food sources (FS) as it crawls on an agar gel. There are about 29 FSs (oats flakes), indicated by the dots. (c) A network of tubes connects many FSs arranged on a lattice. The FSs are represented by white dots. A circular part of the organism extends from the right bottom FS. Only some of the food sources are part of the network. (d) The tube network connects all the FSs on the lattice. The pictures (c) and (d) are reproduced from ref. 55 in which network shapes between many FSs were studied. Scale bar: 1 cm.

Fig. 2 A maze is filled with Physarum, and food sources (FSs) are placed at two exits of the maze. Over time the plasmodium disappears from the dead ends of the maze, and eventually only a strand connecting the food sources by the shortest path remains. (a) Before the placement of the FSs, the plasmodium fills the maze. (b) The transient shape of the organism four hours after the introduction of the FSs. Tubes remain along both solutions to the maze. (c) Eight hours after the placement of the FSs; tubes cover only the shortest path. (d) A graph representing the maze. N₁ and N₂ are the two FSs and M_ij is an edge between two nodes N_i and N_j. Scale bar: 1 cm.

Fig. 3 Ring-shaped network experiment (a,b) and its graphical representation (c). (a, b) Photographs of the plasmodium (10 mg wet weight) extending in a ring, bordered with dashed lines, 0 hr (a) and 4 hr (b) after the nutrient was applied. The final path connecting the two food-sites is emphasized by the white arrow in (b). Scale bars represent 5 mm. AG: the agar block containing the food. (c) N₁,N₂ are nodes that correspond to FSs, and the edges M¹₁₂, M²₁₂ correspond to tubes between the FSs.

As the plasmodium migrates it assumes the form of an interconnected system of tubes that merge to a fan-like structure at the front. Its intelligence is closely related to its ability to form and modify this tubular network. The plasmodium does not have any legs to move, a central nervous system to process information, or a heart to pump fluid. It does have a dynamic circulation system in its tubular network which is used to transport body mass, nutrients, and chemical signals. The information processing in this network is decentralized; any local part of the protoplasm with a volume of approximately 1 mm³ or less can behave as an individual if it is cut off from the main body. Two interesting problems are how the shape of this smart network results from protoplasm dynamics and how the network processes information to exhibit intelligent behavior. As this network totally changes its shape in response to external conditions and stimulation, the Physarum network is a useful experimental system to observe the interplay between self-organization and biological function.

Fig. 1b–d show an example smart network among multiple food sources (FS). The network shape meets two physiological requirements of minimal total length and a fault tolerance so that global connectivity is maintained in the event of accidental disconnections.^9,10 Balancing these two requirements necessitates managing trade-offs, and obtaining an optimal solution is nontrivial. In this review, the dynamics of the self-organization of the functional network in the plasmodium is described through experiments and models. We focus on networks with two FSs. Cases with more than two FSs will be reviewed elsewhere in the future.

The remainder of this paper is organized as follows. In Section 2, we describe the structure and dynamics of the protoplasm. Experimental results on the relationship between shuttle streaming and tube morphogenesis are reviewed in Section 3. A mathematical model of networks that adapt in response to flow was recently developed in order to explore how plasmodia use flow signals to modulate their networks.¹¹ In Section 4, the formulation of this model is reviewed and the behavior demonstrated by the model is summarized. This model gives insight into possible feedback mechanisms in the network, but it does not give information on how such networks are formed. The mechanisms behind the formation of these smart networks is a current area of research. In Section 5 we review previous mechanochemical models of the protoplasm of Physarum and discuss more general models of motile cells that could be adapted to understand the formation of networks by Physarum.

2. Amoeboid movement and the dynamics of protoplasmic soft matter

The protoplasm is differentiated into two phases: a gel phase (ectoplasm) that makes up the walls of the tubular structures and the frontal region, and a sol phase (endoplasm) that flows within the tubes and the channels of the frontal region. The relative amounts of ectoplasm and endoplasm are dynamic and change periodically. The motion of the sol is driven by organized rhythmic contractions of the gel with a period of ca. two minutes. The tension in the gel is due to actin–myosin interaction, which generates internal pressure gradients. The back and forth motion of the sol that results is called shuttle streaming.^12,13 The rhythmic contraction is observed everywhere within the cell and is driven by biochemical oscillations involving Ca²⁺, ATP, H⁺, cAMP, NAD(P)H⁺, phospholipid , etc.^2,14–19 This oscillation is locally self-sustainable throughout the cell, which can be demonstrated by cutting a plasmodium into pieces of millimetre size. These fragments can survive independently and demonstrate the same rhythmicity as the original plasmodium. On the other hand, two plasmodia can spontaneously coalesce to form one large plasmodium upon meeting. Therefore, it is reasonable to regard the plasmodium as a system of spatially distributed coupled oscillators.

The phase of the oscillation varies throughout the cell, and this results in spatial differences of the pressure needed for streaming. Endoplasm flows through narrow cavities according to the pressure difference so that the flux of streaming is larger in wider and shorter cavities. The effect of the cavity thickness strongly influences the flow rate (suppose an approximation of Poiseuille flow, and the conductivity is proportional to the fourth power of the radius).

The plasmodium is made up of a network of tubular elements, which repeatedly bifurcate from thick tubes to smaller tubes. The protoplasm flows through this tubular network, which serves as a circulation system for the cell. When the plasmodium moves, body mass is carried via the network and simultaneously the shape of the network is rearranged. The morphogenesis of the tube network is one mechanism the cell uses to process information. Therefore, describing the dynamics of the tube network is a promising approach to understand how this slimy material of protoplasm exhibits intelligent behavior.

The actin fibers that make up the walls of the tubes show a regular arrangement with a preferred orientation.^12,20–26 In new tubes the fibers are oriented axially, while in older tubes the preferred orientation is in the circumferential direction. The fiber orientations and even the fibers themselves are not stationary but are dynamic. Fragments of actin filament flow within the sol and react with fibers in the gel. The fibers assemble, disassemble, crosslink, and bundle periodically, with the same period (two minutes) as the chemical and mechanical oscillations. The dynamics of the actin filaments cause spatial and temporal variations of the viscosity and elasticity of the ectoplasmic gel and of the viscosity of the endoplasmic sol.

The protoplasm is thixotropic (shear-thinning), which results from its molecular structure.^26,27 Generally, thixotropy is a property observed in solutions of actin filaments.²⁸ The protoplasmic sol does not flow when the pressure gradient is below a critical value, but when the critical pressure gradient is reached the resistance to flow is greatly reduced. Thus a flow-induced instability may be involved in the development of channels in the frontal region of the plasmodium. The frontal region is a sheet-like porous medium without a visible tubular organization. In this frontal sheet, there are channels in which the flow is more vigorous than that in other parts of the sheet but much slower than the flows within the tubes. These channels eventually transform into tubes. They do not move in space once they appear, suggesting that a flow instability is involved in channel formation. In the next section channel and tube development is discussed further.

3. Experiments on tube morphogenesis

In this section we review what is known about the mechanisms for tube morphogenesis based on experimental data. The experiments in ref. 29 were designed to explore the effect of protoplasmic streaming on tube morphogenesis. The direction of shuttle streaming is controlled by entraining the intrinsic oscillation to an external temperature oscillation (Fig. 4). The temperature is varied sinusoidally between 23 and 25 °C with a forcing period 10% shorter than the intrinsic period. Under these conditions, the rhythmic contraction is sometimes entrained to the temperature oscillation. Two halves of a circular shaped organism are forced with the same period but with different phases. One half contracts while the other half relaxes which causes shuttle streaming between the two halves. Fig. 5 shows the results for a circular organism with a preexisting tubular network. The tubes oriented parallel to the flow direction remain unchanged or become thicker while the tubes oriented perpendicular to the flow become thinner or disappear. Fig. 6 shows the results for a sheet-like structure without preexisting tubes. New tubes are formed in the sheet-like structure after 15 to 20 minutes from the initiation of the forcing (about ten periods of the oscillation). These results show that the protoplasmic streaming is one factor in the development and adaptation of the tubular network.

Fig. 4 Experimental set up for varying the temperature and observing the oscillation pattern and cell shape. A Peltier-effect device (PD) was sandwiched by two copper plates (CP), and a heat irradiator (HI) was attached to the lower part. On the upper plates, the agar gel (2–3 mm thick) on which the plasmodium extended was placed in the middle. The temperature of the agar plate was monitored by thermal monitors (TM) on both sides, and readings were transmitted to a personal computer which controlled the PDs. The temperatures on both sides, T₁ and T₂, were varied as T₁ = Asin(2πωt) + T₀ and T₂ = Asin(2πωt + Ψ) + T₀, where T₀ = 25 °C, A = 1 °C, ω = 0.95ω_i and t is time (in seconds). The quantity ω_i is the reciprocal of the contraction period (peak-to-peak time in units of seconds), which was averaged over several changes just before the temperature oscillations were applied. The quantity Ψ was π or (2/3)π to make the phase difference between two parts as large as possible. Because the contraction oscillation synchronized with the temperature oscillation, the contraction pattern could be controlled.^4,29,56 The contraction pattern and the cell shape were simultaneously observed. The spatio-temporal dynamics of the rhythmic contraction were monitored by video image analysis.^29,57,58 The organism was illuminated from above at an angle, and observed from above with a video camera that fed into a microcomputer. Periodic changes in the brightness level which reflected thickness of cell were detected as contractile activity in the cell because the contraction was accompanied by changes in thickness.

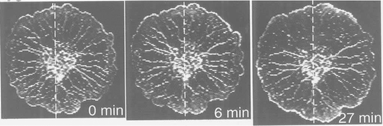Fig. 5 Modulation of tube arrangement by artificial control of the contraction pattern as shown in Fig. 4. Plasmodium at 0, 6, 27 min from the beginning of the oscillatory variations of temperature. The dashed line indicates the position of the narrow gap between the two temperature-controllers. The horizontally oriented veins remained, but the vertical veins diminished. The veins were reinforced along the direction of the phase difference of the contraction, and weakened perpendicular to that direction.²⁹

Fig. 6 Tube generation by artificial control of the contraction pattern. (a) Time course of rhythmic contraction in the right and the left parts separated the dashed line in (b). The oscillations between the two sides were in-phase in the early stage, but became anti-phase 15 min from the beginning of the artificial control (indicated by the arrow). (b) Rectangular piece (ca. 1 cm × 1 cm) of veinless plasmodia at 0, 15 and 25 min from the beginning of artificial control, and a control specimen under artificial control without a phase difference (Ψ = 0). The dashed line indicates the position of the narrow gap between the two temperature controllers. These pictures show the generation of the vein structure along the direction of the phase difference (Ψ = π) of the contraction. Just before the anti-phase contraction at 15 min, there were no new thick veins. Two new thick veins developed perpendicular to the direction of the phase difference of the contraction several minutes after the anti-phase contraction occurred (indicated by the red arrows). Such veins were not observed when the contraction phases were synchronous (Ψ = 0). Consequently, when two regions contracted in different phases for several minutes, tubular structures developed between them.

The experiments described in the previous paragraph show that tubes can develop in the direction of streaming, which was determined by an external oscillation. Next we consider whether streaming precedes the development of new tubes in vivo. This question is addressed by examining two different experimental situations: spontaneous tube formation in an artificial partial partition (Fig. 7) and cell fusion (Fig. 8). In the first experiment, a circular plasmodium with spatially synchronous oscillations is partitioned into two parts connected by a narrow region. The rhythmic contractions in the two halves transition from in-phase to anti-phase after the partitioning. After some time of the anti-phase oscillations, a thick tube develops in the region connecting the two halves. In the second experiment we consider the coalescence of two plasmodia, which occurs naturally when two plasmodia meet. In the early stage of the merger, a thick tube is formed between the two plasmodia in the region of contact. Before the tube forms, the contractions of the two plasmodia are out of phase, so that streaming is directed between the two plasmodia. In each of these two experiments, the plasmodia changed the direction of shuttle streaming, and a tubular structure developed along the direction of streaming. These results indicate that the organism uses shuttle streaming as a signal to form new tubes.

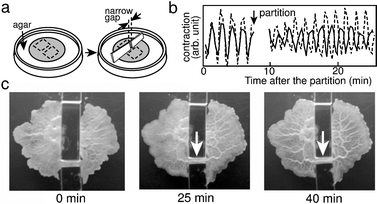Fig. 7 Tube formation and anti-phase oscillations induced by partial partition of the organism. (a) Schematic illustrations of the experiment. The shaded area indicates the plasmodium. A circular shaped plasmodium was partially separated by placing two pieces of cover glass (GW) a short distance (narrow gap) apart on agar gel. (b) Contraction oscillations in the partial partition. The organism was illuminated from below with an infrared emission diode (ca. 950 nm), and observed from above with a video camera that fed into a microcomputer.^29,57,58 The pixel brightness in the image was related to cell thickness, which varied with the contraction movement, as described in Fig. 4. Contraction oscillations were averaged over the area enclosed by the dotted lines, as shown in (a). Anti-phase oscillations resulted from the partition. (c) Pictures of the cell shape. After a period of anti-phase oscillations (see the pictures at 25 and 40 minutes), a thick tube formed between two partially partitioned parts of organism. Scale bar: 1 cm.

Fig. 8 Tube generation and anti-phase oscillations in the fusion of two organisms. (a) Schematic illustrations of the experimental procedures of coalescence (top view). The shaded areas indicate plasmodia. Two plasmodia, placed about 5 mm apart (left figure), extended, met (middle figure) and coalesced (right figure) to form a single plasmodium. (b) Phase relationship of contraction oscillations. How contractions were observed was described in Fig. 7. Contraction oscillations were averaged over the area enclosed by dotted lines in the middle parts, and time courses of contractions in the two parts are shown in the upper panel. The middle panel shows the phase difference between the two oscillations. The two oscillations were clearly anti-phase with one another. In the lower panel, one-dimensional spatial variations of the contraction oscillations are plotted along the dashed line X indicated in (a). Increasing thickness corresponds to black, and decreasing thickness corresponds to white. The oscillations became anti-phase during the early stage of coalescence. After anti-phase oscillations, a thick tube formed between the two parts of the organism, as shown in (c). Thick tubes were formed between the upper and lower parts within 21 minutes after meeting, while no thick tubes were observed just after meeting at 4 minutes.

How does shuttle streaming induce a tube? One possible mechanism involves the alignment of actomyosin filaments. These filaments are preferentially aligned in the axial direction in young tubes and in the circumferential direction in older tubes. These aligned fibers are observed at the interface of endoplasm and ectoplasm, and they form the cytoskeletal framework of the tubular structures. A similar fiber orientation can be artificially induced by stretching the plasmodium. When external tension is applied to a piece of plasmodium, the plasmodium extends a little and then the contraction force resisting the stretching increases rapidly. This increase in contraction force is the result of fiber alignment in the direction of stretching. This effect is known as stretch activation. The alignment of actomyosin fibers in response to stress is a property of networks of chain molecules. A similar phenomenon can be observed by stretching a sheet of transparent vinyl chloride polymer (randomly meshworked structure of chain molecule). When the sheet is stretched it becomes opaque due to the alignment of the polymers within the sheet.

Fibers can be aligned within the plasmodium by applying an external force, but can stretch-induced fiber alignment occur from internal forces within the plasmodium? Within the tubes there are two stresses to consider: the internal pressure that is driving the flow and the viscous stress that results from the flow of the sol (the maximum speed is about 1 mm s⁻¹). The internal pressure exerts a force normal to the surface of the tube which would tend to align fibers circumferentially, and the viscous stress exerts a force tangential to the tube surface which would tend to align fibers axially. We have made rough estimates of these forces and find that they are indeed strong enough for the stretch activation effect. Thus, it is expected that stretch-induced fiber alignment due to protoplasmic streaming plays a major role in the development of tubular structures.

4. Mathematical modeling of the tube-network

In the previous section we presented experimental evidence that the flow of protoplasm causes the formation and growth of tubular structures in plasmodia. In this section we present mathematical models of network adaptation based on the principle that the size of a tube increases as the flux through the tube increases, and it collapses when there is little flow. The models discussed here were developed by Tero, Kobayashi et al. to describe the dynamics of tubular networks in Physarum,^11,30 and this model has also been used to find optimal driving routes.³¹

4.1 Formulation of Tero–Kobayashi model

In the model, the shape of the cell body is represented by a graph: the edges correspond to tubes and nodes correspond to the junctions between tubes. Fig. 2d shows an example graph for a maze-solving experiment, and Fig. 3c shows the graph for the ring-shaped case. The two nodes with food-sources are labeled N₁ and N₂ and the other nodes are numbered N₃,N₄,N₅,…. Edges between node i and j are labeled M_ij, and if there are multiple edges between these nodes, they are labeled M¹_ij,M²_ij,….

Suppose that the pressures at nodes i and j are p_i and p_j, respectively, and that the two nodes are connected by a cylinder of length L_ij and radius r_ij. Assuming a Poiseuille flow, the flux through the tube is

where ξ is the viscosity of the fluid, andis a measure of the conductivity of the tube. Although the tube walls are not rigid and the radius changes over time, the dynamics of tube adaptation are slow enough (10–20 minutes) that the flow can be taken to be in steady state. The state of the network is described by fluxes, Q_ij, and the conductivities, D_ij, of the edges.

The amount of fluid must be conserved, so that at each internal node i (i ≠ 1,2)

Σ_jQ_ij = 0, (3)

so that there is no volume change at these nodes. The nodes that correspond to food sources drive the flow through the network by changing their volume, so that at food sources eqn (3) is modified by a prescribed source (or sink) term

Σ_jQ_ij = S_i, (4)

where i = 1,2. The total volume of fluid in the network does not change, so that

S₁ + S₂ = 0. (5)

These source terms could be periodic in time and drive shuttle streaming through the network. However, because the time scale of network adaptation is an order of magnitude longer than the time scale of shuttle streaming, the sources are taken to be constant.

For a given set of conductivities and source and sink, the flux through each of the network edges can be computed. In Physarum the radii of the tubes change in response to this flux. In the model, the conductivities evolve according to the equation

The first term on the right hand side describes the expansion of tubes in response to the flux. The function f is a monotonically increasing function which satisfies f(0) = 0. The second term represents a constant rate of tube constriction, so that in the absence of flow the tubes will disappear. Each tube interacts with one another because the total amount of fluid in the network must be conserved. If the flux through a tube changes, it affects all the other tubes in the network.

It is instructive to consider the analogy of an electrical circuit. An edge of the network is regarded as a dynamic resistor, with resistance proportional to L⁻¹_ij and r⁴_ij. The shape of the organism is represented as a network of resistors. The fluxes through the edges are analogous to currents through the resistors, and the source/sink terms at the food sources correspond to input currents. The pressures at the nodes correspond to voltages in the circuit. If the current through a resistor is large enough, its resistance decreases and the current through it increases. If the current through is resistor is low, the resistance may tend to infinity, which corresponds to the collapse of the tube.

4.2 Two FSs on a ring

The simplest nontrivial network to study consists of two food sources connected by two edges of different lengths, as shown in Fig. 3. In experiments with plasmodia in this shape, the longer path almost always disappeared and the shorter path remained. However, if the difference in length was small, sometimes both paths remained and occasionally just the longer path remained. In some situations both tubes disappeared, leaving two distinct organisms. The probability of separating into two organisms is influenced by the size of the food sources, as discussed further in Section 4.4. In simulations with the model, which tubes remained depended on the form of the function f(|Q|) as described below. Because there are only two nodes and two edges, the notation is simplified by replacing Lⁱ₁₂, Qⁱ₁₂ and Dⁱ₁₂ (i = 1,2) by Lⁱ, Qⁱ and D_i.

The function f is taken to be of the form

f(|Q|) = |Q|^µ. (7)

The model network exhibits three different behaviors, depending on the value of µ. The results for µ = 1, µ > 1, and µ < 1 are summarized below.

µ = 1. L ¹ ≠ L² (L¹ < L²): In this system, there are two fixed points each corresponding to a graph with only one path connecting the nodes. The equilibrium point corresponding to the shorter path is always stable and the point corresponding to the longer path is always unstable. For any initial state with two paths, the final state is always the stable equilibrium point, which means that the shorter path is always selected.

L ¹ = L²: In this special case, all points on the line which is the common null line for both equations dD¹/dt,dD²/dt are stable fixed points. Thus both paths always remain.

µ > 1. The system has two stable fixed points, so that either of the two paths can be selected. Each fixed point has its own basin of attraction. Which path persists and which disappears depends on the initial conductivities.

0 < µ < 1. There is one stable equilibrium point for which both paths remain. The final thickness of the paths is independent of the initial conditions.

4.3. Maze-solving

In simulating the maze experiment with this model, we assumed that µ = 1 because this was the case for which the model selected the shortest path in the ring simulations. The simulation reproduced the time sequence of network shapes seen in experiments: dead-end paths collapse first, the longer paths connecting the FSs disappear next, and finally the shortest path remains from the four possible paths as shown in Fig. 2.

From these simulations, we expect that this model can select the shortest path connecting two nodes of any network. The algorithm was named Physarum solver when µ = 1, and it has been applied to finding optimal driving routes through a complex network of highways.³¹ It has been mathematically proven that the Physarum solver will select the shortest path from the network.^32,33

4.4 Effects of food size

In the previous sections we described a model that is capable of selecting the shortest path connecting two food sources. Under different conditions the plasmodium either selects the shortest path, maintains multiple paths, or leaves no connections between food sources. The number of paths depends on the ratio of the size of the organism to the quantity of food. Fig. 9 shows the length of time that five paths of different lengths persist for different amounts of food. The number of paths that persist increases as the amount of food decreases. Moreover, regardless of the amount of food, the longer tubes always collapsed before the shorter ones.

Fig. 9 Path selection from five possibilities. (a1) Photograph of the initial shape of the organism. The five connections had different lengths of 2, 4, 6, 8 and 10 cm between two equal food sources (FSs). Scale bar: 1 cm. (a2) A typical result of the experiment. Only the shortest and the second shortest remained (marked by the white arrows) and the others have disappeared. (b) Typical time course for connection survival for different sizes of FS (7, 10, 13 cm²). Each gray bar indicates existence of a connection. (c) Average survival time from 12 experiments for FS sized 10 cm². Higher survival probability corresponds to darker shading.

In order to account for the quantity of food in the mathematical model, we assume that the total volume of protoplasm (V) is divided between two functions: one for nutrient absorption (V_a), the other for tube formation and force generation (V_t). The amount devoted to nutrient absorption increases as the amount of food increases, so that the amount of food provided is expressed by V_a and only V_t = V − V_a affects the ensuing dynamics.

The two FSs generate pressures of p₁ = β(w₁ − s₁) and p₂ = β(w₂ − s₂), where w is related to the volume of protoplasmic sol at the FS, s is the basal volume of protoplasmic sol, and β is related to the stiffness of the protoplasmic gel. For a physiological description of these parameters, see ref. 11,34. The values of s are the prescribed functions

where ω is the frequency and φ_i is the phase. The oscillations are assumed to be out of phase so that φ₁ = 0 and φ₂ = π. The volumes at the nodes change according toNotice that the volume of protoplasm involved in force generation, V_t, appears in the amplitude of the volume oscillations at the food sources.

The conductance again evolves according to eqn (6). The function that describes the increase of conductance as a function of the flux is taken to be

The reasons for choosing this sigmoidal function come from evidence that there is an upper limit of tube thickness in real organisms and that protoplasmic sol is not likely to flow when the pressure difference is sufficiently small because of the thixotropy of protoplasmic sol. This idea has been described in detail previously in ref. 11.

Fig. 10 shows the results from a simulation based on the experiment from Fig. 9. The longer connections collapse earlier while the number of remaining connections declines as the amount of food increases. Two, one, and zero connections remains for food source sizes (V_a) of surface area 5, 10 and 14 for a constant volume of organism (V = 20). The mathematical model thus reproduces the simple experimentally observed rules for selecting connections between two equal FSs. The longer connections are disrupted before shorter ones, and the amount of food determines when the selection process ends. This model suggests a possible mechanism behind this phenomenon: namely, that a large source of food reduces the flow of sol through the network and this in turn leads to the collapse of extra connections.

Fig. 10 Simulation results for path selection in the plasmodial tube network. (a) Graphical representation of the initial shape of the organism: five connections, M_i (i =1 to 5) with lengths of 2, 4, 6, 8 and 10, between two equal FSs, FS₁ and FS₂. (b) Time course of connection survival with food size (V_a) of 5, 10 and 14. V_a + V_t = V, where V = 20.

Finally, we speculate on a biological reason for the relationship between connectivity of the network and size of food sources. Multiple connections provide insurance against the possibility of accidental disconnections from the network. It is risky to use a single connection to a small food source. If this connection is accidentally broken, part of the organism is then stranded in a nutrient-poor region. When nutrient is plentiful the risk of stranding part of the organism without food is low, and so it is wasteful to maintain multiple connections to nutrient-rich locations. Since the organism does not devote much biomass at small FSs, it is reasonable to keep multiple connections to such small sources using the excess volume of the body.

5. Mathematical models of the sol–gel mechanics in motile cells

The network of adaptable tubes present in Physarum is necessary for it to exhibit intelligent behavior. In the previous section we presented mathematical models of a network in which the size of the tube changes in response to the flow through it. These models demonstrated that tasks such as path selection in a maze can be accomplished with simple mechanical feedback in the network. These models did not address how such a network is formed. The development of channels and tubes within the gel is a dynamic process which depends on the local chemical environment and on the motion of the fluid, and so models of this process must consider both chemistry and mechanics. In this section we review some existing mechanochemical models of sol–gel dynamics in Physarum, and then we discuss some more general models of cell motility which may be useful in understanding the mechanochemisty of Physarum.

5.1 Mechanochemical models of sol–gel in Physarum

The first mechanochemical model of the cytoplasm of Physarum is due to Oster and Odell,³⁵ in which the authors describe the factors that contribute to the generation of stress within the cytoplasm and how the stress is affected by calcium. In their model, there are two components to the stress: a passive viscoelastic stress and an active contractile stress. As the calcium concentration increases, the active contractile stress increases but the gel is solated reducing its ability to transmit stress. The result of these two competing processes is a bell-shaped response to increasing calcium concentration in which the contractile stress is maximum for an intermediate level of calcium. Calcium is stored in vesicles that are capable of both releasing it into the cytoplasm and removing it through a pump. There are two positive feedback mechanisms: the release rate from vesicles is an increasing function of calcium level and mechanical strain. The authors use their model of the gel to explore cytoplasmic streaming using a simplified model of a Physarum strand (tube) that is composed of two spherical shells of gel connected by a resistance vessel. When coupled together the shells oscillate out of phase with one another which presumably would produce a flow that could be interpreted as shuttle streaming. When the strain-induced calcium release is too low, the oscillations are damped out. The authors comment that by including more that one chemical species they can get chemical oscillations that drive the mechanical oscillations, but the inclusion of the strain-induced calcium release aids in local synchronization.

A similar model was proposed by Teplov et al.³⁶ to investigate shuttle streaming in Physarum tubes, and this model was applied to circular shaped organisms in ref. 37. Rather than considering just two coupled mechanochemical oscillators as in ref. 35, Teplov et al.³⁶ investigate waves in a gel-walled tube. Again the stress in the gel is the sum of a passive viscoelastic stress and a calcium-sensitive active stress. The stress in the wall generates a pressure on the fluid inside the tube. Spatial differences in pressure induce a flow, which deforms the wall. The release of calcium is a function of strain, but the model for calcium in ref. 36 is simpler than in ref. 35 in that the release rate of calcium is proportional to the strain, but it is not sensitive to the calcium concentration. Analysis of the model shows that when the sensitivity of the release rate to strain is low, the resting state of no flow is stable, but if this sensitivity is increased the no flow state becomes unstable and waves of contraction emerge. The waveforms produced by the model agree qualitatively with experimental data on contraction waves in Physarum.

In the models of Oster and Odell³⁵ and Teplov et al.,^36,37 neither the chemical model nor the mechanical model alone could oscillate, but when coupled together the system produced self-sustaining oscillations and waves. Some experiments suggest that the chemical oscillations occur in the absence of mechanical deformation,³⁸ and thus other models considered the coupling of an autonomous chemical oscillator to a chemically-sensitive mechanical system.^39,40

Smith and Saldana⁴¹ developed a model of the calcium oscillation in Physarum that involved calcium exchange with leaky vacuoles, the binding of calcium to the myosin light chain, and the calcium-sensitive phosphorylation of myosin light chain kinase. The mechanism for the oscillation was inspired by calcium regulation in smooth muscle. In ref. 39 this model was used to explore shuttle streaming by studying the phase difference between coupled oscillators. The mechanical coupling was not modeled explicitly, rather it was a prescribed parameter. The results showed that when the mechanical coupling was weak and the free calcium levels were sufficiently different the calcium oscillators tended to the anti-phase locked state. Phase differences are important because if the mechanical oscillations are spatially uniform, then there are no internal pressure gradients and no shuttle streaming.

Tero et al.⁴⁰ present a mechanochemical model and use it to explore the existence of certain phase patterns observed in Physarum. When a circular plasmodium migrates radially on a flat agar gel, the peripheral region oscillates out of phase with the interior. Near the edges, the gel is not organized into the tubular network as it is in the interior, and the gel is generally less stiff in the peripheral region. The authors hypothesize that the spatial differences in stiffness drive the observed phase patterns. The authors begin with a phenomenological two-variable autonomous oscillator. One variable is interpreted as the amount of sol stored in the gel-walled tubes, and the other variable is interpreted as the amount of a chemical (e.g. calcium) which participates in generating the oscillations. To this system they add a variable corresponding to the amount of fluid in the tubular region, so that the total amount of fluid in the gel and tubes is conserved. The transport rate of fluid in the tubes and the exchange rate of fluid between gel and tube are spatially dependent functions of the stiffness of the gel. Simulations of the model show that indeed spatial differences in the stiffness can account for the phase patterns observed in experiments.

The models described in this section address how the chemistry and mechanics of the cytoplasm interact to produce observed behaviors of Physarum. What these models do not account for is the changing structures within the gel such as the formation of channels and tubes. To model the development of structure, we look to other models of cell motility.

5.2 Models of cell motility

The topic of cell motility is broad, and there are many different modeling approaches. This review is not meant to be comprehensive. Rather, the intention is to discuss techniques which may be useful in modeling motility and gel pattern formation in Physarum. Though Physarum is an unusual cell given its extremely large size, the processes involved in generating force are similar to those in other cells: chemical regulation of solation, gelation, and contraction.

There have been several one-dimensional models of motile cells.^42–45 These models shed light on the relative amounts that different forces contribute to generating motion, but these types of models cannot be used to understand how structures within the gel develop since this is necessarily a multidimensional problem.

Recently, two-dimensional models of crawling cells with free boundaries have been developed for nematode sperm cells⁴⁶ and for fish epidermal keratocytes.^47,48 In each of these models the forces are generated by gelation, solation, and contraction of a gel which is chemically regulated. The modeling approach of each of these works is slightly different. Bottino et al.⁴⁶ compute the forces in the gel using a finite element method. That is, the gel is modeled as a network of discrete mechanical elements. The gel is regulated by the local pH. Solation occurs in acidic environments and gel formation is stimulated by high pH. The cell maintains a pH gradient in its lamellipod so that polymerization occurs at the leading edge which pushes the membrane outward, and depolymerization occurs near the cell body, solating the gel, and pulling the cell forward. Rubinstein et al.⁴⁷ put together models of actin polymerization at the leading edge, depolymerization at the rear, transport of actin in the interior, and the mechanics of an elastic network to simulate the motion of the cell. The force at the leading edge is generated by actin polymerization, and the rate depends on the concentration of monomeric actin and the elastic force. At the rear a one-dimensional model of actin and myosin interaction is used to compute the contraction force. These forces are transmitted through gel in the interior which is treated as a porous elastic solid. Marée et al.⁴⁸ combined a model of regulatory G-proteins with a model of actin polymerization and branching and simulated the movement of the cell using the cellular Potts model.⁴⁹

These models are successful at capturing the cell shape and migration speeds, and provide examples for how to carefully model the gel mechanics. What is different about Physarum is that the tubes and channels within the gel are organized in part by the extremely fast flow of cytoplasm as discussed in Section 3. The fluid mechanics do not play a prominent role in the models discussed in the previous paragraph.

5.3 Two-phase flow models

A model of cytoplasm dynamics in which the fluid mechanics are central is the interpenetrating reactive flow model or two-phase flow model developed by Dembo and co-workers.^50–52 In this model the sol and gel are treated as distinct fluids each with its own velocity field and rheological properties. The sol and gel are assumed to be mixed at every point in space and the composition of the mixture is described by the volume fraction of each phase. The fluid mechanics of the mixture are described by two continuity equations (mass conservation) and two momentum equations, a pair for each phase. These equations are typically of the form

∇ · (θ_sµ_s(∇u_s + ∇u^T_s)) − H(u_s − u_g) − θ_s∇p = 0 (13)

∇ · (θ_gMµ_g(∇u_g + ∇u^T_g)) − H(u_g − u_s) − θ_g∇p + ∇(θ_gΨ) = 0 (14)

θ_s + θ_g = 1, (15)

where θ_s and θ_g are the volume fractions and u_s and u_g are the velocity fields for the sol and gel respectively. Because of the small scale and large viscosity, the inertial terms in the momentum equations (13),(14) have been ignored, and the result is the balance of forces. The forces in the sol phase, eqn (13), are the viscous stress, the interphase drag, and the pressure. The gel equation (14) contains an additional force arising from gel swelling and actin–myosin contractions. There are four unspecified functions: the rate of conversion between sol and gel J, the drag coefficient H, the gel viscosity M, and the swelling/contractile stress Ψ. These four functions can depend on the gel volume fraction and on the concentrations of chemicals such as calcium. For example, in many cells calcium regulates the polymerization and depolymerization of actin (J) and the contractile stress (Ψ).

Dembo used this modeling framework to explore the development of gel structures and the internal flow fields in Amoeba proteus.⁵³ These cells, like Physarum, form channels within the cytoplasm in which the fluid moves rapidly. In ref. 53, the author sought a minimal model which could reproduce the observed structures and flow patterns. The model consists of the equations of motion (11)–(15), and a reaction–advection–diffusion equation for a chemical species. The contractile stress is assumed to be an increasing function of the chemical concentration. The chemical is assumed to be constant at the boundary and is removed in the interior, resulting in a concentration profile which is smallest in the middle of the cell. The contractile stress is lowest in the middle, and this results in the opening of a channel along the center line of the cell. Thus the channel develops as a consequence of the chemical gradient and the chemically-dependent stresses that result.

The channels and tubes in Physarum may be the result of chemical gradients, but as discussed in Section 3, the flow seems to be involved in the development of these structures. A two-phase model of flow-induced channel formation within a gel was recently proposed by Cogan and Keener.⁵⁴ The authors assumed that the gel has two stable preferred volume fractions. Flow through the gel causes local stretching which can act as the mechanism that causes the gel to change from one stable conformation to another.

The two-phase flow model appears to be well-suited to study the internal fluid and gel mechanics of Physarum. So far two-phase models of cytoplasm have used somewhat phenomenological descriptions of the active stresses within the gel and have not included effects such as filament orientation or chemical regulation of the polymerization–depolymerization reactions as has been done in other models of crawling cells.^47,48 However, two-phase models can be adapted to include these effects. The authors of this review believe that such a model would be useful in understanding the internal fluid–gel mechanics of Physarum, and work towards this goal is underway.

6. Concluding remarks

The intelligent behaviors exhibited by Physarum are a result of its ability to create and modify its tubular network. This tubular network provides a means of communicating rapidly with distant parts of the organism. One might assume that chemical signals are transported by the rapid flow, but in this review we have presented experiments and models that demonstrate that this communication can be achieved through local modulation of the material in response to stress, flow, and nutrients. For example, the model in Section 4.4 showed that by decreasing the strength of the oscillation at a food source, less flow goes through the network which results in tubes collapsing. In this way a local chemical signal is transmitted through the network by a mechanical signal.

The models presented in Section 4 show that very simple rules about how the network responds to flow can reproduce the behavior of real plasmodia. However, the question remains as to how the plasmodium develops this network. When the plasmodia are small (≈100 µm in length) there are no channels in the gel and no shuttle streaming. As they increase in size, channels emerge and streaming begins. Experiments with small plasmodia provide an opportunity to observe the development of structures within the gel. Modeling the development of channels and tubes requires accounting for the fluid mechanics as well as the mechanics of the gel which are chemically regulated. Work is underway to develop models of channeling in the protoplasm using multiphase flow models. The goal of this modeling is to understand how processes from the small-scale organization of structures to large scale flow in the network combine to produce the intelligent behavior exhibited by Physarum.

Acknowledgements

The research of RDG was supported in part by NSF grant DMS-0540779. The research of TN was supported by MEXT KAKENHI NO. 18650054.

References

1. W. Gray and C. Alexopoulos, Biology of the Myxomycetes, Ronald Press, New York, 1968.
2. T. Ueda, Phase Transitions, 1993, 45, 93–104.
3. K. Matsumoto, T. Ueda and Y. Kobatake, J. Theor. Biol., 1986, 122, 339–345.
4. K. Matsumoto, T. Ueda and Y. Kobatake, J. Theor. Biol., 1988, 131, 175–182.
5. T. Nakagaki, H. Yamada and A. Tóoth, Nature, 2000, 407, 470.
6. T. Nakagaki, H. Yamada and A. Toth, Biophys. Chem., 2001, 92, 47–52.
7. T. Nakagaki, Res. Microbiol., 2001, 152, 767–770.
8. J. Narby, Intelligence In Nature: An Inquiry Into Knowledge, Tarcher, New York, 2005, ch. 8, pp. 95–108.
9. T. Nakagaki, R. Kobayashi, T. Ueda and Y. Nishiura, Proc. R. Soc. London, Ser. B, 2004, 271, 2305–2310.
10. T. Nakagaki, H. Yamada and M. Hara, Biophys. Chem., 2004, 107, 1–5.
11. A. Tero, R. Kobayashi and T. Nakagaki, J. Theor. Biol., 2007, 244, 553–564.
12. D. Kessler, in Cell biology of Physarum and Didymium, ed. H. C. Aldrich and J. W. Daniel, Academic Press, New York, 1982, pp. 145–196.
13. N. Kamiya, Protoplasmic streaming, Protoplasmatologia, Springer, 1959, vol. 8.
14. E. B. Ridgway and A. C. H. Durham, Protoplasma, 1976, 100, 167–177.
15. Y. Yoshimoto, F. Matsumura and N. Kamiya, Cell Motil., 1981, 1, 433–443.
16. Y. Yoshimoto, T. Sakai and N. Kamiya, Protoplasm, 1981, 109, 159–168.
17. S. Nakamura, Y. Yoshimoto and N. Kamiya, Proc. Jpn. Acad., Ser. B, 1982, 58, 270–273.
18. S. Ogihara, Exp. Cell Res., 1982, 138, 377–384.
19. S. Nakamura and N. Kamiya, Cell Struct. Funct., 1985, 10, 173–176.
20. W. Naib-Majani, W. Stockem and K. E. Wohlfarth-Bottermann, Eur. J. Cell Biol., 1982, 28, 103–114.
21. M. Ishigami, K. Kuroda and S. Hatano, J. Cell Biol., 1987, 105, 381–386.
22. N. Kamiya, Aspects of cell motility, Cambridge University Press, London, 1968, pp. 159–214.
23. R. Nagai, Y. Yoshimoto and N. Kamiya, J. Cell Sci., 1978, 33, 205–225.
24. N. Kamiya, R. D. Allen and Y. Yoshimoto, Cell Motil. Cytoskeleton, 1988, 10, 107–116.
25. W. Stockem and K. Brix, Int. Rev. Cytol., 1994, 149, 145–215.
26. S. Hatano and H. Sugino, Protein, Nucleic Acid Enzyme, 1983, 28, 329–342.
27. T. Hasegawa, S. Takahashi, H. Hayashi and S. Hatano, Biochemistry, 1980, 19, 2677–2683.
28. K. Maruyama, M. Kaibara and E. Fukada, Biochim. Biophys. Acta, 1974, 371, 20–29.
29. T. Nakagaki, H. Yamada and T. Ueda, Biophys. Chem., 2000, 84, 195–204.
30. T. Nakagaki, T. Saigusa, A. Tero and R. Kobayashi, in Proceedings of the International Symposium Topological Aspects in Critical Systems and Networks, World Scientific Publishing Co., 2007, pp. 94–100.
31. A. Tero, R. Kobayashi and T. Nakagaki, Physica A, 2006, 363, 115–119.
32. T. Miyaji and I. Onishi, submitted.
33. T. Miyaji and I. Onishi, Hokkaido Math. J. , in press.
34. R. Kobayashi, A. Tero and T. Nakagaki, J. Math. Biol., 2006, 53, 273–286.
35. G. Oster and G. Odell, Cell Motil., 1984, 4, 469–503.
36. V. Teplov, Y. Romanovsky and O. Latushkin, BioSystems, 1991, 24, 269–289.
37. D. Pavlov, Y. Romanovskii and V. Teplov, Biophysics, 1996, 41, 153–159.
38. Y. Yoshimoto and N. Kamiya, Protoplasma, 1982, 110, 63–65.
39. D. A. Smith, Protoplasma, 1994, 177, 163–170.
40. A. Tero, R. Kobayashi and T. Nakagaki, Physica D, 2005, 205, 125–135.
41. D. A. Smith and R. Saldana, Biophys. J., 1992, 61(2), 368–380.
42. P. A. DiMilla, K. Barbee and D. A. Lauffenburger, Biophys. J., 1991, 60, 15–37.
43. A. Mogilner and D. Verzi, J. Stat. Phys., 2003, 110, 1169–1189.
44. M. E. Gracheva and H. G. Othmer, Bull. Math. Biol., 2004, 66, 167–193.
45. A. T. Dawes, G. B. Ermentrout, E. N. Cytrynbaum and L. Edelstein-Keshet, J. Theor. Biol., 2006, 242, 265–279.
46. D. Bottino, A. Mogilner, T. Roberts, M. Stewart and G. Oster, J. Cell Sci., 2002, 115, 367–384.
47. B. Rubinstein, K. Jacobson and A. Mogilner, Multiscale Model. Simul., 2005, 3, 413–439.
48. A. F. M. Marée, A. Jilkine, A. Dawes, V. A. Grieneisen and L. Edelstein-Keshet, Bull. Math. Biol., 2006, 68, 1169–1211.
49. F. Graner and J. A. Glazier, Phys. Rev. Lett., 1992, 69, 2013–2016.
50. M. Dembo and F. Harlow, Biophys. J., 1986, 50(1), 109–121.
51. M. Dembo, M. Maltrud and F. Harlow, Biophys. J., 1986, 50(1), 123–137.
52. W. Alt and M. Dembo, Math. Biosci., 1999, 156, 207–228.
53. M. Dembo, Biophys. J., 1989, 55(6), 1053–1080.
54. N. G. Cogan and J. P. Keener, SIAM J. Appl. Math., 2005, 65, 1839–1854.
55. T. Nakagaki, Cell behaviors based on self-organization of coupled nonlinear oscillators, PhD thesis, Nagoya University, 1997.
56. Y. Miyake, S. Tabata, H. Murakami, M. Yano and H. Shimizu, J. Theor. Biol., 1996, 178, 341–353.
57. T. Ueda, K. Matsumoto, T. Akitaya and Y. Kobatake, Exp. Cell Res., 1986, 162, 486–494.
58. T. Nakagaki, S. Umemura, Y. Kakiuchi and T. Ueda, Photochem. Photobiol., 1996, 64, 859–862.

---