Hazardous N-containing system: thermochemical and computational evaluation of the intrinsic molecular reactivity of some aryl azides and diazides

Abstract

The exothermic decompositions of the tosyl azide 1, five substituted aryl monoazides 2––6 and two diazides: 1-azido-4-(4-azidophenoxy)benzene 7 and 1-azido-4-[(4-azidophenyl)sulfanyl]benzene 8 were studied experimentally using DSC, weight loss TGA-FTIR and C80-FTIR techniques, and theoretically using the CHETAH software. Numerical modelling and electron impact mass spectrometry (EI-MS) were also performed to investigate the nature of the intrinsic molecular reactivity of azides 1––8, and the possible early stage rate-controlling of an oxidative self-heating process. Significant data were obtained in the instances of 4-methylbenzenesulfonyl azide 1, 4-azido-1,1′-biphenyl-2,2-azido-1,1′-biphenyl 3 and 1-azido-2-(trifluoromethyl)benzene 6. The most likely decomposition pathways of the azides are proposed to explain the observed thermal behavior.

---

Introduction

Organic azides are a vast and important class of compounds which, more than a century after their discovery, remain popular due to both their easy accessibility and their incomparable synthetic utility.^1,2 The last two decades have seen overwhelming interest in these compounds because of various simple routes by which they can be prepared and transformed into different substituents (amines, aza-ylides, isocyanates), reactive species (nitrene, nitrenium ion) and nitrogen-containing heterocycles (triazenes, triazoles, triazolines, azirines, aziridines).

Although the toxic and explosive properties of some metal azides and a few organic azides,^3–5 including tosyl azide,⁶ are well documented, less attention has been paid to the healthy and safe disposal of this class of compounds. In addition, the chemical properties of a series of nitrogen-rich covalent azides, and their potential use as high energy-density materials (HEDM), are presently under investigation.⁷ The azido group is actually a highly energetic functional group that adds 293 kJ mol^–1 to the energy content of a molecule.⁸

The higher energetic content of these oxygen-less compounds is due to the large number of molecular C–N and N–N bonds and to the easy polarization of the –N₃ π-bond, which facilitates N₂extrusion.^9,10 Many organic compounds containing one or more azido groups requires small-scale handling due to their heat- or shock-sensitivity.³ On the other hand, the dissociation of the azido group into a nitrene and molecular nitrogen is known for providing large amounts of energy, which in the presence of high-boiling solvents (controlled conditions) or large substrates is dissipated. At the same time the arising nitrene, in both singlet or triplet state, becomes of great synthetic utility.² Because of this, interest in these molecules has constantly grown as researchers have overcome their awe of the hazard posed by handling azides.^11–13

Only a few heteroarylic azides have been studied by DSC (differential scanning calorimetry),¹⁴ and to our knowledge, no systematic report on the calorimetry of aryl azides can be found in the literature. The only exception would be the DSC analysis of the phenyl azide by T. Grever et al. published as Technical Report (01VD 159/0329) for the Federal German Ministry for Res. Technol., Bonn. 1986, in which the determined energy of decomposition was 1.36 kJ g^–1 at 130–260 °C, with an energy of activation of 119 kJ mol^–1.

From a theoretical point of view, explosive initiation of an energetic compound consists of complex physical and chemical processes, whose iterative and sequential mechanistic aspects occur over a finite time period, and proceed from macroscopic into sub-microscopic composition levels (bulk > crystalline > molecular > atomic). Real initiation starts hence when these processes proceed at a rate that generates enough amounts of energy (heat) to reach the threshold limit in this finite period of time. The rate-controlling N–N₂ bond dissociation can be taken as a significant rate-limiting feature for thermal decomposition (TD) also at high kinetic order, i.e. in polyazido derivatives..¹⁵

In spite of the fact that organic azides are generally stable toward common oxidants and acidic aqueous solutions, azides with large positive heats of formation (Δ_fH) are inherently unstable. The reasons underlying a molecule’s reactivity or lack of stability can be elucidated by examining thermodynamic parameters, and also by scrutinizing kinetic variables, critical temperatures,¹⁶ numerical protocols based on the symmetries and geometries, spatial distributions and energies of a few dominant orbitals, and electric polarizabilities and hyperpolarizabilities.

Therefore, important information could be provided by:

 

(i) Enthalpies of reaction calculated from heats of formation [Δ_rH = ∑ _prodΔ_fH – ∑ _reactΔ_fH].

(ii) Arrhenius activation energy (E_a) of the reactions, from which enthalpies [E_a = ΔH^‡ + RT] and entropies (ΔS_a) of activation could eventually be obtained.

(iii) HOMO–LUMO energies and orbital symmetry.¹⁷ Fast reactivity may be due to a small LUMO–HOMO energy difference.¹⁸

(iv) The polarization of the –N₃ π-bond and –N–N₂ bond energy and length. A higher electric polarizability enhances the instability/reactivity.⁹

(v) Ionization energy. In the general case, this represents the energy required to detach one electron from a neutral molecule (or atom). Qualitative information on the chemical ionization for a selected class of molecules can be obtained using electron impact mass spectrometry (EI-MS).¹⁹

 

In the present study, we measured various thermodynamic variables of the tosyl azide 1, five closely related aryl monoazides 2––6 [4-azido-1,1′-biphenyl 2, 2-azido-1,1′-biphenyl 3, 1-azido-3-methylbenzene 4, 1-azido-4-methylbenzene 5 and 1-azido-2-(trifluoromethyl)benzene 6], and the aryl bisazides: 1-azido-4-(4-azidophenoxy)benzene 7 and 1-azido-4-[(4-azidophenyl)sulfanyl]benzene 8 (Scheme 1). These compounds were selected as significant examples of a series of nitrogen-rich covalent azides whose dangerous threshold values, given by the molecular composition ratio (C + O + S…)/N are ≤ 3, and to shed light on the role of the substituent of the azido group in the TD phenomena.

Scheme 1 Structure of azides 1––8.

Experimental

Materials

The sensitive organic azides 1––8 used in this study (see Scheme 1) were prepared as follows. The tosyl azide 1 was prepared according to a previously described protocol,²⁰ the aryl monoazides 2––6 and the aryl bis-azides 7 and 8, were prepared according to the Dutt–Wormall reaction by diazotization of the corresponding amines (or diamines) and treatment with the azido ion of the resulting diazonium salts.^21,22 The general techniques, compounds, purification and authentication, were performed using standard methods. Chromatographic filtration was carried out on ‘Florisil’ BDH, 60–100 mesh using petroleum ether (distillation range 30–60 °C) as the eluent.

Physical measurements and calculation

IR spectra of 1––8 were measured from films on a Perkin-Elmer Spectrum 2000 FTI-IR spectrometer. The ¹H and ¹³C NMR spectra of each compound were recorded on a Varian Gemini 300 and agree with those reported in the literature.^20–22 The mass spectra of all compounds 1––8 were recorded on VG7070E instruments using electron impact (70 eV) under the same pressure and temperature.

The initial thermochemical calculations are based on the ASTM computer program for chemical thermodynamic and energy release evaluation (CHETAH),²³ Heats of formation obtained by this code were compared with those calculated using a recently released Spartan ‘06 code: the thermochemical recipes ‘T1’, which was developed to fit data from G3(MP2) calculations.²⁴

The experimental TD measurements have been carried on using calorimetric methods (DSC, TG-FTIR, and the Heat-Flux SETARAM C80 calorimeter coupled with an FTIR analyzer) under both oxidative and non-oxidative conditions.

The melting points of the solid azides 2, 3, 7 and 8, taken from the endothermic melting peak in the DSC and C80 thermograms, were 77, 51, 74 and 86 °C, in agreement with the literature values.^21,22 Incidentally, these azides showed DSC (each three runs) experimental values of melting enthalpies of 110, 110, 100 and 110 J g^–1, respectively.

Additional numerical modelling were performed using the standard program Spartan ’06 Windows, running on an AMD K7 processor at 1333 MHz, by which optimized structures and energetics of the N–N₂ bond dissociation have been reasonably obtained.²⁵ Electron impact mass spectrometry (EI, 70 eV) was performed to investigate molecular early stage processes and how the rate-controlling of them could affect the rate-limiting processes in TD of azides 1––8.

Results and discussion

Thermodynamic variables (heats of formation Δ_fH, combustion Δ_cH, and decomposition Δ_dH) and molecular nitrogen loss (%), calculated by using the CHETAH software²³ for azides 1––8, are listed in Table 1. The so-calculated TD enthalpies were found to be in the range –2.86 to –4.50 kJ g^–1, values that are higher than one might have expected.

Table 1 CHETAH calculated energetic parameters (Δ_fH, Δ_cH, Δ_dH) and % N₂ loss for azides 1––8

	1	2	3	4	5	6	7	8
ΔfH/kJ mol^–1	317.5	482.2	482.2	352.8	352.8	–295.6	658.5	837.1
ΔcH/kJ g^–1	–21.37	–32.24	–32.14	–29.70	–29.70	–18.13	–25.16	–25.43
ΔdHmax/J g^–1	–4497	–3331	–3331	–3631	–3631	–2863	–4010	–3677
N2 (%)	21.29	21.51	21.51	31.54	31.54	22.44	33.3	31.3

---

Here, the heats of the decomposition (Δ_dH) for azides 1––5 and 7, 8 were found to be over the threshold of –2.93 kJ g^–1, above which value compounds are considered dangerous, while for azide 6 this value was found to be just within the limit (–2.86 kJ g^–1).

The CHETAH-calculated heats of formation (Δ_fH) for azides 1––8 were compared with those obtained using the less computationally intensive thermochemical recipes ‘T1’,²⁴ which requires geometry optimization at the HF/6-31G* level, revealing that the heat values obtained using the two approaches differ by less than 5%, with the only exception being for azide 1²⁶ (see Table 2)

Table 2 Comparison between CHETAH^a and ‘T1’^b calculated heats of formation (Δ_fH) of azides 1––8

	1	2	3	4	5	6	7	8
ΔfH^a/kJ mol^–1	317.5	482.2	482.2	352.8	352.8	–295.6	658.5	837.1
ΔfH^b/kJ mol^–1	114.2	488.5	496.4	370.3	370.7	–268.1	692.2	860.4

---

The CHETAH predicted data are merely indicative²⁷ even if useful,²⁸ and more realistic results can be obtained by experimental DSC, TG-DTA and SETARAM C80-FTIR calorimetry. These techniques enabled us to characterize the thermal (in)stability of azides 1––8via the determination of physical (pressures P, temperatures T_n and decomposition rates) and energetic (activation energy E_a, enthalpies and entropies of decomposition) parameters.

The experimental data reported on Table 3 account for TD involving differently sensitive compounds, under oxidative (or under nitrogen) heating. In general, the heat capacities of azides measured using the open-vessel in static air (Δ_dH_air) were larger than those measured using a closed-vessel (Δ_dH_SCC)], with the exception of 3, confirming a concerted path; by contrast, under nitrogen only azide 1 exhibited an evident opposite behavior (Δ_dH > Δ_dH_SCC).

Table 3 DSC heats of decomposition (Δ_dH/J g^–1) and temperatures (°C) of the thermal decomposition (TD) of azides 1––8^a

	1	2	3	4	5	6	7	8
a TD data refer to a scan rate (Φ) of 5 °C min^–1. b In static air. c Under nitrogen. d In a closed steel vessel. e Initial decomposition temperature. f Exothermic onset temperature. g Peak decomposition temperature. h Exothermic endset temperature.
ΔdHair^b	–1806	–1318	–1442	–1704	–1519	–1155	–2045	–1340
ΔdH^c	–1640	–1084	–1544	–834	–925	–915	–1562	–1303
ΔdHSCC^d	–1583	–1139	–1585	–1244	–919	–1108	–1715	–1369
T 0 ^e/°C	121	143	134	137	121	141	124	128
T EOT ^f/°C	156	166	240	234	169	175	154	167
T p ^g/°C	184	195	243	253	198	202	177	190
T EET ^h/°C	204	215	245	262	218	222	192	207

---

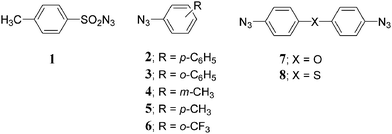
The DSC profiles (Fig. 1), measured at different heating rates in the range 30.0–280.0 °C, were further analyzed using the standard ASTM E698 method²³ for reactions, whose behavior is well described by the Arrhenius equation. From a plot of log b (where b = heating rate in K min^–1) against 1/T (T = peak temperature in K), the apparent activation energies (E_a), the pre-exponential factor A⁰ and the kinetic constant k for each absolute temperature can be calculated.

Fig. 1 Individual TD DSC profiles for DSC runs performed under nitrogen each at scanning rate (Φ) of 2.0, 5.0 and 10.0 °C min^–1, for 2.4, 2.4 and 3.8 mg, respectively, of azide 1.

The TD curves at various temperatures in the range 90–200 °C of azides 1––8 were treated as having first-order kinetics as plots of ln(k/min^–1) vs. T/K, showing a linear trend with correlation coefficients in the range of 0.999–1. The activation energies (E_a) of 1––8 were calculated, with corresponding frequency factor ln(A⁰/min^–1) values. Assuming unimolecular processes, we calculated the activation enthalpies (Δ_aH^‡) and entropies (Δ_aS) from the data (see Table 4)

Table 4 Activation^a energies, enthalpies (Δ_aH)^b and entropies (Δ_aS)^c of reaction calculated from the experimental TD of azides 1––8 using the ASTM E698 method

	1	2	3	4	5	6	7	8
E a ^a/kJ mol^–1	127.5	158.4	99.3	141.9	127.5	99.3	138.6	137.7
ΔrH^b/kJ mol^–1	125.1	155.9	96.8	139.4	125.0	96.8	136.2	135.3
ΔaS^c/K^–1 mol^–1	9.9	78.3	–65.3	35.7	17.6	–49.1	35.2	34.9

---

No thermal data are available in the literature for the azides under investigation, while ‘controlled’ thermal dissociation of azides 1, and 2––5 has been carried out in various solvents, starting from the pioneering works of Breslow et al.²⁹ and Smith and Hall.²¹

In agreement with the data concerning the ‘controlled’ dissociation of the ortho- and para-substituted aryl azides,³⁰ the rate of the TD (t_1/2) at 160 °C of the 4-azidobiphenyl 2 was threefold slower than that of the 2-azidobiphenyl 3, and the corresponding activation energies (E_a) were 158.4 vs. 99.3 kJ mol^–1. This implies a considerable anchimeric assistance, through the phenyl rings, in the quick extrusion of nitrogen from 3, with important formation of carbazole.^31,32 Such a peculiar trend is confirmed by the negative entropy calculated for the o-substituted aryl azide 3.

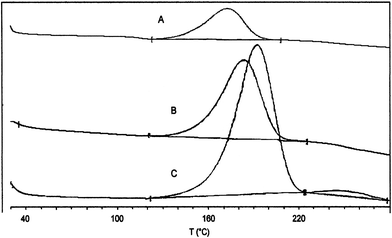
By TG-FTIR and C80-FTIR analyses of azides 1––8, more accurate data for the weight loss, temperatures T_n and heat of decomposition were obtained, along with information on the pressure change associated with the TD process in a closed-vessel. The nature of the TD of 3 was confirmed by SETARAM C80, by which a first endothermic melting peak (108.7 J g^–1) was observed at 51 °C, followed by an exothermic decomposition starting at T₀ = 110 °C, with Δ_dH = –1544 J g^–1 and pressure increments (ΔP) of 6.5 bar. A second endothermic melting peak (79.51 J g^–1) at 245 °C was observed, attributable to the melting of the carbazole³³ partially formed (ca. 36%)³⁴ in the course of the thermal process, the presence of which was also confirmed by FTIR spectra measured at the maximum rate of weight loss. As an example, the C80 curve for azide 3 is shown in Fig. 2.

Fig. 2 C80 curve of azide 3 recorded in the temperature range 30.0–280.0 °C at a scanning rate (Φ) of 0.5 °C min^–1.

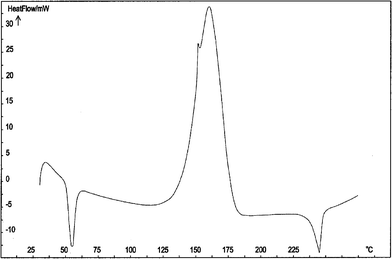
For 1, the C80 analysis (see Fig. 3) detected at least two exothermic processes, at T_i = 103 and 190 °C, with Δ_dH = –1487 and –52 J g^–1, respectively, and a pressure increment (ΔP) of 5 bar. The TG analysis (see Fig. 4) showed that these two processes have corresponding weight losses of 28.6 and 31.4%, which are, respectively higher and lower than the corresponding loss of N₂ and SO₂.

Fig. 3 C80 curve of azide 1 recorded in the temperature range 30.0–280.0 °C at a scanning rate (Φ) of 0.5 °C min^–1.

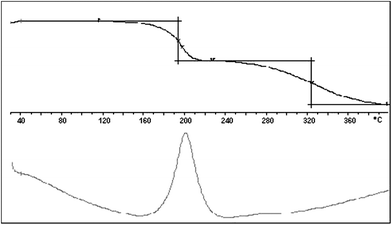Fig. 4 TG curve (upper) and DTA (differential thermal analysis) (lower) of azide 1 recorded in the temperature range 30.0–400.0 °C and at Φ = 20 °C min^–1 under N₂ in an 80 mL min^–1 stream.

The C80 and TG thermal analyses coupled with FTIR spectrometry allowed the identification of the molecular fragments and gases produced by the TDs of the azides. The identified fragments and gases for 1 were carbon dioxide (CO₂), carbon monoxide (CO), sulfur dioxide (SO₂), thioxomethanone (COS), sulfur dioxide (SO₂), ammonia (NH₃) and toluene (C₇H₈). We detected SiF₄, CO₂ and trifluoromethane in the case of azide 6, carbazole for 3 and hydrogen cyanide (HCN), CO₂ and CO for 2, 7 and 8. The C80 and TG techniques brought to evidence the oxidative TD type process for each of azides 1––8 summarized in Table 3 (Δ_dH_air and Δ_dH values).

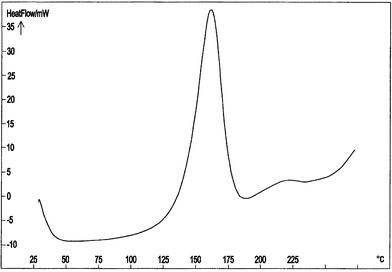
On the other hand, the C80 analyses of diazides 7 and 8 showed in both cases an endothermic melting peak and an exothermic decomposition starting at T_i = 120–125 °C, with Δ_dH = –1.49 and –1.53 kJ g^–1, and pressure increments (ΔP) of 5 and 4 bar, respectively. As an example, the C80 curve for azide 8 is shown in Fig. 5.

Fig. 5 C80 curve of azide 8 performed in the temperature range 30.0–280.0 °C and at Φ = 0.5 °C min^–1.

TG analysis showed that the TD processes for 7 and 8 correspond to a weight loss of 24.6 and 22.4%, which are close to the respective loss of two moles of N₂ (see Fig. 6 for 8).

Fig. 6 TG curve (upper) and DTA curve (lower) of azide 8 performed in the temperature range 30.0–400.0 °C and at Φ = 20 °C min^–1 under N₂ flow of 80 mL min^–1.

A similar behavior was observed in the thermal diagrams of azide 7

Numerical modelling and mass spectra analyses can be used to suggest the possible initial steps of the unimolecular TD of azides 1––8. The main fragmentations obtained by EI-MS (70 eV, m/z) are reported in Table 5, where values in parentheses correspond to the relative intensity, and the asterisk (*) denotes the base peak (100%).

Table 5 Main fragmentations (m/z) and relative intensity (%) obtained by EI-MS for azides 1––8

Comp.	M^+	M – 28	Others
a M – N3. b Identical to the SciFinder spectra ID: WID-DLO-091576-4. c M – Me. d M – 2N2.
1	197 (M^+, 5.7%)		155 (M – 42, 62.4);^a 91*^b
2	195 (M^+, 13.3%)	167*	166 (42.7); 140 (23.1); 139 (25.0)
3	195 (M^+, 6.9%)	167*	166 (37.9); 140 (15.9); 139 (22.7)
4	133 (M^+, 11.8%)	105 (24.9)	119 (18.8);^c 91 (53.6), 57*
5	133 (M^+, 2.5%)	105 (10.8)	57 (18.0); 28*
6	187 (M^+, 12.8%)	159 (71.0)	145 (M – 42, 12.8);^a 139 (50.0); 69*; 63 (88.7); 50 (48.4)
7	252 (M^+, 11.6%)	224 (37.1)	196 (9.8);^d 90*
8	268 (M^+, 22.6%)	240 (48.5)	212 (29.2);^d 211 (26.0), 90*

---

The peaks of the molecular ions (M⁺˙) represent the ionized molecules (Scheme 2). As expected, the primary fragmentations of azides 2––8 involve the loss of neutral N₂ to generate the odd-electron species ArN⁺˙ (M – 28) (see Scheme 2, path I). Conversely azide 1 loses N₃ (M – 42), presumably as a radical from the molecular ion M⁺˙ (otherwise as an anion directly from the starting azide)³⁵ (see Scheme 2, path II and III, respectively).

Scheme 2 Main fragmentation patterns for azides 2––8 and 1 determined by EI-MS spectrometry (70 eV).

The behavior of 2––8 can be adequately described by the normal fragmentation pattern of aryl azides,³⁶ in which the critical energy for ArN₃⁺˙ → ArN⁺˙ + N₂ is equivalent to the dissociation energy of the ArN–N₂ bond plus the ionization energy (I) of the radical ArN⁺˙, because the reverse process is insignificant. The ionization generally requires twice the energy needed for bond dissociation (bond lability). On the other hand, the abnormalazido fragmentation pattern observed for 1 (and only partially verified for the deactivated azide 6) can be interpreted by assuming that under the ion chamber conditions used (T = 220 °C and P = 10^–2 Pa), the reaction ToSO₂–N₃ → ToSO₂⁺ + ^–N₃ (path III) is favored with respect to the ionization process to ToSO₂–N₃^+˙, and hence to other following pathways such as ToSO₂–N₃⁺˙ → ToSO₂–N⁺˙ + N₂ (path I or II).³² No sign of the N₃ cation (m/z 42) was found.

The elucidation of the TD mechanism by numerical modeling of energetic molecules is important for both understanding how the stored energy is released, and gaining information useful for increasing their stabilities. Using density functional theory (DFT) at the B3LYP/6-31G* level, we optimized structures and energetics (including the LUMO–HOMO separations) of the initial states and of the possible transient intermediates, and the structures connecting them. The chemical instability-reactivity of azides 1––8 triggered the interest in calculating the bond N–N₂ dissociation energies (Scheme 2; path I) by the above mentioned protocol.²⁵

The results of these calculations are listed in Table 6.

Table 6 FMO energies (E_HOMO/LUMO) and energies (E) of N–N₂ bond dissociation of 1––8 calculated using B3LYP/6-31G* level

	1	2	3	4	5	6	7	8
a In kJ mol^–1. b Calculated energies of the N–N2 bond dissociation in kJ mol^–1 including ZPE correction.
E HOMO ^a	–710.5	–566.3	–587.0	–590.1	–579.9	–636.8	–559.6	–553.5
E LUMO ^a	–200.0	–114.7	–99.1	–94.9	–93.2	–128.6	–109.3	–126.8
ΔE^a	510.5	451.6	487.9	495.2	486.7	508.2	450.3	426.7
ΔE^b	124.4	141.2	100.2	161.8	131.0	156.4	152.8	156.2

---

For most classes of compounds, the primary cleavage (thermal impact sensitivity) may be taken as a qualitative indicator of the stability of a compound,¹⁵ and thus can be used to compare the stabilities of similar compounds subjected to thermal processes under the same conditions. In this view the energies obtained at the (U)B3LYP level of theory²⁵ for the reaction ToSO₂–N₃ → ToSO₂–N_{(S or T)} + N₂ indicate that the separation between the states of triplet and singlet is 49.5 kJ mol^–1. The calculations of the corresponding energies of bond dissociation involving the ToSO₂–N_(S) in the singlet state (124.4 kJ mol^–1) and triplet state (ToSO₂–N_(T), 74.8 kJ mol^–1) confirmed the expectation that the loss of N₂via a nitrene triplet would be the most favored kinetic process for 1. On the other hand, the corresponding energies of bond dissociation involving the ToSO₂⁺ + ^–N₃ fragmentation (path III) is 218.0 kJ mol^–1, hence higher than expected.

The discrepancy observed between the EI-MS ionization pathway and the above mentioned calculation results, which favors the loss of N₂group rather than the detachment of an N₃ anion (or radical), may be explained considering that the local ionization potential map for azide 1 is mainly localized on the SO₂. This induces weak polarization of the –N₃ π-bond to –N–N₂, and the loss of ^–N₃ anion could be favored when quickly followed by loss of neutral SO₂.

The present data and previous reports on 1²⁹ suggest hence that the early stages of TD of this azide occur via a number of concomitant heterolytic and homolytic bond cleavage pathways, or alternatively, that the sulfonyl–azido bond is not well represented in calculations.

As expected, the o-conjugated aryl azide 3 undergoes N₂ loss via a concerted process that does not involve a ‘free nitrene’ intermediate, as confirmed by the negative entropies of its TD (see Table 4). Previously calculated numerical modelling accounts for the low energy of the reaction path³³ of the o-conjugated aryl azide 3 to carbazole,³⁰ whose controlled TD was thoroughly investigated by several researchers starting from the pioneering work of Smith and Hall.²¹

In addition, we recognized that the path I occurs preferentially via a nitrene singlet when generated both from the strongly deactivated³⁰o-trifluoromethyl substituted azide 6 and the slightly activated 5. Due to the methyl resonance effect, which stabilizes the nitrene favoring the loss of molecular nitrogen, an enhanced reactivity of 5 compared to 4 (and 6) was calculated by DFT. However, the experimentally determined low activation energy (96.8 kJ mol^–1) and negative entropy value in the instance of 6 suggests that the TD of this azide occurs mainly via an intramolecular pathway.

Insofar as diazides 7 and 8 is concerned, relatively high energies were calculated for both the first (152.8 and 156.2 kJ mol^–1) and the second (146.3 and 155.7 kJ mol^–1) azido group dissociation. The inactivity of the expected activating p-directing effect by the heteroatoms (O and S, respectively) is presumably due to weak resonance interaction between the heteroatom and the two aryl rings.²²

Conclusion

We have assessed the thermal decomposition behavior of various organic azides using calorimetric analyses and quantitative structure-property relationships based on molecular modelling. The experimental TD of the tosyl azide 1 and aryl azides 2––8 occurs between 120 and 280 °C with enthalpies of decomposition in the range of –1.1 to –2.0 kJ g^–1. Even if the range falls under the reference threshold limit for explosion, on scaling up reaction of this kind may be hazardous. In addition, we were able to identify the mechanistic rate-controlling bond dissociation via examination of electronic structure correlations and by EI-MS spectra. The general relevance of the initial step, corresponding to the rate-controlling N–N₂ bond dissociation, ultimately affects the energy release rate of a likely energetic material. Rate enhancement, low activation energy and negative reaction entropy characterize the intramolecular thermal cyclisation of the o-substituted azides 3 and 6. Divergent data were observed for azide 1, that shows the highest enthalpy of decomposition and smallest heat of formation for which a thermal process with a number of concomitant heterolytic and homolytic S–N₃ bond-cleavage pathways is suggested. The global thermal processes, evaluated by correlations between numerical modelling and experimental data reported on different kinds of aryl azides and diazides, gives a better understanding of the impact sensitivity from a molecular viewpoint, which should provide help in classifying highly energetic materials.

Acknowledgements

This work was supported by the Ministero Università e Ricerca (PRIN 2005) and partially by the “Progetto di Finanziamento Triennale, Ateneo di Bologna”. We express our most heartfelt gratitude for the work and suggestions given by Prof. Warren J. Hehre.

References

1. S. Bräse, C. Gil, K. Knepper and V. Zimmermann, Angew. Chem., Int. Ed., 2005, 44, 5188–5240.
2. Azides and Nitrenes, Reactivity and Utility, ed. E. F. V. Scriven, Academic, Orlando, FL, 1984.
3. Bretherick’s Handbook of Reactive Chemical Hazards, ed. P. G. Urben, Elsevier, Amsterdam, 7th edn, 2007, vol. 1 and 3.
4. D. S. Breslow, in ref. 2, pp. 509–511.
5. The Chemistry of the Azido Group, ed. M. E. C. Biffin, J. Miller, D. B. Paul and S. Patai, Interscience, London, 1971, pp. 61–63.
6. H. Spencer, Chem. Br., 1981, 17, 106.
7. M.-H. V. Huynh, M. A. Hiskey, D. E. Chavez, D. L. Naud and R. D. Gilardi, J. Am. Chem. Soc., 2005, 127, 12537–12543.
8. R. Haiges, A. Boatz, A. Vij, M. Gerken, S. Schneider, T. Schroer and K. O. Christie, Angew. Chem., Int. Ed., 2003, 42, 5847–5851.
9. D. Spinelli and P. Zanirato, J. Chem. Soc., Perkin Trans. 2, 1993, 1129–1133 , and references therein.
10. Orbital Symmetry and Reaction Mechanism, ed. E. A. Halevi, Springer-Verlag, Berlin, 1992.
11. Organic Chemistry of Explosives, ed. J. P. Agrawal and R. D. Hodgson, Wiley, Chichester, 2007.
12. V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, Angew. Chem., Int. Ed., 2002, 41, 2596–2599.
13. A. Hahma, E. Holmberg, N. Hore, R. Tryman, S. Wallin and H. Oestmark, Int. Annu. Conf. ICT, (Energetic Materials 33rd), 2002, 62, 1.
14. W. Stadlbauer and G. Hojas, J. Biochem. Biophys. Methods, 2002, 53, 89–99.
15. M. Grodzicki, J. M. Seminario and P. Politzer, Theor. Chim. Acta, 1990, 77, 359–367.
16. Critical Temperatures for the Thermal Explosion of Chemicals, ed. T. Kotoyori, Elsevier, Amsterdam, 2005.
17. I. Fleming, Frontier Orbitals and Organic Chemical Reactions, Wiley, London, 1976.
18. N. R. Badders, C. WeI, A. A. Aldeeb, W. J. Rogers and M. S. Mannan, J. Energ. Mater., 2006, 24, 17–33.
19. Interpretation of Mass Spectra, ed. F. W. Mclafferty, University Science Books, Mill Valley, CA, 1980.
20. W. Von E. Doering and C. H. De Puy, J. Am. Chem. Soc., 1953, 75, 5955–5957.
21. P. A. S. Smith and J. H. Hall, J. Am. Chem. Soc., 1962, 84, 480–485.
22. M. Minato and P. M. Lahti, J. Phys. Org. Chem., 1994, 4, 495–502.
23. The ASTM Computer Program for Chemical Thermodynamic and Energy Release Evaluation, CHETAH, ver. 8.0, 2005.
24. T1 is a Prof. Warren J. Hehre product based on thermochemical recipes of different quantum chemical methods that provide thermochemical data. Spartan ‘06 for Windows and Linus, Tutorial and User’s Guide, Wavefunction Inc., Irvine, CA, 2006, (http://www.wavefun.com).
25. These data were obtained using the standard Spartan ’06 Windows DFT method at B3LYP/6-31G* level. see also ref. 37.
26. Heats of formation of 1, kindly calculated by W. J. Hehre using both T1 and G3(MP2) methods, were 120.6 and 126.2 kJ mol^–1, respectively. The discrepancy between the ‘T1' values and the CHETAH-derived ones may be attributed to the fact that the S–azido bonds are not represented in the training set of the ‘T1' method, while the C–azido bonds are instead implemented.
27. W. H. Seaton, J. Chem. Educ., 1989, 66, A137.
28. D. Frurip, L. B. Wenton, J. Going, B. K. Harison, J. Niemier and E. A. Ural, Process Safety Prog., 2004, 23, 266–278.
29. D. S. Breslow, M. F. Sloan, N. M. Newburg and W. B. Renfrow, J. Am. Chem. Soc., 1969, 91, 2273–2279.
30. P. A. S. Smith, in ref. 2, pp. 95–204.
31. R. J. Sundberg, D. W. Gillespie and B. A. DeGraff, J. Am. Chem. Soc., 1975, 97, 6193–6196.
32. K. E. Chippendale, B. Iddon and H. Suschitzky, J. Chem. Soc., Perkin Trans. 1, 1973, 129–133.
33. M.-L. Tsao, N. Gritsan, T. R. James, M. S. Platz, D. A. Hrovat and W. T. Borden, J. Am. Chem. Soc., 2003, 125, 9343–9358.
34. J. S. Chickos, W. E. Acree, Jr and J. F. Liebman, J. Phys. Chem. Ref. Data, 1999, 28, 1535–1673.
35. M. M. Campbell and A. D. Dunn, Org. Mass Spectrom., 1972, 6, 599–600.
36. R. A. Abramovitch, P. Kiba and E. F. V. Scriven, J. Org. Chem., 1971, 36, 3796–3803.
37. D. A. Hrovat, E. E. Waali and W. T. Borden, J. Am. Chem. Soc., 1992, 114, 8698–8699.

---