Analysis of pressure-driven air bubble elimination in a microfluidic device†
Joo H.
Kang
a,
Yu Chang
Kim
ab and
Je-Kyun
Park
*a
aDepartment of Bio and Brain Engineering, Korea Advanced Institute of Science and Technology (KAIST), 335 Gwahangno, Yuseong-gu, Daejeon 305-701, Korea. E-mail: jekyun@kaist.ac.kr; Fax: +82-42-869-4310; Tel: +82-42-869-4315
bKorea Institute of Machinery and Materials (KIMM), 104 Sinseongno, Yuseong-gu, Daejeon 305-343, Korea
First published on 25th October 2007
Abstract
We report an analysis of pressure-driven bubble elimination for a gas-permeable microfluidic device. In this study, we described bubble elimination in a microfluidic device employing a gas permeation model and calculated the removal efficiency of bubbles. The correction factor for the simplified model was estimated with respect to the applied pressure. Based on the established model, the required time to remove a trapped bubble with a certain area was shown to be within an error of 11.58% by comparison with experimental results. Exploiting the model equation, we were able to completely remove the air bubbles appearing during the process of filling a microfluidic device with an aqueous solution.
Introduction
In recent microfluidic technology, the devices manipulating aqueous solutions have become more intricate and are integrated with other functional compartments to achieve microfluidic manifold systems.1 Various novel principles exploited in microfluidic devices are commonly based on laminar flow, generally established in microfluidic channel networks. In spite of a few useful examples of bubbles in microfluidic channels,2 undesirable air bubbles formed in microchannels result in inevitable fatal disorder over the microfluidic systems, spoiling the stable laminar flow and the cell viability. Preparing microfluidic operations, we often encounter the bubble problem and it becomes more inextricable as we fix and remove silicone tubes to and from a device. In particular, for the long-term operation of the microfluidic device,3 bubble removal from the device is crucial to successfully accomplish its purpose because the bubbles grow gradually due to the pressure difference between the outside and inside of the microfluidic polymer channels. To address this problem, several reports have described methods for filling the complex microfluidic devices with aqueous solutions under vacuum.4,5 These methods are simple and useful techniques for the bubble-free preparation of microfluidic devices. However, they require additional vacuum systems and we cannot remove the abruptly appearing bubbles during the microfluidic operation. Even though it has been reported that the trapped bubbles can disappear through a gas permeable polymer such as poly(dimethylsiloxane) (PDMS),6 these qualitative methods are not adequate for microfluidic devices demanding a prediction of the removal rate, such as a gas-generating microfluidic fuel cell device or a pressure-sensitive cell culture device. In addition, it has been reported that the cell viability is subject to a mechanical stress, such as pressure,7 depending on the critical duration-time of the pressure exposure. Consequently, we need not only a more general method to eliminate the bubbles trapped in the microfluidic device but also an analysis model to predict the removal rate of gas bubbles through the gas-permeable microchannel walls.PDMS, one of the most popular polymer materials used in microfluidic devices, has received significant attention because it provides unique properties, such as biocompatibility, surface property and gas permeability, compatible with lab-on-a-chip techniques.8 In particular, the gas permeability and selectivity of PDMS have been exploited by mixed gas separation,9 and recently they were used in microfluidic working principles.5,10
In this paper, a general method and analytical model about the elimination of the gas bubbles trapped in PDMS microfluidic channels have been described using the gas permeation principle. Based on the model equation, we can completely remove the bubbles which appear during the process of filling a microfluidic device with an aqueous solution.
Analytical model for eliminating gas bubbles
An analysis model for the bubble removal is based on the gas permeation equation.11 In the scheme described in Fig. 1, the permeability of a polymer to a permeating gas is defined by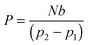 | (1) |
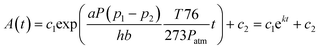 | (2) |
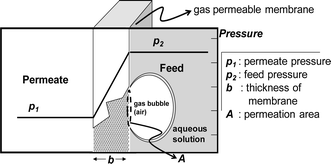 | ||
| Fig. 1 Principle of pressure-driven gas permeation through a polymer membrane. When a pressure difference is generated across the membrane, gas penetrates the membrane according to the pressure difference. | ||
In eqn (2), c1 and c2 are appropriate constants, t is time in seconds, h is the height of the microchannel, and a is a correction factor for the effective permeation area. The correction factor, a, was employed to consider the pathway differences between the practical and theoretical circumstances. The penetration pathway through the PDMS membrane has cross-sectional area (A) and distance (b). The practical penetration pathway, however, is far greater than that in the model geometry. Although this effective penetration pathway can be defined, it would be difficult to develop a generalized expression because the practical features of the PDMS channels are quite diverse depending on their device functions. Therefore, we obtained empirical results for a, which correspond with the fabricated PDMS device we demonstrated in this research (see ESI S1†). To apply this method to a practical use of the bubble removal, we should determine the constants in eqn (2), which depend on the material type of the microfluidic device (permeability (P) of PDMS and PMMA, etc.) and geometric dimensions (microchannel height (h) and thickness of the PDMS substrate (b)) and the applied pressure (p2). In addition to these given constants, it requires obtaining the empirical constant (a) in association with each experimental condition. In general, a presented in this paper can be used for approximation of the bubble removal rate in PDMS microfluidic devices. Occasionally, special experimental conditions, such as the organic solvent-swollen PDMS microchannels and unusual mixing ratios between the PDMS prepolymer and curing agent, require acquiring the proper a in correspondence with each experimental condition. The exponential decay curve for the bubble removal rate is determined by the parameters above and the position of the curve in a rectangular coordinate system depends on c1 and c2 which are related to the initial bubble area (A0) trapped in the PDMS microchannel.
To correlate the measured data with the analysis model in eqn (2), it is necessary to consider several parameters used in the analysis model. As for the permeability of PDMS to the gas, we employed the assumption that the air is composed of a pure gas with a certain permeability. Although a transport study of binary and ternary mixed gases through a PDMS thin membrane has been reported,13 we considered the composition of the air to be a pure gas because this previous literature revealed that a significant difference in permeation was not observed between pure nitrogen gas and oxygen–nitrogen mixed gas (21% of O2, 79% of N2).13 Several reports on gas permeability in the polymer membrane have obtained their results based on their own measurement systems, which may not correspond with each practical experiment, depending on the material preparation details. Moreover, errors that arise from experimental variations become more significant in microscale than in conventional macroscale gas transport because several nanolitres of air bubbles are a critical volume in the microfluidic channel, while they are negligible in conventional large-scale gas permeating systems, such as gas separation apparatus. Therefore, we admitted the simplified permeability and confirmed that using the experimental results.
Experimental
The microfluidic devices were fabricated by PDMS micromolding processes (see ESI S2†). The aqueous solution was injected into the microfluidic channel through the inlet ports and the air bubbles were generated not only when we filled the microchannel having the complicated microstructures (see ESI Fig. S4†) with buffer solution, but also when we changed the silicone tube fitted into the PDMS microchannels to exchange the injected buffer solution. To uniformly apply the pressure over the microchannel, the silicone tube connected with the outlet port was clamped off using a clamp. Using this experimental setup (see ESI Fig. S3†), we simply removed the bubbles trapped in the PDMS microchannels. Even when pressure is accumulated in the microchannels, there is neither leakage at the tube-fitting parts nor break up of bonding between the PDMS and the bottom glass substrate because the maximum applied pressure is much less than the bonding strength (74 psi) of PDMS to glass.13 The area of the air bubble was observed using an inverted microscope and images were captured by CCD every 1 s, and the observed bubble area was analyzed by a commercial image processing program, i-Solution (Image and Microscope Technology, Korea). We demonstrated a continuous perfusion cultivation of MCF-7 human breast cancer cells (mammary gland epithelial cells) in a large-area microfluidic device. Other experimental details about the cell culture are included in the ESI S3†.Results and discussion
The air bubble trapped in the PDMS microchannel was dissipated through the gas permeable microchannel wall, when the pressure difference is formed in a steady-state across the membrane (see ESI Fig. S5†). The bubble removal data measured were plotted in Fig. 2(a), which shows that the trapped air bubbles were diminished according to the first-order exponential decay model described in eqn (2), where P is 1.92 × 10–15 m2 s–1 Pa–1,14T is 298 K, Patm is 76 cmHg, h is 5.0 × 10–3 cm, and b is 0.35 cm. Based on the plotted data, we estimated the correction factor (a) to be 13.39 ± 1.37, 20.12 ± 1.34 and 20.21 ± 1.19 at 2.0, 8.0 and 11.0 psi, respectively (n = 5). As we have explained earlier, it corrects the effective permeation area and the practical permeability of PDMS to air. The correction factor had similar values at relatively high pressures (8.0 and 11.0 psi), but we observed a disparity in different pressure ranges (2.0 psi). This deviation is supposed to result from the deformation effect (see ESI Fig. S6†) of the PDMS channel causing an expanded channel surface area under highly pressurized conditions and the consequent increased permeation flux.15 Using the corrected parameter, we plotted eqn (2) in Fig. 2(a) (line) at the different pressures. The required times to completely remove the trapped air bubble (about 80 nL) in the PDMS channels are 1331.7 s, 318.3 s and 255.76 s at 2.0, 8.0 and 11.0 psi, respectively. This reveals that the error is less than 11.58%, when comparing to experimental results in Fig. 2(a). Fig. 2(b) shows sequential photographs of the air bubble removal processes at 8.0 psi in the PDMS device where the micropillar arrays were patterned for a demonstration of the complicated geometry of the microfluidic device.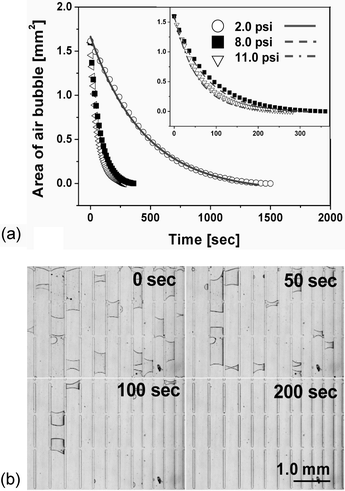 | ||
| Fig. 2 (a) The experimental data plots of reduced bubble area when the PDMS microchannel was constantly pressurized at 2.0, 8.0 or 11.0 psi. Inset shows the magnified view of the data at 8.0 and 11.0 psi. The expected times for complete removal (when y = 0) of air bubbles of about 80 nL were 1500 s, 360 s, and 282 s at 2.0, 8.0, and 11.0 psi, respectively. The line and dashed-line curves represent fitting curves based on eqn (2), employing the correction factors and appropriate parameters. (b) Sequential photographs prove that the air bubbles were successfully removed from the PDMS microchannels at an applied pressure of 8.0 psi according to the exponential decay model. | ||
Conclusion
We have reported a practical analysis model for air bubble removal from gas permeable PDMS microfluidic channels and demonstrated a large-area (1.7 cm2) microfluidic device for cell culture and subculture (see ESI S3†). We expected that the bubble removal rate follows the first-order exponential decay model and proved the model through experimental results, where an adequate correction factor was employed for the correction of errors due to the geometric features and the practical permeability. The proposed model is practical and is simple to optimize the elimination of bubbles trapped in the gas permeable polymer channels. This model can be extended to other kinds of polymers and microfluidic systems, such as a gas-generating microfluidic fuel cell devices,16 for eliminating the generated gas.Acknowledgements
This research was supported by the CHUNG Moon Soul Center for BioInformation and BioElectronics, and by the Nano/Bio Science & Technology Program (M10536090002-05N3609-00210, M10503000218-05M0300-21810) of the Ministry of Science and Technology, Korea.References
- H. Craighead, Nature, 2006, 442, 387–393 CrossRef CAS.
- P. Garstecki, M. J. Fuerstman, M. A. Fischbach, S. K. Sia and G. M. Whitesides, Lab Chip, 2006, 6, 207–212 RSC; P. Garstecki, M. J. Fuerstman and G. M. Whitesides, Nat. Phys., 2005, 1, 168–171 Search PubMed; A. M. Taylor, M. Blurton-Jones, S. W. Rhee, D. H. Cribbs, C. W. Cotman and N. L. Jeon, Nat. Methods, 2005, 2, 599–605 CrossRef CAS; M. Prakash and N. Gershenfeld, Science, 2007, 315, 832–835 CrossRef CAS.
- J. H. Kang and J.-K. Park, Small, 2007, 3, 1784–1791 CrossRef CAS.
- I. Meyvantsson and D. J. Beebe, Vacuum filling of microfluidic devices, Chips & Tips (Lab on a Chip), 23 October 2006. http://www.rsc.org/Publishing/Journals/lc/vacuum_filling.asp; J. Monahan, A. A. Gewirth and R. G. Nuzzo, Anal. Chem., 2001, 73, 3193–3197 Search PubMed.
- K. Hosokawa, K. Sato, N. Ichikawa and M. Maeda, Lab Chip, 2004, 4, 181–185 RSC.
- T. Thorsen, S. J. Maerkl and S. R. Quake, Science, 2002, 298, 580–584 CrossRef CAS; H. Wu, A. Wheeler and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12809–12813 CrossRef CAS; L. Kim, M. D. Vahey, H.-Y. Lee and J. Voldman, Lab Chip, 2006, 6, 394–406 RSC.
- Y. C. Kim, J. H. Kang, S.-J. Park, E.-S. Yoon and J.-K. Park, Sens. Actuators, B, 2007 DOI:10.1016/j.snb.2007.1005.1050; Y. C. Kim, J. H. Kang, S.-J. Park, E.-S. Yoon and J.-K. Park, in Proc. of the 14th Inter. Conf. on Solid-State Sensors, Actuators and Microsystems, Lyon, France, the IEEE, Inc., 2007, pp. 1873–1876 Search PubMed.
- P. Kurian, B. Kasibhatla, J. Daum, C. A. Burns, M. Moosa, K. S. Rosenthal and J. P. Kennedy, Biomaterials, 2003, 24, 3493–3503 CrossRef CAS.
- R. W. Baker, N. Yoshioka, J. M. Mohr and A. J. Khan, J. Membr. Sci., 1987, 31, 259–271 CrossRef CAS.
- M. A. Eddings and B. K. Gale, J. Micromech. Microeng., 2006, 16, 2396–2402 CrossRef.
- K. Ghosal and B. D. Freeman, Polym. Adv. Technol., 1994, 5, 673–697 CrossRef CAS.
- X. Liang, H. Tan, Z. Fu and S. Y. Chou, Nanotechnology, 2007, 18, 025303 CrossRef.
- F. Wu, L. Li, Z. Xu, S. Tan and Z. Zhang, Chem. Eng. J., 2006, 117, 51–59 CrossRef CAS.
- W. L. Robb, Ann. N. Y. Acad. Sci., 1968, 146, 119 CrossRef CAS.
- J. Hinestroza, D. D. Kee and P. N. Pintauro, Ind. Eng. Chem. Res., 2001, 40, 2183–2187 CrossRef CAS.
- C. Litterst, S. Eccarius, C. Hebling, R. Zengerle and P. Koltay, J. Micromech. Microeng., 2006, 16, S248–S253 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: S1 Analytical model, S2 Microfabrication, S3 Experimental setup and cell culture. Fig. S1–S8. See DOI: 10.1039/b712672g |
| This journal is © The Royal Society of Chemistry 2008 |
