Pressure-driven fluidic delivery through carbon tube bundles†
Alexander V.
Bazilevsky
,
Alexander L.
Yarin
* and
Constantine M.
Megaridis
Department of Mechanical and Industrial Engineering, University of Illinois at Chicago, Chicago, IL 60607-7022, USA. E-mail: ayarin@uic.edu; Tel: +1-(312)-996-3472
First published on 31st October 2007
Abstract
The aim of this work is to demonstrate controlled flow through macroscopically long (∼1 cm) carbon tubes (0.5–1.8 µm in radius). A model, high-throughput, pressure-driven fluidic setup, which features a large number of parallel carbon tubes forming a bundle, is fabricated and tested. The carbon tubes are synthesized and self-assembled via co-electrospinning and subsequent carbonization. The setup accommodates pressure-driven flows with flow discharge rates of the order of 1 nL s–1 (73 × 10–11 kg s–1) for low-viscosity liquids and 30 nL s–1 (36.3 × 10–12 kg s–1) for gases into a water pool under imposed pressure drops below 4 bar. The measurements demonstrate the ability to sustain well-controlled laminar flows through these long carbon tube bundles and elucidate the main transport features. A novel procedure is also formulated to recover the flow-carrying tube inner-diameter distribution from the measured dependence of the fluid volumetric or mass flow rate on the imposed pressure drop.
Introduction
Many commercial applications include microscopic flow channels (of the order of 10 to 100 microns) as their key fluid-delivery element. Such applications include DNA and protein analysis, drug development, screening and delivery, optical display technologies and tunable fiber optic waveguides, heat removal from electronic chips and semiconductor lasers, monitoring of hazardous compounds in public areas (airports, etc.), biotechnological and forensic analysis, hydrogen storage in fuel cells, cell biology and manipulation, lab-on-a-chip technologies, mass-limited chemical analysis, development of new materials in highly confined spaces, flow-through reactors and gateable interconnects. All of these technologies rely on micro- and nanofluidic principles and can benefit enormously from further miniaturization.1–4The present work focuses on pressure-driven fluid delivery through macroscopically-long carbon tubes, which have diameters small enough to retain bacteria (including the smallest ones, e.g.E. coli) but large enough to pass dissolved ions, salts and drugs (an ultimate goal in ultrafiltration4). These tubes have diameters of the order of 1 µm, i.e., they are significantly larger than single-wall carbon nanotubes of the order of 1 nm, which attract attention in relation to high-flux membranes (ref. 5 and references therein). In the present work, control over the number of bundled tubes allows tuning of the fluid delivery rates (high rates attained by large numbers of tubes, and vice versa). In principle, the bundle overall diameter can be reduced to 10 µm or less, which makes it attractive for delivery/extraction of different fluid compounds into/from large individual cells, or for simultaneous precise delivery of several immiscible compounds on a lab-on-a-chip environment. Our aim is to create such tube bundles and study hydrodynamic peculiarities of controlled flows in them with a relatively high overall throughput. Moreover, the hydrodynamic findings are used to determine the flow-carrying tube inner-diameter distribution from the measured dependence of the volumetric and mass flow rates on the imposed pressure drop.
Experimental procedures and results
The carbon tubes were produced with the procedures described in ref. 6–9, where core-shell polymethyl methacrylate - polyacrylonitrile (PMMA-PAN) nano/microfibers were co-electrospun. Co-electrospinning was done on a vertically-mounted, sharpened, rotating wheel (electrostatic lens) acting as the ground electrode,10 which produced uniaxially oriented bundles of tens of thousands of core-shell fibers. In a subsequent step, these fiber bundles were heat-treated in a nitrogen atmosphere up to a temperature of 750 °C. As a result of the heating, the PMMA cores were eliminated, whereas the PAN shells carbonized. The resulting tubes consisted of amorphous carbon and had inner radii of the order of 0.5–1.8 µm. They were arranged as bundles of a large number of uniaxially-oriented, parallel carbon tubes. A typical carbonized tube bundle is shown in the different views presented in Fig. 1. It can be seen that the outer walls of adjacent tubes are partly fused together (Fig. 1d), because the distance between the core-shell nozzle and the rotating wheel electrode during co-electrospinning (12–14 cm) was chosen such that the fiber winding around the wheel edge was partially wet upon deposition, i.e., not all the solvent had evaporated yet. Merging among neighboring tube walls partially closed the gaps between the hollow tubes, and prevented larger gaps from forming between the fibers. The gaps that did not close in this process had similar sizes as the tubes themselves (see Fig. 1d) and could act as additional channels in the bundle capable of sustaining more flow. This is improbable, however, since each bundle was inserted through a glass capillary and sealed in place by epoxy, which wet the carbon tubes and probably filled the gaps in between them (thus blocking fluid flow). It is noted that not all fibers in the bundle of Fig. 1d were hollow, which was attributed to intermittent co-electrospinning11 or most probably crimped tube ends during cutting. Moreover, not all carbon tubes that look open in the end view of Fig. 1d, are open along their entire length to allow through flow, as the hydrodynamic results discussed below indicate. Since images of the fiber cross section cannot reveal whether each tube remains open from tip to end, such images cannot be used to produce statistical information on the size distribution of open tubes that can carry flow from the inlet to the exit of the bundle (a tube might be blocked anywhere past the visibly open end). In the present case, flow measurements offer a more reliable method to determine the size distribution of open tubes contributing to the flow. | ||
| Fig. 1 Typical SEM images of a bundle of carbon tubes made via co-electrospinning. Longitudinal views at low (a) and high (b) magnification; Low (c) and high (d) magnification cross-sectional views of the end of the bundle. The large gap shown in the top middle of (c) is a result of handling. Some non-hollow fibers seen in (d) could have been created by intermittent co-electrospinning, or could indicate tube ends crimped during cutting of the bundle. For this particular tube bundle, inner diameters measured from the images were in the range 1.1 ± 0.3 µm (mean value and standard deviation). | ||
The carbon tube bundles collected around the periphery of the rotating wheel electrode were cut in pieces ∼1–2 cm long. These uniaxially oriented bundles of macroscopically-long tubes are ideally suited for pressure-driven nanofluidic systems requiring a wide range of fluid flow rates and relatively easy assembly and handling. If a controlled flow through such tubes can be established, then low flow rates can be attained by using bundles consisting of only a few open tubes. On the other hand, higher flow rates would correspond to an increased number of active (i.e., open) tubes in the bundle. This feature highlights the scalability (as far as flow rate is concerned) of the present approach.
Pressure-driven flows in tubes are attractive because they do not rely on wettability and zeta potential, as in the case of flows arising in the course of capillary imbibition or due to electrokinetic phenomena. Both gases and liquids can be used as flowing media. In addition to pressure and viscous forces, a number of other factors can affect pressure-driven flows in microscopic channels, as discussed in ref. 12. To choose an appropriate theoretical framework, the relevance of these factors in the present case should be estimated first. For gases, the flow type is determined by the value of the mean free path ℓm. At a pressure of the order of 1 bar and room temperature for air, it is ℓm = 60 nm (ref. 13); ℓm is proportional to the inverse pressure and thus at 5 bar, ℓm = 12 nm. The Knudsen number is defined as Kn = ℓm/(2a), where 2a is the characteristic cross-sectional size, say diameter. Taking for the estimate 2a = 1–3 µm (as for the present tubes), and using the previously listed values of ℓm, one can find Kn = 0.004–0.06. Slip at a channel wall is important only in the range Kn > 0.1 (ref. 14). Consequently, gas flow in the present tubes should proceed in the continuum (non-rarefied) regime (the same is obviously true for liquids, which have a much smaller ℓm). Slip and the related slip length λ can also affect flows in microchannels. For diffusive collisions of gas molecules with the channel walls, λ = 2ℓm/3 (ref. 14). On the other hand, the volumetric flow rate increases due to slip by a factor of ψ = (1 + 4λ/a) = [1 + 8ℓm/(3a)] (ref. 14). For ℓm = 12–60 nm and a = 0.5–1.8 µm, the volumetric flow rate could increase by a factor of ψ = 1.018–1.32 due to slip. The lowest value of ψ corresponds to the largest channels, while the highest ψ to the smallest channels. In the case of different channel diameters in a bundle (as in Fig. 1), and for gas release inside water (high surface tension of water makes flow in the smallest channels even less significant; see detailed discussion below), gas will predominantly move through the larger channels, and the deviations from no-slip flow (if any) could hardly exceed several percent. Additionally, pressure is higher and, in turn, ℓm (and thus ψ) is lower inside the channels compared with their exits. All of the above make any deviations from the no-slip flow even less significant in the present case. The experiments discussed below have characteristic velocity in the channels of the order of Ug = 10–1 m s–1 for gas, and Uℓ = 10–3 m s–1 for liquid, as the measurements below show. The corresponding values of the Mach number are of the order of 10–4 and 10–6 for gas and liquid, respectively. At such low values of the Mach number, any compressibility-related (in the gas-dynamic sense) effects are negligibly small. On the other hand, gas density could vary with pressure along the channel, and thus the gas could experience a certain acceleration. The steady equations of motion immediately show that this effect is of the order of ρUg2/p compared to the static driving pressure p, where ρ is the gas density (variable along the tube lengthwise location X). Taking a room temperature estimate for ρ in the applicable range p = 1–5 bar and for Ug = 10–1 m s–1, we deduce ρUg2/p ∼ 10–7, which shows that gas acceleration due to density variation along the channel can be safely neglected. The entrance and exit transition lengths in channels with laminar flows are of the order of 0.1aRe (ref. 15), where the Reynolds number (based on 2a) is of the order of 10–2 and 10–3 (laminar regime) for gas and liquid, respectively. In the present case, the entrance and exit length appear to be much shorter than a ≈ 1 µm. These lengths are negligibly small compared to the channel lengths (of the order of 1 cm) and the flows in the channels could be considered fully developed. Fig. 1d shows that some channels might have elliptical rather than circular cross-sections. This could be due to the fact that the sample in Fig. 1d was cut non-orthogonally with respect to the tube axis, which exaggerates any impression of ellipticity. If r is the aspect ratio of the elliptical cross-section primary axes, it can be shown16 that the volumetric flow rate through a channel with such elliptical cross-section differs from that through a channel of equivalent cross-sectional area and circular shape by a factor of 2/(r + r–1). This factor is 0.995 for r = 1.1, or 0.967 for r = 1.3. Therefore, it is apparent that deviations from circular cross-sectional shape represent only minor volumetric rate effects in the present case. All of the above-mentioned estimates show that for steady conditions, the Poiseuille law should apply for the local volumetric flow rate in the channels of the scale of interest (a ≈ 0.5–1.8 µm)
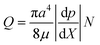 | (1) |
 | (2) |
It is emphasized that eqn (1) and (2) are valid only for bundles of identical channels (all of them assumed to be open tip-to-end), and can be used for preliminary estimates. Estimating the bundle cross-sectional radius R = 100 µm (equivalent, see Fig. 1a) and using a tube radius a = 0.5 µm, we obtain the number of carbon tubes in the bundle as N ∼ (R/a)2 = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. For liquid n-decane (µ = 0.907 × 10–3 Pa s and density ρ = 730 kg m–3 at room temperature) for an applied pressure drop of Δp = 3 bar across the length L = 1 cm, the volumetric flow rate Q obtained from eqn (1) is Q = 32 nL s–1 (2.24 × 10–8 kg s–1). This value of Q for n-decane has been estimated from eqn (1) under the assumption that all N = 40
000. For liquid n-decane (µ = 0.907 × 10–3 Pa s and density ρ = 730 kg m–3 at room temperature) for an applied pressure drop of Δp = 3 bar across the length L = 1 cm, the volumetric flow rate Q obtained from eqn (1) is Q = 32 nL s–1 (2.24 × 10–8 kg s–1). This value of Q for n-decane has been estimated from eqn (1) under the assumption that all N = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tubes in the bundle are open (i.e., carrying liquid). This value is remarkably high compared to the flow rates of the order of 0.25 nL s–1 obtained in some microfluidic devices.3 Consequently, even if 99% of the present carbon tubes were blocked, the device based on the bundle of Fig. 1 (∼40
000 tubes in the bundle are open (i.e., carrying liquid). This value is remarkably high compared to the flow rates of the order of 0.25 nL s–1 obtained in some microfluidic devices.3 Consequently, even if 99% of the present carbon tubes were blocked, the device based on the bundle of Fig. 1 (∼40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tubes) would still be capable of delivering liquid at rates sufficient for many practical applications.
000 tubes) would still be capable of delivering liquid at rates sufficient for many practical applications.
A sketch of the experimental setup is shown in Fig. 2. A typical carbon tube bundle was about 1 cm long and 200 µm in diameter. It was inserted into the open tip of a glass capillary (of 1 mm o.d. and 0.58 mm i.d.) and secured there by epoxy cement (Fig. 3). The epoxy was placed in a manner that did not interfere with the inlet/outlet of any tube in the bundle but penetrated into the gaps between the tubes at the application location. Thus, the capillary orifice was effectively sealed, and fluid could exit only through the tube bundle. The fluid supply system consisted of two standard plastic syringes of volumes 10 and 1 mL, a digital pressure meter, a 7 mL plastic air chamber and two stopcocks. All parts of this apparatus were connected by thin silicon tubing. The chamber was used to adjust air pressure smoothly and maintain it at a nearly constant level during a test. After pressurizing the air chamber by means of the 10 mL syringe (on the left in Fig. 2), the one-way stopcock was closed. To reach higher pressure, this pressurizing step was repeated several times. The pressurized chamber sustained nearly constant pressure during long flow tests, even though air was flowing through the open three-way stopcock into the glass capillary and then into the carbon tube bundle. The second syringe (vertically placed in Fig. 2), which was connected directly to the three-way stopcock, was used only in the liquid-flow experiments to fill (with the liquid) the silicon pipe leading to the glass capillary. This simple system allowed adjustable operational pressure (excess with respect to atmospheric), up to 4 bar, at the carbon tube bundle entrance.
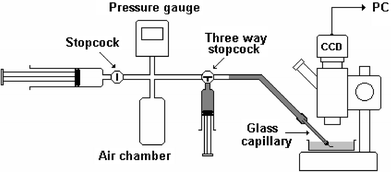 | ||
| Fig. 2 Sketch of the experimental setup. | ||
 | ||
| Fig. 3 (a) Growing air bubble at the tip of the carbon tube bundle immersed in a shallow water pool (Fig. 2). The epoxy secures the conduit bundle at the end of the glass capillary. (b) Growing n-decane droplet in a water pool. (c) Growing n-decane droplet with a gas bubble growing inside it. (d) Gas bubble trapped inside the glass capillary upstream of the solid epoxy plug. (e) This image was captured after the gas bubble shown in (d) was completely depleted. | ||
To visualize discharge of gas (air) or liquid (n-decane) from the carbon tube bundle, the tip of the glass capillary was immersed in a shallow pool of water and observed under a microscope (Fig. 2). As air was being discharged from the bundle tip, macroscopic bubbles were visible in the water (Fig. 3a). On the other hand, when n-decane—which is immiscible with water—was being discharged, a growing droplet was clearly visible in the water pool (Fig. 3b). In the n-decane-discharging-in-water case, a situation was also encountered where the n-decane droplet contained a bubble presumably consisting of air (Fig. 3c). In this case, gas was entrained from a bubble entrapped upstream in the glass capillary in the region inside the capillary where the epoxy plug ended (Fig. 3d); this gas bubble was eventually depleted (Fig. 3e). In all cases, it was possible to visualize and record the growing bubbles/droplets, which emerged at the outer tip of the carbon tube bundle inside the water pool. The consistent appearance of a single bubble/droplet at the tip of the bundle indicated that gas or liquid outflowing from individual tubes merged at the bundle end to form a macroscopic single entity, as seen in Fig. 3. In the case of gas flows, tiny bubbles were sometimes seen at other locations along the outer surface of the tube bundle; however, these bubbles at Δp < 2 bar did not grow fast, thus having little influence on the measured flow rate discharge. But at higher pressure drops, these bubbles did affect the accuracy of the flow rate measurement, as discussed later. It is also noted that attempts to observe n-decane droplets formed at the end of the carbon tube bundle in air (without immersion in water) were unsuccessful, indicating that discharge rates were of the order or less than the evaporation rate of this particular liquid.
The discharge process was observed and recorded at room temperature (20–21 °C) using a simple stereo-zoom microscope (10×– 40×, Edmund Scientific) with a CCD camera. The recorded images were processed to find the value of the volumetric flow rate Q at the tube bundle exit. Typical results of such measurements are shown in Fig. 4, which shows the evolution of volume and diameter of an air bubble formed at the bundle exit under an imposed pressure drop Δp = pi – pe = 0.85 bar. It is clearly seen that the bubble volume in this case increases linearly with time, which indicates a steady exit volumetric flow rate (1.46 nL s–1) for the discharge of air. The flow rate data error was estimated at about 5%. Since measured bubble diameters D were typically above 0.2 mm, the overpressure inside the bubbles (∼4σ/D) was insignificant (below 0.01 bar for σ = 0.072 N m–1; water) in comparison with the imposed pressure Δp at the carbon tube bundle entry. Consequently, bubble pressure was not taken into account and the imposed overall pressure drop Δp (measured with accuracy better than 1%) was used to plot the data.
 | ||
| Fig. 4 Air bubble diameter (D, solid circles) and volume (πD3/6, open triangles) as functions of time. The experimental data are shown by symbols. The straight line is a linear fit for the bubble volume, and corresponds to an exit volumetric flow rate of 1.46 nL s–1 (M = 1.77 × 10–12 kg s–1 = constant at atmospheric exit pressure). The imposed pressure drop in this case was Δp = 0.85 bar. | ||
Repeating the air discharge experiment (as done in Fig. 4) with different values of Δp applied to the same carbon tube bundle, we deduced the exit gas volumetric flow rates Q plotted in Fig. 5. Flow commenced at a threshold pressure slightly above Δp* = 0.8 bar, which corresponds to the opening of tubes with capillary radius a = 2σ/Δp* = 1.8 µm for water (σ = 0.072 N m–1), as defined by the bubble point method.17,18 This radius estimate, which is an upper bound of this quantity, is based on the assumption that the opening occurs when the gas–liquid interface forms a half-sphere with radius equal to the inner radius of an individual tube. It is also noted that this estimate applies to both fully wettable (contact angle θ = 0°; half-sphere initially forms at the inlet of the bundle after water is drawn into the tube) and non-wettable (θ = 180°; half-sphere forms at exit end of bundle, as water resists entry into the tube) situations. For 0.8 bar < Δp* < 1.7 bar in Fig. 5, Q increased almost linearly with Δp, because deviations from linearity are still insignificant at such low pressures (see also discussion below). The first sign of deviation from linear behavior in Fig. 5 is seen at about 3 bar. The expected variation of gas pressure p(X) = [pi2 + (pe2 – pi2)X/L]1/2 indicates a nonlinear behavior at higher values of Δp. But the deviation seen at about Δp = 3 bar in Fig. 5 is not as strong as expected by the nonlinear law; this was attributed to the underestimation of Q at higher pressures because of the random presence of other secondary bubbles along the lateral surface of the bundle and the inability to quantify the contribution of these bubbles to the measured flow rate (cf. Fig. II in the ESI of this paper†). Although the contribution of such “leaks” in measuring Q at the tube exit was not quantifiable, it is worth noting that the reduced value of Q measured at 3 bar in Fig. 5 is still above the linear trend of the low pressure values.
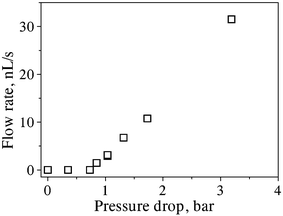 | ||
| Fig. 5 Measured exit volumetric flow rates (squares) of air through the same carbon tube bundle versus the overall pressure drop Δp. | ||
The results for n-decane flow, through the same carbon tube bundle, are shown in Fig. 6–8. The data show a similar response of n-decane flow rate to the applied pressure. In the bubble-free case (see below), a flow onset point at Δp* = 0.7 bar is also observed in Fig. 7 and 8, as in the case of air (Fig. 5), which corresponds to the opening of tubes with capillary radius a = 2σ/Δp* = 1.5 µm (for the decane–water interface σ = 0.053 N m–1; ref. 19). Above this threshold, a linear dependence of Q on Δp is found. It can be seen that the volumetric flow rate of n-decane (Fig. 7 and 8) is much lower than the exit values of Q for air (Fig. 5) for the same carbon tube bundle subjected to the same pressure drop (with the geometric effect, thus excluded). This is due to the fact that n-decane, as a liquid, is much more viscous than air (µ = 0.907 × 10–3 Pa s for n-decane, versusµ = 1.8 × 10–5 Pa s for air).
 | ||
| Fig. 6 Outer diameter (open circles) of n-decane droplet (D1) as a function of time in the arrangement seen in Fig. 3c. The diameter (D2) of the enclosed gas bubble (Fig. 3c) is shown by filled circles. The corresponding liquid n-decane volume π(D13 – D23)/6 is shown by the open triangles. The straight line is a linear fit of the n-decane volume versus time. Its slope characterizes the volumetric flow rate of n-decane in this experiment, namely Q = 0.14 nL s–1 (M = 1.02 × 10–10 kg s–1). The pressure drop in this case was constant at Δp = 1.53 bar. | ||
 | ||
| Fig. 7 N-decane volumetric flow rate versus pressure drop for the carbon tube bundle used in the air experiments of Fig. 5. The open symbol data correspond to the case when a gas bubble inside the glass capillary holder was present (Fig. 3c,d). The filled squares correspond to subsequent stages when the gas bubble trapped in the capillary had been depleted (as in Fig. 3b,e). The lines represent best linear fits. | ||
![Measured volumetric flow rates (squares corresponding to the filled squares in Fig. 7) of n-decane through the same carbon tube bundle and calculated number of open channels N (from eqn 8) versus pressure drop Δp. The upper straight line shows the expected Q(Δp) dependence for a bundle of N* uniform tube channels with a = a*, all carrying the same amount of liquid. This line does not describe the present data. The lower straight line is the best linear fit Q[nL s–1] = 0.2(Δp – 0.7)[bar] of the non-zero values of the experimentally determinedQ.](/image/article/2008/LC/b711446j/b711446j-f8.gif) | ||
| Fig. 8 Measured volumetric flow rates (squares corresponding to the filled squares in Fig. 7) of n-decane through the same carbon tube bundle and calculated number of open channels N (from eqn 8) versus pressure drop Δp. The upper straight line shows the expected Q(Δp) dependence for a bundle of N* uniform tube channels with a = a*, all carrying the same amount of liquid. This line does not describe the present data. The lower straight line is the best linear fit Q[nL s–1] = 0.2(Δp – 0.7)[bar] of the non-zero values of the experimentally determinedQ. | ||
As seen in Fig. 3d, gas can be entrapped in the glass capillary filled with n-decane. As a result, gas is entrained into the carbon tube bundle, thus reducing the volumetric flow rate of n-decane at a given pressure drop. This is shown in Fig. 7 by the open symbols. Such joint flows of liquid and gas do not belong to the validity range of eqn (1), as well as of the kindred equations developed below. Presence of air together with flowing liquid in a channel in general might have multiple effects on the volumetric flow rate Q of liquid: (i) Q might decrease just because a part of the cross-section is occupied by gas; (ii) Q might increase because a continuous gas layer provides lubrication and thus an effective slip for the flowing liquid; (iii) Q might decrease if isolated entrapped bubbles are present and result in additional pressure losses related to moving contact lines. All these situations are out of scope of the present work; the open symbol data from Fig. 7 are not used below for comparison with the theory. Much more detailed information on gas and liquid distribution in the tubes and a more involved theoretical framework are needed to elucidate the real mechanism underlying such cases, which might be a topic of future work. In the case of Fig. 3c,d, gas in the entrapped bubble in the glass capillary is fully depleted eventually, and pure liquid n-decane flows after that through the carbon tube bundle (Fig. 3b,e). In the latter case, the n-decane volumetric flow rate is higher for any given pressure drop, as the filled symbol data in Fig. 7 indicate. In both cases shown in Fig. 7, the volumetric flow rates Q remain proportional to Δp. In the bubble-free case of Fig. 7, which will be used for further discussion and analysis, the flow onset threshold pressure Δp* is ∼0.7 bar, which is slightly lower than the one seen in the air flow case (Fig. 5). This could be expected for n-decane bubbling into water, since Δp* = 2σ/a, and σ for the decane–water interface is 0.053 N m–1, as compared to 0.072 N m–1 for the air–water interface.
According to eqn (1), for incompressible fluids, where |dp/dX| = Δp/L, and for constant values of N, a, L and µ, the volumetric flow rate Q of n-decane is expected to increase linearly with Δp, as shown by the solid straight line passing through the origin in Fig. 8. But the measured Q(Δp) variation in Fig. 7 and 8 indicates a variation Q ∝ (Δp – Δp*), which suggests “memory” with respect to the opening pressure Δp*. This counterintuitive result can be understood by discretizing the opening of tubes (to the flow) as the imposed pressure Δp rises from very low values; see Fig. 9. Initially when Δp < Δp*, the imposed pressure Δp cannot overcome the capillary pressure in the largest-radius tube (or gap), thus no flow can penetrate even the largest tube (or gap) in the bundle. However, as Δp increases, eventually it reaches the opening threshold value Δp*, and the largest tube or gap (radius amax) is opened to the flow. At that moment, it is Δp = Δp* = 2σ/amax. As Δp rises further from Δp*, the flow rate should vary as Q ∝ amax4Δp (see Fig. 9), until the pressure becomes high enough to open the second largest tube (radius amax–1). Then, as Δp rises even further from 2σ/amax–1, the flow rate varies as Q ∝ (amax4 + amax–14)Δp (see Fig. 9), until yet another tube is opened. This cycle continues as Δp rises even further, thus opening gradually smaller tubes to the flow. In this interpretation, between successive tube openings it is Q ∝ Δp, being consistent with the Poiseuille law for liquids (incompressible). If the tube radius distribution is not discrete, but continuous, then the inclined step variation seen in Fig. 9 cannot be resolved experimentally. Instead, the experiment sees the trend depicted by the thick dot-dash line in this Figure; this line intersects the abscissa at Δp*, and indicates an overall Q(Δp) variation that seemingly disagrees with the Poiseuille law for incompressible fluids. It is critical to stress that this disagreement is only superficial, as the interpretation given in Fig. 9 is based on the Poiseuille law. The above mechanism provides a physically meaningful explanation for the measured Q(Δp) variation in liquids (Fig. 7 and 8). As discussed earlier, for gas flowing through the tubes when pi/pe ∼ 1, i.e., Δp is low, p(X) can be approximated by a linear profile and thus Q ∼ Δp (i.e., gas compressibility effects are weak in this regime). Since the values of Δp close to Δp* satisfy this condition, the mechanism depicted in Fig. 9 applies to gases as well.
 | ||
| Fig. 9 Variation of volumetric flow rate vs. pressure drop in between the first two tube opening events. The first opening (to the flow) occurs at the capillary pressure Δp*, corresponding to the largest tube radius (amax) in the bundle. The second largest tube radius is amax–1 (opening pressure 2σ/amax–1). It is important to note that while the Poiseuille law for incompressible fluids applies in between successive tube openings, where Q ∝ Δp, the overall Q(Δp) trend seen in the experiment (dot-dash line) is not consistent with this law. | ||
The volumetric flow rates of n-decane (Fig. 7 and 8) through carbon tube bundles have values ∼2% of those estimated from the Poiseuille law for liquids under the assumption that all channels contribute to the flow (i.e., remain hollow along their entire length, and at no location are too thin to be blocked by capillary forces in the given range of pressure). This means that in the bundles under investigation with one end submerged in water, flow occurred only through several channels. Some channels might also have been blocked because of fabrication defects (visible in the end cross-section shown in Fig. 1d, or not visible in the middle). Below we present a method to calculate the probability density function of the open channel size distribution and the number of channels contributing to the flow.
Discussion and interpretation of results
In the present case, as in many ultrafiltration membranes, direct characterization of the channel-size distribution in a bundle using scanning electron microscope (SEM) imaging, similar to the one in Fig. 1d, cannot be realized, since many tubes might be blocked somewhere between the entry and the exit of the bundle. Transmission electron microscopy (TEM), cannot be employed either, since the tube bundle is far too thick to allow electron transmission. In such cases, a number of indirect characterization methods can be used,18 namely, gas adsorption-desorption, thermoporometry, permporometry, liquid displacement, and fractional rejection measurements. Most of these methods are rather complicated, involving different chemical compounds and due to these and some additional factors cannot be applied to characterize the carbon tube bundles used in the present work, or to interpret the results. Therefore, a novel, to the best of our knowledge, method to reconstruct the open channel size distribution from the recorded Qvs. Δp measurements for liquids is formulated below, and subsequently used to interpret the measurement results for n-decane.According to eqn (1), for liquids where |dp/dX| = Δp/L, for a constant value of N (active channels) and uniform tube radius a, Q is expected to increase linearly with Δp from the origin, as shown by the upper straight line in Fig. 8, which is inconsistent with the obtained experimental data (squares in Fig. 8). Then, the interpretation of the flow rate results presented in Fig. 8 involves the carbon tube diameter distribution and the process of continuous opening of smaller-diameter tubes at higher imposed pressures, as described in the previous section.
In the general case, when the open-tube diameter distribution in a tube bundle is continuous, let us denote the channel-size distribution as f(a). Then, the number of tubes in the radius range (a, a + da) is given by f(a)da; thus the total number of channels in a carbon tube bundle with tube radii from amin to amax is  . The total number of tube channels opened by an imposed pressure Δp is
. The total number of tube channels opened by an imposed pressure Δp is  ; the quantity 2σ/Δp denotes the smallest channel radius opened at a given pressure. Then, the Poiseuille law for an incompressible fluid for a bundle subjected to this pressure drop along its length L yields
; the quantity 2σ/Δp denotes the smallest channel radius opened at a given pressure. Then, the Poiseuille law for an incompressible fluid for a bundle subjected to this pressure drop along its length L yields
 | (3) |
Note, that if at a given Δp there are no channels with a > 2σ/Δp, then f(a) = 0 in eqn (3) in the whole integration range, and thus Q = 0 (imposed pressure is not high enough to overcome the capillary pressure of the largest-diameter tube). On the other hand, for a given Δp and a very narrow channel-size distribution about a radius a* ≥ 2σ/Δp, the channel-size distribution f(a) = N*δ(a – a*), with N* denoting the total number of such channels in the bundle. Then, eqn (3) yields
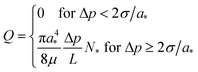 | (4) |
This latter result is presented in Fig. 8 by the upper straight line calculated for a* = 2σ/Δp* = 1.5 µm and N* ≈ 7. This line does not describe the overall experimental dependence of Q on Δp in Fig. 8 (squares), attesting to the fact that the tube inner diameter distribution is polydisperse.
It is emphasized that the measured dependences Q(Δp) for liquids, as in Fig. 8, do allow recovery of the open-channel size distribution in the bundle. Indeed, eqn (3) can be recast as the following integral Volterra equation of the 1st kind
 | (5) |
Equation (5), when solved for ϕ, has the solution ϕ(x) = d[q(x)/x]/dx. Then,
 | (6) |
The number of open finite channels contributing to the flow at a given pressure drop Δp is given by
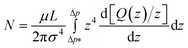 | (7) |
The above expression allows an estimate of the number of open channels for the n-decane data presented in Fig. 8. Fitting the experimental data Q(Δp) in this figure by a linear function Q[nL s–1] = C (Δp – Δp*) [bar], with C being the slope [nL/(s·bar)], in the range Δp* to Δp (>Δp*), and taking Q(Δp) = 0 in the range 0 to Δp*, one can evaluate the integral in eqn (7) to get
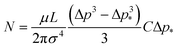 | (8) |
For n-decane flow into water at room temperature µ = 0.907 × 10–3 Pa s, σ = 0.053 N m–1, L = 0.01 m, and Δp = 3.77 × 105 Pa (highest pressure point in Fig. 8), eqn (8) yields N = 454 for C = 0.2 nL/(s·bar) and Δp* = 0.7 bar (from Fig. 8; in this case CΔp*= 0.14 nL s–1). The corresponding radius range of the open channels is from 2σ/Δp = 2 × 0.053/(3.77 × 105) = 0.28 µm to 2σ/Δp* = 2 × 0.053/(0.7 × 105) = 1.5 µm. Equation (8) has been plotted as N(Δp) in Fig. 8 for the values of C = 0.2 nL/(s·bar) and Δp* = 0.7 bar found for n-decane. Partial wettability of carbon tube walls by water from the pool at the opening threshold introduces a cosθ factor (<1) in the value for a* and a factor 1/cos4θ in the value for N in eqn (8). This, for example, when θ = 60° would alter the numerical value of N estimated above, with the radii of the open channels becoming 0.14–0.75 µm and N = 7264. The mathematically-deduced range of the open channel sizes (0.14–0.75 µm) is consistent with the average pore size obtained by examining the SEM image of Fig. 1d, where a = 0.55 ± 0.15 µm. Similarly, the probability density function of the open channels following from eqn (6) is f(a) = 4µLCΔp*/(πσa4).
For gas flows at high pressures Δp, i.e., with significant compressibility effects, the tube-diameter distribution can be recovered via the measured mass flow rate MversusΔp. Then, eqn (3), (6) and (7) are replaced by the following ones using eqn (2)
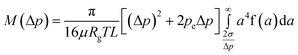 | (9) |
 | (10) |
 | (11) |
Unfortunately, the present instrumentation did not allow the production of reliable data with gases at high pressures, thus the application of the above method for gases is not possible at this time.
Practical significance
Equation (3) for incompressible fluids predicts that flow rate Q is an inverse function of the fluid viscosity µ, while experimental data shows that Q is proportional to (Δp – Δp*). Therefore, for different liquid flows through the same tube bundle, eqn (3) predicts that the product Qµ should be the same for the same pressure. It is of interest to add the product Qµ for the exit volumetric flow rate of air to such a plot, since its possible deviation from linearity, as well as from the n-decane data, would indicate severity of the compressibility effects. The appropriate data for such comparison is shown in Fig. 5 (air flow) and Fig. 7 (filled symbols for pure n-decane flow); the open triangle data points in Fig. 7 correspond to joint liquid/gas flow, for which eqn (3) is inapplicable. Fig. 10 shows the product QµversusΔp for air (Fig. 5) and pure n-decane (Fig. 7) flowing through the same carbon tube bundle. Surprisingly, the data almost collapses onto a single straight line for almost the whole range of Δp, where flow through carbon tubes could be sustained. Only the last point for the highest pressure drop for air in Fig. 10 suggests a possible deviation from the straight line. But as discussed earlier in relation to Fig. 5, Q for air at Δp ∼ 3 bar was underestimated due to the random presence of secondary bubbles along the lateral surface of the tube bundle, whose contribution to the measured flow rate could not be quantified. Consequently, the right-most open square in Fig. 10 is not a reliable indicator of the Q(Δp) trend for gas flow at high pressures. The observed linearity of the air flow data for Q in the range Δp = 1–2 bar and its collapse with the data of n-decane is a manifestation of the fact that at these values the pressure distributions along the tubes do not deviate significantly from the corresponding linear ones, which is also corroborated by calculation of p(X) based on the known inlet and exit pressures (cf. Fig. I in the ESI of this paper†). Consequently, the compressibility effects seem to be still not severe at the present pressures.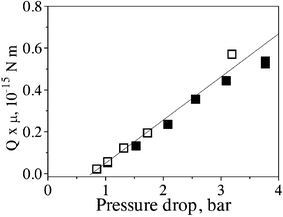 | ||
| Fig. 10 Data from Fig. 5 (air; open symbols) and Fig. 7 (n-decane; filled symbols) plotting the product Qµ versus pressure drop Δp. The straight line shows the best linear fit. | ||
The result shown in Fig. 10 is of significance from both a fundamental and a practical point of view. According to eqn (3) and (9), for this bundle the slope of the Qµ vs.Δp data is proportional to the factor  . The collapse of the data for different fluids on a single line in a certain pressure range in Fig. 10 indicates that the integral factor is essentially the same for both air and pure n-decane. Of course the tube radius distribution f(a) is the same in both cases, as the same bundle was used with both fluids, but the lower limit of the integral (2σ/Δp) is not the same, since σ is different (in one case, air in water, in the other, n-decane in water). The lower value of 2σ/Δp for n-decane–water (compared to water–air) extends the integration to lower values of a, which seem to contribute little to the value of the above integral. This is consistent with the presence of the term a4 multiplying f(a). Physically, eqn (3) and (9) mean that most of the flow is carried by the larger-radius tubes. Thus, variations in the lower limit of the integral essentially do not change the measured Qµvs. (Δp – Δp*) slope (for air Q is the exit value, Q = M/ρe, where ρe is the air density value at pe ≈ 1 bar). From the practical point of view, the collapse of the data on a single line suggests that one can use a single fluid with a given tube bundle to define the Qµ(Δp) line for any pure fluid that can be used thereafter with the same bundle. However, it is also noted that if gases are used in addition to liquids, the gas data is expected to collapse on the liquid data, only for low values of Δp, and not at higher pressures. The collapse of Qµ data on a single line is significant because it suggests that the flow behavior of a tube bundle can be fully characterized for any pure fluid of known viscosity by conducting flow tests with a single test fluid (either gas in the incompressibility range or liquid).
. The collapse of the data for different fluids on a single line in a certain pressure range in Fig. 10 indicates that the integral factor is essentially the same for both air and pure n-decane. Of course the tube radius distribution f(a) is the same in both cases, as the same bundle was used with both fluids, but the lower limit of the integral (2σ/Δp) is not the same, since σ is different (in one case, air in water, in the other, n-decane in water). The lower value of 2σ/Δp for n-decane–water (compared to water–air) extends the integration to lower values of a, which seem to contribute little to the value of the above integral. This is consistent with the presence of the term a4 multiplying f(a). Physically, eqn (3) and (9) mean that most of the flow is carried by the larger-radius tubes. Thus, variations in the lower limit of the integral essentially do not change the measured Qµvs. (Δp – Δp*) slope (for air Q is the exit value, Q = M/ρe, where ρe is the air density value at pe ≈ 1 bar). From the practical point of view, the collapse of the data on a single line suggests that one can use a single fluid with a given tube bundle to define the Qµ(Δp) line for any pure fluid that can be used thereafter with the same bundle. However, it is also noted that if gases are used in addition to liquids, the gas data is expected to collapse on the liquid data, only for low values of Δp, and not at higher pressures. The collapse of Qµ data on a single line is significant because it suggests that the flow behavior of a tube bundle can be fully characterized for any pure fluid of known viscosity by conducting flow tests with a single test fluid (either gas in the incompressibility range or liquid).
Conclusion
The results of the present work show that macroscopically-long parallel bundles of carbon tubes made via co-electrospinning allow fully controlled flows with relatively high overall pressure-driven throughput rates of the order of 30 nL s–1 (36.3 × 10–12 kg s–1) for air and 1 nL s–1 (73 × 10–11 kg s–1) for low viscosity liquids (e.g.n-decane), in the pressure drop range of 0–4 bar and when discharging in water. Being sufficient for many applications, these flow rates could be potentially increased by two orders of magnitude when even higher pressures are used to overcome the blockage of the tiniest carbon tubes by water. Higher flow rates could also be facilitated by an improved quality of the co-electrospun carbon tubes. It was also shown that although the Q(Δp) variation for the liquids first appeared to be inconsistent with the Poiseuille law, this inconsistency could be reconciled using arguments based on this law. In addition, a novel simple method of pore size characterization of nano- and microchannel bundles was formulated and demonstrated. The method employs the measured flow rate vs. pressure drop data to deduce the channel-size distribution in polydisperse tube bundles. Finally, the results have practical significance in suggesting that the flow behavior of a tube bundle can be fully characterized for any fluid of known viscosity by conducting flow tests with a single test fluid (either gas in the incompressibility range or liquid).Acknowledgements
This material is based upon work supported in part by Volkswagen Foundation and the National Science Foundation under Grants NIRT CBET-0609062 and CBET-0543538.References
- H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381–411 Search PubMed.
- A. Greiner, J. H. Wendorff, A. L. Yarin and E. Zussman, Appl. Microbiol. Biotechnol., 2006, 71, 387–393 CrossRef CAS.
- T. T. Huang, D. G. Taylor, K. S. Lim, M. Sedlak, R. Bashir, N. S. Mosier and M. R. Ladisch, Langmuir, 2006, 22, 6429–6437 CrossRef CAS.
- W. A. Phillip, J. Rzayev, M. A. Hillmyer and E. L. Cussler, J. Membr. Sci., 2006, 286, 144–152 CrossRef CAS.
- D. S. Sholl and J. K. Johnson, Science, 2006, 312, 1003–1004 CrossRef CAS.
- E. Zussman, A. L. Yarin, A. V. Bazilevsky, R. Avrahami and M. Feldman, Adv. Mater., 2006, 18, 348–353 CrossRef CAS.
- Y. Dror, W. Salalha, R. Avrahami, E. Zussman, A. L. Yarin, R. Dersch, A. Greiner and J. H. Wendorff, Small, 2007, 3, 1064–1073 CrossRef CAS.
- D. H. Reneker, A. L. Yarin, E. Zussman and H. Xu, Adv. Appl. Mech., 2007, 41, 43–195 Search PubMed.
- A. L. Yarin, E. Zussman, J. H. Wendorff and A. Greiner, J. Mater. Chem., 2007, 17, 2585–2599 RSC.
- A. Theron, E. Zussman and A. L. Yarin, Nanotechnology, 2001, 12, 384–390 CrossRef.
- S. N. Reznik, A. L. Yarin, E. Zussman and L. Bercovici, Phys. Fluids, 2006, 18, 062101 Search PubMed.
- J. C. Harley, Y. Huang, H. H. Bau and J. N. Zemel, J. Fluid Mech., 1995, 284, 257–274 CrossRef CAS.
- G. N. Patterson, Molecular Flow of Gases, Wiley, New York, 1956, p. 38 Search PubMed.
- E. Lauga, M. P. Brenner and H. A. Stone, in Handbook of Experimental Fluid Dynamics, ed. C. Tropea, A. Yarin and J. Foss, Springer, New York, 2007, pp. 1219–1240 Search PubMed.
- L. Prandtl and O. G. Tietjens, Applied Hydro- and Aeromechanics, Dover Publ., New York, 1957, p. 22 Search PubMed.
- L. G. Loitsyanskii, Mechanics of Liquids and Gases, Pergamon, Oxford, 1966, p. 500 Search PubMed.
- E. W. Washburn, Proc. Natl. Acad. Sci. U. S. A., 1921, 115–116 CrossRef CAS.
- M. Mulder, Basic Principles of Membrane Technology, Kluwer, London, 1996, pp. 165–188 Search PubMed.
- A. Goebel and K. Lunkenheimer, Langmuir, 1997, 13, 369–372 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Further details on the pressure distributions in gas flows and an experimental image illustrating gas release at high pressures. See DOI: 10.1039/b711446j |
| This journal is © The Royal Society of Chemistry 2008 |
