A hexacarboxylic open-shell building block: synthesis, structure and magnetism of a three-dimensional metal–radical framework

Abstract

An octahedral hexacarboxylic polychlorotriphenylmethyl radical (PTMHC) and its hydrogenated precursor (αH-PTMHC) have been reacted with Cu(II) and 4,4′-bipyridine to prepare two isomorphic three-dimensional (3-D) coordination polymers of formula [Cu₆(PTMHC)₂(4,4′-bipy)₃(H₂O)₁₂]_n (1) and [Cu₆(αH-PTMHC)₂(4,4′-bipy)₃(EtOH)₆(H₂O)₆]_n (2). Both 3-D structures can be described as two interpenetrating primitive cubic nets connected through bipyridine linkers, which defines an unusual topology with Schläfi symbol of (6²·8¹)·(6⁶·8⁹). Magnetic properties of both metal–organic frameworks have been studied in detail. 2 shows weak antiferromagnetic interactions between Cu(II) ions at low temperature. In contrast, 1 reveals unexpected metal–radical ferromagnetic interactions (θ = 2.1 (2) K). Information on the existence of magnetic ordering and the nature of the ordered phase for 1 has been investigated via very low temperature magnetic susceptibility measurements. Surprisingly, the experimental data indicate the occurrence of 3-D antiferromagnetic ordering below 0.5 K. This latter phenomenon has been explained with specific heat measurements. Experimental results reveal the coexistence of relatively strong ferromagnetic interactions with weaker antiferromagnetic ones, mediated through the bipyridine linkers, which finally determine the low temperature magnetic structure. A deeper study of the data allows the analysis of the magnetic behavior of 1 as a 3-D antiferromagnet, with T_C = 0.39 K, with ferromagnetic exchange interactions that do not propagate with equal strength along the three crystallographic directions above this temperature.

---

Introduction

The so-called “metal–radical approach”, which combines magnetically active metal ions and persistent organic radicals as ligands, has been shown to be a successful strategy to obtain a wide range of magnetic metal–organic materials.¹ The open-shell character of the organic ligands enhances the strength of magnetic interactions and, therefore, the magnetic dimensionality of the molecular material.² Thus far, nitroxide-based radicals,³ derivatives of the verdazyl^1c,4 and dithiadiazolyl⁵ radical families, o-quinone ligands,⁶tetracyanoethylene^7,8 (TCNE) and tetracyanoquinodimethane⁹ (TCNQ) radical anions and diphenylcarbenes,¹⁰ all of them substituted with chemical functions able to coordinate with metal ions, have been fruitfully used. This broad range of coordination functionalities has allowed the construction of multiple complexes, evolving from 0-D to 3-D systems with a great diversity of magnetic properties.³ However, and in spite of the excellent results obtained so far, the construction of extended metal–radical frameworks with specific structural characteristics (topology, connectivity and dimensionality) that should allow better design and control of their magnetic properties still remains an open issue.¹¹

Recent advances in the synthesis of extended metal–organic frameworks (MOFs) with different functionalities such as porosity¹² have made it possible to better understand some of the parameters that influence the final structural characteristics of these solids.¹³ One of these parameters is the geometry of the constituent building blocks. In principle, the proper selection of the geometry of these units is very important to rationally extend them through the space and, therefore, have a certain control of the final topology and dimensionality of the resulting MOFs.¹⁴ An excellent study of how this geometry has an effect on the final topology of MOFs has been recently reported by Yaghi's group.¹⁵ The authors went through a meticulous bibliographic study of more than 700 three-periodic extended MOFs presenting a uninodal net topology reported in the Cambridge Structural Database (CSD). This study allows, in some cases, the prediction of structural characteristics, thus providing a real basis for designing building blocks that allow the construction of specific MOFs with the required topology and dimensionality. For example, it is possible to predict that the use of a tetrahedral building block would afford diamond net types in 70% of the cases, whereas the use of an octahedral one would yield almost exclusively (95% of the cases) metal–organic structures with a primitive cubic net.^15a

Following such a rational strategy, a few years ago we initiated the construction of magnetic molecular materials based on perchlorinated triphenylmethyl (PTM) radicals¹⁶ properly functionalized with carboxylic groups.^17,18 Several aspects make this family of radicals particularly attractive to build up extended metal–radical frameworks. First, the carboxylic groups allow both the coordination to metallic centers and the propagation of magnetic interactions along the whole metal–radical framework.¹⁹ But a second feature that makes these radicals even more interesting is the trigonal geometry of the triphenylmethyl core, which can be decorated with a variable number of coordinating groups at different positions (meta and para) with respect to the central sp²carbon atom.^17,18 This characteristic makes possible the synthesis of a wide diversity of PTM-based building blocks with different connectivities and shapes (considering the carboxylic groups), thereby allowing the formation of multiple metal–radical systems exhibiting different topologies and dimensionalities. For example, we have so far introduced one, two and three carboxylic groups at the para positions of the triphenylmethyl skeleton. This functionalization defines one-, two- and three-connecting building blocks with no, V-shaped and trigonal geometries, respectively, in which the PTM radicals are linked with single Cu(II) metal ions (vide infra). As expected, the use of the monocarboxylic radical creates mononuclear 0-D complexes, whereas the introduction of a second carboxylic group extends these monomers creating 1-D Cu(II)–radical chains. Finally, the dimensionality of the metal–radical framework increases to 2-D Cu(II)–radical layers when the addition of a third carboxylic group is done.²⁰ Therefore, the proper selection of the number and location of carboxylic groups in this type of radical seems to be a powerful strategy to rationally extend the coordination of single metal ions creating metal–radical frameworks. For this reason, we have designed and synthesized a new PTM radical functionalized with six carboxylic groups (PTMHC) located at all meta positions of the phenyl rings with respect to the central carbon atom. A view of the crystal structure of the ligand, which was crystallized from diethyl ether or THF solutions, is shown in Fig. 1. The high molecular C₃ symmetry of the molecule is reflected by the presence of a crystallographic three-fold rotation axis that passes through the central carbon atom (C3), conferring on the molecule the three-bladed propeller-like conformation typically observed in PTM derivatives.²¹ For this radical, the trigonal shape of the triphenylmethyl skeleton and the location of six carboxylic groups at all meta positions confers an octahedral shape to the PTMHC ligand (see Fig. 1). According to this geometry, and based on the previous studies published by Yaghi's group, it is expected that the use of this radical will lead to the formation of 3-D cubic metal–radical networks.^15a

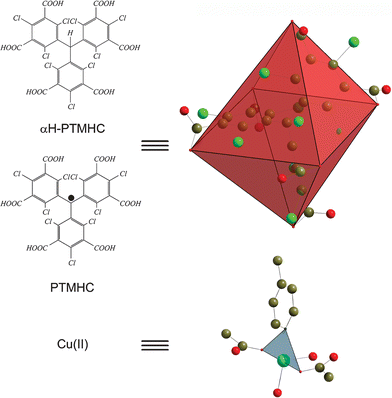Fig. 1 Schematic illustration of the octahedral shape for both the PTMHC radical and the αH-PTMHC ligand and the trigonal geometry of the Cu(II) center.

Herein, we report for the first time the use of this hexacarboxylic radical for the synthesis of a [Cu₆(PTMHC)₂(4,4′-bipy)₃(H₂O)₁₂]_n (1) framework that can be seen as two interpenetrated 3-D metal–radical cubic frameworks connected through 4,4′-bipyridine ligands. Added to the fact that this MOF is one of the scarce examples of 3-D coordination polymers based on a hexacarboxylic ligand,²² this solid represents a promising 3-D metal–radical framework that, in addition to remarkably low temperature magnetic properties, exhibits an unusual (6²·8¹)·(6⁶·8⁹) topology.

Experimental

General considerations

All solvents were reagent grade from SDS, and they were used as received and distilled unless otherwise indicated. All reagents, organic and inorganic, were of high purity grade and obtained from E. Merck, Fluka Chemie and Aldrich Chemical Co. Elemental analyses were obtained from the Servei de Anàlisi de la Universitat Autònoma de Barcelona. FT-IR spectra were obtained using a Perkin-Elmer Spectrum One spectrometer. Crystalline phase purity was checked by X-ray powder diffraction (XRPD) experiments, using a diffractometer (INEL CPS-120) of Debye–Scherrer geometry. X-Ray data collection of the single crystals was performed on a Nonius Kappa CCD equipped with graphite-monochromatized Mo Kα radiation (λ = 0.71073 Å).

Synthesis of [Cu₆(PTMHC)₂(4,4′-bipy)₃(H₂O)₁₂]_n·2.4THF·4.6H₂O (1)

A mixture of PTMHC (0.05 g, 0.063 mmol) and Cu₂(MeCOO)₄·2H₂O (0.038 g, 0.095 mmol) in 10 mL of distillate water was layered with 10 mL of a THF solution of 4,4′-bipyridine (0.030 g, 0.20 mmol). Slow diffusion over 45 days yielded dark red crystals of 1. Yield: 0.025 g (29%). IR (KBr): 1611, 1550, 1418, 1385, 1360, 1331, 1275, 1222, 1115, 1075, 1019, 947, 818, 647, 630, 572, 546 cm⁻¹. Anal. calcd. for C_89.60H_76.4N₆O₄₃Cl₁₈Cu₆: C 36.52, H 2.60, N 2.85; found C 35.65, H 1.82, N 3.02%.²³

Synthesis of [Cu₆(αH-PTMHC)₂(4,4′-bipy)₃(EtOH)₆ (H₂O)₆]_n·3EtOH·H₂O (2)

A mixture of αH-PTMHC (0.05 g, 0.063 mmol) and Cu₂(MeCOO)₄·2H₂O (0.038 g, 0.095 mmol) in 10 mL of distillate water was layered with 10 mL of an ethanol solution of 4,4′-bipyridine (0.030 g, 0.20 mmol). Slow diffusion over 20 days yielded dark green crystals of 2. Yield: 0.045 g (50%). IR (KBr): 1611, 1550, 1419, 1358, 1333, 1306, 1257, 1221, 1076, 1021, 948, 816, 645, 631, 574 cm⁻¹. Anal. calcd. for C₉₈H₉₄N₆O₄₀Cl₁₈Cu₆: C 39.00, H 3.12, N 2.79; found C 38.55, H 2.64, N 2.89%.²³

Magnetic susceptibility measurements

The temperature dependence of the static magnetic susceptibility was measured with a MPMS2 SQUID magnetometer (Quantum Design) at different applied magnetic fields in the temperature range 1.8–300 K. The data were corrected for the contribution of the sample holder and for the diamagnetism of the sample estimated from Pascal's constants.

Low temperature magnetic measurements

Magnetization measurements in the temperature range 0.5–6 K were performed with a high-sensitivity Hall magnetometer,²⁴ installed in a ³He refrigerator. The micro-Hall sensor was made with a high mobility GaAs/GaAlAs hetero-structure. The sample was placed onto one of the three Hall crosses, each of these having an active area of 50 × 400 μm². The external magnetic field was applied perpendicular to the plane of the sensor. Measurements were then performed in a differential mode, which enabled us to compensate for the signal of the empty magnetometer and therefore increased the sensibility up to 0.01 Gauss. The Hall voltage was proportional to the magnetic moment of the sample. In order to get absolute magnetization values, these results were calibrated against data measured with the SQUID in the temperature range where both techniques overlap.

Specific heat measurements

The specific heat of a powdered microcrystalline sample was measured using a commercial multipurpose measurement platform PPMS (Quantum Design). The sample was mixed with Apiezon N grease to increase the thermal contact to the calorimeter and the homogeneity in temperature across the sample. The calorimeter used the relaxation method: the temperature of the calorimeter block was monitored in time after switching on and off pulses of heat power.²⁵ The relaxation time for the decay of the temperature towards its stationary value is proportional to the specific heat of the calorimeter block plus sample. The constant of proportionality depends on the thermal conductivity of the wires coupling the calorimeter to the thermal bath (the cold spot of a ³He refrigerator). Since this conductivity can be extracted from the stationary temperature values, absolute specific heat data can be obtained by this method. The pulses were calibrated to give maximum temperature steps of about 2% of the absolute temperature. The contributions arising from the empty calorimeter and the grease were measured separately, and subtracted from the data to obtain the heat capacity of the sample.

Results and discussion

Synthesis

To our knowledge, not many MOFs built up from hexacarboxylic ligands with all their functional groups coordinating to metal ions have been reported so far. Among them, it is interesting to note that most of these coordination polymers were obtained by using solvo- or hydrothermal techniques. In such a context, in a first approach, we performed numerous reactions by using similar thermal conditions. However, even though different solvent mixtures, reaction times, temperatures and cooling rates were used, only amorphous solids were obtained. Consequently, we decided to change our strategy, and start with a series of crystallizations consisting of a slow diffusion at room temperature.²⁰ After numerous attempts to determine the best conditions, we finally succeeded in obtaining dark prism crystals of the MOF [Cu₆(PTMHC)₂(4,4′-bipy)₃(H₂O)₁₂]_n (1). Such crystals were obtained by diffusing a THF solution of 4,4′-bipyridine onto a water solution of Cu₂(MeCOO)₄·2H₂O and PTMHC radical. Interestingly, an isomorphic structure with formula [Cu₆(αH-PTMHC)₂(4,4′-bipy)₃(EtOH)₆(H₂O)₆]_n (2) was also obtained starting from the non-magnetic counterpart of the PTMHC radical, αH-PTMHC.

Crystallographic studies

Complexes 1 and 2 are isomorphic and crystallize in the trigonal space groupR3̄c (Table 1).†Fig. 2 shows an ORTEP plot of the asymmetric unit of 1 and the link-up to symmetry related atoms by a glide plane, a 2-fold and a 3-fold rotation axis. Representative bond length and bond, torsion and dihedral angles of both complexes are reported in Table 2. Single-crystal structure analysis reveals that the electrically neutral MOFs 1 and 2 are formed by isolated Cu(II) centers, which adopt a square pyramidal geometry. The square base of the coordination polyhedron is composed of two trans-monodentate carboxylic groups, with a conformation close to a syn–anti one, one nitrogen atom of the 4,4′-bipyridine linker and one water molecule. The remaining position on the square pyramid is occupied by an additional water molecule. In the case of complex 2, the latter water molecule is replaced by an ethanol molecule.

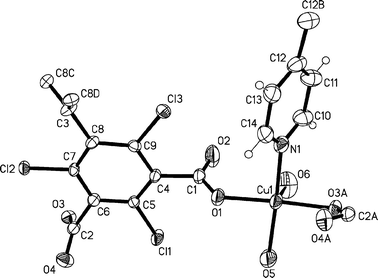Fig. 2 ORTEP view of the asymmetric unit of 1 at 30% probability level, with symmetry-generated atoms of indices A, B, C + D (A: glide plane, B: 2-fold rotation and C + D: 3-fold rotation axis). Solvent molecules are omitted for clarity.

Table 1 Crystal data and structure refinement for 1 and 2

	1	2
Formula	C89.60H76.4Cl18Cu6N6O43	C98H94Cl18Cu6N6O40
FW	2944.51	3015.13
Crystal system	Trigonal	Trigonal
Space group	R3̄c	R3̄c
a/Å	22.3534(4)	22.4479(5)
b/Å	22.3534(3)	22.4479(4)
c/Å	41.1462(3)	41.1720(6)
α/°	90	90
β/°	90	90
γ/°	120	120
V /Å^3	17805.2(4)	17967.3(7)
Z	6	6
T/K	233(2)	233(2)
R 1	0.0656	0.0506
wR 2	0.1883	0.1335
GOF	1.061	1.074

---

Table 2 Selected bond distances (Å) and bond, torsion and dihedral angles (°) of 1 and 2

	1	2
a Φ corresponds to the dihedral angle made by the phenyl rings and the reference plane of the PTM-based ligands.
Φ ^a/°	44.0	44.6
C(5)–C(6)–C(2)–O(4)/°	82.3(8)	79.5(6)
C(9)–C(4)–C(1)–O(2)/°	83.2(9)	85.0(6)
Cu(1)–O(1)/Å	1.947(4)	1.959(3)
Cu(1)–O(3)/Å	1.955(3)	1.947(3)
Cu(1)–O(5)/Å	1.972(5)	1.966(4)
Cu(1)–N(1)/Å	2.001(5)	2.003(4)
Cu(1)–O(6)/Å	2.282(7)	2.262(4)
O(1)–Cu(1)–O(3)/°	169.2(2)	169.0(2)
O(1)–Cu(1)–O(5)/°	86.4(2)	86.1(2)
O(3)–Cu(1)–O(5)/°	92.4(2)	92.5(2)
O(1)–Cu(1)–N(1)/°	90.4(2)	89.5(2)
O(3)–Cu(1)–N(1)/°	88.6(2)	89.8(2)
O(5)–Cu(1)–N(1)/°	168.6(3)	168.6(2)
O(1)–Cu(1)–O(6)/°	100.3(2)	96.36(16)
O(3)–Cu(1)–O(6)/°	90.5(2)	94.63(15)
O(5)–Cu(1)–O(6)/°	95.8(3)	100.2(2)
N(1)–Cu(1)–O(6)/°	95.6(3)	90.70(16)
O(2)–O(1)–O(3a)–O(4a)/°	147.4(3)	144.7(2)

---

The extended structure of 1 is generated by the connection of Cu(II) centers through PTMHC radicals and 4,4′-bipyridine ligands. From this connectivity, the resulting network can be considered as a 3-D net constructed from two interpenetrating connected primitive cubic (pcu or α-Po) metal–radical frameworks. The cubic structures are formed by the connection of each PTMHC radical to six different Cu(II) ions. Fig. 3a shows a representation of one cube composed of eight PTMHC radicals and twelve Cu(II) centers located at the vertices and edges, respectively. The cubic networks are then cross-linked through the Cu(II) centers located at the edges (Fig. 3b and c). Each Cu(II) centre is connected to another Cu(II) ion of a different cubic framework through a 4,4′-bipyiridine ligand. Fig. 4 reveals the unusual topology with a Schläfli symbol of (6²·8¹)·(6⁶·8⁹) displayed by this 3-D structure containing 3-connected Cu(II) centers and 6-connected PTMHC radical units.

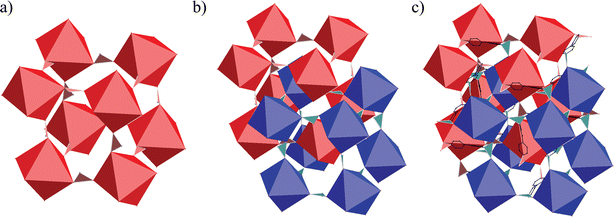Fig. 3 Crystal structure of 1. (a) A metal–radical cube. (b) Two interpenetrated cubes. (c) Illustration of the connectivity between two interpenetrated cubes. PTMHC radicals are represented as octahedra, Cu(II) ions as tri-connected units, and 4,4-bipyridines as black ligands.

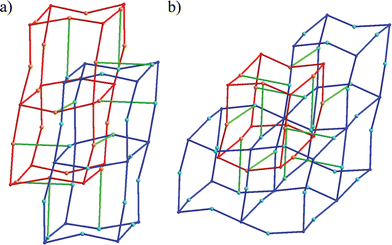Fig. 4 Connectivity of 1. (a) Connectivity between the two interpenetrated cubic networks (red and blue) through linear 4,4′-bipyridine ligands (green). (b) Illustration of the total connectivity of one cube (red) with the other cubic network (blue) through 4,4′-bipyridine ligands (green).

Structural analysis of extended metal–radical frameworks

To address the importance of the shape of multitopic organic radicals to control the topology and dimensionality of metal–radical frameworks, we have analyzed the crystal structures of all coordination polymers built up from single metal ions (considered as spacers) joined by organic radicals registered in the Cambridge Structural Database.²⁶ For this study, we have only selected the frameworks in which the multitopic organic radicals connect metal ions through all their coordinating sites. Table 3 shows a list of such frameworks,²⁷ which have been classified by taking into account the number of coordinating sites of the radicals, the geometry defined by these sites and the dimensionality and topology of the final metal–radical frameworks.

Table 3 Classification of metal-radical frameworks found in the CSD from each open-shell organic building-block connectivity (left) and the resulting framework dimensionality and topology

---

The large majority of metal–radical frameworks are built up from nitroxide radicals (96%), and only two structures are constructed from the use of a tetracyanoethylene (TCNE) radical anion^28,29 and verdazyl radicals.³⁰ Of these, 38 frameworks are constructed from the linkage of metal ions by two-connecting radicals (70%), whereas the number of polymers synthesized by using three- and four-connecting species is smaller (13% and 17%, respectively). We believe that the great abundance of radicals with two coordinating sites is strongly related to the coordination ability of the nitronyl nitroxide radicals^31,32 (R–NN) and of their bis(tert-butyl nitroxide) analogues³³ (R–Ph(tNO)₂), which offer two equivalent N–O coordination sites that define V-shaped and zig-zag geometries, respectively. From these shapes, the formation of extended one-dimensional (1-D) chains would be expected. To date, 38 (100%) chain-like structures that show different magnetic phenomenologies, such as ferro-,^31a ferri-,^31a,h antiferromagnetism,³⁴ 1-D single-chain magnet,^31g,s,32 and spin-glass behavior,³¹ⁱ have been reported.

Even though the use of organic radicals with more than two connecting sites is very important because they are expected to afford metal–radical frameworks with higher structural and consequently magnetic dimensionalities, the number of coordination polymers built up from such open-shell ligands is not very high. Specifically, there are a total of 7 metal–radical networks (44%), which have 1-D structures,^30,35,36 7 show lamellar structures (44%),^28,37,38 and only 2 possess 3-D frameworks (12%).^39,40 Herein, the role played by the shape of the organic radicals in the structure of these metal–radical frameworks is remarkable. For example, 3-connecting trigonal building blocks have been found particularly interesting for the synthesis of layered MOFs. In a similar way, the use of trigonal open-shell ligands based on nitroxide radicals has allowed the synthesis of 2-D metal–radical frameworks. A representative example is the highly symmetric Ph–(Ph–tNO)₃, which connects single Mn(II) ions to create ferrimagnetic honeycomb-like layers with a bulk 3-D magnetic ordering at lower temperatures (T_c = 3.4 K).³⁸ For the 3-D structures, they were obtained by the linkage of Mn(II) ions through the three-connecting NO(Ph-tNO)₂³⁹ and four-connecting tetragonal C(Ph-tNO)₄ radicals.⁴⁰ If one utilizes the study reported by Yaghi's group,^15a the 3-D structures expected from the geometry of both organic building-blocks are the srs (Si in SrSi₂) and the diamond-like networks, respectively. Accordingly, the linkage of Mn(II) ions by these organic radicals results in two coordination polymers that exhibit such topologies.

It is clear from the previous examples that the selection of the shape of multitopic organic radicals is very important for controlling the final structure of the corresponding metal radical frameworks. This observation has been further confirmed in our group with a series of metal–radical complexes synthesized from the linkage of single metal ions by PTM radicals. Our strategy is based on the possibility of controlling the shape of such open-shell ligands by functionalizing their phenyl rings with carboxylic groups. By controlling the number and location of these acidic groups, the topology and dimensionality of metal–radical networks can be rationally modified. Table 4 shows a list of all metal–radical complexes created from the connection of single Cu(II) ions through these radicals. In such complexes, a single Cu(II) ion is coordinated by two radicals in a trans-monodentate mode. The reaction of the monocarboxylic PTMMC radical with Cu(II) ions generates mononuclear Cu(II) complexes. Interestingly, the addition of a second carboxylic group to the organic building block allows these monomers to extend along one direction, leading to the formation of 1-D Cu(II)–radical chains. Following the same principle, those chains can be connected with the addition of a third carboxylic at the para position of the remaining phenyl ring. Indeed, by using the tricarboxylic PTMTC radical, 2-D highly porous honeycomb-like layers are obtained, which can be seen as connected chains through one direction.

Table 4 Classification of metal–radical complexes synthesized from the connection of single Cu(II) ions through carboxylic-based PTM radicals

---

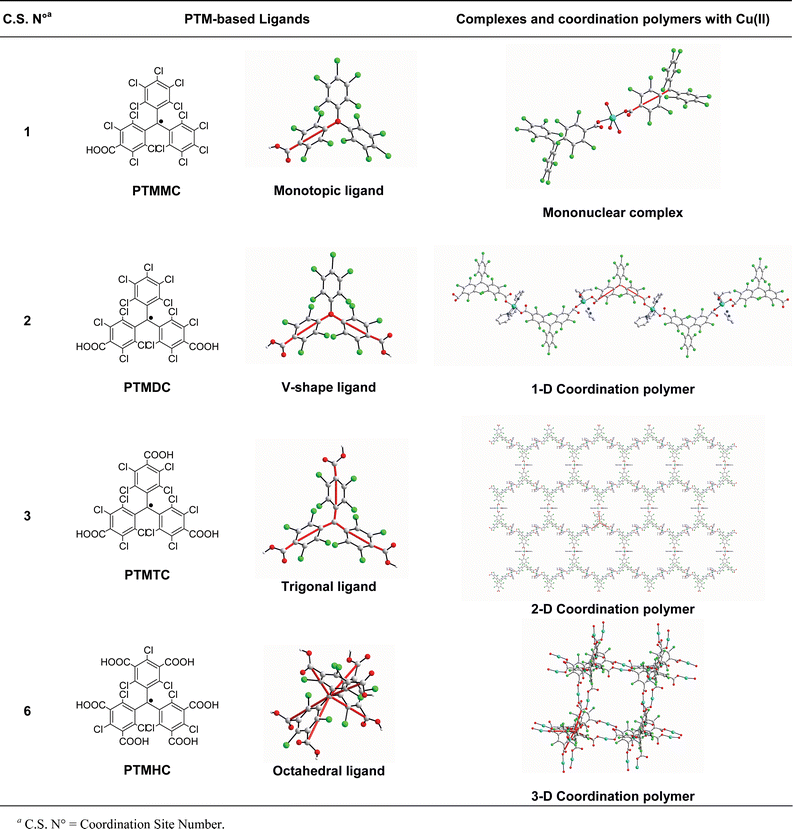
It is in this context that we designed the hexacarboxylic PTMHC radical, in which all six carboxylic groups were introduced at the meta positions of the phenyl rings. This functionalization was done to obtain a six-connecting open-shell ligand with an octahedral geometry (see Fig. 1). Because of this geometry and according to the study published by Yaghi's group,^15a it was expected that the use of this octahedral unit would lead to the formation of a 3-D cubic network with 95% probability. The high frequency of cubic network occurrence from octahedral building blocks was finally confirmed with the formation of 1. Indeed, the connection of single Cu(II) ions through PTMHC radicals defines a slightly distorted cubic net, in which the octahedral radicals occupy the vertices and govern the final topology and dimensionality of the resulting network.

Magnetic properties

Variable temperature magnetic susceptibility data for a crystalline sample of 1 were obtained on a SQUID susceptometer within the temperature range of 2–300 K and an applied magnetic field of 1 Tesla. The resulting χ_molT vs. T plot is shown in Fig. 5.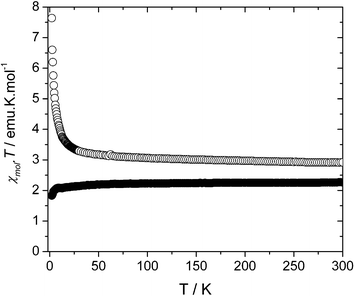

Fig. 5 Plot of χ_molT as a function of temperature for 1 (○) and 2 (●) at an applied magnetic field of 1000 Oe.

As can be seen there, the χ_molT value of 2.94 emu·K·mol⁻¹ at room temperature is in good agreement with that expected for a set of non-interacting Cu(II) ions and PTMHC radicals with a 6 : 2 stoichiometry and spins S_Cu = S_PTMTC = 1/2. As the temperature is lowered, the value of χ_molT remains constant down to approximately 50 K, whereupon it increases smoothly reaching a value of 3.47 emu·K·mol⁻¹ at 20 K. Below 20 K, the χ_molT curve increases abruptly up to a maximum value of 7.64 emu·K·mol⁻¹ around 2 K, indicating the presence of ferromagnetic exchange interactions within the 3-D structure of 1.

Information on the existence of magnetic ordering and the nature of the ordered phase at very low temperatures was obtained from variable temperature magnetic susceptibility experiments performed in a micro-Hall magnetometer. Results for the susceptibility under an applied field μ₀H = 0.1 Tesla in comparison with the susceptibility calculated for non-interacting spins are shown in Fig. 6. The fit of the reciprocal susceptibility above 5 K (linear regime) to a Curie–Weiss law yields a positive value for the Weiss temperature of θ = 2.1 (2) K. This fact, together with the nonlinear behavior of the magnetization under different applied fields below 5 K, confirms the onset of ferromagnetic correlations at low T. However, the value of χ at any temperature above 0.58 K is much smaller than the ferromagnetic limit given by χ_ferro→ 1/N, where N is the demagnetizing field of the sample. Considering the crystals as spheres (N = 4π/3 cm³·emu⁻¹), a theoretical value of χ_ferro≈ 0.24 emu·cm⁻³ is obtained. This value is about 50 times larger than the maximum measured susceptibility. Moreover, the value attained by the magnetization at the lowest temperature (1.33 μ_B (formula unit)⁻¹) under an external field μ₀H = 0.1 Tesla is also far below the saturation magnetization expected for a ferromagnetic state of 8 spins 1/2 (8 μ_B) (Fig. 6). From these observations, we must conclude that, despite the presence of relatively strong ferromagnetic interactions, such couplings do not establish a truly ferromagnetic order. Instead, the experimental data indicate that a phase transition to a magnetically ordered phase with an antiferromagnetic arrangement of spins takes place only below 0.5 K.

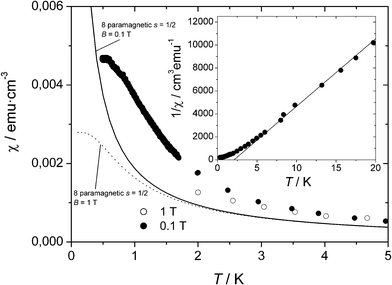Fig. 6 Plot of χ_mol as a function of temperature for 1 at an applied magnetic field of 0.1 T (○) and 1 T (●). Continuous lines show the susceptibility calculated for eight non-interacting species with S = 1/2 at both magnetic fields. Inset shows the inverse of χ_mol as a function of temperature and the corresponding fitting to the Curie–Weiss law (continuous line).

To give more insight into the origin of this phase transition, the magnetic properties of complex 2 were also studied (Fig. 5). The absence of magnetically active organic ligands in 2 should yield information on the occurrence and nature of the Cu(II)–Cu(II) magnetic interactions mediated through pathways other than metal–radical interactions. Such magnetic pathways are mainly defined by the linkage of Cu(II) ions through bipyridine and meta-phenyldicarboxylate bridges. At room temperature, the χ_molT value for 2 is 2.25 emu·K·mol⁻¹. This value is in perfect agreement with that expected for the 6 non-interacting Cu(II) ions present in the repetitive unit. As the temperature is lowered, this value remains constant prior to a decrease for temperatures close to 2 K. This slight decrease of the χ_molT value can be explained by the presence of antiferromagnetic interactions, either viabipyridine ligands or meta-phenyldicarboxylate bridges. In fact, numerous examples of 4,4′-bipyridine based coordination polymers have been magnetically characterized, and this ligand has proved to promote exclusively very weak antiferromagnetic interactions between metallic centres.⁴¹ Taking into account these results, it is reasonable to ascribe the phase transition to the presence of antiferromagnetic interactions between 3-D cubic networks mediated by the bipyridine ligands linking them. Within this picture, the observed ferromagnetic interactions probably correspond to interactions between spins inside each of these networks.

Specific heat measurements

The specific heat c of 1 was measured in a commercial PPMS multipurpose measuring platform that makes use of the relaxation method. Above 7 K, c is dominated by the specific heat c_latt arising from lattice vibrations. Below this temperature, the magnetic specific heat c_mag was estimated by subtracting from the total c the c_latt estimated by fitting the data measured above 10 K to a superposition of two curves, given respectively by Debye's (accounting for acoustic modes) and Einstein's (for the optical phonon modes) models. Results are shown in Fig. 7 in units of the gas constant R per mol of compound. It shows a sharp peak centered around T_c = 0.39 K and broader bump with a maximum near a higher temperature T_L-D = 1.4 K (L-D stands for a low-dimensional order, as is explained below). Both peaks shift towards lower temperatures when a magnetic field of 0.1 Tesla is applied, which confirms their magnetic origin. Above T≈ 3.8 K, c_mag∝T⁻² (see the inset). The low temperature peak confirms our early expectation, extracted from the saturation of χ_dc below 0.6 K, that a phase transition to a long range ordered magnetic state does take place. We have argued before that the ordered phase probably corresponds to an anti-parallel ordering of the two 3-D cubic networks. The facts that a) the Weiss temperature θ > 0 and b) the critical temperature T_c is five times smaller than θ suggest that antiferromagnetic interactions between these two magnetic sublattices are weaker than the ferromagnetic interactions between spins belonging to each of them.^42,43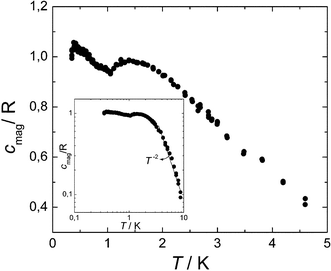

Fig. 7 Changes in the magnetic specific heat c_mag as a function of the temperature for 1. The inset is a double-log scale plot of c_mag in an extended temperature region showing that c_mag decays as T⁻² for temperatures well above T_L-D.

Finally, the presence of a bump above T_c is important. Such a bump does not seem to be associated with a true magnetic phase transition since the magnetic susceptibility does not show any anomaly near T_L-D. Most likely, it might arise from short range magnetic order above T_c or with crystal field effects. The latter possibility is however ruled out by the fact that crystal field terms cannot induce any energy splitting in the case of S = 1/2 spins.⁴⁴ The bump is in fact typical of materials with low-dimensional magnetic character, where short range correlations become enhanced with respect to 3-D lattices.⁴² Indeed, the entropy content ΔS_Tc→∞≈ 2.5R (that is 45% of the total magnetic entropy R ln2 per spin) above T_c is larger than the value ΔS_Tc→∞≈ 2R expected for a 3-D S = 1/2 Heisenberg antiferromagnet.⁴⁵ Remarkably enough, some of our experimental observations, namely the absence of a phase transition at T_L-D, the broad peak in c_mag, the fact that θ > T_L-D, and the deviation of the susceptibility from the Curie–Weiss behavior well above θ, agree qualitatively well with predictions for the Heisenberg model in two or one dimensions.^42,46 This seems surprising at first, since the two nets are nearly cubic. It indicates that the dominant ferromagnetic exchange interactions do not propagate with equal strength along the three crystallographic directions. As a tentative explanation, we associate this remarkable magnetic behavior with the fact that, in each of the two sub-lattices, Cu(II) ions have a very low coordination z = 2, that is, the same they would have in a 1-D chain. The fluctuations of their spins might then give rise, above T_c, to magnetic behavior similar to that predicted for a 1-D system. To support this idea, it is worth mentioning that the height of the bump normalized by the number of Cu ions (c_m(T_L-D)/6 = 0.16R) and its position (T_L-D/θ = 0.67) are both very close to the values predicted for a Heisenberg chain:^46a,b c_m(T_L-D) = 0.134R and T_L-D/θ = 0.7. The low dimensional character of the ferromagnetic interactions in each of the two interpenetrating networks would also explain why these do not give rise to ferromagnetic long-range order. Our compound provides thus one of the rare instances (the archetypical one being the KCuF₃ compound) of a cubic crystal containing Cu(II) ions which shows 1-D magnetic behavior.⁴⁷

Conclusions

The reaction of PTMHC radical with six carboxylic groups at meta-positions and of its hydrogenated precursor αH-PTMHC with Cu(II) ions and 4,4′-bipyridine afforded two isomorphic 3-D coordination polymers 1 and 2. The octahedral geometry and the hexatopic nature of both ligands are directly responsible for the three dimensionality observed for the two structures, which are described as interpenetrated and slightly distorted cubic frameworks connected by their metallic Cu(II) nodes through bipyridine linkers. Such ditopic bridges and the fact that metal ions are acting as linear spacers originate an unusual topology with Schläfi symbol of (6²·8¹)·(6⁶·8⁹). While the structure constructed from the non-magnetic ligand shows Cu(II)–Cu(II) antiferromagnetic interactions at low temperatures, the one based on the radical is characterized by metal–radical ferromagnetic ones. The ferromagnetic nature of such interactions is particularly surprising for coordination polymers based on PTM radicals because all Cu(II)–radical interactions reported so far showed an antiferromagnetic nature. However, this different behavior can be ascribed to the meta-location of the carboxylate groups on the PTM skeleton compared to the previous cases, where all carboxylate groups were located at para-positions. Very low temperature magnetic behavior of this material is directly related to the connection of the metal–radical cubic frameworks by the 4,4′-bipyridine linkers. Experimental results reveal the coexistence of relatively strong ferromagnetic interactions with weaker antiferromagnetic ones, mediated through the bipyridine ligands, which finally determine the low temperature magnetic structure. Such antiferromagnetic couplers limit the propagation of ferromagnetic interactions and afford an overall 3-D antiferromagnetic ordering below 0.39 K. In that sense, this behavior is particularly unusual for a molecular material since the ferromagnetic interactions do not propagate with equal strength along the three crystallographic directions above 0.39 K. In fact, above T_c, the magnetic behavior of 1 is more similar to that predicted for a 1-D system.

Even though these results clearly demonstrate the role played by the 4,4′-bipyridine for both structural and magnetic considerations, they also highlight the advantages offered by PTM radicals for the construction of magnetic coordination polymers compared to the “traditional” nitroxide ones. Changing the number of coordinating sites and their relative positions allows control of both the structure dimensionality and the nature of the metal–radical interactions. As a consequence, the objectives of the work we are currently developing on this research line are twofold. The first one is dedicated to the synthesis of mono-, di- and tri-meta-substituted PTM-based ligands to confirm the occurrence of ferromagnetic metal–radical interactions when the carboxylic groups are introduced in meta-positions. The second one is related to the use of monotopic (such as pyridine derivatives) or even non-coordinating bases (such as amines) during the coordination chemistry reactions involving the PTMHC radical. Such an approach could allow the preparation of 3-D coordination polymers presenting a cubic topology, ferromagnetic ordering and even high porosity if the 4,4′-bipyridine linkers are also responsible for the interpenetrated nature of 1.

Acknowledgements

This work was supported by the Ministerio de Educación y Ciencia of Spain under Consolider-C project EMOCIONa (project CTQ2006-06333/BQU), by the EU under the Marie Curie Research Training Network “QuEMolNa” (contract MCRTN-CT-2003-504880), as well as by NOE MAGMANET (contract NMP3-CT-2005-515767). N. R. thanks the MCRTN for its postdoctoral contract. D. M. acknowledges the Ministerio de Ciencia y Tecnologia for a Ramón y Cajal contract. F. L. and A. C. acknowledge the funding from DGA project PIP039 “NANOMATERIA” and project MAT2005/1272.

References

1. (a) A. Caneschi, D. Gatteschi, R. Sessoli and P. Rey, Acc. Chem. Res., 1989, 22, 392; (b) A. Caneschi, D. Gatteschi and P. Rey, Prog. Inorg. Chem., 1991, 39, 331; (c) H. Iwamura, K. Inoue and T. Hayamizu, Pure Appl. Chem., 1996, 68, 43; (d) M. T. Lemaire, Pure Appl. Chem., 2004, 76, 277.
2. (a) O. Kahn, Molecular Magnetism, VCH, New York, 1993; (b) J. S. Miller, Adv. Mater., 2002, 14, 1105.
3. H. Iwamura and K. Inoue, in Magnetism: Molecules to Materials II, ed. J. S. Miller and M. Drillon, Wiley-VCH, Weinheim, 2001.
4. (a) B. D. Koivisto and R. G. Hicks, Coord. Chem. Rev., 2005, 249, 2612 and references cited therein; (b) J. B. Gilroy, B. D. Koivisto, R. McDonald, M. Ferguson and R. G. Hicks, J. Mater. Chem., 2006, 16, 2618.
5. (a) N. G. R. Hearns, K. E. Preuss, J. F. Richardson and S. Bin-Salamon, J. Am. Chem. Soc., 2004, 126, 9942; (b) M. Jennings, K. E. Preuss and J. Wu, Chem. Commun., 2006, 341; (c) W. Fujita, K. Awaga, R. Kondo and S. Kagoshima, J. Am. Chem. Soc., 2006, 128, 6016; (d) N. G. R. Hearns, K. D. Hesp, M. Jennings, J. L. Korcok, K. E. Preuss and C. S. Smithson, Polyhedron, 2007, 26, 2047; (e) W. Fujita and K. Awaga, J. Am. Chem. Soc., 2001, 123, 3601.
6. (a) D. Ruiz-Molina, J. Veciana, K. Wurst, D. N. Hendrickson and C. Rovira, Inorg. Chem., 2000, 39, 617; (b) A. Caneschi, A. Dei, H. Lee, D. A. Shultz and L. Sorace, Inorg. Chem., 2001, 40, 408; (c) E. Evangelio and D. Ruiz-Molina, Eur. J. Inorg. Chem., 2005, 15, 2957; (d) S. Bin-Salomon, S. H. Brewer, E. C. Depperman, S. Franzen, J. W. Kampf, L. M. Kirk, R. K. Kumar, S. Lappi, K. Peariso, K. E. Preuss and D. A. Shultz, Inorg. Chem., 2006, 45, 4461.
7. J. S. Miller, Dalton Trans., 2006, 2742 and references cited therein.
8. (a) J. S. Miller and A. J. Epstein, Angew. Chem., Int. Ed. Engl., 1994, 33, 385; (b) J. S. Miller and A. J. Epstein, Chem. Eng. News, 1995, 73, 30; (c) K. I. Pokhodnia, N. Petersen and J. S. Miller, Inorg. Chem., 2002, 41, 1996.
9. H. Zhao, M. J. Bazile, Jr., J. R. Galán-Mascaros and K. R. Dunbar, Angew. Chem., Int. Ed., 2003, 42, 1015.
10. (a) M. Gandelman, B. Rybtchinsky, N. Ashkenazi, R. M. Gauvin and D. Milstein, J. Am. Chem. Soc., 2001, 123, 5372; (b) S. Karasawa, H. Kumada, N. Koga and H. Iwamura, J. Am. Chem. Soc., 2001, 123, 9685.
11. (a) H. O. Stumpf, Y. Pei, O. Kahn, J. Sletten and J.-P. Renard, J. Am. Chem. Soc., 1993, 115, 6738; (b) H. O. Stumpf, L. Ouahab, Y. Pei, D. Grandjean and O. Kahn, Science, 1993, 261, 447.
12. D. Maspoch, D. Ruiz-Molina and J. Veciana, Chem. Soc. Rev., 2007, 36, 770.
13. (a) A. K. Cheetham, C. N. R. Rao and R. K. Feller, Chem. Commun., 2006, 4780; (b) M. Du, Z.-H. Zhang, L.-F. Tang, X.-G. Wang, X.-J. Zhao and S. R. Batten, Chem.–Eur. J., 2007, 13, 2578.
14. (a) R. Robson, J. Chem. Soc., Dalton Trans., 2000, 3735; (b) B. Moulton and M. J. Zaworotko, Chem. Rev., 2001, 101, 1629; (c) B. Moulton and M. J. Zaworotko, Curr. Opin. Solid State Mater. Sci., 2002, 6, 117.
15. (a) N. W. Ockwig, O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176; (b) O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acta Crystallogr., Sect. A, 2006, 62, 350.
16. M. Ballester, Acc. Chem. Res., 1985, 12, 380.
17. (a) D. Maspoch, L. Catala, P. Gerbier, D. Ruiz-Molina, K. Wurst, J. Tejada, C. Rovira and J. Veciana, Chem.–Eur. J., 2002, 8, 3635; (b) D. Maspoch, L. Catala, P. Gerbier, D. Ruiz-Molina, K. Wurst, J. Tejada, C. Rovira and J. Veciana, J. Am. Chem. Soc., 2004, 126, 730; (c) D. Maspoch, N. Domingo, D. Ruiz-Molina, G. Vaughan, K. Wurst, J. Tejada, C. Rovira and J. Veciana, Angew. Chem., Int. Ed., 2004, 43, 1828.
18. (a) N. Roques, D. Maspoch, N. Domingo, D. Ruiz-Molina, K. Wurst, J. Tejada, C. Rovira and J. Veciana, Chem. Commun., 2005, 4801; (b) N. Roques, D. Maspoch, K. Wurst, D. Ruiz-Molina, C. Rovira and J. Veciana, Chem.–Eur. J., 2006, 12, 9238.
19. Mono-, di- and trinuclear complexes presenting metal-radical antiferromagnetic interactions have been obtained with the monocarboxylate radical, see: (a) D. Maspoch, D. Ruiz-Molina, K. Wurst, C. Rovira and J. Veciana, Chem. Commun., 2002, 2958; (b) D. Maspoch, D. Ruiz-Molina, K. Wurst, C. Rovira and J. Veciana, Dalton Trans., 2004, 7, 1073; (c) D. Maspoch, J. Gomez-Segura, N. Domingo, D. Ruiz-Molina, K. Wurst, C. Rovira, J. Tejada and J. Veciana, Inorg. Chem., 2005, 44, 6936; (d) D. Maspoch, D. Ruiz-Molina, K. Wurst, C. Rovira and J. Veciana, Polyhedron, 2003, 22, 1929; (e) D. Maspoch, N. Domingo, D. Ruiz-Molina, K. Wurst, J. M. Hernández, F. Lloret, J. Tejada, C. Rovira and J. Veciana, Inorg. Chem., 2007, 46, 1627.
20. (a) D. Maspoch, D. Ruiz-Molina, K. Wurst, N. Domingo, M. Cavallini, F. Biscarini, J. Tejada, C. Rovira and J. Veciana, Nat. Mater., 2003, 2, 190; (b) D. Maspoch, N. Domingo, D. Ruiz-Molina, K. Wurst, J. M. Hernandez, G. Vaughan, C. Rovira, F. Lloret, J. Tejada and J. Veciana, Chem. Commun., 2005, 5035; (c) D. Maspoch, D. Ruiz-Molina, K. Wurst, C. Rovira and J. Veciana, Chem. Commun., 2004, 1164; (d) D. Maspoch, D. Ruiz-Molina and J. Veciana, J. Mater. Chem., 2004, 14, 2713.
21. O. Armet, J. Veciana, C. Rovira, J. Riera, C. Castaner, E. Molins, J. Rius, C. Miravitlles, S. Olivella and J. Brichfeus, J. Phys. Chem., 1987, 91, 5608.
22. To the best of our knowledge, only three examples have been reported in the literature so far: (a) H. K. Chae, M. Eddaoudi, J. Kim, S. I. Hauck, J. F. Hartwig, M. O'Keefe and O. M. Yaghi, J. Am. Chem. Soc., 2001, 123, 11482; (b) J. Wang, L.-L. Zheng, C.-J. Li, Y.-Z. Zeng and M.-L. Tong, Cryst. Growth Des., 2006, 6, 357; (c) S. S.-Y. Chui, A. Siu, X. Feng, Z. Y. Zhang, T. C. W. Mak and I. D. Williams, Inorg. Chem. Commun., 2001, 4, 467.
23. Calculated values in agreement with the found ones are obtained when “guest solvent molecules” are omitted. Calculated values for 1 (C₈₀H₄₈N₆O₃₆Cl₁₈Cu₆, without 2.4 THF and 4.6 H₂O): C 35.71, H 1.79, N 3.12%. Calculated values for 2(C₉₂H₇₄N₆O₃₆Cl₁₈Cu₆, without 3 EtOH and 1 H₂O): C 38.62, H 2.58, N 2.94%.
24. A. D. Kent, S. Vonmolnar, S. Gider and D. D. Awshalom, J. Appl. Phys., 1994, 76, 6656.
25. R. Bachmann, F. J. DiSalvo, Jr., T. H. Geballe, R. L. Greene, R. E. Howard, C. N. King, H. C. Kirsch, K. N. Lee, R. E. Schwall, H.-U. Thomas and R. B. Zubeck, Rev. Sci. Instrum., 1972, 43, 205.
26. Cambridge Structural Database, version 5.28, Cambridge Crystallographic Data Centre, Cambridge, UK, November 2006.
27. The number of structurally characterized magnetic MOFs is very low in comparison with the huge amount of radical ligands possessing 2, 3, 4 or even more connecting sites reported in the literature, a fact that clearly traduces the difficulty of obtaining crystalline materials with these ligands or of obtaining all the connecting sites involved in infinite bonding connectivity.
28. The first structure based on a TCNE⁻ ligand with each CN group involved in the coordination polymer formation was reported at the end of 2006 from powder X-ray diffraction data thanks to Rietveld refinements. See: K. I. Pokhodnya, M. Bonner, J.-H. Her, P. W. Stephens and J. S. Miller, J. Am. Chem. Soc., 2006, 128, 15592.
29. A TCNE-based 3-D structure showing TCNE–metal layers connected through diamagnetic TCNE dimers has also been reported. See: J.-H. Her, P.W. Stephens, K. I. Pokhodnya, M. Bonner and J. S. Miller, Angew. Chem., Int. Ed., 2007, 46, 1521.
30. F. Pointillart, C. Train, P. Herson, J. Marrot and M. Verdaguer, New J. Chem., 2007, 31, 1001.
31. (a) T. Ise, T. Ishida, D. Hashizume, F. Iwasaki and T. Nogami, Inorg. Chem., 2003, 42, 6106; (b) A. Caneschi, D. Gatteschi, P. Rey and R. Sessoli, Inorg. Chem., 1988, 27, 1756; (c) C. Benelli, A. Caneschi, D. Gatteschi, L. Pardi and P. Rey, Inorg. Chem., 1989, 28, 3230; (d) C. I. Cabello, A. Caneschi, R. L. Carlin, D. Gatteschi and P. Rey, Inorg. Chem., 1990, 29, 2582; (e) C. Benelli, A. Caneschi, D. Gatteschi, L. Pardi and P. Rey, Inorg. Chem., 1990, 29, 4223; (f) A. Caneschi, D. Gatteschi, P. Rey and R. Sessoli, Inorg. Chem., 1991, 30, 3936; (g) L. Bogani, C. Sangregorio, D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2005, 44, 5817; (h) A. Caneschi, D. Gatteschi, J.-P. Renard, P. Rey and R. Sessoli, Inorg. Chem., 1989, 28, 3314; (i) M. Minguet, D. Luneau, E. Lhotel, V. Villar, C. Paulsen, D. B. Amabilino and J. Veciana, Angew. Chem., Int. Ed., 2002, 41, 586; (j) A. Caneschi, D. Gatteschi, R. Sessoli, P. Rey and C. I. Cabello, J. Mater. Chem., 1992, 2, 1283; (k) Z.-L. Liu, Q. Zhao, S.-Q. Li, D.-Z. Lia, Z.-H. Jiang and S.-P. Yan, Inorg. Chem. Commun., 2001, 4, 322; (l) M. Handa, Y. Sayama, M. Mikuriya, R. Nukada, I. Hiromitsu and K. Kasuga, Chem. Lett., 1996, 201; (m) M. Handa, Y. Sayama, M. Mikuriya, R. Nukada, I. Hiromitsu and K. Kasuga, Bull. Chem. Soc. Jpn., 1998, 71, 119; (n) C. Benelli, A. Caneschi, D. Gatteschi, L. Pardi and P. Rey, Inorg. Chem., 1989, 28, 275; (o) T. Origuchi, W. Fujita, A. Yamaguchi, T. Okuno, K. Awaga, H. Yano and N. Wada, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 296, 281; (p) E. Ressouche, J.-X. Boucherle, B. Gillon, P. Rey and J. Schweizer, J. Am. Chem. Soc., 1993, 115, 3610; (q) H. Kumagai, Y. Hosokoshi, A. Markosyan and K. Inoue, New J. Chem., 2000, 24, 537; (r) A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio and R. Sessoli, J. Chem. Soc., Dalton Trans., 2000, 3907; (s) A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio, R. Sessoli, G. Venturi, A. Vindigni, A. Rettori, M. G. Pini and M. A. Novak, Angew. Chem., Int. Ed., 2001, 40, 1760; (t) C. Benelli, A. Caneschi, D. Gatteschi and R. Sessoli, Adv. Mater., 1992, 4, 504; (u) D. Zhang, L. Ding, W. Xu, H. Hu, D. Zhu, Y. Huang and D. Fang, Chem. Commun., 2002, 44.
32. KAVKOI isomorphic structures have been obtained with M = Eu, Gd, Tb, Ho, Er and Yb. Cell parameters, space group and experimental diffractograms are similar to those of KAVKOI (M = Dy). See: K. Bernot, L. Bogani, A. Caneschi, D. Gatteschi and R. Sessoli, J. Am. Chem. Soc., 2006, 128, 7947.
33. (a) H. Kumagai and K. Inoue, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 334, 487; (b) H. Kumagai and K. Inoue, Angew. Chem., Int. Ed., 1999, 38, 1601; (c) K. Inoue and H. Iwamura, J. Chem. Soc., Chem. Commun., 1994, 2273; (d) K. Inoue, F. Iwahori, A. F. Markosyan and H. Iwamura, Coord. Chem. Rev., 2000, 198, 219.
34. Y. Yamamoto, T. Suzuki and S. Kaizaki, J. Chem. Soc., Dalton Trans., 2001, 1566.
35. (a) L. M. Field, M. C. Moron, P. M. Lahti, F. Palacio, A. Paduan-Filho and N. F. Oliveira, Jr., Inorg. Chem., 2006, 45, 2562; (b) K. Okada, S. Beppu, K. Tanaka, M. Kuratsu, K. Furuichi, M. Kozaki, S. Suzuki, D. Shiomi, K. Sato, T. Takui, Y. Kitagawa and K. Yamaguchi, Chem. Commun., 2007, 2485.
36. K. Fegy, D. Luneau, E. Belorizky, M. Novac, J.-L. Tholence, C. Paulsen, T. Ohm and P. Rey, Inorg. Chem., 1998, 37, 4524.
37. (a) O. V. Koreneva, G. V. Romanenko, Y. G. Shvedenkov, V. N. Ikorskii and V. I. Ovcharenko, Polyhedron, 2003, 22, 2487; (b) A. Caneschi, D. Gatteschi and R. Sessoli, Inorg. Chem., 1993, 32, 4612; (c) K. Fegy, D. Luneau, T. Ohm, C. Paulsen and P. Rey, Angew. Chem., Int. Ed., 1998, 37, 1270.
38. K. Inoue and H. Iwamura, J. Am. Chem. Soc., 1994, 116, 3173.
39. K. Inoue, T. Hayamizu, H. Iwamura, D. Hashizume and Y. Ohashi, J. Am. Chem. Soc., 1996, 118, 1803.
40. F. Mathevet and D. Luneau, J. Am. Chem. Soc., 2001, 123, 7465.
41. (a) C. Janiak, Dalton Trans., 2003, 2781 and references cited therein; (b) T. K. Maji, M. Ohba and S. Kitagawa, Inorg. Chem., 2005, 44, 9225.
42. L. J. De Jongh and A. R. Miedema, Adv. Phys., 2001, 50, 947.
43. See, for instance, A. H. Morrish, The Physical Principles of Magnetism, John Wiley & Sons, Inc., New York, 1965, ch. 8.
44. A. Abragam and B. Bleaney, Electron paramagnetic resonance of transition ions, Dover, New York, 1986.
45. G. S. Rushbrooke, G. A. Baker, Jr. and P. J. Wood, in Phase Transitions and Critical Phenomena, vol. 3, ed. C. Domb and M. S. Green, Academic Press, London, 1973.
46. (a) J. C. Bonner and M. E. Fisher, Phys. Rev., 1964, 135, A640; (b) G. A. Baker, Jr., G. S. Rushbrooke and H. E. Gilbert, Phys. Rev., 1964, 135, A1272; (c) G. A. Baker, Jr., H. E. Gilbert, J. Eve and G. S. Rushbrooke, Phys. Lett. A, 1967, 25, 207.
47. K. Hirakawa, I. Yamada and Y. Kurogi, J. Phys., 1970, 32, 890.

---

Footnote

† CCDC reference numbers 659802 and 659803. For crystallographic data in CIF or other electronic format see DOI: 10.1039/b713705b

---