Quantitative analysis of carbonaceous aerosols using laser-induced breakdown spectroscopy: a study on mass loading induced plasma matrix effects†
Dibyendu
Mukherjee
and
Meng-Dawn
Cheng
*
Environmental Sciences Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA. E-mail: chengmd@ornl.gov; Tel: +1 (865) 241-5918
First published on 1st October 2007
Abstract
We present results indicating mass loading induced plasma matrix effects on the application of quantitative laser-induced breakdown spectroscopy (LIBS) for estimation of carbon contents in aerosols. An in-house flow-controlled powder-dispersion system generated carbonaceous aerosols with varying bi-modal particle size distributions (∼1 µm and 10 µm median diameters), thereby resulting in a wide mass loading range. For ease of chemical handling and to eliminate toxic effects, common talcum powder was used as our standard aerosol. Normalized atomic species concentrations of C, i.e., [C]/[Si] ratios, were calculated from atomic emission lines of C I (248 nm), Si I (252 nm), and plasma temperatures estimated from a series of Mg I lines. The results show a decrease in [C]/[Si] ratio to about 65% of the initial value as relative mass loadings increased (5.5–100%) due to the increase in number concentrations of larger sized particles (∼10 µm median diameter). As a comparison, normalized ratio of [Mg]/[Si] did not exhibit any marked change with increased mass loading. The normalized total absorption of photon flux across the C I (248 nm) spectral line indicated a strong correlation to the percentage decrease in [C]/[Si] ratio. We used an impactor with a cut-off size of around 10 µm diameter to generate mono-modal aerosolized powders (∼1 µm median diameter) that had lower relative mass loadings (0.32–0.16%). Similar LIBS analysis on these did not indicate any of the matrix effects. We conclude that for aerosol systems with widely varying mass loadings, quantitative LIBS analysis can be significantly affected by plasma matrix effects, specifically for the C I (248 nm) emission line as noticed in this study. This bears significance for the application of quantitative LIBS in the chemical characterization of all forms of carbonaceous aerosols.
Introduction
Laser induced breakdown spectroscopy (LIBS) involves the collection and processing of the spectral signature resulting from a high-irradiance pulsed laser tightly focused to generate a micro-plasma containing an analyte.1 The generic nature of the breakdown has been actively pursued as a robust and conceptually simple method for the elemental characterization of gases, solids, liquids and aerosols. A large volume of literature is available on the various applications of LIBS, beginning with the breakdown of air,2–4 to the physics of LIBS for characterizing the nature of the breakdown process itself.5 More specifically, recent works have extensively studied the LIBS breakdown processes at various levels of energy absorption and the related spatial and temporal profiles of the laser-induced plasma in air.6 Such work clearly demonstrates the relatively small, inhomogeneous and fast changing shape and dynamics of the plasma plume characteristics. In a more recent comprehensive text-book on LIBS, Lee et al.7 cover detailed discussions regarding the theory and instrumentation of LIBS, the related fundamental plasma physics and its wide range of applications.With the advent of advanced optics, high technology lasers and efficient instrumentation, LIBS has increasingly found applications for aerosol analysis and characterization since the pioneering works by Radziemski et al.8 and Essien et al.,9 and later by Hahn and Lunden.10 Hahn21 had carried out one of the earliest works on the application of LIBS for sizing and elemental analysis of discrete aerosols using a known mass concentration as the calibration scheme. One of the key areas of interest in LIBS analysis of aerosols is focused on the dynamics of plasma–particle interactions in the laser-induced plasma plume.22 A substantial amount of work in recent years has delved into details of the importance of particle location within the plasma volume and the effects of focal volume on single-particle analysis using LIBS.23,24
A vast amount of literature has reported the use of LIBS for chemical composition analysis in diverse areas like ambient aerosol monitoring,11,12 trace metals13,14 and toxic emission15–17 detections, characterization of bio-aerosols18,19 and pharmaceutical drugs.20 Owing to the ubiquitous nature of carbon in atmospheric and biological particulate matters, most of these applications involve carbonaceous aerosols in various forms and hence calls for carbon detection. Added to this, there is an increasing interest in the analytical community in detecting biohazardous particulate materials25 and carbonaceous nanoparticles26 that are not environmentally benign and have adverse health effects.27,28 Thus, we have been largely interested in investigating the ability of LIBS for quantitative analysis of carbon content in aerosols.
In recent times, there have been efforts made to use mass spectrometry29,30 and Raman spectroscopy31 for the detection and analysis of various carbon containing particles. Both of these studies had used some form of particle collection on filters that were used for subsequent analysis. Also, thermo-gravimetric analysis coupled with FT-IR studies have been carried out32 to facilitate the carbon analysis of aerosols, but the method required complicated sample and external standards preparation. Thus, there has been a growing interest in LIBS as an analytical tool due to its easy on-field deployment with minimal sample preparation requirement, thereby making it suitable for on-line real-time analysis. Added to this, a more recent study on the oxidation of aluminium nanoparticles33 had established the feasibility of LIBS for quantitative characterization via internal calibration standards.
And yet, except for few papers using LIBS for determining carbon contents in steel,34 soil analyses,35 or in corrosive gas mixtures,36 there have been minimal studies involving LIBS for real-time quantitative characterization of carbonaceous aerosols. Quantitative detection of carbon concentration in fly-ash/pulverized coal37 and single shot analysis of micrometre sized carbonaceous particles38 have been among the few showing the application of LIBS for carbon detection in aerosolized powders. Of these, the latter38 had discussed a particle size dependent phenomenon causing underestimation of the LIBS signal from glucose particles of diameters greater than 5 µm. Carranza et al.39 had suggested an upper particle size limit of 2.1 µm for effective LIBS application in the quantitative analysis of individual aerosol particles. Both of these works suggest incomplete vaporization as the likely cause for such phenomena. In this context, there have also been other efforts that hypothesized an analyte phase dependent dissociation of carbon bearing species in the LIBS plasma plume.40 They proposed hypothetical models that suggest a cut-off size of around 1 µm for solid phase aerosols to exist within the plasma volume, whereas nano-scaled analyte species in gas-phase get depleted from the plume due to outward plasma expansion. While such explanations provide a critical insight into LIBS signal variations for carbon bearing species, they still remain at the hypothetical level and require further validation through extensive experimental work, as suggested by the authors themselves. Also, none of these works clearly elucidate the role of any mass loading related plasma matrix effects in affecting the results for quantitative LIBS analysis of polydisperse carbonaceous aerosols.
Inspired by a recent study indicating mass loading induced matrix effects in laser-ablation ICP-MS,41 and based on a methodology developed for quantitative LIBS,33 we investigate similar effects in LIBS when applied to the estimation of carbon concentrations in aerosols from the C I (248 nm) emission line normalized by an internal standard such as silicon, i.e., the [C]/[Si] ratio. We used common talcum powder as the aerosol sample due to its chemical stability and non-toxic effects. The powders exhibited a bimodal distribution (median diameters of around 1 and 10 µm) with largely varying number counts and hence mass loadings that could be controlled via the flow rate of an in-house built powder-dispersion system. Different particle size distributions (both bi-modal and uni-modal) with varying mass loadings were used in the present study to demonstrate the matrix effects. Our aim was also to see if such mass loading induced matrix effects could also be related to a self-absorption phenomenon specific to the C I (248 nm) transition line. To make the case strong, we looked into the relative impacts of these effects on species like magnesium and silicon also present in the powder, which made the use of talcum powder advantageous to our present study. For all experiments performed, air was used as the background gas, for the sake of uniformity and also since most industrial and atmospheric applications involve air as the carrier gas. All data were collected at optimal gate delays for specific emission lines of the species of interest.
Experimental set-up
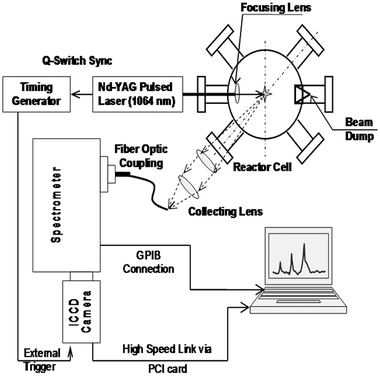
The LIBS experimental system is illustrated in the schematic in Fig. 1. A laser-induced plasma is created with a Q-switched Nd:YAG laser (λ = 1064 nm, New Wave Research, Model Tempest-10) of 10 Hz repetition rate, operated at an energy of 200 mJ per pulse and with a pulse width of 4 ns. The beam is focused with a 25 mm focal length fused silica plano-convex lens (diameter = 25 mm) to provide an estimated fluence of ∼1–1.5 × 1013 W m–2 at the focal point. The subsequent breakdown at the focal point creates a micro-plasma of 1–2 × 10–9 m3 volume within which the excitation temperatures might reach up to 10![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 000–15
000–15![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 000 K. The aerosol flow exits a 0.0635 cm tapered nozzle positioned approximately 1 mm right above the plasma breakdown point at the center of the six-arm reactor cell.
000 K. The aerosol flow exits a 0.0635 cm tapered nozzle positioned approximately 1 mm right above the plasma breakdown point at the center of the six-arm reactor cell.
 | ||
| Fig. 1 Schematics for LIBS experimental set-up. | ||
The plasma fluorescence was collected in the direction of 45° angle to the incoming focused laser beam, which was found to obtain the maximum signal intensity from the plasma plume. The light was collected and collimated by a 200 mm focal length plano-convex lens and was re-focused with a 50 mm focal length plano-convex lens to the tip of a fiber optic collector coupled to the entrance slit of a 0.5 m 1200 grooves mm–1 grating Czerny–Turner spectrometer (Acton Research Corp., Model SpectraPro 500i). The slit width for all experimental runs was kept at around 70 µm for optimal signal intensity and spectral line widths. The dispersed spectra are recorded at the exit focal plane of the spectrometer with a time-gated intensified charge-coupled device (ICCD) detector array (1024 × 1024 CCD) with an effective linear dispersion of approximately 0.014 nm per pixel (Andor Technology, Model DH534-18U-03). The time gating was synchronized with the laser Q-switch and controlled via a digital timing generator (Stanford Research Systems, Model DG535). The spectrograph was calibrated using a standard Hg vapor lamp (Ocean Optics Inc., Model HG-1) with the Hg emission lines spread over a wide range of wavelengths between 250–800 nm.
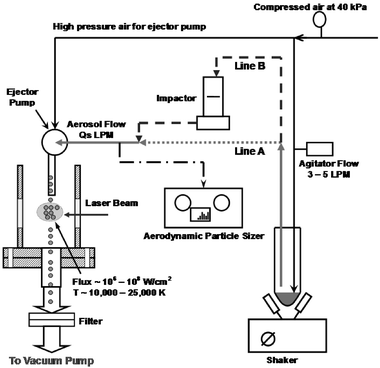
The aerosol flow set-up consisted of an in-house built dry powder dispersion system, as shown in Fig. 2. A simple single stage ejector pump created a suction vacuum level of around 4–4.7 kPa with the aid of a high positive air pressure line of 40 kPa that sucked in the powder from the tube and delivered it at atmospheric pressure into the reactor cell. A low air flow rate of around 3–5 l min–1 was used to agitate and help deliver the powder via the vacuum suction line into the center of the six-arm reactor cell, where the aerosols encounter the laser beam and undergo breakdown. The entire powder-dispersion system is placed in a shaker which prevents the powder from settling down at the bottom of the tube. The agitator flow meter was used to vary the delivery flow rate of the powder in air via the suction line marked as Qs (l min–1 of air) in Fig. 2, which in turn regulated the mass concentrations for the powder delivered into the reactor cell. All mass concentrations were calculated from the particle size distributions data collected for the 4 different flow rates by using an in-line aerodynamic particle sizer (APS) (TSI, Model 3320).
 | ||
| Fig. 2 Schematic for aerosol line set-up. | ||
For the present experiment, we used 4 different delivery flow rates of Qs = 3.5, 4.2, 4.6 and 5.6 l min–1 of air to vary the mass concentrations of powder delivered within a range such that it covered a wide range while allowing a uniform and stable delivery rate for a long enough time to allow sufficient spectral data collection. Beyond a 5.6 l min–1 delivery flow rate, the system was found to become unstable and the delivery rate was irregular. Typically for a powder mass of 4–5 g, we could run the experiments with uniform powder delivery for about 4–5 min, which was sufficient for all our data collection.
For full mass loading cases, powders with complete polydisperse size distributions as generated by the delivery system were fed into the probe volume, shown as line A in Fig. 2. For lower mass loading studies, the powder delivered by the dispersion system was passed through an in-line impactor with cut-off size of around 10 µm at 3 l min–1 of air flow before being delivered into the probe volume. This has been indicated in Fig. 2 as line B. The details for the particle size distribution and mass loading in each of these cases will be discussed in the results and discussion section.
Results and discussion
Aerosol characterization
First, we characterized the powders delivered for LIBS analysis by looking at the particle size distributions (PSD) for our aerosol set-up as described earlier. Data were collected for the 4 different delivery flow rates (Qs = 3.5, 4.2, 4.6 and 5.6 l min–1 of air) using the APS with a dilution ratio of 1:100 to avoid instrument saturation due to high particle count. For aerosols collected via line A in Fig. 2, the typical particle size distributions, as indicated in Fig. 3(a), were found to exhibit an increasingly bimodal distribution with an increase in delivery flow rate, Qs. At the lower flow rate of 3.5 l min–1 of air, the distribution indicated mainly a median aerodynamic diameter (Dp) of around 1 µm, but as the flow rate increased beyond 4.2 l min–1 there was a significant secondary median diameter of around 10 µm, which also contributed largely to the effective mass loading. The mass concentrations as calculated from the distribution shown in Fig. 3(a) were found to range between 3.19–57.85 µg mL–1 of air (approximate mass density of talc42 taken as 2.7 g mL–1). | ||
| Fig. 3 Particle size distribution plotting dN/d(logDp) versus mean aerodynamic diameter (Dp, µm) at different delivery flow rates for: (a) aerosols delivered via line A without any size cut-off; and (b) aerosols delivered via line B after size cut-off using impactor. | ||
We also collected particles via line B (Fig. 2) after passing them through an impactor, as described above. In this case, we eliminated the 10 µm diameter peak in the distribution which also contributes the most to aerosol mass loading. As can be seen in Fig. 3(b), the aerosols delivered now showed a uni-modal distribution with peak median diameter of 1 µm for the 4 different flow rates mentioned above. Also, particle number concentrations for all cases showed a noticeable decrease in Fig. 3(b), which is attributed to particle loss in the impactor. However, this has little impact on our studies since our interest is to reduce the mass loading itself. Although one could dilute the aerosol stream also to achieve this, it is impractical in our system to require an enormous volume of air flow to significantly reduce the mass loading contribution from the 10 µm diameter peak. Hence, for the ease of experimental set-up we chose to reduce the mass loading by removal off the 10 µm diameter peak contributing the most to mass loading in the particle distribution using the impactor technique. The corresponding mass concentrations were found to range between 0.094 and 0.183 µg mL–1 of air. All values for the mass concentrations corresponding to the distributions shown in Fig. 3 (a) and (b) and calculated for different flow rates are listed in Table 1. The respective statistical uncertainties are also indicated. The wide range of aerosol mass loading from the lower end of 0.094 µg mL–1 (flow rate of 3.5 l min–1) to the extreme high loading of 57.85 µg mL–1 (at a flow rate of 5.6 l min–1) can possibly be observed only in certain industrial/chemical processes generating slurries or powdered drugs and in combustion generated emissions. Our motivation here is simply to probe the limitations of LIBS in the extremely high aerosol loading studies involved in on-line monitoring of industrial processes, such as the manufacturing of drug powders.
Validation of quantitative LIBS methodology
On obtaining the particle size distributions, our goal was to look at the effect of mass loadings on subsequent quantitative chemical composition analysis using LIBS. Apart from various forms of carbonaceous materials like sodium bicarbonate, NaHCO3, polysaccharides, etc., one of the main chemical constituents of talcum powder is talc or magnesium silicate,30 Mg3Si4O10(OH)2. Thus, for validation of the LIBS methodology for quantitative analysis, we first estimated the known stoichiometry of [Si]/[Mg] as 1.33 from spectral analysis. For this, the neutral emission lines of Mg I (285.2 nm) and Si I (288.2 nm) were chosen based on their persistently strong emission signals over a wide gate delay range and their presence in a single spectral window for the spectrometer grating used. Atomic data information for these spectral lines is shown in Table 2. The temporal evolution of the S/N ratio of the Mg I and Si I emission lines collected over a delay range of 1–30 µs, shown in Fig. 4, indicated an optimal gate delay of 10 µs with a width of 20 µs. All spectral data were accumulated over 100 shots averaged for 10 different runs. | ||
| Fig. 4 Signal/noise ratio as a function of gate delay times ranging over 1–30 µs for Mg I (285.2 nm) and Si I (288.2 nm) lines indicates an optimal gate delay of 10 µs and width of 20 µs. | ||
| Species | Wavelength/nm | A ki/s–1 | g k | g i | E k/eV | E i/eV |
|---|---|---|---|---|---|---|
| Mg I | 285.213 | 4.91E + 08 | 3 | 1 | 4.345![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 802 802![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 6 6 |
0 |
| Si I | 288.158 | 1.89E + 08 | 3 | 5 | 5.082![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 345 345![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 6 6 |
0.780![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 957 957![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
Based on recent work,33 we used abundant species in the plasma as internal calibration standards for all quantitative estimations of atomic species concentrations calculated from the collected emission intensities (Iem) via the Maxwell–Boltzmann relationship:7
 | (1) |
With Mg and Si being the most abundant species in the plasma, a series of Mg I and Si I transition lines45 were collected at the optimal gate delay setting, as indicated in Table 3, for the calculation of plasma temperatures and as internal calibration standards. The choice of these lines was based on their high relative strengths, transition probabilities and their wavelengths being spread over a wide range of energy levels. Of these, the Mg I transition lines, being most stable at all gate delay ranges, were used for all plasma temperature calculations, whereas all the Mg I and Si I lines were used as the internal calibration standards.
| Species | Wavelength/nm | A ki/s–1 | g k | g i | E k/eV | E i/eV |
|---|---|---|---|---|---|---|
| Mg I | 309.298 | 3.74E + 07 | 5 | 3 | 6.718![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 987 987![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 7 7 |
2.711![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 591 591![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
| Mg I | 309.689 | 4.96E + 07 | 7 | 5 | 6.718![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 983 983![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 0 0 |
2.716![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 639 639![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 7 7 |
| Mg I | 382.936 | 8.99E + 07 | 3 | 1 | 5.945![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 917 917![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 0 0 |
2.709![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 104 104![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
| Mg I | 383.230 | 1.21E + 08 | 5 | 3 | 5.945![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 913 913![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 2 2 |
2.711![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 591 591![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
| Mg I | 383.829 | 1.61E + 08 | 7 | 5 | 5.945![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 915 915![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 4 4 |
2.716![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 639 639![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 7 7 |
| Mg I | 516.732 | 1.13E + 07 | 3 | 1 | 5.107![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 826 826![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 7 7 |
2.709![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 104 104![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
| Mg I | 517.268 | 3.37E + 07 | 3 | 3 | 5.107![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 826 826![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 7 7 |
2.711![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 591 591![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
| Mg I | 518.360 | 5.61E + 07 | 3 | 5 | 5.107![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 826 826![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 7 7 |
2.716![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 639 639![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 7 7 |
| Si I | 250.690 | 4.66E + 07 | 5 | 3 | 4.953![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 794 794![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 9 9 |
0.009![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 561 561![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 0 0 |
| Si I | 251.432 | 6.10E + 07 | 3 | 1 | 4.929![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 646 646![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
0.000![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 000 000![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 0 0 |
| Si I | 251.611 | 1.21E + 08 | 5 | 5 | 4.953![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 794 794![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 9 9 |
0.027![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 667 667![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 9 9 |
| Si I | 251.920 | 4.56E + 07 | 3 | 3 | 4.929![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 646 646![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
0.009![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 561 561![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 0 0 |
| Si I | 252.411 | 1.81E + 08 | 1 | 3 | 4.920![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 084 084![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
0.009![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 561 561![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 0 0 |
| Si I | 252.851 | 7.70E + 07 | 3 | 5 | 4.929![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 646 646![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
0.027![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 667 667![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 9 9 |
| Si I | 570.111 | 3.70E + 06 | 1 | 3 | 7.103![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 783 783![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 4 4 |
4.929![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 646 646![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
| Si I | 577.214 | 3.60E + 06 | 1 | 3 | 7.229![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 723 723![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 8 8 |
5.082![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 345 345![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 6 6 |
The internal calibration technique33 nullifies the artifacts arising due to optical/experimental set-up or time-specific plasma characteristics that affect the Mg I (285.2 nm) and Si I (288.2 nm) emission lines. For each of the 4 different aerosol flow rates (Qs, l min–1) the relative species concentrations of NMg Ii and NSi Ii, calculated from eqn (1), are normalized by respective population densities of magnesium and silicon for the series of Mg I and Si I transition lines listed in Table 3. In each case, all population densities were estimated as discussed above at the delay time of 10 µs for an identical experimental set-up. Finally, with this normalization procedure we get the estimated quantitative stoichiometric ratio of [Si]/[Mg] as:
 | (2) |
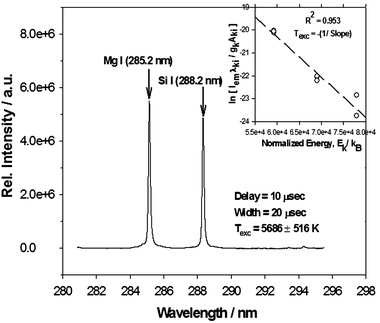 | ||
| Fig. 5 Representative atomic transition line of Mg I (285.2 nm) and Si I (288.2 nm) collected at a delay time = 10 µs and gate width = 20 µs for the case of an aerosol flow rate of 4.2 l min–1. Inset shows the corresponding linear Boltzmann plot (regression coefficient of R2 ∼0.953) for 8 Mg I transition lines (listed in Table 3) used for the calculation of Texc = –1/slope = 5686 ± 516 K at delay time = 10 µs. | ||
![Variation of [Si]/[Mg] ratio normalized to the maximum ideal ratio of [Si]/[Mg] ∼1.33 as a function of relative mass loadings (mass concentrations for different aerosol flow rates normalized by the maximum value at Qs = 5.6 l min–1 case expressed in %). The broken line represents the standard expected value of normalized [Si]/[Mg] ∼1. Error bars indicate uncertainty at 95% confidence interval.](/image/article/2008/JA/b713436n/b713436n-f6.gif) | ||
| Fig. 6 Variation of [Si]/[Mg] ratio normalized to the maximum ideal ratio of [Si]/[Mg] ∼1.33 as a function of relative mass loadings (mass concentrations for different aerosol flow rates normalized by the maximum value at Qs = 5.6 l min–1 case expressed in %). The broken line represents the standard expected value of normalized [Si]/[Mg] ∼1. Error bars indicate uncertainty at 95% confidence interval. | ||
Finally, for ease of comparison between different flow rate cases and hence mass loadings, Fig. 7 shows the [Si]/[Mg] ratios normalized to the maximum ideal stoichiometric value of 1.333 for different flow rate cases plotted as a function of relative mass loading (%). All relative mass loadings (%) in this work refer to the mass loading at any particular flow rate normalized to the maximum mass loading generated at Qs = 5.6 l min–1 for the bi-modal aerosol distribution case (Fig. 3(a)). The error bars indicate the statistical uncertainty at 95% confidence interval. The plot indicates that for varying relative mass loadings, the normalized [Si]/[Mg] ratios of the analyte shows good agreement, within the error limits, with the expected value of 1 (for ideal stoichiometry) indicated in Fig. 7 by the broken line.
 | ||
| Fig. 7 Signal/noise ratio as a function of gate delay times ranging over 700 ns–21 µs for C I (247.8 nm) line, indicating optimal gate delay of 3.5 µs at a width of 10 µs. | ||
Carbon analysis
In this section we further extended the studies to elucidate the effect of aerosol mass loadings on the quantitative LIBS analysis of carbon signals for the given aerosol system. We assume that carbonaceous materials in the talcum powder are uniformly distributed across the particle size distribution. Such an assumption holds good since the particles are mostly in the size range greater than 1 µm and the powder does not contain any semi-volatile organic compound.46 We chose a strong and commonly observed neutral emission line of C I (247.8 nm).38,45 Based on the temporal variations of C I (247.8 nm) emissions over a gate delay range of 700 ns–20 µs, as shown in Fig. 7, a gate delay of 3.5 µs and width of 10 µs was chosen as the optimal setting for all data collected. For statistical accuracy, all C I data were averaged over 10 different runs of 100 shots each.The methodology for all quantitative analysis remained the same as described in our earlier section on validation with the Mg–Si studies. Relative species concentrations were calculated from the Maxwell–Boltzmann distribution (eqn (1)) as discussed earlier and plasma excitation temperatures were determined from linear Boltzmann plots of the Mg I lines collected over 100 shots and listed in Table 3. The only variation was that in the case of LIBS analysis involving the lower aerosol mass loadings generated via the impactor (line B in Fig. 2), signal intensities for a few Mg I lines used for the Boltzmann plot had reduced significantly. Hence, 6–7 of the strongest Mg I lines giving the best linear fit were selected for the Boltzmann plot.
The spectral window with central wavelength of 248 nm shared six strong Si I neutral emission lines along with the C I (247.8 nm) line at the delay of 3.5 µs. Of these the Si I (251.6 nm) line, being persistently strong, was used as the internal calibration standard to normalize the relative species concentrations of C I (NCii). The details for the spectral data of C I (247.8 nm) and Si I (251.6 nm)45 lines can be found in Table 4. Our goal here was to investigate the variation in the normalized species concentration of carbon, i.e., NC I (247.8 nm)i/NSi I (251.6 nm)i as a function of different powder delivery flow rates and aerosol mass loadings.
| Species | Wavelength/nm | A ki/s–1 | g k | g i | E k/eV | E i/eV |
|---|---|---|---|---|---|---|
| C I | 247.856 | 3.40E + 07 | 3 | 1 | 7.684![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 766 766![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 0 0 |
2.684![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 011 011![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 0 0 |
| Si I | 251.611 | 1.21E + 08 | 5 | 5 | 4.953![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 794 794![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 9 9 |
0.027![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 667 667![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 9 9 |
At first, we carried out the LIBS analysis on polydisperse aerosols that exhibit the bi-modal distribution as shown in Fig. 3(a) and generate via the set-up described as line A (indicated in Fig. 2). Typical averaged spectral signatures for C I (247.8 nm) and Si I (251.6 nm) transition lines collected at a delay of 3.5 µs for 4 different flow rates (Qs = 3.5, 4.2, 4.6 and 5.6 l min–1) are shown in Fig. 8(a). The corresponding linear Boltzmann plots are also shown in Fig. 8(b). The linear fits in Fig. 8(b) indicate good regression coefficients (R2 ∼0.90–0.97). The plasma temperatures (Texc) and their uncertainties estimated from these linear fits are also indicated in Fig. 8(b). Their values show a sharp drop-off from around 7181 ± 995 K and 7347 ± 745 K at 3.5 and 4.2 l min–1, respectively, to about 4362 ± 617 K and 4754 ± 409 K at 4.6 and 5.6 l min–1, respectively. We also notice that although Fig. 8(a) shows an expected sharp rise in signal intensities beyond the 4.2 l min–1 case due to higher mass loadings, the Si I (251.6 nm) line intensity exhibits a much enhanced increase beyond the 4.2 l min–1 case as compared with the corresponding increase for the C I (247.8 nm) line. Such a lowering of plasma temperature itself can induce plasma matrix effects that can significantly affect the C I signal as compared with the Si I signal, especially due to the much higher upper energy states of C I (247.8 nm) (refer to Table 4).
 | ||
| Fig. 8 (a) Typical averaged LIBS spectra of C I (247.8 nm) emission lines at gate delay of 3.5 µs and width of 10 s collected for different aerosol flow rates, Qs (l min–1). All spectra have the same scale and have been shifted vertically for ease of visualization. (b) Corresponding Boltzmann plots with linear fits (R2 ∼ 0.897–0.971) generated with Mg I lines for plasma excitation temperature calculations from Texc = (–1/slope). | ||
In order to further analyze this phenomenon and its possible relation to plasma characteristics, we estimated the equivalent widths from net emitted photon flux from the plasma plume that got absorbed across the wavelength of interest, i.e., C I (247.8 nm) for the different aerosol mass loading cases. For this, we used the LIBS signals of C I (247.8 nm) and Si I (251.6 nm) lines obtained for Qs = 3.5 l min–1 as our standard case, relative to which all intensity absorptions were measured. For a given analyte, species concentration ratios at any flow rate, say x l min–1, should remain the same as they were for the 3.5 l min–1 case, i.e., [NC(x)/NSi(x)] ∼ [NC(3.5)/NSi(3.5)]. Thus, theoretically, the emission intensity ratio between C I and Si I at any flow rate case, i.e., IC(x)/ISi(x), is related to the one at the 3.5 l min–1 case through the plasma temperature corrections in the Maxwell–Boltzmann relation (eqn (1)) given as:
 | (3) |
Finally, the difference in photon flux emitted from the plume but absorbed across the wavelengths was calculated by subtracting the expected intensity from the observed values for wavelengths between 247.6 and 248.4 nm. This generated the absorption spectral data for all the flow rate cases relative to the spectral profile for the Qs = 3.5 l min–1 case used as our standard case. The equivalent width for the plasma is estimated by integrating this net photon flux or intensity absorbed across the wavelength of interest for each of the cases and normalizing them to the incident flux density I0 and given as:47
 | (4) |
We used all the spectral data collected to investigate the effect of the above-mentioned observations on the quantitative analysis of carbon for aerosol distributions in Fig. 3(a). Based on the methodology described earlier and the LIBS data collected, the species concentrations NCii and NSi Ii and, finally, the relative concentrations of carbon, i.e., NC I (247.8 nm)i/NSi I (251.6 nm)i denoted as the [C]/[Si] ratio, were calculated by using eqn. 1. For the sake of comparison to a base case, all [C]/[Si] ratios obtained for different flow rates were normalized by its maximum value at Qs = 3.5 l min–1. Fig. 9(a) shows the plot of this normalized [C]/[Si] ratio as a function of the relative mass loadings for different flow rates. It is clearly observed that the normalized [C]/[Si] ratio drops off drastically beyond the 30% mass loading corresponding to the 4.2 l min–1 case, thereby indicating an underestimation of carbon contents for higher aerosol mass loadings as compared with the values estimated at the base case of Qs = 3.5 l min–1.
![Normalized [C]/[Si] ratios (closed circles) and total absorption (open circles) expressed as 2πWλ normalized to the wavelength of C I (247.8 nm) for: (a) full bimodal particle distribution shown in Fig. 3(a); and (b) monomodal particle distribution after size cut-off using impactor as shown in Fig. 3(b).](/image/article/2008/JA/b713436n/b713436n-f9.gif) | ||
| Fig. 9 Normalized [C]/[Si] ratios (closed circles) and total absorption (open circles) expressed as 2πWλ normalized to the wavelength of C I (247.8 nm) for: (a) full bimodal particle distribution shown in Fig. 3(a); and (b) monomodal particle distribution after size cut-off using impactor as shown in Fig. 3(b). | ||
In Fig. 9(a), we also plotted the “total absorption” usually given as 2π times the equivalent width, Wλ (nm)47 calculated from eqn (4) and normalized by the central wavelength of 247.8 nm as a function of relative mass loadings (%). As can be seen from this figure, clearly there was a strong correlation between the reduction in the normalized [C]/[Si] ratio and the corresponding increase in the equivalent width expressed as the normalized total absorption for the C I (247.8 nm) transition line. Thus, we observe a phenomenon driven by mass loading induced plasma matrix effects that results in a strong self-absorption specific to the C I (247.8 nm) transition line, since the phenomenon of self-absorption of C I emissions by the carbon atoms themselves in the lower energy state due to high analyte loading in the plasma is also strongly dependent on the energy states and transition probability of the emission line under consideration. This, in turn, implies a change in the plasma emission characteristics for the C I (27.8 nm) transition line that can severely affect the quantitative estimation of carbon contents in aerosols.
To further support our argument that this phenomenon is driven by aerosol mass loading induced plasma matrix effects, we collected similar LIBS spectral data for C I (247.8 nm) and Si I (251.6 nm) lines at 3.5 µs delay for the uni-modal aerosol distributions shown earlier in Fig. 3(b) and generated via line B in Fig. 2. The relative mass loadings in the range of 0.32–0.16% in this case were much lower as compared with the earlier case study. Similar LIBS analyses for quantitative estimation of [C]/[Si] ratios were carried out from the emission lines of C I, Si I and plasma temperatures, as in the earlier case. As discussed earlier, due to the much lowered aerosol mass loadings the signal intensities of some Mg I lines were considerably reduced. Hence, in this case we used 6 of the strongest emission lines to create the Boltzmann plots, which gave good linear fits within error limits.
Also, similarly to the earlier analysis, we again calculated the equivalent width for the plasma, in this case in the form of total absorption (2πWλ) normalized by 247.8 nm. Both the normalized [C]/[Si] ratios and the normalized total absorptions (2πWλ) were plotted as a function of relative mass loadings (%) in Fig. 9(b). As can be seen from Fig. 9(b) and when compared with the plot in Fig. 9(a), within the error limits the normalized values for [C]/[Si] ratios and total absorptions did not exhibit any noticeable deviation from their respective values at the standard base case of Qs = 3.5 l min–1 study. All error bars in both Fig. 9 (a) and (b) were estimated from uncertainty analysis at the 95% confidence interval based on error propagation of statistical fluctuations on experimental parameters like the emission intensity, Iem, and plasma excitation temperatures, Texc. Here we would like to specifically point out that the uncertainty for the plasma temperature ΔTexc has an expression of the form (ΔTexc/Texc)[ΔEc – ΔESi)/kBTexc] that contributes the most to the total uncertainty in number density measurements through the error propagation. Because of this, the uncertainty in number density measurement can go up to 50–100%, which should be taken into consideration while interpreting the error bars in Fig. 9 (a) and (b).
Such non-linear reductions in the LIBS signal from aerosols have been earlier reported and attributed to an upper particle size limit for incomplete vaporization of particles.38,39 While a few earlier studies8,9 on the LIBS analysis of beryllium aerosols had suggested this particle size to be 10 µm, the latter studies38,39 had 2.1 µm and 5 µm as the particle size limit for such phenomena in the case of silica and carbonaceous particles, respectively. Based on our observations here, we feel that if these phenomena (Fig. 9 (a) and 9 (b)) were purely driven by incomplete vaporization of particles, then this should have uniformly affected all the species signals and hence we should have seen them in our Si–Mg analysis too. But this was not the case as was seen earlier. Secondly, the particle vaporization process should not affect the estimation of atomic species ratios like [Si]/[Mg] or [C]/[Si], since irrespective of the amount of material vaporized, the chemical composition of the analyte remains unchanged.
We had considered the possibility of plasma recombination processes causing the formation of molecular emission lines of CN commonly found in carbonaceous systems. There have been studies that reported such phenomena resulting in spectral interferences leading to depression in carbon signals during LIBS analysis of carbonaceous materials in air or graphite.48,49 In our study here, CN emission lines (388.3 nm, 359 nm and 421.6 nm) were collected at two extreme flow rate cases of 3.5 and 5.6 l min–1. However, we found that the relative intensities (as in signal/noise ratio) of these signals remained unchanged within the error limits.
These observations subsequently led us to explain the present phenomena of underestimation of [C]/[Si] ratios from the perspective of an aerosol mass loading induced matrix effect, as was also observed recently for ICP-MS studies by Kroslakova and Gunther.41 We are also driven to believe that this high mass loading induced matrix effect also manifests itself in the form of strong self-absorption of the emissions for the C I (247.8 nm) transition line by the high concentration of carbon atoms present in the lower energy states. In this regard, we would also like to draw attention to the upper energy states of the different C I, Mg I and Si I lines used here. During the review of this paper, we noticed that the upper energy level for C I (247.8 nm) is around 7.685 eV, whereas those for Si (288.2 nm), Si I (251.6 nm) and Mg I (285.2 nm) lines are only 4.953, 5.082 and 4.346 eV, respectively (refer to Tables 2 and 4 for the spectral details). The same holds true for all the other Si I and Mg lines. Also, the transition probability of 3.40E + 07 s–1 for the C I (247.8 nm) line is almost an order of magnitude lower than those for the Si (288.2 nm), Si I (251.6 nm) and Mg I (285.2 nm) lines, namely, 1.89E + 08, 1.21E + 08, and 4.91E + 08 s–1, respectively. This has an impact on the self-absorption phenomenon since mostly the emitted photons are self-absorbed by species atoms in the lower energy states and their number concentrations, apart from the high analyte loading itself, are also determined by the energy states and the transition probability of the particular line,44,47i.e., C I (247.8 nm) in this case under consideration. Thus, future interesting LIBS work could be extended into analyzing plasma matrix effects for atomic species with varying upper energy levels and transition probabilities to verify the phenomenon observed above.
Furthermore, earlier studies by Evans and Giglio50 on such matrix effects in ICP-MS experiments also suggested that most severe matrix effects are caused by high mass matrix elements with low ionization potentials, while light elements with high ionization potentials get most affected. This appears consistent with our aerosol under study, since silicon and magnesium happen to be the matrix elements with higher atomic weights (28.086 amu for Si and 24.305 amu for Mg), as compared with the lighter atomic mass of carbon (12.01 amu for C). On the other hand, the ionization energy (IE) for carbon is relatively high (1086.5 for the first IE number) when compared with the ionization energies of silicon and magnesium, 786.5 kJ mol–1 and 737.7 kJ mol–1, respectively. This further strengthens our suggested theory of strong aerosol mass loading induced plasma matrix effects playing a significant role in changing plasma dynamics for quantitative LIBS analysis, especially for carbon signals.
Conclusion
We conclude that besides phenomena like incomplete particle vaporization, aerosol mass loadings resulting from widely varying polydisperse distributions can cause severe plasma matrix effects affecting quantitative LIBS determination on specific elements like carbon in this case. Added to this, we also believe that such matrix effects can alter plasma dynamics, resulting in absorption phenomena specific to wavelengths like C I (247.8 nm). This in turn particularly has a serious impact on the use of LIBS for quantitative analysis of carbonaceous aerosols. The present study used a polydisperse aerosol system with a bi-modal size distribution to study the effect of a widely varying mass loading induced matrix effects on application of quantitative LIBS, specifically for carbon analysis. This is an area of interest in the LIBS community due to the various complexities in carbon studies encountered in the past, including its low detection limits and signal fluctuations. Thus, the present study bears significance for applications of LIBS towards real-time carbon analysis of aerosolized drugs, bio-aerosols and/or other forms of carbonaceous aerosols.Acknowledgements
The work was supported by the Strategic Environmental Research and Development Program of the Department of Defense (DM, MDC). This work was partially funded by Powerscope Inc., Minneapolis, through a grant from NIH/National Heart Lung and Blood Institute, Grant # 1R43HL084831-01. Oak Ridge National Laboratory is managed by UT-Battelle, LLC, for the US Department of Energy under contract DE-AC05-00OR22725. The appointment for D. M. to the ORNL Research Associates Program was jointly administered by ORNL and the Oak Ridge Institute for Science and Education. We appreciate the useful comments of the two reviewers who make this manuscript a better paper. In particular, we would like to acknowledge one of the two anonymous reviewers for suggesting the concept of upper energy states of different emission lines as one of the possible explanations for the observed results in this work. This concept has been incorporated into the expanded discussion in this revised manuscript.References
- L. J. Radziemski and D. A. Cremers, in Spectrochemical Analysis Using Laser Plasma Excitation, eds. L. J. Radziemski and D. A. Cremers, Marcel Dekker Inc., New York, 1989, pp. 6107–6118 Search PubMed.
- E. K. Damon and R. G. Thomlinson, Appl. Opt., 1963, 2, 546–547 Search PubMed.
- R. G. Meyerand, Jr and A. F. Haught, Phys. Rev. Lett., 1963, 11, 401–403 CrossRef.
- R. W. Minck, J. Appl. Phys., 1964, 35, 252–254 CrossRef.
- G. M. Weyl, ‘Physics of Laser-Induced Breakdown: An Update’, in Laser-Induced Plasmas and Applications, eds. L. J. Radziemski and D. A. Cremers, Marcel Dekker Inc., New York, 1989, pp. 5978–5985 Search PubMed.
- Y.-L. Chen, J. W. L. Lewis and C. Parigger, J. Quant. Spectrosc. Radiat. Transfer, 2000, 67, 91–103 CrossRef CAS.
- Y.-I. Lee, K. Song and J. Sneddon, in Laser Induced Breakdown Spectrometry, Nova Science Publishers, Huntington, New York, 2000 Search PubMed.
- L. J. Radziemski, T. R. Loree, D. A. Cremers and N. M. Hoffman, Anal. Chem., 1983, 55, 1246–1252 CAS.
- M. Essien, L. J. Radziemski and J. Sneddon, J. Anal. At. Spectrom., 1988, 3, 985–988 RSC.
- D. W. Hahn and M. M. Lunden, Aerosol Sci. Technol., 2000, 33, 30–48 CrossRef CAS.
- J. E. Carranza, B. T. Fisher, G. D. Yoder and D. W. Hahn, Spectrochim. Acta, Part B, 2001, 56(6), 851–864 CrossRef.
- G. A. Lithgow, A. L. Robinson and S. G. Buckley, Atmos. Environ., 2004, 38(20), 3319–3328 CrossRef CAS.
- R. E. Neuhauser, U. Panne and R. Niessner, Anal. Chim. Acta, 1999, 392(1), 47–54 CrossRef CAS.
- M.-D. Cheng, Fuel Process. Technol., 2000, 65–66, 219–229 CrossRef CAS.
- R. E. Neuhauser, U. Panne, R. Niessner and P. Wilbring, Fresenius’ J. Anal. Chem., 1999, 364(8), 720–726 CrossRef CAS.
- M. Martin and M. D. Cheng, Appl. Spectrosc., 2000, 54(9), 1279–1285 CrossRef CAS.
- M.-D. Cheng, Talanta, 2003, 61(2), 127–137 CrossRef CAS.
- J. D. Hybl, G. A. Lithgow and S. G. Buckley, Appl. Spectrosc., 2003, 57(10), 1207–1215 CrossRef CAS.
- P. B. Dixon and D. W. Hahn, Anal. Chem., 2005, 77(2), 631–638 CrossRef CAS.
- L. St-Onge, E. Kwong, M. Sabsabi and E. B. Vadas, Spectrochim. Acta, Part B, 2002, 57(7), 1131–1140 CrossRef.
- D. W. Hahn, Appl. Phys. Lett., 1998, 72(23), 2960–2962 CrossRef CAS.
- V. Hohreiter and D. W. Hahn, Anal. Chem., 2006, 78, 1509–1514 CrossRef CAS.
- G. A. Lithgow and S. G. Buckley, Spectrochim. Acta, Part B, 2005, 60, 1060–1069 CrossRef.
- G. A. Lithgow and S. G. Buckley, Appl. Phys. Lett., 2005, 87, 011501-1–3.
- D. C. S. Beddows and H. H. Telle, Spectrochim. Acta, Part B, 2005, 60(7–8), 1040–1059 CrossRef.
- P. Minutolo, G. Gambi, A. D'Alessio and S. Carlucci, Atmos. Environ., 1999, 33(17), 2725–2732 CrossRef CAS.
- T. Streibel, J. C. Weh, S. Mitschke and R. Zimmermann, Anal. Chem., 2006, 78(15), 5354–5361 CrossRef CAS.
- M. E. Birch, Analyst, 1998, 123(5), 851–857 RSC.
- R. Zimmermann, T. Ferge, M. Galli and R. Karlsson, Rapid Commun. Mass Spectrom., 2003, 17(8), 851–859 CrossRef CAS.
- R. Fisseha, M. Saurer, M. Jaggi, S. Szidat, R. T. W. Siegwolf and U. Baltensperger, Rapid Commun. Mass Spectrom., 2006, 20(15), 2343–2347 CrossRef CAS.
- S. K. Sze, N. Siddique, J. J. Sloan and R. Escribano, Atmos. Environ., 2001, 35(3), 561–568 CrossRef CAS.
- P. Fermo, A. Piazzalunga, R. Vecchi, G. Valli and M. Ceriani, Atmos. Chem. Phys., 2006, 6, 255–266 CAS.
- D. Mukherjee, A. Rai and M. R. Zachariah, J. Aerosol Sci., 2006, 37(6), 677–695 CrossRef CAS.
- J. A. Aguilera, C. Aragon and J. Campos, Appl. Spectrosc., 1992, 46(9), 1382–1387 CAS.
- D. A. Cremers, M. H. Ebinger, D. D. Breshears, P. J. Unkefer, S. A. Kammerdiener, M. J. Ferris, K. M. Catlett and J. R. Brown, J. Environ. Qual., 2001, 30(6), 2202–2206 CAS.
- L. Dudragne, P. Adam and J. Amouroux, Appl. Spectrosc., 1998, 52(10), 1321–1327 CAS.
- M. Noda, Y. Deguchi, S. Iwasaki and N. Yoshikawa, Spectrochim. Acta, Part B, 2002, 57(4), 701–709 CrossRef.
- E. Vors and L. Salmon, Anal. Bioanal. Chem., 2006, 385(2), 281–286 CrossRef CAS.
- J. E. Carranza and D. W. Hahn, Anal. Chem., 2002, 74(21), 5450–5454 CrossRef CAS.
- V. Hohreiter and D. W. Hahn, Anal. Chem., 2005, 77, 1118–1124 CrossRef CAS.
- I. Kroslakova and D. Gunther, J. Anal. At. Spectrom., 2007, 22(1), 51–62 RSC.
- Mineral Database of University of California, Berkeley: http://socrates.berkeley.edu/∼eps2/wisc/glossary2.html.
- S. Yalcin, D. R. Crosley, G. P. Smith and G. W. Faris, Appl. Phys. B: Lasers Opt., 1999, 68(1), 121–130 CrossRef.
- H. R. Griem, in Plasma Spectroscopy, McGraw-Hill Book Co., New York, 1964, ch. 6, pp. 129–152 Search PubMed.
- Yu. Ralchenko, F.-C. Jou, D. E. Kelleher, A. E. Kramida, A. Musgrove, J. Reader, W. L. Wiese and K. Olsen, NIST Atomic Spectra Database, (version 3.1.1) [Online], available from HTUhttp://physics.nist.gov/asd3UTH [2007, March 29], National Institute of Standards and Technology, Gaithersburg, MD Search PubMed.
- H. Tang, E. A. Lewis, D. J. Eatough, R. M. Burton and R. J. Faber, Atmos. Environ., 1994, 28(5), 939–947 CrossRef CAS.
- A. Thorne, U. Litzen and S. Johansson, in Spectrophysics: Principles and Applications, Springer-Verlag, Heidelberg, 1999, ch. 9, pp. 209–211 Search PubMed.
- L. St-Onge, R. Sing, S. Berchard and M. Sabsabi, Appl. Phys. A: Mater. Sci. Process., 1999, 69(suppl.), S913–S916 CAS.
- M. D. Seltzer, Appl. Spectrosc., 1998, 52(2), 195–199 CAS.
- E. H. Evans and J. J. Giglio, J. Anal. At. Spectrom., 1993, 8(1), 1–18 RSC.
Footnote |
| † The mentioning of brand names, trademarks, chemicals, instrument model numbers, and software do not represent ORNL’s or the authors’ endorsement of the commercial products. The submitted manuscript has been authored by a contractor of the US Government under contract DE-AC05-00OR22725. Accordingly, the US Government retains a non-exclusive, royalty-free license to publish or reproduce the published form of this contribution, or allow others to do so, for US Government purposes. |
| This journal is © The Royal Society of Chemistry 2008 |
