Measurement of strontium isotope ratios by MC-ICP-MS after on-line Rb–Sr ion chromatography separation

Abstract

Large volume injection ion chromatography has been evaluated for the precise and accurate measurement of strontium isotope ratios by multicollector ICP-MS. On-line coupling of the ion chromatograph to the MC-ICP-MS instrument allowed the complete separation of isobaric rubidium and other matrix elements (Ca, Mg, Na and K) and the measurement of strontium isotope ratios on flat-topped chromatographic peaks of ca. 3 minutes duration. No drift in the strontium isotope ratios was observed during strontium elution and mass bias could be corrected using either the ⁸⁶Sr/⁸⁸Sr isotope ratio (internal correction) or the observed ⁸⁷Rb/⁸⁵Rb isotope ratio (external correction) in the real samples. Typical internal precisions obtained with the selected measurement and correction conditions were about 2 times lower than the precisions obtained with continuous sample introduction for a solution 50 ng g^–1 of Sr NIST SRM 987 in HNO₃ 2% (typical standard deviations of 0.00022–0.00036 for the corrected ⁸⁷Sr/⁸⁶Sr ratio in comparison to 0.00014–0.00020 for continuous sample introduction). The method was applied to the measurement of strontium isotope ratios in cider samples and the results agreed with previous data obtained after an off-line Rb–Sr separation procedure using the Sr-Spec chelating material. The precision obtained for the real samples was poorer than previous data due to the low concentration of strontium in the measured samples. The method was also applied to other sample types (soil leachates, apple leaves and apples) to study the transference of strontium isotope ratios in the soil–tree–cider system.

---

Introduction

Highly precise and accurate isotope ratio measurements are crucial in geological, environmental and biological research. Some important applications in these fields are quantification by isotope dilution analysis, tracer studies with highly enriched stable isotopes, dating of geological samples and the determination of isotope variations in nature.¹ Strontium has four natural occurring stable isotopes, ⁸⁴Sr, ⁸⁶Sr, ⁸⁷Sr and ⁸⁸Sr, with relative natural abundance variations of 0.55–0.58%, 9.75–9.99%, 6.94–7.14% and 82.29–82.75%, respectively, according to the IUPAC.² Only ⁸⁷Sr is radiogenic and its abundance is increased by the radioactive β-decay of ⁸⁷Rb. In this sense, the ⁸⁷Sr/⁸⁶Sr isotope ratio and the Rb/Sr elemental ratio in minerals are the basis of the Rb–Sr dating method.³ Additionally, the ⁸⁷Sr/⁸⁶Sr isotope ratio has been employed as a tracer in provenance studies of archaeological,⁴ environmental,⁵ and food samples.^6,7

High precision strontium isotope ratio measurements have been routinely achieved with thermal ionisation mass spectrometry (TIMS) which can be considered as the reference technique with reported values of 0.002% RSD for ⁸⁷Sr/⁸⁶Sr isotope ratios.^8–10 Recently, multicollector (MC) ICP-MS instruments have also provided high precision strontium isotope ratio measurements (0.002% RSD)^11–13 with improved sample throughput in comparison to TIMS. For the accurate determination of Sr isotope ratios by TIMS or MC-ICP-MS, an effective separation of Rb from Sr is necessary before isotope ratio measurement in order to eliminate the isobaric interference of ⁸⁷Rb on ⁸⁷Sr. Additionally, for MC-ICP-MS instruments, matrix elements may interfere with the measurements by modifying the mass discrimination factor used for correction, particularly when external mass bias correction is used. In this sense, most pre-treatment methods employed traditionally for TIMS strontium isotope ratio measurements are now applied for MC-ICP-MS.^14–17 However, all these off-line separations need to be carried out under ultra-clean conditions in order to minimise sample contamination risks.

The on-line coupling of a chromatographic separation with a multicollector ICP-MS instrument could overcome some of the problems of the off-line separations, providing additional advantages such as improved sample throughput and the use of alternative mass bias correction procedures instead of the traditional ⁸⁶Sr/⁸⁸Sr internal correction. This coupling has been evaluated by different authors using either gas chromatography^18–20 or liquid chromatography.^21,22 The results obtained for short transient signals (typically from 3 s for GC up to about 60 s for HPLC) using MC-ICP-MS detection showed a drift in the isotope ratios during peak elution^18,20–22 together with a worsening of the isotope ratio precision up to a factor of ten²¹ in comparison to continuous sample introduction. This isotope ratio drift was reported to be due to a slow response of the Faraday cup amplifiers used in current MC-ICP-MS instruments^18,22,23 or to isotopic fractionation effects during chromatographic separations²⁰ or thermal desorption processes.²⁴ Hence, it would be advisable to develop chromatographic procedures which showed no isotopic fractionation effects and eliminate the need for fast response in the Faraday cup amplifiers. Recent work in our laboratory²⁵ on the on-line separation of Rb and Sr using ion chromatography showed that flat-topped chromatographic peaks of several minutes could be obtained using large volume injection (3 mL) and a mobile phase containing 900 mM nitric acid in the presence of 5 mM 18-crown-6 ether. The chromatographic method was optimised using a quadrupole ICP-MS instrument and showed that Rb and other matrix elements (such as Ca, Mg, K and Na) eluted at the dead volume, while Sr was strongly retained and eluted as a flat-topped chromatographic peak. From the developed chromatographic method,²⁵ it was clear that isotope fractionation effects would be absent and no fast response amplifiers would be required at the flat top of the peak.

Therefore, the aim of the present work was the evaluation of this procedure for the measurement of Sr isotope ratios using a MC-ICP-MS instrument. Evaluated samples included ciders with different geographical origin, vegetal materials and associated soil extracts within the framework of an origin authentication project using Sr isotope ratio measurements.

Experimental

Instrumentation

The separation of rubidium from strontium was performed using a Dionex DX-120 ion chromatograph (Sunnyvale, CA, USA) equipped with a cation-exchange column Dionex IonPac CS2 (4 × 250 mm) with sulfonated substrate surface and a 3 mL PFA (perfluoroalcoxy) (Omnifit, Cambridge, England) sample loop. The efficiency of the separation of strontium from other elements was evaluated using an Agilent 4500 ICP-MS instrument (Agilent Technologies, Manchester, UK).

On-line Sr isotope ratio determinations were carried out by coupling the chromatographic system to a Neptune high resolution MC-ICP-MS (Thermo Fisher Scientific, Bremen, Germany), with a forward Nier–Johnson geometry and equipped with 9 Faraday collectors along the focal plane, eight movable cups and one fixed centre channel. HPLC coupling was made through a 0.3 mm id PFA tube connected to the sample introduction system consisting of a PFA-100 microconcentric nebuliser and a cyclonic spray chamber. Sampler and skimmer Ni cones were employed. Lens settings were optimised daily for maximum analyte sensitivity. Collector positions were adjusted for peak overlap of signals in L2 (⁸⁴Sr, ⁸⁴Kr), L1 (⁸⁵Rb), C (⁸⁶Sr, ⁸⁶Kr), H1 (⁸⁷Sr, ⁸⁷Rb) and H2 (⁸⁸Sr) cups. Instrumental operating conditions and data acquisition parameters are shown in Table 1. Electronic baseline was measured before each block of measurements.

Table 1 Instrumental operating conditions and data acquisition parameters

DX-120 Chromatographic parameters
Column	Dionex Ion Pac CS2
Eluent	900 mM HNO3, 5 mM 18-crown-6 ether
Mode	isocratic
Flow rate	1 mL min^–1
Sample injection volume	3 mL

---

Neptune MC-ICP-MS parameters
Instrument settings
Rf power	1200 W
Cool gas flow	14 L min^–1 Ar
Auxiliary gas flow	0.9 L min^–1 Ar
Sample gas flow	0.935 mL min^–1 Ar
Sampler and skimmer cones	Ni
Data acquisition parameters
Collection mode	Static
Cup configuration	L4	82	Kr
	L3	83	Kr
	L2	84	Sr/Kr
	L1	85	Rb
	C	86	Sr/Kr
	H1	87	Sr/Rb
	H2	88	Sr
Resolution mode	low
Continuous sample introduction
Acquisition method	5 blocks, 10 cycles, 4.194 s integration, 3 s idle
HPLC coupling
Acquisition method	1 block, 280 cycles, 4.194 s integration, 0.5 s idle

---

Off-line Sr isotope ratio measurements on cider samples were carried out using a VG Axiom MC-ICP-MS (Thermo-Elemental, Winsford, England) according to the procedure described previously.⁷

Reagents and materials

Rubidium and strontium certified standard solutions were supplied by Merck (Merck, Darmstadt, Germany). Additionally, solid RbNO₃ (Merck, ProAnalysis) and another rubidium certified standard solution (CPI International, Amsterdam, Holland) were evaluated as a possible source of natural isotope abundance rubidium. NIST SRM 987 strontium carbonate (NIST, Gaithersburg, MD, USA), with certified isotopic composition, was used to evaluate the analytical procedure. Daily working solutions were prepared by gravimetric dilution of the stock solutions and stored in HDPE (high density polyethylene) (Brand, Wertheim, Germany) bottles. All solutions were prepared using ultra-pure water with a resistivity of 18.2 MΩ cm^–1 obtained from Milli-Q water purification system (Millipore, Bedford, MA, USA). Analytical grade nitric acid (Merck, Darmstadt, Germany) was purified by subboiling distillation using a Savillex PFA apparatus (Savillex, Minnetonka, MN, USA) and an infrared lamp.

The chromatographic eluent was freshly prepared using subboiled nitric acid and puriss. p.a. grade 18-crown-6 ether (Fluka, Buchs, Switzerland) and degassed with helium prior its use. PVDF (polyvinylidene fluoride) 0.45 µm syringe filters (Teknokroma, Barcelona, Spain) were used for sample filtration.

Subboiled nitric acid, suprapur hydrogen peroxide 30% (v/v) and suprapur hydrofluoric acid 48% (v/v) were employed for the apple and apple leaves digestion using a microwave digestion apparatus Milestone mls 1200 mega (Milestone, Leutkirch, Germany). Extraction of soils was performed using subboiled nitric acid or analytical grade ammonium nitrate. All these reagents for sample digestion or extraction were provided by Merck.

Chromatographic separation

The optimisation of the ion chromatographic separation using large volume injection is described in detail elsewhere.²⁵ In brief, Rb and Sr were chromatographically separated using 900 mM nitric acid and 5 mM 18-crown-6 ether eluent using 3 mL volume sample injection. Flat-topped chromatographic peaks, with about 3 minutes of stable plateau for on-line data acquisition at both Rb and Sr peaks, were obtained when the composition of the mobile phase was identical to the sample solution. Under those conditions, similar chromatographic separations in isocratic mode for samples and standards were also obtained. Selected chromatographic conditions are also shown in Table 1.

Sample selection

Ciders, vegetal materials (apples and apple leaves) and soils samples were analysed within this study. Cider samples, with different Rb and Sr content and originating from England and Spain, were selected to test the on-line MC-ICP-MS measurement of Sr isotope ratios. In a previous work,⁷ Sr isotope ratios were measured in other aliquots of the same cider samples by Sr-selective chromatographic extraction and continuous sample introduction MC-ICP-MS. In addition, cider, apples, apple leaves and soils were collected from a local apple production site (Lué, Asturias, Spain), in order to evaluate the Sr isotope ratio transference through a soil–apple tree–cider system.

Sample preparation

Sample preparation for cider samples consisted of a simple 1 : 10 dilution after the addition of nitric acid and 18-crown-6 ether in order to obtain the same concentration of nitric acid and 18-crown-6 ether in the sample solution as in the HPLC eluent. Apple and apple leaves samples were digested under MW irradiation and high pressure PFA bombs using ca. 3 g and 0.2 g of solid material, respectively, and 3 mL of HNO₃, 1 mL of H₂O₂ and 0.1 mL of HF. After digestion, samples were diluted to 20 g with ultra-pure water. A final dilution, 1 : 5 and 1 : 10, respectively, was performed before analysis, after the addition of nitric acid and 18-crown-6 ether to obtain the same concentration of nitric acid and 18-crown-6 ether in the sample solution as in the HPLC eluent.

Soil samples were air-dried and sieved (<300 µm). Extraction was performed by shaking, for 24 hours, 1 g of soil sample and 10 g of 1 M NH₄NO₃ or 0.2 M HNO₃. The ammonium nitrate extract represented the mobile fraction, which includes water soluble and non-specifically adsorbed metals and easily soluble metallo-organic complexes. The extracts were further diluted (1 : 10) and the concentration of nitric acid and 18-crown-6 was adjusted to match that in the eluent.

Procedural blanks were evaluated following all the sample measurement process but using ultra-pure water instead of the sample.

Results and discussion

The first attempt to measure on-line Sr isotope ratios after a chromatographic separation was described by Latkoczy et al.²⁶ for prehistoric bones and associated soil samples using a single collector sector-field ICP-MS instrument. Unfortunately, no separation of strontium from other matrix elements (such as calcium) could be accomplished and this could affect measurements using MC-ICP-MS instruments. The chromatographic procedure used here²⁵ separates strontium from other alkaline and alkaline earth elements which eluted in the dead volume. Additionally, carbon containing compounds in cider, detected as ¹³C in the quadrupole instrument, eluted well before the strontium peak. So, no mass bias effects from overlapping components should be expected.

Strontium isotope ratio measurement in transient signals

The classical approach for the determination of isotope ratios on transient signals using scanning mass spectrometers is whole peak integration followed by the calculation of the peak area ratio of the integrated peak areas obtained for the respective isotopes.²⁷ In that case, an indicator of the data precision is the external precision expressed as the reproducibility from several replicate injections of the same sample (repeated runs). However, when using multicollector instruments, internal precision can be evaluated as well during peak elution due to the simultaneous measurement process for all isotopes. Then, this internal precision can be compared with data obtained on steady-state signals.

In spite of improved precision of multicollector ICP-MS compared to scanning mass spectrometers for short transient signals, current procedures published for the on-line coupling of chromatographic separations to MC-ICP-MS instruments showed that internal precision worsened up to a factor of ten²¹ in comparison to steady-state signals and a drift on isotope ratio measurements could be observed during peak elution. In order to overcome these problems, we have developed an IC-MC-ICP-MS procedure in which the large volume injection (3 mL) led to efficient Rb and Sr separation with flat-topped peaks of about 3 min of stable plateau (for both Rb and Sr)²⁵. As an example, Fig. 1 shows the chromatogram obtained for the separation of a Rb standard (Merck) and the Sr NIST SRM 987. Under the chromatographic conditions used, Rb is practically unretained and elutes at the dead volume whereas Sr elutes at a retention time between 8–14 min. As can be observed in the chromatogram, no dilution of Rb or Sr in the mobile phase occurs, in contrast to traditional LC separations. Other matrix elements, such as Ca, Mg, Na and K, also elute at the dead volume showing an efficient separation from Sr. Flat-topped peaks provided a steady-state signal on the plateau that allowed isotope ratio measurements (point to point) during ca. 3 minutes. Under these conditions, only data points corresponding to signal intensities higher than 90% of the maximum intensity were considered, so that between 20 and 122 strontium isotope ratios can be measured on the signal plateau depending on the integration and idle time used. Therefore, isotope ratios for a single injection were determined as the mean obtained from all data points on the plateau of the flat-topped peak. The internal precision was calculated, similarly for continuous sample introduction, as the standard deviation of the isotope ratio values for each point on the plateau of the flat-topped peak within the same chromatographic run. Additionally, external precision can be evaluated by repeated injections of the same sample.

Fig. 1 Separation of a standard solution containing 50 ng g^–1 of Rb (Merck) and 50 ng g^–1 of Sr NIST SRM 987 by IC-MC-ICP-MS under the chromatographic conditions shown in Table 1.

Correction of spectral interferences

The main spectral interferences in the measurement of Sr isotope ratios are caused by ⁸⁴Kr⁺ and ⁴⁴Ca⁴⁰Ar⁺ on ⁸⁴Sr; ⁸⁶Kr⁺ on ⁸⁶Sr; ⁸⁷Rb⁺ on ⁸⁷Sr; and, ⁴⁸Ca⁴⁰Ar⁺ on ⁸⁸Sr. So, spectral interferences on the measured strontium isotope ratios can arise from the tail of the rubidium peak or from rubidium contamination in the chromatographic eluent. Additionally, the presence of krypton impurities in the argon gas could produce spectral interferences at masses 84 and 86 for strontium. Therefore, it was decided to perform a double correction of spectral interferences. First, the baseline signal (B) was computed for all measured isotopes as the average signal for the first 60 seconds after injection (before the dead volume of the chromatographic system) and it was subtracted from all subsequent data points. This correction should eliminate the contribution from Kr in the argon gas and possible Rb (and also Sr) contamination in the eluent. Then, the contribution of the tail of ⁸⁷Rb on ⁸⁷Sr could be corrected using the measured ⁸⁵Rb intensity and the experimentally measured ⁸⁷Rb/⁸⁵Rb isotope ratio or the theoretical ⁸⁷Rb/⁸⁵Rb isotope ratio from IUPAC. The experimental ⁸⁷Rb/⁸⁵Rb isotope ratio was preferred instead of the IUPAC natural abundance ratio in order to take into account mass bias effects and possible rubidium isotope fractionation effects in samples or standards. For the correction of the ⁸⁷Sr/⁸⁶Sr isotope ratio, the following equations were used:

(a) Rb baseline correction.

where S denotes the signal at the corresponding masses; and, B the average baseline calculated from the initial data points of the chromatogram. Baseline was corrected also for the other measured isotopes at masses 84, 86 and 88. After baseline correction only those isotope ratios obtained at the flat top of the chromatographic peak (>90% of peak maximum criteria) were considered for further calculations both for Rb and Sr. The average measured isotope ratio on rubidium, R^87/85_Rb, measured at the top of the Rb peak was used to correct for the tailing of the ⁸⁷Rb signal on ⁸⁷Sr.

(b) Rb tail correction.

⁸⁷Sr = S⁸⁷ – S⁸⁵R^87/85_Rb (2)

After that correction, the isotope ratios 84/86, 87/86 and 88/86 for strontium were computed at the top of the strontium peak. Fig. 2 shows the uncorrected and corrected ⁸⁷Sr/⁸⁶Sr isotope ratios (left Y-axis) together with the intensity of the chromatographic signals for mass 88 (right Y-axis) versus time. Uncorrected ⁸⁷Sr/⁸⁶Sr isotope ratios were not completely stable through the transient signal due to these spectral interferences. The correction of baseline and, mainly, the correction of the contribution of residual ⁸⁷Rb on ⁸⁷Sr, coming from a small but noticeable Rb peak tail, eliminated this problem. As can be observed, the ⁸⁷Sr/⁸⁶Sr isotope ratios corrected for baseline and Rb interference were stable throughout the peak (intensities higher than 90% of maximum). It was also observed that the contribution of Kr at masses 84 and 86 was negligible.

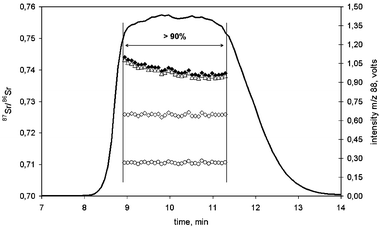Fig. 2 ⁸⁷Sr/⁸⁶Sr isotope ratios across the 50 ng g^–1 Sr NIST SRM 987 transient signal separated from Rb by IC-MC-ICP-MS: experimental data (filled diamond); corrected for baseline (open triangles); corrected for baseline and Rb interference (open diamond); and, corrected for baseline, Rb interference and mass bias (open circles). The Sr elution is represented by the ⁸⁸Sr intensity signal. Only intensity data above 90% of the maximum at mass 88 were used for isotope ratio measurements.

Mass bias correction

Several algorithms for mass bias correction have been published^28,29 including the linear, power law and exponential model.²⁹ The Russell equation³⁰ is the exponential model which is applied nowadays in the geological literature using multicollector ICP-MS instruments³¹ and provides results similar to the exponential model used in the analytical literature. In this paper, mass bias was corrected by applying the “analytical” exponential law.^28,29 Two types of correction for mass bias were evaluated: internal and external correction. For internal correction, the mass discrimination factor was evaluated using as reference value the isotope abundance ratio ⁸⁸Sr/⁸⁶Sr in the sample, assuming that this value is invariant in nature (⁸⁸Sr/⁸⁶Sr = 8.37861 ± 0.00325, certified value for the standard NIST SRM 987). This procedure can be considered as standard for Sr isotope ratio measurements. The equations used for this correction are given below:

(a) Determination of the mass bias factor.

Mass bias per mass unit, K, was calculated for internal mass bias correction according to the exponential model equation:

where R^88/86_Sr,meas is the average of the measured ⁸⁸Sr/⁸⁶Sr isotope ratio at the top of the Sr peak; R^88/86_Sr,ref is the ⁸⁸Sr/⁸⁶Sr reference isotope ratio used; and, Δm_Sr88 is the mass difference between the isotopes ⁸⁸Sr and ⁸⁶Sr.

(b) Correction of mass bias on the strontium isotope ratios.

The mass bias corrected ⁸⁷Sr/⁸⁶Sr isotope ratio, R^87/86_Sr,cor, was then calculated as:

R^87/86_Sr,cor = R^87/86_Sr,meas × exp(K × Δm_Sr87) (4)

where R^87/86_Sr,meas is the average measured ⁸⁷Sr/⁸⁶Sr isotope ratio at the top of the Sr peak and Δm_Sr87 is the mass difference between the isotopes ⁸⁷Sr and ⁸⁶Sr. Fig. 2 shows also the final ⁸⁷Sr/⁸⁶Sr isotope ratios after correction for mass bias using the internal correction method. As can be observed, the final corrected ratio is very close to the certified value for the ⁸⁷Sr/⁸⁶Sr ratio of 0.71034.

Additionally, the on-line coupling of the chromatographic separation to the MC-ICP-MS instrument allowed the measurement of all three Sr isotope ratios and the ⁸⁷Rb/⁸⁵Rb isotope ratio in the sample within the same chromatographic run. The measured ⁸⁷Rb/⁸⁵Rb isotope ratio could be used to calculate the mass discrimination factor, acting as a reference value for external mass bias correction of Sr isotope ratios assuming that the variability of the ⁸⁵Rb/⁸⁷Rb value in nature (⁸⁷Rb/⁸⁵Rb = 0.38562 ± 0.00017, obtained from the IUPAC Table 2) is negligible. Recently, Nebel et al.³² showed that no natural variations in the Rb isotope composition of terrestrial samples could be observed within ±0.5 δ⁸⁷Rb. Therefore, this alternative procedure will be also evaluated for the real samples.

Table 2 Obtained ⁸⁷Sr/⁸⁶Sr isotope ratio for a standard solution containing 50 ng g^–1 of Sr NIST SRM 987 and 50 ng g^–1 Rb after on-line IC separation and MC-ICP-MS measurement with different integration and idle times. Uncertainties are expressed as 95% confidence interval of the mean (2s/√n)

Integration time/s	0.1 s idle time			3 s idle time
	^87Sr/^86Sr	s^a	n^b	^87Sr/^86Sr	s^a	n^b
a Standard deviation of the corrected ^87Sr/^86Sr isotope ratios across the flat-topped peak.b Number of acquisition points considered for the calculation of the Sr isotope ratios (intensities for ^88Sr > 90% of maximum).
0.131	—	—	—	0.71047 ± 0.00053	0.00167	39
1.049	0.71036 ± 0.00013	0.00071	122	0.71034 ± 0.00032	0.00094	35
2.097	0.71033 ± 0.00014	0.00057	69	0.71060 ± 0.00018	0.00047	28
4.194	0.71044 ± 0.00011	0.00030	30	0.71045 ± 0.00018	0.00041	20

---

Measurement conditions: integration and idle time

Data acquisition parameters for measurement on transient signals have to be optimised considering the time profile of analyte signal. In Gaussian chromatographic peaks, signal intensity varies significantly along the transient signal so integration time for short transient signals should be shorter than for steady-state signals, although it implies lower precision.²¹ In our study, data acquisition parameters (integration and idle time) were optimised to obtain a stable isotope ratio in the ca. 3 minutes plateau of the flat-topped peak with maximum internal precision for the measurement of Sr isotope ratios.

Although precision of Sr isotope ratios was dependent on analyte concentration, concentrations of 50 ng g^–1 Rb (Merck) and 50 ng g^–1 Sr NIST SRM 987 were selected as representative of typical contents of these elements in the evaluated samples. Strontium isotope ratios and internal precision were evaluated by on-line IC-MC-ICP-MS for integration times of 0.13, 1, 2.1 and 4.2 s, and for idle times of 0.1 and 3 s, the minimum and recommended value for dynamic measurements, respectively, with a standard solution containing Rb (Merck) and Sr NIST SRM 987. The idle time affects the total acquisition time of the method and the number of points per acquisition run, even though it is not critical for static measurements by MC-ICP-MS, as is the case of our measurements. Table 2 shows the obtained results. As can be observed, after spectral interferences and internal mass bias correction using ⁸⁸Sr/⁸⁶Sr, all ⁸⁷Sr/⁸⁶Sr isotope ratio values and their uncertainties overlapped with the certified interval given in the certificate of the reference material NIST SRM 987 (⁸⁷Sr/⁸⁶Sr = 0.71034 ± 0.00026, 95% confidence). However, internal precision for the ⁸⁷Sr/⁸⁶Sr isotope ratio was improved for longer integration times, between 0.13 and 4.2 s, and at constant idle time. As reported in Table 2, the standard deviation (s) of data points on the plateau of the flat-topped peak decreased for increasing integration times, as well as the standard deviation on the mean (2s/√n) even though the reduced number of data points. For a fixed integration time, standard deviation was similar for both (0.1 and 3 s) idle times, although standard deviation on the mean was lower for 0.1 s idle since more data points were obtained. Nevertheless, signal fluctuations were observed for the short idle time of 0.1 s which affected the correction procedures applied. This effect was not observed at 0.5 s idle time, so an integration time of 4.2 s and idle time of 0.5 s were selected for precise isotope ratio measurements and stable signal in the plateau of the flat-topped peak.

Under the selected data acquisition parameters, between 25 and 30 data points, which showed intensities above 90% of the maximum, were obtained in all replicate chromatograms measured for the standard solution containing Rb and Sr NIST SRM 987. Typical internal precisions obtained with the selected measurement and correction conditions were about 2 times lower than the precisions obtained with continuous sample introduction for a solution of the same concentration of Sr NIST SRM 987 in HNO₃ 2% (typical standard deviations of 0.00022–0.00036 for the corrected ⁸⁷Sr/⁸⁶Sr ratio in comparison to 0.00014–0.00020 for continuous sample introduction). It should be noted that the integration time used for steady-state signals from continuous sample introduction was 4.2 s integration and 3 s idle times, measuring 50 data points per acquisition run.

Uncertainty propagation

The measurement uncertainty was propagated considering all corrections performed to the raw data (eqn (1) to (4)) using the spreadsheet procedure described by Kragten.^33,34 This procedure takes into account all stated uncertainties in the measurement method calculating, in a stepwise form, the uncertainty in the Sr isotope ratios originating from the uncertainty in all parameters used for the corrections and including the experimental uncertainty in the measurement procedure itself. The contribution of the uncertainty of all corrections to the total uncertainty of the ⁸⁷Sr/⁸⁶Sr isotope ratio is summarised in Table 3 for the chromatogram shown in Fig. 1. As can be observed, nine parameters were considered for uncertainty propagation, the five baseline intensities (in volts) at masses 84, 85, 86, 87 and 88 measured after injection, the experimental ⁸⁷Rb/⁸⁵Rb isotope ratio used for the correction of the tail of the Rb peak, the experimental uncertainty of the measured ⁸⁷Sr/⁸⁶Sr ratio and the uncertainties in the measured and reference ⁸⁸Sr/⁸⁶Sr ratio used for mass bias correction. The final combined uncertainty increased from 0.000228 (experimental standard deviation of the ⁸⁷Sr/⁸⁶Sr isotope ratio) to 0.00037. Please note that all values and uncertainties are given with 6 significant figures in Table 3 except for the final isotope ratio and uncertainty which is given with only 5 significant digits. Kragten’s method allows also establishing the relative importance of all uncertainty sources. In this case, it was observed that the baseline correction for rubidium (85B and 87B) accounted for ca. 50% of the total variance while the experimental uncertainty contributed only 38% to the total variance. Mass bias correction using ⁸⁸Sr/⁸⁶Sr does not contribute significantly to the total variance.

Table 3 Propagation of uncertainty using Kragten’s method for the ⁸⁷Sr/⁸⁶Sr isotope ratio using internal mass bias correction (⁸⁸Sr/⁸⁶Sr as reference)

Uncertainty (s)		0.000029	0.000049	0.000032	0.000035	0.000058	0.000070	0.000228	0.00185	0.00162
Mean value		84B	85B	86B	87B	88B	^87Rb/^85Rb	^87Sr/^86Sr	^88Sr/^86Sr	^88Sr/^86Sr ref
84B (V)	0.000105	0.000134	0.000105	0.000105	0.000105	0.000105	0.000105	0.000105	0.000105	0.000105
85B (V)	0.004717	0.004717	0.004766	0.004717	0.004717	0.004717	0.004717	0.004717	0.004717	0.004717
86B (V)	0.000591	0.000591	0.000591	0.000623	0.000591	0.000591	0.000591	0.000591	0.000591	0.000591
87B (V)	0.002238	0.002238	0.002238	0.002238	0.002273	0.002238	0.002238	0.002238	0.002238	0.002238
88B (V)	0.004906	0.004906	0.004906	0.004906	0.004906	0.004963	0.004906	0.004906	0.004906	0.004906
^87Rb/^85Rb	0.403374	0.403374	0.403374	0.403374	0.403374	0.403374	0.403444	0.403374	0.403374	0.403374
^87Sr/^86Sr	0.726030	0.726030	0.726030	0.726030	0.726030	0.726030	0.726030	0.726258	0.726030	0.726030
^88Sr/^86Sr	8.74701	8.74701	8.74701	8.74701	8.74701	8.74701	8.74701	8.74701	8.74886	8.74701
^88Sr/^86Sr ref	8.37861	8.37861	8.37861	8.37861	8.37861	8.37861	8.37861	8.37861	8.37861	8.38023
^87Sr/^86Sr cor	0.71058	0.710576	0.710706	0.710652	0.710352	0.710592	0.710575	0.710805	0.710501	0.710645
UR	0.00037	0.00	1.67 × 10^–8	5.66 × 10^–9	5.04 × 10^–8	2.44 × 10^–10	3.00 × 10^–12	5.19 × 10^–8	5.67 × 10^–9	4.75 × 10^–9
Contribution (%)		0.0	12.4	4.2	37.2	0.2	0.0	38.4	4.2	3.5

---

Comparison of internal and external mass bias correction

As previously mentioned, two different methods for mass bias correction were evaluated: internal mass bias correction using the isotope ratio ⁸⁸Sr/⁸⁶Sr in the sample as the reference value (eqn (3)) and, external mass bias correction using as reference value the ⁸⁷Rb/⁸⁵Rb isotope ratio in the sample measured within the same chromatographic run. For external mass bias correction the equation used was: where R^87/85_Rb,meas is the average of the measured ⁸⁷Rb/⁸⁵Rb isotope ratio at the top of the Rb peak, R^87/85_Rb,ref is the ⁸⁷Rb/⁸⁵Rb IUPAC reference isotope ratio used and Δm_Rb is the mass difference between the isotopes ⁸⁷Rb and ⁸⁵Rb. The advantage of external mass bias correction is that the traditional reference ratio ⁸⁸Sr/⁸⁶Sr can be corrected as well and compared with the reference values.

In the first experiments, using the Merck Rb standard and the NIST SRM 987, Sr isotope ratio values obtained by external mass bias correction were significantly lower than those obtained by internal mass bias correction and well below the certified interval given for the reference material NIST SRM 987. However, when cider samples were injected, the values obtained for ⁸⁷Sr/⁸⁶Sr using the internal correction were in agreement with those values obtained using external Rb correction. This disagreement was initially attributed to isotopic effects in the Merck standard which would be absent for the real samples. As no Rb isotopically certified standard was available, it was decided to use the NIST SRM 987 as reference to calculate the isotopic composition of different Rb standards present in the laboratory. In this way, two different lots of Merck certified Rb standard, a solid RbNO₃ standard, and a CPI certified Rb standard were measured by MC-ICP-MS under continuous nebulisation using the NIST SRM 987 standard as reference for mass bias correction. The results obtained, compared with the published IUPAC values, are given in Fig. 3. It was observed that the mass bias corrected ⁸⁷Rb/⁸⁵Rb isotope ratio value for all Merck Rb standards was, on average, 0.38649 ± 0.00008 which was higher than the IUPAC value of 0.38562 ± 0.00017. Additionally, Rb fractionation effects on the chromatographic procedure used here were rejected since the obtained value for the ⁸⁷Rb/⁸⁵Rb isotope ratio after the chromatographic separation of the Merck standard and the NIST SRM 987 Sr reference material, calculated using the NIST as reference, was 0.38639 ± 0.00008, in agreement with the value obtained by continuous nebulisation. Finally, cider samples injected under the same conditions as the Merck standard, but using the found ⁸⁸Sr/⁸⁶Sr as reference for mass bias correction, gave rubidium isotope ratios of 0.38557 ± 0.00018, in agreement with the IUPAC values. Such deviation of ⁸⁷Rb/⁸⁵Rb isotope ratio from IUPAC value can be attributed to possible fractionation effects during the process of purification of the Rb standard. Although other publications on measurement of Rb isotope ratios by MC-ICP-MS^32,35 did not provide isotopic data on non-certified Rb standard solutions, fractionation of Rb isotopes in cation exchange chromatography was already described on the literature.³⁶

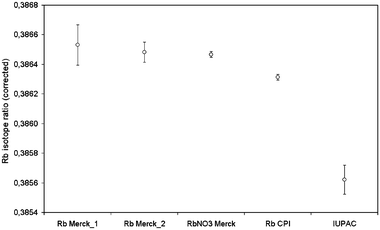Fig. 3 ⁸⁷Rb/⁸⁵Rb isotope ratios measured by continuous nebulisation of different rubidium standards at 200 ppb levels (n = 3) using the NIST SRM 987 for mass bias correction (ratio ⁸⁸Sr/⁸⁶Sr). Uncertainties indicate standard deviation of the triplicate measurement.

Strontium isotope ratios and their propagated uncertainty was evaluated for six consecutive injections of a standard solution containing 50 ng g^–1 Sr NIST SRM 987 and 50 ng g^–1 Rb (Merck). Both internal and external mass bias correction are given in Table 4. The equation used to calculate the standard uncertainty of the average was:

where s_i are the standard deviations obtained for each measurement divided by the square root of the number of measurements (in this case 25–30 measurements on the flat top peak) and n = 6. As can be observed, for internal correction, the average values obtained by the IC-MC-ICP-MS hyphenated procedure were 0.71054 ± 0.00008. For external mass bias correction, the measurement uncertainty was calculated in the same way but considering the measured ⁸⁷Rb/⁸⁵Rb (0.38649) isotope ratio as reference. As can be also observed, the propagated uncertainty on the corrected ⁸⁷Sr/⁸⁶Sr isotope ratio was similar to that obtained using internal mass bias correction. The deviation from the certified values for external correction was always below 0.05% for both the 87/86 and the 88/86 ratios.

Table 4 Comparison of internally and externally mass bias corrected Sr isotope ratios and their uncertainties, obtained for a standard solution containing 50 ng g^–1 Sr NIST SRM 987 and 50 ng g^–1 Rb using IC separation coupled to MC-ICP-MS detection

Injection number	Internally corrected ^87Sr/^86Sr	UR	Externally corrected ^87Sr/^86Sr	UR	Externally corrected ^88Sr/^86Sr	UR
1	0.71058	0.00037	0.71066	0.00037	8.3807	0.0034
2	0.71053	0.00041	0.71059	0.00041	8.3799	0.0035
3	0.71052	0.00033	0.71066	0.00033	8.3818	0.0028
4	0.71057	0.00043	0.71067	0.00043	8.3811	0.0043
5	0.71050	0.00030	0.71060	0.00031	8.3808	0.0032
6	0.71053	0.00042	0.71073	0.00042	8.3833	0.0037
Average	0.71054	0.00008	0.71065	0.00009	8.3812	0.0014
Certified	0.71034	0.00026	0.71034	0.00026	8.3786	0.0033
Error (%)	+0.028		+0.044		+0.031

---

Strontium isotope ratios in ciders

In order to test the analytical performance of the hyphenated procedure, the ⁸⁷Sr/⁸⁶Sr isotope ratios obtained using the developed on-line IC-MC-ICP-MS procedure were compared with values obtained for the same cider samples measured in a previous work by off-line Sr-selective chromatographic extraction and continuous sample introduction MC-ICP-MS.⁷

Five cider samples originating from England and Spain, and containing different Rb and Sr concentrations, were selected to evaluate the analytical procedure. The obtained ⁸⁷Sr/⁸⁶Sr isotope ratios after both off-line⁷ and on-line separation are shown in Table 5. For on-line separation both internal correction, using the ⁸⁸Sr/⁸⁶Sr ratio, and external correction, using the ⁸⁷Rb/⁸⁵Rb ratio, are given. The isotope ratio uncertainties for on-line separation were calculated using the Kragten’s method as described before. However, for the off-line separation only the contribution of the ⁸⁸Sr/⁸⁶Sr ratio for internal correction was taken into account for the propagation of the uncertainties.⁷

Table 5 Comparison of the measured ⁸⁷Sr/⁸⁶Sr isotope ratios in cider samples by IC coupled to MC-ICP-MS (Neptune, Thermo Scientific) and by Sr-selective chromatographic extraction and continuous sample introduction MC-ICP-MS (VG Axiom)

Sample	Sr (ppb)^a	Rb (ppb)^a	IC-MC-ICP-MS (Neptune)				Continuous sample introduction MC-ICP-MS (Axiom)
			Internally corrected ^87Sr/^86Sr	UR	Externally corrected ^87Sr/^86Sr	UR	Internally corrected ^87Sr/^86Sr	UR
a Concentrations in the measured solution after 1:10 dilution of the samples.
England
KX	36	47	0.7098	0.0006	0.7096	0.0006	0.70951	0.00007
Gaymer’s Olde	33	13	0.7099	0.0005	0.7097	0.0005	0.70951	0.00007
Spain (Asturias)
M. Busto	9.8	74	0.7088	0.0016	0.7086	0.0018	0.70899	0.00007
DOP7	7.8	116	0.7131	0.0024	0.7130	0.0024	0.71253	0.00008
Fugitivo	6.6	34	0.7097	0.0011	0.7097	0.0011	0.70941	0.00007

---

As can be observed, English samples contained a higher concentration of strontium which resulted in lower isotope ratio uncertainties in comparison with Spanish ciders. On the other hand, no difference could be observed between internal and external correction both in terms of the measured isotope ratios and their uncertainties indicating that matrix effects on the mass bias measured for rubidium were not present even as rubidium eluted at the dead volumne of the column. The levels of rubidium in all samples were high enough to allow external mass bias correction. Finally, the observed values for on-line separation were in agreement with those obtained previously by off-line separation. The most striking difference between both procedures was the lower uncertainties of the off-line procedure. This is due to the large difference in concentration of strontium in the measured solutions (between 20 and 200 times higher for the off-line procedure) after the off-line Sr-Spec preconcentration. It is clear then that the main disadvantage of the propossed procedure in comparison with the off-line separation of Rb and Sr is the lack of any suitable preconcentration procedure for samples containing low Sr concentrations. As can be observed in Table 4, similar uncertainties can be obtained after repeated injections of the sample.

Strontium isotope ratios in other samples

The on-line MC-ICP-MS measurement of Sr isotope ratios was evaluated on different types of samples, including ciders, apples, apple leaves and soils coming from the same production site, in order to: (i) test the applicability of this hyphenated procedure to the measurement of high precision strontium isotope ratio in acid sample solutions resulting from acid digestion of solid or liquid samples; and, (ii) evaluate the ⁸⁷Sr/⁸⁶Sr isotope ratios through the soil–tree–apple–cider system within the framework of an origin authentication project using Sr isotope ratio measurements. Example chromatograms of these different sample types are shown in Fig. 4. Please note that the separation of rubidium and strontium changes slightly depending on the matrix of the sample but adequate separations were obtained in all cases.

Fig. 4 Chromatograms obtained under the selected chromatographic conditions for real samples: (a) cider, (b) apples, and (c) soil extract in ammonium nitrate.

The obtained ⁸⁷Sr/⁸⁶Sr isotope ratios for cider, apples, apple leaves and soil extracts from the same production site are shown in Table 6. For all samples, internal correction is compared with external correction both in terms of ⁸⁷Sr/⁸⁶Sr isotope ratios and their uncertainties. For cider and apples, the concentration of strontium in the measured solutions was always below 5 ppb, and that explains the high uncertainty obtained. For apple leaves and soil extracts the strontium concentrations were one order of magnitude higher and, therefore, the uncertainties decreased considerably. For external correction the uncertainties were similar to those found by internal correction except for those samples were the concentration of rubidium was very low as for the nitric acid extract as can be observed in Table 6.

Table 6 ⁸⁷Sr/⁸⁶Sr isotope ratios, internally and externally corrected, after on line IC-MC-ICP-MS determination in cider, apples, apple leaves and soil extracts samples originating from the same production site

Sample	Sr (ppb)^a	Rb (ppb)^a	Internally corrected ^87Sr/^86Sr	UR	Externally corrected ^87Sr/^86Sr	UR
a Concentrations in the measured solution after 1 : 10 dilution of the samples.
Cider	2.9	75	0.7085	0.0053	0.7074	0.0054
Apples	3.9	64	0.7101	0.0090	0.7089	0.0092
Apple leaves	17	6.3	0.7105	0.0012	0.7097	0.0011
Soil (HNO3 extract)	41	1.9	0.7109	0.0003	0.7106	0.0024
Soil (NH4NO3 extract)	48	4.7	0.7107	0.0011	0.7086	0.0014

---

Conclusions

A procedure for the on-line separation of rubidium and strontium by ion chromatography coupled to multicollector ICP-MS was developed. The procedure allowed a complete separation of strontium from isobaric and matrix elements, and strontium isotope ratios could be measured in a flat-topped chromatographic peaks of about three minutes duration. A complete uncertainty study was carried out using Kragten’s method for uncertainty propagation showing that baseline correction from residual ⁸⁵Rb and ⁸⁷Rb was the main source of uncertainty. Both internal (⁸⁸Sr/⁸⁶Sr) and external (⁸⁷Rb/⁸⁵Rb) mass bias correction were evaluated and results indicated that both correction methods were equivalent for real samples. It was also observed that the isotopic composition of rubidium analytical standards is different from the natural ratio.

Using this on-line methodology the uncertainties in the ⁸⁷Sr/⁸⁶Sr isotope ratios depended strongly on the concentration of strontium in the samples. In comparison with off-line procedures, where preconcentration factors up to 20 are common, cider samples have to be diluted ten times resulting in much poorer uncertainties. Typical internal precisions obtained with the selected measurement and correction conditions were only 2 times lower than the precisions obtained with continuous sample introduction for a solution of the same concentration of Sr NIST SRM 987. It is clear that samples containing much higher strontium concentrations, in comparison to those measured in this work, will provide comparable isotope ratio uncertainties to off-line procedures with simplified sample preparation. The application of this procedure to other sample types, such as mineral digests and ancient bones is under progress in our laboratory.

Acknowledgements

We acknowledge Jorge Millos (CACTI, University of Vigo) for his collaboration during the measurements on the Neptune MC-ICP-MS. S. García-Ruiz is grateful to the Spanish Ministry of Education and Science (MEC) for her pre-doctoral fellowship. M. Moldovan thanks to the European Social Fund and the MEC for the funding through the “Juan de la Cierva Programme”. Financial support was granted through the CICYT (BQU2003-03438 project) and a Marie Curie European Reintegration Grant (contract UE-05-MERG-CT-6-2005-014874).

References

1. J. S. Becker, J. Anal. At. Spectrom., 2005, 20, 1173–1184.
2. J. K. Bohlke, J. R. de Laeter, P. de Bievre, H. Hidaka, H. S. Peiser, K. J. R. Rosman and P. D. P. Taylor, J. Phys. Chem. Ref. Data, 2005, 34, 57–67.
3. G. Faure, in Principles of Isotope Geology, John Wiley & Sons, New York, 1986, pp. 117–140.
4. T. Prohaska, C. Latkoczy, G. Schultheis, M. Teschler-Nicola and G. Stingeder, J. Anal. At. Spectrom., 2002, 17, 887–891.
5. P. Négrel and S. Roy, Appl. Geochem., 1998, 13, 941–952.
6. G. Fortunato, K. Mumic, S. Wunderli, L. Pillonel, J. O. Bosset and G. Gremaud, J. Anal. At. Spectrom., 2004, 19, 227–234.
7. S. García-Ruiz, M. Moldovan, G. Fortunato, S. Wunderli and J. I. García Alonso, Anal. Chim. Acta, 2007, 590, 55–66.
8. B. W. Stewart, R. C. Capo and O. A. Chadwick, Geochim. Cosmochim. Acta, 2001, 65, 1087–1099.
9. A. Sillen, G. Hall, S. Richardson and R. Armstrong, Geochim. Cosmochim. Acta, 1998, 62, 2463–2473.
10. A. Rossmann, G. Haberhauer, S. Hölzl, P. Horn, F. Pichlmayer and S. Voerkelius, Eur. Food Res. Technol., 2000, 211, 32–40.
11. L. Balcaen, I. de Schrijver, L. Moens and F. Vanhaecke, Int. J. Mass Spectrom., 2005, 242, 251–255.
12. S. Ehrlich, I. Gavrieli, L.-B. Dor and L. Halicz, J. Anal. At. Spectrom., 2001, 16, 1389–1392.
13. M. Barbaste, K. Robinson, S. Guilfoyle, B. Medina and R. Lobinski, J. Anal. At. Spectrom., 2002, 17, 135–137.
14. F. Vanhaecke, G. de Wannemacker, L. Moens and J. Hertogen, J. Anal. At. Spectrom., 1999, 14, 1691–1696.
15. C. M. Almeida and M. T. S. D. Vasconcelos, J. Anal. At. Spectrom., 2001, 16, 607–611.
16. E. P. Horwitz, M. L. Dietz and D. E. Fischer, Anal. Chem., 1991, 63, 522–525.
17. C. Pin and C. Bassin, Anal. Chim. Acta, 1992, 269, 249–255.
18. E. M. Krupp and O. F. X. Donard, Int. J. Mass Spectrom., 2005, 242, 233–242.
19. E. M. Krupp, C. Pécheyran, S. Meffan-Main and O. F. X. Donard, Anal. Bioanal. Chem., 2004, 378, 250–255.
20. S. Wehmeier, R. Ellam and J. Feldmann, J. Anal. At. Spectrom., 2003, 18, 1001–1007.
21. I. Günther-Leopold, B. Wernli, Z. Kopajtic and D. Günther, Anal. Bioanal. Chem., 2004, 378, 241–249.
22. I. Günther-Leopold, J. Kobler Waldis, B. Wernli and Z. Kopajtic, Int. J. Mass Spectrom., 2005, 242, 197–202.
23. T. Hirata, Y. Hayano and T. Ohno, J. Anal. At. Spectrom., 2003, 18, 1283–1288.
24. R. D. Evans, H. Hintelmann and P. J. Dillon, J. Anal. At. Spectrom., 2001, 16, 1064–1069.
25. S. García-Ruiz, M. Moldovan and J. I. García Alonso, J. Chromatogr., A, 2007, 1149, 274–281.
26. C. Latkoczy, T. Prohaska, M. Watkins, M. Teschler-Nicola and G. Stingeder, J. Anal. At. Spectrom., 2001, 16, 806–811.
27. P. Rodríguez-González, J. M. Marchante-Gayón, J. I. García Alonso and A. Sanz-Medel, Spectrochim. Acta, Part B, 2005, 60, 151–207.
28. P. K. Appelblad and D. C. Baxter, J. Anal. At. Spectrom., 2000, 15, 557.
29. C. P. Ingle, B. L. Sharp, M. S. A. Horstwood, R. R. Parrish and D. J. Lewis, J. Anal. At. Spectrom., 2003, 18, 219.
30. W. A. Russell, D. A. Papantastassious and T. A. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075.
31. R. Schoenberg and F. Von Blanckenburg, Int. J. Mass Spectrom., 2005, 242, 257.
32. O. Nebel, K. Mezger, E. E. Scherer and C. Münker, Int. J. Mass Spectrom., 2005, 246, 10–18.
33. J. Kragten, Analyst, 1994, 119, 2161–2166.
34. Quantifying Uncertainty in Analytical Measurements, ed. S. Ellison, M. Rosslein and A. Williams, Eurachem/CITAC, 2000.
35. T. Waight, J. Baker and B. Willigers, Chem. Geol., 2002, 186, 99–116.
36. M. Hosoe, T. Oi, K. Kawada and H. Kakihana, J. Chromatogr., A, 1988, 438, 225–231.

---