A comparative study of the hydrated morphologies of perfluorosulfonic acid fuel cell membranes with mesoscopic simulations
Received
6th June 2008
, Accepted 25th June 2008
First published on 23rd July 2008
Abstract
The hydrated morphology of Nafion, the short-side-chain (SSC), and 3M perfluorosulfonic acid (PFSA) fuel cell membranes have been investigated through dissipative particle dynamics (DPD) simulations as a function of ionomer equivalent weight (EW) and degree of hydration. Coarse-grained mesoscale models were constructed by dividing each hydrated ionomer into components consisting of: a common polytetrafluoroethylene backbone bead, ionomer specific backbone beads, a terminal side chain bead, and a bead consisting of a cluster of six water molecules. Flory–Huggins χ-parameters describing the interactions between the various DPD particles were calculated. Equilibrated morphologies were determined for the SSC and 3M PFSA membranes both at EW's of 678 and 978, and Nafion with an EW of 1244. The hydration level was varied in each system with water contents corresponding to 5, 7, 9, 11, and 16 H2O/SO3H. The high EW ionomers exhibit significantly greater dispersion of the water regions than the low EW membranes. Water contour plots reveal that as the hydration level is increased, the isolated water clusters present at the lower water contents increase in size eventually forming continuous regions resembling channels or pores particularly at a hydration of 16 H2O/SO3H. The DPD simulations reveal differences in the hydrated morphology when only the side chain length was altered and indicate that the 3MPFSA ionomer exhibits much larger clusters of water when compared to the SSC ionomer at the same EW and water content above 9 H2O/SO3H. The average size of the clusters were estimated from the water–water particles’ RDFs and vary from about 2 nm to nearly 13 nm for hydration levels from λ = 5 to λ = 16. Finally, computed Bragg spacing in each of the hydrated membranes indicate separation of the domains containing the water from 2 to 6 nm, exhibiting an approximately linear relationship with hydration.
Introduction
Fuel
cells have increasingly attracted interest since their implementation in NASA's Gemini and Apollo space exploration missions in the 1960’s. During the last two decades, a world-wide effort has been mounted into the research and development of polymer electrolyte membrane (PEM) fuel cells for portable, stationary, and vehicular applications; the latter due to the significant demand for efficient and ‘green energy’ systems for transportation. Central to this effort has been the synthesis and characterization of novel materials meetings the requirements of the operation of the device with little or no humidification and over a broad temperature range (i.e. −20 to 120 °C).
The proton exchange membrane is the central component of the fuel cell whose function is the conduction of protons and separation of the electrodes and fuel, typically humidified hydrogen gas, from the oxidant (oxygen gas). Perfluorinated ionomers remain the most widely utilized fuel cell electrolyte with Nafion®, the archetypal perfluorosulfonic acid (PFSA) membrane.1 The most commonly employed form is Nafion 117 with an equivalent weight (EW) of ≈ 1100 g mol−1, corresponding to the number of grams of dry Nafion per mole of sulfonic acid. Mauritz and Moore2 recently summarized the efforts during the last two decades towards understanding the morphology, structure and properties of Nafion. Although Nafion has received the most extensive studies among the various fuel cell membranes, it still has some serious limitations including a restrictive range of thermal stability, high manufacturing cost and a significant degree of hydration required in order to achieve sufficient proton conductivity.3 Therefore, the development of new materials with advanced characterization is taking a central role in fuel cell research. Various chemical homologues of Nafion exist including: Flemion® and Aciplex® from Asahi Glass;4,5 the short-side-chain (SSC) PFSA membrane, originally synthesized by the Dow Chemical Company and now commercialized by Solvay Solexis as Hyflon®;6–9 and a PFSA membrane developed by the Fuel Cell Components program at 3M with slightly longer –O(CF2)4SO3H side chains.10 Both membranes exhibit higher proton conductivity than Nafion 1100 when synthesized with an EW of approximately 800. The evaluation of the SSC PFSA membrane in fuel cells indicated that current densities nearly three times higher were possible at a potential of 0.5 V.11 Although this material did not see widespread application in fuel cells, recently it has attracted considerable attention due to the development of the much simpler synthesis route by Solvay Solexis.8
Experimental and modeling studies have been undertaken to understand the properties of PFSA membranes under a wide range of conditions. A variety of diffraction experiments, including small-angle X-ray scattering (SAXS), small-angle neutron scattering (SANS), and wide-angle X-ray diffraction (WAXD), have been implemented to study the morphologies of Nafion as a function of absorbed water and other species. Different models have been proposed to interpret the results from these experiments. The original cluster-network (or cluster-channel) model proposed by Gierke et al. has been the most widely referenced model in the history of PFSA ionomers.12–14 Following this early work a host of additional models were developed including: the modified (depleted-zone) core-shell proposed by Fujimura et al.,15 a lamellar model proposed by Litt,16 a sandwich-like model proposed by Haubold et al.,17 a rod-like model proposed by Rubatat et al.,18 a channel network model by Kreuer,19 and most recently a parallel cylindrical channel model by Schmidt-Rohr.20 Although these models differ significantly in the geometry and spatial distribution of the ionic clusters, they still have the common feature of the segregation of hydrophobic regions from hydrophilic domains. Experimental work to date has only provided a framework for understanding the hydrated morphologies of PFSA membranes but not as yet the specific details.
Modeling and simulation of PFSA membranes have recently been carried out to provide additional insight into membrane structure and function. The theoretical treatments of modeling of morphology and proton transport mechanisms in PFSA membranes have been reviewed by several authors.21–23 Various simulation scales have been considered and can basically be divided into molecular-level modeling and mesoscopic modeling. The former include ab initio electronic structure calculations concerning the effects of structure and local chemistry on proton dissociation and separation in PEM fragments,24–28 classical molecular dynamics (MD) simulations of morphology and transport,29–38 empirical valence bond models of proton hopping.39,40 and coarse-grained mesoscale modeling.41–44 Here we concentrate on mesoscopic simulations that are capable of examining length and time scales that are several orders of magnitude greater and longer than atomistic simulations. Yamamoto and Hyodo have used dissipative particle dynamics (DPD) simulations to study mesoscopic structure of Nafion membranes at varying degrees of hydration.41 Another study by Galperin and Khokhlov used a self-consistent mean field (SCMF) simulation to study morphological changes in Nafion upon alteration of temperature and water content.44 They found that there can exist a cluster-network morphology at low hydration levels and a sponge-like structure at higher hydration levels, similar to the results of Yamamoto and Hyodo. A more recent mesoscale simulation on the morphology of hydrated PFSA membranes analogous to Nafion 117 was carried out by Wescott et al., using the MESODYN code,43 which is based on mean-field free energy functional approach, but produced very similar results to previous DPD simulations.
We have undertaken DPD simulations in the current study to investigate the effect of side chain chemistry of the ionomer on the hydrated morphologies of PFSA membranes including: SSC, 3M, and Nafion over a range of EWs and at different water contents corresponding to intermediate levels of hydration. The PFSA polymer molecules have been modeled by chains connected soft spherical particles, which represent groups of several atoms. Water has also been modeled as a collection of six water molecules. After geometry optimization of the particles, their corresponding Flory–Huggins χ-parameters were calculated. Based on these parameters, the DPD interaction parameters were derived and used in mesoscopic simulations to determine the morphologies of the PFSA membranes. The radial distribution functions (RDFs) of water particles have been generated and used to characterize the average sizes of water clusters and average separation of the domains containing the water. The paper is structured as follows: firstly we briefly review the DPD methodology and parameterization methods used in this study, and how the RDFs were used to compute estimates of the size and separation of the water domains from the resulting models, before summarizing results from three different types of membranes at varying levels of hydration. Finally, we discuss the implications of the generated morphologies on the ionomer chemistry, before presenting our conclusions.
Model and theoretical methodology
I.
DPD simulations
The DPD method was first introduced by Hoogerbrugge and Koelman for simulating complex hydrodynamic behavior of isothermal fluids,45,46 and further developed by Español who included stochastic differential equations and conservation of energy.47,48 The formulation used here is due to Groot and Warren.49 Although this is now know to have a number of shortcomings, in that it can reproduce only a fixed quadratic equation of state and has no simple relationship between input parameters and transport coefficients, it has nevertheless been used in a number of different studies to successfully reproduce realistic morphologies of dense amphiphilic polymer systems.50,51 Only a brief outline of the method is presented here to provide context. The change in position and velocity of the DPD particles (or beads) are governed by Newton's equation of motion:| |  | (1) |
In general, the interaction between two DPD particles can be written down as the sum of a conservative force FCij, a dissipative force FDij, a random force FRij and an additional spring force FSij for a system:
| | 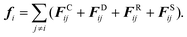 | (2) |
The conservative force is derived from a scalar potential exerted on particle i by the j-th particle,49 and treated as a soft repulsion acting along the line of centers with the form:52,53
| | 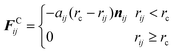 | (3) |
where
aij is a maximum repulsion force between particle
i and
j,
rc is a selected cutoff radius of the interaction,
rij =
ri −
rj,
rij = |
rij|, and
nij =
rij/|
rij|. The dissipative force is due to viscous drag and is given by:
| |  | (4) |
where
γ is a friction coefficient,
ωD(
rij) is a weight function, and
vij =
vi −
vj. The random force corresponds to thermal motion and is related to the noise parameter
σ and weight function
ωR(
rij) as follows:
| | 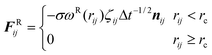 | (5) |
The random number ζij has zero mean and unit variance, and the appearance of Δt−1/2 is used to control step-size dependence of the random force.49 The spring force is given by the derivative of a harmonic potential defined between pairs of connected beads and is given by:
| | | FSij = −C(r0 − rij)nij | (6) |
where
C is the spring constant and
r0 is the equilibrium bond length.
The positions and velocities of the DPD particles may be solved in accordance to the above equations by implementing a modified version of the velocity-Verlet algorithm:49
| |  | (7) |
where the masses of the particles are defined as 1.
II.
DPD model for the perfluorosulfonic acid membranes
The monomeric molecular structures of the SSC, 3M, and NafionPFSA membranes are shown in Fig. 1. We chose m = 15, giving molecular weights of between 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 20
000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 for the oligomers, but acknowledge that there are probably at least 90 monomers in the real ionomers.54 We selected n = 9, 15 for the SSC membrane; and n = 7, 13 for the 3M membrane, resulting in a similar pair of EWs of 678 and 978 for both ionomers. These membranes were compared to Nafion with an EW of 1244 where n = 17. The ionomers were modeled by connecting spherical soft particles (beads), which contain groups of atoms and/or molecules. The differing structure of the side chains prevents a single set of beads being adopted for the three membranes unless the size of each bead was made much smaller. Hence, the DPD particles used to construct the different PFSA membranes used in the simulations are: –CF2CF2CF2CF2CF2CF2–, –CF2CF2CF2CF(OCF3)–, –CF2CF(OCF2CF2CF3)–, –OCF2C(CF3)FOCF2–, and CF3SO3H·3H2O; and designated: A, B, B′, B″, and C, respectively. As our primary interest in modeling these PFSA membranes is due to the higher proton conductivity in both the SSC and 3M membranes at low EWs and intermediate hydration levels,55 we chose to include the majority of the water molecules of the first hydration shell of the terminal sulfonic acid group in the C bead. Another independent water particle, W, was constructed from six water molecules (i.e., (H2O)6). We realize that this, of course, limits the water contents that can be examined in the simulations, i.e. λ ≥ 3. The volume of a single molecule is about 30 Å3 and hence the volume of the W particle is therefore about 180 Å3. Considering our simulated density, ρr3c = 3, a cube with a volume of rc contains three particles and corresponds to a volume of 540 Å3. Thus, the interaction radius, rc, is determined to be
000 g mol−1 for the oligomers, but acknowledge that there are probably at least 90 monomers in the real ionomers.54 We selected n = 9, 15 for the SSC membrane; and n = 7, 13 for the 3M membrane, resulting in a similar pair of EWs of 678 and 978 for both ionomers. These membranes were compared to Nafion with an EW of 1244 where n = 17. The ionomers were modeled by connecting spherical soft particles (beads), which contain groups of atoms and/or molecules. The differing structure of the side chains prevents a single set of beads being adopted for the three membranes unless the size of each bead was made much smaller. Hence, the DPD particles used to construct the different PFSA membranes used in the simulations are: –CF2CF2CF2CF2CF2CF2–, –CF2CF2CF2CF(OCF3)–, –CF2CF(OCF2CF2CF3)–, –OCF2C(CF3)FOCF2–, and CF3SO3H·3H2O; and designated: A, B, B′, B″, and C, respectively. As our primary interest in modeling these PFSA membranes is due to the higher proton conductivity in both the SSC and 3M membranes at low EWs and intermediate hydration levels,55 we chose to include the majority of the water molecules of the first hydration shell of the terminal sulfonic acid group in the C bead. Another independent water particle, W, was constructed from six water molecules (i.e., (H2O)6). We realize that this, of course, limits the water contents that can be examined in the simulations, i.e. λ ≥ 3. The volume of a single molecule is about 30 Å3 and hence the volume of the W particle is therefore about 180 Å3. Considering our simulated density, ρr3c = 3, a cube with a volume of rc contains three particles and corresponds to a volume of 540 Å3. Thus, the interaction radius, rc, is determined to be  Å ≈ 8.14 Å by the method used by Groot and Rabone.53 The simulated time step in absolute units corresponds to rc√m/kBT ≅ 5.35 ps and the systems were equilibrated for a minimum of 5.35 ns.
Å ≈ 8.14 Å by the method used by Groot and Rabone.53 The simulated time step in absolute units corresponds to rc√m/kBT ≅ 5.35 ps and the systems were equilibrated for a minimum of 5.35 ns.
 |
| | Fig. 1 General molecular structure of the PFSA acid membranes used in the simulations: (a) SSC; (b) 3M; and (c) Nafion. | |
The structures of particles A, B, B′, B″, and W were optimized by molecular mechanics with COMPASS parameters using the Forcite module in Materials Studio.56 The particles A and B, B′, or B″ were taken as repeat units in the polymer for the optimizations. However, the structure of particle C was optimized using density functional theory (DFT) at the B3LYP/6-31G** level with Gaussian 03.57 This treatment of the C bead was deemed necessary due to the observed dissociation of a sulfonic acid molecule in presence of 3 or more water molecules.58 Therefore, it required a quantum mechanical treatment in order to obtain an accurate description as a starting point for later simulations.
III.
DPD simulation parameters and conditions
It is clear from eqn (3) that the repulsive interaction parameters, aij, are required for the calculation of the conservative forces. As the reduced density ρ in our simulations was chosen to be 3, the repulsion parameters are related to the Flory–Huggins χ-parameters according to:49,52where aii is the repulsion parameter between particles of the same type and has the value of 25kBT, which gives a pure DPD fluid a compressibility similar to that of liquid water. The Flory–Huggins χ-parameters were calculated using the Blends module in Materials Studio and the derived DPD repulsion parameters are collected for the SSC, 3M, and Nafion ionomers in Tables 1, 2, and 3, respectively.
Table 1 Computed χ-parameters and corresponding repulsion parameters describing pair wise interactions of the selected beads for the SSC PFSA ionomer
| Paira |
χ
|
a
ij
(kBT) |
|
DPD beads in pair are: A, –CF2CF2CF2CF2CF2CF2–; B, –CF2CF2CF2CF(OCF3)–; C, CF3SO3H·3H2O; and W, 6H2O.
|
|
A–B |
0.15 |
25.5 |
|
A–C |
6.86 |
47.4 |
|
A–W |
3.28 |
35.7 |
|
B–C |
6.24 |
45.4 |
|
B–W |
3.15 |
35.3 |
|
C–W |
1.24 |
29.0 |
Table 2 Computed χ-parameters and corresponding repulsion parameters describing pair wise interactions of the selected beads for the 3MPFSA ionomer
| Paira |
χ
|
a
ij
(kBT) |
|
DPD beads in pair are: A, –CF2CF2CF2CF2CF2CF2–; B′, –CF2CF(OCF2CF2CF3)–; C, CF3SO3H·3H2O; and W, 6H2O.
|
|
A–B′ |
−0.03 |
24.9 |
|
A–C |
7.07 |
48.1 |
|
A–W |
3.30 |
35.8 |
|
B′–C |
7.04 |
48.0 |
|
B′–W |
3.47 |
36.3 |
|
C–W |
1.53 |
30.0 |
Table 3 Computed χ-parameters and corresponding repulsion parameters describing pair wise interactions of the selected beads Nafion
| Paira |
χ
|
a
ij
(kBT) |
|
DPD beads in pair are: A, –CF2CF2CF2CF2CF2CF2–; B″, –OCF2C(CF3)FOCF2–; C, CF3SO3H·3H2O; and W, 6H2O.
|
|
A–B′′ |
1.23 |
29.0 |
|
A–C |
7.44 |
49.3 |
|
A–W |
3.36 |
36.0 |
|
B′′–C |
2.70 |
33.8 |
|
B′′–W |
1.53 |
30.0 |
|
C–W |
1.48 |
29.9 |
A unit cell of side length 40 nm was chosen as the initial condition of our DPD simulations; hence using a density ρ = 3 there were 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 DPD particles in total. The spring constant was set to the default value 4.0kBT/r2c in the DPD module in Materials Studio. The topologies of the SSC and 3M PFSA ionomers studied are: (A 1 [B or B′ 1] [C 1])15, (A 2 [B or B′ 1] [C 1])15 and (A 3 [B or B′ 1] [C 1])15, and for Nafion (A 3 [B″ 1] [C 1])15.
000 DPD particles in total. The spring constant was set to the default value 4.0kBT/r2c in the DPD module in Materials Studio. The topologies of the SSC and 3M PFSA ionomers studied are: (A 1 [B or B′ 1] [C 1])15, (A 2 [B or B′ 1] [C 1])15 and (A 3 [B or B′ 1] [C 1])15, and for Nafion (A 3 [B″ 1] [C 1])15.
IV. Radial distribution functions and scattering intensities.
While the bead positions in the DPD simulations are themselves continuous, the output consists of a distribution of bead densities on a cubic grid of lattice sites. It was assumed in this work that the displacements of beads about a lattice point P will have a Gaussian form:59| |  | (9) |
in which r is the distance from a reference lattice point, N is the number density on the reference lattice point, and σ is a standard deviation representing the spread of beads around an individual lattice point. When one considers the distribution of beads on a certain lattice point other than the reference site, a more useful asymmetric distribution function will be given by:| |  | (10) |
where rP is the distance from a lattice point P to the reference lattice point N. By summing distributions from all the lattice points around the reference lattice point, one obtains:59| |  | (11) |
where n is the average number density, and G(r) is the radial distribution function (RDF).
The scattering intensities I(Q) can be related to radial distribution function G(r) by Fourier transformation,60,61 according to:
| |  | (12) |
where
Q is the magnitude of the scattering vector and
ρ is the average density over all space. It can be approximately limited for our finite-sized system to:
| |  | (13) |
Results and discussion
I. Morphologies at various hydration levels
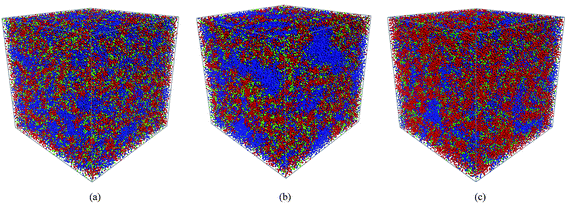
The SSC, 3M and NafionPFSA membranes at various hydration levels corresponding to λ = 5, 7, 9, 11, and 16 were simulated (where λ has its usual definition of the number of water molecules per sulfonic acid group). These hydration levels correspond to water volume concentrations of: 25, 31.8, 37.5, 45.8, and 51.6% for the SSC and 3M PFSA membranes with an EW = 678; 19.2, 25, 30, 34.5, and 43.2% for the SSC and 3M PFSA membrane with an EW = 978, and 15.6, 20.6, 25, 28.9, and 37.2% for Nafion with EW = 1244. The equilibrated morphologies of the SSC and 3M PFSA membranes at the lower EW are compared to Nafion all with a hydration level where λ = 9 are shown in Fig. 2. Both of the membranes with the shorter side chains clearly display the anticipated larger fraction of water than the high EW Nafion where the majority of the simulation box appears to consist of the backbone beads (i.e., –CF2CF2CF2CF2CF2CF2– and –OCF2C(CF3)FOCF2−–) which are shown in red. The water in the SSC membrane appears to be slightly more dispersed than in the 3M membrane, an observation that is further substantiated when the water content is increased. Fig. 3 displays the hydrated morphologies of the same three membranes but at a significantly higher water content where λ = 16. It is clear in comparison to the morphologies at the lower water content (Fig. 2) that the phase separation has increased in all of the ionomers with the water occupying larger clusters of up to several nanometers in dimension, particularly with the 3M membrane where relatively large domains containing only water beads are evident. Clearly, the DPD simulations are capable of capturing the effects of differences in the side chain chemistry as evidenced by the two membranes with the same EW (Fig. 3(a) and (b)) possessing different morphologies at the same hydration level. Furthermore, it can be seen that the shape of the clusters of water are not spherical as proposed in the cluster-network model12 but irregular, which is in agreement with the simulation results on Nafion by others using both mesoscale methods41,44 and fully atomistic MD simulations.31,36,38
 |
| | Fig. 2 The morphologies of the SSC, 3M and NafionPFSA membranes at a hydration level where λ = 9: (a) SSC with an EW = 678; (b) 3M with an EW = 678; and (c) Nafion with an EW = 1244. The backbone beads: A, B, B′, B″ (see text for molecular description) are shown in red, the terminal portion of side chain C bead in green; and the water, W, bead in blue. | |
 |
| | Fig. 3 The morphologies of the SSC, 3M and NafionPFSA membranes at a hydration level where λ = 16: (a) SSC with an EW = 678; (b) 3M with an EW = 678; and (c) Nafion with an EW = 1244. The backbone beads: A, B, B′, B″ (see text for molecular description) are shown in red, the terminal portion of side chain C bead in green; and the water, W, bead in blue. | |
Further insight into the hydrated morphologies may be obtained from two dimensional (2D) contour plots detailing the density distribution of water in each of the ionomers. These are obtained by making slices (in the y–z plane) of the simulation boxes (as depicted in Fig. 2 and 3) and plotting the average density of the water beads. The density distribution of water in the SSC PFSA membrane at an EW = 678 and hydration levels where λ = 9 and 16 are shown in Fig. 4(a) and (b), respectively, and for the same membrane and similar with water contents but at the higher EW = 978 in Fig. 4(c) and (d). The density of the water beads is the same for all plots and the scale is provided at the bottom right corner of the figure. These plots clearly indicate that the DPD simulations are able to capture significant differences in the distribution of the water when either the EW is fixed and the water content varied or when the hydration is fixed at the EW is changed. When the EW is increased from 678 to 978 the water is distributed into domains that are more isolated and far less connected particularly at the lower water content (Fig. 4(c)). The morphology of the SSC ionomer is generally irregular in shape and only resembles that of channels at the lower EW and higher water content.
 |
| | Fig. 4 Contour plots of the density of water, as W beads, shown as a two dimensional cross section for the SSC PFSA membrane: (a) EW = 678 and λ = 9; (b) EW = 678 and λ = 16; (c) EW = 978 and λ = 9; and (d) EW = 978 and λ = 16. The darker the color the greater the density of the water beads. | |
A similar set of 2D contour plots for the 3MPFSA membrane are displayed in Fig. 5 where again the water density of the ionomer at two different EWs (678 and 978) and two different water contents (λ = 9 and 16) are compared. The plots clearly show the previously observed greater connectivity of the water in the ionomer with the lower EW at both hydration levels. However, in comparison to the SSC ionomer, the average density of water is greater within the regions containing the water (i.e., in the figures the region is darker indicating greater density). This is particularly evident at a hydration level where λ = 16 where the water appears to accumulate into larger domains when compared to the SSC membrane at the same EW and water content. Clearly, the DPD simulations are able to capture differences in the hydrated morphologies of the SSC and 3M PFSA membranes in systems where the only structural difference in the monomer is a single tetrafluoroethylene unit (i.e., a –CF2CF2– present in the backbone of the SSC ionomer but in the side chain of the 3M ionomer). This seemingly small difference in the structure of the ionomers of the same EW apparently changes the local and extended distribution of the water in the ionomers at least within the sampled intermediate hydration levels. It could be reasoned that the longer side chain simply allows greater aggregation of the sulfonate terminated side chains thereby resulting in the formation of larger water domains. Further investigations with atomistic simulations (i.e. MD) would be necessary, however, to examine whether this simply relationship to side chain length is always valid.
 |
| | Fig. 5 Contour plots of the density of water, as W beads, shown as a two dimensional cross section for the 3MPFSA membrane: (a) EW = 678 and λ = 9; (b) EW = 678 and λ = 16; (c) EW = 978 and λ = 9; and (d) EW = 978 and λ = 16. | |
Finally, the density distribution of water in the 1244 EW Nafion system at hydration levels where λ = 9 and 16 is presented in Fig. 6(a) and (b), respectively. This considerably higher EW (when compared to the PFSA ionomers with the shorter side chains) clearly brings about significant isolation of the water with large regions of the 2D plots at both hydration levels occupied by the perfluorinated components of the ionomer backbone and side chain (white regions in the plots). It is interesting to note that the DPD simulations suggest that the water occupies regions that markedly resemble channels or pores (or certainly elongated domains) at the highest hydration level only. This latter feature is quite different than that observed in either the SSC or 3M PFSA membranes at a similar hydration level (i.e., Fig. 5(d) and 6(d)), but similar channel morphologies have been deduced from the fitting of SAXS spectra in prior studies.19,20
 |
| | Fig. 6 Contour plots of the density of water, as W beads, shown as a two dimensional cross section for Nafion with an EW = 1244: (a) λ = 9; and (b) λ = 16. | |
II. RDFs and Bragg spacing
Water particle–water particle radial distribution functions, G(r), were computed at three different hydration levels (i.e., λ = 7, 9, and 16) in order to further quantify the average size of the domains containing the water and their average separation (i.e., Bragg spacing) in the three PFSA membranes. The RDFs for the SSC, 3M, and Nafion membranes are plotted in Fig. 7, 8, and 9, respectively.
 |
| | Fig. 7 Radial distribution functions, G(r)’s, of water particles for the SSC PFSA membrane at the two different EW's of: (a) 678; and (b) 978, plotted at three distinct water contents. | |
 |
| | Fig. 8 Radial distribution functions, G(r)’s, of water particles for the 3MPFSA membrane at the two different EW's of: (a) 678; and (b) 978, plotted at three distinct water contents. | |
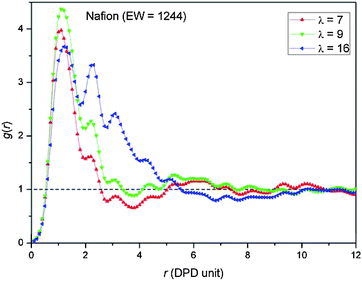 |
| | Fig. 9 Radial distribution functions, G(r)’s, of water particles for Nafion at three distinct water contents. | |
The G(r)’s for the SSC PFSA membranes at the two distinct EWs of 678 and 978 are compared in Fig. 7(a) and (b), respectively, and underscore the qualitative observations described above as observed in the water contour plots. Clearly, at the lowest water content where λ = 7 the vast majority of the water is in a single cluster with a slight dispersion (shoulder in the G(r) just beyond 2 DPD units. As the degree of hydration is increased the percentage of water residing in the first peak in the G(r) decreases and a second peak and third peak emerge indicating an increase in the size and dispersion of the water domains. The RDFs at these two EWs are qualitatively similar particularly at the lowest water content, but the lower EW ionomer does indicate a higher proportion of larger clusters at λ = 16 in the simulation box. The tails of the G(r)’s in the lower EW ionomer also extend further before crossing the mean density of the water in the systems (i.e., G(r) = 1).
RDFs were generated for the 3MPFSA membrane at EW's of 678 and 978 over a similar set of water contents and are shown in Fig. 8(a) and (b), respectively. In comparison with the SSC membrane, only the G(r)’s at the lowest water content appear similar, with the majority of the water in a single cluster with a slight dispersion (shoulder in the G(r) just beyond 2 DPD units). The G(r) for the membrane of higher EW at a hydration where λ = 9 possesses only a single peak with a small shoulder (similar to that at λ = 7) unlike that seen in the RDF of the SSC PFSA membrane at the same EW where 3 distinct peaks are present (see Fig. 7(b)). However, the most significant difference in the G(r)’s of the 3M membranes when compared to the SSC membranes is at the highest water content where 7 or 8 peaks are present and very long tails (i.e. not cutting the mean water density until more than 8 DPD units). This latter result is consistent with what is seen in the water contours plots where very large water domains are observed (Fig. 5(b) and (d)).
A corresponding set of RDFs are plotted for Nafion at EW = 1244 in Fig. 9. The G(r) at λ = 7 is very similar to both of the other two PFSA membranes at EW = 978 with the clear indication that the water resides in single small clusters. Evidently at very low water contents the DPD simulations do not indicate any significant differences in the hydrated morphology when either the side chain chemistry or EW is altered. At the highest water content, the G(r) has 5 peaks and qualitatively resembles the SSC membrane at the same water content, but with a tail that is quite a bit longer cutting the mean water density at about 5.5 DPD units. While this tail is not any where near as long as observed in the 3M membrane (Fig. 8(b)) this again suggests that a longer side chain will result in larger sized water domains at sufficiently high levels of hydration.
Quantification of the average size of the water domains in each of the PFSA membranes was further evaluated by considering the width of the first two breaking points where G(r) = 1. The resulting average ‘cluster’ radius of the water in each of the PFSA membranes is plotted as a function of hydration level in Fig. 10. These plots reveal that the average diameter of the water domains in the membranes vary from about 2 nm to nearly 13 nm for hydration levels from λ = 5 to λ = 16. Consistent with what was discussed above, at the lower hydration level (λ ≤ 9) the size of the domains of the various membranes is similar and seems to be unaffected by changes in the monomer chemistry. As the water content is increased the radius of the water clusters increases for all the membranes. This increase is roughly linearly for both the Nafion and SSC PFSA membranes. The plots for the SSC ionomer across the entire hydration range of 5 to 16 H2O/SO3H show that the average size of the water domains are quite similar (at some water contents identical) for both EW's. This is in contrast to the 3M ionomer where the increase is very rapid and the average size much larger for the lower EW ionomer above λ = 9.
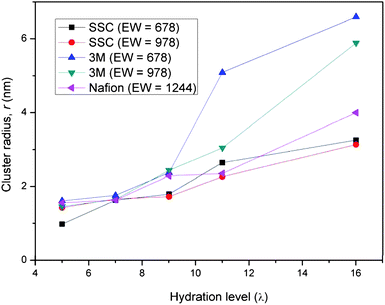 |
| | Fig. 10 Average radius of the water domains of the three PFSA membranes simulated in this investigation as a function of the hydration level. The water clusters in the 3M membranes are significantly larger at the higher water contents. | |
Finally, scattering intensities, I(Q), are evaluated from the Fourier transformation of the radial distribution function to quantify the average separation of the water clusters within the polymeric matrix. The first peak at the maximum small angle scattering vector Qm is associated with the ionomer peak appearing in a SAXS or SANS spectrum. The physical dimension or Bragg spacing (d) associated with the ionomer peak position may be calculated from the Bragg relationship, d = 2π/Qm. Plots of d as a function of hydration level for the three ionomers is shown in Fig. 11 (only EW = 978 is shown for the SSC and 3M membranes). The spacing of the water domains range from 2 to 6 nm, and exhibit an approximately linear increase with increasing hydration. The Nafion membrane has the largest separation consistent with its substantially higher EW. The plots also indicate that the average separation of the water domains is greater in the 3M ionomer than in the SSC ionomer despite the membranes having the same equivalent weight. This latter is certainly what is evidenced in the water contour plots which do show that on average the domains in the 3MPFSA ionomer are larger and consistently more separated.
 |
| | Fig. 11 Bragg spacing, d, in the higher EW (978 and 1244) PFSA membranes examined in this study as a function of the hydration level. | |
Conclusions
We have investigated the hydrated morphology of Nafion, the SSC, and 3M PFSA fuel cell membranes as a function of ionomer EW and degree of hydration with DPD simulations. Specifically, equilibrated morphologies were determined for the SSC and 3M PFSA membranes at EW's of 678 and 978, and Nafion with an EW of 1244. The hydration level was varied in each system with water contents corresponding to 5, 7, 9, 11, and 16 H2Os/SO3H. Our simulations suggest that the high EW ionomers exhibit significantly greater dispersion of the water regions than the low EW membranes and contour plots of the water density reveal that as the hydration level is increased, the isolated water clusters present at the lower water contents increase in size eventually forming continuous regions resembling channels or pores particularly at a hydration of 16 H2Os/SO3H. The DPD simulations also revealed differences in the hydrated morphology when only the side chain length was altered and suggest that the 3MPFSA ionomer exhibits much larger clusters of water when compared to the SSC ionomer at the same EW and water content. This small structural difference in the ionomers of similar EW seems to change the local and extended distribution of the water with the longer side chains resulting in greater aggregation of the sulfonate groups and consequently the formation of larger water domains. The average size of the clusters were estimated from the water–water particles’ RDFs and vary from about 2 nm to nearly 13 nm for hydration levels from λ = 5 to λ = 16 with the largest domains found in the 3M membrane with an EW = 678. The average separation of the water domains was estimated from computed Bragg spacing for each membrane and show an approximately linear relationship with hydration.
Acknowledgements
The authors acknowledge the support for this work by the U.S. Army Research Laboratory, under contract number W911NF-07-1-0085 and the DOE under contract number DE-FG36-07G017006. DOE support does not constitute an endorsement by DOE of the views expressed in this work.
References
- P. P. Kundu and A. Pal, Rev. Chem. Eng., 2006, 22, 125–153 Search PubMed.
- K. A. Mauritz and R. B. Moore, Chem. Rev., 2004, 104, 4535–4585 CrossRef CAS.
- K. D. Kreuer, ChemPhysChem, 2002, 3, 771–775 CrossRef CAS.
- M. Saito, N. Arimura, K. Hayamizu and T. Okada, J. Phys. Chem. B, 2004, 108, 16064–16070 CrossRef CAS.
- N. Yoshida, T. Ishisaki, A. Watakabe and M. Yoshitake, Electrochim. Acta, 1998, 43, 3749–3754 CrossRef CAS.
- R. B. Moore and C. R. Martin, Macromolecules, 1989, 22, 3594–3599 CrossRef CAS.
- G. Gebel and R. B. Moore, Macromolecules, 2000, 33, 4850–4855 CrossRef CAS.
- V. Arcella, A. Ghielmi and G. Tommasi, Ann. N. Y. Acad. Sci., 2003, 984, 226–244 CrossRef CAS.
- A. Ghielmi, P. Vaccarono, C. Troglia and V. Arcella, J. Power Sources, 2005, 145, 108–115 CrossRef CAS.
- M. Emery, M. Guerra, G. Haugen, K. Hintzer, K. H. Lochhaas, P. Pham, D. Pierpont, M. Schaberg, A. Thaler, M. Yandrasits and S. Hamrock, ECS Trans., 2007, 11, 3–14 Search PubMed.
- K. Prater, J. Power Sources, 1990, 29, 239–250 CrossRef CAS.
- T. D. Gierke, G. E. Munn and F. C. Wilson, J. Polym. Sci., 1981, 19, 1687–1704 Search PubMed.
- W. Y. Hsu and T. D. Gierke, Macromolecules, 1982, 15, 101–105 CrossRef CAS.
- W. Y. Hsu and T. D. Gierke, J. Membr. Sci., 1983, 13, 307–326 CrossRef CAS.
- M. Fujimura, T. Hashimoto and H. Kawai, Macromolecules, 1981, 14, 1309–1315 CrossRef CAS.
- M. H. Litt, Polym. Prepr., 1997, 38, 80–81 CAS.
- H. G. Haubold, T. Vad, H. Jungbluth and P. Hiller, Electrochim. Acta, 2001, 46, 1559–1563 CrossRef CAS.
- L. Rubatat, A. L. Rollet, G. Gebel and O. Diat, Macromolecules, 2002, 35, 4050–4055 CrossRef CAS.
- K. D. Kreuer, J. Membr. Sci., 2001, 185, 29–39 CrossRef CAS.
- K. Schmidt-Rohr and Q. Chen, Nat. Mater., 2008, 7, 75–83 CrossRef CAS.
- S. J. Paddison, Annu. Rev. Mater. Res., 2003, 33, 289–319 CrossRef CAS.
- K. D. Kreuer, S. J. Paddison, E. Spohr and M. Schuster, Chem. Rev., 2004, 104, 4637–4678 CrossRef CAS.
- J. A. Elliott and S. J. Paddison, Phys. Chem. Chem. Phys., 2007, 9, 2602–2618 RSC.
- M. Eikerling, S. J. Paddison and T. A. Zawodzinski, J. New Mater. Electrochem. Syst., 2002, 5, 15–23 Search PubMed.
- S. J. Paddison and J. A. Elliott, J. Phys. Chem. A, 2005, 109, 7583–7593 CrossRef CAS.
- S. J. Paddison and J. A. Elliott, Phys. Chem. Chem. Phys., 2006, 8, 2193–2203 RSC.
- S. J. Paddison and J. A. Elliott, Solid State Ionics, 2006, 177, 2385–2390 CrossRef CAS.
- S. J. Paddison and J. A. Elliott, Solid State Ionics, 2007, 178, 561–567 CrossRef CAS.
- A. Vishnyakov and A. V. Neimark, J.
Phys. Chem. B, 2000, 104, 4471–4478 CrossRef CAS.
- S. S. Jang, V. Molinero, T. Cagin and W. A. Goddard, J. Phys. Chem. B, 2004, 108, 3149–3157 CrossRef CAS.
- S. Urata, J. Irisawa, A. Takada, W. Shinoda, S. Tsuzuki and M. Mikami, J. Phys. Chem. B, 2005, 109, 4269–4278 CrossRef CAS.
- S. Urata, J. Irisawa, A. Takada, W. Shinoda, S. Tsuzuki and M. Mikami, J. Phys. Chem. B, 2005, 109, 17274–17280 CrossRef CAS.
- N. P. Blake, M. K. Petersen, G. A. Voth and H. Metiu, J. Phys. Chem. B, 2005, 109, 24244–24253 CrossRef CAS.
- N. P. Blake, G. Mills and H. Metiu, J. Phys. Chem. B, 2007, 111, 2490–2494 CrossRef CAS.
- A. Venkatnathan, R. Devanathan and M. Dupuis, J. Phys. Chem. B, 2007, 111, 7234–7244 CrossRef CAS.
- R. Devanathan, A. Venkatnathan and M. Dupuis, J. Phys. Chem. B, 2007, 111, 8069–8079 CrossRef CAS.
- R. Devanathan, A. Venkatnathan and M. Dupuis, J. Phys. Chem. B, 2007, 111, 13006–13013 CrossRef CAS.
- I. H. Hristov, S. J. Paddison and R. Paul, J. Phys. Chem. B, 2008, 112, 2937–2949 CrossRef CAS.
- D. Seeliger, C. Hartnig and E. Spohr, Electrochim. Acta, 2005, 50, 4234–4240 CrossRef CAS.
- S. Dokmaisrijan and E. Spohr, J. Mol. Liq., 2006, 129, 92–100 CrossRef CAS.
- S. Yamamoto and S. A. Hyodo, Polym. J., 2003, 35, 519–527 CrossRef CAS.
- P. G. Khalatur, S. K. Talitskikh and A. R. Khokhlov, Macromol. Theory Simul., 2002, 11, 566–586 CrossRef CAS.
- J. T. Wescott, Y. Qi, L. Subramanian and T. W. Capehart, J. Chem. Phys., 2006, 124, 134702 CrossRef.
- D. Y. Galperin and A. R. Khokhlov, Macromol. Theory Simul., 2006, 15, 137–146 CrossRef CAS.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- J. M. V. A. Koelman and P. J. Hoogerbrugge, Europhys. Lett., 1993, 21, 363–368 CrossRef CAS.
- P. Español and P. B. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- P. Español, Europhys. Lett., 1997, 39, 605–610 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- P. Español, M. Serrano and H. C. Ottinger, Phys. Rev. Lett., 1999, 83, 4542–4545 CrossRef CAS.
- M. Serrano and P. Espanol, Phys. Rev. E, 2001, 6404.
- R. D. Groot and T. J. Madden, J. Chem. Phys., 1998, 108, 8713–8724 CrossRef CAS.
- R. D. Groot and K. L. Rabone, Biophys. J., 2001, 81, 725–736 CrossRef CAS.
- D. E. Curtin, R. D. Lousenberg, T. J. Henry, P. C. Tangeman and M. E. Tisack, J. Power Sources, 2004, 131, 41–48 CrossRef.
- K. D. Kreuer, M. Schuster, B. Obliers, O. Diat, U. Traub, A. Fuchs, U. Klock, S. J. Paddison and J. Maier, J. Power Sources, 2008, 178, 499–509 CrossRef CAS.
-
Materials Studio, Accelrys Software Inc., San Diego, Release 4.1 edn, 2006 Search PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. M. Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Gaussian Inc., Wallingford, CT, Revision C.02 edn, 2004 Search PubMed.
- S. J. Paddison, J. New Mater. Electrochem. Syst., 2001, 4, 197–207 Search PubMed.
- B. J. Yoon, M. S. Jhon and H. Eyring, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 6588–6591 CrossRef CAS.
- J. J. Salacuse, A. R. Denton and P. A. Egelstaff, Phys. Rev. E, 1996, 53, 2382–2389 Search PubMed.
- J. J. Salacuse, A. R. Denton, P. A. Egelstaff, M. Tau and L. Reatto, Phys. Rev. E, 1996, 53, 2390–2401 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2008 |
Click here to see how this site uses Cookies. View our privacy policy here. 
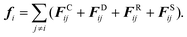
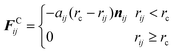

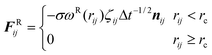

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 20
000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 for the oligomers, but acknowledge that there are probably at least 90 monomers in the real ionomers.54 We selected n = 9, 15 for the SSC membrane; and n = 7, 13 for the 3M membrane, resulting in a similar pair of EWs of 678 and 978 for both ionomers. These membranes were compared to Nafion with an EW of 1244 where n = 17. The ionomers were modeled by connecting spherical soft particles (beads), which contain groups of atoms and/or molecules. The differing structure of the side chains prevents a single set of beads being adopted for the three membranes unless the size of each bead was made much smaller. Hence, the DPD particles used to construct the different PFSA membranes used in the simulations are: –CF2CF2CF2CF2CF2CF2–, –CF2CF2CF2CF(OCF3)–, –CF2CF(OCF2CF2CF3)–, –OCF2C(CF3)FOCF2–, and CF3SO3H·3H2O; and designated: A, B, B′, B″, and C, respectively. As our primary interest in modeling these PFSA membranes is due to the higher proton conductivity in both the SSC and 3M membranes at low EWs and intermediate hydration levels,55 we chose to include the majority of the water molecules of the first hydration shell of the terminal sulfonic acid group in the C bead. Another independent water particle, W, was constructed from six water molecules (i.e., (H2O)6). We realize that this, of course, limits the water contents that can be examined in the simulations, i.e. λ ≥ 3. The volume of a single molecule is about 30 Å3 and hence the volume of the W particle is therefore about 180 Å3. Considering our simulated density, ρr3c = 3, a cube with a volume of rc contains three particles and corresponds to a volume of 540 Å3. Thus, the interaction radius, rc, is determined to be
000 g mol−1 for the oligomers, but acknowledge that there are probably at least 90 monomers in the real ionomers.54 We selected n = 9, 15 for the SSC membrane; and n = 7, 13 for the 3M membrane, resulting in a similar pair of EWs of 678 and 978 for both ionomers. These membranes were compared to Nafion with an EW of 1244 where n = 17. The ionomers were modeled by connecting spherical soft particles (beads), which contain groups of atoms and/or molecules. The differing structure of the side chains prevents a single set of beads being adopted for the three membranes unless the size of each bead was made much smaller. Hence, the DPD particles used to construct the different PFSA membranes used in the simulations are: –CF2CF2CF2CF2CF2CF2–, –CF2CF2CF2CF(OCF3)–, –CF2CF(OCF2CF2CF3)–, –OCF2C(CF3)FOCF2–, and CF3SO3H·3H2O; and designated: A, B, B′, B″, and C, respectively. As our primary interest in modeling these PFSA membranes is due to the higher proton conductivity in both the SSC and 3M membranes at low EWs and intermediate hydration levels,55 we chose to include the majority of the water molecules of the first hydration shell of the terminal sulfonic acid group in the C bead. Another independent water particle, W, was constructed from six water molecules (i.e., (H2O)6). We realize that this, of course, limits the water contents that can be examined in the simulations, i.e. λ ≥ 3. The volume of a single molecule is about 30 Å3 and hence the volume of the W particle is therefore about 180 Å3. Considering our simulated density, ρr3c = 3, a cube with a volume of rc contains three particles and corresponds to a volume of 540 Å3. Thus, the interaction radius, rc, is determined to be  Å ≈ 8.14 Å by the method used by Groot and Rabone.53 The simulated time step in absolute units corresponds to rc√m/kBT ≅ 5.35 ps and the systems were equilibrated for a minimum of 5.35 ns.
Å ≈ 8.14 Å by the method used by Groot and Rabone.53 The simulated time step in absolute units corresponds to rc√m/kBT ≅ 5.35 ps and the systems were equilibrated for a minimum of 5.35 ns.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 DPD particles in total. The spring constant was set to the default value 4.0kBT/r2c in the DPD module in Materials Studio. The topologies of the SSC and 3M PFSA ionomers studied are: (A 1 [B or B′ 1] [C 1])15, (A 2 [B or B′ 1] [C 1])15 and (A 3 [B or B′ 1] [C 1])15, and for Nafion (A 3 [B″ 1] [C 1])15.
000 DPD particles in total. The spring constant was set to the default value 4.0kBT/r2c in the DPD module in Materials Studio. The topologies of the SSC and 3M PFSA ionomers studied are: (A 1 [B or B′ 1] [C 1])15, (A 2 [B or B′ 1] [C 1])15 and (A 3 [B or B′ 1] [C 1])15, and for Nafion (A 3 [B″ 1] [C 1])15.














