Multi-objective optimization of a polymer electrolyte fuel cell membrane electrode assembly

Abstract

A multi-objective multi-variable gradient-based fuel cell optimization framework is presented in order to optimize fuel cell membrane electrode assembly fabrication. The optimization target is to simultaneously maximize the cell current density at a given voltage and minimize its production costs. The design variables are electrode composition parameters such as platinum loading and porosity. To develop this framework, a two-dimensional through-the-channel single-phase membrane electrode assembly model is implemented and coupled to an optimization algorithm. In order to solve the optimization problem in a reasonable time, a gradient-based optimization method in conjunction with analytical sensitivities of the electrode model with respect to design parameters such as amount of electrolyte are used. Results show the trade-offs between performance and cost and illustrate that large gains in performance and reductions in production costs are possible. They also highlight the problems associated with formulating the optimization problem without taking into account production costs.

---

1 Introduction

Reducing production cost and improving performance, reliability and durability remain critical prerequisites for commercialization of polymer electrolyte membrane fuel cells. Past investigations on electrode design for optimal performance^1–5 and low platinum loading^6–8 have been mainly based on trial-and-error and parametric studies. When the number of design variables becomes large, a more systematic and rational approach to optimization of the electrode structure and composition is necessary. One such case is when trying to design a complete membrane electrode assembly (MEA).

The anode and cathode gas diffusion layer (GDL) and catalyst layer (CL) have multiple functions that require a combination of different materials and structures. For example, in the GDL, the electron conductive material provides the necessary electrical conductivity, while the porous structure allows reactant transport. In order for the fuel cell to provide the best possible performance at a minimum cost, the optimal porosities and amounts of different materials in the GDL and CL need to be determined. Since all these design parameters are coupled, the task of finding the optimal amount of material to reduce production cost and maximize performance becomes in fact a multi-objective, multi-variable problem that depends on the fuel cell operating and geometric conditions. To date, only four research groups – Song et al.,^9,10 Grujicic et al.,^11–13 Mawardi et al.¹⁴ and Secanell et al.^15–18 – have attempted to perform single cell fuel cell optimization using a physical or theoretical model. In all cases, a single objective optimization problem was solved and only Song et al.^9,10 and Secanell et al.,^15–18 have attempted to optimize electrode composition by using a one-dimensional cathode model and a two-dimensional cathode and anode model respectively.

In this paper, a numerical optimization methodology recently developed by the authors^16,17 and used to investigate the optimal cathode composition of standard fuel cells is extended to allow determination of the optimal composition and structure of an entire membrane electrode assembly. Section 2 of this paper describes the MEA model. Section 3 presents the optimization formulation and the computational framework. Using the computational framework, a multi-objective problem is solved and Pareto fronts for cost and performance are obtained in section 4, and the amounts of ionomer or electrolyte, platinum and carbon in both the anode and cathode CLs and the porosities in the GDL determined from the optimization process are presented and analyzed. The results demonstrate the importance of using a multi-objective formulation and highlight in particular the trade-offs between cost and performance. To the knowledge of the authors this represents the first attempt in the literature to apply numerical optimization to solve a multi-objective optimization problem for a complete membrane electrode assembly.

2 Membrane electrode assembly model

In this section, a model accounting for the salient transport phenomena in a complete membrane electrode assembly is outlined. A review of these phenomena and associated computational modelling strategies is given in ref. 19. The fuel cell model used here is based on our previous work;^16,17,20 this model considers a two-dimensional section of the fuel cell and is based on the following assumptions:

 

• The fuel cell is at steady state and operates at constant temperature and pressure.

• The cathode is fed with humidified air.

• The anode is fed with humidified hydrogen.

• The gas diffusion layers are composed of a porous fibrous matrix.

• The catalyst layer is formed by agglomerates made of a mixture of platinum supported on carbon and ionomer membrane electrolyte, and surrounded by void space.¹⁷

• The electrochemical reaction occurs inside the agglomerates.

• The transport of reactants from the gas channels to the catalyst layer occurs only by diffusion to the agglomerate surface and then by dissolution and diffusion through the ionomer to the reaction site.

• The transport of water inside the electrolyte in the membrane and CL is driven by electro-osmotic drag and diffusion.^20–22

• The water content in the membrane and the gas phase in the CL are assumed to be in equilibrium throughout the CL, therefore they are related by means of the sorption isotherm.

• The transport of protons takes place only through the ionomer phase and is governed by Ohm's law.

• The transport of electrons takes place only through the solid phase, i.e. the carbon fibers in the GDL and the mixture of carbon supported platinum in the catalyst layer, and is governed by Ohm's law.

2.1 Model equations

The governing equations for the complete MEA are:where the unknowns are the oxygen mole fraction, x_O2; the water mole fraction, x_w; the electrolyte (membrane) and electronic potentials, ϕ_m and ϕ_S, respectively; and, the membrane water content, λ. The effective transport parameters D^eff_O2, D^eff_w, D^eff_λ, σ^eff_m and σ^eff_S are different in the membrane, GDL and CL and depend nonlinearly on the design variables.¹⁷ The solution methodology requires all equations to be solved in all the domains, i.e. GDL, CL and membrane. However, some of the corresponding transport processes only take place in appropriate domains. The redundancy is simply addressed by setting the corresponding transport parameters to be essentially nil.

The source terms in the system of equations are given by:

andwhere λ_eq is given by the sorption isotherm reported by Hinatsu et al.²³ at the corresponding water vapour activity value in the specific location in the CL.

The term ∇·i is in fact a nonlinear function that depends on the unknowns and the design variables. As an example, in the cathode the volumetric current density, ∇·i, is

with units of A cm⁻³ and with the reaction kinetics, k_c, given as a function of the state variables

The different parameters in k_c are only a function of the design variables and they are described in detail in previous published work.¹⁷ The parameter A_ν represents the active area available for the reaction given the platinum loading, type of catalytic particles and catalyst layer thickness. It accounts for the platinum loading and the platinum activity depending on the particle size and dispersion on the carbon support according to the cyclic voltammetry data reported by the catalyst manufacturer, in this case E-TEK data is used.²⁴ Note that eqn (8) does not account for catalyst poisoning and therefore all sites are assumed to be available for the reaction. To account for CO poisoning an approach similar to those reported in refs. 25 and 26 should be used. An overview of the anode model and source terms is given in ref. 18. A detailed derivation of the governing equations as well a numerical and experimental validation of the model can be found in refs. 17 and 20.

2.2 Computational domain and boundary conditions

The two-dimensional cross-section representation of the membrane electrode assembly should include both CLs and GDLs and the membrane with appropriate boundary conditions for the gas channel–GDL and current collector–GDL interfaces. It is assumed here that the solution is continuous on the interfaces between layers. Taking advantage of geometric symmetry, the computational domain includes only half of the gas channel and half of the current collector, as shown in Fig. 1. The boundary conditions assume a zero flux boundary condition for all state variables, except at the anode and cathode current collector interfaces (segments A–F and B–C in Fig. 1) where solid phase voltage is specified, and at the anode and cathode gas channel interfaces (segment F–E and C–D) where the mole fraction of the reactants is given.

Fig. 1 Computational domain and initial grid used to solve the equations of the MEA model.

2.3 Input parameters

The input parameters to the membrane electrode assembly model are specified in Tables 1, 2, 3 and 4 for the operating conditions and geometry, anode electrode, membrane and cathode electrode respectively. The data presented here is obtained from the literature and the source of the data is specified next to the value.

Table 1 Membrane electrode assembly geometry and operating conditions

Geometry
Anode GDL thickness, La^gdl/cm	2.5 × 10^−2, [65]
Anode CL thickness, La^cl/cm	1.0 × 10^−3, [65]
Membrane thickness, L^m/cm	0.89 × 10^−2, Nafion 1135
Cathode CL thickness, Lc^cl/cm	1.0 × 10^−3, [65]
Cathode GDL thickness, Lc^gdl/cm	2.5 × 10^−2, [65]
Channel width/cm	0.1, [65]
Current collector width/cm	0.1, [65]
Cell operating conditions
T/K	353, [65]
Anode operating conditions
p/atm	3, [65]
x H2	0.88326 (75% RH)
x w	0.11674 (75% RH)
Cathode operating conditions
p/atm	3, [65]
x O2	0.18549 (75% RH)
x N2	0.69777 (75% RH)
x w	0.11674 (75% RH)

---

Table 2 Anode gas diffusion layer and catalyst layer physical and electro-chemical properties

Constants
ρ Pt /g cm^−3	21.5, [9]
ρ c/g cm^−3	2.0, [9]
ρ N /g cm^−3	2.0, [9]
Anode GDL and CL physical properties
D H2,w/cm^2 s^−1	0.34952, [66]
H H2,N/Pa cm^3 mol^−1	6.69 × 10^10, [64]
D H2,N/cm^2 s^−1	12.8 × 10^−6, [64]
σ ^gdl S, XX/S cm^−1	16.03
σ ^gdl S, YY/S cm^−1	272.78
σ ^cl S/S cm^−1	88.84
Anode GDL and CL structural properties
ε V ^gdl	0.6
m Pt /mg cm^−2	0.2, [27]
Pt|C	0.2, [27]
r agg/μm	1.0, [65]
ε agg	0.35, this work
δ agg/nm	80, [65]
Anode CL electrochemical properties
j OT /A cm^−2	0.47, [33]
j OH /A cm^−2	0.01, [33]
γ	1.2, [33]
C H2/mol cm^−3	0.59 × 10^−6, [64,67]

---

Table 3 Membrane physical and electro-chemical properties

EW /g mol^−1	1100, [21]
ρ dry/g cm^−3	2.0, [21]
k/s^−1	10000, this work

---

Table 4 Cathode gas diffusion layer and catalyst layer physical and electro-chemical properties

Constants
ρ Pt /g cm^−3	21.5, [9]
ρ c/g cm^−3	2.0, [9]
ρ N /g cm^−3	2.0, [9]
Cathode GDL and CL physical properties
D O2,N2/cm^2 s^−1	0.091368, [66]
D w, N2/cm^2 s^−1	0.098919, [66]
H O2,N/Pa cm^3 mol^−1	3.1664 × 10^10, [65]
D O2,N/cm^2 s^−1	8.45 × 10^−6, [65]
σ ^gdl S, XX/S cm^−1	16.03
σ ^gdl S, YY/S cm^−1	272.78
σ ^cl S/S cm^−1	88.84
Cathode GDL and CL structural properties
ε V ^gdl	0.6
m Pt /mg cm^−2	0.2, [27]
Pt|C	0.2, [27]
r agg/μm	1, [65]
ε agg	0.35, [65]
δ agg/nm	80, [65,32]
Cathode CL electrochemical properties
α	1, [34,35,68]
n	4, [34,35,65]
γ	1.0, [34,35,65]
i ^ref 0/A cm^−2	2.707 × 10^−8, [34,35]
C ^ref O2/mol cm^−3	0.725 × 10^−5, [34,35]

---

The geometrical parameters in Table 1 are prescribed standard values for the GDL and CL. The thickness of the membrane is that of a Nafion 1135 membrane. The operating conditions are the same as for Bender et al..²⁷ These operating conditions are chosen to readily validate the computational model (see section 2.4). Note that the relative humidity (RH) is set to be 75% since the authors in ref. 27 report humidification levels slightly below 100% RH.

The physical, structural and electrochemical parameters for the anode and cathode electrode are given in Tables 2 and 4, respectively. These values are also obtained from the literature. The diffusion coefficients and Henry's law constant are reported for the given operating conditions. The values for GDL and CL conductivities are obtained by curve fitting experimental data, such as that reported by Pantea et al.²⁸ for carbon black. The methodology for fitting these parameters is given in refs. 18 and 20. The structural parameters are given by the MEA information provided in ref. 27 for model validation. Finally, the amount of electrolyte inside the agglomerate is a fitting parameter and is set to ensure a reasonable volume fraction of each material in the CL. The structural parameters in Table 2 result in solid phase, electrolyte and porosity values of 0.409, 0.384 and 0.207, respectively. Note that the composition parameters and porosities are set for validation and the base case conditions, but are allowed to vary in the optimization process which in fact does yield different values as will be discussed subsequently. There is great uncertainty regarding the agglomerate radius and thin film surrounding the agglomerate. Experimental observations from TEM and SEM images suggest values ranging from 0.01 to 3 μm and 0 to 80 nm, respectively.^5,29–32 The values of 1 μm and 80 nm are used because they lie within the range of values reported in the literature and provide a good fit to the experimental polarization curve in ref. 27. The electrochemical data used for the anode corresponds to the recently proposed dual-path kinetics model.³³ For the cathode, the low voltage kinetics data reported by Parthasarathy et al.^34,35 is used.

The membrane properties are given in Table 3. Of these parameters, the constant k is the most important as it is used to properly couple the membrane water content to the water content in the catalyst layer. This constant needs to be set at a sufficiently large value to ensure consistency with the sorption isotherm. As such, k should not be considered to represent an adsorption/desorption rate.

2.4 Experimental validation

The (through-the-channel) two-dimensional model presented here does not account for convective transport and consumption of reactants along the gas flow direction, and is thus representative of operating conditions corresponding to very high stoichiometries in both cathode and anode channels. Thus low stoichiometry experimental data commonly used for validation, e.g. Wang et al.,^36,37 is not appropriate here. Since polarization curves at high stoichiometries are seldom published, data from the first segment of a segmented cell study is used for validation. Several research group have developed and performed such segmented cell experiments.^27,38–44 In this paper, the data from Bender et al.²⁷ is used for validation, as this work documents in detail the MEA properties and experimental setup. Tables 1, 2, 3 and 4, provide the input data for the simulations. All the data used for the validation is taken either from the experimental setup given in ref. 27 or sources referenced in section 2.3.

Fig. 2 compares the polarization curve reported by Bender et al. for the first segment of the cell and the curve obtained using the present numerical model. It should be noted that the humidifier temperature in the experiments was equal to the cell temperature and the inlet air should be fully saturated. However, Bender et al. report that even in this case, the air was not fully humidified. Therefore, polarization curves for both 75 and 100% relative humidities were computed and are plotted in Fig. 2. The experimental curve falls between the two predicted polarization curves, and good overall agreement between numerical and experimental data is obtained over the whole range of operating voltages.

Fig. 2 Polarization curves from experimental data and numerical data at 75 and 100% RH.

3 Optimization problem

The mathematical formulation for multi-objective optimization is presented with a focus on simultaneous optimization of the MEA in terms of both performance (minimum losses) and production costs (minimum platinum content).

3.1 Objective functions

Fuel cell performance is commonly described in terms of its polarization behavior, i.e. voltage versus current density. Performance can be improved either at a single operating voltage (single-point optimization) or in a specific range of operating conditions (multi-point or robust optimization). If the goal is to optimize the performance of current MEA designs at a given operating point, e.g. at a fixed cell voltage, the objective function can be expressed simply as the current density at the given voltage. On the other hand, if the goal is to maximize performance in a given operating range, the design objective is less straightforward to define and express mathematically. A possible representation of the objective would be to either optimize a weighted sum of current densities at several points in the operating range or to optimize the integral of the polarization curve in the given range. Multi-point optimization is an active area of research and there are several issues regarding the choice of the objective.^45,46 In this work we focus on single-point optimization problems where the objective function that quantifies performance is given by the current density at the desired voltage.

Cost reduction is the second objective of the optimization. A recent study by General Motors researchers identifies polymer electrolyte membrane and platinum (Pt) costs as the key barriers to achieving the US $30/kW target for large scale commercialization.^47,48 Whereas the cost of platinum is not expected to decrease, the cost of polymer electrolyte membranes could potentially be reduced by a factor of ten according to electrolyte manufacturers such as DuPont and Asahi Chemical.⁴⁹ Consequently in this first attempt at addressing the issues of cost and performance using a systematic methodology, it is assumed that platinum loading is a good indicator of a PEMFC cost and is thus used here as the objective function representing cost. The costs of the electrolyte, bipolar plates, balance of plant and control system are assumed constant. Future work should incorporate a more comprehensive cost analysis module that accounts for the additional materials and components as well as their amortization depending on fuel cell degradation rates.

3.2 Design variables

The anode and cathode catalyst layer structure and compositions are characterized by five parameters: platinum loading, m_Pt; mass percentage of platinum catalyst on the support carbon black, Pt|C; agglomerate radius, r_agg; agglomerate thin film thickness, δ_agg; and electrolyte volume fraction inside the agglomerate, ε_agg.¹⁷ Three of these parameters can be controlled during manufacturing and are thus used as design variables: the platinum loading; the mass percentage of platinum catalyst on the support carbon black; and, the electrolyte volume fraction inside the agglomerate. The GDL porosity is also included as a design variable.

The platinum loading can be controlled when dispensing the amount of catalyst in the ink used to create the CL. The platinum to carbon ratio can also be controlled by selecting the appropriate catalytic particles. Manufacturers usually provide a selection of catalytic particles with different platinum to carbon ratios ranging from 0.05 wt% platinum on carbon to platinum black.^50,51 The ionomer film and the amount of ionomer inside the agglomerate provide the total amount of electrolyte in the catalyst layer. It is difficult to discern how much of the electrolyte will become part of the agglomerate and how much will be used to create an electrolyte film. A study performed by Lee et al.³² suggests that the thickness of the electrolyte film surrounding the agglomerate increases rapidly when the electrolyte content in the catalyst layer increases from zero to 10 wt% and then remains almost constant. Following Lee et al., in this work it is assumed that the electrolyte film surrounding the agglomerate is constant and equal to 80 nm. Adjustments to this value should be considered when using different methods of preparation of the catalyst layer. The radius of the agglomerate is also considered constant, even though, Song et al.⁵² suggest that this value can also be varied by using different manufacturing processes and ink preparations. The effect of the agglomerate radius and the thin film was already discussed in a our previous work,¹⁷ where it was shown that these two parameters should not be included as design variables in the optimization problem because they do not present any trade-offs. These parameters represent mass transport resistances due to current CL manufacturing methods and, their optimization is trivial and yields values of zero.

3.3 Optimization of the MEA cost and performance

The problems of maximizing performance and minimizing cost need to be solved simultaneously. There is a large array of methods to solve multi-objective problems and to obtain the set of Pareto optimal solutions;^53–58 one of the most widely used methods is the weighted sum method.⁵⁴ In this method, the multiple objectives are transformed into a single objective function by multiplying each objective by a weighting factor and summing up all contributions such that the final objective is:

J_weightedsum = w₁J₁ + w₂J₂ + … + w_nJ_n (9)

where w_i are the weighting factors. If the sum of all weights is equal to one, then the weighted sum is said to be a convex combination of objectives, and if all objectives are convex, the weighted sum objective will also be convex.

In general, in a multiple objective optimization problem there is no global optimum; specifically for the problem at hand there exists a set of optimal solutions corresponding to a set of weighting factors. These solutions are represented as a so-called Pareto curve, whereby for a performance–cost objective function problem moving from one point on the curve to the other improves one objective and worsens the other. None of these points are intrinsically superior, and the choice of optimized solution depends on techno–economic considerations specific to the application (e.g. portable vs. automotive). The Pareto front can be obtained by systematically changing the weights and solving the given optimization problem. The weighted sum method is easy to implement and it is readily understood, however it has two drawbacks: (1) a uniform spread of weight parameters rarely produces a uniform spread of points on the Pareto set; and (2) non-convex parts of the Pareto set cannot be obtained.⁵⁹

In this paper, the weighted sum method is used because we are mainly interested in a small number of solutions in the Pareto set and the physical meaning of the weights is easy to understand. Furthermore, the method is shown to provide good results for most engineering applications and is readily implemented in DAKOTA,⁶⁰ the OpenSource optimization program used.

The MEA multi-objective optimization problem is formulated using a simple weighted sum method as

where i(dV) represents the current density at a given voltage across the MEA, the subscripts c and a represent the design variables in the cathode and anode respectively; ε^cl_{V, c}, ε^cl_{S, c} and ε^cl_{N, c} are constraints in the volume fraction of each material in the CL; w₁ + w₂ = 1 and where a negative sign has been added in front of the performance objective, i.e. the current density, in order for the two objectives to be minimization problems. In order for the weighted sum method to search the Pareto set effectively, objectives must be scaled to have similar values.⁶¹ In this case, both current density and total platinum loading are of the same order of magnitude and scaling is not necessary.

In addition to the constraints shown in eqn (10) all design variables are bounded. The design variable bounds are shown in Table 5.

Table 5 Initial upper and lower bounds for the design parameters used to optimize the catalyst layer

Design variable	Upper bound	Lower bound
m Pt , c and mPt, a/mg cm^−2	1.0	1 × 10^−4
ε agg, c and εagg, a	0.9	0.1
Pt|Cc and Pt|Ca	1.0	0.05
ε ^gdl V , c and ε^gdlV, a	0.9	0.1

---

In the optimization problem above, one of the objective functions is given by the fuel cell current density at a given MEA voltage. The current density per unit area of a fuel cell can be obtained during postprocessing by integrating the volumetric current density over the volume of either the anode or the cathode CL,

where ∇·i is given in eqn (7), H is the height of the domain and L is the width of the domain, i.e. the thickness of the CL. The second objective, the platinum loading, is given directly by the platinum loading design variables. The constraint equations in the optimization problem in eqn (10) are directly given by the analysis model. Hence, no extra computations are required to determine the second objective and the constraints.

In order to solve the optimization problem effectively using gradient-based optimization algorithms, the analytical sensitivity equations of the model with respect to the design variables are obtained, as opposed to the commonly used forward differences.^9,11,12 The use of analytic sensitivity equations increase accuracy of the sensitivities and reduces the computational cost of the design framework, an important consideration for development of a design framework that can be used for large scale optimization of fuel cells. The mathematical formulation used to obtain the sensitivity equations is introduced in the ESI.†

3.4 Design and optimization numerical framework

The MEA model together with the analytic sensitivity equations of the objective function and constraints are discretized using finite elements and solved using the deal.II finite element libraries.^62,63 The MEA finite element model is then coupled to the optimization package DAKOTA,⁶⁰ as shown in Fig. 3, where the three main iterative loops can be identified. The inner or analysis loop is used to solve the nonlinear governing equations by means of Newton's algorithm and the finite element method. The middle or adaptive refinement loop is used to check the accuracy of the solution and adapt the computational mesh as necessary using an a posteriori error estimator. The outer or optimization loop is used to change the design parameters in order to obtain an improved design. Convergence of the optimization algorithm is achieved either when the relative change in the objective function is less that 10⁻³ or the L₂ norm of the gradient of the objective function is less than 10⁻³. A more detailed explanation of the design framework can be found in ref. 20.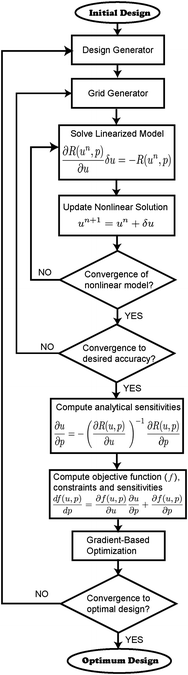

Fig. 3 Implementation of the multivariable optimization framework with adaptive refinement and analytic sensitivities.

4 Discussion and results

In this section, Pareto optimal solutions are obtained for six sets of weights. Table 6 shows the values for the weights. w₁ is the current density weight and w₂ is the cost weight. The weights are selected to assign different importance to each objective. Set 1 is equivalent to solving a single objective performance maximization problem. Sets 2 and 3 ascribe higher importance to performance, but at the same time, penalize cost. Set 4 gives similar importance to performance and cost. Notice, however, that the weights being equal does not imply that the two objectives are given exactly equal importance since this will also depend on the values of both objectives. Set 5 and 6 put more weight on cost than performance. Notice that a set with w₂ equal to one is not considered as it leads to a trivial and impractical solution: the minimum cost with no performance constraint is obtained with zero amount of catalyst, which would result in no reaction and a zero current density.

Table 6 Weights used to obtain Pareto optimal solutions

	w 1	w 2
Set 1	1.0	0.0
Set 2	0.9	0.1
Set 3	0.75	0.25
Set 4	0.5	0.5
Set 5	0.25	0.75
Set 6	0.1	0.9

---

Since optimization is performed at a given operating voltage, three Pareto fronts are also obtained at three different operating voltages. The Pareto fronts at different operating voltages represent the optimal designs that can be obtained when optimizing the fuel cell for that specific voltage and are obtained by solving the optimization problem in eqn (10) for the sets of weights in Table 6. Note that it might not be possible to achieve a design that lies on top of all three Pareto fronts simultaneously.

Fig. 4 shows an approximation of the three Pareto fronts obtained by solving the optimization problem in eqn (10) with the weights in Table 6 for three operating points corresponding to cell operation at low, medium and high current densities, i.e. at low, medium and high MEA voltage losses. All optimization problems converged, except for set 6 at high current densities. Fig. 5 shows the evolution of the two objectives and the combined objective (left) and the evolution of the design variables for Set 3 at 0.6 V voltage across the MEA. The lack of convergence for set 6 at dV = 0.8 V was due to convergence problems in the analysis code at high currents and low platinum contents. The design variables for the initial design are {m_{Pt, c}, ε_{agg, c}, Pt|C_c, ε^gdl_{V, c}, m_{Pt, a}, ε_{agg, a}, Pt|C_a, ε^gdl_{V, a}} = {0.2, 0.35, 0.2, 0.6, 0.2, 0.35, 0.2, 0.6}, which corresponds to values for a typical MEA with the same composition for anode and cathode.²⁷ An optimization run with a given set of weights usually converges after approximately 20 iterations and 30 min of CPU time on a 2 GHz Mac PowerPC G5.

Fig. 4 Pareto front at three different operating conditions.

Fig. 5 Evolution of the objectives (left) and the design variables (right) during the multiobjective optimization problem with w₁ = 0.75 and w₂ = 0.25 at an operating voltage of dV = 0.6 V.

In Fig. 4, the points that are on the right of the Pareto fronts represent those points for the weight set 1, i.e. maximum performance regardless of cost. As the points move towards the left, the optimal Pt cost and performance for the optimal designs obtained by solving the optimization problem for weight sets 2–6 are shown. The trivial solution of zero current density for zero catalyst is also shown. Examining the Pareto front it is clear that there is a trade-off between performance and cost. The highest values of current density are obtained when the platinum loadings are high, i.e. of the order of 2 mg cm⁻². Once cost is included as an objective, the platinum loading is reduced at the expense of performance.

Fig. 4 also shows three very distinct areas. At the far right, the slope of the Pareto fronts is small. This means that at any operating voltage a large increase in cost is necessary for a small increase in performance. Similarly, at the far left, the slope is very steep. In this area, in order to obtain an optimal design with a low Pt cost, a very large drop in performance is required. In the middle of the graph, for platinum loadings between 0.1 and 0.6 mg cm⁻² is where the best trade-offs between Pt cost and performance are achieved. Looking at the Pareto fronts it is clear that the designs obtained using maximum performance only as an objective are not the best designs. These designs are extremely expensive when compared to the design obtained from weight set 2 which provides current densities well above 0.8 A cm⁻² at 0.6 V across the MEA at one third of the price. This highlights the advantages of using multi-objective optimization. Inside the range of platinum loadings between 0.1 and 0.6 mg cm⁻², all designs offer some advantages and it is up to the designer to select the most appropriate design depending on the application. For example, if the fuel cell is to be used for a mass-produced automobile, maybe a design with a platinum loading of 0.2 mg cm⁻² provides the necessary performance. However, for a one-of-a-kind high performance automobile, a design with higher platinum loadings of around 0.6 mg cm⁻² might be more appropriate. Platinum loadings above 0.6 mg cm⁻² are not likely to be used because the achieved performance increase by increasing platinum loading do not justify the extra cost.

Regarding the applicability of the weighted sum method, the results in Fig. 4 using the different weights are well spaced and resolve the Pareto front adequately. Only for very large weights for cost the weight sum method starts to cluster points in the Pareto set. However, at those values performance is already unacceptably low for any application. Therefore, in this case the sum weighted residual is an appropriate method to obtain the Pareto curve. Fig. 6 shows a well-populated Pareto front and the weights used to obtain the Pareto plot for a voltage across the MEA of 0.6 V. The figure shows the convexity of the Pareto front and no discontinuities are observed, further confirming the applicability of the weighted sum method in this case. The front is well populated in all areas but at very high performance. The latter is due to the large impact of introducing cost as an objective. The blue points in Fig. 6 are selected as example of a set of well distributed weights. They show that such set yields a well distributed Pareto front.

Fig. 6 Pareto front (left) and the set of weights used to obtain the Pareto front (right) at operating condition of dV = 0.6 V.

Figs. 7 and 8 show the value of the cathode design variables and the CL volume fraction for all designs in the Pareto curves in Fig. 4 at the three different operating voltages. Looking at the figures from right to left, they show the evolution of the design variables and the volume fraction as cost is considered more important for the optimal design at each of the three design voltages. The most interesting parameters from these curves are the platinum loading and the platinum to carbon ratio. For all operating conditions, for the optimal Pareto design with set 1, platinum loading reaches its upper bound of 1 mg cm⁻². As the cost objective is ascribed increasing importance, both platinum loading and platinum to carbon ratio start to decrease. Initially with a sharp drop, from set 1 to 2, and then more gradually. Furthermore, both curves follow a very similar trend. This can be explained by examining the evolution of the solid phase volume fraction in Fig. 8. Even though, the platinum loading drops sharply, the solid phase volume fractions remain quite similar with a slight decrease as cost becomes more important. The slight decrease is mainly due to the reduction in current density for the latter designs and therefore; a decrease for the necessity for highly electrical conductive material in the CL. From the figures, it is clear that there is a strong coupling between these two parameters so that electrical conductivity in the CL is maintained. The electrolyte volume fraction inside the agglomerate and the GDL porosity remain almost constant regardless of the Pareto optimal solution.

Fig. 7 Cathode design variable values for the design given by weights sets 1–6 at operating conditions of dV = 0.4, 0.6 and 0.8 V.

Fig. 8 Cathode CL solid, void and electrolyte phase volume fractions for the design given by weights sets 1–6 at operating conditions of dV = 0.4, 0.6 and 0.8 V.

Comparing the designs obtained at different operating voltages in Fig. 7, an increase in electrolyte volume fraction inside the agglomerate is observed as the voltage across the MEA is increased. Note that an increase in the voltage across the MEA results in an increase in current density. GDL porosity increases steadily with increased operating voltage across the MEA. The latter most likely due to the increase in oxygen consumption with increasing current density. The increase in GDL porosity results in a reduction of the mass transport limitations. Finally, for the different voltages, the Pt loading and the platinum to carbon ratio follow similar trends. However, at lower MEA voltages, the Pt loading appears to be more reluctant to decrease for the same set of weights. This is because at low MEA voltage, i.e. low overpotential, the fuel cell is limited by the ORR kinetics. Looking at the CL volume fractions in Fig. 8 similar trends are observed. As the voltage across the MEA is increased, CL porosity increases. In the CL the total amount of electrolyte is highest at medium operating voltages, this is because at medium current densities Ohmic losses in the electrolyte dominate. Finally, the solid phase volume fraction decreases as current increases to leave more space to the other two phases.

Figs. 9 and 10 show the value of the anode design variables and the CL volume fraction for all designs in the Pareto curves. Looking at Fig. 9, the platinum loading is reduced by almost one order of magnitude almost immediately after cost is added to the objective. For set 1 (maximum performance at any cost) the platinum loading was of the order of 0.5 mg cm⁻². This value drops to almost 0.05 mg cm⁻² in set 2 and then remains almost constant for sets 3–6. Similarly to the cathode, the platinum to carbon ratio follows the platinum loading behaviour due to their close coupling. The large reduction in platinum loading from set 1 to set 2 comes at a small expense in performance. This result is consistent with the results published recently by Karan⁶⁴ and Secanell et al.,¹⁸ where an anode model was used to minimize platinum loading at a given current density, as well as with the experimental observations of Gasteiger et al..⁴⁸ It was also shown by the authors that reducing the anode CL thickness could result in further platinum loading reductions; therefore, highlighting the possibility to introduce geometric design variables into the design process. The electrolyte volume fraction inside the agglomerate and the GDL porosity follow similar trends to the cathode. An interesting difference between the anode and the cathode is the extremely low GDL and CL porosity in the anode design at low operating voltages. This porosity is found to increase at high current densities. This increase occurs in order to improve water transport to the membrane rather than hydrogen transport.

Fig. 9 Anode design variable values for the design given by weights sets 1–6 at operating conditions of dV = 0.4, 0.6 and 0.8 V.

Fig. 10 Anode CL solid, void and electrolyte phase volume fractions for the design given by weights sets 1–6 at operating conditions of dV = 0.4, 0.6 and 0.8 V.

4.1 Final remarks

Comparing the results obtained from the previous optimization formulations^16,17,20 and the proposed multi-objective optimization formulation, it is clear that cost must be included in the optimization objective. If only performance is optimized, the outcome is a very expensive electrode. The results also show the importance of designing MEAs with different anode and cathode electrodes in order to save on Pt costs. The presented optimization results suggest that platinum reductions in the anode to values of less than 0.05 mg cm⁻² could be achieved with very little penalty in performance. Furthermore, competitive performances at any operating condition can be obtained with total platinum loadings on the order of 0.2–0.1 mg cm⁻². Looking at Fig. 4, for a cell voltage of 0.593 V, a current density of 0.7 and 0.8 A cm⁻² can be achieved with platinum loadings of 0.1 and 0.2 mg cm⁻². These values represent a Pt-specific power density of the cell with an optimized MEA of 0.241 and 0.422 g_PtkW⁻¹, respectively. The target for large-scale implementation is 0.4 g_PtkW⁻¹.⁴⁸ Therefore, the results show that, by optimizing current PEMFC MEAs, targets could be met for future fuel cell commercialization. These results are even more encouraging considering there is potentially further room for improvement from optimization of geometrical and/or operating conditions parameters.

5 Conclusion

A fuel cell analysis and design framework has been presented. This analysis and design tool consists of a two-dimensional, through-the-channel fuel cell model coupled to a gradient-based optimization algorithm. A multi-objective optimization problem has been formulated, implemented and solved using this design framework. The results illustrate and quantify the existing trade-offs between cost and performance. The Pareto fronts presented show that there is only a specific range of designs that present a good trade-off between Pt costs and performance. This is shown to be true for any design regardless of the desired operating voltage. The designs that offer the best trade-off between Pt cost and performance have total Pt loadings between 0.1 and 0.6 mg cm⁻² and produce current densities in the range of 1.25–1.35, 0.7–0.85 and 0.1–0.25 A cm⁻² depending on the operating voltage for which the design is optimized, i.e. 0.8, 0.6, 0.4 V across the MEA, respectively. The optimal designs exhibit a very different composition for anode and cathode, demonstrating the advantages of developing MEAs with different anodes and cathodes. The optimal designs that offer the best trade-offs have anode Pt loadings that are one to two orders of magnitude less than the cathode ones.

The new MEA design methodology presented in this paper is rational and systematic, and its application demonstrates the potential benefits of using multi-objective optimization for fuel cell design. An important aspect of this methodology is its applicability to large scale optimization of fuel cells. However, further work is required on several fronts. The results presented here are obtained taking into account only two objectives. The optimal CL compositions might change once durability and reliability are included in the optimization. The results depend of course on the physico-chemical processes accounted for in the model; the model presented here does not for instance account for possible CO poisoning in the anode. The introduction of this phenomena might yield designs requiring higher Pt loadings in the anode. The multi-objective approach highlights the need for a holistic approach for designing optimal fuel cell systems. Given the large number of design objectives and design parameters, such an approach is only feasible by means of numerical optimization.

Acknowledgements

Financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC), Hydrogen and Fuel Cells Canada and the Canada Research Chairs Program are gratefully acknowledged.

References

1. G. Sasikumar, J. Ihm and H. Ryu, Electrochim. Acta, 2004, 50(2–3), 601–605.
2. E. Passalacqua, F. Lufrano, G. Squadrito, A. Patti and L. Giorgi, Electrochim. Acta, 2001, 46, 799–805.
3. E. Antolini, L. Giorgi, A. Pozio and E. Passalacqua, J. Power Sources, 1999, 77, 136–142.
4. Z. Xie, T. Navessin, K. Shi, R. Chow, Q. Wang, D. Song, B. Andreaus, M. Eikerling, Z. Liu and S. Holdcroft, J. Electrochem. Soc., 2005, 152(6), A1171–A1179.
5. P. Gode, F. Jaouen, G. Lindbergh, A. Lundblad and G. Sundholm, Electrochim. Acta, 2003, 48, 4175–4187.
6. N. Cunningham, E. Irissou, M. Lefevre, M.-C. Denis, D. Guay and J.-P. Dodelet, Electrochem. Solid-State Lett., 2003, 6(7), A125–8.
7. S. Mukerjee, S. Srinivasan and A. J. Appleby, Electrochim. Acta, 1993, 38(12), 1661–1669.
8. M. S. Saha, A. F. Gulla, R. J. Allen and S. Mukerjee, Electrochim. Acta, 2006, 51(22), 4680–4692.
9. D. Song, Q. Wang, Z. Liu, T. Navessin, M. Eikerling and S. Holdcroft, J. Power Sources, 2004, 126(1–2), 104–111.
10. D. Song, Q. Wang, Z. Liu, M. Eikerling, Z. Xie, T. Navessin and S. Holdcroft, Electrochim. Acta, 2005, 50(16–17), 3359–3374.
11. M. Grujicic and K. Chittajallu, Appl. Surf. Sci., 2004, 227, 56–72.
12. M. Grujicic and K. Chittajallu, Chem. Eng. Sci., 2004, 59, 5883–5895.
13. M. Grujicic, C. Zhao, K. Chittajallu and J. Ochterbeck, Mater. Sci. Eng. B, 2004, 108, 241–252.
14. A. Mawardi, F. Yang and R. Pitchumani, J. Fuel Cell Sci. Technol., 2005, 2(2), 121–135.
15. M. Secanell, B. Carnes, A. Suleman, and N. Djilali, in III European Conference on Computational Mechanics. ECCOMAS, 2006.
16. M. Secanell, B. Carnes, A. Suleman and N. Djilali, Electrochim. Acta, 2007, 52(7), 2668–2682.
17. M. Secanell, K. Karan, A. Suleman and N. Djilali, Electrochim. Acta, 2007, 52(22), 6318–6337.
18. M. Secanell, K. Karan, A. Suleman and N. Djilali, J. Electrochem. Soc., 2008, 155(2), B125–B134.
19. N. Djilali, Energy, 2007, 32(4), 269–280.
20. M. Secanell, Computational Modeling and Optimization of Proton Exchange Membrane Fuel Cells, PhD thesis, University of Victoria, 2007.
21. T. Springer, T. Zawodzinski and S. Gottesfeld, J. Electrochem. Soc., 1991, 138(8), 2334–2342.
22. P. Sui and N. Djilali, ASME J. Fuel Cell Sci. Technol., 2005, 2(3), 149–155.
23. J. T. Hinatsu, M. Mizuhata and H. Takenaka, J. Electrochem. Soc., 1994, 141(6), 1493–1498.
24. E-TEK, http://www.etek-inc.com/, Data accessed on February 2, 2007.
25. T. Springer, T. Rockward, T. Zawodzinski and S. Gottesfeld, J. Electrochem. Soc., 2001, 148(1), A11–A23.
26. A. Shah, P. Sui, G. S. Kim and S. Ye, J. Power Sources, 2007, 166, 1–21.
27. G. Bender, M. S. Wilson and T. A. Zawodzinski, J. Power Sources, 2003, 123(2), 163–171.
28. D. Pantea, H. Darmstadt, S. Kaliaguine and C. Roy, Appl. Surf. Sci., 2003, 217(1–4), 181–193.
29. K. Broka and P. Ekdunge, J. Appl. Electrochem., 1997, 27(3), 281–289.
30. K. More, R. Borup and K. Reeves, ECS Trans., 2006, 3(1), 717–733.
31. F. Jaouen, G. Lindbergh and G. Sundholm, J. Electrochem. Soc., 2002, 149(4), A437–A447.
32. S. Lee, S. Mukerjee, J. McBreen, Y. Rho, Y. Kho and T. H. Lee, Electrochim. Acta, 1998, 43(24), 3693–3701.
33. J. X. Wang, T. E. Springer and R. R. Adzic, J. Electrochem. Soc., 2006, 153(9), A1732–A1740.
34. A. Parthasarathy, S. Srinivasan, A. J. Appleby and C. R. Martin, J. Electrochem. Soc., 1992, 139(9), 2530–2537.
35. A. Parthasarathy, S. Srinivasan, A. J. Appleby and C. R. Martin, J. Electrochem. Soc., 1992, 139(10), 2856–2862.
36. L. Wang, A. Husar, T. Zhou and H. Liu, Int. J. Hydrogen Energy, 2003, 28(11), 1263–1272.
37. L. Wang and H. Liu, J. Power Sources, 2004, 134(2), 185–196.
38. J. Stumper, S. A. Campbell, D. P. Wilkinson, M. C. Johnson and M. Davis, Electrochim. Acta, 1998, 43(24), 3773–3783.
39. A. Hakenjos, K. Tüber, J. Schumacher and C. Hebling, Fuel Cells, 2004, 4(3), 185–189.
40. D. Natarajan and T. V. Nguyen, AIChE J., 2005, 51(9), 2587–2598.
41. D. Natarajan and T. V. Nguyen, AIChE J., 2005, 51(9), 2599–2608.
42. D. Natarajan and T. V. Nguyen, J. Power Sources, 2004, 135(1), 95–109.
43. D. J. L. Brett, S. Atkins, N. P. Brandon, V. Vesovic, N. Vasileiadis and A. R. Kucernak, Electrochem. Commun., 2001, 3(11), 628–632.
44. T. Hottinen, M. Noponen, T. Mennola, O. Himanen, M. Mikkola and P. Lund, J. Appl. Electrochem., 2003, 33, 265–271.
45. W. Li, L. Huyse and S. Padula, Struct. Multidiscipl. Optim., 2002, 24, 38–50.
46. D. W. Zingg and S. Elias, AIAA J., 2006, 11(44), 2787–2792.
47. M. F. Mathias, R. Makharia, H. A. Gasteiger, J. J. Conley, T. J. Fuller, C. J. Gittleman, S. S. Kocha, D. P. Miller, C. K. Mittelsteadt, T. Xie, S. G. Van and P. T. Yu, Electrochem. Soc. Interface, 2005, 14(3), 24–35.
48. H. Gasteiger, J. Panels and S. Yan, J. Power Sources, 2004, 127, 162–171.
49. P. Costamagna and S. Srinivasan, J. Power Sources, 2001, 102, 242–252.
50. C. Marr and X. Li, J. Power Sources, 1999, 77(1), 17–27.
51. E-TEK, http://www.etek-inc.com, (Accessed Nov. 2006).
52. D. Song, Q. Wang, Z. Liu, T. Navessin and S. Holdcroft, Electrochim. Acta, 2004, 50, 731–737.
53. I. Kim and O. de Weck, Struct. Multidiscipl. Optim., 2005, 29, 149–158.
54. I. Kim and O. de Weck, Struct. Multidiscipl. Optim., 2006, 31, 105–116.
55. J. G. Lin, IEEE Trans. Autom. Control, 1976, 21(5), 641–650.
56. I. Das, http://www-fp.mcs.anl.gov/otc/Guide/OptWeb/multiobj, (Accessed July 2007).
57. A. Messac and C. A. Mattson, AIAA J., 2004, 42(10), 2101–2111.
58. I. Das and J. Dennis, SIAM J. Optim., 1998, 8, 631–657.
59. I. Das and J. Dennis, Struct. Optim., 1997, 14, 63–69.
60. M. Eldred, A. Giunta, B. van Bloemen Waanders, J. S. F. Wojtkiewicz, W. Hart and M. Alleva Dakota, A multilevel parallel object-oriented framework for design optimization, parameter estimation, uncertainty quantification, and sensitivity analysis. version 3.0 users manual. Technical Report 2001–3796, Sandia National Laboratory, 2003.
61. G. Vanderplaats, Numerical Optimization Techniques for Engineering Design with Applications, McGraw-Hill, 1984.
62. W. Bangerth, R. Hartmann and G. Kanschat, ACM Trans. Math. Softw., 2007, 33(4) , article 4.
63. deal.II differential equations analysis library, Technical reference. W. Bangerth, R. Hartmann and G. Kanschat.
64. K. Karan, Electrochem. Commun., 2007, 9(4), 747–753.
65. W. Sun, B. A. Peppley and K. Karan, Electrochim. Acta, 2005, 50(16–17), 3347–3358.
66. E. L. Cussler, Diffusion: Mass Transfer in Fluid Systems, Cambridge University Press, Cambridge, UK, 2nd edn, 1997.
67. S. Chen and A. Kucernak, J. Phys. Chem. B, 2004, 108(10), 3262–3276.
68. K. C. Neyerlin, W. Gu, J. Jorne and H. A. Gasteiger, J. Electrochem. Soc., 2006, 154(10), A1955–A1963.

---

Footnote

† Electronic supplementary information (ESI) available: Mathematical formulation used to obtain the sensitivity equations. See DOI: 10.1039/b804654a

---