Optical micromanipulation

Abstract

Optical micromanipulation has engendered some major studies across all of the natural sciences at the mesoscopic scale. Though over thirty-five years old, the field is finding new applications and has lost none of its dynamic or innovative character: a trapped object presents a system that enables a calibrated minuscule force (piconewtons or less) to be exerted at will, enabling precision displacements right down to the angstrom level to be observed. The study of the motion of single biological molecular motors has been revolutionised and new studies in the physical sciences have been realised. From the chemistry and microfluidic viewpoint, optical forces may remotely actuate micro-components and perform micro-reactions. Overall, optical traps are becoming a key part of a wider “optical toolkit”. We present a tutorial review of this technique, its fundamental principles and a flavour of some of the recent advances made.

---

Kishan Dholakia

Kishan Dholakia is Professor of Physics at the University of St Andrews, Scotland and an honorary adjunct Professor at the Center for Optical Sciences at the University of Arizona. He heads a large (20+) group working in various aspects of photonics including micromanipulation and biophotonics. He has published over 300 journal/conference papers and his group won the European Optics Prize in 2003. He was elected to the position of Fellow of the Royal Society of Edinburgh in 2007.

Peter Reece

Peter Reece is a Postdoctoral Research Associate working at the University of St Andrews in the United Kingdom. He received his PhD in Physics (2005) from the University of New South Wales, Sydney, Australia and a BSc (Hons 1) in Medical Physics (1999) from the same institution. He has wide ranging experience in photonics and his current research activities are focused on advanced optical trapping techniques and optical force induced self-organization.

Min Gu

Professor Min Gu, a University Distinguished Professor, is Director of the Centre for Micro-Photonics at Swinburne University of Technology. He is a sole author of two standard reference books and has over 450 publications in nano/biophotonics. He is a Past President of the International Society of Optics within Life Sciences and a Vice President of the International Commission for Optics. He is a member of the editorial board of 13 internationally leading journals in optical science and photonics. He is an elected Fellow of the Australian Academy of Science, the Australian Academy of Technological Sciences and Engineering, the Australian Institute of Physics, the Optical Society of America and the International Society for Optical Engineering.

---

Introduction

Few would have predicted the tremendous impact the laser has had across all of the natural sciences or indeed in a myriad applications in our everyday lives since its arrival over forty years ago. Laser technology in tandem with microscopy has fuelled a revolutionary advance in biology and chemistry. Microscopic methods have allowed scientists to observe cells and single molecules in action and study the behaviour of proteins and lipids and other biological macromolecules. Real-time observation and tracking of cellular processes has yielded a wealth of bioscience. Imaging techniques such as confocal imaging and two-photon excitation are established techniques for visualising cells and molecules in three dimensions. However the influence of light is not restricted to such a passive mode such as imaging—light may move, hold, guide and exert a very controllable yet calibratable force on mesoscopic objects. This is the area of optical micromanipulation that is the topic of this article.

We need to turn to a famous astronomer rather than a biologist however to find the roots of this field: four centuries ago, the famous astronomer Johannes Kepler was intrigued by his observation that the tail of a comet pointed away from the sun at all times which he attributed to some kind of solar pressure. Scientific developments around 100 years ago reinforced these ideas: light could indeed exert a force and thus carried momentum. Terrestrial experiments coupled with our understanding of the wave–particle duality of light mean we know that this photon momentum is very small, in turn leading to a force of the order of piconewtons. Thus on Earth, we are restricted to influencing the motion of microscopic or nanoscale objects rather than a comet! Excitingly this is the size scale where there is immense interest particularly from the biology and chemistry communities. These ideas came of age with the novel use of the laser: a light source of concentrated, coherent photons in a pencil-like beam signalled the advent of the field of optical micromanipulation: moving or trapping objects non-invasively using light.

It is over twenty years now since the conception of the most popular form of optical micromanipulation, the single beam optical trap termed “optical tweezers”.¹ However the first experiments in this field date back much earlier than 1986. In 1970 Ashkin performed his original experimental studies:² with a single weakly focused propagating beam, particles were seen to propel themselves along the beam axis and through the beam centre: this is optical guiding. Further work showed that two such gently focused counter-propagating beams were seen to make the first true trap: the dual beam trap. This counter-propagating beam geometry was superseded by the single beam gradient trap (optical tweezers) which has become the most popular incarnation of this field. Nevertheless, the dual beam trap has retained much interest due to its divergent light fields and in 1993 was realised in a robust geometry using optical fibres.³

This tutorial article cannot hope to cover the full extent or diversity of the field but aims to give the reader an introduction to optical micromanipulation indicating the latest advances and challenges in the field. It is organised as follows: we explain the basic mechanisms of light–matter interaction to achieve trapping in the next section including theoretical considerations. We follow this by a discussion of the biological advances that may be achieved with optical traps. We then explore schemes to generate multiple arrays of optical traps, including novel light fields and use of near field geometries. We aim to give particular emphasis on the interdisciplinary nature of the work and mention some of the studies that have been performed. We describe applications in the arena of microfluidics and the combination of trapping with other modalities within a microscope. We conclude with challenging themes in the field.

How does optical trapping work?

The light–matter interaction is at the heart of optical trapping and the subsequent forces may be visualised in a number of ways. Fig. 1 shows how we may picture the operation of optical trapping when considering particles that are an order of magnitude larger than the laser trapping wavelength: the so-termed Mie regime. This is perhaps the most straightforward regime to consider. Here we can see that any light scattering should result in a force actually in the direction of light propagation and any refraction of the light results in a force attracting the particle (if of higher refractive index than its surroundings) to the region of highest light intensity. The scattering and gradient forces arise from the reflection and refraction of light. The Fresnel equations tell us how much light is reflected or refracted between the boundaries of the object and the sample media and, in the Mie regime, we may use a geometrical optics approach to determine the forces present. As in most optical trapping experiments, we choose a source such that we avoid any absorption by the sample. Basically we may consider the trapped object as a microscopic lens that focuses the light field. This focusing effect (with accompanying change in photon momentum) causes the particle to move to the position of highest light intensity as may be seen in Fig. 1.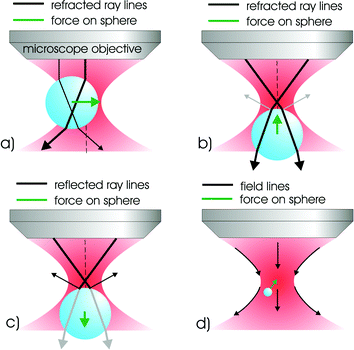

Fig. 1 This diagram illustrates the principles of optical trapping for a simple gradient force optical tweezers. For transparent objects displaced perpendicularly to the propagation axis (a) the focused light is refracted through the particle and imparts momentum to the particle which conserves the change in direction experienced by the light. The particle moves under this action until it reaches an equilibrium position at the centre of the symmetric beam. Similar ray-tracing arguments (b) may be applied to predict the stable trapping position in the z-direction near the focus. There is the additional effect of radiation pressure (c), which tends to destabilise the trap. For the Rayleigh particles (d) it is the polarisability of the particle, rather than transparency, which is important for optical trapping. The electric field of the light produces an induced dipole in the particles which align to regions of high field gradient (in the static field approximation).

Overall we can see from this simplified diagram that gradients of intensity both in the lateral and axial direction are the key to operation of this technique with the interplay between the gradient and scattering force dictating the exact equilibrium position of the trapped object. Naturally we cannot use this picture for objects that are a lot smaller than the wavelength: in this Rayleigh regime, it is more appropriate there to consider the particle as a dipole that minimises its energy in the field gradient created by the light. Typically optical trapping is implemented at neither the Rayleigh or Mie regime but rather where the particle dimensions are close to the wavelength of the light. This so-called Lorentz–Mie regime is difficult to model.

The single beam trap, or optical tweezers, is based around a standard microscope which uses a high numerical aperture objective lens and requires a tightly focused light beam for operation. The high numerical aperture objective ensures this confinement in 3D is achieved through gradients in both the lateral and axial directions. This is the most widely used version of optical trapping but we will also describe briefly other traps, notably dual counter-propagating beam optical traps (analogous to the first trap realised by Ashkin in 1970)² that use rather weakly focused light fields and also surface traps created by evanescent waves. The requirement for creating as small a focus as possible in turn requires that the trapping laser source has a high degree of spatial coherence. Interestingly temporal coherence is not such an issue and one may use short pulse femtosecond light sources or even a “white light” laser source based on broadband supercontinuum generation. Most optical tweezers use monochromatic continuous wave (CW) sources with the overriding criteria being good beam pointing stability and low absorption of the light by the trapped material, especially when using biological samples.

Setting up an optical trap

Alignment of single and dual beam traps has been addressed in detail elsewhere.^4,5 and indeed detail has been given as to the parts required to set up a system. Here we give a brief overview and Fig. 2 shows the typical optical arrangement for trapping. To achieve an optical spot that is diffraction-limited at the focal plane, a high-magnification microscope objective lens with a high numerical aperture is a natural choice. Modern microscope objectives consist of compound lenses and produce an image at infinity. Thus a “tube lens” is necessary to produce an image on your camera or detector of choice. Such “infinity corrected” objectives place no particular constraint on the physical dimensions of the optical trapping apparatus and may permit one readily to place other optical components in the beam path which is usually a pre-requisite for trapping where one uses highly collimated laser sources.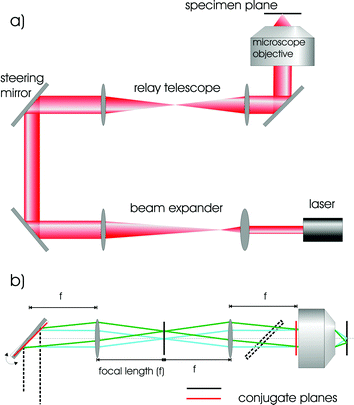

Fig. 2 (a) Typical arrangement of delivery optics for a gradient force optical tweezers; including beam expanding optics to match the beam waist to the back-aperture of the microscope objective; relay and beam steering optics for delivering the beam and a high NA microscope objective for focusing the beam to a diffraction limited spot. (b) Details of the operation of the beam steering optics. The conjugate plane of the steering mirror (narrow line) is imaged onto the back focal plane of the microscope objective via a relay telescope. This enables the position of the beam in the focal plane to be controlled whilst maintaining optimal back-aperture filling; an important factor for trap efficiency.

The microscope objective is not the only optical component that one needs to consider. Naturally high quality dielectric mirrors and anti-reflection coated lenses within the optical system are used to minimise power loss. For tweezing, we need to invoke beam steering so we may translate the beam across the sample stage yet ensure it does not “walk off” or is deviated in a way that might cause it to miss or clip any apertures in the beam path, notably the back entrance aperture of the microscope objective upon which the trapping beam should be centred at all times. Beam steering across the sample plane is realised by using the idea of optical conjugates: we image the back aperture of the microscope objective onto a mirror: thus positioning the light onto that mirror is equivalent to positioning the beam through the objective: tilting the mirror in the lateral plane now moves the beam at the sample plane but does not move it across the back of the microscope objective thus ensuring the beam path retains its direction through this pupil aperture (see Fig. 2). Typically a telescope is required in the beam path to ensure that we slightly overfill the back aperture of the microscope objective. This filling ensures we attain the tightest possible beam focus at the sample plane and thus achieve true three dimensional trapping. The lenses used for creating the optical conjugates may also serve as the telescoping lenses or one may decouple both processes into different optical systems. The working distance with such objectives means we are restricted to trapping only a few tens of microns into the sample medium. The sample itself typically consists of two thin (<100 µm thickness) cover slips with a spacer of thickness 100 µm. Colloidal particles are typically dispersed in water and approximately 10 µl is placed on the sample. If cell studies are performed, they are typically suspended in a suitable buffer medium.

Choice of laser system for micromanipulation

The optimum laser wavelength is a key decision for optical micromanipulation and as already mentioned monochromatic continuous wave (CW) laser beams are usually used. We wish to avoid laser absorption by the sample which leads to damage or “optocution”. When studying biological samples, the near infra-red wavelength range of 750–1100 nm is a good choice due to the transparency of many biological samples in this wavelength window and substantial studies have been performed within this wavelength range. Exposure to infra-red trapping wavelengths of 830 nm and 970 nm is shown to be optimum for E. coli and Chinese hamster ovary (CHO) cells through subsequent cloning.⁶ It is important to bear in mind that two-photon absorption may occur even when using continuous wave laser sources, resulting in cell damage.⁷ It appears sensible to perform tests of cell viability in the trap for your cells of choice for such damage in optical trapping experiments. Colloidal particles (e.g. silica, polymer beads) are typically inert and we have less concern with such damage due to absorption. However here too choice of laser wavelength is an important consideration as heating may occur due to absorption not in the particle but within the surrounding medium that may influence the particle dynamics.⁸ In this instance the use of heavy water D₂O may be useful which has a lower absorption coefficient than normal water at typical trapping wavelengths. Short pulse or modelocked lasers have been used in optical micromanipulation.⁹ They may be used where one wishes to look at nonlinear excitation (e.g. second harmonic generation) within the particle at the same time as trapping or combining modalities such as multiphoton imaging with optical trapping but would likely be avoided for most biological studies due to the prospects of two-photon damage within the sample.

Aberrations may also occur due to refractive index mismatches in the optical system that mean trap performance is degraded when operating deep into the sample. Notably spherical aberration degrades the trap strength performance when working well beyond the cover slip, deep into a sample. Aberrations may be obviated by use of dynamic holographic or deformable mirror technology by imposing correction terms of the appropriate Zernicke polynomials upon the input wavefront of the trapping beam.¹⁰

Theoretical considerations for traps

Modelling of the optical forces for trapping has been key to a detailed understanding of this field. We consider the case of a single particle within an optical tweezers trap. In many respects, optical trapping has relied largely on experimentally determined calibration rather than rigorous comparison between theory and experiment to gain an understanding of the underlying mechanisms of physical or biological systems.

The size of the trapped particle relative to the size of the incident wavelength influences how we treat the modelling and interpretation of the forces induced. In the Rayleigh regime (particle diameter a ≪ λ), we have forces resulting in the scattering force, and gradient force though such a distinction is perhaps not the best way to proceed in the Lorentz–Mie regime (a ≈ λ) or the Mie region (a ≫ λ). In the Rayleigh size scale the trapped object may be considered as an induced dipole that minimises its energy in the trapped light field.¹¹ Suitable references for theoretical approaches to trapping may be found elsewhere.⁶

Trapping may move objects the scale of a large cell (upwards of 10 µm) right down to a few tens of nanometres. The key point is that we need to consider the polarisability of the particle as the key criterion; the depth of any generated optical potential U for a given object must greatly exceed the thermal motion of kT where k is Boltzmann's constant and T is the temperature.

Issues naturally arise due to the exact description of an optical beam near the focus of a high numerical aperture optical system where the paraxial limit is no longer valid. Higher order contributions to the transverse and longitudinal electric and magnetic fields are included to ensure the description satisfies Maxwell's equation. Consideration needs also to be given to diffraction and the description of the polarisation of light in the focus, thus one discusses not just intensity of the light field but would ideally require a full electromagnetic description. The generalised Lorentz–Mie formalism may be used for particles of similar size to the wavelength and this breaks down the optical forces into three components of the radiation pressure: it is an extension of the Mie scattering model.^11,12

It is worth commenting on the link between optical micromanipulation and the fields of laser cooling and cold quantum gases (which have received Nobel Prizes in Physics 1997 and 2001). For an atomic system, the scattering force may be considered as arising at this scale from absorption followed by spontaneous emission whereas the dipole force (analogous to the gradient force for tweezers) is considered as absorption followed by stimulated emission. The dipole force is enhanced by placing the laser close to a suitable resonance but of course this typically results in enhanced absorption. The issue of exploiting resonances for optical trapping at the mesoscale remains promising, in analogy to the atom trapping or guiding (transport) where the laser detuning plays a key role. In particular this would be useful for future prospects of trapping quantum dots or molecular species and some indication of this effect has been observed for metal nanoparticles and molecules.¹³ Molecular trapping use is complicated by their internal vibrational and rotational levels in addition to the issue of Brownian motion.

An often asked question is why are optical tweezers so important in elucidating the motion of single molecules and indeed to explore displacement at the nanometre or angstrom level? Surely we are dealing with optics and as such how do we attain such resolution much smaller than the diffraction limited optical spot size (∼wavelength of light). To answer this question we begin by exploring the mathematical description of a trapped object in an optical beam. The optical forces exerted on the particle mean it acts rather like a microscopic version of Hookean spring: that is force is proportional to displacement. The trapping laser yields a parabolic potential energy basin within which the object may reside. The restoring force, over distances up to several hundred nanometres, is a linear function of displacement x. The motion may be described for a trapped mass, m, in a medium that gives a viscous damping γ₀ (see below) at a temperature T by the famous Einstein–Ornstein–Uhlenbeck theory for Brownian motion and leads to a Langevin equation of the following form:

where κ denotes the trap stiffness which linearly increases with trapping laser power and k_B is Boltzmann's constant. The damping in this system is crucial in many respects—all biological studies are performed with the object in an aqueous medium. A trapped object may be considered as an example of a simple harmonic oscillator. The term (2k_BTγ₀)^1/2η(t) represents the random Gaussian noise process and accounts for all the Brownian forces on the trapped particles at a temperature T, with η(t) denoting the stochastic process of motion of the object as a function of time. The presence of the aqueous medium means we have to consider the object as a highly overdamped system and thus the oscillation frequencies fall well short of the value one would obtain if we assumed the particle was subjected to little or no damping (e.g. in a vacuum) once we take into account the Stokes drag forces in moving in a fluid of density ρ, kinematic viscosity ν. The Stokes' drag term (viscous damping), γ₀, for a particle of radius r is given by γ₀ = 6πrρν.

For a typical biological application of traps, we find that the roll-off frequency well below 1 kHz. This is much lower than the resonant frequency, confirming the very over-damped nature of the oscillations. We are in the low Reynolds number regime: viscosity dominates and inertial and gravitational forces can largely be ignored altogether. In addition to providing the damping force, the surrounding fluid has the advantage of providing cooling to minimise the heating effect of the laser light. It is important to explain how we might calibrate and use a trap to exploit this knowledge. Visualising and tracking the motion of a trapped bead naturally leads to an in situ measurement of the trap stiffness and shape and depth of the optical potential: this determination of the exact centre of the trapped bead can lead to resolutions well in excess of the wavelength of light. Video techniques may be used to infer trap stiffness using the variance of the trap position but the technique of choice is to image the particle onto a quadrant photodiode with a large bandpass in frequency (several kHz). The equipartition theorem leads us to understand that the particle excursions within the trap have an exponential distribution following Boltzmann's law P = (–U/kT). In turn this gives us the form of the optical potential U which is parabolic in nature for a standard trap (see Fig. 3). The quadrant photodiode works by recording the centre of gravity of the particle position. Importantly this may be performed to a far higher accuracy than the optical wavelength: thus we readily achieve resolution on the nanometre scale with this technique.

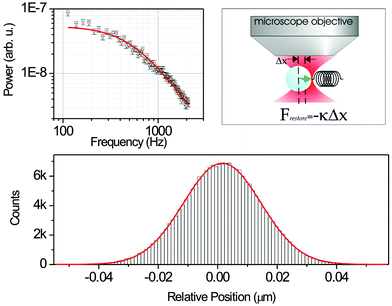Fig. 3 Force calibration of optical tweezers using Brownian dynamics and sub-nanometre position sensing of particles has been very important in expanding the role of optical tweezers as a force transducer. Microscopic objects trapped in an optical trap may be treated as Brownian particles sitting in a harmonic potential; the kinetically driven thermodynamic motion experienced by the particle is counteracted by a restoring force (similar to that of a mass on a spring) from the optical tweezers proportional to the displacement of the bead from the centre of the trap (a). By studying these fluctuations the stiffness of the trap may be discerned with a high precision. From a power spectrum analysis of the time series fluctuation of the particle position, the trap stiffness may be readily extracted (b). The bottom panel (c) is a histogram showing the Gaussian distribution of the particle position in the trap; if the quadrant photodiode (QPD)is calibrated then a full three dimensional map of particle position may be determined with sub-nanometre resolution.

An alternative method by which to characterise the trap is to measure what is denoted the Q value for the trap. This is a simple method where one translates the sample stage at known velocities and records the velocity at which the trapped bead falls out of the trap.¹¹ As we drag the bead at velocity ẋ it moves its equilibrium position up the side of the potential well and is displaced from the trap centre. We equate the Stokes drag force to the force exerted by a laser (power P) in the following manner: firstly one may show that the light momentum transferred to an object leads to a force given by

where c denotes the velocity of light and n is the refractive index of the sample medium. Multiplying this equation by a dimensionless parameter and equating to the Stokes drag gives us a value for Q. Typically Q is around 0.1–0.2 and is a measure of how well the optical momentum of the trapping light field couples to the sphere and incorporates factors such as aberrations in the trapping system. We may equate optical forces with Stokes forces as follows:

Further corrections to this equation may be necessary to take into account close proximity to a boundary (the Flaxen correction). Whilst this is a valid way to characterise the force and appreciate how well a trap is performing, the Q value is not a particularly productive way to perform quantitative biology with optical traps. It has been very useful to compare one laser wavelength versus another or for exploring the influence of differing beam shapes in optical traps.¹⁴

Single molecule studies using optical tweezers

The advent of optical tweezers, the single beam trap, heralded a new era of research into single molecule biophysics. Until the advent of optical tweezers in the mid 1980s, biologists’ knowledge of biomolecular processes was limited to studies on bulk biological samples. In a true revolution, optical tweezers have enabled the possibility of studying the mechanics of such interactions at the molecular level, providing an unprecedented level of insight into biological molecular motors and other biopolymers. Such motors are in all living cells and play a central role in the biology of living organisms. Optical tweezers have permitted ground-breaking studies of actin–myosin interactions, kinesin motion along microtubules, and DNA folding and transcription amongst other systems. The most powerful implementation of optical tweezers has been as a force transducer measuring (down to) sub-femtonewton forces for such molecular motors. This application as a force transducer stems from the theoretical considerations we have given above. The forces exerted by optical tweezers are small and are certainly unlikely to break a covalent bond (∼1 µN) but certainly may be able to break up a DNA double helix structure, study protein–protein interactions (∼a few tens of piconewtons) and indeed are ideally placed to look at motor proteins (∼a few pN). In fact Rohrbach measured the smallest switchable forces known to date (25 fN) using optical tweezers.¹⁵ A more detailed discussion of the implementation of tweezers in biology may be found elsewhere including other references for a thorough discussion of the practical aspects of the system.⁶

The trapped object is held at room temperature and bombarded by molecules from the sample medium. Using the equipartition of energy where x is the direction of movement, we may evaluate the fluctuation of the object at a given temperature, which is around 10 nm at room temperature. This small excursion means the object stays well confined within the trap dimension of λ/2 for tightly focused light beam of wavelength λ. Whilst 10 nm appears small it is not insignificant when considering motion of biological macromolecules at the nanoscale and reinforces too the requirement of excellent optics, lasers and robust apparatus for precision studies.

The true potential of optical tweezers is realised when we consider the use of the trapped object as an “anchor” or “handle”, attached to the biomolecule of interest. The attachment may be performed with suitable surface chemistry e.g.biotin–streptavidin links. Tweezers thus typically do not hold the molecule of interest directly (which in turn reduces the risk of photodamage) but do so indirectly via the bead (see Fig. 4). We may monitor excursions of the trapped particle within the trap by imaging the particle onto a quadrant photodiode as already mentioned. These excursions are well characterised, thus when a biological molecule is attached and interaction occurs between the molecule and its environs we are able to observe it in real time. The pertinent point to note is that the centre of gravity position of the sphere may be determined to a very high accuracy, typically at the nanometre scale or even better: it is important to stress that this is two orders of magnitude less that the diffraction limit of the trapping light itself (100 nm). Very recently a major step forward in this field has been reported where researchers have attained resolution down to the few angstrom level.¹⁶

Fig. 4 Applying and sensing piconewton forces and sub-nanometre fluctuations with optical tweezers allows the study of individual biomolecular interactions, as well as probing the fundamental nature of non-equilibrium thermodynamics. In these studies an optically trapped colloid is attached to a bio-molecule via a tether and the interactions of the molecule with other proteins perturbs the sphere within the traps, which may be monitored with a QPD detection system. Also, force loading studies may be done by deliberately displacing the colloid in the trap.

One of the first studies with optical traps as force transducers looked at kinesin moving along a fixed microtubule track.¹⁷ Surface chemistry permitted the kinesin molecule to adhere to a microparticle which was positioned close to the microtubule track. This is a linear molecular motor and gains energy from the hydrolysis of adenosine triphosphate (ATP) to adenosine diphosphate (ADP) and phosphate. The motion of kinesin along the microtubule was dictated by the arrival of an ATP molecule and single molecule chemical reactions of ATP to ADP resulted in a juddering motion of the kinesin along the microtubule in steps of size 8 nm. The intermittent nature of the motion was due to the motor waiting for the arrival of the next ATP molecule to continue its progression. The actin–myosin system involved interactions between two molecules and thus the use of a single calibrated trap was insufficient. A dual tweezer system was devised that permitted a single action molecule to be suspended between the two traps. A myosin coated bead was placed in close proximity. The buffer solution contained ATP and again when a reaction occurred between both molecules a jerky tug was exerted that, for each ATP to ADP conversion, gave a kick to the bead position. Numerous events of this nature could be observed. As mentioned a major step forward has recently occurred where step sizes at the angstrom level have been observed.¹⁶ This system was used to explore the motion of RNA polymerase (RNAP) as it moved along a DNA template. Transcriptional elongation of E. coliRNAP was monitored and steps of 3.7 Å were observed. To achieve this level of resolution the Block group enclosed the whole trapping apparatus in helium: helium has a refractive index close to the vacuum reducing any beam wander due to turbulence (rather akin to removing the twinkling of distant starlight). Their dual beam trapping system used a novel form of force clamp: one of the beads was positioned well away from trap centre where the force versus distance graph was largely flat, thus exerting a constant force for a range of displacements on one end of the molecule. The other trap was used to monitor the motion of RNA polymerase along the DNA chain (see Fig. 5).

Fig. 5 The direct observation of base-pair stepping of RNA polymerase by Abbondanzieri et al. is an illustrative example of the power of optical tweezers for studying biomolecular interaction. The design of an ultra-stable trapping system with a passive force clamp mechanism (a) allowed the study of biomolecular interactions with an angstrom scale resolution (b)–(d). Reprinted by permission from Macmillan Publishers Ltd: Nature,¹⁶ copyright (2005).

Thermodynamics is linked inherently to energy exchange and describes macroscopic systems. Biology and its link to thermodynamics is an intriguing subject. Notably, when we have thermal fluctuations these may begin to dictate the overall system behaviour as the scale of the system decreases. A mesoscopic non-equilibrium system may exhibit behaviour that deviates from some average ensemble value: molecular motors as described and other sub-cellular processes may exhibit such features and optical traps are a good technique to elucidate the process. The molecular world can take thermal fluctuations and rectify them using energy from ATP to ADP conversion. The experiment already described using RNAP moving along DNA for transcription is a good example: evidence suggests the enzyme rectifies thermal energy to instigate forward motion.¹⁶ Fundamental laws of non-equilibrium thermodynamics at the microscopic scale have been explored in some ground breaking experiments that include the use of colloidal particles as well as single molecule studies.¹⁸ Considering the fluctuation theorem, they explored entropy production: that is the rate at which the system exchanges heat with a surrounding bath. Timescales matter in such systems: by dragging optically confined beads, and carefully computing their trajectory through water, the Evans group showed that for short times (in the millisecond range) entropy-consuming trajectories were observed, thus “violating” the second law of thermodynamics whereas longer times revealed the more well known entropy producing behaviour.¹⁹

At the cellular level, optical trapping continues to provide much insight into biological processes. Indeed the first studies after the conception of the optical tweezers moved viruses, bacteria and cells around.²⁰ Other studies have also elucidated the properties of red blood cells. Notably, recent work using a counter-propagating system has been used to explore the elastic properties of cells as a method for differentiating healthy and cancerous cells. Here due to momentum conservation at the interfaces between the medium and the cell (considered as a dielectric of higher refractive index than the medium) a force actually elongates and deforms the cell towards each of the two counter-propagating beams creating an “optical stretcher”—a rather unintuitive response.²¹ The ellipticity of the stretched cells in this system is indicative of their state: healthy and abnormal cells behave differently permitting one to distinguish between them.

Optical traps have enabled a very wide, diverse and important range of scientific research. It is becoming apparent that for next generation studies in the biosciences, optical micromanipulation will likely be combined with one or more other techniques. Optical traps were combined over thirty years ago with an optical scalpel or optical scissors by Berns and co-workers: they used a second laser, typically a pulsed system, used to ablate and cut material with another laser to tweeze. A comprehensive history of the laser ablation (“laser scissors”) as well as other related applications may be found in the recent book in the series Methods in Cell Biology.²²Chromosomes or cells may be isolated in this way. Optical tweezers may be combined with Raman spectroscopy, confocal imaging or multiphoton imaging. Raman offers a unique chemical fingerprint that may be used for diagnosis. The Raman signal is an individual fingerprint of biological macromolecules present in a biological system: the combination of this spectroscopic method with trapping means we can isolate a single cell and explore it in detail. We can move the cell away from any local surface thus reducing any extraneous scattering or background signal. This may form the basis of future micro-analysis when this is combined with microfluidic flow chambers. Optical tweezers have also been combined with single molecule fluorescence in a number of ways⁶ including studies of unzipping duplex regions of DNA and with multiphoton microscopy.²³

Sculpting the wavefront: optical traps multiply

A recent resurgence in optical micromanipulation has in part been fuelled by advanced optical patterning in two and three dimensions. Standard optical tweezers use a microscope objective lens and a normal Gaussian laser beam. The trap region is ellipsoidal in nature with the major axis of the ellipse along the beam propagation direction. However this constrains the trap geometry in that we cannot easily sculpt or change the optical potential in two or three dimensions to a specification. Firstly, it is important to acknowledge why such beam shaping is important: sculpting the laser intensity profile in itself should lead to exciting new advances. For single molecule studies we may need more sophisticated control of force versus extension possibilities for single molecule measurements. Another example is axial trapping: this is significantly enhanced if we use a beam devoid of light right at the centre retaining strong light intensity at the beam periphery: thus we need an annular beam.²⁴ This means we reduce the backscattering contribution that originates from photons along the beam axis which act to push the particle away from the beam focus position (see Fig. 1). The very same profile of light beam is key to trapping low index particles such as microbubbles—these behave such that they are repelled by the light field thus we need to cage them in some sense with light and restrict them to a dark “light free” region.²⁵ There are chemistry applications such as droplet mixing. In other studies the trapping and ultrasonic cavitation of low index particles such as ultrasound contrast agent can perform cell lysis.

Sculpting the wavefront to form arrays of traps create what are termed optical potential energy landscapes. Particle or cell motion within such landscapes is a vibrant area of research and leads to new studies in colloidal science^26,27 and biological sorting of cells. Colloids at all mesoscopic sizes are fascinating: in tandem with Brownian motion, a colloidal dispersion can lower its free energy and self organise. They are excellent model systems where we are readily able to tune the interactions between the particles (e.g.via the solvent) as well as impose our “known” potential energy landscape. The behaviour of colloidal systems parallels that of atomic and molecular systems. Important insights into condensed matter such as melting, freezing²⁸ and the glass transition may be gleamed from studies as well as re-entrant behaviour.²⁹ Colloidal science has undergone a major renaissance in recent times and remains an area where optical trapping continues to make seminal impacts. Notably colloidal interactions are complex in nature as they are solvent-mediated. Multiple trap sites and energy landscapes can be used to measure hydrodynamic interactions between increasingly larger arrays of particles.

The most straightforward extension of the single beam trap to two adjacent traps has been a key development. Such dual optical tweezers have proved crucial for numerous molecular motor studies as already seen. Dual traps may be created by a number of methods, most popularly by time sharing the beam with an acousto-optic deflector or splitting the beam amplitude using a Mach Zender type arrangement.⁵ Acousto-optic deflectors (AODs) time share the light beam between each site. The slow diffusion (random walk) of trapped objects mean this method is very powerful due to the rapid switching time (microseconds) of AODs but of course there is a limit to how long the laser may be absent from a given trap site which may be determined by the Einstein diffusion relation. Instead of time sharing the light field we can use methods to create the light field of choice, be it discrete traps, arrays or more elaborate patterns including patterns in three dimensions. This may be realised using holographic techniques or phase contrast methods and involve no time sharing. We may readily compute the desired final energy landscape at the trap plane and use a suitable algorithm. This may be performed in two or three dimensions. Holographic trapping can influence not only the local intensity but also the phase profile of the trapping light creating three dimensional landscapes and unusual light modes. Other methods use advanced techniques in spatial filtering such as the generalised phase contrast (GPC) approach which is direct imaging and not holographic thus reducing the computational complexity. This method has recently been extended to a three dimensional trapping system using a counter-propagating geometry.³⁰ The implementation of diffractive optics in optical micromanipulation is well over a ten years old: Fournier and co-workers proposed their use and looked at the use of Talbot imaging for trapping in multiple planes. Recently dynamic projection of holograms and advance spatial filtering has been shown using a spatial light modulator: this is a dynamic hologram in essence and comprises an array of liquid crystals that may be either optically or electrically addressed to induce a phase change from 0 to 2π at the design wavelength. The efficiency and power handling capability of these systems is improving as is the resolution in which does not typically match that which may be created in static diffractive optic elements. Dynamic holograms created on spatial light modulators have been used with various algorithms³¹ and may organise micro-particles into pre-described geometries³²—one can envisage these forming nucleation sites for larger colloidal crystals or even templates for advanced studies of cell growth, signalling or differentiation.

Novel light modes for optical micromanipulation

The Laguerre–Gaussian (LG) light beam³³ has been one such example of an unusual sculpted light mode of interest that offers different possibilities compared to the Gaussian beam. Two of these possibilities have already been mentioned: improved axial trapping²⁴ and the confinement of low index particles.²⁵ These light fields are circularly symmetric and are described by two indices. The radial mode index denotes the number of rings in the mode whereas the other index, the azimuthal index l tells us the number of cycles of 2π phase we accumulate as we traverse the mode circumference. Forms of this mode with this azimuthal term have a dark centre. If we visualise the circumference of the mode we see that it must form a spiralling helical surface: rather akin to a helter skelter. At the centre of the spiral all the radial phase points meet: thus we have destructive interference which in turn means that the area in the centre is dark (the phase is ill-defined): this is referred to as an optical vortex (see Fig. 6).

Fig. 6 Novel light propagating modes enable unique ways of trapping and manipulation particles. Modes such as Laguerre–Gaussian beams (a, b) and higher order Bessel beams may carry both spin and orbital angular momentum, which may be transferred to a particle to make it spin and gyrate. Laguerre–Gaussian modes are circular symmetric higher order modes characterised by radial mode index, p (determines radial structure), and an azimuthal mode index, l (determines helicity). Image (c) shows a birefringent particle trapped in the first ring of a higher order Bessel beam, rotating simultaneously (i) around its own axis due to spin angular momentum and (ii) around the beam's axis due to orbital angular momentum. (Fig. 6b reproduced by permission from ref. 39. Copyright 2003 the American Physical Society.)

The energy flow of any light field is described by the Poynting vector. The LG light field has helical phasefronts so its motion includes an azimuthal component to the Poynting vector that results in an orbital angular momentum content the light field. This is in addition to the spin angular momentum that results from the polarisation state of the photon. A linearly polarised Laguerre–Gaussian beam has an angular momentum of lħ per photon. The use of such beams in micromanipulation has shown the transfer of OAM by a variety of mechanisms including scattering and absorption. Such LG modes, created holographically, were used in traps and through absorption showed the transfer of orbital angular momentum to a trapped metal oxide particle.³⁴ Subsequent work showed methods to transfer orbital angular momentum by scattering. Using a mode with high azimuthal index and interferometric versions of these light modes have shown the first creation of three dimensional cubic structures in traps³⁵ as well as controlled rotation of chromosomes. Spin angular momentum may be transferred to microscopic particles too held in tweezers, creating a microscopic version of Beth's famous experiment of 1936.³⁶ Rotating particles holds immense promise for microrheology: here the rotational Stokes drag torque given by τ_D = 8πγr³Ω (γ₀ is the dynamic viscosity, r the particle radius and Ω the angular velocity) is equated by the torque supplied by the light field due to a change in the polarisation state. As the system is overdamped it reaches equilibrium with the rotating object permitting a local measurement of viscosity. Future research is aiming to study local viscosity in a variety of fluids (including non-Newtonian fluids) and within cells.³⁷

Diffraction is associated with the wave nature of light. Researchers in optics have long been questioning how one might obtain beams that avoid such diffractive spreading that is common to a standard Gaussian beam. A class of such beams termed Bessel beams³⁸ has created much recent interest in the arena of optical trapping (see Fig. 7). These beams satisfy the Helmholtz equation and are termed propagation invariant due to the fact they retain their cross-sectional intensity profile upon propagation. They are “pseudo non-diffracting” such that the central maximum of a zeroth order Bessel beam keeps its dimension over many times the Rayleigh range of an equivalent Gaussian beam. The beam consists of a series of concentric rings with either a bright spot (zeroth order) or dark region (higher order) in the middle. Bessel modes have been used for a number of studies including extended guiding of particles as we are not restricted by the Rayleigh range of a beam. Studies of the spin and orbital angular momentum have also been performed looking particularly at mapping out quantitatively the angular momentum density in a light field using the trapped object as a probe³⁹ (see Fig. 6c). The Bessel mode may be decomposed into a number of waves travelling on the surface of a cone, which all interfere to give the beam its characteristic form. It has the unusual characteristic of self-healing or reconstruction and this has been used to trap and move objects in a single line when the objects are relatively far apart.⁴⁰

Fig. 7 Bessel beams, generated using a conical shaped optical element (axicon), are “pseudo non-diffracting” beams, which have a very narrow rod-like core that is maintained over extended distances. This makes it possible to trap multiple particles along the axis of the beam. The beam profile of a Bessel beam (a) has a narrow core surrounded by concentric rings of decreasing line-width, producing an optical potential with a corrugated appearance (b). By adjusting the profile, a tilted washboard potential may be generated for accumulating particles to the central core (c). Microscopic particles with different optical properties (e.g. different cell types) can be separated (optical fractionation) when placed on the modulated optical potential, such as different cell types (d).

The Bessel beam and indeed other interference patterns may realise an optical washboard potential. Particle behaviour in a periodic pattern will be dictated by the size of the object relative to the pitch of the pattern. An object smaller than the width of a ring of the Bessel beam will lock into the rings and only thermally activate and thus move relatively slowly to the more intense beam centre. A larger object may actually not see the underlying periodic nature of the pattern but rather be influenced by the beam envelope of the beam and thus run into the beam centre more quickly (see Fig. 7). Interference between two Bessel beams has created long arrays of microscopic traps that may be translated: initiating and optical conveyor belt: this may transport sub-micron objects over millimetre distances. The standard Bessel beam has shown passive sorting of lymphocytes and erythrocytes, with no flow present, where the lymphocytes are guided in the beam centre and may be collected by a capillary⁴¹ (see Fig. 7d).

Near-field optical trapping

Most optical trapping is performed in what is termed the far-field. However, operating in the near-field offers some advantages. Here the laser trapping forces used for manipulating a microparticle result from an evanescent wave. The fact that the strength of an evanescent wave decays rapidly with the distance from the place where the evanescent field is generated may result in a significantly reduced trapping region. This concept builds upon the demonstration of near field optical guiding by Kawata and colleagues in a prism geometry.⁴² The radiation pressure force for guiding is generated by an evanescent wave produced at the interface between two media under total internal reflection conditions. However, as the evanescent wave field is not laterally localised, it is difficult to achieve laser trapping in this case, though one can do this with two counter propagating beams.

To overcome this drawback, a metallic tip illuminated by a laser beam has been proposed to produce a localised evanescent field by the surface plasmon effect so that a particle of a few nanometres in size, suspended in water or air, can be trapped. Another proposed method involves the use of the evanescent field near a nanoaperture. Although these theoretical proposals are exciting and important, it is difficult to implement them in practice. Firstly, it is difficult to control the distance between the probe and samples, which is in the range of tens of nanometres due to the evanescent nature of illumination. Thus, the use of a sharp tip or a nanoaperture may hamper the manipulation operation such as rotation. Second, although a metallic tip leads to an enhanced evanescent wave, the heating effect caused by surface plasmons associated with a metallic tip may significantly reduce the stability of trapping and tweezing. Finally one should note that the light throughput of near-field tips or apertures is quite low.

Recently, a new near-field trapping and tweezing mechanism that utilizes the focused evanescent wave illumination has been proposed and demonstrated.⁴³ The focused evanescent field is produced by the use of a ring beam produced by a high numerical aperture objective that is centrally obstructed, as shown in Fig. 8a. The opaque disk has such a size that the minimum angle of convergence of a ray is larger than the critical angle determined by the refractive indices of the two media. As a result, each incident ray results in total internal reflection and thus an evanescent wave on the interface. Due to the circular symmetric nature of illumination, the resulting evanescent wave constructively interferes at the centre of the focus, enhancing the strength of the evanescent field. The transverse profile of the evanescent focal spot leads to a gradient force as shown in Fig. 8a, pushing a small particle toward the centre of the focus. Due to the fast decaying nature of the evanescent field, there exists an upward gradient force with a reduced trapping depth (Fig. 8). Therefore optical trapping and tweezing of a micro-sphere can be achieved under evanescent wave illumination. Fig. 8b shows the trapping efficiency mapping for an objective of numerical aperture, NA = 1.65, calculated by a physical model that is based on the vectorial diffraction by a high NA objective under the total internal reflection condition and scattering by a small particle with a focused evanescent wave. It confirms the existence of transverse and axial trapping forces under the focused evanescent wave illumination, which has been experimentally demonstrated in the visible and near-infrared wavelength region.⁴³

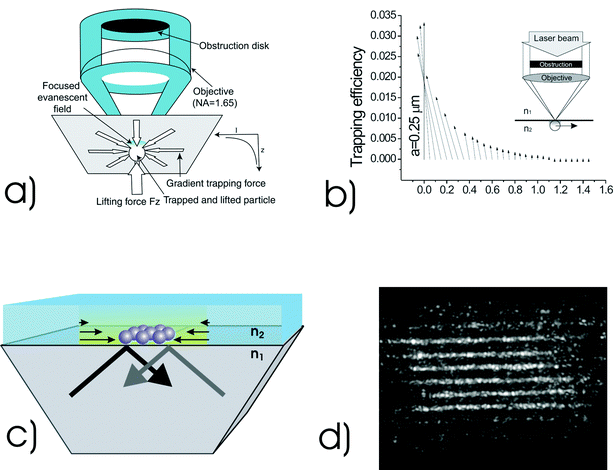Fig. 8 (a) Concept of optical trapping under focused evanescent wave illumination: an obstruction is used at the back of a total internal reflection (TIR) microscope objective to block all but rays which arrive under TIR conditions. (b) Trapping efficiency mapping for a polystyrene particle of radius a, scanned in the x direction (light polarisation direction) across the focused evanescent field. Numerical aperture = 1.65, λ = 532 nm, ε = 0.85 (normalised obstruction size), n₁ = 1.78 and n₂ = 1.33. (c) Generating evanescent waves over an extended area using total internal reflection through a prism allows arrays of particles to be simultaneously manipulated and also enables optically induced self-organisation of particles to be studied, (d). In a near field geometry using a large area prism one may see enhancement of the field and colloidal organisation on the surface: See ref. 44 for more details. (Fig. 8a reproduced with permission from ref. 43. Copyright 2004 American Institute of Physics. Fig. 8b reproduced with permission from ref. 58. Copyright 2004 Optical Society of America.)

The method shown in Fig. 8a has no potential heating, the distance between the trapping site and the objective is sufficiently large for micro-manipulation, and the light throughput is improved significantly due to the use of a high numerical aperture objective. The most important advantage of the focused evanescent wave tweezers is its significant reduction of the axial trapping region pulling particles close to the surface and the potential for a reduced trapping volume. In the far-field case, the focal spot of a high NA objective is elongated along the axial direction. Therefore the axial size of the trapping volume, as denoted by the optical beam shape and to which a particle may be confined, is approximately three times larger than that in the transverse direction. Although far-field laser trapping technique is powerful, the axially elongated trapping volume may lead to a significant region to which a particle may be attracted and ultimately confined. This difficulty can be overcome by the introduction of near-field illumination or evanescent wave illumination. For the example shown in Fig. 8a, the axial size of the trapping region, defined by the position where the optical intensity drops to 50% of that at the interface, is reduced to approximately 60 nm. This is approximately one order of magnitude shorter than that in the far-field case.

One of the future developments in the focused evanescent wave tweezers is to reduce the lateral size of the trapping volume. As near-field optics are not constrained by the diffraction limit, they may also offer the potential for creating an optical trapping volume, or notably a periodicity within an optical landscape that is significantly smaller than can be achieved in conventional optical tweezers. Further experiments in this area have shown the guiding⁴² and trapping of objects upon a prism in what is termed the Kretschmann geometry. One may create an enhancement of the strength of an evanescent wave field in such a geometry. Techniques for surface enhancement include surface plasmons or dielectric resonators⁴⁴ (Fig. 8c and 8d).

When we consider the creation of multiple trap sites generating optical landscapes, be it in the near-field or far-field, we typically ignore the very scattering or redistribution of light by a given object in this light field and how it may influence the position of its nearest neighbours. Such light–matter interactions are termed “optical binding” and this may manifest itself in a form either transverse to or in the direction of (longitudinal) the optical beam propagation. There are various types of “optical binding”: Golovchenko and co-workers investigated transverse optical binding⁴⁵ where the interaction of coherently induced dipole moments of the spheres were said to interact to bind matter. In an evanescent wave system in the Kretschmann geometry, such binding has recently been shown to result in intriguing patterns formed by arrays of microparticles both with and without actually patterning or sculpting the optical landscape.⁴⁶

Optical organisation through interactions of scattering in the beam propagation direction has been recently seen and allows interactions between micro-particles separated by distances an order of magnitude larger than their individual diameters. This is longitudinal optical binding and has been observed by several groups⁴⁷ and has shown some perhaps surprising behaviour. There are rich dynamics in such systems, including observations of bistability as well as correlated behaviour between bound objects. It is noteworthy of emphasis that such “optical binding” is radically different from individually trapping each micro-object: the very interaction between an object and its nearest neighbours creates a self consistent solution that may allow in future a method to create a large scale colloidal array. Transverse and longitudinal binding need further studies to see how these interesting effects actually link together.

Chemistry in optical traps

From a chemist's standpoint, optical tweezers are emerging as an interesting tool in many respects. Reactions between vesicles composed of polymer bilayers are being investigated for use as microreaction containers.^48a These are essentially small nanovials. The advantage of such nanovials over liposomes is a much reduced leakage rate of encapsulated small molecules, they are more robust and not easily deformable. Polymersomes can be prepared by reverse evaporation or electroformation and are more easily trappable than liposomes.

Liposomes may be tens of microns in diameter. They may be used to perform chemical reactions in closed nanovials involving only picolitres of reagent. The experiment uses two optical traps to hold two individual liposomes, which are then brought into contact. A single pulse of ultraviolet laser light induces the fusion between liposomes (see Fig. 9a). As a consequence the fusion reagents that are encapsulated in the liposomes mix and react. The newly formed fused liposome is typically spherical and that volume is conserved in this process. This avoids any unwanted leakage of precious encapsulated molecules. This novel approach may open the way for quantitative studies of mixing of chemicals, realising combinatorial chemistry with only picolitres of reagent. Optical micromanipulation is broadening its applicability: and fusion studies with single liposomes have recently prompted the promising suggestion that vesicles filled with different reagents could be fused to initiate reactions involving very small volumes in a controlled microreactor.^48a Holographic methods may now move and coalesce multiple droplets⁴⁹ (see Fig. 9b). At smaller scales, as already stated there are indications now that molecules may even be directly trapped.¹³

Fig. 9 (a) The ability to control and manipulate microscopic objects has demonstrable importance in studying the properties of chemical reactions in femtolitre volumes. Helmerson and co-workers^48a have shown that optically trapped lipid vesicles may act as microreaction vessels. Individual reagents are loaded into separate vesicles and brought into contact using optical tweezers. A UV laser focused onto the membrane promotes fusion of the two vesicles which in turn initiates the reaction. (b) This may also be achieved by controllably trapping and fusing aerosol droplets containing different reagents; a technique that has recently been highlighted by Burnham et al.^48b using holographic optical tweezers. The images (sequence as indicated by the time lapsed) show a matrix of eight aerosol particles trapped in an array being coagulated in a process controlled by the spatial light modulator (SLM). The images for 9(b) are provided courtesy of D. Burnham.

The power of surface chemistry on inert microbeads may also be seen in a different way with work on the binding reactions of antigen–antibodies. Here two traps each containing a bead coated in ligand and receptor molecules were used. The receptor and ligand to freely bind and dissociate when the traps are placed in close proximity and the movement of the beads monitors the interaction. Excitingly, recent work has also looked at moving and growing in situlysozyme crystals in a standard optical tweezers.⁵⁰ Varying the pH and lysozyme concentration during growth changed the length to width ratio of the crystals which in turn affected their orientation in the trap. Real-time observation of crystal growth was directly seen by adding protein to the sample solution.

Micromanipulation and microfluidics

In biology and chemistry there has been recently a tendency to perform experiments with minimal amounts of analyte. This concept relates to the notion of a lab-on-a-chip. In this domain we deal with nanolitres of analyte. When at this size scale, the behaviour of liquids is somewhat non-intuitive to our macroscopic view of fluid flow. At the micro level, we are in the low Reynolds number regime where viscosity dominates and inertial effects may largely be ignored. Turbulence that plays a key role in phenomena such as mixing is now largely absent. For purposes of mixing and even separation of microparticles one may not rely on features such as turbulence which are not present: rather diffusion dominates which can be very slow: in turn this poses interesting problems for separation at the micro and nanoscale. Optical forces at the microscale may be used to drive and actuate micro-components, for example micro-cogs⁵¹ or even initiate small pumps, notably thought transfer of spin or orbital angular momentum. Even new forms of integrated, wholly portable optical traps may be generated placing the trapping lasers adjacent to the microfluidic flow.⁵² The reconfigurabilty and non-invasive nature of light seems to be attractive in many respects but one finds the throughput for such systems in this form is not very high.

Separation of cells, colloidal particles and other microscopic objects remains an important enabling technology. The current industry standard is the fluorescence activated cell sorter (FACS). This established technology is based on a flow cytometer. This device records the scattering distribution of a single cell as it traverses a laser beam. A FACS is a special type of flow cytometer: fluorescent markers (fluorescently labelled monoclonal antibodies) allow specific cells to be recognised and subsequently separated. Separation in FACS is based upon a wide range of parameters. It may record up to a dozen different fluorescent colours in addition to two scattering parameters, all of which can be used to discriminate in the sorting process. FACS has a variety of uses and has found numerous applications including the diagnosis of leukaemia and the testing of patients for compatibility in transplant surgery. The current drive to microfluidic environments as the name implies involves the use of optical forces to select out particles of interest, particularly in a microfluidic system where diffusion is too slow. It is important to distinguish between what may be termed passive sorting versus active sorting. Active sorting is the process occurring for example in fluorescence activated cell sorting devices (FACS machines). In such a system the particles of interest are identified using a laser to induce fluorescence: this can take the form of fluorescent markers within the cells expressing, for example, green fluorescent protein (GFP). As they pass through a detection region, the fluorescence signal is recorded and then they subsequently pass through a detection region that incorporates a deflection or trapping laser that then collects this particle in an appropriate reservoir. Whilst this method has proven to be very powerful, new separation methods have emerged that do not need inherent marking of the selected objects but are based on their individual physical attributes. Such a system might be able to achieve very high throughput as we would be relying on the response of the objects to an optical landscape that could take the form of an extended light pattern in 2D or 3D. We have already briefly described one form of sorting of blood cells when discussing the Bessel beam. Placing a particle anywhere on an optical landscape results in energy considerations dictating the particle's equilibrium position.⁵³ Furthermore, we have to deal with Stokes drag which may increase linearly with velocity. Such sorting or separation has recently been observed for colloidal particles⁵⁴ and offers a new potential for selection and enrichment of cell phenotypes in a rapid fashion. It is an interesting future theme to see whether this could be applied to the sorting of DNA or other biological macromolecules or quantum dots where sorting is certainly a requirement. The forces scale with size such that this may prove difficult without dramatic change of wavelength or the possible use of resonance enhancement.

Conclusions

Optical micromanipulation is established as a powerful technique spanning numerous fields and operating at mesoscopic size scales, from the single molecule to a large cell. Multiplexed light patterns offer new possibilities particularly for the biology and chemistry communities. Exciting advances using holographic and time shared optical traps are permitting new studies to be undertaken. The central role of a single beam trap as an unprecedented force transducer is enduring: the displacements that one is able to measure are now routinely at the nanometre scale or below and there are good prospects for new studies of polymers and biological macromolecules New techniques (such as the photonic force microscope)⁵⁵ allow fN resolution by true 3D positioning of microparticles and new studies within cells. From a chemist's viewpoint the technology is in its early days: micro-reactions and the interactions between multiple trapped droplets will lead to new science. Separating or fractionating objects by optical separation has worked well on colloidal material and, to a lesser extent, biological cells but can it work for viruses or proteins? Multiple traps may be used for simultaneous studies of forces on cellular structures though key issues of trap calibration at all generated trap sites is an issue. Recent work has seen the trapping of gold nanoparticles for use as optical handles⁵⁶ following original studies in the 1980s. However it remains to be seen how far this work progresses as the absorption of such nanoparticles causes large temperature rises in the trap.

To create multiple trap sites over large areas the use of holographic technology and evanescent field geometries have led the way but new methods are emerging: this includes the recent development of light induced dielectrophoresis where gradient forces to trap and move objects may be generated with an optically enabled electrode.⁵⁷ Notably using only milliwatts of optical power from a light emitting diode numerous particles were organised and moved due to the high photoconductive gain of the material.

The impact and diversity of the field is increasing with each passing year and it is quite stunning to see the diverse and rich science that this technology has spawned in the last four decades: the future is indeed very bright.

Acknowledgements

KD and MG would like to thank the UK Engineering and Physical Sciences Research Council for the award of a visiting fellowship grant. KD thanks Klaus Metzger for assistance with the figures.

References

1. A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm and S. Chu, Op. Lett., 1986, 11, 288.
2. A. Ashkin, Phys. Rev. Lett., 1970, 24, 156.
3. A. Constable, J. Kim, J. Mervis, F. Zarinetchi and M. Prentiss, Opt. Lett., 1993, 18, 1867.
4. S. P. Smith, S. R. Bhalotra, A. L. Brody, B. L. Brown, E. K. Boyda and M. Prentiss, Am. J. Phys., 1999, 67, 26.
5. E. Fallman and O. Axner, Appl. Opt., 1997, 36, 2107.
6. K. C. Neuman and S. M. Block, Rev. Sci. Instrum., 2004, 75, 2787.
7. K. Konig, H. Liang, M. W. Berns and B. J. Tromberg, Opt. Lett., 1996, 21, 1090.
8. E. J. G. Peterman, F. Gittes and C. F. Schmidt, Biophys. J., 2003, 84, 1308.
9. B. Agate, C. T. A. Brown, W. Sibbett and K. Dholakia, Opt. Express, 2004, 12, 3011.
10. Y. Roichman, A. Waldron, E. Gardel and D. G. Grier, Appl. Opt., 2006, 45, 3425.
11. N. Malagnino, G. Pesce, A. Sasso and E. Arimondo, Opt. Commun., 2002, 214, 15.
12. Y. Harada and T. Asakura, Opt. Commun., 1996, 124, 529.
13. H. T. Li, D. J. Zhou, H. Browne and D. Klenerman, J. Am. Chem. Soc., 2006, 128, 5711.
14. H. Felgner, O. Muller and M. Schliwa, Appl. Opt., 1995, 34, 977.
15. A. Rohrbach, Opt. Express, 2005, 13, 9695.
16. E. A. Abbondanzieri, W. J. Greenleaf, J. W. Shaevitz, R. Landick and S. M. Block, Nature, 2005, 438, 460.
17. S. M. Block, L. S. B. Goldstein and B. J. Schnapp, Nature, 1990, 348, 348.
18. C. Bustamante, J. Liphardt and F. Ritort, Phys. Today, 2005, 58, 43.
19. G. M. Wang, E. M. Sevick, E. Mittag, D. J. Searles and D. J. Evans, Phys. Rev. Lett., 2002, 89, 050601.
20. A. Ashkin and J. M. Dziedzic, Science, 1987, 235, 1517.
21. J. Guck, R. Ananthakrishnan, H. Mahmood, T. J. Moon, C. C. Cunningham, R. Hallworth and J. Kas, Biophys. J., 2001, 80, 277A.
22. Laser Manipulation of Cells and Tissue, Methods in Cell Biology, ed. M. W. Berns and K. O. Greulich, Academic Press, Elsevier, London, vol. 82, 2007.
23. M. Goksor, J. Enger and D. Hanstorp, Appl. Opt., 2004, 43, 4831.
24. N. B. Simpson, D. McGloin, K. Dholakia, L. Allen and M. J. Padgett, J. Mod. Opt., 1998, 45, 1943.
25. K. T. Gahagan and G. A. Swartzlander, Opt. Lett., 1996, 21, 827.
26. J. P. Hoogenboom, D. L. J. Vossen, C. Faivre-Moskalenko, M. Dogterom and A. van Blaaderen, Appl. Phys. Lett., 2002, 80, 4828.
27. P. T. Korda, M. B. Taylor and D. G. Grier, Phys. Rev. Lett., 2002, 89, 128301.
28. A. Chowdhury, B. J. Ackerson and N. A. Clark, Phys. Rev. Lett., 1985, 55, 833.
29. Q. H. Wei, C. Bechinger, D. Rudhardt and P. Leiderer, Phys. Rev. Lett., 1998, 81, 2606.
30. P. J. Rodrigo, V. R. Daria and J. Gluckstad, Appl. Phys. Lett., 2005, 86, 074103.
31. J. E. Curtis, B. A. Koss and D. G. Grier, Opt. Commun., 2002, 207, 169.
32. J. Leach, G. Sinclair, P. Jordan, J. Courtial, M. J. Padgett, J. Cooper and Z. J. Laczik, Opt. Express, 2004, 12, 220.
33. L. Allen, M. W. Beijersbergen, R. J. C. Spreeuw and J. P. Woerdman, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 8185.
34. H. He, M. E. J. Friese, N. R. Heckenberg and H. Rubinszteindunlop, Phys. Rev. Lett., 1995, 75, 826.
35. M. P. MacDonald, L. Paterson, K. Volke-Sepulveda, J. Arlt, W. Sibbett and K. Dholakia, Science, 2002, 296, 1101.
36. M. E. J. Friese, T. A. Nieminen, N. R. Heckenberg and H. Rubinsztein-Dunlop, Nature, 1998, 394, 348.
37. G. Knoner, S. Parkin, N. R. Heckenberg and H. Rubinsztein-Dunlop, Phys. Rev. E, 2005, 72, 031507.
38. D. McGloin and K. Dholakia, Contemp. Phys., 2005, 46, 15.
39. V. Garces-Chavez, D. McGloin, M. J. Padgett, W. Dultz, H. Schmitzer and K. Dholakia, Phys. Rev. Lett., 2003, 91, 093602.
40. V. Garces-Chavez, D. McGloin, H. Melville, W. Sibbett and K. Dholakia, Nature, 2002, 419, 145.
41. L. Paterson, E. Papagiakoumou, G. Milne, V. Garces-Chavez, S. A. Tatarkova, W. Sibbett, F. J. Gunn-Moore, P. E. Bryant, A. C. Riches and K. Dholakia, Appl. Phys. Lett., 2005, 87, 123901.
42. S. Kawata and T. Sugiura, Optics Lett., 1992, 17, 772.
43. M. Gu, J. B. Haumonte, Y. Micheau, J. W. M. Chon and X. S. Gan, Appl. Phys. Lett., 2004, 84, 4236.
44. P. J. Reece, V. Garces-Chavez and K. Dholakia, Appl. Phys. Lett., 2006, 88, 221116.
45. M. M. Burns, J. M. Fournier and J. A. Golovchenko, Phys. Rev. Lett., 1989, 63, 1233.
46. C. D. Mellor and C. D. Bain, ChemPhysChem, 2006, 7, 329.
47. S. A. Tatarkova, A. E. Carruthers and K. Dholakia, Phys. Rev. Lett., 2002, 89, 283901.
48. (a) S. Kulin, R. Kishore, K. Helmerson and L. Locascio, Langmuir, 2003, 19, 8206; (b) D. R. Burnham and D. McGloin, Opt. Express, 2006, 14, 4176–4182.
49. D. R. Burnham and D. McGloin, Opt. Express, 2006, 14, 4175.
50. W. Singer, H. Rubinsztein-Dunlop and U. Gibson, Opt. Express, 2004, 12, 6440.
51. P. Galajda and P. Ormos, Appl. Phys. Lett., 2001, 78, 249.
52. S. Cran-McGreehin, T. F. Krauss and K. Dholakia, Lab Chip, 2006, 6, 1122.
53. P. Zemanek, A. Jonas and M. Liska, J. Opt. Soc. Am. A, 2002, 19, 1025.
54. M. P. MacDonald, G. C. Spalding and K. Dholakia, Nature, 2003, 426, 421.
55. A. Rohrbach, C. Tischer, D. Neumayer, E. L. Florin and E. H. K. Stelzer, Rev. Sci. Instrum., 2004, 75, 2197.
56. P. M. Hansen, V. K. Bhatia, N. Harrit and L. Oddershede, Nano Lett., 2005, 5, 1937.
57. P. Y. Chiou, A. T. Ohta and M. C. Wu, Nature, 2005, 436, 370.
58. D. Ganic, X. Gan and M. Gu, Opt. Express, 2004, 12, 5533.

---