The non-covalent functionalisation of carbon nanotubes studied by density functional and semi-empirical molecular orbital methods including dispersion corrections
Jonathan P.
McNamara
,
Raman
Sharma
,
Mark A.
Vincent
,
Ian H.
Hillier
* and
Claudio A.
Morgado
School of Chemistry, University of Manchester, Oxford Road, Manchester, UK M13 9PL. E-mail: Ian.Hillier@manchester.ac.uk; Fax: +44 (0)161 275 4734; Tel: +44 (0)161 275 4686
First published on 25th October 2007
Abstract
Density functional theory (DFT-D) and semi-empirical (PM3-D) methods having an added empirical dispersion correction have been used to study the binding of a series of small molecules and planar aromatic molecules to single-walled carbon nanotubes (CNTs). For the small molecule set, the PM3-D method gives a mean unsigned error (MUE) in the binding energies of 1.2 kcal mol−1 when judged against experimental reference data for graphitic carbon. This value is close to the MUE for this method compared to high-level ab initio data for biological complexes. The PM3-D and DFT-D calculations describing the adsorption of the planar organic molecules (benzene, bibenzene, naphthalene, anthracene, TCNQ and DDQ) on the outer-walls of both semi-conducting and metallic CNTs give similar binding energies for benzene and DDQ, but do not display a stronger adsorption on [6,6] compared to [10,0] structures shown by another DFT study.
Introduction
Non-covalent (intermolecular) interactions are of importance in many areas of biological, supramolecular and materials chemistry.1–3 One area where such interactions are expected to play a crucial role is in the chemistry of the fullerenes and carbon nanotubes (CNTs).4 However, despite their promising potential in a range of nanoelectronic devices,5,6 relatively little is known regarding the magnitude and nature of the interactions between adsorbed molecules and the inner- and outer-walls of single-walled CNTs.Structurally a CNT can be considered as essentially a graphene sheet (a single-atom thick layer of graphite) rolled into a cylinder, with a diameter of ca. 1 nm and a length several orders of magnitude larger. The different structures are described by a chiral vector, denoted by a pair of indices [n,m] which describe the way in which the graphene sheet is wrapped. As such, the different structures are commonly referred to as ‘zigzag’ (m = 0) and ‘armchair’ (n = m), whilst all other tubes are denoted ‘chiral’. Importantly, the transport properties of CNTs are determined by their structure, with armchair CNTs being metallic and all others being semi-conducting.5
Quantum chemical calculations are now being used to gain insight into how molecules in different orientations interact with both the inner- and outer walls of a range of CNTs.7–17 However, such calculations remain a formidable challenge since the proper description of the extended π-system of the tubes ideally requires the use of large models and a highly-correlated quantum mechanical method [e.g. MP2 or CCSD(T)], even though the size of such calculations generally precludes the use of such an approach. It is for this reason that density functional theory (DFT) methods involving either plane-wave7–14 or localised basis sets15–17 are now being used to understand the interaction of a number of closed and open-shell molecules with the extended π-system of CNTs. In particular, the interaction with CNTs, of aromatic molecules ranging from benzene to 2,3-dichloro-5,6-dicyano-1,4-benzoquinone (DDQ) have been studied by DFT methods.8–12π-stacking interactions are expected to be important here,18 although similar interactions in biological systems such as base-pairs have been shown to be generally poorly described using standard density functionals.19,20 This is attributed to the problem of correctly describing the important dispersive interactions.18,19 This problem has been tackled both by developing new functionals21,22 and by the addition of an empirical dispersion correction to DFT to give the so-called DFT-D method.18,19,23,24 A similar strategy has recently been shown to be extremely successful in correcting semi-empirical molecular orbital methods such as PM3 and AM1 to give the PM3-D and AM1-D methods.25,26
In view of the success of the DFT-D and PM3-D methods in modelling a wide range of biological interactions,25–28 we here explore their use to study the non-covalent interactions between the inner- and outer walls of metallic and semi-conducting CNTs and a range of small molecules. Recently the DFT-D method has been used to study the interaction of methane with CNTs18 and also the non-covalent interactions between graphene sheets and multi-shell fullerenes.29 However, the relatively low computational cost of the PM3-D method compared to the DFT-D approach makes it an attractive alternative for the study of more realistic CNT models. Herein we use the PM3-D method to study the interaction of a large number of quite small molecules with CNTs. For these systems there are reference physical adsorption potentials involving a graphitic surface.30 This paper provides a summary of key data on 250 gas–surface interactions, giving ‘best values’ for many systems, but no estimates of the error. We also use both the DFT-D and PM3-D approaches to study the interaction of a number of aromatic molecules with CNTs.
Computational details
In the DFT-D approach,19,23 a pair-wise additive potential of the form C6/R6 is used to account for long-range dispersion effects that can be particularly poorly described both with some density functionals and with current semi-empirical methods (AM1, PM3).31,32 For each model, the dispersion corrected total energy is given by: | (1) |
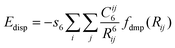 | (2) |
 | (3) |
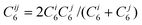 | (4) |
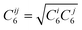 | (5) |
The DFT-D calculations reported herein have been performed using a locally modified version of GAUSSIAN 0334 with the dispersion corrected BLYP35,36 method (BLYP-D)27,28 and the TZV(2d,2p) basis set.37,38 As in previous calculations, we do not consider basis set superposition errors (BSSE) in view of the quite large basis sets employed.19 This is justified by the success of the DFT-D method in reproducing the interaction energies of a large database of interactions calculated by high level methods at the basis set limit.27 We have also compared some of the results of our DFT-D calculations with those using a number of alternative density functionals suggested to be appropriate for the description of π-stacking interactions. Thus, DFT calculations with the BHandH,39SVWN40 and PWB6K21 functionals were carried out using GAUSSIAN 03, with a local implementation of the PWB6K functional. As in the case of the DFT-D calculations, the numerical integration was performed employing the weighting scheme of Becke along with grids of ultrafine quality. Reported interaction energies refer to electronic energies; zero-point vibrational as well as thermal corrections are not included. Zero point corrections are only about 0.3 kcal mol−1 for the benzene dimer,18 and are thus not expected to be important here.
The semi-empirical calculations reported herein were performed using our local semi-empirical program.41 In line with our previous work, the calculations (PM3-D) use the combination rule given in eqn (4) and the associated C6, R0, s6 and α parameters (Table 1) along with the modified semi-empirical parameters for H, C, N and O.25 We note that although some of the calculations involve chlorine atoms, optimisation of the PM3 chlorine parameters did not significantly change the final results and as such we chose to use the published PM3 chlorine parameters. Finally, all the PM3-D calculations reported herein are closed-shell since the DFT-D calculations indicate that using the triplet rather than the singlet electronic state for the CNT does not significantly alter the values of the interaction or binding energies.
Finally, all calculations reported herein involve only the isolated CNT-molecule complexes, consistent with gas-surface experimental data.30
Computational results and discussion
(1) Benchmark calculations for biological interactions
Before considering non-covalent interactions in nanomaterials, we first note the performance of the DFT-D and PM3-D methods for the calculation of biological non-covalent interactions. The DFT-D (BLYP-D) method has been successfully used to calculate the binding energies of 156 non-covalent biological complexes taken from the combined S22 and JSCH-2005 databases1 of Hobza and co-workers. On average, the BLYP-D method yields binding energies to within 0.7 kcal mol−1 of the high-level ab initio values [MP2 or CCSD(T)].27 For this same database, the PM3-D method yields interaction energies to within, on average, 1.2 kcal mol−1 of the high-level ab initio values.25(2) PM3-D binding of small molecules to the inner- and outer walls of CNTs
An understanding of the mode of interaction of small molecules with the inner- and outer walls of CNTs is important for the development of future gas storage materials, novel monitoring technology (e.g. pollutant detection) and also heterogeneous catalyst supports.42–46 We have calculated the binding geometries and energies for a series of small molecules for which reference physical adsorption potential data for graphitic carbon are available from the work of Vidali et al.30 In order to realistically model the extended delocalised π-system of a CNT we chose as our model a ca. 30 Å length of a zigzag [10,0] CNT involving 280 carbon atoms, the tube being terminated with 20 hydrogen atoms. We have calculated the binding geometries and energies of the molecules CH4, C2H2, C2H4, C2H6, C6H6, CO, CO2, H2O, NH3, H2 and N2 in different orientations on both the inner- and outer walls of the model CNT. For each system, full geometry optimisation (without any constraints) was employed for both the tube and the adsorbed molecule. The final results (binding energies and geometries) are presented in Tables 2 and 3. We note that here the binding energy (ΔEbind) is defined as the difference in energy between the optimised complex and the optimised monomer units, whereas the interaction energy (ΔEint) is defined as the difference in energy between the optimised complex and the isolated (non-relaxed) monomer units. The dispersive contributions to the binding energies (ΔEdisp) are also reported. In Fig. 1 we depict the different adsorption sites; T (top of a carbon atom), B (the centre of a C–C bond), C (top of the centre of a carbon hexagon).![Different possible adsorption sites on the (a) [10,0] CNT and (b) [6,6] CNT. T (top of a carbon atom), B (top of the centre of a C–C bond) and C (top of the centre of a carbon hexagon).](/image/article/2008/CP/b711498b/b711498b-f1.gif) | ||
| Fig. 1 Different possible adsorption sites on the (a) [10,0] CNT and (b) [6,6] CNT. T (top of a carbon atom), B (top of the centre of a C–C bond) and C (top of the centre of a carbon hexagon). | ||
| PM3-D | Referenced | ||||||
|---|---|---|---|---|---|---|---|
| Moleculea | Coordinationb | R | ΔEbind | ΔEdispc | R | ΔEbind | |
a Long molecular axis perpendicular to [10,0] CNT axis (⊥). Long molecular axis parallel to [10,0] CNT axis (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ).
b Refer to Fig. 1 for coordination sites for PM3-D calculations only. Italics denote binding site. COM (centre of mass).
c PM3-D dispersion contribution.
d Vidali et al. and references therein.30
e Closest hydrogen to C-site distance 2.473 Å.
f Average hydrogen (down) to closest CNT carbon atom distance 2.697 Å.
g Average hydrogen to closest CNT carbon atom distance. ).
b Refer to Fig. 1 for coordination sites for PM3-D calculations only. Italics denote binding site. COM (centre of mass).
c PM3-D dispersion contribution.
d Vidali et al. and references therein.30
e Closest hydrogen to C-site distance 2.473 Å.
f Average hydrogen (down) to closest CNT carbon atom distance 2.697 Å.
g Average hydrogen to closest CNT carbon atom distance.
|
|||||||
| CH4 | C to Ce | 3.313 | −3.95 | −4.46 | 3.45 | −2.91 | |
| C2H2 | Centre of C–C to B | 3.263 | −3.51 | −4.83 | −4.10 | ||
| C2H4 | Centre of C–C to B | 3.248 | −4.08 | −5.61 | −4.52 | ||
| C2H6 | Centre of C–C to Tf | 3.294 | −6.60 | −7.38 | −4.75 | ||
| C6H6 | COM (benzene) to B | 3.192 | −10.32 | −14.69 | 3.38 | −6.41 | |
| CO | C to T | 3.301 | −1.61 | −2.34 | −2.53 | ||
| O to T | 3.283 | −1.29 | −1.88 | ||||
| CO2 | ⊥ | O to T | 3.256 | −1.37 | −2.04 | 3.2 | −4.11 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Centre of C–O to B | 3.404 | −2.41 | −4.01 | |||
| H2O | H-down | H to Tg | 2.628 | −3.35 | −3.13 | −3.71 | |
| O-down | O to T | 3.185 | −1.29 | −1.79 | |||
| NH3 | H-down | H to Cg | 2.803 | −4.07 | −4.65 | −2.42 | |
| N-down | N to T | 3.216 | −2.15 | −2.54 | |||
| H2 | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Centre of H–H to B | 3.394 | −0.50 | −0.66 | 2.87 | −0.96 |
| ⊥ | H to T | 2.631 | −0.94 | −1.13 | |||
| N2 | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Centre of N–N to B | 3.373 | −2.07 | −3.03 | 3.34 | −2.40 |
| ⊥ | N to T | 3.213 | −1.72 | −2.34 | |||
We see that the computed binding energies are generally in good agreement with the data of Vidali et al. with the ordering of the hydrocarbon binding energies, C6H6 > C2H6 > C2H4 > C2H2, being in-line with the reference data,28 although in the absence of the dispersive correction all the interactions are essentially repulsive. For the case of methane there are data for the adsorption on CNTs themselves which give an adsorption energy of −5.1 kcal mol−1,47 significantly greater than the value on graphene (−2.91 kcal mol−1, Table 2).30 We note that our PM3-D estimate (−3.95 kcal mol−1) is between these two values. The mean unsigned error (MUE) for the binding energies (compared to the reference values) is just 1.2 kcal mol−1, very close to the MUE obtained for the PM3-D calculations of 156 complexes taken from the combined S22 and JSCH-2005 biological databases (1.21 kcal mol−1).25 In the present study, the largest difference between the reference and semi-empirical values occurs for the π-stacked benzene complex where the binding energy is overestimated by 3.9 kcal mol−1 (−10.32 kcal mol−1) compared to the value reported by Vidali et al. [−6.41 kcal mol−1, Table 2].30 However, there is some disagreement as to the actual value for the heat of adsorption of benzene on graphitic carbon. Thus, the heat of adsorption of benzene on carbon black surfaces has been reported to be −9.4 kcal mol−1, a value closer to our PM3-D estimate.48
The calculated PM3-D binding energies range from −0.50 kcal mol−1 for H2 (parallel to CNT axis) to –10.32 kcal mol−1 for benzene (π-stacked) and the dispersive contributions range from –0.66 kcal mol−1 (H2, parallel to CNT axis) to −14.69 kcal mol−1 (benzene). We may compare our results with the work of Feng et al.15 who have estimated the binding of ammonia to a single-walled CNT from SCC-DFTB-D (dispersion) calculations of NH3 binding to coronene. Their calculated binding energy (−3.42 kcal mol−1) is in fact quite close to our PM3-D values obtained with a more realistic CNT model (−2.15 and −4.07 kcal mol−1, Table 2).
We have extended our calculations to consider the interaction of the same small molecules with the inner walls of a model [10,0] CNT. We find that for each of these molecules, with the exception of benzene, the inner-wall binding energies are significantly larger than the corresponding outer-wall values (Table 3). As expected, the dispersive contributions to binding are important as in the absence of the correction, the various molecule–CNT interactions are again repulsive. The increased inner-wall binding energies largely reflect the increased availability of non-covalent contacts with the surrounding CNT walls. Interestingly, for benzene the inner-wall binding energy is reduced by 1.3 kcal mol−1 compared to the outer-wall value. This decrease may be due to the distortion of the [10,0] CNT whose diameter has increased by ca. 0.5 Å in order to accommodate the benzene molecule, the benzene hydrogens now being within 2.2–2.4 Å of the nearest CNT carbon atom. The corresponding increase in the intermolecular interactions is further highlighted by the fact that the dispersive contribution for the inner-wall complex is −55.5 kcal mol−1 (Table 3), nearly four times the value for the corresponding outer-wall structure (−14.7 kcal mol−1, Table 2).
(3) DFT-D and PM3-D interaction of planar organic molecules on [10,0] and [6,6] CNTs
The chemical properties of CNTs may be tailored by appropriate functionalisation in order to achieve better solubility and processability, and, as such, two possible routes exist for their modification. Firstly, by the covalent attachment of chemical groupsvia chemical reaction onto the π-conjugated tube walls (e.g.hydrogenation; cycloadditions; radical, electrophilic and nucleophilic additions; ozonolysis),49 and secondly, the non-covalent adsorption or wrapping of various functional molecules around the tubes themselves.4 Of these two approaches, the latter provides a way of modifying the chemical properties of the CNT without destroying its geometric and electronic properties. These relatively weak non-covalent interactions often involve π–π stacking, and as such, planar aromatic organic molecules are found to readily interact with the walls of CNTs.4 As a result, a great deal of attention is now being given to the study of the interaction of planar organic molecules of varying sizes, such as benzene, bibenzene, naphthalene, anthracene, 7,7′,8,8′-tetracyanoquinodimethane (TCNQ) and DDQ with both the semi-conducting zigzag and metallic armchair single-walled CNTs.8–12 We have therefore extended our DFT-D and PM3-D calculations to study the interaction of various planar organic molecules with model [10,0] and [6,6] CNTs.We first consider the calculation of the interaction energy of benzene with a model [10,0] CNT. To date, dispersion corrected DFT (or semi-empirical) methods have yet to be used to investigate the binding of benzene to CNTs. Such calculations are important since previous computational studies have not reached a consensus regarding the magnitude of binding of π-stacked benzene to CNTs.8–12
In order to realistically model the outer-wall of the [10,0] CNT, our model involves a CNT of ca. 10 Å in length, having 80 carbon atoms and is terminated with 20 hydrogen atoms, a size similar to that used by Grimme et al. for their DFT-D calculations of methane adsorption on a [6,6] CNT.18 In view of the associated computational expense of the DFT-D calculations (up to 2574 basis functions) and the excellent results obtained using the PM3-D method (Table 2) we chose to optimise the geometry of the benzene + [10,0] CNT complex using the PM3-D method followed by the evaluation of the energy at the BLYP-D/TZV(2d,2p) level. Optimisation of the complex at the PM3-D level led to a structure in which the benzene was bound at the B coordination site (Fig. 1a). At the DFT-D level the corresponding interaction energy is −7.3 kcal mol−1. Previous DFT calculations by Tournus and Charlier (employing periodic boundary conditions) on the binding of benzene to zigzag and armchair CNTs yield smaller values (−4.0 to −4.7 kcal mol−1) which argues for the importance of the dispersive correction.9 Moreover, the DFT-D value is considerably larger than the values obtained by Luet al.12 (using ultrasoft pseudopotentials and plane-wave basis sets) for the binding of benzene to [10,0] and [6,6] CNTs (−2.5 and −2.3 kcal mol−1). We also note that previous calculations of Mavarandonakis et al. indicate that the lowest electronic state of the CNT is in fact a triplet and not a singlet.16 This finding is supported by our DFT-D calculations which predict the triplet to be lower than the singlet but by only 1.8 kcal mol−1. However, the overall effect on the interaction energy for this complex is negligible; for the triplet CNT the interaction energy for benzene increases by only 0.1 kcal mol−1 to −7.4 kcal mol−1 (Table 4).
| Complex | Coordination | BHandHd | SVWN d | PWB6Kd | BLYP-D d |
|---|---|---|---|---|---|
| a Triplet. CNT model involves 80 carbon atoms, terminated by 20 hydrogen atoms. b Singlet. Long molecular axis of DDQ is parallel to tube axis. CNT model involves 80 carbon atoms, terminated by 20 hydrogen atoms. c Singlet. Long molecular axis of DDQ is rotated ca. 60° to tube axis. CNT model involves 84 carbon atoms, terminated by 24 hydrogen atoms. d TZV(2d,2p) basis set. | |||||
| C6H6 + [10,0]a | B | −5.3 | −6.4 | −1.6 | −7.4 |
| DDQ + [10,0]b | B | −23.1 | |||
| DDQ + [6,6]c | B | −20.7 |
We have also compared the results of our DFT-D calculations for the benzene–CNT complex with those using a number of alternative functionals, suggested to be appropriate for the description of π-stacking interactions.21,39,40 The results of the additional DFT calculations are summarised in Table 4. Overall the DFT-D method yields the largest interaction energy (−7.4 kcal mol−1) and also the closest value to the measured heat of adsorption of benzene on carbon black surfaces (−9.4 kcal mol−1).48 The other functionals yield a range of smaller values, −1.6 (PWB6K), −5.3 (BHandH) and −6.4 kcal mol−1 (SVWN). We find that at the PM3-D level the binding energy for benzene on a [10,0] CNT (−10.32 kcal mol−1, Table 2) is in fact closer to the heat of adsorption of benzene on carbon black surfaces (−9.4 kcal mol−1)48 than any of these DFT values, although the SVWN value is closer to the value on graphene.30
One of the most important steps during the processing of CNTs is the separation of metallic and semi-conducting tubes, and, as such, Luet al. have carried out DFT calculations to understand the interaction of various planar organic molecules with both semi-conducting [10,0] and metallic [6,6] CNTs.12 Their calculations predict that the charge-transfer molecules (TCNQ, DDQ) interact more strongly with metallic [6,6] CNTs compared to their semi-conducting counterparts, [10,0] CNTs, thus providing a possible mechanism for the separation of these two types of CNT. For example, their DFT calculations give the binding energies for the perpendicular orientation of TCNQ to be −6.0 kcal mol−1 on the [10,0] and −13.6 kcal mol−1 on the [6,6]; for the parallel orientation of DDQ the binding energies are −13.1 kcal mol−1 on the [10,0] and −26.3 kcal mol−1 on the [6,6]. To further investigate this possible effect, we have carried out calculations at the PM3-D and the DFT-D level of the adsorption of a number of planar organic molecules on model [10,0] and [6,6] CNTs.
For the DFT-D calculations, as with those calculations of benzene adsorption, all geometries were optimised at the PM3-D level, interaction energies being calculated at the BLYP-D/TZV(2d,2p) level. The model [10,0] CNT was the same as that used to calculate the binding of benzene, and the [6,6] CNT was modelled using a tube of ca. 10 Å in length, having 84 carbon atoms and being terminated with 24 hydrogen atoms. Optimisation at the PM3-D level led to structures in which the DDQ was bound at the B site on both the [10,0] and [6,6] CNTs (Fig. 1). We note that for the complex involving the [6,6] CNT the long molecular axis of the DDQ molecule rotated by ca. 60° as a result of the use of a truncated CNT model. At the BLYP-D level, the interaction energies for DDQ on the [10,0] and [6,6] CNTs were calculated to be −23.1 and −20.7 kcal mol−1, respectively, which do not display the strong differential effect shown by the calculations of Luet al.12
A more extensive set of molecules were studied using the PM3-D method. Benzene, bibenzene, naphthalene, anthracene, TCNQ and DDQ were considered in two different orientations, firstly, where the long molecular axis of the adsorbed molecule is parallel to the tube axis and secondly, where the long molecular axis is perpendicular to the tube axis. We chose the [10,0] CNT model to be the same as the one used to study the small molecule interactions (i.e. length of ca. 30 Å). The [6,6] CNT model involved 300 carbon atoms (terminated by 24 hydrogens), again ca. 30 Å in length. We have calculated the binding energies for each molecule in the fully optimised tube–molecule complex. The binding energies and interaction distances for adsorption on the [10,0] and [6,6] CNTs are given in Table 5, with the binding geometries being shown in Fig. 2 and 3.
![Adsorption motifs of planar organic molecules in parallel () and perpendicular (⊥) arrangements on the outer walls of a [10,0] CNT: benzene, (a); bibenzene, (b), (c); naphthalene, (d), (e); anthracene, (f), (g); TCNQ, (h), (i); DDQ, (j), (k).](/image/article/2008/CP/b711498b/b711498b-f2.gif) | ||
Fig. 2 Adsorption motifs of planar organic molecules in parallel (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ) and perpendicular (⊥) arrangements on the outer walls of a [10,0] CNT: benzene, (a); bibenzene, (b), (c); naphthalene, (d), (e); anthracene, (f), (g); TCNQ, (h), (i); DDQ, (j), (k). ) and perpendicular (⊥) arrangements on the outer walls of a [10,0] CNT: benzene, (a); bibenzene, (b), (c); naphthalene, (d), (e); anthracene, (f), (g); TCNQ, (h), (i); DDQ, (j), (k). | ||
![Adsorption motifs of planar organic molecules in parallel () and perpendicular (⊥) arrangements on the outer-walls of a [6,6] CNT: benzene, (a); bibenzene, (b), (c); naphthalene, (d), (e); anthracene, (f), (g); TCNQ, (h), (i); DDQ, (j), (k).](/image/article/2008/CP/b711498b/b711498b-f3.gif) | ||
Fig. 3 Adsorption motifs of planar organic molecules in parallel (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ) and perpendicular (⊥) arrangements on the outer-walls of a [6,6] CNT: benzene, (a); bibenzene, (b), (c); naphthalene, (d), (e); anthracene, (f), (g); TCNQ, (h), (i); DDQ, (j), (k). ) and perpendicular (⊥) arrangements on the outer-walls of a [6,6] CNT: benzene, (a); bibenzene, (b), (c); naphthalene, (d), (e); anthracene, (f), (g); TCNQ, (h), (i); DDQ, (j), (k). | ||
| [10,0] | [6,6] | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Molecule | Coordinationa | R d/Å | Site | ΔEbind/kcal mol−1 | ΔEdisp/kcal mol−1 | Site | R d/Å | ΔEbind/kcal mol−1 | ΔEdisp/kcal mol−1 |
a Refer to Fig. 2 and 3 for coordination sites. Molecular axis perpendicular to tube axis (⊥). Molecular axis parallel to tube axis (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ).
b
7,7′,8,8′-Tetracyanoquinodimethane.
c
2-3-Dichloro-5,-dicyano-1,4-benzoquinone.
d Distance from centre of mass of molecule to adsorption site (B, C, or T).
e Distance from centre of carbon ring to binding site is 3.122 Å.
f Distance from centre of carbon ring to binding site is 3.228 Å. ).
b
7,7′,8,8′-Tetracyanoquinodimethane.
c
2-3-Dichloro-5,-dicyano-1,4-benzoquinone.
d Distance from centre of mass of molecule to adsorption site (B, C, or T).
e Distance from centre of carbon ring to binding site is 3.122 Å.
f Distance from centre of carbon ring to binding site is 3.228 Å.
|
|||||||||
| Benzene | 3.192 | B | −10.32 | −14.69 | B | 3.248 | −10.56 | −15.12 | |
| Bibenzene | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
3.322 | C | −19.72 | −28.20 | B | 3.258 | −19.95 | −33.50 |
| ⊥ | 3.098 | C | −18.14 | −26.34 | C | 3.122 | −17.92 | −30.80 | |
| Naphthalene | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
3.389 | B | −16.11 | −22.99 | B | 3.338 | −16.10 | −22.44 |
| ⊥ | 3.252 | C | −15.57 | −22.23 | B | 3.204 | −15.72 | −22.52 | |
| Anthracene | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
3.224 | T | −21.92 | −31.29 | B | 3.268 | −22.59 | −32.59 |
| ⊥ | 3.026 | B | −19.72 | −28.80 | B | 3.081 | −20.01 | −29.21 | |
| TCNQ b | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
3.158 | T | −23.04 | −32.65 | C | 3.360 | −22.10 | −31.28 |
| ⊥ | 2.701e | B | −20.52 | −32.91 | B | 2.793f | −21.88 | −32.47 | |
| DDQ c | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
3.230 | B | −29.71 | −26.49 | B | 3.289 | −18.78 | −26.74 |
| V | 3.099 | B | −27.63 | −26.41 | B | 3.104 | −19.11 | −27.02 | |
As far as the interaction of planar organic molecules with the extended π-system of the CNT is concerned, it is anticipated that molecules with their long molecular axis aligned with that of the CNT will have increased binding energies due to an increased contact area with the tube (compared to the perpendicular orientation). This is essentially the trend observed (Table 5), where the differences between the binding energies of the parallel and perpendicular orientations range from 0.22 to 2.58 kcal mol−1. Again the dispersive contributions to binding are significant. In contrast to the DFT results of Luet al.12 the PM3-D calculations generally show no strong differential adsorption energies between the [10,0] and [6,6] structures, (Table 5), with the exception of DDQ. Here, the PM3-D binding energies for DDQ in the parallel orientation on both the [10,0] and [6,6] CNTs (−29.7 and −18.8 kcal mol−1, Table 5) in common with the DFT-D values for the smaller CNT models (−23.1 kcal mol−1 and −20.7 kcal mol−1, Table 4), predict a stronger binding on [10,0] compared to [6,6] structures.
(4) PM3-D interaction of C60 with [10,10] CNT
There is currently considerable interest in the supramolecular chemistry of the fullerenes with regards to developments in nanoscience and nanotechnology. One such area involves the encapsulation of C60 into single-walled CNTs to form supramolecular assemblies where the C60 molecules are arranged in a 1D array, the so-called nanoscopic ‘peapod’ structure.50,51 Such structures are of great interest as potentially they could be tailored to give nanomaterials having unique electronic properties. However, very little is actually known about such assemblies, other than structural characterisation. Thus, we have extended our PM3-D calculations to evaluate the interaction energy for a single C60 molecule inside a [10,10] CNT. Our model involves a ca. 50 Å length of a [10,10] CNT, a tube with sufficiently large diameter (ca. 13–14 Å) to accommodate C60. Overall, the CNT model involves 880 atoms and therefore such models are impractical to treat at the DFT-D level. Even at the PM3-D level, a full semi-empirical treatment is quite expensive, although with code parallelisation, energies can be obtained for systems of the order of 1000 atoms in several hours on a dual-core, dual-processor node (2.5 GHz AMD Opteron) cluster computer.For C60, the interaction energy inside the [10,10] CNT is, as expected, much larger (−122 kcal mol−1) than the corresponding value for benzene inside a [10,0] CNT (Table 3) and the dispersive contribution is even larger (−156.2 kcal mol−1). Thus we have demonstrated that the PM3-D method can be used to calculate interaction energies for very large molecular clusters which could not be easily performed using DFT-D or ab initio methods.
Conclusions
We have shown in this work that the DFT-D and PM3-D methods are capable of accurately describing the non-covalent interactions between small molecules and the inner- and outer walls of singled-walled CNTs, thus extending their use from intermolecular biological interactions, which are now well documented.25–28 The PM3-D binding energy MUE of 1.2 kcal mol−1 obtained for the small molecule adsorption on the outer-walls of the [10,0] CNT is close to the corresponding value obtained for the combined S22 and JSCH-2005 databases (1.2 kcal mol−1) of biological interactions.25 Both DFT-D and PM3-D methods give similar binding energies for a series of planar aromatic molecules on both [10,0] and [6,6] nanotubes, except for DDQ where both corrected methods predict a stronger adsorption on [10,0] compared to [6,6] structures. Thus the DFT-D and PM3-D calculations do not display stronger interactions with the metallic compared to the semi-conducting species, shown by a previous DFT study.12 Although further validation of the PM3-D and DFT-D methods is clearly needed, they are both attractive methods for the study of new and important problems involving nanotubes and fullerenes in the area of nanoscience and nanotechnology. Even though these DFT and semi-empirical methods with a R−6 correction may be deemed to be more ‘approximate’ than DFT methods requiring a specific functional, they do however represent a good compromise between high level ab initio methods and empirical force-field schemes.Acknowledgements
We thank the North West Development Agency (NWDA), the NWGrid Consortium for the provision of computing resources, Professor S. Yeates for helpful discussions and Dr N. A. Burton for the implementation of the PWB6K functional.References
- P. Jurečka, J. Šponer, J. Černy and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985 RSC.
- P. Hobza and J. Šponer, Chem. Rev., 1999, 99, 3247 CrossRef CAS.
- K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143 CrossRef CAS.
- D. A. Britz and A. N. Khlobystov, Chem. Soc. Rev., 2006, 35, 637 RSC.
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 2005 Search PubMed.
- M. Terrones, W. K. Hsu, H. W. Kroto and D. R. M. Walton, Top. Curr. Chem., 1999, 199, 189 CAS.
- J. Zhao, A. Buldum, J. Han and J. Ping Lu, Nanotechnology, 2002, 13, 195 CrossRef CAS.
- J. Zhao, J. Ping Lu, J. Han and C.-K. Yang, Appl. Phys. Lett., 2003, 82, 3746 CrossRef CAS.
- F. Tournus and J.-C. Charlier, Phys. Rev. B, 2005, 71, 165421 CrossRef.
- F. Tournus, S. Latil, M. I. Heggie and J.-C. Charlier, Phys. Rev. B, 2005, 72, 075431 CrossRef.
- R. G. A. Veiga and R. H. Miwa, Phys. Rev. B, 2006, 73, 245422 CrossRef.
- J. Lu, S. Nagase, X. Zhang, D. Wang, M. Ni, Y. Maeda, T. Wakahara, T. Nakahodo, T. Tsuchiya, T. Akasaka, Z. Gao, D. Yu, H. Ye, W. N. Mei and Y. Zhou, J. Am. Chem. Soc., 2006, 128, 5114 CrossRef CAS.
- (a) E. L. Sceats and J. C. Green, Phys. Rev. B, 2007, 75, 245441 CrossRef; (b) E. L. Sceats and J. C. Green, J. Chem. Phys., 2006, 125, 154704 CrossRef.
- R. Carter, J. Sloan, A. I. Kirkland, R. R. Meyer, P. J. D. Lindan, G. Lin, M. L. H. Green, A. Vlandas, J. L. Hutchison and J. Harding, Phys. Rev. Lett., 2006, 96, 215501 CrossRef.
- X. Feng, S. Irle, H. Witek, K. Morokuma, R. Vidic and E. Borguet, J. Am. Chem. Soc., 2005, 127, 10533 CrossRef CAS.
- A. Mavarandonakis, S. C. Farantos and G. E. Froudakis, J. Phys. Chem. B, 2006, 110, 6048 CrossRef.
- V. A. Basiuk, J. Phys. Chem. B, 2004, 108, 19990 CrossRef CAS.
- S. Grimme, J. Antony, T. Schwabe and C. Mück-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741 RSC.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Comput. Theory Comput., 2007, 3, 289 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 2701 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef.
- X. Wu, M. C. Vargas, S. Nayak, V. Lotrich and G. Scoles, J. Chem. Phys., 2001, 115, 8748 CrossRef CAS.
- J. P. McNamara and I. H. Hillier, Phys. Chem. Chem. Phys., 2007, 9, 2362 RSC.
- C. A. Morgado, J. P. McNamara, I. H. Hillier, N. A. Burton and M. A. Vincent, J. Chem. Theory Comput., 2007, 3, 1656 CrossRef CAS.
- C. Morgado, M. A. Vincent, I. H. Hillier and X. Shan, Phys. Chem. Chem. Phys., 2007, 9, 448 RSC.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287 RSC.
- S. Grimme, C. Mück-Lichtenfeld and J. Antony, J. Phys. Chem. C, 2007, 111, 11199 CrossRef CAS.
- G. Vidali, G. Ihm, H. Kim and M. W. Cole, Surf. Sci. Rep., 1991, 12, 133 CrossRef CAS.
- M. J. S. Dewar, E. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1993, 115, 5348 CrossRef CAS.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209 CrossRef CAS.
- T. A. Halgren, J. Am. Chem. Soc., 1992, 114, 7827 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03, (Revision C.02), Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- A. Schäfer, C. Huber and R. J. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- S. J. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- M. Mohr, J. P. McNamara, H. Wang, S. A. Rajeev, J. Ge, C. Morgado and I. H. Hillier, Faraday Discuss., 2003, 124, 413 RSC.
- Q. Zhao, M. Buongiorno Nardelli, W. Lu and J. Bernholc, Nano Lett., 2005, 5, 847 CrossRef CAS.
- A. Javey, R. Tu, D. B. Farmer, J. Guo, R. G. Gordon and H. Dai, Nano Lett., 2005, 5, 345 CrossRef CAS.
- W. Li, C. Liang, W. Zhou, J. Qiu, Z. Zhou, G. Sun and Q. Xin, J. Phys. Chem. B, 2003, 107, 6292 CrossRef CAS.
- R. H. Baughman, A. A. Zakhidov and W. A. de Heer, Science, 2002, 297, 787 CrossRef CAS.
- G. G. Wildgoose, C. E. Banks and R. G. Compton, Small, 2006, 2, 182 CrossRef CAS.
- S. E. Weber, S. Talapatra, C. Journet, A. Zambano and A. D. Migone, Phys. Rev. B: Condens. Matter, 2000, 61, 13150 CrossRef CAS.
- P. A. Elkington and G. Curthoys, J. Phys. Chem., 1969, 73, 2321 CrossRef CAS.
- D. Tasis, N. Tagmatarchis, A. Bianco and M. Prato, Chem. Rev., 2006, 106, 1105 CrossRef CAS.
- B. Smith, M. Monthioux and D. E. Luzzi, Nature, 1998, 396, 323 CrossRef CAS.
- D. J. Hornbaker, S.-J. Kahng, S. Misra, B. W. Smith, A. T. Johnson, E. J. Mele, D. E. Luzzi and A. Yazdani, Science, 2002, 295, 828 CrossRef CAS.
| This journal is © the Owner Societies 2008 |
