Effect of water molecules on the fluorescence enhancement of Aflatoxin B1 mediated by Aflatoxin B1:β-cyclodextrin complexes. A theoretical study
Guillermo
Ramírez-Galicia
*a,
Ramón
Garduño-Juárez
a and
M.
Gabriela Vargas
b
aInstituto de Ciencias Físicas, UNAM, PO Box 48-3, 62251, Cuernavaca Morelos, México. E-mail: grg@fis.unam.mx; Fax: +52-55-5622-7775
bDepartamento de Química Analítica, FES-Cuautitlán, Universidad Nacional Autónoma de México, 54700, Edo. de México, México
First published on 24th November 2006
Abstract
In order to explain the observed fluorescence enhancement of Aflatoxin B1 (AFB1) when forming AFB1:β-cyclodextrin (AFB1:β-CD) inclusion complexes, we have performed a theoretical (quantum chemistry calculations) study of AFB1 and AFB1:β-CD in vacuum and in the presence of aqueous solvent. The AM1 method was used to calculate the absorption and emission wavelengths of these molecules. With the help of density functional theory (DFT) and time-dependent DFT (TDDFT) vibrational frequencies and related excitation energies of AFB1 and AFB1·(H2O)m = 4,5,6,11 were calculated. On the basis of these calculations we propose a plausible mechanism for the fluorescence enhancement of AFB1 in the presence of β-CD: (1) before photoexcitation of AFB1 to its S1 excited state, there is a vibrational coupling between the vibrational modes involving the AFB1 carbonyl groups and the bending modes of the nearby water molecules (CG + WM); (2) these interactions allow a thermal relaxation of the excited AFB1 molecules that results in fluorescence quenching; (3) when the AFB1 molecules form inclusion complexes with β-CD the CG + WM interaction decreases; and (4) this gives rise to a fluorescence enhancement.
1 Introduction
Aflatoxin B1 (AFB1) is one of the most potent carcinogenic metabolites found in nature since 1 µg kg−1 of AFB1 on contaminated food is able to induce liver cancer in test animals.1 AFB1 is produced by the mould fungi Aspergillus flavus and it is a contaminant which is widespread in human and animal food by-products.2,3 The European Union (EU) and the Food and Drug Administration of the USA have established specific guidelines on the acceptable levels of aflatoxins. On the EU this level is 5 ppb on several foodstuffs,4 whereas on the USA the level is 20 ppb on human food and animal feed.5AFB1 fluoresces at λex = 365 nm and λem = 440 nm, a property that is enhanced when forming inclusion complexes in cyclodextrins (CDs).6–13 This observation has prompted the use of CDs for AFB1 detection through molecular fluorescence.14 This phenomenon is not exclusive for aflatoxins, there are other reports of analyte fluorescence enhancement upon forming of a β-cyclodextrin (β-CD) inclusion complex in aqueous solution.15–24
Cyclodextrins are cyclic oligosaccharide molecules with a chiral toroidal configuration, and a hydrophobic cavity that can act as a container for different types of small molecules through non-covalent interactions, such as van der Waals interactions and/or hydrogen bonding. The α-, β- and γ-CDs have six, seven and eight glucose units, respectively, and their physical and chemical properties are well described in the literature.25 In recent years CDs have been used extensively in analytical chemistry.
Fluorescence enhancement is a process that has been studied over many years. Various mechanisms have been suggested as the reason of this phenomenon: (1) restriction of the chromophore conformational flexibility inside the rigid environment of the CD cavity,16 (2) solvent exclusion,26 (3) intersystem crossing to the triplet state,27 (4) monophotonic photoionization,28 (5) intramolecular charge transfer,29 and (6) specific solvent–solute interactions.30–32 Regarding the AFB1 fluorescence enhancement, it has been suggested that it is due to a change in the emission oscillator strength through an interaction between the furan double bond and the inner or the outer surface of the β-CD. However, the mechanism involved in fluorescence enhancement is not yet completely understood.
In this article we present the results of applying two quantum chemical methods to AFB1 molecular complexes in order to explain fluorescence enhancement in the presence of β-CD. First, the AM1 method was applied to the AFB1 molecule, three solvated AFB1·(H2O)n = 26,36,89 complexes and the AFB1:β-CD inclusion complex. Secondly, a density functional theory (DFT) study was performed on the AFB1 molecule and four solvated AFB1·(H2O)m = 4,5,6,11 complexes in order to establish the role of water molecules on the fluorescence enhancement. After careful analysis of the results we propose a plausible mechanism that explains the origin of this phenomenon.
2 Method of calculation
2.1 Initial setup
AFB1 and the solvated AFB1·(H2O)n = 26,36,89 geometries were built and optimized using the MM+ molecular mechanics method and the periodic box option included in the HyperChem package.33 The numeration used for AFB1 is shown in Fig. 1. The β-CD initial geometry was taken from the neutron diffraction crystallographic data of the dodecahydrated β-CD crystal,34,35 and further optimized by molecular mechanics in HyperChem. | ||
| Fig. 1 AFB1 structure and numeration used on this paper. | ||
After β-CD optimization, four inclusion complexes were proposed and energy minimized. Two different penetration modes were identified, one of these corresponds to the inclusion of the AFB1 I and II rings (or furan sites) and the other corresponds to the inclusion of the AFB1 IV and V rings (or carbonyl groups). These inclusion complexes were denoted IC1, IC2, IC3 and IC4, respectively. The AFB1 fragments were included in the β-CD cavity from both the wide and narrow rims (Fig. 2).
 | ||
| Fig. 2 AFB1:β-CD inclusion complexes. IC1 and IC2 are the complexes with E and A–B rings inside of the wide rim of β-CD respectively, and IC3 and IC4 are the complexes with A–B and E rings inside of the narrow rim of β-CD. | ||
The oxygen at the glycosidic plane was taken as a reference of how deep AFB1 was introduced inside of the β-CD cavity. A perpendicular position of the included AFB1 rings inside of β-CD was found in the IC1 and IC3 complexes. On the other hand, IC2 and IC4 are about 10 and 32° out of the perpendicular position, respectively. As a result the IC2 and IC3 complexes (carbonyl groups outside of β-CD cavity) are more stable than the IC1 and IC4 complexes (carbonyl groups inside of β-CD cavity), since these are conformers that form more non-polar (hydrogen-hydrogen) interactions with distances below 3.0 Å. The non-polar interactions are mainly between C–H of furan groups and C–H of glucose groups on β-CD; moreover, IC2 and IC3 are also the complexes with the largest number of hydrogen bonds.
The four AFB1·(H2O)m = 4,5,6,11 geometries used to calculate the IR and UV-Visible spectra were prepared as follows. The MM+ optimized AFB1(H2O)26 geometry was used as the template to obtain the AFB1(H2O)4 complex by selectively removing 22 water molecules and leaving 4 water molecules surrounding the AFB1 molecule. These four water molecules were placed in such a way that three of them were close to the AFB1 carbonyl groups and one more around the oxygen of ring II (Fig. 3(a)). The AFB1(H2O)5 complex was built from the AFB1(H2O)4 geometry by adding one water molecule around O21 (Fig. 3(b)). The AFB1(H2O)6 complex was built from the AFB1(H2O)5 geometry by adding one water molecule around water molecules B and C (Fig. 3(c)). The AFB1(H2O)11 complex was built from the AFB1(H2O)6 geometry by reflecting water molecules B, C, D, E and F to their new positions B′, C′, D′, E′ and F′ (Fig. 3(d)). This reflection was about the plane containing rings IV and V in order to simulate the solvation sphere around their carbonyl groups.
 | ||
| Fig. 3 Distribution of water molecules on the optimized geometries of the AFB1·(H2O)m = 4,5,6,11 complexes calculated with the B3LYP/6-31G* functional. The given values correspond to the solvation energies of these complexes: (a) AFB1·(H2O)4, (b) AFB1·(H2O)5, (c) AFB1·(H2O)6, (d) AFB1·(H2O)11. | ||
2.2 Quantum chemical methodology
The AM1 method36 contained in the AMSOL package37 was used to SCF optimize the geometry of the β-CD, the AFB1 ground state (S0) and the AFB1 first excited state (S1) in both inclusion and n-water cluster complexes. The location of the energy minima was carried out employing the eigenvector following method.38 Solvent effects were simulated with the SM5.4A model.39 The RHF closed-shell calculations were performed using configuration interactions (CI) with 100 microstates. The resulting AFB1 geometries were used to prepare the input geometries of the AFB1:β-CD inclusion complexes. The solvated AFB1·(H2O)n = 26,36,89 geometries optimized at the molecular mechanics level were further optimized at the CI/AM1 SCF level.Since we aimed at a good description of the AFB1 ground and excited state energies within the density functional theory (DFT), we used the B3LYP hybrid functional40 with the 6-31G* basis set, as coded in the Spartan package,41 to further optimize the corresponding AM1 optimized geometries. The same level of theory was used to calculate the vibrational frequencies of the AFB1 molecule, and the solvated AFB1·(H2O)m = 4,5,6,11 complexes. For all optimal geometries, there were no imaginary frequencies in the vibrational analysis, which proves that the geometric configurations of the complexes are stable. The ground-state UV-visible spectra of these molecules were calculated using the time-dependent DFT (TDDFT) method.
2.3 Absorption and emission energies calculation
In order to assess the effect of the solvent on the AFB1 fluorescence enhancement when forming AFB1:β-CD inclusion complexes, we performed electronic energy calculations on the isolated and geometrically SCF optimized AFB1 molecule for the S0 and S1 electronic states, both in vacuum and with solvent effects. In all cases the calculated energies correspond to the electronic transitions S1(v = 0)←S0(v = 0) or S0(v = 0)←S1(v = 0). This was followed by a vibrational analysis of AFB1:β-CD inclusion complexes and the solvated AFB1·(H2O)n complexes.To circumvent the treatment of explicit solvent effect on the geometries of the fluorescence electronic states, we used the fact that fluorescence electronic states are long living species, with approximate lifetimes three orders of magnitude larger than the time of a molecular vibration and solvent shell relaxation, in order to propose a relaxation cycle that helps the understanding of the fluorescence enhancement if AFB1 in β-CD inclusion complexes. The proposed relaxation cycle consists of:
(1) CI calculation and SCF geometry optimization of the AFB1 S0 state.
(2) Single point (1SCF) calculation of the AFB1 S1 state. The geometry used for this calculation was the optimized ground-state geometry of the respective spin state.
(3) CI calculation and SCF geometry optimization of the AFB1 S1 state.
(4) Single point (1SCF) calculation of the AFB1 S0 energy at the S1 optimized geometry.
In this way the instantaneous S1←S0 electronic emission can be estimated correctly. This relaxation cycle is shown in Fig. 4. Thus, the HOMO and LUMO from the S0 ground state are transformed to SOMO1 and SOMO2 in the S1 excited state. Conversely, from the S1 excited state to the S0 ground state, SOMO1 and SOMO2 are transformed to HOMO and LUMO.
 | ||
| Fig. 4 Scheme (2) is based on molecular orbital energy balance. | ||
3 Results and discussion
3.1 AFB1 molecular geometry
The optimized B3LYP/6-31G* ground-state geometry is in good agreement with the available X-ray data.42 The average deviation of all predicted bond lengths and bond angles from the experimental values in the solid state is 0.02 Å and 1.5°, respectively. According to these calculations AFB1 rings II, III, IV and V are coplanar, this is partially due to the rigid ring system of AFB1. It is found that the two carbonyl groups on rings IV and V repel each other, that the bond angle O1–C2–O20 is smaller than 120°, and that the bond angle C3–C4–O21 is larger than 120°; this effect is better observed on the AM1 calculations. The carbonyl repulsion has been also reported by Billes et al.43Small changes in the AFB1 geometry were observed during the electronic excitation (S1← S0). The largest variations were found in rings III and IV, particularly at the C3–C7, C7–C8, C8–C9 bonds whose distances changed from 1.376 to 1.433 Å, from 1.426 to 1.375 Å and from 1.420 to 1.460 Å, respectively. No significant changes on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances were found.
O bond distances were found.
The HOMO and LUMO of AFB1 in the S0 state (Fig. 5) show π symmetry. The main contributions to the HOMO come from the rings III and IV, the double bond of ring I and the oxygens at the carbonyl groups. The LUMO has similar contributions but presents a greater number of nodes. As for the SOMO1 and SOMO2 on the S1 state (Fig. 5), they present similar symmetries to their respective HOMO and LUMO in spite of the absence of the double bond contribution in ring I.
 | ||
| Fig. 5 Molecular orbitals on the ground (S0) and excited (S1) states of AFB1. | ||
3.2 AFB1 fluorescence
The best approximation to the AFB1 fluorescence is through the Franck–Condon (FC) principle since the CI calculation of the AFB1 S1 state in the S0 geometry shows that S1 is mainly a combination of two configurations with electronic transfer of one electron from the HOMO to LUMO (see Fig. 6). Both configurations correspond to 84.26% of S1 state. In addition, there are three triplet states with lower energy than the S1 state (Fig. 7), the first one (T1) corresponds to a similar combination as S1, but with a change of electron spin. Equivalent configurations are found when the solvent effect was added. | ||
| Fig. 6 CI window, three MO occupied and two MO unoccupied, of AFB1 in its S0 and S1 states. Values are the coefficients of the linear combination. | ||
 | ||
| Fig. 7 Lowest energy CI levels of AFB1 in its ground and excited states. | ||
In order to explain the origin of the AFB1 fluorescence based in the FC principle, we examined three different electronic schemes.
In scheme (1), we calculated the absorption and emission wavelengths between S1←S0 and S0←S1, both in vacuum and with solvent effects; however, these values are not in agreement with the experimentally observed quantities. The best approximations are about 27 nm (for excitation) and 65 nm (for emission) below the experimental quantities (see Fig. 7 and Table 1).
| Molecular complex | Scheme (1) | Scheme (2) | Scheme (3) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vacuum | Aqueous | Vacuum | Aqueous | Vacuum | Aqueous | |||||||
| S1←S0 | S0←S1 | S1←S0 | S0←S1 | S1←S0 | S0←S1 | S1←S0 | S0←S1 | S1←S0 | S0←S1 | S1←S0 | S0←S1 | |
| AFB1 | 334 | 375 | 338 | 372 | 318 | 431 | 239 | 428 | — | 447 | — | 428 |
| AFB1 + 26H2O | 340 | 373 | 339 | 372 | 229 | 425 | 235 | 417 | — | 435 | — | 439 |
| AFB1 + 36H2O | 341 | 375 | 340 | 374 | 229 | 419 | 234 | 419 | — | 430 | — | 439 |
| AFB1 + 89H2O | 347 | 372 | 348 | 377 | 231 | 420 | 260 | 416 | — | 428 | — | 445 |
| IC1 | 335 | 374 | 338 | 372 | 230 | 427 | 229 | 415 | — | 442 | — | 433 |
| IC2 | 334 | 374 | 339 | 371 | 228 | 429 | 234 | 410 | — | 445 | — | 427 |
| IC3 | 333 | 375 | 337 | 372 | 228 | 429 | 233 | 412 | — | 445 | — | 429 |
| IC4 | 337 | 373 | 338 | 372 | 230 | 425 | 229 | 411 | — | 438 | — | 430 |
| Exptl.6 | 365 | 440 | ||||||||||
In scheme (2), we used an energy balance procedure based on the MO changes proposed in the relaxation cycle (Fig. 4). Following this energy balance, the S1←S0 transition energy is given by the relation ES0←S1 = 2εSOMO2_1SCF + εSOMO1_1SCF − 2εHOMO − εLUMO, where we have considered the following three steps: one electron from the HOMO is transferred to SOMO2 (εSOMO2_1SCF − εHOMO), followed by LUMO stabilization (εSOMO2_1SCF − εLUMO) and HOMO destabilization (εSOMO1_1SCF − εHOMO). Under this scheme, the S0←S1 transition energy is given by the relation ES1←S0 = εHOMO_1SCF + εLUMO_1SCF − 2εSOMO1, where one electron from SOMO2 is transferred to SOMO1 (εSOMO2 − εSOMO1) and followed by SOMO2 destabilization (εLUMO_1SCF − εSOMO2) and SOMO2 stabilization (εHOMO_1SCF − εSOMO1). Here only the emission wavelength improves, but it is still lower than the experimental quantity by about 9 to 12 nm. In this scheme the excitation wavelength values worsen in the implicit solvent treatment, being 126 nm below the experimental result (see Table 1).
In scheme (3), the S0←S1 transition energy is considered as arising from the εSOMO2 − εSOMO1 energy gap. In vacuum it is the best approximation to the AFB1 emission wavelength, being 7 nm above the experimental result, while in the solvent approximation it is 12 nm below the experimental value.
3.3 AFB1·(H2O)n fluorescence
The AM1 optimized geometries of the AFB1·(H2O)n = 26,36,89 clusters and the corresponding box dimensions are given in Fig. 8 and Table 2, respectively. In these geometries the coplanar rings of AFB1 are parallel to the X–Z plane. In the first box, the water molecules are localized around of carbonyl groups and the oxygens of furan rings. In the second box, the length of the Y-axis was increased to allow a larger number of water molecules around the AFB1 molecule. Finally, in the third box the length of the X- and Z-axes were increased to simulate the bulk. The calculated solvation energy (εsolv = ΔHfcomplex − ΔHfAFB1 − nΔHfH2O; where n = 26, 36 and 89) shows that water molecules localized above and below the coplanar rings of AFB1 destabilize the complex, whereas 89 water molecules adequately represent the effect of the bulk. The wavelengths of excitation and emission for these complexes are given in Table 1.| Axis | Smallest box | First box | Second box | Third box Å |
|---|---|---|---|---|
| X/Å | 8.17 | 12.0 | 12 | 16 |
| Y/Å | 3.70 | 5.0 | 10 | 10 |
| Z/Å | 9.91 | 13.0 | 13 | 20 |
| No. of water molecules | — | 26 | 36 | 89 |
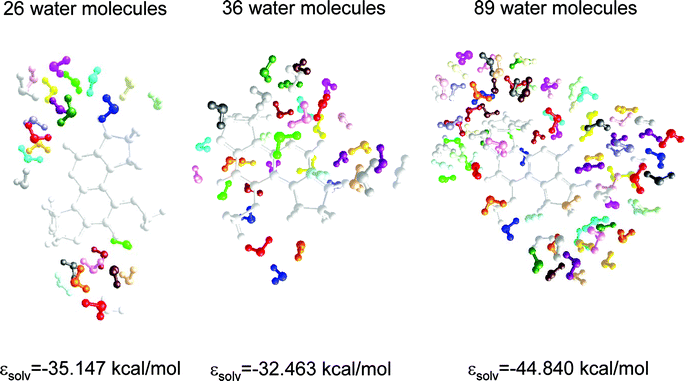 | ||
| Fig. 8 Optimized geometry of the water distribution around the AFB1 molecule as solvated by 26, 36 and 89 water molecules. The coplanar rings of AFB1 are parallel to the X–Z plane. Further addition of water molecules did not increase the stabilization of the system. | ||
The data presented in Table 1 show that the FC approximation (scheme (1)) to excitation of these solvated AFB1 complexes, is consistently better than schemes (2) and (3) in reproducing the experimental value. The best approximation to the experimental excitation wavelength was given by the AFB1(H2O)89 complex.
As for the emission wavelength calculations, scheme (3) appears to be the best approximation to the experimental value. For instance, the AFB1(H2O)26 and AFB1(H2O)36 complexes reproduce well this value within 1 nm the experimental result; while the AFB1(H2O)89 complex gives a wavelength 5 nm over the same value.
Scheme (2), while an interesting exercise, does not explain correctly the excitation or the emission process for AFB1.
It is important to mention that the MOs of the explicit water molecules do not participate in the AFB1 HOMO–LUMO electronic transfer in the ground state or to the SOMO1–SOMO2 in the S1 state (Fig. 9). Furthermore, the symmetry of the resulting molecular orbitals (MO) is similar to the MO of free AFB1 (shown in Fig. 5). However, scheme (3) indicates that the presence of hydrogen bonds coming from the explicit water molecules and the presence of the “bulk” effect as a continuum is a good approximation to calculate the AFB1 fluorescence in aqueous solution.
 | ||
| Fig. 9 Molecular orbitals of ground (S0) and excited (S1) states of AFB1 + 26H2O. | ||
3.4 Fluorescence of AFB1:β-cyclodextrin inclusion complexes.
The experimental wavelength of excitation is best reproduced from the FC approximation upon the solvated AFB1:β-CD complexes, in particular the IC2 complex. In general, these results have the same level of precision as the calculation on free AFB1. Similar results are observed for the emission wavelengths.The β-CD MOs do not participate in the AFB1 HOMO/LUMO and SOMO1/SOMO2 molecular orbitals (Fig. 10). Moreover, the atomic orbital contribution to those molecular orbitals on free AFB1 and AFB1·(H2O)n complexes is identical. Thus it is not surprising to obtain similar values for the excitation and emission wavelengths of free AFB1, since neither the shell of water molecules or β-CD participate in the electronic transfer.
 | ||
| Fig. 10 Molecular orbitals of ground (S0) and excited (S1) states of AFB1:β-CD (IC1). | ||
3.5 Carbonyl groups and water molecules vibrational frequencies coupling
The DFT optimized AFB1·(H2O)m = 4,5,6,11 geometries are shown in Fig. 3. The AFB1(H2O)5 optimized geometry shows a hydrogen bond net between water molecules C, D and E (Fig. 3(b)). The extra water molecule F in the AFB1(H2O)6 geometry does not change significantly the distribution of the previous five water molecules (i.e. those present in the AFB1(H2O)5 complex); however, it contributes to the formation of a small water cluster that involves mainly the B, C, E and F water molecules surrounding the carbonyl groups of rings IV and V (Fig. 3(c)). Five extra water molecules (B′, C′, D′, E′ and F′) were added to the AFB1(H2O)6 geometry in order to obtain the AFB1(H2O)11 complex (Fig. 3(d)). This was done by reflection of the B, C, D, E and F water molecules cluster about the plane made by rings IV and V of AFB1. In this way ten water molecules formed a larger cluster of water molecules that covers completely the carbonyl groups on these rings.After geometry optimization of the AFB1(H2O)11 complex, it was found that the relative position of its B, C, D, E and F water molecules did not change significantly with respect to the same water molecules in the AFB1(H2O)6 complex. In Table 3 we present the internal coordinates of water molecules B and D as determined before and after the addition of B′, C′, D′, E′ and F′ water molecules. It is observed that their relative internal coordinates only showed small changes in bond distances and bond angles. Although there are significant changes in their dihedral angle values, these changes are due to a rotation of the water hydrogen atom opposite to the one forming the hydrogen bond, followed by a small displacement of the water oxygen atom. This effect is more evident for water molecule B as shown in Fig. 11(b). Likewise, it was observed that rings II, III, IV and V of the AFB1 molecule deviate from planarity by about 5° when it forms the AFB1(H2O)6 complex (Fig. 11(a)), and that the planarity is recovered in the AFB1(H2O)11 complex (Fig. 11(b)). In this configuration the effect of water molecules on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond lengths is evident. In going from the free AFB1 to the AFB1(H2O)11 complex the C2
O bond lengths is evident. In going from the free AFB1 to the AFB1(H2O)11 complex the C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O20 and C4
O20 and C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O21 bond lengths changed from 1.201 to 1.232 Å and from 1.214 to 1.238 Å, respectively.
O21 bond lengths changed from 1.201 to 1.232 Å and from 1.214 to 1.238 Å, respectively.
| Water molecule D | ||
|---|---|---|
| a Reference atoms. b Taken from the optimized geometries before and after (in parenthesis) adding extra five water molecules to the AFB1(H2O)6 complex to form the AFB1(H2O)11 complex. | ||
| HD1⋯O20a | HD1⋯O21–C4 | HD1⋯O21–C4–C3 |
| 1.915 (1.942)b | 133.28 (129.83) | −109.52 (−76.67) |
| OD–HD1 | OD–HD1⋯O21 | OD–HD1⋯O21–C4 |
| 0.977 (0.977) | 148.52 (166.82) | 72.15 (16.32) |
| HD2–OD | HD2–OD–HD1 | HD2–OD–HD1⋯O21 |
| 0.981 (0.979) | 102.49 (104.13) | 49.34 (81.51) |
 | ||
| Fig. 11 Relative position of B, C; D; E and F water molecules on the hydrated AFB1 molecule. (a) Lateral view of AFB1·(H2O)6 complex as shown in Fig. 3(c). (b) Lateral view of AFB1·(H–O)11 complex as shown in Fig. 3(d). The position of these water molecules remain about the same in both complexes. | ||
The wavelengths of excitation for AFB1 molecule and its complexes are collected in Table 4. The wavelength of free AFB1 is far from the experimental value, however when the number of water molecules increase in the solvated AFB1 complexes, the excitation wavelength moves towards the experimental value with a maximum of 334 nm for the AFB1(H2O)11 complex. This behavior is also observed in the semiempirical results. The calculated excitation wavelength intensity is maximum for the AFB1 molecule and is minimum for the tetrahydrated AFB1 complex; from this point on, this value increases as the number of water molecules increase around the AFB1 molecule. We interpret this as a signal of the influence that water molecules in the hydration shell, and those in the bulk, have on the AFB1 fluorescence quenching.
| Molecular complex | λ excitation/nm (intensity) | Vibrational frequency/cm−1 (intensity) | Vibrational mode |
|---|---|---|---|
| a SS = Symmetric stretch, b AS = Asymmetric stretch, c S = Scissors. | |||
| AFB1 | 296.67 (0.3922) | 1878.61 (674.44) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os SSa Os SSa |
| 1803.63 (127.68) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os ASb Os ASb |
||
| AFB1·4H2O | 322.98 (0.1024) | 1835.45 (784.09) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os SS + HOH (B and C) Sc Os SS + HOH (B and C) Sc |
| 1750.91 (210.31) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, C and D) S Os AS + HOH (B, C and D) S |
||
| 1743.93 (138.41) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, C and D) S Os AS + HOH (B, C and D) S |
||
| 1697.96 (121.14) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (C) S Os AS + HOH (C) S |
||
| AFB1·5H2O | 321.51 (0.1528) | 1829.27 (645.19) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os SS + HOH (B, C and D) S Os SS + HOH (B, C and D) S |
| 1779.00 (107.02) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, C, D and E) S Os AS + HOH (B, C, D and E) S |
||
| 1765.54 (366.08) | C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O21 AS + HOH (B, C, D and E) S O21 AS + HOH (B, C, D and E) S |
||
| 1748.89 (105.53) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, C, D and E) S Os AS + HOH (B, C, D and E) S |
||
| 1736.58 (278.70) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, C, D and E) S Os AS + HOH (B, C, D and E) S |
||
| AFB1·6H2O | 320.63 (0.1530) | 1826.41 (694.32) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os SS + HOH (B, C, D, E and F) S Os SS + HOH (B, C, D, E and F) S |
| 1765.93 (391.34) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, C, D, E and F) S Os AS + HOH (B, C, D, E and F) S |
||
| 1740.15 (172.23) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, C, E and F) S Os AS + HOH (B, C, E and F) S |
||
| 1728.07 (132.26) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (A, B, C, D, E and F) S Os AS + HOH (A, B, C, D, E and F) S |
||
| AFB1·6H2O | 334.77 (0.1677) | 1799.39 (397.34) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os SS + HOH (B to F′) S Os SS + HOH (B to F′) S |
| 1779.21 (223.53) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B to F′) S Os AS + HOH (B to F′) S |
||
| 1773.65 (106.71) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os SS + HOH (B, C, E, F, B′, C′ E′ and F′) S Os SS + HOH (B, C, E, F, B′, C′ E′ and F′) S |
||
| 1762.62 (363.54) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os SS + HOH (B to E′) S Os SS + HOH (B to E′) S |
||
| 1745.11 (298.72) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os SS + HOH (B to E and B′ to E′) S Os SS + HOH (B to E and B′ to E′) S |
||
| 1684.52 (719.10) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, D, E, B′, D′ and E′) S Os AS + HOH (B, D, E, B′, D′ and E′) S |
||
| 1666.39 (307.12) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os AS + HOH (B, D and B′) S Os AS + HOH (B, D and B′) S |
||
Since the strongest interactions between the AFB1 and the water molecules are through the carbonyl groups of rings IV and V, in the calculated spectra we looked for those frequencies that involved vibrational coupling between these chemical groups and the nearby water molecules. The results of this analysis are condensed in Table 4. We found that there exists a vibrational coupling between the bending modes of the water molecules hydrogen bonded to the AFB1 carbonyl groups through their symmetric and asymmetric modes. These couplings are in the range of 1835 to 1697 cm−1 for AFB1(H2O)4, 1829 to 1736 cm−1 for AFB1(H2O)5, 1826.41 to 1728.07 cm−1 for AFB1(H2O)6, and 1799.39 to 1666.39 cm−1 for AFB1(H2O)11. These data are in good agreement with the simulated AFB1 IR spectrum reported by Billes et al.43
Based in these findings we propose a plausible mechanism for the AFB1 fluorescence quenching in aqueous solution and its further enhancement when forming an inclusion complex with β-CD. It is proposed that when the AFB1 molecules are solvated by water molecules and photons are radiating, the AFB1 molecules would undergo an electronic excitation while coupled to the particular vibrational modes involving the AFB1 carbonyl groups and the bending modes of the nearby water molecules (CG + WM). In this case, part of the absorbed radiation will be driven away in the form of heat generated by the system intercrossing between a given vibrational mode of the AFB1 excited state and the GC + WM vibrational modes. The net result would be fluorescence quenching.
When β-CD (native or modified) is added to the solution and inclusion complexes are allowed to be formed, the AFB1 molecule could adopt any of the four penetration modes shown in Fig. 2. None of these geometries allow the AFB1 to form a complete set of interactions with the surrounding water molecules, thus the amount of CG + WM coupling will decrease. The result would be an enhancement of the fluorescence intensity. A schematic diagram illustrating the mechanisms of fluorescence quenching and fluorescence enhancement for AFB1 is presented in Fig. 12.
 | ||
| Fig. 12 A schematic diagram illustrating the mechanisms of fluorescence quenching and fluorescence enhancement of AFB1 under the effect of βCD in aqueous solution. | ||
In support of our proposed AFB1 fluorescence enhancement mechanism, there is strong experimental evidence suggesting that the low fluorescence quantum yields observed for some dyes in solution is due to easy vibrational deexcitation.44,45 By contrast, florescence enhancement is observed when these dyes are encapsulated into solvent free cavities, such as protein binding pockets46 or cyclodextrins,6 due to the restriction of the guest vibrations and/or conformational flexibility, thus hindering any thermal relaxation pathway and increasing fluorescence emission.
4 Conclusions
In this article we have explored several electronic and vibrational mechanisms of AFB1 in vacuum, implicit solvent and in the presence of explicit water molecules, in order to understand the fluorescence enhancement of AFB1 when forming inclusion complexes with β-CD. A plausible mechanism for this phenomenon is proposed applying AM1 and DFT methods to AFB1, AFB1: β-CD inclusion complexes and solvated AFB1·(H2O)n complexes. These methods provided geometrical and electronic data in good agreement with the experimental results. The computational analysis was performed upon the ground and excited states and energies, where the best approximation for excitation is provided by the Franck–Condon approximation, and the best approximation to emission is provided by the εSOMO2 − εSOMO1 energy gap.We have shown that vibrational coupling between the bending modes of the water molecules hydrogen bonded to the symmetric and asymmetric modes of AFB1 carbonyl groups (CG + WM), could provide a way for a thermal relaxation leading to fluorescence quenching. We have also shown that when these carbonyl groups are imbedded in the β-CD cavity the CG + WM coupling would be reduced, and as a consequence a florescence enhancement would be observed.
Acknowledgements
G. R. G. is thankful to DGAPA-UNAM for a postdoctoral fellowship. Fruitful discussions with Dr J. Peón-Peralta are gratefully acknowledged. DGSCA-UNAM are acknowledged for free allotment of computer time in their Cray Origin 2000 computer. This work was partially supported by a CONACyT grant 46061R to R. G. J. The authors acknowledge Springer Publishing Company for permission to reproduce the central figure of the graphical abstract from ref. 6.References
- J. S. Wang and J. D. Groopman, Mutat. Res., 1999, 424, 167 CrossRef CAS.
- P. M. Scott, J. Assoc. Off. Anal. Chem., 1987, 70, 276.
- J. Leitao, G. De Saint Blanquat, J. R. Bailly and Ch. Paillas, J. Chromatogr., A, 1998, 435, 229.
- R. Krska, G. Kos and H. Lohniger, http://www.ifa-tulln.ac.at.
- The Food and Drug Administration Focus, 1992, 10, 6 Search PubMed.
- C. Dall'asta, G. Ingletto, R. Corradini, G. Galavena and R. Marchellini, J. Inclusion Phenom. Macrocycl. Chem., 2003, 45, 257 Search PubMed.
- O. J. Francis, G. P. Kirschenhenter, G. M. Wase, A. S. Carman and S. S. Kuan, J. Assoc. Off. Anal. Chem., 1988, 71, 725 CAS.
- G. M. Janini, G. M. Muschik and H. J. Hissaq, J. Chromatogr., B, 1996, 683, 29 CrossRef CAS.
- J. Wei, E. Okerberg, J. Dunlap, C. Ly and J. B. Shear, Anal. Chem., 2000, 72, 1360 CrossRef CAS.
- J. Horsky and J. Pitha, J. Pharm. Sci., 1996, 85, 96 CrossRef CAS.
- M. L. Vazquez, A. Cepeda, P. Prognon, G. Mahuzier and J. Blais, Anal. Chim. Acta, 1991, 255, 343 CrossRef CAS.
- M. L. Vazquez, C. M. Franco, A. Cepeda, P. Prognon and G. Mahuzier, Anal. Chim. Acta, 1992, 269, 239 CrossRef CAS.
- M. L. Vazquez, C. A. Fente, C. M. Franco, A. Cepeda, P. Prognon and G. Mahuzier, Anal. Commun., 1999, 36, 5 RSC.
- P. Prognon, A. Kasselouri, M. C. Desroches and G. Mahuzier, Analusis, 2000, 28, 664 CrossRef CAS.
- F. Cramer, W. Saenger and H. Spatz, J. Am. Chem. Soc., 1967, 89, 14 CrossRef CAS.
- A. Harada, M. Furue and S. Nozakura, Macromolecules, 1976, 10, 676.
- M. Hocino, M. Imamura, K. Ikehara and Y. Hama, J. Phys. Chem., 1981, 85, 1820 CrossRef CAS.
- J. Nishijo, M. Nagai, M. Yasuda, E. Ohno and Y. Ushidora, J. Pharm. Sci., 1995, 84, 1420 CrossRef CAS.
- M. Eddaoudi, A. W. Coleman, P. Prognon and P. Lopez-Mahia, J. Chem. Soc., Perkin Trans. 2, 1996, 955 RSC.
- A. Kasselouri, M. Eddaoudi, C. Donze, P. Prognon, A. W. Coleman and G. J. Mahuzier, Fluorescence, 1997, 7, 15S Search PubMed.
- S. Letellier, B. Maupas, J. P. Gramond, F. Guyon and P. Goreil, Anal. Chim. Acta, 1997, 315, 357.
- M. Moofi, J. J. Aaron, M. C. Mahedero and F. Salinas, Appl. Spectrosc., 1998, 52, 91 CrossRef.
- I. Oh, M. Y. Lee, Y. B. Lee, S. C. Shin and I. Park, Int. J. Pharm., 1998, 175, 215 CrossRef CAS.
- D. Demore, A. Kasselouri, O. Bourdon, J. Blais, G. Mahuzier and P. Prognon, Appl. Spectrosc., 1999, 53, 523 CrossRef CAS.
- A. Sozsef, Cyclodextrin Technology, Kluwer, Dordrecht, 1988 Search PubMed.
- J. Szejtli, Chem. Rev., 1998, 98, 1743 CrossRef CAS.
- C. J. Seliskar and L. Brand, J. Am. Chem. Soc., 1971, 93, 5414 CrossRef CAS.
- P. J. Sadkowski and G. R. Fleming, Chem. Phys., 1980, 54, 79 CrossRef CAS.
- E. M. Kosower and H. Kanety, J. Am. Chem. Soc., 1983, 105, 6236 CrossRef CAS.
- C. Cappelli, S. Monti and A. Rizo, Int. J. Quantum Chem., 2005, 104, 744 CrossRef CAS.
- T. W. Ebbensen and C. A. Ghiron, J. Phys. Chem., 1989, 93, 7139 CrossRef CAS.
- S. Tobita, K. Ida and S. Shiobara, Rev. Chem. Intermed., 2001, 27, 205 Search PubMed.
- HyperChem TM Release 7.1 for Windows Molecular Modeling System, 1115 NW 4th Street, Gainesville, FL 32601, USA, 2002.
- C. Betzel, W. Saenger, B. E. Hingerty and G. Brown, J. Am. Chem. Soc., 1984, 108, 7545 CrossRef.
- www.ccdc.cam.ac.uk .
- M. J. S. Dewar, E. G. Zeoblish, E. F. Healy and J. J. Stewart, J. Am. Chem. Soc., 1985, 107, 3902 CrossRef.
- G. D. Hawkins, D. J. Giesen, G. C. Lynch, C. C. Chambers, I. Rossi, J. W. Storer, J. Li, D. Rinaldi, D. A. Liotard, C. J. Cramer and D. G. Truhlar, AMSOL version 6.5.3, University of Minnesota, 1998 Search PubMed.
- J. Baker, J. Comput. Chem., 1986, 7, 385 CrossRef CAS.
- C. C. Chambers, C. J. Cramer and D. G. Truhlar, J. Phys. Chem., 1996, 100, 16385 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- Spartan 04, Wavefunction Inc. 18401 Von Karman Avenue, Suit 370, Irvine, CA 92612, 2005.
- T. C. van Soest and A. F. Peerdeman, Acta Crystallogr., Sect. B, 1970, 26, 1940 CrossRef CAS.
- F. Billes, A. M. Móricz, E. Thika and H. Mikosch, Spectrochim. Acta, Part A, 2006, 64, 600 CrossRef.
- J. R. Babendure, S. R. Adams and R. Y. Tsien, J. Am. Chem. Soc., 2003, 125, 14716 CrossRef CAS.
- S. B. Baptista and G. L. Indig, J. Phys. Chem. B, 1998, 102, 4678 CrossRef CAS.
- B. Perman, V. Šrajer, Z. Ren, T. Teng, C. Pradervand, T. Ursby, D. Bourgeois, F. Schotte, M. Wulff, R. Kort, K. Hellingwerf and K. Moffat, Science, 1998, 279, 1946 CrossRef CAS.
| This journal is © The Royal Society of Chemistry and Owner Societies 2007 |
