Computational design of Brønsted neutral organic superbases—[3]iminoradialenes and quinonimines are important synthetic targets

Abstract

The gas-phase proton affinities and basicities of a large number of extended π-systems possessing imino nitrogens as the most basic sites, which are parts of the [3]iminoradialene or quinonimine “spearheads”, are examined by the DFT B3LYP/6-311+G(2df,p)//B3LYP/6-31G(d) method. Some of the systems are neutral organic superbases exhibiting the gas phase proton affinities over 300 kcal mol⁻¹ and basicity values in the range of 245.3–294.7 kcal mol⁻¹. The backbone of the polycyclic π-electron networks contains either [3]radialene, methylenecyclopropene or quinoid substructures. Construction of the “tails” of planar organic superbases was at the focus of the research efforts. It is shown that the =P(NR₂)₃ and =C(NR₂)₂ fragments as well as the 1,3-diamino-2-methylenecyclopentene ring enable very efficient cationic resonance across the extended linear π-system, thus considerably contributing to the amplified basicity. Conclusive evidence is provided that protonation triggers aromatization of the quinoid six-membered ring (as well as that of the 1,3-diamino-2-methylenecyclopentene) particularly if they are linearly aligned. Triadic analysis has shown: (1) that the extremely large basicities are obtained, if a synergistic effect is obtained between the three contributions corresponding to the initial state, intermediate stage and final state triadic terms, and (2) that the methyl groups enhance basicity predominantly via destabilization of the principal molecular orbitals of the initial bases. It is argued that powerful organic superbases should lead to a spontaneous proton transfer, when interacting with (organic and inorganic) superacids. Formation of their ion pair might provide new interesting molecular materials.

---

Introduction

Brønsted neutral organic (super)bases are indispensable reagents in base mediated chemical reactions,^1–3 since they have a number of distinct advantages over their ionic inorganic counterparts. They exhibit very good stability at low temperatures,⁴ efficient solubility, enhanced reactivity with the naked anions forming poorly associated ion pairs upon deprotonation⁵etc. Last but not least, they provide good catalysts, particularly if immobilized on appropriate surfaces,^6–9 being recyclable at the same time. Thus, they are a part of green chemistry, which is a desirable feature. Finally, neutral organic (super)bases proved useful in both catalytic and stoichiometric asymmetric syntheses.¹⁰

The work on proton affinities and proton transfer reactions has been reviewed in several review articles.^11–18 There are several families of compounds exhibiting high basicity. They include cyclic and acyclic guanidines,^10,19–24 phosphazenes,^25–27 cyclopropenimines,²⁸ quinonimines,²⁹ quinolyl-boranes,³⁰ extended 2,5-dihidropyrolimines³¹ and C₂ diamines³² and compounds with the S=N functionality.³³ Somewhat surprisingly, it was found that a phosphorus atom could be a very basic centre in proazaphosphatranes,^34–37 tris(tetramethylguanidinyl)phosphine and tris(hexamethyl-aminophosphazenyl)phosphine.^38,39 Numerous combined theoretical and experimental studies of neutral bases and superbases including design, synthetic work and measurements of basicity in solutions of Koppel, Leito and co-workers should be emphasized.^26,39–43 Particular attention deserve superbases employing multiple intramolecular hydrogen bonding (IMHB) pattern.^44–46 In a way, this was a generalization of the single IMHB motif introduced by Alder’s paradigmatic proton “sponge” DMAN [1,8-bis(dimethylamino)naphthalene)] some 35 years ago.⁴⁷ Alder’s seminal idea has resulted in a large number of related organic superbases utilizing amino nitrogen as a proton attractor and amino groups as chelating functionalities.^48–59

A useful extension of the DMAN pattern was materialized recently by syntheses of TMGN [1,8-bis(tetramethylguanidino)naphthalene]^60,61 and HMPN [1,8-bis(hexamethyltriaminophosphazenyl)naphthalene].⁶² This type of superbase has better kinetics and exhibits some other advantageous features compared to phosphazenes.^60–62 It appears that replacement of the NMe₂ groups by hexamethyltriaminophosphazenyl fragments in HMPN provides a new powerful superbase with the absolute proton affinity (APA) of 305.4 kcal mol⁻¹ in the gas phase and with the pK_a value in MeCN of 44.8 units as predicted by DFT study.⁶³

In spite of the fact that all these compounds offer a wide variety of nonionic organic superbases, there is a constant need for new alternative systems exhibiting different properties including (super)basicity. Namely, it is of paramount importance to construct a ladder of strong organic superbases possessing as many rungs as possible for a number of reasons: (1) in the first place, because of their use in preparative laboratory investigations and industrial applications as suitable catalysts, (2) their employment in the experimental determination of basicity of new bases by the bracketing technique, (3) formation of the new families of ion pairs (by spontaneous proton transfer reactions),^64–67 which might well lead to novel materials possessing remarkable features. Thus, continuing our interest in designing new organic superbases, we present here results of the theoretical study of some extended π-systems involving [3]iminoradialene and quinonimine substructures and their combinations with quinone and/or methylenecyclopropene building blocks. These fragments will be distributed both in a linear and angular fashion, which should in principle lead to systems possessing different features. In doing so one should distinguish between the head of a molecule (the moiety containing most basic centre), or better to say a “spearhead”, and a tail (specific terminal fragment) placed opposite to the protonation site. A strong emphasis will be laid down on the choice of the terminal structural and electronic patterns, since they could exert a significant influence on the extent of the cationic resonance in the conjugate acids, thus affecting basicity. Further, we shall consider their methyl derivatives possessing sometimes record APA values due to additional inductive effect produced by the CH₃ groups. In order to put the present paper in the proper perspective, it should be mentioned that it is an outgrowth of our earlier work on the related cyclopropenimines and quinodiimines, where it was shown that these moieties undergo aromatic stabilization triggered by protonation.^28,29 In addition to the design of new neutral superbases, which is important per se, we would also like to contribute towards the understanding of proton affinities, which is one of the central notions in chemistry. Therefore, special attention will be devoted to the interpretation of the results, in order to reveal the underlying mechanisms controlling superbasicity in simple and intuitively appealing concepts and terms.

Strategy, theoretical method and computational procedure

Tailoring of uncharged organic bases and superbases requires a systematic search of new molecular systems exhibiting specific structural and electronic features, which needs a suitable strategy. The latter is embodied in a set of rules named the Aufbau principle of organic superbases.⁶⁸ These rules include: (a) identification of the basic atom usually within a particular functional group possessing high intrinsic basicity (imine nitrogen, carbene C˙˙ atom, tricoordinated phosphorus …), (b) selection of a molecular backbone carrying the functional group containing the highly basic centre (polyguanide and phosphazene structures, dihydropyrrolimines…), (c) fine tuning by insertion of judiciously selected substituents (alkyl groups, NMe₂, OMe…) at the strategic sites, and (d) special buttressing effects (steric and angular strain, IMHB corona effect…). We have shown that this strategy was capable of providing a large catalogue of bases and powerful superbases.^{23,27–29,31,38,44–46,61–63} In the present paper we shall explore in great detail compounds containing [3]iminoradialene and quinonimine moieties, serving as the “spearheads” of the larger π-electron systems in scavenging the proton. Further, various backbones formed by methylenecyclopropene and quinone building blocks will be used. Finally, several “tails” of these systems will be tested in tailoring new organic superbases in spe. Methyl groups placed at the N atoms will be examined as the simplest electron donating substituents.

The theoretical framework for calculating the absolute proton affinities (APAs) as a negative value of the enthalpy change for the protonation reaction (eqn (1)) in the gas phase is given by eqn (2)–(4):

B + H⁺ → B_αH⁺ (1)

APA(B_α) = (ΔE_el)_α + (ΔE_vib)_α + (5/2)RT (2)

(ΔE_el)_α = E(B) − E(B_αH)⁺ (3)

(ΔE_vib)_α = E_vib(B) − E_vib(B_αH)⁺ (4)

The base in question and its conjugate acid are denoted by B and B_αH⁺, respectively, while α denotes the site of proton attack. (ΔE_el)_α is the electronic contribution to proton affinity, E_vib includes the zero point vibrational energy and temperature corrections to the room-temperature enthalpy, whereas (5/2)RT accounts for the translational energy of the proton as well as the Δ(pV) term. The gas-phase basicity is defined as a Gibbs free energy change of eqn (1). Basicity values will be given latter in order to make easier comparison with future experiments. However, the main body of the paper will be devoted to proton affinities and their interpretation, which in turn provide the simplest and the most important indicator of molecular basicity in the gas phase.

Numerical realization of eqn (2) requires careful selection of a theoretical model and its validation by extensive computational/computer experiments. We have shown that the Hartree–Fock (HF) model is capable of providing APAs fairly close to the MP2 values, if properly scaled.⁶⁹ This approach is applicable to molecular systems consisting of hundreds of atoms. However, if quantitative accordance with experiment is desired, explicit account of the correlation effect should be made. It appears that the density functional theory (DFT) is a good compromise between accuracy and feasibility provided the B3LYP^70,71 method is employed if flexible basis sets are used. Hence, the molecular structures were calculated by the B3LYP formalism employing efficient 6-31G(d) basis set, whereas the final molecular energies were obtained by a more intricate and subtle 6-311+G(2df,p) basis set in single point calculations, thus giving rise to the B3LYP/6-311+G(2df,p)//B3LYP/6-31G(d) scheme. The true minima on Born–Oppenheimer potential energy hypersurface (BO) were verified by the vibrational frequencies analysis at the B3LYP/6-31G(d) level, which were subsequently used in the zero point vibrational energies (ZPVEs) and thermal correction calculations without scaling.

An important task of the theoretical work is the interpretation of the experimentally measured or theoretically predicted data on molecular properties. A strong emphasis is given here on the rationalization of the calculated APAs. We found that a triadic (trichotomy) formula was well suited for this purpose.⁷² It reads:

(APA)_α = −(IE)_α,n^Koop + E(ei)_α,rex⁽ⁿ⁾ + (BAE)_α˙⁺ + 313.6 kcal mol⁻¹ (5)

where (IE)_n^Koop refers to the nth Hartree–Fock occupied orbital energy ε_n. It corresponds to the nth ionization energy computed in the clamped nuclei and frozen electron density (Koopmans’) approximation.⁷³ It should be noted that the highest occupied molecular orbital (HOMO) will be denoted by a subscript n = 1, and that lower MOs will be signified by n > 1. The latter is a very important ingredient of the triadic analysis, since the frontier HOMO orbital is not necessarily the most important orbital participating in the protonation. Instead, the pivotal MO will be invariably the one describing the lone pair of the imine's nitrogen atom for an obvious reason. Generally, the MO playing the leading role in a chemical reaction under scrutiny will be termed the principal molecular orbital or PRIMO. Furthermore, the bond association energy (BAE)_α˙⁺ term yields the exothermic energy release upon formation of a new bond between the α atom of the molecular radical cation and the hydrogen atom. It should be kept in mind that Koopmans’ ionization term corresponds to the sudden electron ejection event. This is not so crude approximation as it might be conjectured at the first glance. There is abundant evidence that the one-electron picture is very useful in rationalizing the photoelectron spectra.^74–76 There is also a growing evidence that the concept of molecular orbital has a touch of reality itself,^77–80 which means that frozen MOs used in description of the ionization (by employing a properly selected PRIMOs) do reflect properties of the initial state rather well. We cannot resist mentioning in this respect that polarized hybrid AOs, which host either one or two (lone pair) electrons, also possess a grain of truth, since they are closely related to a large number of local molecular properties, which would be unrelated otherwise.^81–83 Having said that and going back to the interpretation of proton affinities, we should always bear in mind that true ionization occurs in a real time. It is generally accepted that the relaxation of the molecular radical cation is completed at the end of the ionization process. Hence, the relaxation effect should be considered as an intermediate step on its own. The corresponding energy is given by:

E(ei)_α,rex⁽ⁿ⁾ = (IE)_α,n^Koop − (IE)₁^ad (6)

It should be explicitly taken into account in full description of the electron ejections and in the quantitative prediction of the APAs. In eqn (6) the first adiabatic ionization energy is signified by (IE)₁^ad. It is worth noting in this connection that formation of a new chemical bond by attachment of the H^˙ atom to the imino nitrogen in the radical cation also causes some reorganization of the nuclei and electron density. This kind of relaxation stabilization is included in a collective (BAE)˙⁺ term in an implicit way. Generally, we do not consider it separately, but in some characteristic cases the final state relaxation energy will be explicitly included in the triadic analysis, in order to elucidate its role in determining the bond association energies (see later).

To epitomize, the initial state effect is mirrored in the PRIMOs, which describe a sudden ionization in Koopmans’ approximation, thus reflecting genuine features of the base in question. The latter are stored in the fixed geometry and frozen electron density of the reactant (base). The final state effect is given by the bond association (BAE)_α˙⁺ term, which completes the protonation process and yields the product (conjugate acid). The relaxation of the molecular radical cation yields interplay between the initial and final state effects representing an intermediate step on its own right. Interpretive advantages of the triadic approach were discussed at length by Deakyne.⁸⁴ We note in passing that this approach proved useful in rationalizing the substituent effects as well.^85–88 As a final remark, it should be mentioned that Koopmans’ (IE)_n^Koop orbital energies were computed by the HF/6-311+G(2df,p)//B3LYP/6-31G(d) model. All calculations have been carried out by GAUSSIAN 03 program.⁸⁹

Results and discussion

General remarks

Molecules explored here are depicted in Fig. 1. They represent cyclic or extended polycyclic π-systems possessing planar or nearly planar structures. The calculated APAs span a range between 251.4–305.7 kcal mol⁻¹ and are given in Table 1. The limits belong to 1a and 33b systems, respectively. Thus, the [3]iminoradialene structural and bonding pattern exhibits the lowest basicity. It has to be said that in accordance with Fig. 1, all molecules with R = H are denoted with a letter “a” together with a corresponding number in bold, while systems possessing R = Me are listed with a letter “b” in the same way. It appears that the methyl derivatives, obtained by replacement of all N–H bonds by the N–Me groups exhibit invariably higher proton affinities, which is compatible with their electron donating character. Hence, the inductive effect of the methyl groups contributes toward complete dispersion of the excess positive charge over the corresponding conjugate acids thus leading to their stabilization. The gross effect is exerted, however, by the cationic resonance induced by protonation. It is illustrated by the resonance structures in the simplest system 1 in Scheme 1.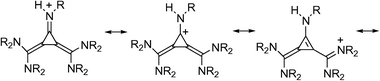

Scheme 1

Fig. 1 Schematic representation of the studied neutral organic superbases and their numbering for R = H and Me. The proton affinities are given below molecules with the data for methyl derivatives encompassed by square parentheses. The NICS(1) values defined as negative numbers are placed near the respective rings. The data referring to the corresponding conjugate acids are given in the square parentheses.

Table 1 The calculated gas-phase absolute proton affinities (APAs), basicities (GB), the first adiabatic ionization energies and resolution of the APAs via the triadic formula eqn (5) in units of kcal mol^−1a

Molecule	IEn^Koop	IE1^ad	E(ei)^(n)rex	BAE˙^+	APA	ΔAPA	GB
a The relative absolute proton affinities are calculated relative to the 1a system.
1a	240.5HOMO–2	133.4	107.1	71.2	251.4	0.0	245.2
1b	216.3HOMO–2	122.1	94.2	71.1	262.6	11.2	256.5
2a	234.7HOMO–2	124.7	110.0	70.6	259.5	8.1	252.5
2b	224.5HOMO–2	118.3	106.2	66.1	261.4	10.0	255.4
3a	235.2HOMO–2	112.6	122.6	60.8	261.8	10.4	255.2
3b	222.6HOMO–2	105.3	117.3	58.1	266.4	15.0	258.8
4a	219.5HOMO–2	107.1	112.4	60.5	267.0	15.6	261.2
4b	205.3HOMO–2	100.2	105.1	63.2	276.6	25.2	269.8
5a	229.6HOMO–2	150.0	79.6	89.6	253.2	1.9	245.8
5b	222.5HOMO–2	148.1	74.4	89.8	255.3	3.9	248.1
6a	225.1HOMO–2	139.4	85.7	83.4	257.6	6.2	249.6
6b	218.0HOMO–2	131.5	86.5	78.7	260.8	9.4	253.9
7a	223.3HOMO–2	127.1	96.2	75.9	262.4	11.0	255.0
7b	215.7HOMO–2	117.8	97.9	70.5	266.3	14.9	259.2
8a	218.3HOMO–2	107.0	111.3	65.5	272.1	20.7	264.9
8b	209.4HOMO–2	98.4	111.0	60.1	275.3	23.9	269.4
9a	234.6HOMO–4	117.0	117.6	68.1	264.7	13.3	258.6
10a	225.5HOMO–4	106.5	119.0	67.5	274.6	23.2	268.4
11a	215.2HOMO–6	97.0	118.2	65.1	281.7	30.3	274.4
12a	248.7HOMO–2	147.1	101.6	102.7	269.2	17.8	261.9
12b	225.8HOMO–2	134.1	91.7	96.7	276.2	24.8	268.4
13a	244.0HOMO–2	143.3	100.7	101.7	272.0	20.6	265.3
13b	221.2HOMO–2	129.5	91.7	96.0	280.1	28.7	273.5
14a	239.6HOMO–3	139.3	100.3	100.3	274.6	23.2	266.8
14b	217.4HOMO–3	126.4	91.0	95.7	282.9	31.5	276.2
15a	231.9HOMO–2	133.6	98.3	100.8	280.8	29.4	274.5
15b	211.9HOMO–2	123.7	88.2	95.9	285.8	34.4	278.7
16a	250.1HOMO–2	167.4	82.7	110.5	256.7	5.3	249.5
16b	233.3HOMO–1	159.6	73.7	104.9	258.9	7.5	252.0
17a	243.5HOMO–4	127.1	116.4	95.8	282.3	30.9	275.1
18a	239.3HOMO–4	124.2	115.1	95.5	284.9	33.5	277.6
19a	234.3HOMO–4	121.6	112.7	95.1	287.1	35.7	278.2
20a	228.1HOMO–4	115.0	113.1	94.7	293.3	41.9	285.6
21a	244.2HOMO–3	139.0	105.2	99.4	274.0	22.6	267.3
22a	235.3HOMO–5	114.1	121.2	92.5	292.0	40.6	284.1
23a	230.8HOMO–5	111.6	119.2	92.2	294.2	42.8	286.5
24a	225.3HOMO–5	109.4	115.9	92.1	296.3	44.9	287.4
25a	220.5HOMO–4	102.9	117.6	91.9	302.6	51.2	294.7
26a	238.9HOMO–4	123.0	115.9	94.4	285.0	33.6	277.1
27a	252.8HOMO–4	137.9	114.9	94.2	269.9	18.5	263.7
28a	234.7HOMO–4	116.5	118.2	88.7	285.8	34.4	277.9
29a	247.8HOMO–5	122.1	125.7	88.4	279.9	28.5	273.1
30a	241.7HOMO–7	111.0	130.7	83.4	286.0	34.6	279.4
31a	226.7HOMO–7	98.1	128.6	77.2	292.7	41.3	286.4
32a	242.5HOMO–6	122.3	120.2	89.3	280.6	29.2	274.4
33a	275.0HOMO–6	157.7	117.3	96.8	252.7	1.3	245.3

---

It should be pointed out that the cationic resonance effect implies a combination of the inductive effect and conjugation effect transmitted by the mobile π-electrons. The fact of the matter is that protonation of the nitrogen lone pair increases electronegativity of the attacked nitrogen. As a consequence, the protonated N atom pulls the electron density from the attached carbon via the σ-channel forming the σ-”hole” at the atom C, which is subsequently filled up by the π-electron residing on that carbon. The created π-“hole” is then delocalized over the π-network, thus spreading the positive charge over remote parts of the system. This picture is essentially correct and it will be heavily used in what follows. We would like to issue a warning, however, that stabilization of the conjugate acids is not necessarily the most important effect leading to high basicity, as we shall see by using triadic analysis later.

The resonance effect propagates along the alternating double and single bonds, which in this case above implies that the basal bond in 1H⁺ does not participate in the cationic resonance. This statement should be taken with a due caution, because the resonance structures depicted in Scheme 1 represent just a part (albeit an important one) of the full quantum mechanical description of 1H⁺ conjugate acid. In fact, some delocalization within the three-membered ring cannot be excluded either in the neutral base 1 or in the 1H⁺ protonated form. It is, however, fair to say that the aromatization of the ring in 1H⁺ does not take place unlike in the protonated cyclopropenimine moiety as shown for comparison in Scheme 2.

Scheme 2

The double π-bond does circulate around the perimeter of the ring in the protonated cyclopropenimine, as indicated by the resonance structures. This is also reflected in the nucleus independent chemical shift^90–92 (NICS) values calculated at the point 1 Å above the electron density critical point in the ring interior. The latter is pinpointed by the analysis performed within the atoms in molecule theory of Bader.⁹³ The NICS(1) values are calculated by the HF/6-31G(d)//B3LYP/6-31G(d) model employing GIAO orbitals and estimated for the CH₃ derivatives, if not stated otherwise. The NICS(1) values are presented in Fig. 1 near respective rings with the values corresponding to the protonated species given within square parentheses. It turns out that NICS(1) in 1b is −6.7, which does not imply that the three-membered ring is partially aromatic. On the contrary, it is perfectly nonaromatic as evidenced by the NICS(1) value in cyclopropene, which is −7.8. More important is that the NICS(1) value is slightly diminished in the protonated form 1bH⁺ (−5.8). This is in harmony with the increased conjugation over the lateral C–C bonds in the ring indicated by the resonance structures on Scheme 1. On the other hand, the NICS(1) values in 1,2-diamino-cyclopropeneimine and the corresponding conjugate acid are −10.5 and −11.9, respectively, which indicate slight aromatization of the neutral base and its minute increase upon protonation. We note in passing here that the NICS(1) value in the planar aromatic cyclopropenyl cation is −16.0. It appears that the APA value for 1,2-diaminocyclopropenimine (R = H) is slightly increased relative to 1a being 254.7 kcal mol⁻¹, whereas it is virtually the same in the permethyl derivatives of 1,2-diamino-cyclopropenimine and [3]iminoradialene 1b (262.6 kcal mol⁻¹).

A survey of the proton affinities, presented in Fig. 1, offers several interesting observations pertaining the importance of the “tails”, i.e. the peripheral substructures opposite to the protonation centre. Let us first consider the [3]iminoradialene-like series 1–4. It appears that the amino groups embedded in the five membered rings in 2 and 3 amplify basicity more than the C(NR₂)₂ endings in 1, which in turn represents the gauge molecule. It is noteworthy that the 1,3-diamino-2-methyl-cyclopentene-like rings are more efficient in this respect than the 1,3-diamino-2-methyl-cyclopentane-like, which seems to be a general feature. This is reflected in the NICS(1) values (Fig. 1). They are increased (i.e. the absolute value is decreased) in the five-membered rings in 2b and decreased in 3b upon protonation (Fig. 1). The point is that the positive charge arriving at the 1,3-diaminocyclopentene moiety forms an aromatic sextet within the ring. The NICS(1) value of −7.2 units in 3bH⁺ indicates that some aromatic character might be expected. The NICS(1) value of cyclopentene and cyclopentadiene are −3.0 and −5.6, respectively. It should be strongly pointed out that there is not a direct relation between NICS(1) index and the aromatic stabilization energy. Consequently, all conclusions derived by the NICS(1) parameters are only qualitative. The groups enhancing basicity the most are P(NR₂)₃ ones (4), which provide very efficient tails. The series 5–8 illustrates importance of the NR₂ substituents in amplifying and fine tuning of basicity. The latter gradually increases with the number of the amino groups and with the number of the methyl substituents. The permethyl derivative 8b attains a respectable APA of 275.3 kcal mol⁻¹. Once again, it is interesting to notice that [3]radialene moiety increases, whereas methylenecyclopropene fragment decreases their NICS(1) values upon protonation, which means that the latter building-blocks amplify delocalization and increase stability of the conjugate acids. Also, inspection of the NICS(1) values in 5b and 8b shows that the presence of the terminal NR₂ groups stimulates delocalization within the cyclopropene rings both in the neutral bases and resulting conjugate acids. The NICS(1) value in 8bH⁺ (−11.3) comes close to that in the protonated 1,2-diamino-cyclopropenimine (−11.9). Comparison of 1, 8 and 10 is instructive. The quinoid fragments in 10 increase basicity more than the methylenecyclopropene-like moieties in 8 relative to a standard system 1. Surprisingly, the quinoid fragments are only slightly aromatized in 10bH⁺ although formation of the aromatic sextets might have been expected. Apparently, the angular bifurcation of the quinoid rings is not as favourable as the linear network (vide infra). Extended system 11 containing additional cyclopentene-like rings achieve remarkable APAs of 281.7 and 287.2 kcal mol⁻¹ for R = H and R = Me, respectively. It illustrates a known fact that the more extended π-systems exhibit the more pronounced basicity.^{23,28,29,31,94} It is noteworthy that the five-membered 1,3-dimethylamino-2-methyl-cyclopentene ring seems to be more stabilized in 11bH⁺ than the six-membered quinoid substructure in 10bH⁺ according to the NICS(1) criterion (−8.5 vs. −4.4). A caveat emptor should be issued here, since NICS(1) values are not directly comparable between rings of different size.⁹⁵ Hence, the same NICS(1) values in different rings do not automatically mean the same aromatic stabilization. Quinonimine structure 12 on the other hand undergoes substantial aromatization of the six-membered ring upon protonation, which is reflected in NICS(1) value (−10.0) of 12bH⁺, thus causing appreciable increase in the APA relative to 1 by 17.8 (R = H) and 13.6 (R = Me) kcal mol⁻¹. This is compatible with a higher susceptibility of the quinoid six-membered ring to aromatization compared to delocalization in [3]iminoradialene moiety triggered by protonation provided the imino nitrogen is directly attached to the ring in question. Basicity gradually increases by replacement of the =C(NR₂)₂ terminal fragment by 2-methylenecyclopentane and 2-methylenecyclopentene-like rings with inserted amino nitrogen at positions 1 and 3 in 13 and 14, respectively. A powerful superbase is obtained by =P(NR₂)₃ structural group in 15 as evidenced by the APAs 280.8 [285.4] kcal mol⁻¹. On the other hand, substitution of the structural C=C(NR₂)₂ fragment in 12 by N–Me structural subunit as in 16 leads to appreciably lower basicity compared to the related systems 12–15. Extended quinoid systems 17–20 exhibit pronounced basicities as evidenced by APA values 282.3 [287.9], 284.9 [291.8], 287.1 [294.2] and 293.3 [297.1] kcal mol⁻¹, respectively, where data for methyl derivatives are given within the square parentheses as usual. The reason behind is the aromatic tandem-effect, since both six-membered rings are aromatized in the corresponding conjugate acids. This is reflected in the NICS(1) values of approximately −11 units in both six-membered rings. The linear arrangement of the quinoid subunits is obviously crucial. It is found once again that the five-membered ring in 19b has a noteworthy NICS(1) = −10.0. Similarly, the aromatic domino-effect gives rise to some superbasic record APA values in the series 22–26. They assume 292.0 [296.9], 294.2 [300.7], 296.3 [302.7], 302.6 [305.7] and 285.0 [285.5] kcal mol⁻¹ in 22, 23, 24, 25, and 26, respectively. The domino effect is spread over all rings the cyclopentane-like being an exception (Fig. 1). This is very nicely illustrated by the NICS(1) values in the corresponding conjugate acids. They are approximately constant and close to benzene value in all rings. One should mention that all four rings participate in the domino effect in 24. It follows that 1,3-dimethylamino-2-methylenecyclopentene building block represents one of the most important tails in the extended π-systems leading to remarkably high basicities in 3, 11, 19 and 24 compounds.

It is interesting that calixene-like structures 27 and 28 possess respectable basicity, which is further increased in propeller systems 29–32 in spite of a very moderate propagation of the delocalization over the peripheral rings, if we accept NICS(1) as a viable index of the cationic resonance. Obviously, branching of the quinoid substructures departing the central [3]radialene relay in 10, 30–33 systems prohibits a more pronounced aromatization of the peripheral parts. There is no bifurcation of the quinoid building blocks in 29 and a notable aromatization does occur in the remote ring. Once again the =P(NR₂)₃ terminal groups are the most efficient in enhancing basicity particularly in systems 28b and 31b.

It follows as a corollary that the aromatic domino-effect is efficiently spread over all rings only in linearly arranged quinoid fragments leading to extremely high proton affinities in 22–25, both with and without methylation of the N–H bonds. It should be mentioned at this point that methylation (alkylation) of the N–H bonds is strongly encouraged in order to prevent the hydrogen walk (tautomerism) in the initial bases. The same applies to alkylation of the C–H bonds attached to the C=C double bonds. To conclude, the very high proton affinities obtained here in several extended π-systems match the deprotonation energies of inorganic and organic superacids, which might be of great importance, because interaction of strong superacids and superbases should lead to spontaneous proton transfer without an energy barrier.^64–67

Triadic analysis

A description of the conjugate acids in terms of the cationic resonance including the aromatic tandem- and domino-effects is useful in rationalizing their global features providing some qualitative information on their stability. This belongs, however, partly to the intermediate stage and the final state of the protonation process. A more detailed and balanced insight into the basicity is provided by the triadic analysis, because it treats the initial, intermediate and final state effects on an equal footing offering quantitative information at the same time. For this purpose we shall employ a succinct description of the trend of changes relative to a parent molecule (compound 1a) by using differences between the corresponding triads:

Δ[APA(B_α)] = APA(B_α) − APA(1) = [−Δ(IE)_α,n^Koop; ΔE(ei)_α,rex⁽ⁿ⁾; Δ(BAE)_α˙⁺] (7)

where the squared parentheses imply summation of the three terms within, which explicitly read:

Δ(IE)_α,n^Koop = (IE)_α,n^Koop(B_α) − (IE)_β,m^Koop(1) (8)

ΔE(ei)_α,rex⁽ⁿ⁾ = E(ei)_α,rex⁽ⁿ⁾(B_α) − E(ei)_β,rex^(m)(1) (9)

Δ(BAE)_α˙⁺ = (BAE)_α˙⁺(B_α) − (BAE)_β˙⁺(1) (10)

Here B_α stands for the base under consideration. Notice that indices α and β as well as n and m could be different in general. Partitioning of the APAs into triadic components is given in Table 1 (in kcal mol⁻¹). We shall consider R = H cases, if not stated otherwise. Let us consider the series 1a–4a. Inspection of Fig. 2 reveals that PRIMOs are HOMO–2 orbitals (n = 3). The corresponding triads are Δ[APA(2a)] = [5.8; 2.9; −0.6] = 8.1; Δ[APA(3a)] = [5.3; 15.5; −10.4] = 10.4 and Δ[APA(4a)] = [21.0; 5.3; −10.7] = 15.6. It appears that a modest increase in proton affinity of 2a arises due to a combined effect of Koopmans’ ionization and relaxation terms. Interestingly, the relaxation effect is considerably more pronounced in 3a, which overcomes the smaller bond association energy. The larger relaxation energy seems to be compatible with a strong cationic resonance, which includes the cyclopentene-like rings. It is worth noting that amplified basicity of 4a is a consequence of significant destabilization of the PRIMO (HOMO–2) orbital (Fig. 2), which means that the price of releasing an electron from the lone pair of the imine nitrogen is considerably lower than in 1a. Thus the contribution of Koopmans’ term is large and positive.

Fig. 2 Principal molecular orbitals for some selected superbases given within parentheses.

The underlying picture behind the variation in APA along the series 5a–8a is somewhat different. Let us explicitly consider the first and the last member of the series. The corresponding triads read Δ[APA(5a)] = [10.9; −27.5; 18.4] = 1.8 and Δ[APA(8a)] = [22.2; 4.2; −5.7] = 20.7. It turns out that the relaxation energy in 5a is appreciably smaller than in the parent compound 1a. This is not surprising, because it is well known that the amino groups strongly enhance the cationic resonance as exemplified by polyguanides.¹⁵ Consequently, it is already large in 1aH⁺ being 107.1 kcal mol⁻¹. On the other hand the basicity of 5a is amplified by the Koopmans’ and (BAE)˙⁺ terms. The final APA is a result of a strong interplay of all three contributions. Dressing of 8a by four amino groups increases the relaxation energy, which becomes slightly higher than that in 1a. The main contribution comes, however, from the Koopmans’ term, due to destabilization of the PRIMO orbital (Fig. 2). Analysis of systems 10a and 11a is also instructive, since the trend is the same as in 8a. Their triads are Δ[APA(10a)] = [15.0; 11.9; −3.7] = 23.2 and Δ[APA(11a)] = [25.3; 11.1; −6.1] = 30.3, respectively. The principal molecular orbital in 10a is deep below HOMO being HOMO–4 (Fig. 1S, see ESI†) and yet it is less stable than its counterpart in 1a by 15 kcal mol⁻¹. An even more dramatic case is found in 11a, where PRIMO is HOMO–6 orbital, which contributes to proton affinity 25.3 kcal mol⁻¹. These two cases convincingly show that the frontier HOMOs would be absolutely unsuitable for description of the protonation process. In both systems 10a and 11a the amplified basicity is a result of a combined initial (Koopmans’) and intermediate (relaxation) effects, while the (BAE)˙⁺ bond association energy decreases basicity being lower than in 1a.

We shall focus now on the quinoid systems 12a–16a. The first four triads take a form: Δ[APA(12a)] = [−8.2; −5.5; 31.5] = 17.7, Δ[APA(13a)] = [−3.5; −6.4; 30.5] = 20.6, Δ[APA(14a)] = [0.9; −6.8; 29.1] = 23.2 and Δ[APA(15a)] = [8.6; −8.8; 29.6] = 29.4 showing that the overriding influence is exerted by the final state reflected in the bond association energy, which is approximately 30 kcal mol⁻¹ higher than in 1a. These findings call for rationalization (vide infra). The PRIMOs are more stable in 12a and 13a than in the parent 1a system leading in this way to a decrease in basicity. In contrast, they are less stable in 14a and 15a thus contributing to the increased basicity. The relaxation is moderately lower in all four systems. Compound 16a exhibits features closely related to 12a with a distinct difference that the relaxation is significantly lower than in 1a. Two series 17–20 and 22–25 behave in a similar way. Therefore, we shall analyze only the latter one, because its members have very high basicities thus being more interesting. The triads corresponding to 22a–25a are Δ[APA(22a)] = [5.2; 14.1; 21.3] = 40.6, Δ[APA(23a)] = [9.7; 12.1; 21.0] = 42.8, Δ[APA(24a)] = [15.2; 8.8; 20.9] = 44.9 and Δ[APA(25a)] = [20.0; 10.0; 20.7] = 50.7 meaning that strong basicity is a consequence of the synergy of three effects. There is a large contribution of the (BAE)^˙+ term being about 21 kcal mol⁻¹. A striking feature of the systems possessing = P(NH₂)₃ terminus like in 20a and 25a lies in the destabilization of their PRIMOs, which leads to large positive contributions of Koopmans’ term by 12.4 and 20.0 kcal mol⁻¹, respectively. The highest basicity of 25b (R = Me) evidenced by APA = 305.7 kcal mol⁻¹ is a consequence of synergistic effects like in 25a, but on top of that comes the inductive effect of the methyl group. The latter increases proton affinity by 3 kcal mol⁻¹.

Finally, in considering systems 27–33 we shall make just a couple of remarks, since the data in Table 1 speak for themselves. The outstanding feature of 28a and 31a is a significant role of Koopmans’ term in amplifying basicity as might has been expected on the basis of similar behaviour found in the related compounds 4a, 15a, 20a and 25a. All three terms are positive making propeller system 31 extremely basic as reflected in the APAs 292.7 [300.5] kcal mol⁻¹. Specifically, Δ[APA(31a)] = [13.8; 21.5; 6.0] = 41.3 implies that the overwhelming effect is exerted by relaxation. The synergy of three effects acting in concert is decisive. Notice that high basicity is attained despite the fact that the distal quinoid moieties are not aromatized in the conjugate acid (viz. Fig. 1). The rest of the compounds in this group (i.e.27a, 29a, 30a, 32a and 33a) have negative Koopmans’ term implying that their PRIMOs are more stable than in 1a. Consequently, their increase in basicity is lesser.

The methyl group affects proton affinities predominantly via Koopmans’ term. A characteristic and the largest effect is found in 1b as evidenced by the difference APA(1b) − APA(1a) = 11.2 kcal mol⁻¹. Its breakdown into triadic components yields [24.2; −12.9; −0.1] = 11.2 kcal mol⁻¹, thus proving the point that destabilization of the PRIMO is a decisive factor in harmony with our previous results on the proton affinities of some simple imines.⁷² Undoubtedly, the strongest effect found in 1b is a consequence of a large number of the methyl groups (9). In contrast, 2b and 3b derivatives have only five CH₃ substituents and the effect is smaller. The second largest effect is found in 4b, which has 13 methyl groups. The origin of the CH₃ substituent effect in 4b is the same. More specifically, APA(4b) − APA(4a) = [14.2; −7.3; 2.7] = 9.6 kcal mol⁻¹.

Let us briefly comment on the (BAE)˙⁺ term, which assumes high values in some quinonimine systems like 12a–16a as well as in 27a. They are by some 30 kcal mol⁻¹ larger than in the parent molecule 1a. The first spontaneous idea would be to seek an answer in the more pronounced relaxation energy in the final state, i.e. in the additional stabilization of the whole system during creation of a new localized N–H bond between the radical cation and hydrogen atom. The following analysis shows that this is not the case. Let us take frozen geometries of the radical cations 1a˙⁺, 12a˙⁺ –16a˙⁺, and 27a˙⁺ and place the incoming H˙ atom near the imino nitrogen of the molecular “spearhead” at a position that both N–H bonds are equivalent. Subsequently, the systems are relaxed until they attain geometries of the conjugate acids. The difference between these two energies yields relaxation effect caused by attachment of the H˙ atom to the molecular radical cations. The final state relaxation energies are 10.8, 3.7, 3.6, 3.4, 3.2, 3.5 and 13.0 (in kcal mol⁻¹) in the same order as above. It appears that the collective stabilization caused by formation of a new N–H bond is the lowest in quinonimine systems (around 4 kcal mol⁻¹), whereas it is large in cyclopropenimine system 1a being 10.8 kcal mol⁻¹. Hence, it follows that the strong N–H bonds in the quinonimine protonated cations are genuine features of the six-membered ring, since it depends relatively little on the molecular tails in the systems 12a–16a, as it is easily deduced from the data presented in Table 1. Concomitantly, it is evident that molecular systems possessing quinonimine “spearheads” are well prepared for the final bond formation once the ionization is brought to its end. Examination of the geometries of the corresponding radical cations (not shown here) reveals that they are similar to those of the conjugate acids, thus proving the argument.

Before completing this section, a comparison between the cationic resonance and the relaxation energy release occurring in the radical cation upon ejection of an electron is in place here. The former is a property of the final state only, being a combination of the inductive effect triggered by protonation and followed by subsequent π-conjugation (vide supra). The relaxation effect is on the other hand the intermediate stage in the triadic picture, being a preparation of the radical cation for the final formation of the N–H bond with the incoming H˙ atom. Although both effects lead to stabilization of the conjugate acids exhibiting sometimes a broad similarity, they are different by their very definitions. Consequently, they should be strongly distinguished.

Structural characteristics

A detailed description of the geometries of all systems considered here and their protonated forms is beyond the scope of the present paper. Instead, we shall briefly discuss the most important facets of some characteristic spatial structures, which bear relevance on the interpretation of the phenomenon of protonation. We shall also confine our comments to the unsubstituted organic bases (R = H). It will become obvious that the cationic resonance and in particular the aromatic tandem-domino effects exert a decisive influence on the structural characteristics of conjugate acids. For that purpose we shall make use—inter alia—of information on the pyramidalization of the nitrogen atoms, which very actively participate in the cationic resonance effect. A degree of pyramidalization is readily calculated by eqn (11):where DP(%) stands for the degree of pyramidalization (in percent), while summation is extended over the three bond angles merging at the pyramidal atom in question.⁹⁶ It is easily checked that the maximal pyramidalization (100%) occurs if all three bond angles are 90°, whereas DP(%) = 0 for a planar trigonal atom.

Let us examine the geometry of the parent molecule 1a and its protonated form 1aH⁺ (Fig. 3). The bond lengths of 1aH⁺ [given in square parentheses] clearly show that the double bonds are elongated whereas the single bonds are shortened by protonation. A significant shrinkage of the C–NH₂ bonds is indicative of a strong cationic resonance interaction. The basal C–C bond is stretched to 1.479 Å in 1aH⁺ implying that a modest delocalization within the three-membered ring in the neutral base is further diminished upon protonation in accordance with the NICS(1) values discussed earlier (vide supra). It is worth noting in this connection that the lateral C–C bonds in 1aH⁺ are shorter assuming 1.388 Å, thus implying that the cationic resonance is propagated from the protonation centre to the amino groups in a most direct way avoiding the basal C–C bond. Concomitantly, the pyramidalization of the amino nitrogen atoms is considerably lessened upon protonation (Fig. 3).

Fig. 3 Selected bond distances (in Å) and pyramidalization indices for systems 1a and 3a and their conjugate acids [given within square parentheses] as obtained with the B3LYP/6-31G(d) level of theory.

Similar structural features are found in 3a and 3aH⁺. However, the changes in the bond lengths in 3aH⁺ are more pronounced indicating a stronger cationic resonance effect. Particularly interesting are the single bonds in the five-membered ring, which are significantly shortened, whereas the double bond is slightly elongated. This finding is in accordance with aromatization of the ring, which tends to achieve the π-electron sextet. It should be noticed in this connection that the five-membered rings are more planar in the conjugate acid as evidenced by small DP(%) values.

Very strong aromatization triggered by protonation occurs in quinonimine systems 12aH⁺ and 14aH⁺ (Fig. 4). The N–C bond at the spearhead in the conjugate acids 12aH⁺ and 14aH⁺ is increased by 0.5 Å, while the C=C bonds of the tails are stretched to 1.444 Å and 1.439 Å, respectively. The terminal C–NH₂ bonds in 12aH⁺ are considerably shrunk to 1.339 Å, whereas the NH₂ groups become planar. Obviously, these data reflect a strong cationic resonance. By the same token, the five-membered ring in 14aH⁺ is planar and the variation in the bond distances is less pronounced upon protonation as a result of aromatization. One can safely say that 14aH⁺ system exhibits the aromatic tandem effect indeed. Similarly, the 15aH⁺ undergoes strong aromatization too as evidenced by the data presented in Fig. 4.

Fig. 4 Selected bond distances (in Å) and pyramidalization indices in systems 12a, 14a and 15a and their conjugate acids [given within square parentheses] as obtained with the B3LYP/6-31G(d) level of theory.

As a final comment, we shall discuss the aromatic domino effect in 24aH⁺ and 25aH⁺ (Fig. 5). The feature striking the most is that aromatization of the six-membered rings is more pronounced in 24aH⁺ and 25aH⁺, than in the corresponding smaller systems 14aH⁺ and 15aH⁺, in accordance with the NICS(1) values given in Fig. 1. It is important to notice that the aromatic rings are rotated relative to each other by a dihedral angle ϕ ∼ 30° in a tendency to avoid perturbation of the aromatic sextets as much as possible. In contrast, dihedral angles are considerably smaller in neutral molecule 24a ranging between 4°–9° (Fig. 5). The 1,3-dimethylamino-2-methylenecyclopropene in 24aH⁺ is planar and twisted relative to the last six-membered ring by dihedral angle of 22°. It is noteworthy that the structure of the five-membered ring in 24aH⁺ is comparable to that in 14aH⁺. It is planar before and after the protonation of the bases’ spearheads. Elongation of the C=P bond in 25aH⁺ is even larger than that in 15aH⁺. Thus, the aromatic domino effect is vindicated (Q.E.D.).

Fig. 5 Selected structural parameters in 24a and 25a and their conjugate acids [given within square parentheses] as obtained with the B3LYP/6-31G(d) level of theory.

Conclusion

We have conclusively shown that [3]iminoradialene and quinonimine can serve as spearheads of the highly basic polycyclic π-systems with imino nitrogen as a protonation site. It is taken for granted that the molecular backbone of these extended π-networks is composed of the [3]radialene, quinoid and methylenecyclopropene structural subunits dressed by NR₂ (R = H, Me) substituents. Particular attention is dedicated to design of the molecular tails. The useful endings of superbases, which considerably enhance basicity include some characteristic fragments or rings encompassing =C(NR₂)₂, >N–Me, =P(NR₂)₃, 1,3-diamino-2-methylenecyclopentane and 1,3-diamino-2-methylenecyclopentene subunits. It turned out that =P(NR₂)₃ and =C(NR₂)₂ fragments as well as 1,3-diamino-2-methylenecyclopentene ring are the most effective in enhancing the basicity. The role of the amino groups NR₂ (R = H, Me) is important in amplifying the cationic resonance in conjugate acids particularly for R = Me. It is unequivocally established that polycyclic systems involving quinoid moieties and a 1,3-diamino-2-methylenecyclopentene subunit at the end of a molecule undergo strong aromatization upon the proton attack.

Triadic analysis shows that the influence of the Me groups in increasing basicity arises due to the destabilization of the principal molecular orbitals, which is a predominating effect. Partitioning of the proton affinity into three contributions related to the initial, intermediate and final state properties by triadic formula, reveals that very high basicity can be attained only by synergistic action of all three effects. In these cases proton affinities close to 300 kcal mol⁻¹ and over 300 kcal mol⁻¹ in the gas phase can be obtained.

Basicity of systems like 14b, 19b and 24b could be additionally increased by attaching two NR₂ groups to the double-bond of the five-membered ring. Moreover, systems possessing =P(NR₂)₃ tail could be made considerably more basic by replacing amino groups with the methylated guanidino groups. All compounds should exhibit higher basicity, if the corona motif^44,45 is utilized at the molecular =N–R spearhead with R = CH₂–CH₂–CH₂–N(CH₃)₂. It should be stressed that peralkylation of potential superbases is strongly recommended in order to prevent intramolecular self-protonation of the most basic sites. This could lead to systems of lower basicity.

We are confident that superbases exhibiting proton affinities, which exceed the deprotonation energies of the strongest mineral and organic acids, are within the synthetic reach. Their preparation and interaction with superacid would lead to a spontaneous proton transfer and formation of ion pairs. The latter might well provide new molecular materials possessing some extraordinary properties. Finally, the basicity values are given in order to enable easier comparison with the experimental data.

Acknowledgements

We would like to thank the Computing Centre of the University of Zagreb (SRCE) for granting computation time on the ISABELLA cluster.

References

1. M. Oediger, F. Möller and K. Eiter, Synthesis, 1972, 591.
2. F. Hibbert and K. P. P. Hunte, J. Chem. Soc., Perkin Trans. 2, 1983, 1895.
3. Encyclopedia of Reagents for Organic Synthesis, ed. L. A. Paquette, John Wiley & Sons, Chichester, 1995.
4. R. Schwesinger and H. Schlemper, Angew. Chem., Int. Ed. Engl., 1987, 26, 1167.
5. T. Pietzonka and D. Seebach, Chem. Ber., 1991, 124, 1837.
6. D. J. Macquarrie, Green Chem., 1999, 1, 195.
7. U. Schuchardt, R. M. Vargas and G. J. Gelbard, J. Mol. Catal. A: Chem., 1996, 109, 37.
8. D. J. Macquarrie and D. B. Jackson, Chem. Commun., 1997, 1781.
9. G. Gelbard and F. Vielfaure-Joly, Tetrahedron Lett., 1998, 39, 2743.
10. T. Ishikawa and T. Isobe, Chem.–Eur. J., 2002, 8, 552–557.
11. R. W. Alder, Tetrahedron, 1990, 46, 683.
12. A. L. Llamas-Saiz, C. Foces-Foces and J. Elguero, J. Mol. Struct., 1994, 328, 297.
13. D. Kuck, Angew. Chem., Int. Ed., 2000, 39, 125–130.
14. E. D. Raczyńska, M. Decouzon, J.-F. Gal, P.-C. Maria, G. Gelbard and F. Vielfaure-Joly, J. Phys. Org. Chem., 2001, 14, 25.
15. J.-F. Gal, P.-C. Maria and E. D. Raczyńska, J. Mass Spectrom., 2001, 36, 699.
16. M. Alcami, O. Mó and M. Yáñez, Mass Spectrom. Rev., 2001, 20, 195.
17. M. Alcami, O. Mó and M. Yáñez, J. Phys. Org. Chem., 2002, 15, 174.
18. D. Kuck, Int. J. Mass Spectrom., 2002, 213, 101–144.
19. E. D. Raczyńska, P.-C. Maria, J.-F. Gal and M. Decouzon, J. Phys. Org. Chem., 1994, 7, 725.
20. R. Schwesinger, Angew. Chem., Int. Ed. Engl., 1987, 26, 1164.
21. R. Schwesinger, M. Misfeldt, K. Peters and M. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1987, 26, 1165.
22. S. T. Howard, J. A. Platts and M. P. Coogan, J. Chem. Soc., Perkin Trans. 2, 2002, 899.
23. Z. B. Maksić and B. Kovačević, J. Org. Chem., 2000, 65, 3303.
24. U. Köhn, W. Günther, H. Görls and E. Anders, Tetrahedron: Asymmetry, 2004, 15, 1419.
25. R. Schwesinger, H. Schlemper, C. Hasenfratz, J. Willaredt, T. Dimbacher, T. Brener, C. Ottaway, M. Fletschinger, J. Boele, M. Fritz, D. Putzas, H. W. Rotter, F. G. Bordwell, A. V. Satish, G.-Z. Ji, E.-M. Peters and H. G. von Schnering, Liebigs Ann., 1996, 1055.
26. I. A. Koppel, R. Schwesinger, T. Brener, P. Burk, K. Herodes, I. Koppel, I. Leito and M. Mishima, J. Phys. Chem. A, 2001, 105, 9375.
27. B. Kovačević, D. Barić and Z. B. Maksić, New J. Chem., 2004, 28, 284.
28. Z. B. Maksić and B. Kovačević, J. Phys. Chem. A, 1999, 103, 6678.
29. Z. B. Maksić and B. Kovačević, J. Phys. Chem. A, 1998, 102, 7324.
30. G. Bucher, Angew. Chem., Int. Ed., 2003, 42, 4039.
31. Z. B. Maksić, Z. Glasovac and I. Despotović, J. Phys. Org. Chem., 2002, 15, 499.
32. R. W. Alder, J. Am. Chem. Soc., 2005, 127, 7924.
33. E. D. Raczyńska, K. Woźniak, E. Dolecka and M. Darowska, J. Phys. Org. Chem., 2002, 15, 706.
34. C. Lensink, S. K. Xi, L. M. Daniels and J. G. Verkade, J. Am. Chem. Soc., 1989, 111, 3478.
35. J. G. Verkade, Acc. Chem. Res., 1993, 26, 483–489.
36. J. G. Verkade, Coord. Chem. Rev., 1994, 137, 233–295.
37. J. Tang, J. Dopke and J. G. Verkade, J. Am. Chem. Soc., 1993, 115, 5015–6020.
38. B. Kovačević and Z. B. Maksić, Chem. Commun., 2006, 14, 1524–1526.
39. A. A. Kolomeitsev, I. A. Koppel, T. Radina, J. Barten, E. Lark, G. V. Röschenthaler, I. Kaljurand, A. Kütt, I. Koppel, V. Mäemets and I. Leito, J. Am. Chem. Soc., 2005, 127, 17656–17666.
40. I. Kaljurand, A. Kütt, L. Sooväli, T. Rodima, V. Mäemets, I. Leito and I. A. Koppel, J. Org. Chem., 2005, 70, 1019–1028.
41. I. Kaljurand, T. Rodima, A. Pihl, V. Mäemets, I. Leito, I. A. Koppel and M. Mishima, J. Org. Chem., 2003, 68, 9988–9993.
42. T. Rodima, I. Kaljurand, A. Pihl, V. Mäemets, I. Leito and I. A. Koppel, J. Org. Chem., 2002, 67, 1873–1881.
43. I. Kaljurand, T. Rodima, I. Leito, I. A. Koppel and R. Schwesinger, J. Org. Chem., 2000, 65, 6202–6208.
44. B. Kovačević, Z. Glasovac and Z. B. Maksić, J. Phys. Org. Chem., 2002, 15, 765.
45. Z. Gattin, B. Kovačević and Z. B. Maksić, Eur. J. Org. Chem., 2005, 3206.
46. Z. Glasovac, B. Kovačević, E. Metrović and M. Eckert-Maksić, Tetrahedron Lett., 2005, 46, 8733.
47. R. W. Alder, P. S. Bowman, R. W. S. Steele and D. R. Winterman, Chem. Commun., 1968, 723.
48. H. A. Staab and T. Saupe, Angew. Chem., 1998, 100, 895.
49. R. W. Alder, Chem. Rev., 1989, 89, 1215.
50. H. A. Staab, A. Kirsch, T. Barth, C. Krieger and F. A. Neugebauer, Eur. J. Org. Chem., 2000, 1617.
51. A. F. Pozharskii, O. V. Ryabtsova, V. A. Ozeryanskii, A. V. Degtyarev, O. N. Kazheva, G. G. Alexandrov and O. A. Dyachenko, J. Org. Chem., 2003, 68, 10109.
52. T. Yamasaki, N. Ozaki, Y. Saika, K. Ohta, K. Goboh, F. Nakamura, M. Hashimoto and S. Okeya, Chem. Lett., 2004, 33, 928.
53. S. A. Reiter, S. D. Nogai, K. Karaghiosoff and H. Schmidbaur, J. Am. Chem. Soc., 2004, 126, 15833.
54. V. A. Ozeryanskii, A. F. Pozharskii, A. J. Bienko, W. Sawka-Dobrowolska and L. Sobczyk, J. Phys. Chem. A, 2005, 109, 1637.
55. V. A. Ozeryanskii, A. F. Pozharskii, M. G. Koroleva, D. A. Shevchuk, O. N. Kazheva, A. N. Chekhlov, G. V. Shilov and O. A. Dyachenko, Tetrahedron, 2005, 61, 4221.
56. A. L. Llamas-Saiz, C. Foces-Foces and J. Elguero, J. Chem. Soc., Perkin Trans. 2, 1995, 923.
57. J. A. Platts, S. T. Howard and W. Woźniak, J. Org. Chem., 1994, 59, 4647.
58. J. A. Platts and S. T. Howard, J. Org. Chem., 1996, 61, 4480.
59. V. A. Ozeryanskii, A. A. Milov, V. I. Minkin and A. F. Pozharskii, Angew. Chem., Int. Ed., 2006, 45, 1453–1456.
60. V. Raab, I. Kipke, R. Gschwind and J. Sundermeyer, Chem.–Eur. J., 2002, 8, 1682.
61. B. Kovačević and Z. B. Maksić, Chem.–Eur. J., 2002, 8, 1694.
62. V. Raab, E. Gauchenova, A. Merkoulov, K. Harms, J. Sundermeyer, B. Kovačević and Z. B. Maksić, J. Am. Chem. Soc., 2005, 127, 15738.
63. B. Kovačević and Z. B. Maksić, Tetrahedron Lett., 2006, 47, 2553–2555.
64. I. Alkorta and J. Elguero, Struct. Chem., 2000, 11, 335.
65. I. Alkorta, I. Rozas and J. Elguero, Chem. Soc. Rev., 1998, 27, 163.
66. O. Mó, M. Yáñez, L. Gonzalez and J. Elguero, ChemPhysChem, 2001, 2, 465.
67. I. Alkorta, I. Rozas, O. Mó, M. Yáñez and J. Elguero, J. Phys. Chem. A, 2001, 105, 7481.
68. B. Kovačević and Z. B. Maksić, John von Neumann Institute for Computing Publication Series, 2003, 20, 71.
69. Z. B. Maksić, B. Kovačević and D. Kovaček, J. Phys. Chem. A, 1997, 101, 7446–7453.
70. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
71. C. Lee, M. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
72. Z. B. Maksić and R. Vianello, J. Phys. Chem. A, 2002, 106, 419.
73. T. Koopmans, Physica, 1933, 1, 104.
74. S. P. McGlynn, K. Wittel and L. Klasinc, in Theoretical Models of Chemical Bonding, Part 3, Molecular Spectroscopy, Electronic, Structure and Intramolecular Interactions, ed. Z. B. Maksić, Springer Verlag, Berlin-Heidelberg, 1991, p. 63.
75. E. Honneger and E. Heilbronner, in Theoretical Models of Chemical Bonding, Part 3, Molecular Spectroscopy, Electronic Structure and Intramolecular Interactions, ed. Z. B. Maksić, Springer Verlag, Berlin-Heidelberg, 1991, p. 99.
76. M. Eckert-Maksić, in Theoretical Models of Chemical Bonding, Part 3, Molecular Spectroscopy, Electronic Structure and Intramolecular Interactions, ed. Z. B. Maksić, Springer Verlag, Berlin-Heidelberg, 1991, p. 153.
77. (a) A. H. Zewail, Angew. Chem., Int. Ed., 2001, 40, 4371; (b) A. H. Zewail, Nature, 2001, 412, 279.
78. (a) J. Hataui, J. Levesque, D. Zeitler, H. Niikura, H. Pépin, J. C. Kieffer, P. B. Corkum and D. M. Villeneuve, Nature, 2004, 432, 867; (b) J. Hataui, J. Levesque, D. Zeitler, H. Niikura, H. Pépin, J. C. Kieffer, P. B. Corkum and D. M. Villeneuve, Phys. Rev. Lett., 2005, 94, 123902.
79. H. Stapelfeldt, Nature, 2004, 432, 809.
80. W. H. E. Schwarz, Angew. Chem., Int. Ed., 2006, 45, 2.
81. Z. B. Maksić, Pure Appl. Chem., 1983, 55, 307.
82. Z. B. Maksić, in Symmetry—Unitying Human Understanding, ed. I. Hargittai, Pergaman Press, New York, 1986, p. 697.
83. Z. B. Maksić, in Theoretical Models of Chemical Bonding, Part 2, The Concept of the Chemical Bond, ed. Z. B. Maksić, Springer Verlag, Berlin-Heidelberg, 1990, p. 137.
84. C. A. Deakyne, Int. J. Mass Spectr., 2003, 227, 601.
85. R. Vianello and Z. B. Maksić, J. Phys. Org. Chem., 2005, 18, 699.
86. R. Vianello and Z. B. Maksić, Tetrahedron, 2006, 62, 3402.
87. R. Vianello, H. Maskill and Z. B. Maksić, Eur. J. Org. Chem., 2006, 2851.
88. Z. B. Maksić and R. Vianello, J. Chem. Phys. A, 2006, 110, 10651–10652.
89. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 (Revision B.03), Gaussian, Inc., Wallingford, CT, 2004.
90. H. Jiao and P. v. R. Schleyer, Angew. Chem., Int. Ed. Engl., 1996, 35, 2383.
91. G. Subramanian, P. v. R. Schleyer and H. Jiao, Angew. Chem., Int. Ed. Engl., 1996, 35, 2638.
92. H. Jiao and P. v. R. Schleyer, J. Phys. Org. Chem., 1998, 11, 655.
93. R. F. W. Bader, Atoms in Molecules, A Quantum Theory, Oxford University Press, Oxford, 1990.
94. B. Kovačević, Z. B. Maksić and R. Vianello, J. Chem. Soc., Perkin Trans. 2, 2001, 886.
95. (a) P. v. R. Schleyer, H. J. Jiao, N. Hommes, V. G. Malkin and O. L. Malkina, J. Am. Chem. Soc., 1997, 119, 12669; (b) A. Stanger, J. Org. Chem., 2006, 71, 883–893.
96. Z. B. Maksić and B. Kovačević, J. Chem. Soc., Perkin Trans. 2, 1999, 2623–2629.

---

Footnote

† Electronic supplementary information (ESI) available: Principal molecular orbitals for selected superbases. See DOI: 10.1039/b611980h

---