How does confinement affect the catalytic activity of mesoporous materials?

Abstract

So-called confinement effects in porous materials are known to strongly affect diffusion, phase transformations, catalytic properties, etc. In the field of catalysis, it is generally admitted that antagonistic effects at the mesoscale result in the existence of an optimal catalytic efficiency depending on pore size. Herein we highlight some recent examples of pore size effects and their proposed mechanisms. Confinement studies on periodically organised mesoporous materials must be developed because they should provide a certain clearness of arguments and understanding.

---

Frédéric Goettmann

After receiving his degree from the Ecole Polytechnique in Palaiseau, France, Frédéric Goettmann worked at Ciba SC in Basel, Switzerland on a new synthesis for cyclohexyl phenyl ketone under the supervision of Dr Reinhard Sommerlade. He received his PhD from the University Pierre et Marie Curie in Paris, France, where he worked under the supervision of Dr Clément Sanchez on the catalytic applications of mesostructured hybrid materials. He is currently occupying a post-doctoral position at the Max Planck Institute of Colloids and Interfaces in Potsdam, Germany, under the supervision of Dr Arne Thomas in the group of Prof. Markus Antonietti. His interest focuses on the catalytic activity of organic solids and the development of metal free heterogeneous catalysis.

Clément Sanchez

Clément Sanchez is Director of Research at the French National Center for Scientific Research (CNRS) and Director of the “Laboratoire de Chimie de la Matière Condensée de Paris” at the University of Pierre and Marie Curie of Paris. He received an engineering degree from the Ecole Nationale Supérieure de Chimie de Paris in 1978 and a “thèse d'état” (PhD) in physical chemistry from the University of Paris VI in 1981. He did post-doctoral work at the University of California, Berkeley, and is currently performing research at the University Pierre and Marie Curie in Paris. He was professor at the Ecole Polytechnique (Palaiseau) from 1991 to 2003. He currently leads a research group of a dozen scientists and specialises in the field of chemistry and physical properties of nanostructured porous and non-porous transition metal oxide based gels and porous and non-porous hybrid organic–inorganic materials shaped as monoliths, microspheres and films. He received the French IBM prize for materials science in 1988 and the Société Chimique de France prize for Solid State Chemistry in 1994. He was the recipient of the Silver Medal of the CNRS for chemistry in 1995 and the prize of the French Academy of Sciences for Application of Science to Industry in 2000. He has organised several international meetings associated with the fields of soft chemistry, hybrid nanocomposite materials and related bio-aspects. He is a member of the Materials Research Society and the Société Chimique de France. He is the co-author of over 285 scientific publications, 11 book chapters and more than 55 proceedings, co-editor of 9 books or proceedings related to the chemistry and properties of hybrid materials and has more than 29 patents. He has delivered over 80 invited lectures at international meetings and more than 100 invited seminars in academic or industrial research centers.

---

Introduction

Nowadays, nanoporous materials can be synthesized following a large set of different chemical and physicochemical strategies (sol–gel, hydrothermal, templated growth, surfactant assisted templating, nanomolding, etc.).^1–5 According to the classification made by IUPAC,⁶ porous solids can be divided into three main categories, depending on their pore size (diameter d): micro- (d < 2 nm), meso- (2 nm < d < 50 nm), and macroporous materials (d > 50 nm). Zeolites, for example, constitute a great family of crystalline microporous materials, presenting pore sizes smaller than about 1 nm. The applications of zeolite based materials are widespread. Although mostly aimed at industrial catalytic processes, (i.e., chemical and petroleum industries), zeolites also hold their place in everyday life (phosphate-free cleaning products, isolating purposes, etc.).⁷ Indeed, these microporous solids are very effective as selective ion-exchange agents and sorbents, due to the high mobility of water and cations, and their high and well-defined porosity.

These remarkable properties of nanoporous solids explain the interest of hundreds of research groups world-wide, in the study and synthesis of novel materials with controlled porosity. The development of soft chemistry derived inorganic or hybrid networks templated by organized surfactant assemblies (structure directing agents) resulted in the emergence of a new family of nanostructured porous materials in the mesoscopic scale (2–50 nm) processed as powders or films.^2,4,5,7,8 More recently a new generation of crystalline microporous hybrid solids (Metal–Organic Frameworks (MOFs)) enabled the tailoring of a large variety of nanoporous solids exhibiting very high surface areas (up to 5000 m² g⁻¹) and presenting hydrogen uptakes of about 3.8 wt% at 77 K.^9–16 These nanoporous hybrid MOFs are very promising candidates for applications in the field of catalysis, gas purification or gas adsorption.¹⁷ However, in contrast to microporous zeolites the understanding of the basic mechanisms of adsorption in the confined hybrid microporosity associated with MOF structures is still in its infancy.

Microporous solids (zeolites, MOFs) and periodically organized mesoporous solids (mesoporous silica and aluminosilicates, mesoporous transition metal oxides, and mesoporous hybrid organic–inorganic nanocomposites) are giving rise to a constellation of innovative advanced materials with promising applications in many fields like optics, electronics, ionics, mechanics, membranes, protective coatings, catalysis, sensors, and biological applications (immobilization, recognition, drug delivery,…).^7,18–22 However, to date, the understanding of the effects of the chemical nature of the pore wall and its degree of crystallinity, the pore size and shape and porosity connectivity on the resulting physico-chemical properties of the porous materials still remains an important challenge in particular for mesoporous solids and microporous hybrid MOFs.

Pore size is obviously an important parameter that impacts not only the physico-chemical properties of porous material but also the properties of chemical species inside their pores. In this respect, the alterations of the properties of a mesoconfined phase are very similar to those of clusters, in which thermodynamics is known to totally break down.²³ These modifications of the behaviour of a phase within pores are usually called confinement effects and were intensively studied for zeolitic materials. Interfacial interactions, symmetry breaking, curvature as well as structural frustration and confinement-induced entropy losses are known to play important roles in determining molecular organisation within physically confined environments.

In the specific case of catalysis, two types of effects were identified and led to the opinion that a pore size optimum for catalytic activity does exist. On the one hand, diffusion limitations were naturally envisaged for explaining activity decreases with smaller pore sizes.⁷ On the other hand, confinement effects were thought to increase the catalytic activity in more constricted systems.

The outstanding success of zeolites in industry, especially as catalysts,²⁴ prompted many studies intending to evidence the links between the truly physical effects of confinement in their pores and their catalytic activity. This field can now be considered as mature because many relations between structure and property are quite well understood. This piece of work may thus be a kind of guideline for what still has to be done in the mesoscopic systems, which gave birth to a large set of interesting but complex porous materials.

Indeed, in the case of mesoporous materials (mainly oxides, most of all silica), there is not one clearly identified mechanism accounting for these size effects. On the contrary, experimental evidence of the existence of size depending physico-chemical properties in porous solids usually relies on their own specific mechanism.

By highlighting some relevant phenomena involved in controlling the activity of zeolites and some of the most important works on confinement in mesoporous materials, we would like to suggest that there still is the need for comprehensive mechanistic investigations of the impact of confinement at the mesoscale in catalysis.

Confinement effects in zeolites

Zeolites are crystalline, microporous silicates or aluminosilicates, forming high surface three-dimensional networks. Being the most successful heterogeneous industrial catalyst up to now, the various features impacting their catalytic activity have been extensively studied. Among them, pore size (or curvature, which is related to both pore size and geometry) is one of the most important.

Blum et al. proposed a model based on the Gaussian curvature of zeolitic structures and dispersion self-energy of molecules to account for the adsorption properties of zeolites.²⁵ Their approach permitted the correlation of the adsorption heat of a given molecule on a given zeolite (this released heat playing a major role in the catalytic process as the released energy may match the activation energy of the wanted reaction, see below) to both the geometry of this molecule and the curvature of the considered zeolite. In a conceptually similar, but for chemists more intuitive, approach, Derouane proposed that zeolites could be considered as solid solvents and thus the behaviour of molecules inside the zeolites as resulting from solvation effects.²⁶ Many examples strongly support this assertion, such as the fact that ZSM-5 zeolite, with a mean pore size of 0.55 nm, can easily accommodate benzene molecules, even though their van der Waals radius is 0.6 nm, or that the “solvation” energy released by adsorbing p-xylene on SAPO-11 zeolite reaches 90 kJ mol⁻¹ and is thus comparable to the activation energy of many reactions involving p-xylene. Another approach to these phenomena, developed by Garcia and co-workers, suggests that molecules in zeolites are confined at the molecular level; this means that the molecular orbitals are strongly perturbed by the solid. They showed, for instance, that the aromaticity of anthracene in zeolites was strongly disrupted due to limitation of the π-orbital spatial extension induced by the pore walls proximity (as depicted in Fig. 1).^27,28

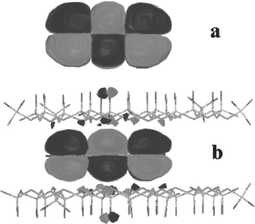Fig. 1 Calculated spatial extension of the HOMO of anthracene in the gas phase (a) and confined between two sheets of mica (b). Adapted from ref. 27 © 2000 with permission from the American Chemical Society.

These three models nicely exemplify how the evolution of measurable or at least calculable physical quantities (adsorption heat and limitation of the spatial extension of molecular orbitals) with changing pore size or curvature could be related to the varying catalytic properties of zeolites. Despite the huge number of studies concerning mesoporous materials, it seems not to be as simple to make the same link in the latter case.

Confinement at the mesoscale

Physico-chemical evidence of confinement effects

With the strong expansion of the field of organised mesoporous materials, precise characterisation of mesoporosity became an increasingly important topic. Besides diffraction and microscopic techniques, numerous indirect methods relying on specific properties of chemical phases adsorbed inside the pores were developed. Along with their great interest for characterising porous solids, the underlying physics sheds light on the mechanisms of confinement at the mesoscale.

- Adsortion/desorption measurements. Capillary condensation can be described by the Kelvin equation [eqn (1)], which describes how the equilibrium pressure of a spherical droplet increases when its radius decreases (where γ stands for the surface tension, V_m for the molar volume of the condensed phase, r is the radius of the pore, R is the gas constant and T the temperature). Even if this equation does not provide an exact evaluation of the equilibrium pressure of a phase absorbed on a mesoporous material, the underlying phenomenon has been widely used to measure surface areas, pore sizes and pore size distribution of many solids (typically with N₂, mercury or water as adsorbed phases) by measuring the amount of adsorbed gas at a given partial pressure. More sophisticated information can be obtained by collecting other data. In the case of N₂ and CO the combination of these data with Monte-Carlo calculations showed that in very small pores the adsorbed molecules had to pack so closely together that they tended to self organise.²⁹ On the other hand, Trens et al. showed that curvature strongly altered the liquefaction free energy of hexane in MCM type materials.³⁰ In the case of mesoporous thin layers, for which standard adsorption–desorption isotherms are hardly obtainable, similar data could be obtained by plotting the evolution of the refractive index of the films against the partial pressure of water.³¹ This so-called ellipsometric porosimetry also allows one to evidence the contraction of the film upon capillary condensation within the matrix.

- Thermoporometry. The freezing behaviour of liquids is also pore size dependent. Alba-Simionesco et al. recently wrote a comprehensive review on the theoretical (relying on the Gibbs–Thomson equation) and experimental background of this effect.³² This shift in freezing point towards lower temperatures can be measured by calorimetry, NMR or diffraction techniques and led to a method of pore characterisation known as thermoporometry.³³ Recently Findenegg and co-workers applied this technique to water confined in a series of mesoporous materials confirming that the shift of the transition temperature was inversely proportional to the pore radius.³⁴ These two items, namely adsorption/desorption behaviour and melting/freezing in confined systems, were comprehensively reviewed by Gelb et al. together with other phase separations such as liquid/liquid equilibria and layering transitions.³⁵

- NMR and ESR techniques. The relaxation time of nuclear or electronic spins provides valuable information on the dynamics of the chemical species bearing this spin. Such NMR measurement performed in porous media allowed Korb et al. to show that correlation times increased with decreasing pore size (i.e. that molecules are “moving” more slowly in smaller pores. Please note that this trend may be true for mesopores but not necessarily for micropores.²⁶) and that molecular motion was strongly anisotropic close to the pore walls.^36,37 Working at a different time scale similar results were recently obtained by Okazaki and Toriyama by means of ESR experiments.³⁸ Among the various nuclei that can be used as NMR probes ¹²⁹Xe plays a peculiar role. It is a NMR responsive non-reactive gas, the chemical shift of which is strongly dependent on its chemical environment.³⁹ Cros et al. showed that the chemical shift of ¹²⁹Xe adsorbed on mesoporous silica was also pore size dependent (Fig. 2).⁴⁰ One explanation of this phenomenon is that adsorbed xenon atoms being rapidly exchanging with free ones, the observed chemical shift can be regarded as the average between those of the free atoms and of the adsorbed ones. As a consequence the chemical shift of confined xenon has to vary with the surface/volume ratio of the pores.

Fig. 2 Experimental chemical shifts observed for confined ¹²⁹Xe. Extracted from ref. 40 © 2000 with permission from the American Chemical Society.

- X-Ray and neutron diffraction techniques. At relatively large angles, diffraction techniques also provide information on the molecular structures of liquids. Large Angle X-ray Scattering has been used in the case of methanol confined in MCM-41 silicas to demonstrate that the confined liquid was indeed highly ordered within the pores, which is consistent with the above mentioned anisotropy of confined liquids.⁴¹ Interestingly, neutron diffraction combined with molecular dynamics calculations allowed Morineau and co-workers to ascertain that the density of confined methanol was higher than that of bulk methanol and varied regularly along the diameter of the pore, as can be seen from Fig. 3.⁴²

Fig. 3 Calculated variation along a pore diameter of the density of carbon atoms for confined methanol. Shaded areas correspond to molecules in strong interaction with the wall of the solid. Adapted from ref. 42 © 2005 with permission from Elsevier.

This list of physical properties of confined fluids, which can vary with pore size, is not intended to be comprehensive. We only wanted to underline that this topic has already been widely explored. Important features for our focus are the fact that surface effects tend to become dominant in fluids confined at the mesoscale and that molecular properties are strongly anisotropic. Nevertheless, as mentioned in the title our focus was catalysis with mesoporous catalysts or catalyst supports. In this field, there are far less studies and no general mechanism.

The impact of pore size on catalysis

There are some examples ascertaining that confinement affects the catalytic behaviour of mesoporous materials. J. M. Thomas et al. reported enantioselectivity enhancement induced by pore size reduction. Indeed, the authors electrostatically immobilised various chiral rhodium and palladium complexes on mesoporous silicas of varying pore sizes. The resulting hybrid catalysts were then tested in hydrogenation reactions. The origin of the observed enantioselectivity increase with decreasing pore size was shown to be the fact that a more curved structure permitted better control of the catalytic centre.^43,44 Iwamoto et al. reported a strong rate enhancement in cyclohexanone acetalisation catalysed by aluminosilicates with lower pore sizes. This observation however seemed to rely on the relative ease of dehydration of the various powders in the pre-treatment step and not on true confinement effects during the catalysis.⁴⁵ Finally, A. Thomas et al. observed that nanoconfinement affected the rate of pyrene excimer formation, partly because of the fact that below a given concentration the probability of finding two pyrene molecules in the same hole becomes very small.⁴⁶ Interestingly none of these examples resorted to any of the above mentioned “physical” confinement effects. Nevertheless, Tanchoux and coworkers recently observed a correlation between the pore size dependence of the activity of mesoporous aluminosilicates in the catalytic isomerization of 1-hexene and the variation of absorption heat of hexane on the corresponding non-acidic mesoporous silicates.⁴⁷ This very nice piece of science constitutes a notable exception to the general absence of link between physical confinement and catalytic behaviour.

The field of periodically organized mesoporous organic–inorganic hybrids⁴⁸ provides a large number of systems in which mesoscopic confinement effects may be evidenced especially in catalytic applications. An emerging idea in the world of hybrids is that the control of the interface between the organic and the inorganic part of those materials could play a key role in enhancing their catalytic activity.⁴⁹ This assumption is nicely supported by the outstanding success of surface organometallic catalysis (SOMC)⁵⁰ as exemplified by the works of Basset⁵¹ and Katz⁵² and their coworkers. Our modest contribution to this new domain was the discovery of so-called Hybrid Bidentate Ligands (HBL) in which an anchored organic ligand chelates a metal centre through one usual organic arm and a part of its anchoring function (Fig. 4). The first member of this new family was a phosphanorbornadiene rhodium complex immobilised on various periodically organized mesoporous silica supports that proved to be active in hydrogenation and hydroformylation reactions.^53,54 Surprisingly, the supported complexes showed increased activities compared to their homogeneous counter parts (up to 1 order of magnitude). In order to gain more insight into this phenomenon, we synthesised three MCM-41 type powders swelled with mesitylene⁵⁵ to reach pore sizes of 20, 50 and 80 Å respectively. The choice of MCM-41 powders not only permitted access to various pore sizes without changing the pore geometry and the porous organisation, it also enabled systems without any microporosity to be obtained, which would have added one more parameter yielding a more complex system. They were functionalised with 1-phospha-3,6-diphenyl-4,5-dimethyl-2-triethoxysilyl norbornadiene rhodium(I) complexes⁵⁴ and tested in 1-hexene hydrogenation. The activities (measured on the basis of hydrogen consumption) observed in methanol and isopropanol at room temperature, under 7 bars of H₂ with 0.1 mol% of catalyst are summarised in Fig. 5.

Fig. 4 Structure of one of the first hybrid bidentate ligands.

Fig. 5 Catalytic activity of a rhodium complex tethered on mesoporous MCM-41 type silicas of various pore sizes in 1-hexene hydrogenation. Comparison between the activities in methanol and isopropanol is given.

These results prove the existence of a pore size optimum, confirming that at least two antagonist effects are at work. More interestingly, the pore size optimum depends strongly on the dimensions of the molecules of the used solvent. A first explanation would be that bulkier solvents, such as ⁱPrOH, strengthen the diffusion limitations, shifting the optimum towards higher pore sizes. But this would also imply an overall decrease in the catalytic activity, which is obviously not found. Thus, the size of the solvent molecules must also play a role in “positive” confinement effects. As we did not find any obvious explanation for these observations we felt that this could be a case where physical confinement effects had a direct effect on the catalytic activity.

The previously mentioned Kelvin equation predicts that the saturating vapour pressure of gases depends on pore size. It thus seems reasonable to assume that the microscopic pressure within a confined liquid (or at least chemical activity) could depend on pore size because of their curvature. Incidentally, the solubility of a gas within this liquid phase should be modified by the porosity. The observed activity increase with decreasing pore size might thus be attributed to a higher H₂ concentration in smaller pores. Preliminary tests on the solubility of hydrogen in methanol, however, showed that the effect of a suspension of 5 nm pore sized mesoporous SBA-15 powders was below the detection limit.† This indicates that if there is such an effect, the solubility increases by less than 50% and can thus not account for our observed catalytic activity enhancement.

Another effect of confinement is the lowering of entropic barriers,⁵⁶ which can easily be understood considering the above mentioned ordering of the solvent molecules near the pore wall. Moreover, the number of molecules in a spherical mesopore is relatively low, reducing the number of realisation possibilities, thus impacting the partition function. Both features certainly favour catalytic paths relying on associative transition states. Nevertheless, evaluating the change in entropy at mesoscopic scales remains a difficult task.⁴⁶ Thus far we did not find a suitable mechanism for explaining our observations.

Outlook

These considerations underline the current need for a predictive model of confinement effects at the mesoscale in order to design technical catalysts based on mesoporous materials.‡ Mesoporous periodic solids, because of their regular pore assemblies, will probably help to shed some light on the role of confinement in catalytic activities and on the construction of a robust model. The development of such a model is far beyond the scope of this highlight article and would require a closer collaboration between physicists and chemists focusing on catalytic applications of mesoporous solids.

In this respect, we would like to propose two directions that would perhaps be worth exploring in such a collaboration. The first one would be to have a closer look at energy exchanges at the solid/liquid interface. Indeed, even if the overall energy flux through this interface is null, the flux of a given energy form could be different from zero. For example, considering the radiative flux, MeOH is likely to have a higher Stefan coefficient than silica and thus to radiate more than the solid at the same temperature. There must therefore be another mechanism allowing silica to give this excess energy back to the solvent. This could possibly take place very close to the surface and make the collisions of methanol molecules with the surface inelastic, in such a way that the molecules would leave the surface with more kinetic energy than when they arrived. This would be a microscopic equivalent of the system studied by Falcon and coworkers. This group showed recently that aggregates could form in vibration excited granular media in low gravity.⁵⁷ Their 2-D granular medium, consisting of 0.3–0.4 mm bronze spheres, was placed in microgravity and fluidised by a horizontal oscillating motion. For given surface concentrations, the spheres began to form clusters in the middle of the box (Fig. 6). This behaviour was rationalised as follows. The collisions between the spheres are not conservative; a part of the kinetic energy is consumed for deforming the spheres. In order to keep the system moving, it is necessary to reinject some energy. This happens through the collisions with the oscillating box walls. Therefore the spheres’ speed is higher after encountering the wall than before, leading to the particles’ concentration at the middle edge of the box (given that the particle density is high enough, i.e. that the sphere mean free path is shorter than half of the box typical dimension). The direct analogy between this system and mesopores is obviously too adventurous but stresses the fact that energy exchanges at the interface can play a major role in controlling the behaviour of a given phase.

Fig. 6 Pictures of the 2-D aggregation of bronze sphere in oscillating boxes. Adapted from ref. 57.

Another phenomenon that could, in our opinion, be advantageously taken into account for analyzing the catalytic behaviour of mesoporous solids is the wetting of nanorough surfaces.⁵⁸ It was, indeed, recently shown that partial dewetting in confined structures could result in strong pressure increases within the confined liquid.⁵⁹ Moreover, the well known ability of light alcohols to esterify the silanols of silica based materials should allow the formation of a hydrophobic belt at the silica porous surface enhancing the dewetting phenomenon of polar hydrophilic MeOH (ε = 33) or ⁱPrOH (ε = 18) solvent molecules. Such partial dewetting effects could occur in systems featuring both meso- and micro-porosity, such as for instance SBA-15. It is worth noticing here that, incidentally, SBA-15 is the system which yielded the highest catalytic activity for HBLs in hydrogenation catalysis.⁵⁴

Conclusions

Confinement in mesoscopic porous solids still yields surprising results, like the observations by Tanchoux and co-workers (unpublished thus far⁶⁰) that the positions of IR vibrations of super-critical CO₂ (which vary linearly with the applied pressure in the bulk) corresponded to formally higher pressures than the applied one, once confined inside a periodically organized mesoporous material. This clearly points the fact that further work, both experimental and theoretical, has to be done to access a full comprehension of the involved phenomena. We hope that this paper will contribute to open fruitful discussions between the concerned scientists to access a comprehensive overview of confinement in very promising periodically organized mesoporous materials. This overview is not only needed for academic concerns but also because it will allow tailoring of the properties of industrially very relevant porous materials.

Acknowledgements

The authors would like to thank Dr Francesco di Renzo and Prof. Dr Markus Antonietti for fruitfull discussions.

References

1. C. G. Goltner and M. Antonietti, Adv. Mater., 1997, 9, 431.
2. C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C. Vartuli and J. S. Beck, Nature, 1992, 359, 710.
3. S. Mann, S. L. Burkett, S. A. Davis, C. E. Fowler, N. H. Mendelson, S. D. Sims, D. Walsh and N. T. Whilton, Chem. Mater., 1997, 9, 2300.
4. F. Schuth, Chem. Mater., 2001, 13, 3184.
5. G. J. D. Soler-Illia, C. Sanchez, B. Lebeau and J. Patarin, Chem. Rev., 2002, 102, 4093.
6. K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquerol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603.
7. A. Corma, Chem. Rev., 1997, 97, 2373.
8. D. Grosso, C. Boissière, L. Nicole and C. Sanchez, J. Sol–Gel Sci. Technol., 2006 , in press.
9. A. K. Cheetham and C. N. R. Rao, MRS Bull., 2005, 30, 93.
10. G. Ferey, Chem. Mater., 2001, 13, 3084.
11. G. Ferey, C. Mellot-Draznieks, C. Serre and F. Millange, Acc. Chem. Res., 2005, 38, 217.
12. S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334.
13. H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276.
14. T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Ferey, Chem.–Eur. J., 2004, 10, 1373.
15. J. L. C. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3.
16. O. M. Yaghi, G. M. Li and H. L. Li, Nature, 1995, 378, 703.
17. U. Mueller, M. Schubert, F. Teich, H. Puetter, K. Schierle-Arndt and J. Pastre, J. Mater. Chem., 2006, 16, 626.
18. D. M. Ford, E. E. Simanek and D. F. Shantz, Nanotechnology, 2005, 16, S458.
19. N. Z. Logar and V. Kaucic, Acta Chim. Slov., 2006, 53, 117.
20. L. Nicole, C. Boissiere, D. Grosso, A. Quach and C. Sanchez, J. Mater. Chem., 2005, 15, 3598.
21. A. Taguchi and F. Schuth, Microporous Mesoporous Mater., 2005, 77, 1.
22. M. Vallet-Regí, Chem.–Eur. J., 2006, 12, 5934.
23. E. Roduner, Chem. Soc. Rev., 2006, 35, 583.
24. A. Corma, J. Catal., 2003, 216, 298.
25. Z. Blum, S. T. Hyde and B. W. Ninham, J. Phys. Chem., 1993, 97, 661.
26. E. G. Derouane, J. Mol. Catal. A, 1998, 134, 29.
27. F. Marquez, H. Garcia, E. Palomares, L. Fernandez and A. Corma, J. Am. Chem. Soc., 2000, 1222, 6520.
28. F. Marquez, C. Zicovich-Wilson, A. Corma, E. Palomares and H. Garcia, J. Phys. Chem. B, 2001, 105, 9973.
29. C. Schumacher, J. Gonzalez, P. A. Wright and N. A. Seaton, Phys. Chem. Chem. Phys., 2005, 7, 2351.
30. N. Tanchoux, P. Trens, D. Maldonato, F. Di Renzo and F. Fajula, Colloids Surf., A, 2004, 246, 1.
31. C. Boissiere, D. Grosso, S. Lepoutre, L. Nicole, A. B. Bruneau and C. Sanchez, Langmuir, 2005, 21, 12362.
32. C. Alba-Simionesco, B. Coasne, G. Dosseh, G. Dudziak, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, J. Phys.: Condens. Matter, 2006, 18, R15.
33. M. Brun, A. Lallemand, J. F. Quinson and C. Eyraud, Thermochim. Acta, 1977, 21, 59.
34. A. Schreiber, I. Ketelsen and G. H. Findenegg, Phys. Chem. Chem. Phys., 2001, 3, 1185.
35. L. D. Gelb, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, Rep. Prog. Phys., 1999, 62, 1573.
36. J. P. Korb, S. Xu, F. Cros, L. Malier and J. Jonas, J. Chem. Phys., 1997, 107, 4044.
37. J. P. Korb, L. Malier, F. Cros, S. Xu and J. Jonas, Phys. Rev. Lett., 1996, 77, 2312.
38. M. Okazaki and K. Toriyama, J. Phys. Chem. B, 2005, 109, 13180.
39. J. L. Bonardet, J. Fraissard, A. Gedeon and M. A. Springuel-Huet, Catal. Rev. Sci. Eng., 1999, 41, 115.
40. F. Cros, J. P. Korb and L. Malier, Langmuir, 2000, 16, 10193.
41. T. Takamuku, H. Maruyama, S. Kittaka, S. Takahara and T. Yamaguchi, J. Phys. Chem. B, 2005, 109, 892.
42. R. Guegan, D. Morineau and C. Alba-Simionesco, Chem. Phys., 2005, 317, 236.
43. R. Raja, J. M. Thomas, M. D. Jones, B. F. G. Johnson and D. E. W. Vaughan, J. Am. Chem. Soc., 2003, 125, 14982.
44. M. D. Jones, R. Raja, J. M. Thomas, B. F. G. Johnson, D. W. Lewis, J. Rouzaud and K. D. M. Harris, Angew. Chem., Int. Ed., 2003, 42, 4326.
45. M. Iwamoto, Y. Tanaka, N. Sawamura and S. Namba, J. Am. Chem. Soc., 2003, 125, 13032.
46. A. Thomas, S. Polarz and M. Antonietti, J. Phys. Chem. B, 2003, 107, 5081.
47. S. Pariente, P. Trens, F. Fajula, F. Di Renzo and N. Tanchoux, Appl. Catal., A, 2006, 307, 51.
48. F. Hoffmann, M. Cornelius, J. Morell and M. Froba, Angew. Chem., Int. Ed., 2006, 45, 3216.
49. J. M. Notestein and A. Katz, Chem.–Eur. J., 2006, 12, 3954.
50. R. Anwander, Chem. Mater., 2001, 13, 4419.
51. C. Coperet, M. Chabanas, R. P. Saint-Arroman and J. M. Basset, Angew. Chem., Int. Ed., 2003, 42, 156.
52. J. M. Notestein, E. Iglesia and A. Katz, J. Am. Chem. Soc., 2004, 126, 16478.
53. F. Goettmann, C. Boissière, D. Grosso, F. Mercier, P. Le Floch and C. Sanchez, Chem.–Eur. J., 2005, 11, 7416.
54. F. Goettmann, D. Grosso, F. Mercier, F. Mathey and C. Sanchez, Chem. Commun., 2004, 1240.
55. A. Galarneau, D. Desplantier, R. Dutartre and F. Di Renzo, Microporous Mesoporous Mater., 1999, 27, 297.
56. R. Zangi, J. Phys.: Condens. Matter, 2004, 16, S5371.
57. E. Falcon, R. Wunenburger, P. Evesque, S. Fauve, C. Chabot, Y. Garrabos and D. Beysens, Phys. Rev. Lett., 1999, 83, 440.
58. S. M. M. Ramos, E. Charlaix, A. Benyagoub and M. Toulemonde, Phys. Rev. E, 2003, 67, 031604.
59. C. Cottin-Bizonne, C. Barentin, E. Charlaix, L. Boequet and J. L. Barrat, Eur. Phys. J. E, 2004, 15, 427.
60. P. M. Papineschi, N. Tanchoux, P. Trens, F. Di Renzo and F. Fajula, presented at Congrès Zéolithe Catalyse, Autrans, Vercors, 2003.

---

Footnotes

† In a typical test, 500 mg of SBA-15 type powder with a specific surface area of 800 m² g⁻¹, a mean pore diameter of 5 nm and a pore volume of 0,5 cm³ g⁻¹ were suspended in 5 ml of MeOH. The suspension was placed in a 30 ml stainless steel autoclave fitted with a glass vessel and a magnetic stirrer. The autoclave was pressurised with 4.00 ± 0.05 bar of H₂. Five minutes after the starting of stirring the pressure had dropped to 3.80 ± 0.05 bar and then stabilized, due to the dissolution of H₂ in methanol. A reference test without mesoporous powder showed the same pressure loss. Owing to the detection limits there could be a maximum discrepancy between those results of 0.1 bar (i.e. 2.5%). As 5% of the methanol is within the pores the possible increase in solubility within the pores is lower than 50%.

‡ It is well known that polymodal porous materials having both nano- and macroporosities provide optimum adsorption and diffusion (optimal flow) behaviour needed for applications like chromatography and catalysis.

---