Plasma diagnostics and numerical simulations: insight into the heart of analytical glow discharges

Abstract

This review paper gives an overview of the fundamental studies, both by plasma diagnostics and numerical modelling, that have been carried out for analytical glow discharges. After some introduction about the basic aspects of a glow discharge, the various plasma diagnostic techniques that have been described in the literature for analytical glow discharges will be outlined, including a discussion on their strong and weak points, and a presentation of some characteristic results. The major part of the paper, however, focuses on modelling activities for a better description of glow discharges. An overview is given of possible modelling approaches for glow discharges in general, as a means to point out why we have chosen to describe analytical glow discharges by a hybrid modelling network, consisting of various sub-models. The latter will be briefly described, and typical calculation results will be outlined, mainly for glow discharges in direct current (dc) mode, which are nowadays well described by numerical modelling. The modelling of radiofrequency (rf) glow discharges was found to be more complicated, as described in this review, but we believe that the most important aspects of the rf glow discharge are also correctly predicted. For pulsed discharges, on the other hand, some unanswered questions remain, mainly related to the so-called afterpeak behaviour. Hence, this will need further attention in the future, by modelling and/or plasma diagnostic measurements.

---

1. Introduction

Glow discharges are used for the analysis of solid materials, typically in combination with mass spectrometry (GDMS) or optical emission spectrometry (GD-OES). Although these techniques are routinely applied to many different materials,^1–4 quite a few aspects of the glow discharge are still not completely understood. For instance, the formation of a peak in signal intensity in pulsed glow discharges upon pulse termination cannot yet be fully explained by existing theories (see also below, Section 4.5 and refs. 5 and 6). The effect of impurity gases, such as H₂, N₂, O₂ and H₂O, on signal intensities is also not yet fully understood: for instance the rise in the optical emission intensities of some lines upon addition of small traces of H₂, and the decreasing trend of some other lines.⁷ Also, the effects of molecular emission in glow discharge sources, and the consequences for elemental depth profile analysis, need further investigation.⁸ To improve the analytical capabilities, a better understanding of the glow discharge behaviour is desirable. This can be acquired, on one hand, by measurements inside the glow discharge plasma, i.e., by so-called “plasma diagnostics”, and on the other hand, by computer simulations of the plasma behaviour. In this paper, an overview will be given of plasma diagnostic measurements as well as numerical simulations that have been performed in the past, for a better characterization of the glow discharge plasma, in direct current (dc), radiofrequency (rf) and pulsed operation modes. First, the basic aspects (i.e., typical operating conditions, important plasma species and processes) of a glow discharge will be summarized in Section 2. In Section 3, an overview will be presented of the plasma diagnostic methods that have been used for analytical glow discharges. The major part of the review paper, however, deals with computer simulations of analytical glow discharges, showing what can be predicted with the modelling and also stressing the unresolved questions.

2. Basic aspects of a glow discharge

2.1. Operating conditions of analytical glow discharges

Before going into detail about the plasma diagnostic methods and the computer simulations, the basic physical aspects of a glow discharge will be briefly reviewed. A glow discharge is created in its simplest form by applying a potential difference (of the order of 1 kV) between two electrodes, which are inserted in a cell or form the cell walls. For analytical glow discharges, the solid sample to be analyzed acts as the cathode of the glow discharge. The cell is filled with a gas, usually argon, at a pressure ranging from below 100 Pa to several hundreds of Pa, depending mainly on the cell design. The two basic types of glow discharge cells, used nowadays commercially and in research laboratories, are the VG9000 type⁹ and the Grimm-type.¹⁰ In general, the VG9000 glow discharge cell operates at a pressure around 50–100 Pa, and the electrical current, which arises as a result of the potential difference, is of the order of a few mA. The Grimm-type cell operates typically at a pressure of several hundreds of Pa, and the resulting electrical current is around 20 mA for a Grimm-cell with anode tube of 4 mm diameter (which is most common in analytical practice), and of the order of 40–80 Pa for a 8 mm anode tube. Of course, other home-built glow discharge sources also exist, and they operate typically at a pressure of 100–200 Pa, giving rise to a current of the order of 10 mA.

The potential difference can be applied in constant mode (direct current, dc) or can be varied in time, often with a sinusoidal time-profile in the radiofrequency (rf) range, or in pulsed mode with millisecond or microsecond time duration.

2.2. Basic processes in the glow discharge

The most important basic processes occurring in an analytical glow discharge are schematically illustrated in Fig. 1. Note that analytical glow discharges usually take place in a noble gas, and for economic reasons argon is normally chosen. It should be realized that Fig. 1 gives a strongly simplified picture, because in reality many more different plasma species and processes come into play.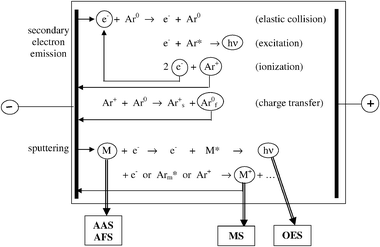

Fig. 1 Schematic picture of the most important basic processes that take place in an analytical glow discharge plasma. Note that the subscripts f and s stand for “fast” and “slow”, and the superscripts 0 and * denote the ground state and excited states, respectively. Ar_m* symbolizes the Ar metastable atoms. AAS, AFS, MS and OES stand for atomic absorption spectrometry, atomic fluorescence spectrometry, mass spectrometry and optical emission spectrometry.

Simply speaking, the glow discharge is sustained by a combination of two processes, i.e., secondary electron emission from the cathode and ionization in the plasma. Secondary electron emission from the cathode occurs as a result of a bombardment of mainly positive ions. Owing to the potential difference between cathode and anode, these electrons will be accelerated away from the cathode into the plasma, where they give rise to collisions with the (argon) gas atoms. These collisions can be subdivided into elastic collisions and inelastic collisions. In elastic collisions, only kinetic energy is exchanged, and because of the large mass difference between electrons and atoms the energy loss of the electrons is negligible. Hence, elastic collisions mainly result in scattering of the electrons. In inelastic collisions, the kinetic energy of the electrons is transferred to the atom as internal (potential) energy. In analytical glow discharges, the two most important electron impact inelastic collisions are excitation and ionization. The excitation collisions, followed by radiative decay to a lower energy level, are responsible for the characteristic name of “glow” discharges. The ionization collisions create a new electron and a positive ion. The electrons can again give rise to inelastic collisions, creating new ion–electron pairs. The positive ions can be accelerated to the cathode, resulting in secondary electron emission. Hence, the combination of these two processes results in an electrical current flowing through the glow discharge and makes the glow discharge self-sustaining.

The positive ions bombarding the cathode give rise not only to secondary electron emission, but also to the release of atoms of the cathode material. This is called sputtering, and can be compared to sand-blasting on an atomic level. Sputtering results not only from positive ion bombardment but also from the bombardment of energetic gas atoms, which are created by elastic (or charge transfer) collisions from the positive ions with the gas, on their way towards the cathode. Moreover, sputtering can also be accomplished by energetic ions of the cathode material, which is called “self-sputtering”.

The sputtered atoms arrive into the glow discharge plasma, where they are also subject to various kinds of collisions. Again, the two most important collisions are excitation and ionization. Excitation collisions result in the formation of excited atoms, which emit characteristic photons, which can be detected with optical emission spectrometry (GD-OES). Ionization collisions give rise to ions of the cathode material, which leave the glow discharge cell through an exit slit and can be measured with mass spectrometry (GDMS). The sputtered atoms can also be detected directly with atomic absorption or fluorescence spectrometry (GD-AAS, GD-AFS), but the latter combinations find considerably fewer applications.

Whereas for the argon gas atoms, excitation and ionization result mainly from electron impact (as well as by impact by energetic Ar⁺ ions and Ar atoms; see below, Section 4.3(c)), for the sputtered atoms, two specific ionization (and excitation) processes come into play, i.e., Penning ionization by argon metastable atoms (denoted as Ar_m*) (M⁰ + Ar_m* → M⁺ + Ar⁰ + e⁻) and asymmetric charge transfer with Ar⁺ ions (M⁰ + Ar⁺ → M⁺ + Ar⁰). The latter process is only important when there is a close resonance between the energy levels of the Ar⁺ ions and the ionic energy levels of the atoms to be ionized (M). A more detailed discussion about the relative importance of these three ionization processes will follow in Section 4.3.

2.3. Spatial regions in a glow discharge

The potential difference applied between the two electrodes of the glow discharge does not drop linearly between cathode and anode, but it drops completely in the first millimetres in front of the cathode. This is schematically illustrated in Fig. 2. This region is called the “cathode dark space” (CDS) or “cathode sheath”, and it is dark because the strong electric field, associated with the potential drop, accelerates the electrons emitted from the cathode (see above) to energies which are too high for efficient ionization and excitation (and hence, emission of light). Moreover, this region is characterized by a positive space charge, because of the much higher mobility (lower mass) of the electrons compared with positive ions.

Fig. 2 Schematic picture of the three spatial regions typically present in an analytical glow discharge, and the characteristic potential distribution throughout the discharge.

The major part of the glow discharge is filled with a region called “negative glow” (NG) or “plasma bulk”, which is characterized by a very weak electric field, or in other words a constant and slightly positive potential, called the “plasma potential” (see Fig. 2). Moreover, this region has nearly charge neutrality (because of equal number densities of electrons and positive ions) and high luminosity (because the electrons have lost energy by collisions, and have now suitable energy for ionization and excitation).

When the distance between anode and cathode is very long, such as in glow discharges used for laser applications and fluorescent lamps, two more regions can be distinguished between the negative glow and the anode, i.e., the so-called Faraday dark space and the positive column, where a slightly negative electric field ensures that sufficient electrons can reach the anode, necessary to maintain the electrical current. However, in most analytical glow discharges, the distance between cathode and anode is rather short, so that the negative glow is only followed by a short “anode zone”, in which the positive plasma potential returns back to zero at the grounded anode (see Fig. 2). Note that the length of the different regions, especially of the CDS, depends also on pressure: a higher pressure results in shorter regions, so that for a fixed distance between cathode and anode, a Faraday dark space and positive column can even be formed.

3. Plasma diagnostics of a glow discharge

A large number of plasma diagnostic techniques exist for performing measurements inside a glow discharge plasma. In the following, a brief overview of these techniques will be given, with special emphasis on the measurements carried out in analytical glow discharges.

3.1. Langmuir probe measurements

Langmuir probes are undoubtedly the most widely used of all plasma diagnostic techniques for glow discharge plasmas.^11–18 The technique consists of inserting a wire into the plasma, to which a known voltage is applied, relative to the grounded electrode. By varying the voltage and recording the corresponding current, the current–voltage characteristic of the probe is obtained, from which in principle the electron and positive ion number densities, the plasma potential, the electron temperature(s) and electron energy distribution can be deduced. Although the construction of the Langmuir probe and the recording of the current–voltage characteristics are relatively straightforward, the data analysis for recovering the actual plasma quantities is very complex. There is no general theory, valid for all plasma parameters and probe shapes (cylindrical, spherical or flat), but some approximate equations need to be used, corresponding to different limiting regions of plasma parameters. Moreover, the Langmuir probe must be very small, otherwise the plasma will be disturbed, and the measured quantities will not reflect the real plasma. Marcus and co-workers have developed a computer-controlled Langmuir probe diagnostic technique for a low pressure dc glow discharge,¹³ and applied it later to an rf glow discharge also.¹⁴ In ref. 15, they designed a data acquisition system and a processing software package for automated Langmuir probe diagnostics, and the software was published in Spectrochimica Acta Electronica.¹⁵ Finally, the effect of He as plasma gas was investigated by a combination of Langmuir probe and emission intensity studies.¹⁶ Furthermore, Heintz and Hieftje carried out Langmuir probe measurements in rf and pulsed glow discharges, and in an rf planar magnetron source (i.e., a kind of glow discharge with additional magnetic field).¹⁷ They observed an afterpeak current at the Langmuir probe in the pulsed discharge, attributed to both an expanding collection volume of the probe and the generation of electrons from metastable argon ionization. In the magnetron source, higher electron number densities were obtained, which probably accounts for the higher emission and ion intensities as generally observed.¹⁷ We performed also Langmuir probe measurements in a Grimm-type dc glow discharge, operating at higher pressures than the above experiments.¹⁸ As illustrated in Fig. 3, the measured electron number densities were found to be in reasonable agreement with calculation results from our model described below (see Section 4.2). Both calculated and measured electron number densities rise in the same way with voltage and pressure. Quantitatively, a factor of 2 difference was obtained in the absolute values at the two lowest pressures investigated, and a slightly larger difference at the highest pressure investigated (note the different scales in the y-axes). This is, however, still reasonable, because it is well below the expected errors of both the model calculations (e.g., uncertainties in input data) and the experimental data (e.g., possible disturbance of the plasma by the Langmuir probe, possible contamination due to deposition on the probe, and approximations in the Langmuir probe theory).

Fig. 3 Comparison of calculated (solid lines, left axis) and measured (broken lines, right axis) electron number densities, as a function of voltage, at three different pressures, both obtained for a Grimm-type glow discharge. Note the different scales of the y-axes. The calculated densities¹⁵⁶ are depicted at the maximum of their profiles, whereas the measured data were obtained with the Langmuir probe at 7 mm from the cathode.¹⁸

3.2. Optical emission spectrometry

Optical emission spectrometry is a non-invasive plasma diagnostic method, which is one of its major advantages compared to Langmuir probe measurements. From the intensities, the intensity ratios or the widths of optical spectral lines, information can be obtained about electron densities and different “temperatures” in the plasma, i.e., the gas temperature, excitation, ionization and rotational temperatures.

When a source is in local thermal equilibrium (LTE), each process is balanced by the reverse process and the population of atoms, ions or molecules of the species at the different energy levels all follow Boltzmann distributions. The corresponding temperatures may be obtained by measuring the intensities, I, of a large number of spectral lines, and plotting ln(Iλ³/A) against the excitation energy of the upper levels, where A is the Einstein spontaneous transition probability of the transition and λ the wavelength. A straight line should be obtained, and from the slope of this plot (the so-called Boltzmann plot) the temperature, often called excitation temperature, can be deduced. A large number of such measurements have been reported for analytical glow discharges,^18–24 since they are relatively easy to perform. Nevertheless, the experiments can be time consuming because a large number of spectral lines have to be measured, and care has to be taken that the spectral lines are not subject to interferences. Moreover, unless complex methods are used to obtain spatial resolution, the measured intensities give the total intensity in the line of sight and only spatially averaged data are obtained. Care must also be taken to avoid lines subject to self-absorption. In addition, accurate values of the transition probabilities of the measured lines are required, and these are not always available. Finally, since glow discharge plasmas are not in LTE, a straight line may not be obtained, and in any case, the measured “temperature” does not have a real physical meaning as an excitation temperature.

Similarly, the ionization temperature can in principle be estimated from spectral lines of atoms and ions of the same species (e.g., Ar I and Ar II).^18,24 We estimated that values of the ionization temperature of Ar vary from 2600 to 8000 K, for the range of discharge conditions shown in Fig. 3.¹⁸ However, even for one set of operating conditions, the ionization temperatures were found to vary depending on the combination of atom–ion spectral lines. This illustrates that the glow discharge plasma is indeed not in LTE, because that would result in only one value for the ionization temperature, being equal to the excitation temperature.

Also, rotational temperatures can be obtained by optical emission spectrometry from a Boltzmann plot of the rotational energy levels of molecules. Since the energy differences between rotational energy levels are small, the excited rotational states are in equilibrium with the kinetic energy of the molecules. Therefore, the rotational temperatures can be considered as a reasonable approximation for the kinetic gas temperature. Ohorodnik and Harrison²² determined the rotational temperature from the N₂⁺ rotational emission spectra, and obtained values in the range between 500–620 K. This was slightly higher than the gas temperature measured with a thermocouple (i.e., 380–430 K). This could be due to the low pressure in the source, requiring a longer time for the thermocouple probe to reach equilibrium with the surrounding gas. However, the spatial profiles of gas temperature obtained optically and by the thermocouple were found to be very similar.

The gas temperature can also be obtained from the Doppler broadening of atomic spectral lines. Kuraica et al.²¹ deduced the gas temperature from the Ar I 696.54 nm line, which resulted in values between 400 and 1400 K, depending on the operating conditions and on the position in the plasma (i.e., highest value near the cathode). Ferreira et al.²⁵ used the Ar I 415.8 nm line, as well as three metal atomic lines, for the gas temperature determination, yielding values between 700 and 1300 K depending again on discharge conditions and position in the plasma.

For Ar I lines, the line shape is indeed only determined by Doppler broadening, and Stark broadening is generally negligible. However, note that this is only true in the absence of self-absorption, and many lines are affected by self-absorption. Hydrogen (H_β) or He I lines, on the other hand, are broadened by the Stark effect, and the shape of these lines can be used to determine electron number densities in the plasma. This was demonstrated for a Grimm-type glow discharge by Kuraica et al.²¹ and Ferreira et al.²⁵ for the H_β line and a He I line, respectively, and by Brackett et al.²⁶ for the H_β line in a diode-type glow discharge source operating under similar conditions, and typical electron number densities in the range of 10¹⁴ cm⁻³ were obtained.^21,25,26

Stark spectroscopy has also been applied to measuring the electric field distribution in a Grimm-type glow discharge.^27,28 Because the energy levels of hydrogen and helium atoms in an external electric field are split due to the Stark effect, the spectral lines emitted as a transition between such split levels consist of a number of components, and from the peak-to-peak separation between these components the electric field strength can be deduced.^27,28 It should, however, be mentioned that the introduction of another gas, such as hydrogen, for measurement purposes may affect the quantity being measured.

Moreover, from the investigation of some optical emission lines, new insights can be obtained about the excitation (and ionization) mechanisms of certain levels. The occurrence of asymmetric charge transfer for the ionization of specific elements was demonstrated by measuring the intensities of certain emission lines.^29–33 In another study of a number of Ar lines, the relative contribution of cascading from upper levels to 2p levels to the total production of these 2p levels was estimated.³⁴

Several authors^7,35–40 have also investigated the effects of controlled addition of impurity gases, such as hydrogen, nitrogen or oxygen, on the optical emission intensities, as well as on the electrical current and sputtering rate, of an argon glow discharge. It was found that some emission line intensities of certain elements increase, whereas other lines decrease in intensity. Moreover, some new spectral features are observed, such as emission bands of new compounds and a continuous background. In the case of hydrogen, the same effects occur whether the hydrogen is introduced into the plasma gas or is a constituent of the sample, i.e., the effects are independent of the method of introducing hydrogen.^7,37–40 Hence, these studies of controlled addition of impurity gases are important for achieving better insights into the effect of sample impurities on chemical analysis.

Optical emission spectrometry was also applied by Perez et al.^41–43 in comparative studies of dc and rf glow discharges, and by Kodama and Wagatstuma⁴⁴ to study the excitation mechanisms for Ni and Ar lines in rf glow discharges with dc bias current introduction. It was found that the emission intensities of Ni atomic lines were elevated by a dc bias current, especially when the excitation energy was in the order of 5 eV. This could be explained by additional excitation through collisions with introduced electrons with kinetic energies favorable for excitation of such Ni atomic lines. However, this excitation mechanism appeared to be less effective for excited states of the Ni⁺ ions, Ar atoms and Ar⁺ ions, because their excitation energies were probably too high.

Furthermore, optical emission spectroscopy, often in combination with mass spectrometry and atomic absorption spectrometry (see below), can provide interesting information on fundamental plasma processes in (millisecond and microsecond) pulsed discharges.^45–52 Optical emission and mass spectrometry signals of analyte atoms and ions appear to reach sharp maxima shortly after pulse termination, which is attributed to the dominance of Penning ionization.⁴⁶ A set of interesting studies was performed by King and co-workers for a millisecond pulsed glow discharge.^48–52 Two-dimensional spatial distributions of emission intensities were plotted at different times during and after the pulse.⁴⁸ It was found that the plateau time (i.e., during the pulse) is dominated by spectral lines originating from low excited levels of analyte atoms, whereas lines originating from higher levels predominate during the afterglow (i.e., immediately after pulse termination), attributed to electron–ion recombination. Two-dimensional distributions of Ar metastable atoms were measured as well, by optical emission spectroscopy, atomic absorption and fluorescence spectrometry.⁴⁹ Electron and energetic Ar⁺ ion and Ar atom impact excitation seem to dominate during the plateau time, whereas electron–ion recombination is probably a more important production mechanism of metastables during the afterglow. In ref. 50, the authors added N₂ for diagnostic measurements, i.e., the rotational temperature gives information on the gas temperature. However, N₂ addition also affects the transient signals of argon and sputtered analyte atoms, especially in the afterglow region, because N₂ reduces the number of Ar⁺ ions available for recombination, and moreover, vibrationally excited states of N₂ slow down the thermalization of electrons thereby decreasing the recombination efficiency. It was concluded from the optical emission measurements in ref. 52 that the glow discharge plasma is highly ionizing in nature during breakdown, with lower excited states being overpopulated; the plateau time is also ionizing in nature, but the post-pulse period displays a recombining behaviour, characterized even by population inversion for some selected species.

Finally, the spatial profiles of optical emission lines allow some interesting information about excitation mechanisms. It was demonstrated by Phelps and co-workers^53,54 and by Donko and colleagues^55,56 that some Ar I lines are not only produced by electron impact excitation, which occurs mainly in the NG, but also by the impact of energetic Ar⁺ ions and Ar atoms in the CDS, where the Ar⁺ ions have gained sufficient energy from the strong electric field, and the energetic atoms are created from collisions of the Ar⁺ ions with the background gas. We have made a comparison of measured spatial profiles of some characteristic Ar I, Ar II and Cu I lines, for a range of different glow discharge conditions, with calculation results obtained with the model described below (Section 4.2) at exactly the same conditions.⁵⁷ The experimental and calculated data were in fairly good agreement, as is clear from Fig. 4. The Ar I 750.3 nm line, which originates from a highly excited 4p level, exhibits a maximum at the beginning of the NG due to electron impact excitation, as well as a minor peak near the cathode in the so-called cathode glow (CG), which could be attributed to energetic Ar⁺ ion and Ar atom excitation. For the Ar I 811.5 nm line, which originates from a low 4p level, the peak in the CG is higher than the peak in the NG, as is clear from Fig. 4. This made us conclude that high 4p levels are predominantly populated by electron impact excitation, which is generally accepted, but that for the low 4p levels the most important production process is ion and atom impact excitation, at the typical conditions of analytical glow discharges. The Ar II lines are characterized by a peak in the NG due to electron impact excitation. Indeed, for the argon ion excited levels, ion and atom impact excitation are not important, because the ion and atom energy necessary to excite the ionic levels is much higher than the ion and atom energies typical for the analytical glow discharge operating conditions. Finally, the Cu I lines are also mainly characterized by a peak in the NG. This peak is rather broad for the Cu I 324.7 nm line, as can be seen in Fig. 4. Indeed, this line is a resonance line (i.e., decaying to the ground state), which is subject to self-absorption. In general, a very good agreement has been reached between the calculated and experimental results, suggesting that the model takes into account the correct excitation mechanisms, and hence, can be used, in combination with the experiment, to predict the relative importance of these mechanisms.

Fig. 4 Comparison of calculated (a) and measured (b) optical emission intensities, as a function of distance from the cathode, in a dc cylindrically symmetrical glow discharge cell, at a pressure of 80 Pa and five different currents and voltages, for the lines Ar I (750.3 nm), Ar I (811.5 nm), Ar II (476.4 nm), Cu I (324.75 nm) and Cu I (510.55 nm).⁵⁷

3.3. Mass spectrometry

The ion peaks in the mass spectrum sometimes yield information about ionization processes in the plasma. Eckstein et al.⁵⁸ measured the Cu⁺ ion current with GDMS in an rf glow discharge, and its behaviour as a function of gas pressure and rf power was found to be proportional to the product of the copper atom and neon metastable atom densities, both determined by atomic absorption spectrometry. This suggested that Penning ionization is a dominant ionization mechanism for the sputtered copper atoms. A similar study on the importance of Penning ionization was performed by Hess and Harrison⁵⁹ by the combination of mass spectrometry and optogalvanic spectroscopy.

As with optical emission spectrometry, mass spectrometry can also yield information on ionization mechanisms, important during different time-periods of pulsed glow discharges. Klingler et al.⁶⁰ demonstrated that the prepeak at the beginning of the pulse, which occurs mainly for ions of the discharge gas, was related to electron impact ionization, whereas the afterpeak, which is characteristic for the analyte ion signals, is associated with Penning ionization due to metastable atoms. Wang and Harrison⁶¹ applied mass spectrometry to measure the diffusion times of sputtered atoms from the cathode surface to the sampling orifice, in order to obtain more insight into the diffusion, ionization and sampling process in a pulsed glow discharge. King and co-workers⁶² used time-of-flight mass spectrometry to investigate the internal energy distributions in a millisecond pulsed glow discharge, using tungsten hexacarbonyl (W(CO)₆) as a “thermometer molecule”. Vapour of this compound was introduced into the plasma and subjected to various ionization and excitation mechanisms. By monitoring the resulting molecular and fragment ions, in combination with the known energetics of W(CO)₆, internal energy distributions could be constructed. Different internal energy distributions were noticeable during the prepeak, plateau region and afterpeak, which suggests that the pulsed glow discharge affords excellent energy tunability to perform selective ionization and fragmentation for molecular, structural and elemental information.

Again, similar to optical emission spectrometry, mass spectrometry can provide better insight into the effect of reactive gases in glow discharges. Hastings and Harrison⁶³ investigated the effect of reactive gases (N₂ or O₂) on the ion signals, both in dc and pulsed glow discharges, and found that both N₂ and O₂ addition leads to significant loss of Ar⁺ and ArH⁺ ion signals. The influence of H₂ addition on dc glow discharges was also measured with TOF-MS by Menendez et al.^64,65 It was observed that the Ar²⁺ signals increase upon H₂ addition, whereas the Ar₂⁺ ions did not show such an enhancement and sometimes even a signal decrease was observed. For the analyte signals, enhancements were obtained in most cases. A strong peak was also measured at m/z = 3, corresponding to H₃⁺ ions, which is in agreement with our modelling calculations described below. Newman et al.⁶⁶ studied the effect of H₂ addition to an Ar plasma by fast flow glow discharge mass spectrometry, and a rise in signal intensities was again observed for most elements. The effect of water vapour on glow discharge plasma atomization and ionization has also been investigated with mass spectrometry by Ratliff and Harrison.⁶⁷ Mass spectra taken with water concentrations up to 5% reveal that the primary glow discharge species arise from ion–molecule reactions and water dissociation in the plasma. Similarly, Ohorodnik et al.⁶⁸ applied optical and mass spectrometric diagnostics for studying the chemical reactivity of the plasma impurity species in an rf glow discharge source, and the important effect of cryogenic cooling was demonstrated. In general, the presence of certain cluster peaks in the mass spectra makes it possible to speculate about production and/or destruction mechanisms of certain molecular species in the plasma.^69,70

However, it should be realized that mass spectrometry cannot give direct information about plasma properties, and this can sometimes lead to wrong conclusions, as was pointed out by Steers³⁰ concerning the relative importance of Penning ionization and asymmetric charge transfer for the ionization of sputtered analyte atoms. Indeed, in their early mass spectrometric studies,⁷¹ Coburn and Kay considered Penning ionization as the most important ionization mechanism. They ruled out the possibility of asymmetric charge transfer, because they assumed that the analyte ions are formed in the ground state and hence the energy difference with the gas ion levels was then too large. Mass spectrometry can, indeed, give no information about excited states, but Steers demonstrated by optical emission spectrometry that the analyte ions are mainly formed in excited states, so that the energy difference with gas ion levels is much smaller, and asymmetric charge transfer can occur.³⁰

Finally, mass spectrometry has also been used to measure ion energy distributions. This was reported mainly for technological plasmas, with a combination of a quadrupole mass spectrometer and an electrostatic energy analyzer.^72–76 van Straaten et al.⁷⁷ recorded the energy distributions of ions bombarding the cathode of an analytical glow discharge cell, by varying the acceleration voltage of a double-focusing VG9000 mass spectrometer and keeping the magnetic field constant. Fig. 5 illustrates the measured energy distribution of Ar⁺ ions at the cathode (b), in comparison with calculation results obtained with the model described below (a). The measured energy distribution is characterized by a dip at low energy, as well as a peak at negative energy. This is probably the result of experimental artifacts. Indeed, it was suggested that low energy ions were subject to charge transfer collisions immediately outside the discharge cell, in the acceleration region of the mass spectrometer. This gives rise to some loss of low energy ions, explaining the dip, as well as some production (i.e., a peak) at negative energy, because these ions have not attained the maximum acceleration voltage. Therefore, the expected “real” energy distribution is indicated by the broken line in Fig. 5(b), and the latter agrees qualitatively with the calculated results of Fig. 5(a). Fairly good agreement was also reached between the measured and calculated energy distributions of the Cu⁺ ions bombarding the cathode, as is shown in Fig. 6 (a), (b). In contrast to the Ar⁺ ions, which exhibit a decreasing energy distribution towards high energies, the Cu⁺ ions (and the ions of the cathode material in general) are characterized by a pronounced peak at maximum energy. Indeed, these ions do not lose their energy very efficiently in charge transfer collisions, as is the case for the Ar⁺ ions, because of the much lower Cu atom density. Note that the measured energy distribution is plotted for three estimated pressure values, because the pressure could actually not be measured inside the glow discharge cell during the experiments. Exact quantitative comparison cannot, therefore, be carried out, but the qualitative agreement between calculated and experimental results is quite convincing.

Fig. 5 Comparison of calculated (a) and measured (b) flux energy distributions of Ar⁺ ions in the VG9000 glow discharge cell (GDMS). The calculation results are obtained at different positions from the cathode, for 1000 V, 75 Pa and 3.5 mA.¹⁵⁴ The measured data were obtained at the cathode, at 1000 V and 3 mA (pressure not measured).⁷⁷

Fig. 6 Comparison of calculated (a) and measured (b) flux energy distributions of Cu⁺ ions in the VG9000 glow discharge cell. The calculation results are obtained at different positions from the cathode, for 1000 V, 75 Pa and 3.5 mA.¹⁵⁴ The measured data were obtained at the cathode, at 1000 V and three pressure values.⁷⁷

3.4. Retarding field analyzer to measure energy distributions

Energy distributions of both ions and electrons in a glow discharge can also be measured with a retarding field analyzer.^78–80 The analyzer typically consists of a sampling orifice, followed by a metal screen having a circular aperture, and a Faraday collector situated immediately behind the aperture. A certain potential is applied to the retarding screen, so that only ions/electrons with sufficiently high energies can pass through the aperture and reach the Faraday collector. By gradually decreasing the potential, ions/electrons with lower energies can pass, and hence the total energy distribution can be deduced.

This method has also been applied to analytical rf glow discharges by Jäger et al.⁸¹ and by Christopher et al.⁸² Jäger et al. measured ion energy distributions by two different methods, i.e., by scanning the acceleration voltage between the electrostatic and magnetic analyzer of a double focusing mass spectrometer, and by applying a variable retarding potential at a grid placed between the ion source and the mass spectrometer.⁸¹ With the latter method, it was possible to determine the absolute value of the average kinetic energy for different ionic species. In general it was found that the kinetic energy of ions of the discharge gas (Ar⁺) and of impurities (e.g., CO⁺ ions) lies about 10 eV lower than the kinetic energy of the sample ions. Note that the ions were sampled here from the grounded electrode. This explains why the energy difference is only 10 eV, because the bias voltage in front of the grounded electrode is only of that order of magnitude. On the other hand, the ion energy distributions measured in ref. 77, and illustrated above, were for ions sampled from the cathode, which could be accelerated by the large potential drop in the CDS in front of the cathode. By a suitable choice of the width and position of the energy window of the electrostatic analyzer of the mass spectrometer, it was found possible in ref. 81 to reduce the intensity of the detected CO⁺ and Ar⁺ ions relative to the intensity of the sample ions, by more than one order of magnitude, which helps to improve the analytical capabilities of rf-GDMS. Christopher, Ye and Marcus⁸² measured ion energy distributions, which were characterized by a broad, low energy peak, extending from 0 to 20 eV, with a high energy shoulder, which is indicative for rf modulation effects.

3.5. Atomic absorption spectrometry

Atomic absorption spectrometry (AAS) can be carried out to obtain absolute number densities of the plasma species. Ferreira, Strauss and Human^83–85 had already performed such measurements in the early 1980s for the argon metastable atoms and the sputtered atoms in a Grimm-type glow discharge, using a hollow cathode lamp as primary source. The argon metastable atoms exhibit a maximum density near the cathode, and the sputtered atoms reach their maximum slightly further away from the cathode. The obtained number densities were of the order of 10¹² cm⁻³ for the metastable atoms, and of the order of 10¹³ cm⁻³ for the sputtered (matrix) atoms. Similar measurements, but with a diode laser as primary source, were carried out by Uzelac and Leis,⁸⁶ for the argon metastable atoms in a microwave boosted Grimm source. Moreover, Hoppstock and Harrison⁸⁷ and Absalan et al.⁸⁸ monitored two-dimensional spatial distributions of sputtered atoms in a dc and an rf glow discharge, respectively, but only relative profiles (i.e., absorbance data) were obtained. Finally, Larkins⁸⁹ investigated the effect of traces of water vapour on the amount of absorption by sputtered atoms. The water vapour appeared to reduce the number of sputtered atoms, but the effect depended on the type of sample being sputtered and the discharge current. The reduction is explained due to interferences with the sputtering process, and to some gas phase reactions between the sputtered atoms and the water molecules or fragments.⁸⁹

A disadvantage of conventional AAS experiments is the need for accurate knowledge of the absorption coefficient or calibration with known standards in order to obtain absolute density profiles. This drawback is overcome by the so-called “concentration-modulated absorption spectrometry (COMAS)”, applied by Mason and co-workers,^90,91 where two laser beams are shone through the glow discharge. The first beam, called pump beam, is modulated. When the pump beam is “on”, it is absorbed in the glow discharge and causes perturbation in the concentration difference between the two states, coupled with the incident radiation. The second beam, called probe beam, is sent through the discharge and will not be absorbed to any large extent because the concentration of the lower state is depleted. However, when the pump beam is turned “off” no concentration perturbation occurs, and the probe beam will be absorbed to a greater extent. The difference in intensity of the probe beam after passing through the glow discharge is measured, and the gain created on the probe beam provides a direct measure of the concentration of the absorber. Because the experiment is on a relative scale, there is no need for calibration with a known concentration or for an accurate knowledge of the absorption coefficient. We applied this method and compared it with our model calculations, to investigate the effect of sticking coefficients at the walls, on the sputtered atom density profiles.⁹² Lithium was chosen in this study, because it has a strong transition at 670.8 nm, which is within the range of 620–680 nm of the tunable dye laser.

Another interesting absorption technique, which is based on measuring the absorption rate instead of the absorption itself, is so-called “cavity ring-down spectroscopy”.^93–95 A light pulse, e.g., from a laser, is sent through a cavity, which is filled by plasma and surrounded by two mirrors at both sides (see Fig. 7: left-hand side). In this way, the light intensity passes through the plasma a large number of times, thereby significantly increasing the sensitivity. A small fraction of the light intensity is able to escape through one of the mirrors, and this light intensity is measured as a function of time (see Fig. 7: right-hand side). When there is no plasma inside the cavity, the only loss factor is the loss of reflectivity at the mirrors, and the light intensity will decrease exponentially as a function of time, with a time constant (the so-called “ring-down-time”) of:

where d is the distance between the mirrors, c is the speed of light, and R is the reflectivity of the mirrors. In practice, R is nearly equal to 1, so that the above equation can be approximated by:
When plasma is present inside the cavity, the light intensity will still drop exponentially, under the condition that the plasma species obey the Lambert–Beer law. The ring-down-time becomes then equal to:
where the sum is taken over all absorbing species, with (frequency-dependent) cross section, and spatially-integrated species density. By measuring the ring-down-time with and without plasma, the integrated species density can be obtained. This is a very powerful technique, often used in technological plasmas for measuring various reactive species densities,^94,95 but to our knowledge, it has not yet been applied to analytical glow discharges.

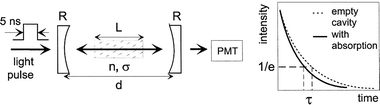Fig. 7 Schematic picture of the set-up of cavity ring-down spectroscopy (left-hand side). R and d stand for the reflectivity of the mirrors, and the distance between the mirrors. L, n and σ represent the distance in the plasma (i.e., where absorbing species are present), the number density of the absorbing species and their absorption cross section. The right-hand side shows how the light intensity decays as a function of time, with and without plasma absorption.

3.6. Laser induced fluorescence spectroscopy

Laser induced fluorescence (LIF) spectroscopy is a powerful technique for obtaining two-dimensional density profiles. This is indeed not straightforward with AAS, where typically integrated values are obtained. We measured two-dimensional density profiles of Ar metastable atoms and of sputtered Ta atoms and ions in a (cylindrically symmetrical) glow discharge with LIF.^96,97 The absolute values were obtained by properly calibrating the gain of the electronics and the response of the monochromator and photomultiplier tube. Moreover, for the Ta atoms, a combination of LIF and AAS measurements has been carried out as well: the LIF experiment yielded the two-dimensional relative density profiles, whereas the AAS measurement allowed us to put an absolute number on these profiles. The combined LIF + AAS experiments typically yielded values a factor of three lower than the pure LIF measurements.⁹⁷Figs. 8, 9 and 10 illustrate the measured density profiles (a) of the Ar metastable atoms, sputtered Ta atoms and Ta⁺ ions, respectively, at 1000 V, 1 Torr and ca. 2 mA, in comparison with results obtained from our modelling calculations described below, at the same discharge conditions and cell geometry (b). Ta was chosen as the cathode material for this comparison, because it has fluorescent lines in the suitable wavelength range of the laser available for the experiment.⁹⁷ For the argon metastable atoms, Fig. 9 shows that both measured and calculated density profiles exhibit a maximum near the cathode, and a second maximum further on in the NG. In the calculations, however, this maximum near the cathode seems too high and the secondary maximum too low, in comparison with the measurements. This pronounced maximum near the cathode is attributed to energetic Ar⁺ ion and Ar atom impact excitation, as was also discussed above, in relation to Fig. 4. The discrepancy with experimental observation therefore suggests that some loss mechanisms might not have been included in the model, which would be important near the cathode, but up to now, we have not yet identified from the literature such an additional loss mechanism for the metastables. For the sputtered Ta atoms (Fig. 10), the agreement is quite satisfactory, both in shape and in absolute values of the densities, certainly keeping in mind that both model and experiment are subject to uncertainties (at least a factor of three for the experiment, cf. above). The different behaviour near z = 0 is due to an approximation in the model, i.e., the cell used for the experiments was open at z = 0 (because the cathode was mounted on an insertion probe), whereas the model assumed a wall at z = 0. Finally, Fig. 11 illustrates the results for the Ta⁺ ions. The experimental and calculated density profiles exhibit the same shape, but the absolute values differ by a factor of 10. Because the measured and calculated Ta atom densities were in fairly good agreement, this may indicate that the calculated amount of ionization is too low, either because an important ionization mechanism is not incorporated, or because the rate coefficients for Penning ionization and asymmetric charge transfer used in the model are too low. The latter can indeed be the case, because these rate coefficients are very difficult to find in the literature, and hence the values assumed in the model are subject to large uncertainties. On the other hand, the experimental results are also prone to some errors, as mentioned above for the Ta atoms. Probably, the observed discrepancy is a combination of uncertainties and approximations in the model and the experiment (e.g., conversion of LIF intensities into ion number densities). After all, a difference of a factor of 10 is not too bad, if one realizes that such model calculations and experiments have never been carried out and confronted before.

Fig. 8 Comparison of measured (left) and calculated (right) number density profiles of the Ar metastable atoms, in a cylindrically symmetrical dc glow discharge, at 1000 V, 1 Torr and ca. 2 mA. The cathode is represented by the black rectangle at the left side, whereas the other borders of the figure denote the cell walls (at anode potential). The remaining part of the left side was open in the measurements, whereas anode walls were assumed in the calculations.⁹⁶

Fig. 9 Comparison of measured (a) and calculated (b) number density profiles of the sputtered Ta atoms, in a cylindrically symmetrical dc glow discharge, at 1000 V, 1 Torr and ca. 2 mA. The tantalum cathode is represented by the black rectangle at the left side, whereas the other borders of the figure denote the cell walls (at anode potential). The remaining part of the left side was open in the measurements, whereas anode walls were assumed in the calculations.⁹⁷

Fig. 10 Comparison of measured (a) and calculated (b) number density profiles of the Ta⁺ ions, in a cylindrically symmetrical dc glow discharge, at 1000 V, 1 Torr and ca. 2 mA. The tantalum cathode is represented by the black rectangle at the left side, whereas the other borders of the figure denote the cell walls (at anode potential). The remaining part of the left side was open in the measurements, whereas anode walls were assumed in the calculations.⁹⁷

3.7. Thomson and Rayleigh scattering

Thomson and Rayleigh scattering also make use of a laser as primary source. Thomson scattering occurs when an electromagnetic wave interacts with charged particles. Since the scattered radiant power is inversely related to the square of the charged particle mass, scattering occurs mainly from electrons. The electrons have rather high velocities in the glow discharge: hence, the light scattered by the electrons will be strongly Doppler shifted, and this shift will increase with the velocity of the electrons. From the collection of the complete Doppler shift spectrum produced by the electrons, the electron velocity (and energy) distribution can be deduced. Moreover, since the integrated intensity under the Doppler shift spectrum is proportional to the total number of electrons, the electron density can also be obtained from this experiment. A very interesting review paper on Thomson scattering from analytical plasmas was published in 2002 by Hieftje and co-workers.⁹⁸

In Rayleigh scattering, the laser light is scattered by, for instance, the Ar gas atoms. The intensity of the scattered light is linearly related to the gas atom density. Since the latter is inversely proportial to the gas temperature, through the ideal gas law, information on the gas temperature can be determined.

Neither method requires LTE conditions in the plasma, nor a Maxwellian energy distribution of electrons. Furthermore, they are more or less non-invasive methods, and are probably more reliable than, for instance, Langmuir probe measurements. Finally, when a pulsed laser is used as the light source, the latter can be focused to a small region in the plasma, and the observation direction and incident laser beam can overlap at only a single point in the discharge, which results in both high spatial and temporal resolution. However, the technique suffers from poor sensitivities, as low intensities of Thomson-scattered light need to be detected in the presence of intense plasma radiation and significant stray light levels, due to the use of high-powered lasers. These requirements dictate the use of a rather complicated and expensive instrumental setup, in order to reduce the stray light and detect the weak Thomson-scattering signals. This is especially true for analytical glow discharge plasmas, which are characterized by relatively low electron number densities in comparison with, for instance, an inductively coupled plasma. Nevertheless, the technique of combined Thomson and Rayleigh scattering has been successfully applied by Hieftje and co-workers for analytical glow discharges.^99–102 Gamez et al.⁹⁹ described the performance of the instrument, as well as the significance of the results. In refs. 100 and 101 a comparison was performed with our modelling calculations described below. The measured gas temperature was found to reach maximum values (i.e., near the cathode) between 600 and 1000 K for discharge conditions in the range of 500–1000 V, 1–3 Torr, and 2.5–65 mA. The electron density was found in the order of 2 × 10¹¹–6 × 10¹² cm⁻³, for the same set of discharge conditions. The experimental values for the gas temperature and electron number densities were in fairly good agreement with the calculated values. As far as the electron energy distribution and average electron energy are concerned, comparison between model and experiment is not straightforward. Indeed, the experiment can detect only low-energy electrons, because the high-energy electrons result in very weak signals. The model, on the other hand, focuses more on the high-energy electrons, which are most important in the glow discharge plasma, i.e., for excitation, ionization, and sustaining the discharge. Hence, model and experiment can be considered complementary to each other in providing information on the electron energy and energy distribution function. Finally, the power of Thomson and Rayleigh scattering in temporal and spatially resolved plasma diagnostics has been demonstrated recently for a millisecond-pulsed glow discharge.¹⁰² For this purpose, the detection optics of the original instrument⁹⁹ were modified and a photon-counting imaging technique was employed to allow the simultaneous observation of Thomson scattering from multiple spatial positions. The measured data provided very interesting information regarding the temporal behaviour of the various plasma parameters, especially during the prepeak and the afterglow period (see also the discussion below in Section 4.5).

4. Computer simulations of a glow discharge

4.1. Overview of existing modelling approaches

Besides plasma diagnostics, better insight into the plasma behaviour can also be obtained by computer simulations. Detailed numerical modelling of analytical glow discharges dates back only to the early 1990s. However, before that period a great number of models were already developed for glow discharges used for technological applications, mainly for deposition purposes and in the semiconductor industry (e.g., refs. 103–115). Several different modelling approaches have been used to describe glow discharge plasmas.

In so-called analytical models,^103,104 the plasma behaviour is decribed with a number of analytical formulae, derived from plasma physics theory. This yields a fast description of the plasma but it is, of course, an approximation, only valid under specified operating conditions.

In a fluid model,^105–107 the different plasma species are considered as separate fluids, and their behaviour is described with continuity equations for mass, momentum and energy. In practice, an energy balance equation is typically only applied for the electrons, because the other plasma species can be considered more or less in thermal equilibrium with the background gas. Moreover, the momentum conservation equations are commonly reduced to transport equations, based on the so-called drift-diffusion approximation, i.e., transport by diffusion, and for the charged species, also by migration (drift) in the electric field. When the mass continuity and flux equations for the different species and the electron energy balance equation are solved simultaneously with the Poisson equation, a self-consistent electric field distribution can be calculated. Indeed, the charged species densities, as obtained from the mass continuity equations, are inserted into the Poisson equation, which yields an electric field distribution that is in turn used in the charged species transport equations (migration-term). In this way, a complete picture of the glow discharge behaviour can be obtained. This model approach is also rather fast, although it can be tricky to solve the coupled differential equations. However, the plasma species are assumed to be more or less in equilibrium with the electric field, i.e., the energy gained by the electric field is more or less balanced by the energy lost through collisions. This is not completely true, especially for the electrons, which can gain a lot of energy from the strong electric field in the CDS.

The non-equilibrium behaviour of the plasma species is fully accounted for in the so-called Boltzmann model,^108,109 which is based on solving the full Boltzmann transport equation for every plasma species. Hence, this kind of model is more accurate, but it becomes mathematically very complicated, especially if one tries to model the glow discharge in more than one dimension. Simplifications to the Boltzmann equation are possible, but are only valid under certain conditions.

Another modelling approach, which is very accurate and moreover, mathematically very simple, is possible via Monte Carlo (MC) simulations,^110–112 which treat the plasma species as individual particles. A number of so-called super-particles are followed, which represent a large number of real particles, as is defined by their “weight”. During successive time-steps, the movement of these super-particles, under the influence of the electric field, is simulated with simple Newton’s laws, and their collisions during every time-step (i.e., occurrence and kind of collision, new energy and direction after the collision) are treated with random numbers. By following a large number of super-particles in this way, their behaviour can be statistically simulated. However, in order to reach statistically valid results, long calculation times are required, especially for slow-moving species. Moreover, this model approach is not fully self-consistent, because the electric field, needed to simulate the species’ trajectories, has to be given as input in the model.

The latter drawback can be circumvented for in the so-called particle-in-cell–Monte Carlo (PIC-MC) simulations,^113–115 where the above description of the super-particles is complemented in every time-step with the solution of the Poisson equation, i.e., the charged species densities, necessary to solve the Poisson equation, are obtained from the positions of all (charged) super-particles at every time-step, as calculated with Newton’s laws. In this way, a fully self-consistent description of the plasma behaviour can be obtained. However, by coupling the statistical description of the super-particles with the solution of the Poisson equation, the PIC-MC simulations are even more time-consuming.

It is clear that every modelling approach has its own advantages and disadvantages. Therefore, we have developed a so-called hybrid modelling network, which is a combination of the above models. For instance, for the energetic plasma species, which are not in equilibrium with the electric field, such as the electrons and energetic ions in the CDS, MC simulations are applied, whereas for other plasma species, which can be considered more or less in thermal equilibrium, such as thermal ions and electrons as well as neutral species, the much faster fluid approach is valid and, moreover, ensures a self-consistent description of the glow discharge behaviour. In this way, the drawbacks of the different modelling approaches are avoided, and the benefits of the models are fully realized. More details about this hybrid modelling network will be given in Section 4.2.

The models that we developed for the analytical glow discharges, are partly based on the models developed for technological plasmas, and described in the literature. However, the latter focus mainly on the electrical characteristics and the discharge gas behaviour, whereas for analytical applications, the behaviour of the sputtered atoms and ions, the Ar atoms in metastable levels, as well as the level populations of excited atoms and ions (for OES purposes) are of fundamental importance. Hence, we have included the analytically important species and the relevant chemical reactions in our modelling network as well (see Section 4.2).

Before going into detail about our own modelling network, it is worth mentioning the efforts of some other research groups to model analytical or related glow discharges. Donko^116–120 has developed a number of MC and hybrid MC–fluid models for dc glow discharges, which are not specifically applied to analytical spectrometry, but which operate under similar conditions to analytical glow discharges, although mainly in helium as the discharge gas. The model approach is similar to the one used in our modelling network (see below, Section 4.2), but it focuses only on the electrons and ions of the discharge gas. Pitchford, Boeuf and colleagues applied a similar hybrid MC–fluid model for argon to a dc glow discharge used as ion source for mass spectrometry, and they studied the effect of cathode geometry (i.e., pin-type and disk-type) on the ion currents arriving at the entry plane of the mass spectrometer, but they did not include any sputtered species either.¹²¹ They also calculated the gas temperature profile in dc argon glow discharges, in a similar way to that included in our hybrid modelling network (see below, Section 4.2), but applied the model to relatively low voltages and currents, where the contribution of the sputtered atoms can be neglected.¹²² Finally, they also applied the hybrid MC–fluid model to an rf glow discharge in order to calculate the electrical characteristics (see also below; Section 4.4).¹²³ Another electrical model for an rf glow discharge was developed by Payling et al., based on a simplified parallel equivalent circuit.¹²⁴ The resulting model was used to calculate plasma resistances based on the matching box settings, and as a test of the model these plasma resistances were used as emission yield corrections in a multi-matrix calibration. Also, Wilken et al.¹²⁵ used a plasma equivalent circuit for an rf glow discharge for quantification purposes. It is shown that the cathode voltage and active cathode current describe the sputtering and excitation well.¹²⁵

As was mentioned above, for analytical glow discharges, the processes of sputtering and the behaviour of the sputtered species is of great importance. In 1972 Boumans derived a linear relationship between the mass sputtered per unit time and per unit current, and the operating voltage, based on measured sputtering rates for various metals and alloys.¹²⁶ More than 20 years later, Payling^127,128 identified the threshold voltage constant in the Boumans equation as the sum of the turn-on voltage and the minimum voltage required for sputtering,¹²⁷ and presented a modified form of the Boumans sputtering equation, supported by measurements on thin films and on bulk samples.¹²⁸ Finally, the impact of this new equation on bulk analysis and quantitative depth profiling was also described.

Ferreira et al.⁸³ formulated a simple diffusion model to predict the density distribution of sputtered atoms, and the agreement with their measured atomic absorption data was found to be very reasonable. However, the measured density profiles exhibit a maximum at about 1 mm from the cathode, which could not be explained by the model because the latter predicted a steadily decreasing density with increasing distance from the cathode. The characteristic density profile, with a maximum shifted away from the cathode, was obtained later on by van Straaten et al., also using a simple diffusion model, in one dimension¹²⁹ and two dimensions,¹³⁰ but taking into account a thermalization profile of sputtered atoms as source term for the diffusion model (see also Section 4.2). Furthermore, van Straaten et al.¹²⁹ calculated the sputter rate, based on Boltzmann equations for the electrons, Ar⁺ ions and energetic Ar atoms in the CDS, and obtained satisfactory agreement with measured etch rates. Based on the sputtering and back diffusion flux, information could also be obtained on the crater profile due to sputtering.¹³⁰ Finally, it was shown that slight modifications of the boundaries of the glow discharge cell could result in a more efficient sputtered atom density distribution in the cell.¹³⁰

Based on a simple sputter model, Mason et al.¹³¹ derived a theoretical expression that describes the experimental parameter dependence of the erosion rate. They also developed a simple model to calculate the flux and average energy of fast atoms in a glow discharge, based on charge transfer from energetic Ar⁺ ions.¹³² By using experimental values from the literature, it is predicted that the fast atom flux is at least twice as large as the ion flux, but with an average energy only slightly lower than for the ions, so that the sputtering of the cathode material is probably caused mainly by fast Ar atom bombardment.¹³² Finally, Hagelaar and Pitchford¹³³ presented a simple model to estimate the mass loss due to sublimation of cathode material (zinc) in a glow discharge. It was concluded that sublimation can contribute to the mass loss of a cathode with a low point of sublimation, and hence to the density of sample atoms in the glow discharge, if the cathode surface temperature is sufficiently high.

Finally, in order to be able to explain and even predict variations in relative sensitivity factors (RSFs) or relative ion yields (RIYs) for various elements in GDMS, some simplified empirical models have been described in literature.^134–137 These models generally reach a more or less satisfactory agreement between calculated and experimental RSF values—one model being better than the other—but all of them are based on the assumption of some kind of equilibrium in the plasma, which certainly does not exist. Moreover, they are based on fitting parameters, in order to reach the best agreement between experiment and theory. In this way one can, of course, always achieve some agreement with experiment, but because of their weak theoretical basis, the fitting parameters do not always have a real physical meaning. The empirical model that describes the physical processes in GDMS in the most realistic way is that of Vieth and Huneke.¹³⁶ However, it is also based on fitting parameters, which can take arbitrary, physically unrealistic, values when comparing experimental and calculated RSFs. Moreover, the observed discrepancy between experimental and calculated RSFs for some elements cannot yet be explained. Using the physical insights acquired by our model calculations, and applying them to the theory of ref. 136, we have been able to offer a rationalization of the experimental RSF values without the need of fitting parameters.¹³⁸ This will be illustrated below, in Section 4.3.

4.2. Comprehensive modelling network for the analytical glow discharge

As was mentioned above, we have developed a comprehensive modelling network for the analytical glow discharge in Ar, with a cathode made of Cu. The species incorporated in the model, and the sub-models used to describe their behaviour, are listed in Table 1.

Table 1 Species taken into account in the hybrid modelling network, and sub-models used to describe their behaviour

Species	Model
Ar gas atoms	No model (assumed thermal + uniformly distributed)
	Alternatives (dc)
	gas heating: heat conduction model
	gas flow: computational fluid dynamics
Electrons	MC model (energetic electrons)
	Fluid model (thermal electrons in NG)
Ar^+ ions	Fluid model (entire discharge)
	MC model in CDS
Fast Ar atoms	MC model in CDS
Ar atoms in excited levels	Collisional–radiative model
Sputtered Cu atoms	Sputtering: empirical formula
	Thermalization: MC model
Cu atoms and Cu^+ ions in ground state + excited levels	Collisional–radiative model
Cu^+ ions	MC model in CDS

---

The Ar gas is usually assumed to be thermal and uniformly distributed, with a gas temperature around or slightly above room temperature. However, we have also developed a model to calculate the gas heating¹³⁹ with a heat conduction equation, where the power input was obtained from collisions of energetic plasma species (electrons, ions and fast atoms) with the Ar background gas, as calculated in the MC models (see below).

The gas temperature in the plasma depends strongly on the temperature at the cathode surface, as was discussed thoroughly in ref. 139. Because the cathode surface temperature can rise to fairly high values, which are apparently not straightforward to measure, we have applied a model to calculate the cathode temperature by means of a heat conduction equation,¹⁴⁰ and this model correctly predicted high temperatures at the cathode surface, depending on the degree of cathode cooling.

In some glow discharge cells there is a considerable gas flow; hence, the assumption of a uniformly distributed background gas is then not valid any more. Therefore, we have also calculated the gas flow with a commercial computational fluid dynamics (CFD) model, i.e., FLUENT, and its effect on the plasma behaviour was obtained by coupling this model with our self-written codes.¹⁴¹

The electrons are split up in two groups: the behaviour of the energetic electrons, i.e., with total (= sum of potential + kinetic) energy above the threshold for inelastic collisions, is simulated with a MC model,^142–144 whereas the thermal electrons are treated with a fluid model.^143,144 Electrons are transferred from the MC to the fluid model when their total energy has dropped below this threshold for inelastic collisions. Indeed, applying a MC model for these thermal electrons would be too time-consuming. Because their major role in the glow discharge plasma is to carry the electrical current and provide negative space charge, as they cannot give rise to inelastic collisions any more, they can as well be described by the (much faster) fluid approach.

The Ar⁺ions are handled, together with the thermal electrons, with a fluid model.^143,144 The continuity and flux equations of electrons and Ar⁺ ions are coupled to the Poisson equation, to obtain a self-consistent electric field distribution (see above). In the case of a dc glow discharge, we have also extended this fluid model for electrons and Ar⁺ ions with two additional ionic species, i.e., the Ar²⁺and Ar₂⁺ions, to investigate their role in the glow discharge.¹⁴⁵ It was found that they constitute typically a few % of the ionic population. Moreover, in another study, we have incorporated hydrogen-related ions (ArH⁺, H⁺, H₂⁺and H₃⁺) in the fluid model for a dc glow discharge, in a mixture of Ar–H₂, with up to 10% H₂.^146–148

Because the Ar⁺ions can gain significant amounts of energy by the strong electric field in the CDS, their behaviour was not only simulated with a fluid model, but additionally with a MC model in the CDS.^142,149 This yields, among other things, the flux energy distribution function of the Ar⁺ ions at the cathode (see above; Fig. 5), which is important in calculating the amount of sputtering (see below).

On their way towards the cathode, the energetic Ar⁺ ions collide with the Ar background gas, creating energetic Ar atoms, which can also bombard the cathode and give rise to sputtering. Therefore, the behaviour of these energetic Ar atoms is also simulated with a MC model in the CDS, keeping in mind, of course, that the atoms do not feel the influence of an electric field.^142,149

Ar atoms can also become excited by the impact of energetic electrons, Ar⁺ ions or Ar atoms, and the behaviour of these excited Ar levels is, therefore, also described in a model. The most suitable model for this purpose is a so-called collisional–radiative model.¹⁵⁰ This is a kind of fluid model based on a set of continuity equations (i.e., balance equations, with different production and loss terms) and flux equations for every excited level. In total, 64 excited levels are taken into account; some of these are individual levels, such as the four lowest (4s) levels, but most of them are so-called effective levels, i.e., a combination of different individual levels with similar excitation energies and quantum numbers. More information can be found in ref. 150. The production and loss processes incorporated in this model include electron, ion and atom impact excitation and de-excitation between all levels, ionization from and ion–electron recombination to all levels, as well as radiative decay between all excited levels. For the four 4s levels, of which two are metastable and two are resonant levels, some additional processes are taken into account, because they play an important role in the glow discharge due to their longer lifetime. These additional processes include metastable–metastable collisions, two-body and three-body collisions with Ar ground state atoms, and Penning ionization of sputtered atoms for the metastable levels, and radiative decay to the ground state, followed by re-absorption of the emitted radiation (i.e., so-called radiation trapping) for the two resonant levels. Because the production processes of one level correspond to the loss processes of other levels, the 64 balance and flux equations for the different levels are coupled to each other.

The amount of sputtering from the (Cu) cathode is calculated with an empirical formula for the sputter yield as a function of the bombarding energies,¹⁵¹ multiplied by the flux energy distributions of the plasma species bombarding the cathode, i.e., the Ar⁺ ions and energetic Ar atoms, as well as the Cu⁺ ions (see below), which are calculated with the MC models.

Once the Cu atoms are sputtered, they have typical energies in the order of 5–15 eV. They lose this energy rapidly by collisions with the Ar background gas, until they are thermalized, which occurs typically a few millimetres from the cathode. This thermalization process is simulated with a MC model,¹⁵² which yields, among others, the so-called thermalization profile, i.e., the fraction of atoms thermalized as a function of position from the cathode.

When the Cu atoms are thermalized, their further transport is diffusion-dominated. Moreover, the Cu atoms can become excited and ionized. The behaviour of the Cu atoms and Cu⁺ions, in ground state and excited levels, is also treated with a collisional–radiative model.¹⁵³ 8 Cu atomic levels and 7 Cu⁺ ionic levels are considered, as well as the Cu²⁺ ions. The production and loss processes are similar as for the Ar collisional–radiative model (see above). The ionization processes of Cu atoms, taken into account in the model, are electron impact ionization, Penning ionization by Ar metastable atoms and asymmetric charge transfer with Ar⁺ ions (see Section 2.2 above).

Finally, the Cu⁺ions are also treated with a MC model¹⁵⁴ in the CDS, where they can gain a significant amount of energy from the strong electric field. This MC model yields, among other things, the flux energy distribution of the Cu⁺ ions, which is also necessary to calculate the amount of sputtering at the cathode, i.e., so-called self-sputtering.

The various sub-models are coupled to each other, due to the interaction processes between the different species, and they are solved iteratively, until final convergence is reached.¹⁵⁵ In this way, a complete picture of the glow discharge behaviour can be obtained. More information about these models and about the coupling procedure can be found in the cited references.

4.3. Modelling of a dc glow discharge

The modeling network explained above has been developed initially for a dc glow discharge, and has been most extensively tested with experimental data for this operation mode. Table 2 gives an overview of the results obtained with our modelling network. These results are calculated using as input only the discharge voltage and gas pressure, the gas temperature (although the latter can also be calculated self-consistently; see above), the cell geometry, and the necessary data for reactions in the plasma (cross sections, rate constants) and at the cell walls (secondary electron emission coefficient, parameters for sputtering yield, other reaction probabilities). For the interested reader, references are also given to the papers where these calculation results are presented, as well as to the papers where comparison with experimental data is performed.

Table 2 Overview of the typical results that have been obtained with our hybrid modelling network for a dc glow discharge, and references for comparison with experimental data, to validate these modelling results. The range of conditions for which the calculations were obtained can roughly be subdivided into two groups, and are indicated by the superscripts (a) and (b): (a) 50–100 Pa, 600–1200 V, 1–10 mA (such as is typical for the VG9000 glow discharge cell, and other laboratory-built sources); (b) 300–700 Pa, 600–1200 V, 10–100 mA (such as is typical for a Grimm-type source). Most results were obtained for the range of conditions (a), because initially the modelling network was developed for these conditions, but later on the model was also applied to the range of conditions (b), and it should be realised that all results mentioned here can also be calculated for conditions (b), even if not indicated in the table

Calculated quantities (+ references for more information)		References for comparison with experiment
Electrical characteristics:
Current–voltage–pressure relations	149 ^(a),156^(b)	149 ^(a),157^(a),158^(b)
Potential, electric field distributions:
3D potential distributions	144 ^(a),156^(b),159–161^(a)	—
3D axial and radial electric field distributions	144 ^(a)	—
Lengths of the different regions (CDS, NG)	149 ^(a),156^(b),160^(a)	162 (CDS length ∼ Aston formula)
3D density profiles of:
Ar atoms (due to gas heating or gas flow)	139 ^(a,b),141^(b)	—
Ar^+, Ar^2+ and Ar2^+ ions	144 ^(a),145^(a),156^(b),159–161^(a)	—
Fast Ar atoms	142 ^(a),144^(a),156^(b)	—
Ar metastable atoms	150 ^(a),163^(a),96^(a),156^(b)	96 ^(a) (LIF)
Other Ar excited levels	150 ^(a),156^(b)	—
Fast electrons	142–144 ^(a),101^(a,b)	101 ^(a,b) (Thomson)
Thermal electrons	142–144 ^(a),156^(b),101^(a,b)	11 ^(b) (Langmuir probe), 101^(a,b) (Thomson)
Atoms of the cathode material	153 ^(a),154^(a),156^(b),164^(a),97^(a)	97 ^(a) (LIF)
Ions of the cathode material	153 ^(a),154^(a),156^(b),164^(a),97^(a)	97 ^(a) (LIF)
Cathode atoms + ions in excited levels	153 ^(a)	—
Ion fluxes of various Ar and cathode ions at the exit slit of the cell to the mass spectrometer	145 ^(a),160^(a),161^(a)	165 ^(a) (intensity ratios in glow discharge mass spectra)
Ionization degrees of Ar and cathode atoms	156 ^(b),164^(a),97^(a)	97 ^(a) (based on LIF results)
3D energy distributions and mean energies of:
Electrons	142 ^(a),143^(a),156^(b),157^(a)	—
Ar^+ ions	142 ^(a),157^(a)	77 ^(a) (at cathode, measured with MS)
Fast Ar atoms	142 ^(a),157^(a)	—
Cathode ions	154 ^(a),157^(a)	77 ^(a) (at cathode, measured with MS)
Information about collision processes:
Collision rates of the various collision processes of electrons, Ar^+ ions and fast Ar atoms	142 ^(a),143^(a),144^(a),149^(a), 156^(b),157^(a)	—
Rates of Penning ionization, asymmetric charge transfer and electron impact ionization of sputtered atoms; relative contributions to the total ionization	153 ^(a),154^(a),156^(b),157^(a), 164^(a)	—
Rates and relative contributions of the various populating and depopulating processes (see text) of the metastable and other excited Ar levels	150 ^(a),156^(b),157^(a),163^(a)	—
Rates and relative contributions of the various populating and depopulating processes (see text) of the excited Cu atom + ion levels	153 ^(a)	—
Information about sputtering:
Sputtering (erosion) rates at the cathode	154 ^(a),156^(b),157^(a),158^(b), 166^(a),167^(b)	158 ^(b), 166^(a), 167^(b)
Thermalization profiles of the sputtered atoms	152 ^(a)	—
Amount of re-deposition on the cathode by backscattering or back diffusion	152 ^(a),166^(a),167^(b)	—
Relative contributions of Ar^+ ions, fast Ar atoms and cathode ions to the sputtering process	142 ^(a),154^(a),156^(b),166^(a), 167^(b)	—
2D crater profiles due to sputtering at the cathode	166 ^(a),167^(b)	166 ^(a),167^(b)
Emission spectra and spatial distributions of emission intensities for Ar and Cu atoms + ions	57 ^(a),158^(b),168^(a),169^(a)	158 ^(b),168^(a),57^(a)
Effect of cell geometry	160 ^(a),161^(a)	—
Effect of H2 impurities on an Ar glow discharge	146–148 ^(a)	—
Gas temperature (+ spatial distribution)	139 ^(a,b)	—
Temperature of the cathode surface	140 ^(b)	—
Prediction of variations in relative sensitivity factors (RSFs) for GDMS	138 ^(a)	138 ^(a)

---

It should be realized that experimental data on fundamental plasma properties for analytical glow discharge plasmas are rather limited, since it is not so easy to measure the various plasma quantities (see Section 3 above). The most straightforward comparison between calculated and measured results, not only in dc mode, but also in rf and pulsed mode (see below, Sections 4.4 and 4.5), is given by current–voltage–pressure characteristics. Indeed, the latter can quite easily be measured, although it must be mentioned that the exact gas pressure is not always readily available. From the calculations side, the discharge voltage and gas pressure are used as input values, and the electrical current is calculated based on the microscopic fluxes of the charged plasma species (i.e., electrons and ions). Therefore, a comparison of the current–voltage–pressure characteristics is always a first way to check the model calculations. In general, we obtained typically a satisfactory correlation between calculated and measured electrical characteristics, which indicates that the other—microscopic—plasma quantities (such as number densities of plasma species, importance of collision processes in the plasma) are also realistic predictions.

In the following, some characteristic examples of calculation results will be illustrated.

(a) Number densities of the plasma species. Table 3 summarizes the range of typical number densities that have been calculated for the various plasma species in an Ar glow discharge with Cu cathode. The Ar gas density can simply be calculated from the ideal gas law, based on the (known or assumed) gas pressure and temperature, and assuming a uniform density profile. However, as mentioned above in Section 4.2, if significant gas heating occurs, a non-uniform gas density profile will result. This is illustrated in Fig. 11, which shows a calculated gas temperature distribution (a), as well as the resulting Ar gas density profile (b), for a glow discharge at 800 V, 500 Pa and about 30 mA. Note that the cathode is located at the left-hand side of the figure, whereas the other borders of the figure are at anode potential. It is clear that significant heating can occur near the cathode, where the plasma species have considerable energy, and transfer this to the background gas. As a consequence, the Ar gas is found to be depleted in front of the cathode. It should be mentioned that at lower pressure and lower power the temperature does not rise to such a large extent, and the gas atom density remains more constant throughout the discharge.

Fig. 11 Calculated gas temperature distribution in Kelvin (a) and corresponding Ar gas atom number density distribution in cm⁻³ (b), obtained for a Grimm-type glow discharge, at 800 V, 500 Pa and about 30 mA.¹³⁹ The cathode is situated at the left side of the figure, whereas the other borders of the figure are at anode potential. Note that only the first 1.5 cm near the cathode of the Grimm-type cell are shown. Reproduced from N. Jakubowski, A. Bogaerts and V. Hoffmann, ‘Glow discharges in emission and mass spectrometry’ in Atomic Spectroscopy in Elemental Analysis, ed. M. Cullen, Blackwell Publishing, Sheffield, 2003.

Table 3 Overview of the typical range of number densities for the various plasma species, as calculated with the model, in the characteristic range of analytical glow discharge conditions (i.e., voltage of 500–1400 V, pressure of 50–700 Pa, gas temperature of 300–1000 K, electrical current of 1–100 mA)

Species	Calculated range of number densities/cm^−3
Ar gas atoms	10^16–10^17
Ar^+ ions	10^11–10^14
Ar^2+ and Ar2^+ ions	10^9–10^11
Electrons	10^11–10^14
Ar atoms in 4s metastable levels	10^11–10^13
Sputtered (Cu) atoms	10^12–10^14
Cu^+ ions	10^9–10^12

---

On the other hand, the uniform gas density profile can also be disturbed when there is a considerable gas flow. Such a gas flow pattern (axial and radial convection velocities of the Ar gas), and the resulting Ar gas density distribution, are depicted in Fig. 12 for a modified Grimm-type cell used as ion source with high gas flow rate for GDMS.¹⁷⁰ The cathode and the positions of gas inlet and outlet are indicated. The gas flow rate at the inlet is 100 sccm, and the background pressures at the gas outlet positions amount to 3.4 Pa and 73 Pa (at the outlet towards the mass spectrometer and the additional outlet, respectively). The calculated axial velocity is highly negative (i.e., directed towards the left) at the gas inlet position, but in most of the cell geometry, it is positive, i.e., directed towards the right (away from the cathode towards the entrance of the mass spectrometer), with typical values ranging from a few 10 s to 100 m s⁻¹, as is apparent from the colour (or shading) scale in Fig. 12(a). It increases, particularly near the outlet to the mass spectrometer, to values of several 100 m s⁻¹. The radial convection velocity is characterized by somewhat lower values than the axial velocity, as is clear from Fig. 12(b). It is highly negative, i.e., directed towards the cell axis, near the gas inlet in front of the cathode, and highly positive, i.e., directed towards the sidewalls of the cell, at the additional gas outlet. In the main part of the discharge cell, the radial convection velocity is, however, rather small, with values between +10 and −10 m s⁻¹. Hence, from the combination of axial and radial convection velocities, the trajectory of the Ar gas flow can be interpreted as follows: the Ar gas, which enters the gas inlet, moves with a high velocity in the direction of the cathode; then it turns and moves away from the cathode through the whole discharge cell, until it is accelerated at both gas outlet positions.

Fig. 12 Calculated axial (a) and radial (b) flow velocities of the Ar gas, as obtained by the CFD program FLUENT, and the resulting Ar gas density distribution (c), for a modified Grimm-type cell used as an ion source with high gas flow rate for GDMS. The cathode and the positions of gas inlet and outlet are indicated. The gas flow rate at the inlet is 100 sccm, and the background pressures at the gas outlet positions are 3.4 Pa (at the outlet towards the mass spectrometer) and 73 Pa (at the additional outlet).¹⁴¹

The gas flow appears to have only limited influence on the density distribution of the Ar background gas, which is slightly non-uniform, with values between 4 × 10¹⁶ and 5 × 10¹⁶ cm⁻³, as is depicted in Fig. 12(c). These values are realistic for the conditions under investigation, because they correspond to an overall gas pressure and temperature of about 500 Pa and 800 K, when calculated with the ideal gas law. As is apparent from the figure, the Ar density reaches higher values near the gas inlet, and lower values at both gas outlet positions, as expected.

Note that the majority of our modelling calculations were performed assuming a uniform Ar gas density distribution, i.e., without considerable gas heating or gas flow. Therefore, the remaining results that will be illustrated in this paper were obtained without gas heating or gas flow, in order not to further complicate the situation, and to focus on the behaviour of these other species. Indeed, the gas heating and gas flow had no major effect on the other calculation results presented here.

It is important to realise that beside the thermal Ar gas atoms, there is a fraction of energetic Ar atoms, with a maximum near the cathode; however, their density is typically about four orders of magnitude lower that the thermal Ar gas atom density,^142,143,156 so that it does not affect the total Ar gas density distribution.

For the sputtered (e.g., Cu) atoms, a non-thermal and a thermal component can also be distinguished, as was explained in Section 4.2 above. This is illustrated in Fig. 13, for the same conditions as in Fig. 11. The non-thermal Cu fraction (Fig. 13 (top)), which arrives in the plasma directly after sputtering, reaches a maximum of 5 × 10¹² cm⁻³ near the cathode, and drops rapidly as a function of distance from the cathode. It is also clearly of lower importance compared with the thermal Cu atom density profile, depicted in Fig. 13 (bottom)). The latter is characterized by a maximum of 2 × 10¹⁴ cm⁻³ at a few mm from the cathode. This maximum shifted away from the cathode can be explained because the sputtered atoms will first become thermalized after sputtering from the cathode, resulting in a thermalization profile, which serves as starting condition for the further diffusion (see also above; Section 4.1 and 4.2). This density profile is typically in reasonable agreement with experimental density profiles, as was shown for the sputtered Ta atoms in Fig. 9 above. Finally, note that the sputtered atom density is typically 3–5 orders of magnitude lower than the Ar atom density.

Fig. 13 Calculated non-thermal (top) and thermal (bottom) sputtered Cu atom density distribution, for the same conditions as in Fig. 11.¹⁵⁶

A typical calculated density profile for the Ar⁺ ions is shown in Fig. 14 for the same conditions as in Fig. 11. The Ar⁺ ion density is low and fairly constant in the first few mm from the cathode (i.e., the CDS), and reaches a maximum in the middle of the plasma. The electron number density has a very similar profile in the NG, resulting in near charge neutrality, but it is virtually zero in the CDS, giving rise to a positive space charge region. This explains, based on the Poisson equation, why the potential exhibits a significant drop in the CDS, and is more or less constant in the NG, as was schematically illustrated in Fig. 2. The density profiles of all other ionic species in the plasma (i.e., Ar₂⁺, Ar²⁺, as well as the ions of the cathode material, and even hydrogen-related ions, such as ArH⁺, H⁺, H₂⁺, H₃⁺ ions, when small admixtures of H₂ are added to the Ar gas^146–148) were found to be characterized by a very similar shape as the Ar⁺ ion profile, but the densities were typically several orders of magnitude lower (see Table 3). For the Ta⁺ ions, a comparison was performed with LIF measurements (see above: Fig. 10), and reasonable agreement was obtained, especially as far as the shape of the profile is concerned.

Fig. 14 Calculated Ar⁺ ion density distribution, for the same conditions as in Fig. 11.¹⁵⁶ Reproduced from N. Jakubowski, A. Bogaerts and V. Hoffmann, ‘Glow discharges in emission and mass spectrometry’ in “Atomic Spectroscopy in Elemental Analysis”, ed. M. Cullen, Blackwell Publishing, Sheffield, 2003.

From the ratio of the ion to atom number densities, information can be obtained on the typical ionization degree in the glow discharge plasma. For argon, this yields values in the range of 0.001%–0.01%. For the sputtered atoms (e.g., Cu) somewhat higher values are obtained, i.e., typically ranging from 0.001% up to a few %, increasing with voltage, pressure and current. This is attributed to the additional ionization mechanisms which come into play for the sputtered atoms, i.e., Penning ionization and asymmetric charge transfer (see below).

The calculated densities of the Ar atoms in excited levels, at the maximum of their spatial profiles, are plotted as a function of their excitation energy in Fig. 15, for the same conditions as in Fig. 11. Note that the level populations, as depicted in Fig. 15, are divided by the statistical weight of the levels, because the higher levels are combined into effective levels with correspondingly much higher statistical weight (see above: Section 4.2). The density of the Ar atoms in the four 4s levels is clearly higher than the populations of the higher excited levels. Indeed, two 4s levels are metastable, i.e., they do not get lost to lower levels (the ground state) by radiative decay, and they play an important role in the glow discharge, i.e., for ionization of the sputtered atoms by Penning ionization (see below). The other two 4s levels are so-called resonant levels, which can be depopulated by radiative decay to the ground state, but the latter can easily reabsorb the emitted radiation, because of its large number density. This is called “radiation trapping”, and the so-called “escape factor”, i.e., the fraction of emitted radiation which is not reabsorbed again but can escape from the plasma, is typically of the order of 10⁻³−10⁻⁴.¹⁵⁰ Hence, the two 4s resonant levels are also characterized by rather high densities. It appears from Fig. 15 that the populations of the higher excited levels decrease steadily as a function of increasing energy, but they do not follow a real Boltzmann distribution. The Ar* (3p⁵) 4p, 5s, 3d and 5p levels still have a considerable population density (albeit several orders of magnitude lower than the 4s metastable and resonant levels), but the higher excited levels have still much lower population densities.¹⁵⁰

Fig. 15 Calculated level populations at the maximum of their profiles, divided by the statistical weight of the levels, for the Ar atoms in various excited states, plotted as a function of their excitation energy, for the same conditions as in Fig. 11.¹⁵⁶ Reproduced from N. Jakubowski, A. Bogaerts and V. Hoffmann, ‘Glow discharges in emission and mass spectrometry’ in “Atomic Spectroscopy in Elemental Analysis”, ed. M. Cullen, Blackwell Publishing, Sheffield, 2003.

A similar plot of level populations for the Cu atoms and Cu⁺ ions in ground state and excited levels, again divided by the statistical weight of the levels, is illustrated in Fig. 16, for the same conditions as in Fig. 11.¹⁵³ Again, it is clear that most of the Cu atoms and Cu⁺ ions are present in the ground state, and that the level populations decrease for higher excited levels. Note that the Cu⁺ 3d⁹4p (³P₂) level is characterized by a significantly higher level population than the other 3d⁹4p levels. Indeed, it follows from the model that this level is very efficiently created by asymmetric charge transfer of Cu atoms with Ar⁺ ions. This high density can indeed explain the anomalously high intensity of the 224.7 nm line, originating from this level, as was observed for typical GD-OES discharge conditions by Steers et al.²⁵ Finally, it can be deduced from Fig. 16 that both the ratio of Cu⁺/Cu⁰ and Cu²⁺/Cu⁺ are of the order of 10⁻².

Fig. 16 Calculated level populations at the maxima of their profiles, divided by the statistical weight of the levels, for the Cu atoms and Cu⁺ ions in the ground state and various excited states, as well as for the Cu²⁺ ions, plotted as a function of their excitation energy, for the same conditions as in Fig. 11.¹⁵³ Reproduced from N. Jakubowski, A. Bogaerts and V. Hoffmann, ‘Glow discharges in emission and mass spectrometry’ in “Atomic Spectroscopy in Elemental Analysis”, ed. M. Cullen, Blackwell Publishing, Sheffield, 2003.

(b) Energies of the plasma species. The calculated energy distributions of the Ar⁺ and Cu⁺ ions have already been depicted for an argon glow discharge in Figs. 5(a) and 6(a), where the comparison with measurements was illustrated. It was shown that the Ar⁺ ions are characterized by a decreasing energy distribution towards higher energies, whereas the Cu⁺ ions exhibit a peak at maximum energy, because they do not lose their energy so efficiently by collisions, in comparison with the Ar⁺ ions. As indicated in Table 4, the maximum energy of the Ar⁺ ions (i.e., when bombarding the cathode) is on average about 10–15% of the total discharge voltage, at typical VG9000 GDMS conditions (i.e., 50–100 Pa, 600–1200 V, 1–10 mA), and about 15–30% at typical Grimm-type conditions (i.e., 300–700 Pa, 600–1200 V, 10–100 mA). The higher energy values at Grimm-type conditions might be a bit unexpected at first sight, because it would be expected that at higher pressures the ions are subject to more collisions, resulting in lower energies. However, the higher pressures give rise to a shorter CDS, so that in absolute terms, the total number of collisions in the CDS is lower.¹⁵⁶ The maximum energy of the Cu⁺ ions is on average about 50–80% of the total discharge voltage, as appears from Table 4, which is indeed much higher than for the Ar⁺ ions.

Table 4 Calculated fraction (on average) of the maximum energy obtained for the Ar⁺ ions, Cu⁺ ions, energetic Ar⁰ atoms and electrons, with respect to the total discharge voltage. Values are given for two different ranges of operating conditions, corresponding to typical VG9000 GDMS¹⁵⁷ and Grimm-type¹⁵⁶ conditions, respectively

	Fraction of maximum energy (on average), with respect to the total discharge voltage
Species	Typical VG9000 conditions^157 (600–1200 V, 50–100 Pa, 1–10 mA)	Typical Grimm-type conditions^156 (600–1200 V, 300–700 Pa, 10–100 mA)
Ar^+ ions	10–15%	15–30%
Cu^+ ions	60–80%	50%
Energetic Ar^0 atoms	3%	4–7%
Energetic electrons	50%	60–80%

---

The energetic Ar atoms also bombard the cathode with considerable energy, because they are created by elastic (including charge transfer) collisions of the energetic Ar⁺ ions with the Ar background gas. Hence, they are also characterized by a similar energy distribution to the Ar⁺ ions, as is illustrated, for example, in refs. 154 and 157. However, because they cannot gain additional energy from the electric field on their way towards the cathode, their energy distribution is shifted to lower energies, and the maximum energy is on average only about 3–7% of the discharge voltage. Note that this is only related to the small group of energetic Ar atoms, because the overall Ar gas atom population is characterized by thermal energy.

Finally, the electrons gain energy when they travel away from the cathode, in the CDS, but they also lose energy by inelastic collisions with the Ar background gas (i.e., excitation, ionization). Hence, their maximum energy is on average about 50% of the discharge voltage at typical VG9000 GDMS conditions, and of the order of 60–80% of the total discharge voltage for typical Grimm-type conditions (see Table 4). Note that this maximum energy is reached at the end of the CDS. Indeed, in the NG, the electrons do not gain significant energy any more from the electric field, which is very weak in this region, and they lose their energy more efficiently by inelastic collisions.

(c) Information about collision processes in the plasma. The modelling network also gives information about the various collision processes occurring in the plasma. Table 5 gives an overview of the relative importance of various ionization and excitation processes, calculated at the characteristic operating conditions of 800 V, 500 Pa and about 30 mA. For the Ar background gas, electron impact ionization is the most important ionization mechanism, but energetic Ar⁺ ions and Ar⁰ atoms also contribute to the overall ionization, for about 1–4% and 2–14%, respectively, depending on the discharge conditions.^156,157 The relative importance of these processes is nearly independent of the pressure, but they become more important at higher voltages, which is logical, because the ions and atoms can reach higher energies, and the cross sections of these processes rise with energy, in the energy range of interest for analytical glow discharges. Moreover, the inclusion of these processes in the model appeared to be really essential for reproducing the correct current–voltage–pressure characteristics. Indeed, in ref. 143, they were not yet included in the model, and the calculated electrical current did not rise with voltage any more above voltages of about 600 V, but reached saturation, which was in discrepancy with experimental data. When energetic Ar⁺ ion and Ar atom impact ionization were incorporated in the model, the correct current–voltage characteristics could be reproduced,¹⁴⁹ indicating that these processes really play an essential role for a correct description of the glow discharge behaviour.

Table 5 Overview of the calculated relative importance of various collision processes, i.e., for ionization of Ar atoms and sputtered Cu atoms, and for production and loss of Ar metastable atoms, integrated over the entire glow discharge cell, for the conditions of 800 V, 500 Pa and about 30 mA

Process	Calculated relative contribution
Ionization of Ar background gas
By energetic electron impact	93%
By energetic Ar^+ ion impact	2%
By energetic Ar atom impact	5%
Ionization of sputtered Cu atoms
Electron impact ionization	3%
Penning ionization by Ar metastables	63%
Asymmetric charge transfer with Ar^+ ions	34%
Production of Ar metastables (4s ^3P2 level)
Electron impact excitation	4.3%
Energetic Ar^+ ion impact excitation	2.6%
Energetic Ar atom impact excitation	18.2%
Electron impact de-excitation from higher 4s levels	33.4%
Radiative decay from higher levels (mainly 4p)	41.4%
Loss of Ar metastables (4s ^3P2 level)
Electron impact excitation to higher 4s levels	58.6%
Metastable–metastable collisions	20.2%
Penning ionization of sputtered atoms	14.0%
Electron impact excitation to 4p levels	6.2%
Electron impact ionization	0.5%
Two-body and three-body collisions with Ar atoms	0.4%

---

For the sputtered (e.g., Cu) atoms, two other ionization processes, besides electron impact ionization, needed to be considered, i.e., Penning ionization by Ar metastable atoms and asymmetric charge transfer with Ar⁺ ions. Note that energetic Ar⁺ ion and Ar⁰ atom impact ionization are not included in the model as ionization processes for the sputtered atoms, because nothing is known about their cross sections and these processes would anyway be negligible compared with Penning ionization and asymmetric charge transfer. Indeed, the latter two processes are found to be of major importance for the sputtered atoms, as also appears from Table 5. In general, it was found that electron impact ionization is of minor importance (2–5%) in the whole range of analytical glow discharge conditions. The contribution of Penning ionization ranges from 40 to 85%, decreasing with increasing pressure and also slightly with rising voltage. The variation of the contribution of asymmetric charge transfer is exactly the opposite; it is only about 10% at low voltages and pressures, and increases to nearly 60% at the highest voltage and pressure investigated for analytical glow discharges. Hence, it appears that in general Penning ionization is the dominant ionization process, but at high voltages and pressures asymmetric charge transfer becomes increasingly important. This trend is consistent with experimental observations from the literature.¹⁷¹ However, it should be realized that asymmetric charge transfer can only play a significant role when the sputtered elements have ionic levels lying close enough to the Ar⁺ ionic levels that they are in close resonance. This will be discussed in more detail below, in relation to variations in relative sensitivity factors (RSFs). Finally, the fact that the ionization degree of the sputtered atoms is calculated to be higher than for the discharge gas (see above) can be explained now, because the sputtered atoms can be ionized more efficiently by Penning ionization and asymmetric charge transfer, which do not occur for the Ar atoms. Moreover, asymmetric charge transfer depletes the Ar⁺ ion density, thereby decreasing the ionization degree of argon.

Table 5 also illustrates the calculated relative contributions of the various production and loss processes of the Ar metastable atoms. The numbers refer to the 4s ³P₂ metastable level, which is the most important metastable level, but the corresponding data for the other 4s levels, as well as for higher excited levels, can be found in ref. 156. It appears that the energetic Ar⁺ ions, and especially the Ar⁰ atoms, play a quite important role for excitation of the 4s levels, even more than the electrons. This explains why the calculated Ar metastable density profile exhibits a pronounced maximum near the cathode (see Fig. 8 (right) above). This maximum was found to be too high compared with the measured maximum (Fig. 8 (left)), suggesting that either the production process by energetic Ar⁺ ion and Ar⁰ atom impact excitation is overestimated (although it is based on published cross sections from literature) or that an additional loss mechanism near the cathode needs to be included in the model (but up to now we are not aware of the existence of such an additional loss mechanism: see the discussion above, in Section 3.6). Other important population processes for the lowest Ar metastable 4s level, as listed in Table 5, include radiative decay from the higher lying 4p levels, as well as electron impact de-excitation from the higher 4s levels. The latter indicates that the 4s levels are closely coupled by electron impact. As far as the loss processes are concerned, electron impact excitation to higher 4s levels is the dominant loss mechanism for the same reason. Other important loss processes are metastable–metastable collisions, and Penning ionization of the sputtered atoms, as well as electron impact excitation to the higher 4p levels. Electron impact ionization, and two-body and three-body collisions with Ar gas atoms, are of minor importance, as is clear from Table 5.

For the higher excited levels, production occurs mainly by electron impact excitation and energetic Ar⁺ ion and Ar atom impact excitation (the latter processes becoming gradually less important for higher excited levels: see also section 3.2 above), as well as radiative decay from higher levels. The latter process is also the dominant loss mechanism for the higher excited Ar atoms.¹⁵⁶ Similar conclusions can be drawn for the excited levels of the sputtered Cu atoms and Cu⁺ ions, as is presented in detail in ref. 153.

(d) Information about sputtering at the cathode. Beside the collision processes in the plasma, the model gives also more information about the sputtering at the cathode. Fig. 17 illustrates some calculated crater profiles (continuous lines, right axis), for a Grimm-type glow discharge with 2.5 mm anode diameter, at a current of 5 mA and different voltages, in comparison with the measured profiles (broken lines, left axis) at the same operating conditions.¹⁶⁷ For each case, the sputtering time (used in the experiment and in the model) is also indicated. The agreement between calculated and measured craters is quite reasonable. The absolute values sometimes differ by a factor of two (note the different depth scales of the measured and calculated profiles, left and right axes), but the shape is in excellent correlation, except at the lowest voltage. At low voltage, both experiment and model predict a concave crater shape. At increasing voltage, the crater shows a convex–concave curvature (i.e., deepest at the sides and in the centre, and shallower in between). At still higher voltage, the crater shape becomes convex (i.e., deeper at the sides than in the centre). Neither experiments nor model predict a completely flat crater bottom: however, around 880 V, the crater shape can be considered as optimal in both experimental and calculated data. Moreover, the obtained crater shapes for the Grimm-type glow discharge are much better than the crater profiles predicted (and measured) for the VG9000 glow discharge source.¹⁶⁶ Because of the satisfactory agreement between calculated and measured crater profiles, the model can, in principle, be used to predict under which operating conditions optimum crater profiles can be obtained. Moreover, the insights gained from the modelling work enable us to explain the crater shape from the microscopic point of view, i.e., based on the calculated potential distributions in front of the cathode, the fluxes and energies of plasma species bombarding the cathode, and the flux of back-diffusing (and hence redepositing) atoms at the cathode surface.^166,167

Fig. 17 Calculated (continuous lines, right axis) and measured (broken lines, left axis) crater profiles, for a Grimm-type glow discharge with 2.5 mm anode diameter, at a current of 5 mA and different voltages. Also shown on the left are the sputtering times used to obtain the crater profiles in both the experiment and the model.¹⁶⁷ The left and right y-axes have different scales, in order to allow the best comparison between the shapes of the calculated and measured crater profiles.

From the calculated fluxes and energy distributions of the energetic Ar⁺ ions, Ar⁰ atoms and Cu⁺ ions bombarding the cathode, information can also be obtained on the relative importance of these species to the sputtering process. These data are plotted in Fig. 18, as a function of discharge voltage, for different pressure values, typical for VG9000 and Grimm-type cell conditions. In spite of their lower energy, the energetic Ar⁰ atoms appear to be the most important sputtering species, especially at low pressure or low voltages. This is attributed to their high flux. Indeed, the flux of energetic Ar⁰ atoms is typically two orders of magnitude higher than the Ar⁺ ion flux. The energetic Ar⁺ ions contribute about 20–30% to the sputtering process. Finally, the Cu⁺ ions also play a non-negligible role in sputtering (i.e., so-called “self-sputtering”), with a relative contribution of less than 1% at the lowest voltage and pressure investigated, but increasing up to about 60% at high voltage and pressure, hence typical for Grimm-type conditions. This is quite remarkable in view of the much lower flux of Cu⁺ ions (typically less than 1% of the Ar⁺ ion flux), and it is attributed to the higher energy of the Cu⁺ ions (cf., Figs. 5 and 6, above).

Fig. 18 Calculated relative contributions to sputtering of the fast Ar atoms (continuous lines, closed circles), Ar⁺ ions (small broken lines, closed rectangles) and Cu⁺ ions (wide broken lines, stars), as a function of voltage at different pressures, for typical GD-OES conditions (a) and GDMS conditions (b).^154,156

(e) Optical emission intensities. From the level populations of the excited levels, it is possible to obtain the optical emission intensities of the various spectral lines. This was illustrated in Section 3.2, where a comparison was made between measured and calculated spatial distributions of the intensities of some selected spectral lines (cf. Fig. 4). Another example is given in Fig. 19, which shows a full spectrum of (605) Ar lines, as calculated from the level populations of all Ar levels included in the collisional–radiative model (see Section 4.2 and refs. 150 and 168 for more details), for the conditions of 1000 V, 133 Pa and 2 mA. It is clear that the lines originating from the Ar 4p levels, i.e., the so-called red lines, lying between 700 and 1000 nm, dominate the spectrum, followed by the so-called blue lines, lying between 400 and 450 nm, originating from the Ar 5p levels. The other lines were all found to be less intense, as illustrated in Fig. 19. A comparison was made with a spectrum found in literature for a hollow cathode glow discharge at 150 mA and 133 Pa¹⁷² and reasonable agreement was reached,¹⁶⁸ demonstrating that the collisional–radiative model takes into account the correct processes.

Fig. 19 Calculated optical emission spectrum of (605) Ar I lines, for the conditions of 1000 V, 133 Pa and 2 mA.¹⁵³

(f) Prediction of relative sensitivity factors (RSFs) and relative ion yields (RIYs) for GDMS. One of the benefits of GDMS is the fairly uniform sensitivity for multi-elemental analysis. The so-called relative sensitivity factors (RSFs) lie generally within one order of magnitude. The RSF in GDMS is defined as the multiplication factor that has to be applied to the measured ion current ratio in order to obtain the relative concentration of the elements in the sample. It has therefore actually the meaning of unsensitivity factor.

For quantitative analytical results, the RSF values have to be known as accurately as possible. We have therefore applied our model to predict variations in RSFs, or rather in so-called relative ion yields (RIYs), which are more or less the inverse of the RSFs. Based on the model by Vieth and Huneke,¹³⁶ it was assumed that differences in RIYs are attributed to transport of the sputtered atoms and to ionization efficiency. Transport, as well as electron impact ionization and Penning ionization are, however, rather unselective processes, because their cross sections and rate coefficients do not vary to a great extent from one element to another. Asymmetric charge transfer with Ar⁺ ions, on the other hand, is a very selective process, because it depends on the availability of suitable ionic energy levels having good overlap with the Ar⁺ ionic levels (also as discussed above). Hence, based on our model predictions, we suggested that asymmetric charge transfer could be responsible for the variations in RIYs or RSFs.¹³⁸ However, rate constant data for asymmetric charge transfer are not readily available for most elements. Therefore, we had to work in the reversed order.

In first instance, the process of asymmetric charge transfer was neglected in this study. Because electron impact ionization was also found to be of minor importance, relative ion yields were calculated, taking only the transport and Penning ionization contributions into account. The calculated RIYs were then compared with the experimental RIYs¹³⁶ and the relative differences were calculated. Simultaneously, a systematic investigation was carried out, to look for the individual ionic energy levels of 42 elements of the periodic system that lie close to the Ar⁺ ion ground state or metastable level, and which could therefore be important for asymmetric charge transfer. We found an excellent correlation between the availability of such ionic energy levels and the relative difference between experimental and calculated RIYs, as is demonstrated in ref. 138. This excellent correlation strongly suggests that the occurrence or absence of asymmetric charge transfer can explain the variations in the RIYs or RSFs of the various elements.

4.4. Modelling of an rf glow discharge

After a full description of dc glow discharges had been obtained, we extended our modelling network in order to describe rf glow discharges as well. This appeared to be more complicated than the modelling of a dc glow discharge. Indeed, the problem is related to the description of thermal electrons. In the dc modelling network, these thermal electrons are transferred from the MC model to the fluid model, where they can be further treated by continuity equations. Indeed, they are not able to give rise to inelastic collisions any more; their only role in the plasma is to provide negative space charge and to carry electrical current, which can as well be described in a fluid model. In the rf discharge, however, thermal electrons can be heated again by the fluctuating rf electric field. Hence, these electrons might again give rise to ionization (so-called alpha-ionization¹⁷³) which, in principle, can be simulated most accurately with a MC model. The description of these thermal electrons, and their contribution to ionization, appeared, however, to be a non-trivial modelling task.

In the rf model that we originally developed,¹⁷⁴ all electrons starting from the rf electrode (due to secondary electron emission), and the ones created by ionization in the plasma, were simulated with a MC method irrespective of their energy. However, a model comparison between a dc and an rf discharge revealed that the rf discharge yielded less ionization, and hence required higher voltages (rf amplitude and dc bias voltage) for the same values of pressure and power as the dc discharge, which was in contrast to experimental observations where the opposite is generally found. This suggested that the behaviour of the electrons and their ionization mechanisms were not yet correctly described in that early rf model. Indeed, the electron density, calculated in the MC model, appeared to be lower than the density predicted from the fluid model (based on the electric field distribution and the Poisson equation), which means that the thermal electron group, and therefore also their contribution to ionization (after being heated by the fluctuating rf electric field), were underestimated in the rf model.

Several attempts to describe this large group of thermal electrons (which will be built up after a very long time, from the avalanche of the electrons starting at the rf electrode) in the MC model failed, mainly due to extremely long calculation times. Therefore, in the second version of our rf model, the thermal electrons were treated in the fluid model. However, they were allowed to be heated by the fluctuating rf electric field, and they could give rise to ionization. The latter, i.e., alpha-ionization, was described in the fluid code by a simple empirical formula for the ionization rate as a function of the mean electron energy, which was also calculated in the code.¹⁷⁵ With this new model, the comparison of electrical characteristics (voltage, current, power) between a dc and an rf discharge yielded reasonable agreement with the experimental data.¹⁷⁶ However, it should be mentioned that both the calculations of the ionization rate and of the mean electron energy in the fluid code are only approximations, which has to be accepted to avoid the long computation times.

Moreover, beside these difficulties encountered in our own rf models, a paper by Belenguer et al. has been published,¹²³ which showed discrepancies with our results. Indeed, by using a hybrid MC–fluid model (but treating all electrons with the MC method, and not describing the energetic Ar⁺ ions and Ar atoms with a MC method), the authors found that the rf glow discharge used for GD-OES had a capacitive electrical behaviour (i.e., voltage and current out of phase by π/2 with respect to each other) which appeared to arise from a dominant contribution of the displacement current to the overall electrical current,¹²³ whereas we found, in both versions of our rf model,^174,175 that the displacement current was of minor importance at typical analytical operating conditions, and consequently that the rf glow discharge used for analytical purposes (such as the Grimm-type source) has a resistive character (i.e., voltage and current in phase with each other).

This discrepancy between our model results and those by Belenguer et al. (who have a long experience with the modelling of rf glow discharges, albeit for technological applications), as well as the approximation that we had to carry out in our second version of the rf model (i.e., alpha-ionization treated with the fluid model) were the driving forces for us to further improve our model attempts for the rf glow discharge.¹⁷⁷ In this new approach, all electrons, including the large thermal electron group in the bulk plasma, are treated with the MC model. The difference with ref. 174, however, was that the earlier version of the model simulated the behaviour of electrons created at the rf electrode (from secondary electron emission) and the electrons created by ionization of these gamma-electrons (i.e., the so-called avalanche electrons). It takes, however, a very long time before these avalanche electrons have multiplied themselves until they reach the large—steady-state—population of thermal electrons, and it appeared that the MC model of ref. 174 did not treat all these thermal electrons properly. In the improved rf model,¹⁷⁷ we have overcome this problem of extremely long calculation times before the thermal electron group is built up (typical computation times of several days on today’s fast computers). Indeed, the thermal electron group is introduced now at time-step t = 0 in the MC model, from the fluid calculations. Note that in addition to the MC simulations, the thermal electron density is indeed also calculated with the fluid model now. Strictly speaking, this is not necessary, but it appeared to be numerically simpler to maintain the three coupled differential equations (i.e., electron and ion continuity equations, as well as the Poisson equation), as in the dc fluid code (see above: Section 4.2). Hence, the electrons are treated simultaneously in two models: a MC model and a fluid model. The MC model is especially important to yield the accurate electron impact ionization rates (used as input in the fluid model) whereas the fluid model is used to calculate the electron density, coupled to Poisson’s equation, which can then be inserted as input in the MC model (see above). It is found that most of the thermal electrons in the MC model will remain thermal and do not contribute to the ionization. However, a fraction of them will be sufficiently heated to produce alpha-ionization. In this way, all electrons, including the thermal ones, are correctly treated in the MC model, within a reasonable time-scale. Moreover, in order to further reduce the calculation time, a method of combining the thermal electrons into a lower number of “super-electrons” with a higher weight factor is applied.

As expected, the major difference in calculation results between our improved rf model¹⁷⁷ and our previous hybrid rf model¹⁷⁵ is observed in the electron impact ionization rate, at least at the time phase in the rf-cycle when the potential at the powered electrode is positive (ωt = π/2). However, the calculated electrical characteristics, i.e., voltage, electrical current and power as a function of time in the rf cycle, remain essentially the same.

The improved model confirms our earlier findings that the plasma displacement current is lower than the ion and electron conduction currents at the typical analytical rf glow discharge conditions, and therefore that the plasma current and voltage are in phase with each other, which is indicative for the resistive character of analytical rf glow discharges, Moreover, our obtained calculation results are in excellent agreement with experimental observations, where attention is paid, of course, to measuring only the real plasma current.¹⁷⁸ This is illustrated in Fig. 20, where both calculated and measured voltage and electrical current are plotted as a function of time during one rf-cycle. It is clear, both from the calculations and the experiment, that voltage and current are in phase with each other. Also the calculated dc bias voltage correlates almost perfectly with the measured dc bias voltage.

Fig. 20 Comparison of calculated (continuous lines) and measured (broken lines) voltages and electrical current (upper and lower parts of figure, respectively), as a function of time in one rf-cycle, at a pressure of 850 Pa and a voltage of 578 V. Also shown in the upper figure are the calculated and measured dc bias voltages (continuous and broken thin lines, respectively).¹⁷⁸

Besides the electrical characteristics and the behaviour of electrons, the behaviour of energetic Ar⁺ ions and Ar atoms, Ar atoms in excited levels, as well as sputtered Cu atoms and Cu⁺ ions, has also been described in this model for the rf glow discharge. This was performed with MC models and collisional–radiative models, much in the same way as in the dc glow discharge (see above). More details can be found in refs. 179–181. In general, the results obtained for rf and dc operation modes were found to be quite similar, although a somewhat greater amount of ionization, ion and electron densities, erosion rates and optical emission intensities were predicted for the rf mode compared with the dc mode.^180–182

4.5. Modelling of a pulsed glow discharge

Finally, we have also applied our modelling network to pulsed glow discharges, of both microsecond (μs) and millisecond (ms) pulse duration. The calculated results, as summarized in Table 2 for the dc mode, have been obtained as a function of time during and after the pulse. However, some peculiarities were observed when comparing the calculated results with experimental data. These are related to the so-called pre-peak and the after-peak behaviour.

The peculiarity in the pre-peak behaviour is again concerned with the electrical characteristics (i.e., electrical current as a function of time). Indeed, in the μs-pulsed (Grimm-type) glow discharge, experimental data¹⁸³ revealed a pronounced peak in the electrical current at the beginning of the pulse, i.e., the so-called pre-peak. When applying the same voltage profile in the model as was measured experimentally, this characteristic current behaviour could only be reproduced when the gas temperature in the plasma was allowed to vary with time as well.¹⁸⁴ This time-evolution of the gas temperature was a bit unexpected for us, and it distinguishes the pulsed model from our previous models for dc and rf discharges, where the gas temperature was assumed to be constant in time. It could, however, be qualitatively explained by significant gas heating at the beginning of the pulse, when the electrical power was high, followed by cooling down when the power was off.¹⁸⁴ However, in connection with the discussion about this characteristic behaviour of the electrical current, Harrison and co-workers repeated their experiments and found out that the initial current peak had to be attributed to the measuring circuit (capacitive effects) and not to the real plasma current.¹⁸³ Hence, our assumptions about the time-behaviour of the gas temperature are probably not relevant any more, certainly not to the same extent as is outlined in ref. 184. This was also confirmed by gas temperature measurements as a function of time, obtained by Rayleigh scattering, albeit for a ms-pulsed glow discharge.¹⁰²

The other point of discussion, which emerged from our modelling calculations, both for a μs-pulsed¹⁸⁵ and a ms-pulsed⁵ glow discharge, is the presence of the peak in excited level populations, optical emission intensities and analyte ion signals in the afterglow, i.e., when the applied voltage pulse is terminated. This experimentally observed “afterpeak” is attributed in the literature^46,48,49,60 to electron–ion recombination. However, when we applied our modelling network to a (μs or ms) pulsed glow discharge, using the calculated electron and ion densities and the rate constants for electron–ion recombination (adopted from literature), electron–ion recombination appeared not to be important enough to give rise to such an afterpeak.^5,185 The same conclusion was independently also drawn by Jackson.⁶ This suggested that maybe some physical processes were still overlooked in the model, which might be important in the afterglow. Therefore, a detailed study⁵ was performed to investigate the afterglow mechanisms (i.e., various possible electron–ion recombination processes), by comparing our model with the detailed diagnostic measurements for a ms-pulsed glow discharge, performed by King and collaborators.^6,48,49 We have estimated how large the recombination rates (both for Ar and sputtered Cu) must be in order to account for the experimentally observed after peaks, and based on these estimates, we have investigated which electron–ion recombination mechanisms (i.e., radiative recombination, collisional–radiative recombination, neutral-stabilized recombination or dissociative recombination) might play a role, and what should be the corresponding rise in electron number density.⁵ This study suggested that collisional–radiative recombination (i.e., three-body recombination with an electron as the third body) is the most plausible candidate, but it requires a rise in electron number density in the early afterglow of about two orders of magnitude, in comparison with the value at the end of the pulse. However, recent Thomson-scattering measurements¹⁰² did not reveal at all such a rise in electron number density. Hence, this still leaves the question unanswered about how electron–ion recombination can account for the afterpeak in pulsed glow discharges. A possible alternative would be dissociative recombination with molecular ions (e.g., Ar₂⁺) in high vibrational levels.⁵ However, this possibility is currently based on several speculations; hence, more experimental data and modelling studies will be needed for further consideration of this mechanism.

5. Conclusions

This review paper attempts to give the reader more insight into what is known about the mechanisms and behaviour of analytical glow discharges. After a brief introduction about the basic aspects of glow discharges, we have given an overview of the various plasma diagnostic techniques that have been applied in the literature for analytical glow discharges. We have outlined some of their benefits and limitations, and given some practical examples of measurements. In the last and major part of the review paper, we have focused on modelling activities for a better description of glow discharges. An overview is given of possible modelling approaches for glow discharges in general, as well as of previous modelling initiatives taken for analytical glow discharges. Subsequently, the comprehensive modelling network that we have developed for analytical glow discharges is explained, and the typical calculation results are outlined. For dc glow discharges, most of the plasma behaviour is now well described, and is also validated against experimental data as much as possible. For rf glow discharges, the modelling approach appeared to be more complicated, but we believe that most important aspects of the rf glow discharge are now also correctly predicted. For pulsed discharges, on the other hand, some unanswered questions still remain, mainly related to the so-called after peak behaviour, and the mechanisms of electron–ion recombination. Hence, this needs further attention in the future, both from the modelling side and from the plasma diagnostics point of view, in order to elucidate the after peak behaviour.

Other challenges for the modelling activities include the description of gaseous impurities in the model for an Ar glow discharge, because this is of importance for analytical measurements. As indicated in Table 2, such studies were carried out for Ar–H₂ discharges, but it would be interesting to develop similar models for describing the effect of impurities originating from N₂, O₂ and H₂O. Another aspect of analytical importance is a more quantitative prediction of variations in RSFs in GDMS, but this will only be possible if exact rate constants for asymmetric charge transfer become available (from experiments or computational chemistry). This leads us to the general conclusion that the availability (or unavailability) of rate constant data is one of the weakest points of the modelling work. Indeed, many different processes can occur in the glow discharge plasma (certainly when reactive gas impurities are taken into account, and when the detailed behaviour of excited levels is considered), and their rate constants are not always well known. These uncertainties limit or course the accuracy of the calculation results. Nevertheless, we may conclude that the modelling work has improved our understanding of the complexity of glow discharge behaviour.

References

1. R. K. Marcus, Glow Discharge Spectroscopies, Plenum Press, New York, 1993.
2. Glow Discharge Optical Emission Spectrometry, eds. R. Payling, D. Jones and A. Bengtson, Wiley, New York, 1997.
3. Glow Discharge Plasmas in Analytical Spectroscopy, eds. R. K. Marcus and J. A. C. Broekaert, Wiley, Chichester, 2003.
4. N. Jakubowski, A. Bogaerts and V. Hoffmann, Glow discharges in emission and mass spectrometryin Atomic Spectroscopy in Elemental Analysis, ed. M. Cullen, Blackwell, Sheffield, 2003.
5. A. Bogaerts, R. Gijbels and G. P. Jackson, J. Anal. At. Spectrom., 2003, 18, 533–548.
6. G. P. Jackson, PhD Dissertation, West Virginia University, 2002.
7. V.-D. Hodoroaba, V. Hoffmann, E. B. M. Steers and K. Wetzig, J. Anal. At. Spectrom., 2000, 15, 951.
8. A. Bengtson, “Molecular species in glow discharge emission—a connection with matrix effects?”, Poster at the FACSS Conference, Lake Buena Vista (FL, USA), September 24–28, 2006.
9. M. van Straaten, A. Vertes and R. Gijbels, Spectrochim. Acta, Part B, 1991, 46, 283–290.
10. W. Grimm, Spectrochim. Acta, Part B, 1968, 23, 443.
11. I. Langmuir and H. Mott-Smith, General Electric Review, 1924, XXVII, pp. 449, 538, 616, 762 and 810.
12. J. D. Swift and M. J. R. Schwar, Electrical Probes for Plasma Diagnostics, Iliffe Books, London, 1970.
13. D. Fang and R. K. Marcus, Spectrochim. Acta, Part B, 1990, 45, 1053.
14. Y. Ye and R. K. Marcus, Spectrochim. Acta, Part B, 1995, 50, 997.
15. Y. Ye and R. K. Marcus, Spectrochim. Acta, Part B, 1997, 52, 2025.
16. M. Belkin, J. A. Caruso, S. J. Christopher and R. K. Marcus, Spectrochim. Acta, Part B, 1998, 53, 1197.
17. M. J. Heintz and G. M. Hieftje, Spectrochim. Acta, Part B, 1996, 51, 1629.
18. A. Bogaerts, A. Quentmeier, N. Jakubowski and R. Gijbels, Spectrochim. Acta, Part B, 1995, 50, 1337.
19. M. Kubota, Y. Fujishiro and R. Ishida, Spectrochim. Acta, Part B, 1981, 36, 697.
20. C. van Dijk, B. W. Smith and J. D. Winefordner, Spectrochim. Acta, Part B, 1982, 37, 759.
21. M. Kuraica, N. Konjevic, M. Platisa and D. Pantelic, Spectrochim. Acta, Part B, 1992, 47, 1173.
22. S. K. Ohordnik and W. W. Harrison, J. Anal. At. Spectrom., 1994, 9, 991.
23. K. Wagatsuma, Spectrochim. Acta, Part B, 2003, 58, 565.
24. P. E. Walters, T. L. Chester and J. D. Winefordner, Appl. Spectrosc., 1977, 31, 1.
25. N. P. Ferreira, H. G. C. Human and L. R. P. Butler, Spectrochim. Acta, Part B, 1980, 35, 287.
26. J. M. Brackett, J. C. Mitchell and T. J. Vickers, Appl. Spectrosc., 1984, 38, 136.
27. I. R. Videnovic, N. Konjevic and M. M. Kuraica, Spectrochim. Acta, Part B, 1996, 51, 1707.
28. M. M. Kuraica, N. Konjevic and I. R. Videnovic, Spectrochim. Acta, Part B, 1997, 52, 745.
29. P. B. Farnsworth and J. P. Walters, Spectrochim. Acta, Part B, 1982, 37, 773.
30. E. B. M. Steers and R. J. Fielding, J. Anal. At. Spectrom., 1987, 2, 239.
31. E. B. M. Steers and F. Leis, Spectrochim. Acta, Part B, 1991, 46, 527.
32. E. B. M. Steers and A. P. Thorne, J. Anal. At. Spectrom., 1993, 8, 309.
33. K. Wagatsuma and K. Hirokawa, Spectrochim. Acta, Part B, 1996, 51, 349.
34. Z. M. Jelenak, Z. B. Velikic, J. V. Bozin, Z. Lj. Petrovic and B. M. Jelenkovic, Phys. Rev. E, 1993, 47, 3566.
35. K. Wagatsuma, Spectrochim. Acta, Part B, 2001, 56, 465.
36. P. Smid, E. B. M. Steers, Z. Weiss and J. Vlcek, J. Anal. At. Spectrom., 2003, 18, 549.
37. V.-D. Hodoroaba, V. Hoffmann, E. B. M. Steers and K. Wetzig, J. Anal. At. Spectrom., 2001, 16, 43.
38. C. Fernandez, N. Bordel, C. Perez, R. Pereiro and A. Sanz-Medel, J. Anal. At. Spectrom., 2002, 17, 1549.
39. V.-D. Hodoroaba, E. B. M. Steers, V. Hoffmann, W. E. S. Unger, W. Paatsch and K. Wetzig, J. Anal. At. Spectrom., 2003, 18, 521.
40. Z. Weiss, E. B. M. Steers and P. Smid, J. Anal. At. Spectrom., 2005, 20, 839.
41. C. Perez, R. Pereiro, N. Bordel and A. Sanz-Medel, Spectrochim. Acta, Part B, 1998, 53, 1541.
42. C. Perez, R. Pereiro, N. Bordel and A. Sanz-Medel, J. Anal. At. Spectrom., 1999, 14, 1413.
43. C. Perez, R. Pereiro, N. Bordel and A. Sanz-Medel, J. Anal. At. Spectrom., 2000, 15, 67.
44. K. Kodama and K. Wagatsuma, Spectrochim. Acta, Part B, 2004, 59, 429.
45. D. Pollmann, K. Ingeneri and W. W. Harrison, J. Anal. At. Spectrom., 1996, 11, 849.
46. F. L. King and C. Pan, Anal. Chem., 1993, 65, 735.
47. X. Yan, K. Ingeneri, W. Hang and W. W. Harrison, J. Anal. At. Spectrom., 2001, 16, 819.
48. C. L. Lewis, G. P. Jackson, S. K. Doorn, V. Majidi and F. L. King, Spectrochim. Acta, Part B, 2001, 56, 487.
49. G. P. Jackson, C. L. Lewis, S. K. Doorn, V. Majidi and F. L. King, Spectrochim. Acta, Part B, 2001, 56, 2449.
50. G. P. Jackson and F. L. King, Spectrochim. Acta, Part B, 2003, 58, 185.
51. C. L. Lewis, L. Li, J. T. Millay, S. Downey, J. Warrick and F. L. King, J. Anal. At. Spectrom., 2003, 18, 527.
52. G. P. Jackson and F. L. King, Spectrochim. Acta, Part B, 2003, 58, 1417.
53. A. V. Phelps and B. M. Jelenkovic, Phys. Rev. A, 1988, 38, 2975.
54. D. A. Scott and A. V. Phelps, Phys. Rev. A, 1991, 43, 3043.
55. K. Rozsa, A. Gallagher and Z. Donko, Phys. Rev. E, 1995, 52, 913.
56. Z. Donko, G. Bano, L. Szalai, K. Rozsa, M. Pinheiro and N. Pinhao, J. Phys. D: Appl. Phys., 1999, 32, 2416.
57. A. Bogaerts, Z. Donko, K. Kutasi, G. Bano, N. Pinhao and M. Pinheiro, Spectrochim. Acta, Part B, 2000, 55, 1465.
58. E. W. Eckstein, J. W. Coburn and E. Kay, Int. J. Mass Spectrom. Ion Phys., 1975, 17, 129.
59. K. R. Hess and W. W. Harrison, Anal. Chem., 1988, 60, 691.
60. J. A. Klingler, C. M. Barshick and W. W. Harrison, Anal. Chem., 1991, 63, 2571.
61. W. Hang and W. W. Harrison, Anal. Chem., 1997, 69, 4957.
62. L. Li, J. T. Millay, J. P. Turner and F. L. King, J. Am. Soc. Mass Spectrom., 2004, 15, 87.
63. E. P. Hastings and W. W. Harrison, J. Anal. At. Spectrom., 2004, 19, 1268.
64. A. Menendez, J. Pisonero, R. Pereiro, N. Bordel and A. Sanz-Medel, J. Anal. At. Spectrom., 2003, 18, 557.
65. A. Menendez, R. Pereiro, N. Bordel and A. Sanz-Medel, Spectrochim. Acta, Part B, 2005, 60, 824.
66. K. Newman, R. S. Mason, D. R. Williams and I. P. Mortimer, J. Anal. At. Spectrom., 2004, 19, 1192.
67. P. H. Ratliff and W. W. Harrison, Spectrochim. Acta, Part B, 1994, 49, 1747.
68. S. K. Ohorodnik, S. De Gendt, S. L. Tong and W. W. Harrison, J. Anal. At. Spectrom., 1993, 8, 859.
69. J. S. Becker, G. Seifert, A. I. Saprykin and H.-J. Dietze, J. Anal. At. Spectrom., 1996, 11, 643.
70. J. S. Becker and H.-J. Dietze, Fresenius’ J. Anal. Chem., 1997, 359, 338.
71. J. W. Coburn and E. Kay, Appl. Phys. Lett., 1971, 18, 435.
72. B. E. Thompson, K. D. Allen, A. D. Richards and H. H. Sawin, J. Appl. Phys., 1986, 59, 1890.
73. W. M. Greene, M. A. Hartney, W. G. Oldham and D. W. Hess, J. Appl. Phys., 1988, 63, 1367.
74. S. Kumar and P. K. Ghosh, Int. J. Mass Spectrom. Ion Processes, 1993, 127, 105.
75. J. K. Olthoff, R. J. Van Brunt and S. B. Radovanov, J. Appl. Phys., 1992, 72, 4566.
76. J. K. Olthoff, R. J. Van Brunt, S. B. Radovanov, J. A. Rees and R. Surowiec, J. Appl. Phys., 1994, 75, 115.
77. M. van Straaten, A. Bogaerts and R. Gijbels, Spectrochim. Acta, Part B, 1995, 50, 583.
78. K.-U. Riemann, U. Ehlemann and K. Wiesemann, J. Phys. D: Appl. Phys., 1992, 25, 620.
79. U. Kortshagen and M. Zethoff, Plasma Sources Sci. Technol., 1995, 4, 541.
80. P. Gill and C. E. Webb, J. Phys. D: Appl. Phys., 1977, 10, 299.
81. R. Jäger, J. S. Becker, H.-J. Dietze and J. A. C. Broekaert, Int. J. Mass Spectrom. Ion Processes, 1997, 171, 183.
82. S. J. Christopher, Y. Ye and R. K. Marcus, Spectrochim. Acta, Part B, 1997, 52, 1627.
83. N. P. Ferreira and H. G. C. Human, Spectrochim. Acta, Part B, 1981, 36, 215.
84. J. A. Strauss, N. P. Ferreira and H. G. C. Human, Spectrochim. Acta, Part B, 1982, 37, 947.
85. N. P. Ferreira, J. A. Strauss and H. G. C. Human, Spectrochim. Acta, Part B, 1982, 37, 273.
86. N. I. Uzelac and F. Leis, Spectrochim. Acta, Part B, 1992, 47, 877.
87. K. Hoppstock and W. W. Harrison, Anal. Chem., 1995, 67, 3167.
88. G. Absalan, C. L. Chakrabarti, J. C. Hutton, M. H. Back, C. Lazik and R. K. Marcus, J. Anal. At. Spectrom., 1994, 9, 45.
89. P. L. Larkins, Spectrochim. Acta, Part B, 1991, 46, 291.
90. R. M. Allott, M. Kubinyl, A. Grofcsik, W. J. Jones and R. S. Mason, J. Chem. Soc., Faraday Trans., 1995, 91, 1297.
91. R. S. Mason, J. C. Naylor, M. G. Hatcher and W. J. Jones, J. Appl. Phys., 1998, 84, 1179.
92. A. Bogaerts, J. Naylor, M. Hatcher, W. J. Jones and R. Mason, J. Vac. Sci. Technol., A, 1998, 16, 2400.
93. K. W. Busch and M. A. Busch, Cavity ringdown spectroscopy: an ultratrace-absorption measurement technique, American Chemical Society, Washington, 1999.
94. R. Engeln, K. G. Y. Letourneur, M. G. H. Boogaarts, M. C. M. van de Sanden and D. C. Schram, Chem. Phys. Lett., 1994, 310, 405.
95. J. Benedikt, M. Wisse, R. V. Woen, R. Engeln and M. C. M. van de Sanden, J. Appl. Phys., 2003, 94, 6932.
96. A. Bogaerts, R. D. Guenard, B. W. Smith, J. D. Winefordner, W. W. Harrison and R. Gijbels, Spectrochim. Acta, Part B, 1997, 52, 219.
97. A. Bogaerts, E. Wagner, B. W. Smith, J. D. Winefordner, D. Pollmann, W. W. Harrison and R. Gijbels, Spectrochim. Acta, Part B, 1997, 52, 205.
98. K. Warner and G. M. Hieftje, Spectrochim. Acta, Part B, 2002, 57, 201.
99. G. Gamez, M. Huang, S. A. Lehn and G. M. Hieftje, J. Anal. At. Spectrom., 2003, 18, 680.
100. G. Gamez, A. Bogaerts, F. Andrade and G. M. Hieftje, Spectrochim. Acta, Part B, 2004, 59, 435.
101. A. Bogaerts, R. Gijbels, G. Gamez and G. M. Hieftje, Spectrochim. Acta, Part B, 2004, 49, 449.
102. G. Gamez, A. Bogaerts and G. M. Hieftje, J. Anal. At. Spectrom., 2006, 21, 350.
103. S. V. Berezhnoi, I. D. Kaganovich, L. D. Tsendin and V. A. Schweigert, Appl. Phys. Lett., 1996, 69, 2341.
104. Y. T. Lee, M. A. Lieberman, A. J. Lichtenberg, F. Bose, H. Baltes and R. Patrick, J. Vac. Sci. Technol., A, 1997, 15, 113.
105. J. P. Boeuf, J. Appl. Phys., 1988, 63, 1342.
106. J. D. P. Passchier and W. J. Goedheer, J. Appl. Phys., 1993, 74, 3744.
107. D. Herrebout, A. Bogaerts, M. Yan, W. Goedheer, E. Dekempeneer and R. Gijbels, J. Appl. Phys., 2001, 90, 570.
108. D. Loffhagen and R. Winkler, J. Comput. Phys., 1994, 112, 91.
109. F. Sigeneger and R. Winkler, Eur. Phys. J.: Appl. Phys., 2002, 19, 211.
110. J. P. Boeuf and E. Marode, J. Phys. D: Appl. Phys., 1982, 15, 2169.
111. Z. Donko, K. Rozsa and R. C. Tobin, J. Phys. D: Appl. Phys., 1996, 29, 105.
112. M. Ohuchi and T. Kubota, J. Phys. D: Appl. Phys., 1983, 16, 1705.
113. E. Neyts, M. Yan, A. Bogaerts and R. Gijbels, J. Appl. Phys., 2003, 93, 5025.
114. I. Kolev, A. Bogaerts and R. Gijbels, Phys. Rev. E, 2005, 72, 056402.
115. V. Georgieva, A. Bogaerts and R. Gijbels, J. Appl. Phys., 2003, 93, 2369.
116. Z. Donko and M. Janossy, J. Phys. D: Appl. Phys., 1992, 25, 1323.
117. Z. Donko, K. Rozsa, R. C. Tobin and K. A. Peard, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 3283.
118. Z. Donko, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 3934.
119. Z. Donko, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 7126.
120. Z. Donko, J. Appl. Phys., 2000, 88, 2226.
121. A. Fiala, L. C. Pitchford, J. P. Boeuf and S. Baude, Spectrochim. Acta, Part B, 1997, 52, 531.
122. I. Revel, L. C. Pitchford and J. P. Boeuf, J. Appl. Phys., 2000, 88, 2234.
123. Ph. Belenguer, L. C. Pitchford and J. C. Hubinois, J. Anal. At. Spectrom., 2001, 16, 1.
124. R. Payling, O. Bonnot, E. Fretel, O. Rogerieux, M. Aeberhard, J. Michler, T. Nelis, U. Hansen, A. Hartmann, P. Belenguer and P. Guillot, J. Anal. At. Spectrom., 2003, 18, 656.
125. L. Wilken, V. Hoffmann and K. Wetzig, Appl. Surf. Sci., 2005, 252, 261.
126. P. W. J. M. Boumans, Anal. Chem., 1972, 44, 1219.
127. R. Payling, Surf. Interface Anal., 1994, 21, 785.
128. R. Payling, Surf. Interface Anal., 1994, 21, 791.
129. M. van Straaten, A. Vertes and R. Gijbels, Spectrochim. Acta, Part B, 1991, 46, 283.
130. M. van Straaten, R. Gijbels and A. Vertes, Anal. Chem., 1992, 64, 1855.
131. R. S. Mason and M. Pichelingi, J. Phys. D: Appl. Phys., 1994, 27, 2363.
132. R. S. Mason and R. M. Allott, J. Phys. D: Appl. Phys., 1994, 27, 2372.
133. G. J. M. Hagelaar and L. C. Pitchford, J. Anal. At. Spectrom., 2002, 17, 1408.
134. R. W. Smithwick III, J. Am. Soc. Mass Spectrom., 1992, 3, 79.
135. R. W. Smithwick III, D. W. Lynch and J. C. Franklin, J. Am. Soc. Mass Spectrom., 1993, 4, 278.
136. W. Vieth and J. C. Huneke, Spectrochim. Acta, Part B, 1991, 46, 137.
137. M. Saito, Anal. Chim. Acta, 1997, 355, 129.
138. A. Bogaerts and R. Gijbels, J. Anal. At. Spectrom., 1996, 11, 841.
139. A. Bogaerts, R. Gijbels and V. V. Serikov, J. Appl. Phys., 2000, 87, 8334.
140. A. Bogaerts and R. Gijbels, J. Anal. At. Spectrom., 2004, 18, 1206.
141. A. Bogaerts, A. Okhrimovskyy and R. Gijbels, J. Anal. At. Spectrom., 2002, 17, 1076.
142. A. Bogaerts, M. van Straaten and R. Gijbels, Spectrochim. Acta, Part B, 1995, 50, 179.
143. A. Bogaerts, R. Gijbels and W. J. Goedheer, J. Appl. Phys., 1995, 78, 2233.
144. A. Bogaerts, R. Gijbels and W. J. Goedheer, Anal. Chem., 1996, 68, 2296.
145. A. Bogaerts and R. Gijbels, J. Appl. Phys., 1999, 86, 4124.
146. A. Bogaerts and R. Gijbels, Spectrochim. Acta, Part B, 2002, 57, 1071.
147. A. Bogaerts and R. Gijbels, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2002, 65, 056402.
148. A. Bogaerts, J. Anal. At. Spectrom., 2002, 17, 768.
149. A. Bogaerts and R. Gijbels, J. Appl. Phys., 1995, 78, 6427.
150. A. Bogaerts, R. Gijbels and J. Vlcek, J. Appl. Phys., 1998, 84, 121.
151. N. Matsunami, Y. Yamamura, Y. Itikawa, N. Itoh, Y. Kazumata, S. Miyagawa, K. Morita, R. Shimizu and H. Tawara, At. Data Nucl. Data Tables, 1984, 31, 1.
152. A. Bogaerts, M. van Straaten and R. Gijbels, J. Appl. Phys., 1995, 77, 1868.
153. A. Bogaerts, R. Gijbels and R. J. Carman, Spectrochim. Acta, Part B, 1998, 53, 1679.
154. A. Bogaerts and R. Gijbels, J. Appl. Phys., 1996, 79, 1279.
155. A. Bogaerts and R. Gijbels, Plasma Phys. Rep., 1998, 24, 573.
156. A. Bogaerts and R. Gijbels, Spectrochim. Acta, Part B, 1998, 53, 437.
157. A. Bogaerts, PhD Dissertation, University of Antwerp, 1996.
158. A. Bogaerts, L. Wilken, V. Hoffmann, R. Gijbels and K. Wetzig, Spectrochim. Acta, Part B, 2001, 56, 551.
159. A. Bogaerts and R. Gijbels, Spectrochim. Acta, Part B, 1997, 52, 553.
160. A. Bogaerts and R. Gijbels, J. Anal. At. Spectrom., 1997, 12, 751.
161. A. Bogaerts and R. Gijbels, J. Am. Soc. Mass Spectrom., 1997, 8, 1021.
162. F. W. Aston, Proc. R. Soc. London, Ser. A, 1907, 79, 80.
163. A. Bogaerts and R. Gijbels, Phys. Rev. A, 1995, 52, 3743.
164. A. Bogaerts and R. Gijbels, Anal. Chem., 1996, 68, 2676.
165. P. Kennis, PhD Dissertation, University of Antwerp, 1996.
166. A. Bogaerts and R. Gijbels, Spectrochim. Acta, Part B, 1997, 52, 765.
167. A. Bogaerts, W. Verscharen and E. Steers, Spectrochim. Acta, Part B, 2004, 59, 1403.
168. A. Bogaerts, R. Gijbels and J. Vlcek, Spectrochim. Acta, Part B, 1998, 53, 1517.
169. A. Bogaerts and R. Gijbels, J. Anal. At. Spectrom., 1998, 13, 721.
170. C. Beyer, I. Feldmann, D. Gilmour, V. Hoffmann and N. Jakubowski, Spectrochim. Acta, Part B, 2002, 57, 1521.
171. M. K. Levy, D. Serxner, A. D. Angstadt, R. L. Smith and K. R. Hess, Spectrochim. Acta, Part B, 1991, 36, 253.
172. D. E. Gray, American Institute of Physics Handbook, 3rd edn., McGraw Hill, New York, 1972.
173. V. A. Godyak and A. S. Kanneh, IEEE Trans. Plasma Sci., 1986, PS-14, 112.
174. A. Bogaerts, R. Gijbels and W. J. Goedheer, Jpn J. Appl. Phys., Part 1, 1999, 38, 4404.
175. A. Bogaerts, M. Yan, R. Gijbels and W. Goedheer, J. Appl. Phys., 1999, 86, 2990.
176. A. Bogaerts, R. Gijbels and W. J. Goedheer, Spectrochim. Acta, Part B, 1999, 54, 1335.
177. A. Bogaerts, R. Gijbels and W. Goedheer, J. Anal. At. Spectrom., 2001, 16, 750.
178. A. Bogaerts, L. Wilken, V. Hoffmann, R. Gijbels and K. Wetzig, Spectrochim. Acta, Part B, 2002, 57, 109.
179. A. Bogaerts and R. Gijbels, IEEE Trans. Plasma Sci., 1999, 27, 1406.
180. A. Bogaerts and R. Gijbels, Spectrochim. Acta, Part B, 2000, 55, 263.
181. A. Bogaerts and R. Gijbels, Spectrochim. Acta, Part B, 2000, 55, 279.
182. A. Bogaerts and R. Gijbels, J. Anal. At. Spectrom., 2000, 15, 1191.
183. W. W. Harrison, personal communication.
184. A. Bogaerts and R. Gijbels, J. Anal. At. Spectrom., 2000, 15, 895–905.
185. A. Bogaerts and R. Gijbels, J. Anal. At. Spectrom., 2001, 16, 239–249.

---

Footnote

† The HTML version of this article has been enhanced with a colour image.

---