Purification of Hf in silicate materials using extraction chromatographic resin, and its application to precise determination of ¹⁷⁶Hf/¹⁷⁷Hf by MC-ICP-MS with ¹⁷⁹Hf spike

Abstract

A two-stage column purification method for Hf from Zr and other elements in silicate samples using the extraction chromatographic resin, UTEVA has been developed. In the first column, using an anion-exchange resin, AG 1X8, Hf, Zr and Ti were collected. In the second, using UTEVA, and after eliminating F⁻ by evaporation with HClO₄ and re-dissolution with H₂O₂–HNO₃, Hf was purified from Ti and Zr, based on characteristic of the UTEVA resin that Hf distribution coefficient (K_d) decreases from 770 to 40, while K_d of Zr decreases less from 890 to 200, in 9 and 6 mol l⁻¹ HNO₃, respectively. The recovery yield of Hf was ∼88% and total blank was ∼4 pg. A MC-ICP-MS Hf isotope ratio determination method was also developed, which uses ¹⁷⁹Hf spike for simultaneous determination of the Hf concentration and ¹⁷⁶Hf/¹⁷⁷Hf ratio. Combining the chemistry and ICP-MS techniques, ¹⁷⁶Hf/¹⁷⁷Hf ratios in silicate reference materials were determined with and without the spike, which gave identical results, showing the applicability of this method.

---

Introduction

The Hf isotope ratio, ¹⁷⁶Hf/¹⁷⁷Hf, is a powerful tracer in geochemistry, because the parent isotope ¹⁷⁶Lu decays to ¹⁷⁶Hf (t_1/2 = 38 Gy) and Lu/Hf fractionation is widely observed in melting processes especially where garnet remains in the residue. Furthermore, this isotope system is well suited for dating of Archaean rocks because of its high resistance to metamorphism or alteration based on immobility of Lu and Hf. For its application, precise ¹⁷⁶Hf/¹⁷⁷Hf ratio measurement is required by thermal ionization mass spectrometry (TIMS) or multi-collector ICP mass spectrometry (MC-ICP-MS). In TIMS, Hf separation from all other elements including Zr and Ti is required,¹ however, in MC-ICP-MS, Hf separation from Zr is not a prerequisite.²

Purification of Hf, especially the separation of Hf from Zr is difficult. For this purpose, cation³ and anion exchange⁴ and extraction^5–8 resins are used. However, there are some drawbacks to each method, such as usage of organic acids³ or H₂SO₄,^4,9 which interferes with MC-ICP-MS measurements,¹⁰ difficulty in obtaining stable elution,^5,6 and matrix effects from Fe and ClO₄⁻.⁸

Le Fèvre and Pin¹¹ used UTEVA resin, which is an extraction resin based on dipentyl pentyl phosphonate, for separation of Hf and Zr from Ti. The UTEVA resin is also used for separation of Ti from Hf + Zr,¹² but no separation of Hf from Zr has been attempted using this resin.

In this study, we have successfully developed a new method to separate Hf from other elements including Zr and Ti in silicate rock samples using the extraction chromatographic resin, UTEVA. This newly developed Hf purification method is applied to precise determination of ¹⁷⁶Hf/¹⁷⁷Hf by MC-ICP-MS. We have also developed a calculation method for ¹⁷⁶Hf/¹⁷⁷Hf with ¹⁷⁹Hf tracer (spike). The use of ¹⁷⁹Hf spike has the advantage that the concentration of Hf in the sample can be estimated by Q-pole ICP-MS before starting the Hf separation, and when the Hf amount in this sample solution is sufficient for the Hf isotope ratio measurement, the solution can then be used for the Hf separation. In contrast, the commonly used ¹⁸⁰Hf spike method requires W separation for determination of Hf because of the isobaric interference of ¹⁸⁰W. The utility of the chemical and mass spectrometric techniques developed in this study, are demonstrated by analyzing Hf isotopic data and Hf concentration in geological reference materials.

Experimental

Reagents and silicate reference materials

Water, HF and mannitol were purified as described elsewhere.¹³ The materials used were Ultrapur H₂O_2, EL-grade HCl and HNO₃ from Kanto Chemical Co. Inc. (Japan) and HClO₄ (TAMAPURE-AA-100) from Tama Chemicals Co. Ltd (Japan).

Enriched isotopes of ¹⁷⁹Hf in oxide form, purchased from Oak Ridge National laboratory (Oak Ridge, TN, USA), were dissolved and then diluted to form a 0.5 mol l⁻¹ HF solution.¹⁴

Two types of the Hf spike solution were prepared. The first was Hf–Zr mix spike, which was purified using AG 1X8 anion exchange resin to remove Ta.¹⁵ The other was pure Hf spike. The former was used for all samples, and the latter was partly used for JB-2, JB-3 and JA-1 analyses.

Three pure Hf solutions were used in this study as the Hf isotope ratio standard. At the early stage of this study, 1000 μg ml⁻¹ Hf standard solution for atomic absorption spectrophotometry (AAS), purchased from Aldrich Chemicals Company Inc. (USA), was used for the Hf–Zr spike isotope ratio calibration. The 10 000 μg ml⁻¹ Hf plasma standard solution (Cat. No. 14374) from Alpha Aesar (USA), named JMC 14374 in this study, was used to calibrate the isotope ratio of the pure Hf spike and spike concentrations in both spikes. JMC 14374 was measured in every analytical session to check machine conditions as the in-house Hf isotope ratio standard. JMC 475, which is the most popular Hf standard, was used to calibrate the ¹⁷⁶Hf/¹⁷⁷Hf ratio of JMC 14374 against JMC 475. All standard solutions were dissolved into 0.5 mol l⁻¹ HF solution.

AG 1X8 (200–400 mesh, Bio-Rad Laboratories, USA), UTEVA resin (100–150 μm, Eichrom Technologies, Inc., USA) and Amberchrom CG-71C (Rohm and Haas Co., USA) were used. AG 1X8 was alternately washed with HCl and water, UTEVA was soaked in 0.5 mol l⁻¹ HNO₃, and washed with water, and CG-71C stored in ethanol was washed and soaked with water prior to use.

Silicate reference materials from Geological Survey of Japan (GSJ), JB-1, JB-2, JB-3 (basalt), JA-1, JA-2, JA-3 (andesite) and JP-1 (peridotite); and those from US Geological Survey (USGS), BHVO-1 (basalt) and AGV-1 (andesite) were analyzed in this study. GSJ samples were further pulverized to enhance homogeneity in an alumina swing mill or by the silicon nitride pestle and mortar (only JP-1).¹⁶

Sample decomposition

The sample decomposition method used in this study was the same as that developed for B–Zr–Nb–Hf–Ta determination,^14,15,17 20–30 mg of basalt and andesite rock powders were weighed into a polypropylene bottle. The sample was then soaked in 0.1% m/v mannitol solution, and a known amount of the Hf–Zr spike or pure Hf spike solutions were added if necessary. When the Hf–Zr spike was used, B–Mo–Sn–Sb spikes were also added.¹⁵ 30 mol l⁻¹ HF was added and the sample was decomposed in an ultrasonic bath. The sample solution was then evaporated to dryness, 5 ml of 0.5 mol l⁻¹ HF was added, and the bottle was agitated in an ultrasonic bath. The insoluble fluorides were removed by centrifuging and the supernatant of 1–4 ml was taken, the amount depending on the Hf concentration in the supernatant solution. 6 mol l⁻¹ HCl was then added to the sample aliquot so that the final concentration was 0.4 mol l⁻¹ HCl–0.5 mol l⁻¹ HF.

The Teflon bomb digestion was employed for the peridotite JP-1. Approximately 50 mg of sample powder was weighed into the bomb. Hf spike and 30 mol l⁻¹ HF were then added, and the bomb was sealed and heated at 478 K for 15 h. After cooling, the sample was transferred into a polypropylene bottle and the mannitol solution was added. The sample solution was then treated in a similar manner to the ultrasonic digestion.

Chemical separation of Hf

A two-step column chemistry has been developed for this study. The first column uses anion exchange resin to remove major elements. The second column employs extraction resin to purify Hf from Ti and Zr. In the first column, 0.3 ml of the anion exchange resin, AG 1X8, was packed in a polypropylene column (29 mm length × 3.5 mm in diameter). The resin was subsequently washed with 3 ml of 6 mol l⁻¹ HCl–0.5 mol l⁻¹ HF mix acid, and conditioned with 1 ml of 0.4 mol l⁻¹ HCl–0.5 mol l⁻¹ HF mix acid. Then the sample solution (1–4 ml) was loaded onto the resin. The resin was subsequently washed with 2 ml of the 0.4 mol l⁻¹ HCl–0.5 mol l⁻¹ HF mix acid to remove major and trace elements such as Al and Fe. Finally Hf, together with Zr and Ti, was recovered by addition of 2 ml of the 6 mol l⁻¹ HCl–0.5 mol l⁻¹ HF mix acid into a 7 ml Teflon beaker. The resin was discarded after use. The HCl–HF mix acid was employed to prevent hydrolysis of Ti, Zr and Hf forming soluble fluoro-complexes.

The solution obtained from the first column was dried with three drops of HClO₄ at 393 K in a draft chamber with clean air. After drying, three drops of concentrated HClO₄ and one drop of concentrated HF were added and solution was heated for 5–10 h at 388 K to eliminate F⁻. Precipitates of HClO₄ are often observed on the beaker wall after heating, but it does not interfere with later column chemistry. The sample solution was then dissolved in one drop of 30% H₂O₂ and 1 ml of 9 mol l⁻¹ HNO₃. The solution should show an orange color, due to formation of the stable complex [Ti(O₂)OH_aq]⁺. If the drying temperature is too high, or if the drying time is too long, the solution shows a pale yellow color or white precipitates. This means that Ti forms stable TiO₂ which can not be dissolved by H₂O₂ + HNO₃, resulting in poor Hf yield because TiO₂ can incorporate Hf. If this happens, the elimination procedure of F⁻ with addition of HClO₄ + HF should be repeated.

In the second column, a two-layered resin bed was used. 0.15 ml of CG-71C was packed at the bottom of a polyethylene column, with the same dimensions as the first column, to absorb organic compounds released from UTEVA. 0.15 ml of UTEVA was packed in the upper layer. This two-layered resin bed was washed with 3 ml 0.5 mol l⁻¹ HNO₃ and conditioned with 1 ml 9 mol l⁻¹ HNO₃. Then the sample solution was loaded onto the column. Showing no absorption on the resin, Ti and other elements were washed away by subsequent addition of 4 ml of 9 mol l⁻¹ HNO₃. Then Hf was collected by 8 ml of 6 mol l⁻¹ HNO₃. The solution was evaporated and finally dissolved in 0.5–1 ml with 0.5 mol l⁻¹ HF for analyses by MC-ICP-MS. The new resin was used in each separation.

Mass spectrometry

The multiple collector inductively coupled plasma magnetic sector field mass spectrometer (MC-ICP-MS), Neptune (Thermo Electron Corp., Germany) in PML, was used for the analysis of Hf isotope ratios. Details of MC-ICP-MS operating conditions are shown in Table 1. ¹⁷⁹Hf/¹⁷⁷Hf = 0.7325 was used for normalization, assuming the exponential law for samples without spike. The sample solution was aspirated through the Aridus desolvating nebulizer (CETAC Technologies, USA). The operating condition of the desolvator is also shown in Table 1. Ar and N₂ gas flow rates for the desolvator were finely tuned daily to get maximum intensity using the 1 ng ml⁻¹ Hf standard solution. 0.5 mol l⁻¹ HF is used for carrier and washing solution. The sensitivity of Hf was 6 × 10⁻¹² A ng⁻¹ ml, corresponding to total ion yields of 1%.

Table 1 MC-ICP-MS operating conditions

1. ICP conditions
Plasma power	1.2 kW
Torch	Quartz glass torch with a sapphire injector
Plasma Ar gas flow rate	15 l min^−1
Auxiliary Ar gas flow rate	0.80 l min^−1
Nebulizer Ar gas flow rate	0.90 l min^−1

---

2. Desolvator conditions
Desolvator	ARIDUS (CETAC Technologies, USA)
Nebulizer	Micro-flow PFA nebulizer, PFA-20 (ESI, USA), self-aspiration
Flow rate	60 μl min^−1 (observed)
Spray chamber temperature	383 K
Desolvator temperature	433 K
Sweep gas (Ar)	6.5 l min^−1
Nitrogen gas	3 ml min^−1

---

3. Interface
Sampling cone	Made of Ni
Skimmer cone	Made of Ni (X-skimmer)

---

4. Data acquisition conditions
Washing time	800 s after measurement
Uptake time	80 s
Background data integration	4 s for 1 scan, 40 scans in one run
Sample data integration	4 s for 1 scan, 70 scans in one run

---

Eight Faraday cups were used. Isotopes of ¹⁷¹Yb, ¹⁷³Yb, ¹⁷⁵Lu, ¹⁷⁶Hf, ¹⁷⁷Hf, ¹⁷⁸Hf, ¹⁷⁹Hf and ¹⁸⁰Hf were monitored using the L4, L3, L2, L1, C (center), H1, H2 and H3 Faraday cups. The gains of each amplifier were calibrated each day using a constant current source in the mass spectrometer. The sample data was integrated for 4 s, accumulating 70 ratios. After an 800 s wash, 40 background ratios were measured for each sample before the sample measurement. The 100 ng ml⁻¹ JMC 14374 standard solution was measured every fourth sample to check the stability of the mass spectrometer, however, there were no drifts of its isotope ratio over a year or during a day.

To examine the accuracy of the Hf measurement by MC-ICP-MS, 100 ng ml⁻¹ JMC 475 was alternately measured with JMC 14374, which gave 0.282 150 ± 0.000 006 (2σ, n = 9) and 0.282 182 ± 0.000 006 (2σ, n = 12), respectively. Considering the difference between this study and the commonly accepted value of JMC 475 of 0.282 160,¹ a multiple of 1.000 035 was applied to all ¹⁷⁶Hf/¹⁷⁷Hf ratios presented in this study. The value of 0.282 192 is proposed to be the reference value of JMC 14374, which is consistent with the result of 0.282 183 ± 0.000 016 (2σ).¹⁸

Interference correction of Yb and Lu on Hf

Isobaric interferences of ¹⁷⁶Yb and ¹⁷⁶Lu on ¹⁷⁶Hf were corrected during data acquisition by monitoring ¹⁷¹Yb, ¹⁷³Yb and ¹⁷⁵Lu. Mixed solutions of Hf and Yb, and Hf and Lu were made with various ratios up to 0.4 and 0.01, respectively. The Hf isotope ratio of each solution was then measured and interference correction methods were examined. Yb correction, based on the exponential mass discrimination correction^18–20 monitoring a ¹⁷¹Yb/¹⁷³Yb ratio and Lu correction with ¹⁷⁶Lu/¹⁷⁵Lu = 0.026 78, gave the most accurate results. The following interference correction were performed:

¹⁷⁶Hf_corr = ¹⁷⁶Hf_obs − (¹⁷⁶Yb/¹⁷³Yb)_c(M₁₇₆/M₁₇₃)^F(¹⁷³Yb_obs) − (¹⁷⁶Lu/¹⁷⁵Lu)_c¹⁷⁵Lu_obs (1)

F = ln  [(¹⁷¹Yb/¹⁷³Yb)_c/(¹⁷¹Yb_obs/¹⁷³Yb_obs)]/ln (M₁₇₁/M₁₇₃) (2)

where ¹⁷⁶Hf_corr is the interference corrected ¹⁷⁶Hf intensity; ¹⁷⁶Hf_obs, ¹⁷¹Yb_obs, ¹⁷³Yb_obs and ¹⁷⁵Lu_obs are observed intensities at masses of 176, 171, 173 and 175; (¹⁷⁶Yb/¹⁷³Yb)_c and (¹⁷¹Yb/¹⁷³Yb)_c are constant ¹⁷⁶Yb/¹⁷³Yb and ¹⁷¹Yb/¹⁷³Yb ratios in the natural sample; (¹⁷⁶Lu/¹⁷⁵Lu)_c is 0.026 78; F is the mass discrimination correction factor of Yb. Measurements of the Yb standard solution gave (¹⁷⁶Yb/¹⁷³Yb)_c = 0.793 76 ± 0.000 03 (2σ, n = 5) with the normalizing value of (¹⁷¹Yb/¹⁷³Yb)_c = 0.8848,²⁰ which is similar to ¹⁷⁶Yb/¹⁷³Yb = 0.793 81.²⁰ After two-stage column chemistry, Lu/Hf and Yb/Hf ratios are generally <1 × 10⁻⁵ in natural silicate sample analysis, resulting in no significant difference in the ¹⁷⁶Hf/¹⁷⁷Hf ratio before and after the interference correction.

Mass discrimination correction for the spiked sample

The following method was used to calculate the Hf isotope ratio of spiked samples. This method calculates the mass discrimination factor, F, the mole ratio of ¹⁷⁸Hf between the spike and sample, R, and the ¹⁷⁶Hf/¹⁷⁷Hf ratio in the sample by iteration.

The mass discrimination of the sample-spike mixture is corrected using the exponential law:

(^JHf/¹⁷⁷Hf)^corr_mix = (^JHf/¹⁷⁷Hf)_mix^obs(M_J/M₁₇₇)^F (3)

F = ln [P/(¹⁷⁹Hf/¹⁷⁷Hf)_mix^obs]/ln (M₁₇₉/M₁₇₇) (4)

where J = 176 or 178; (^JHf/¹⁷⁷Hf)_mix^obs and (¹⁷⁹Hf/¹⁷⁷Hf)_mix^obs are observed ^JHf/¹⁷⁷Hf and ¹⁷⁹Hf/¹⁷⁷Hf ratios of the sample-spike mixture; (^JHf/¹⁷⁷Hf)^corr_mix is a mass discrimination corrected ^JHf/¹⁷⁷Hf ratio of the mixture; M_J, M₁₇₇ and M₁₇₉ are the weights of the Hf isotopes, ^JHf, ¹⁷⁷Hf and ¹⁷⁹Hf; F is the mass discrimination correction factor; and P is the normalizing ratio, which is equivalent to (¹⁷⁹Hf/¹⁷⁷Hf)^corr_mix.

The normalizing ratio, P is given by the linear combination of the sample and spike Hf isotope ratios using the mole ratio of ¹⁷⁸Hf, R (mole of ¹⁷⁸Hf in spike/mole of ¹⁷⁸Hf in sample) as:

P = [R(¹⁷⁹Hf/¹⁷⁷Hf)_spike/(¹⁷⁸Hf/¹⁷⁷Hf)_spike + (¹⁷⁹Hf/¹⁷⁷Hf)_sample/(¹⁷⁸Hf/¹⁷⁷Hf)_sample ]/[R/(¹⁷⁸Hf/¹⁷⁷Hf)_spike + 1/(¹⁷⁸Hf/¹⁷⁷Hf)_sample] (5)

where (¹⁷⁸Hf/¹⁷⁷Hf)_spike and (¹⁷⁸Hf/¹⁷⁷Hf)_sample are ¹⁷⁸Hf/¹⁷⁷Hf ratios of the spike and sample; and (¹⁷⁹Hf/¹⁷⁷Hf)_spike and (¹⁷⁹Hf/¹⁷⁷Hf)_sample are ¹⁷⁹Hf/¹⁷⁷Hf ratios of the spike and sample, respectively. These ratios are the mass discrimination corrected ratios. (¹⁷⁸Hf/¹⁷⁷Hf)_sample = 0.7325 and (¹⁷⁹Hf/¹⁷⁷Hf)_sample = 1.467 25 were used. The latter was obtained by numerous measurements of JMC 14374 during this study. Similarly, using eqn (3) and R, (¹⁷⁶Hf/¹⁷⁷Hf)^corr_mix and (¹⁷⁸Hf/¹⁷⁷Hf)^corr_mix are expressed as:

(¹⁷⁶Hf/¹⁷⁷Hf)^corr_mix = [R(¹⁷⁶Hf/¹⁷⁷Hf)_spike/(¹⁷⁸Hf/¹⁷⁷Hf)_spike + (¹⁷⁶Hf/¹⁷⁷Hf)_sample/(¹⁷⁸Hf/¹⁷⁷Hf)_sample]/[R/(¹⁷⁸Hf/¹⁷⁷Hf)_spike + 1/(¹⁷⁸Hf/¹⁷⁷Hf)_sample] (6)

(¹⁷⁸Hf/¹⁷⁷Hf)^corr_mix = (R + 1)/[R/(¹⁷⁸Hf/¹⁷⁷Hf)_spike + 1/(¹⁷⁸Hf/¹⁷⁷Hf)_sample] (7)

where (¹⁷⁶Hf/¹⁷⁷Hf)_spike and (¹⁷⁶Hf/¹⁷⁷Hf)_sample are the ¹⁷⁶Hf/¹⁷⁷Hf ratios of the spike and sample, respectively.

The iterative calculation started by assuming F is 1 and R is then calculated from:

R = [1 − (¹⁷⁸Hf/¹⁷⁷Hf)^corr_mix/(¹⁷⁸Hf/¹⁷⁷Hf)_sample ]/[(¹⁷⁸Hf/¹⁷⁷Hf)^corr_mix/(¹⁷⁸Hf/¹⁷⁷Hf)_spike − 1] (8)

which is obtained from eqn (7). The raw ratio of (¹⁷⁸Hf/¹⁷⁷Hf)_mix^obs is initially used for (¹⁷⁸Hf/¹⁷⁷Hf)^corr_mix, and it is then obtained from eqn (3) in subsequent calculations. Using this R, P is calculated after eqn (5), and then F is recalculated using eqn (4). This calculation is repeated until the change of F becomes <10⁻⁶. Finally, using these values for F, P and R, (¹⁷⁶Hf/¹⁷⁷Hf)_sample is obtained from eqn (6).

The mass discrimination corrected spike isotope ratios of (^JHf/¹⁷⁷Hf)_spike (J = 176, 178) and (¹⁷⁹Hf/¹⁷⁷Hf)_spike are determined as follows. We make various mixture of the spike-sample mixtures using the Hf standard solution with a precisely known ¹⁷⁶Hf/¹⁷⁷Hf ratio. The mixtures are then measured, and ¹⁷⁶Hf/¹⁷⁷Hf of the standard solution is calculated using (¹⁷⁶Hf/¹⁷⁷Hf)_spike, (¹⁷⁸Hf/¹⁷⁷Hf)_spike and K which is (¹⁷⁹Hf/¹⁷⁷Hf)_spike. The normalizing calculation is similar to eqn (3) and (4):

(^JHf/¹⁷⁷Hf)_spike = (^JHf/¹⁷⁷Hf)_spike^obs(M_J/M₁₇₇)^F_s (9)

F_s = ln [K/(¹⁷⁹Hf/¹⁷⁷Hf)_spike^obs ]/ln (M₁₇₉/M₁₇₇) (10)

K is determined to minimize the difference between ¹⁷⁶Hf/¹⁷⁷Hf ratios of the standard solution with and without spike. Thus (¹⁷⁶Hf/¹⁷⁷Hf)_spike, (¹⁷⁸Hf/¹⁷⁷Hf)_spike and (¹⁷⁹Hf/¹⁷⁷Hf)_spike were determined to be 0.165554, 2.76843 and 69.4620 for the Hf–Zr mix spike, and 0.145933, 3.00663 and 81.8170 for the pure Hf spike, respectively. This difference in the Hf–Zr mix spike is due to Hf blanks from the Zr spike.

Results and discussion

K _d of Hf, Zr and Ti on UTEVA resin in nitric acid

The distribution coefficient (K_d) of Hf, Zr and Ti on the UTEVA resin in the nitric acid medium was measured. F⁻-free Hf–Zr–Ti solution in H₂O₂ (1% v/v)–HNO₃ mixture prepared by evaporation with HClO₄, was mixed with the UTEVA resin, the concentration of Hf, Zr and Ti on the supernatant was measured by ICP-MS, and K_d was calculated as the ratio of the concentration in the resin (ng ml⁻¹; the volume is the wet resin volume) against the concentration in the solution (ng ml⁻¹).

K _d values of Zr and Hf are shown in Fig. 1. Ti shows no absorption and is therefore not plotted in Fig. 1. Both the K_d values of Hf and Zr decrease as the HNO₃ concentration increases from 1 to 2 mol l⁻¹, then almost stay constant and finally increase between 2 to 10 mol l⁻¹ HNO₃. The large change and difference of K_d in Fig. 1 indicates that mutual separation of Hf and Zr by the UTEVA resin is possible. In order to obtain higher K_d at sample loading, 9 mol l⁻¹ HNO₃ is used for the loading (K_d values are 770 and 890 for Hf and Zr), and 6 mol l⁻¹ HNO₃ is used for Hf and Zr separation (K_d values are 40 and 200 for Hf and Zr) to make the K_d difference between Hf and Zr large. 4 mol l⁻¹ HNO₃ gives the largest difference in K_d between Hf and Zr, but is not employed because breakthrough of Zr during Hf separation is expected when the resin volume is small, such as the 0.15 ml used as this study.

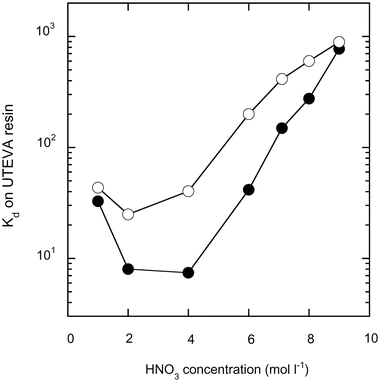Fig. 1 Distribution coefficient (K_d) of Hf (solid circles) and Zr (open circles) on UTEVA resin at various HNO₃ concentrations.

Purification of Hf

Perfect removal of F⁻ is required before attempting to apply ion exchange and extraction resins for the separation of Hf from Zr and Ti, otherwise F⁻ forms stable HfF₆²⁻ and ZrF₆²⁻, resulting in no absorption on TEVA and UTEVA. The first column is effective in reducing the total amount of F⁻ needed to be removed,^2,12,21 otherwise three to four prolonged fuming steps with HClO₄ are required.^8,22

An alternative is to separate Hf through one step column chemistry using flux fusion techniques, instead of using HF sample digestion. However, the blank contribution from the flux reagents are large, resulting in an extremely high procedural Hf blanks of 330 pg by cation exchange resin;²³ 50–100 pg by TEVA resin;²⁴ 55 pg by UTEVA.¹¹

Fig. 2 shows the elution curves of Al (Fe), Ti, Hf (Zr), Nb and W in the first column. As Fe and Zr behaved similarly to Al and Hf, respectively, they are not shown in Fig. 2. 4 ml of sample solution, containing ∼20 mg of the JB-3 basalt was loaded on the resin bed to obtain the elution curves. Measurements were done by ICP-QMS in our laboratory. Elution curves for 1 ml of loading solution are substantially the same. Therefore, 1–4 ml of sample solution can be used. Small amounts of Mo and Ta were detected in the last fraction in Fig. 2, but not in the Hf fraction. Thus the Hf fraction contains Ti, Zr, Hf and small amounts of W. The merit of sample solution with HF is that Mg, Ca, REEs and Th are removed from the solution as insoluble fluorides.^14,25,26

Fig. 2 Elution curves of Al (solid circles), Ti (open circles), Hf (solid squares), Nb (solid triangles) and W (open diamonds) in the first column. The vertical axis is the recovery yield for each element, calculated by normalizing the intensity of each fraction to the total intensity. 0.4 mol l⁻¹ HCl–0.5 mol l⁻¹ HF and 6 mol l⁻¹ HCl–0.5 mol l⁻¹ HF mix acids were used for the wash and the Hf fraction, respectively.

Fig. 3 shows the elution curves of Ti, Zr, Hf and W in the second column. The elution curve was obtained using a multi-element standard solution containing these elements and measured by ICP-QMS. In yield experiments, using 29–38 mg of JB-3 (n = 4), the total Hf recovery was 86–90% (the average is 88%). The Zr yield in the Hf fraction was also measured by ICP-QMS, and found to be 2%. Zr can be better separated by repeating the second column or using a larger resin volume. However, this level of Zr in the Hf fraction is too low to affect Hf isotope ratio measurements by MC-ICP-MS, because it has been shown that Zr/Hf ratios as high as ∼40 in the Hf fraction, which means no separation of Hf from Zr, does not affect the measurement.² If the Hf amount in the loading solution is ample, the last 2 ml fractions can be discarded without significantly affecting the Hf yield, because Hf in these 2 ml solution is <2%. Total blanks, for both the ultrasonic and bomb methods, were similar and were 1–10 pg (the average is 4 pg; n = 12) and therefore negligible. Thus, there is no need for blank correction on the Hf ratio in this study.

Fig. 3 Elution curves of Ti (open circles), Zr (×10, solid triangles), Hf (solid squares) and W (open diamonds) in the second column. The vertical axis is the recovery yield of each element, calculated by normalizing the intensity of each fraction to the total intensity. The yield of Zr is enlarged 10 times, and calculated based on the Zr yield in the Hf fraction of 2%. The sample was loaded in 1 ml of 1% H₂O₂–9 mol l⁻¹ HNO₃ mixture, shown as L. For the wash and the Hf fraction, 9 mol l⁻¹ HNO₃ and 6 mol l⁻¹ HNO₃ were used, respectively.

There are also techniques for Hf purification using other extraction chromatographic resins. Bis(2-ethylhexyl) hydrogen phosphate (HEDHP) is doped on the Teflon powder, and various concentrations of HCl-HF are used to separate Ti, Zr and Hf.^5,6 The Ln-Spec resin, which is a commercially available extraction resin using HEDHP, was used.^7,27 Münker et al.⁷ developed a one-step column separation method for separating Hf and Lu from Ti and Zr, however, the elution volume is extremely large (Hf is collected after 150 ml elution of eluants with the 1 ml resin), resulting in a far larger blank (<100 pg⁷) than in this study. An extraction chromatographic resin, using trioctylmethylammonium chloride (Aliquat 336), is also used (commercially available as TEVA resin) to mutually separate Ti, Zr and Hf,⁸ however, as separation using Aliquat 336 is based on anion exchange, the separation is affected by Fe ions and trace amounts of ClO₄⁻, which is used to remove F⁻. In addition, the elution volumes are large (∼30 ml with 2.1 ml resin).⁸ Recently Connelly et al.²⁸ used a new TODGA resin for the separation of Hf but no Zr separation was performed.

Accuracy and precision of spiked samples

Various concentrations (3.2–103 ng ml⁻¹) of unspiked JMC 14374 were used to determine the precision and reproducibility of the method. The results are shown in Fig. 4. As the Hf concentration, namely, ¹⁷⁷Hf intensity increases from 0.18 to 12 × 10⁻¹¹A, both precision (2σ_m) and reproducibility (2σ) improve from 0.000 025 to 0.000 002 6 and 0.000 038 to 0.000 002 7, respectively. The ¹⁷⁷Hf intensity was used to represent the Hf intensity, because the ¹⁷⁷Hf abundance in the spikes is low, so the ¹⁷⁷Hf intensity is not affected by the amount of spike. When the intensity of ¹⁷⁷Hf is <1 × 10⁻¹¹A, the reproducibility is slightly poorer than the precision, but at higher intensity, the reproducibility becomes similar to the precision.

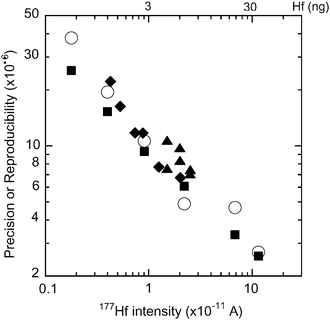Fig. 4 Precision (2σ_m; solid squares) and reproducibility (2σ; open circles) in ¹⁷⁶Hf/¹⁷⁷Hf ratio measurements at various ¹⁷⁷Hf intensities (×10⁻¹¹A). The vertical axis is enlarged 10⁶ times. The solid diamonds and the solid triangles indicate the precision (2σ_m) in the measurement of the spike-standard mixture using the Hf–Zr mix spike and the pure Hf spike, respectively. The scale at the top of the figure indicates the Hf amount (ng) used to obtain the corresponding intensity of the bottom scale.

Various mixtures of the spike and the standard solution were prepared, and the ¹⁷⁶Hf/¹⁷⁷Hf ratios obtained. The difference between the ¹⁷⁶Hf/¹⁷⁷Hf ratio of the mixture that of the standard without spike is plotted in Fig. 5. In this test, the Aldrich Hf standard solution and JMC 14374 were used for the Hf–Zr spike and pure Hf spike solutions, respectively. ¹⁷⁹Hf/¹⁷⁸Hf ratios of the mixture were increased from the natural ratio of 0.499 to as high as 8.9 for the Hf–Zr spike and 10.6 for the pure Hf spike, without producing a systematic shift in the measured ratio, after errors are taken into account. Therefore, it is concluded that measurements of the spiked samples have a similar accuracy to the samples without spike.

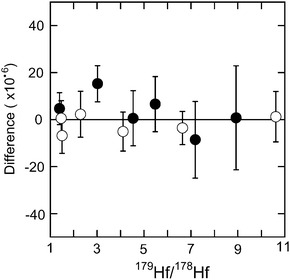Fig. 5 Difference (×10⁻⁶) of ¹⁷⁷Hf/¹⁷⁶Hf ratio of spike-standard mixtures using the Hf–Zr mix spike (solid circles) and the pure Hf spike (open circles) with various mixing ratios from that of the standard without spike. The horizontal axis is the ¹⁷⁹Hf/¹⁷⁸Hf ratio of the mixture. ¹⁷⁹Hf/¹⁷⁸Hf ratios of the standard, Zr–Hf spike and pure Hf spike solutions used in this study are 0.499 233, 25.0907 and 27.2122, respectively. The error bar indicates the precision (2σ_m) of each measurement with the spike.

The precision against the ¹⁷⁷Hf intensity for the spiked samples is also plotted in Fig. 4. The precision of the spiked samples is slightly higher than that of the samples without spikes. The regression line between log [intensity (×10¹¹)] (= X) and log [precision] (= Y) for the sample without spike in Fig. 4 gives a good correlation, with Y = 0.974 − 0.544X and R² = 0.998. Using this equation, deterioration of the precision for the spiked samples from those without spike at the same intensity is calculated to be 5–51% (the average is 25%). However, these levels are not significant, because the reproducibility is generally similar in silicate analyses (see Table 2).

Table 2 ¹⁷⁶Hf/¹⁷⁷Hf in reference materials without and with spike

Sample	^176Hf/^177Hf (without spike)	n	^176Hf/^177Hf (with spike)	n	Ref.
Errors are reproducibility (2σ), and correspond to the last two digits.a The average of results using the Hf–Zr mixed spike and the pure Hf spike.
Basalt
JB-1	0.282963 ± 06	4	0.282967 ± 06	5	0.282965 ± 89^3	0.282951 ± 26^7
					0.282965 ± 11^23	0.282996 ± 30^29
JB-2	0.283244 ± 06	4	0.283243 ± 13^a	5	0.283283 ± 16^29
JB-3	0.283223 ± 07	8	0.283220 ± 06^a	10	0.283245 ± 34^29
BHVO-1	0.283095 ± 06	4	0.283089 ± 05	5	0.283082 ± 14^10	0.283113 ± 05^11
					0.283105 ± 12^24	0.283108 ± 07^28
					0.283109 ± 04^30	0.283102 ± 10^31
					0.283106 ± 13^32
Andesite
JA-1	0.283264 ± 08	4	0.283262 ± 07^a	9	0.282858 ± 10^11	0.283292 ± 57^29
JA-2	0.282875 ± 04	4	0.282873 ± 06	5	0.282874 ± 83^29
JA-3	0.283063 ± 09	3	0.283070 ± 03	5	0.283084 ± 23^29
AGV-1	0.282971 ± 02	4	0.282969 ± 07	5
Peridotite
JP-1	0.282310 ± 13	3	0.282297 ± 24	5

---

The most widely used Hf spike is ¹⁸⁰Hf spike.² However, this method requires the contribution from the spike on ¹⁷⁶Hf to be <4–6 ppm. In contrast, in our method, there is no such limitation, and the calculation method gives accurate values up to a spike contribution on ¹⁷⁶Hf of ∼16%.

Lapen et al.¹⁰ used ¹⁷⁸Hf spike. Although molar spike-to-sample ratio between 0.11–0.62 can be applied, they used a double-normalizing technique, in which mass discrimination of the sample was roughly corrected using a bracketing technique involving a standard Hf solution and a linear mass discrimination law. The spike contribution was then subtracted assuming a linear law. Compared to this calculation method, our method directly applies the exponential law without the assumption of the constant degree of the mass fractionation between the standard and the bracketed sample. David et al.⁹ used ¹⁷⁹Hf spike as this study, but the calculation details are not shown, and reproducibility of actual samples is not as good (2σ error was 0.000 052) as for our method.

¹⁷⁶Hf/¹⁷⁷Hf ratio determination in silicate samples without spike

¹⁷⁶Hf/¹⁷⁷Hf ratios for basalts (JB-1, JB-2, JB-3, BHVO-1) using 25–87 mg, andesites (JA-1, JA-2, JA-3 and AGV-1) using 21–44 mg, and peridotite (JP-1) using 56–66 mg, without spike were repeatedly measured after sample digestion and results are shown in Table 2. The average value of the multiple measurements and reproducibility (2σ) are given in the table. The precision of each measurement (2σ_m) is 0.000 002–0.000 010. Basalts (JB-1, JB-2, JB-3, BHVO-1) and andesites (JA-1, JA-2, JA-3 and AGV-1) measurements show a reproducibility of 0.000 002–0.000 008. JP-1 shows a slightly larger reproducibility of 0.000 013, which may be caused by sample heterogeneity and the relatively low Hf concentration (0.124 μg g⁻¹, see Table 2), resulting in low signal intensity.

¹⁷⁶Hf/¹⁷⁷Hf ratios in other studies^{3,7,10,11,23,24,28–32} are also shown in Table 2. ¹⁷⁶Hf/¹⁷⁷Hf ratios of JB-1 and BHVO-1 in other studies^3,7,23,29 are similar to those obtained in this study. The published ¹⁷⁶Hf/¹⁷⁷Hf ratios for JA-1 are 0.282 858 ± 10¹¹ and 0.283 292 ± 57.²⁹ The former seems to be too high, and the latter is similar to 0.283 264 ± 08 obtained in this study. Although the spread in values of the study of Hanyu et al.²⁹ are large, the data for JB-3, JA-2 and JA-3 are also similar to those of this study. Thus, most data in our study are consistent with those in other studies. However, the Hf purification procedure and the mass spectrometry of this study give better accuracy and precision.

¹⁷⁶Hf/¹⁷⁷Hf ratio and Hf concentration determination in silicate samples with spike

The Hf isotope ratios were also measured with addition of spikes. Hf spike was added to 17–28 mg of basalts, 16–30 mg of andesites, and 46–57 mg of peridotite, Hf was recovered, and the Hf isotope ratio was measured. The average value of the multiple measurements and reproducibility (2σ) are shown in Table 2. There was no significant difference between the Hf isotope ratios obtained whether a mixed Hf–Zr spike was used or a pure Hf spike. The ¹⁷⁶Hf/¹⁷⁷Hf ratio of samples with and without spike are identical. The precision of each measurement (2σ_m) is 0.000 002–0.000 010. The basalt and andesite measurements show reproducibility of 0.000 003–0.000 013, which is also similar to that without spike. JP-1 shows larger reproducibility of 0.000 024 for its unspiked measurement.

Hf concentrations simultaneously determined by MC-ICP-MS using ID, are shown in Table 3. The analytical results are similar to those obtained in other studies as shown in Table 3. Tanaka et al.²⁶ examined the spike-sample equilibrium of Hf in various composition, and concluded that they are mixed well in the digestion procedure employed in this study. The reproducibility of most measurements is 0.1–0.7% (mean 0.4%) except for JP-1, which may also be caused by sample heterogeneity and low signal intensity.

Table 3 Concentration of Hf (μg g⁻¹) in silicate reference materials

	Concentration	Reproducibility (%)	n	Ref.
a The average of results using the Hf–Zr mixed spike and the pure Hf spike.
Basalt
JB-1	3.48	0.3	5	3.18,^14 3.42,^15 3.31^33
JB-2^a	1.47	0.4	5	1.45,^14 1.45,^15 1.49^33
JB-3^a	2.68	0.6	10	2.56,^14 2.66,^15 2.67^33
BHVO-1	4.39	0.4	5	4.35,^14 4.42,^15 4.484,^28 4.38,^34 4.53,^35 4.26^37
Andesite
JA-1^a	2.47	0.7	9	2.47,^14 2.45,^15 2.42,^33 2.53^36
JA-2	2.96	0.4	5	2.91,^14 2.92,^15 2.86^33
JA-3	3.21	0.1	5	3.18,^14 3.18,^15 3.42^33
AGV-1	5.10	0.2	5	5.3,^14 5.10,^15 5.1,^34 4.94^37
Peridotite
JP-1	0.124	8.1	5	0.12,^14 0.124,^15 0.2^33

---

Conclusion

A new chemical procedure for purifying Hf from other elements including Zr in silicate materials with low blank has been developed. This separation method was applied to precise determination of ¹⁷⁶Hf/¹⁷⁷Hf by MC-ICP-MS, resulting in reproducibility of less than 0.000 010. A simultaneous determination method for ¹⁷⁶Hf/¹⁷⁷Hf and Hf concentration was also developed using ¹⁷⁹Hf spike, which gave similar analytical results to those without spike.

Acknowledgements

We are grateful to T. Moriguti, T. Yokoyama, H. Kitagawa, A. Ishikawa and all other members of PML for analytical help and maintaining the clear laboratory. We also thank to I. Campbell for improving the manuscript and N. Belshaw who kindly donated us the precious JMC 475 solution. This study was supported by the Ministry of Education, Culture, Sports, Science and Technology to A. M. and E. N. and by the program of the “Center of Excellence for the 21^st Century in Japan”.

References

1. G. M. Nowell, P. D. Kempton, S. R. Noble, J. G. Fitton, A. D. Saunders, J. J. Mahoney and R. N. Taylor, Chem. Geol., 1998, 149, 211–233.
2. J. Blichert-Toft, C. Chauvel and F. Albarede, Contrib. Mineral. Petrol., 1997, 127, 248–260.
3. P. J. Patchett and M. Tatsumoto, Contrib. Mineral. Petrol., 1980, 75, 263–267.
4. K. M. Barovich, B. L. Beard, J. B. Cappel, C. M. Johnson, T. K. Kyser and B. E. Morgan, Chem. Geol., 1995, 121, 303–308.
5. H. Fujimaki, M. Tatsumoto and K. J. Aoki, J. Geophys. Res., [Atmos.], 1984, 89, 662–672.
6. V. J. M. Salters, Anal. Chem., 1994, 66, 4186–4189.
7. C. Münker, S. Weyer, E. Scherer and K. Mezger, Geochem. Geophys. Geosyst., 2001 , Paper No 2001GC000183.
8. X. J. Yang and C. Pin, Anal. Chem., 1999, 71, 1706–1711.
9. K. David, J. L. Birck, P. Telouk and C. J. Allègre, Chem. Geol., 1999, 157, 1–12.
10. T. J. Lapen, N. J. Mahlen, C. M. Johnson and B. L. Beard, Geochem. Geophys. Geosyst., 2004, 5, Q01010,  DOI:10.1029/2003GC000582.
11. B. Le Fèvre and C. Pin, Anal. Chem., 2001, 73, 2453–2460.
12. A. Makishima, X.-K. Zhu, N. S. Belshaw and R. K. O’Nions, J. Anal. At. Spectrom., 2002, 17, 1290–1294.
13. E. Nakamura, A. Makishima, T. Moriguti, K. Kobayashi, C. Sakaguchi, T. Yokoyama, R. Tanaka, T. Kuritani and H. Takei, Inst. Space Astron. Sci. Rep., 2003, SP No. 16, 49–101.
14. A. Makishina, E. Nakamura and T. Nakano, Geostand. Newsl., 1999, 06, 7–20.
15. Y. H. Lu, A. Makishima and E. Nakamura, Chem. Geol., 2006 DOI:10.1016/j.chemgeo.2006.08.007.
16. A. Makishima and E. Nakamura, Geostand. Newsl., 1997, 21, 307–319.
17. A. Makishima, E. Nakamura and T. Nakano, Anal. Chem., 1997, 69, 3754–3759.
18. P. Xu, F.-Y. Wu, L.-W. Xie and Y.-H. Yang, Chinese Sci. Bull., 2004, 49, 1642–1648.
19. N.-C. Chu, R. N. Taylor, V. Chavagnac, R. W. Nesbitt, R. M. Boella, J. A. Milton, C. R. German, G. Bayon and K. Burton, J. Anal. At. Spectrom., 2002, 17, 1567–1574.
20. I. Segal, L. Halicz and I. T. Platzner, J. Anal. At. Spectrom., 2003, 18, 1217–1223.
21. J. Blichert-Toft, Geostand. Newsl., 2003, 25, 41–56.
22. X. J. Yang and C. Pin, Analyst, 2000, 125, 453–457.
23. I. C. Kleinhanns, K. Kreissig, B. S. Kamber, T. Meisel, T. E. Nägler and J. D. Kramers, Anal. Chem., 2002, 74, 67–73.
24. M. Bizzarro, J. A. Baker and D. Ulfbeck, Geostand. Newsl., 2003, 27, 133–145.
25. T. Yokoyama, A. Makishima and E. Nakamura, Chem. Geol., 2001, 181, 1–12.
26. R. Tanaka, A. Makishima, H. Kitagawa and E. Nakamura, J. Anal. At. Spectrom., 2003, 18, 1458–1463.
27. Y. Nebel-Jacobsen, E. E. Scherer, C. Münker and K. Mezger, Chem. Geol., 2005, 220, 105–120.
28. J. N. Connelly, D. G. Ulfbeck, K. Thrane, M. Bizzarro and T. Housh, Chem. Geol., 2006, 233, 126–136.
29. T. Hanyu, S. Nakai and R. Tatsuta, Geochem. J., 2005, 39, 83–90.
30. J. Blichert-Toft, F. Frey and F. Albarède, Science, 1999, 285, 879–882.
31. D. Ulfbeck, J. Baker, T. Waight and E. Krogstad, Talanta, 2003, 59, 365–373.
32. J. D. Vervoort, P. J. Patchett, U. Söderlund and M. Baker, Geochem. Geophys. Geosyst., 2004, Q11002,  DOI:10.1029/2004GC00721 , ISSN: 1525–2027.
33. N. Imai, S. Terashima, S. Itoh and A. Ando, Geochem. J., 1995, 29, 91–95.
34. K. Govindaraju, Geostand. Newsl., 1994, 18, 1–158.
35. X. J. Yang and C. Pin, Anal. Chim. Acta, 2002, 458, 375–386.
36. B. Le Fèvre and C. Pin, Geostand. Newsl., 2002, 26, 161–170.
37. M. Willbold and K. P. Jochum, Geostand. Geoanal. Res., 2005, 29, 63–82.

---