Spectroscopy and potential energy surface of the H2–CO2 van der Waals complex: experimental and theoretical studies†‡
Lin
Wang
ab,
Minghui
Yang
a,
A. R. W.
McKellar
c and
Dong H.
Zhang
d
aState Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan, 430071, China. E-mail: yangmh@wipm.ac.cn
bGraduate School of Chinese Academy of Sciences, Beijing, 100039, China
cSteacie Institute for Molecular Sciences, National Research Council of Canada, Ottawa, Ontario, Canada K1A 0R6. E-mail: robert.mckellar@nrc-cnrc.gc.ca
dCenter for Theoretical & Computational Chemistry and State Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, 457 Zhongshan Road, Dalian, Liaoning 116023, China
First published on 28th November 2006
Abstract
A 4-D ab initio potential energy surface is calculated for the intermolecular interaction of hydrogen and carbon dioxide, using the CCSD(T) method with a large basis set. The surface has a global minimum with a well depth of 212 cm−1 and an intermolecular distance of 2.98 Å for a planar configuration with both the O–C–O and H–H axes perpendicular to the intermolecular axis. Bound state calculations are performed for the H2–CO2 van der Waals complex with H2 in both the para and ortho spin states, and the binding energy of paraH2–CO2 (50.4 cm−1) is found to be significantly less than that of orthoH2–CO2 (71.7 cm−1). The surface supports 7 bound intermolecular vibrational states for paraH2–CO2 and 19 for orthoH2–CO2, and the lower rotational levels with J ≤ 4 follow an asymmetric rotor pattern. The calculated infrared spectrum of paraH2–CO2 agrees well with experiment. For orthoH2–CO2, the ground state rotational levels allowed by symmetry are found to have (Ka, Kc) = (even, odd) or (odd, even). This somewhat unexpected fact enables the previously observed experimental spectrum to be assigned for the first time, in good agreement with theory, and indicates that the orientation of hydrogen is perpendicular to the intermolecular axis in the ground state of the orthoH2–CO2 complex.
I. Introduction
Carbon dioxide, nitrous oxide, and carbonyl sulfide form an isovalent “CO2 family” of linear molecules. The van der Waals (vdW) complexes containing these molecules have received much attention in both experimental and theoretical investigations.1–8 It is found that the vdW complexes containing the CO2 family have similar intermolecular interactions and spectra, as illustrated, for example, by He–CO2,6 He–N2O,7 and He–OCS.8 These three complexes all have a T-shaped structure and a rotational energy level structure which can be explained with an asymmetric rotor Hamiltonian, at least for lower energies. Ab initio potential energy surfaces (PES) for these complexes have been constructed and tested by bound state calculations, usually including two degrees of freedom (the vdW stretch and bend) with the linear molecule (CO2, N2O, OCS) taken as a rigid rotor. In general the experimental rotational spectra could be explained with the accuracy of about 10−2 cm−1 in these calculations. More accurate models have also been developed to account for the other experimental data, for example, Xie et al.9 have considered the asymmetric vibrational mode of N2O in the Hamiltonian to explain the blue shift of the band origin for He–N2O.vdW complexes containing hydrogen molecules are of particular interest, in part due to hydrogen’s cosmic abundance and the possibility of complex formation in interstellar space.10–19 Recently, McKellar and co-workers have reported the infrared spectra of vdW complexes formed by the CO2 family and hydrogen. For complexes containing OCS20 and N2O21 attached to the experimentally accessible hydrogen species (paraH2, orthoH2, orthoD2, paraD2, and HD), rotation-vibration spectra were recorded in the region of the asymmetric stretch mode of the triatomic molecules and fitted to a model Hamiltonian. It was found that all these spectra corresponded to those of T-shaped asymmetric rotors with predominantly a-type transitions (ΔKa = 0) (since the a inertial axis is approximately parallel to the O–C–S or N–N–O molecular axis). Pure rotational microwave spectra have also been obtained for H2–OCS.22 To date, the only theoretical study of these systems was reported by Paesani and Whaley for H2–OCS.15 In their work, a PES was calculated with explicit dependence on the OCS ν3 vibrational mode, and predicted transition frequencies agreed with the observed values within 0.09 cm−1 or better. Qualitative aspects of the energy level patterns of weakly bound complexes relevant to systems containing H2 were discussed some time ago in a paper by Nesbitt and Naaman.23
Due to the spin statistics of the indistinguishable 16O nuclei, half the rotational energy levels of CO2 are missing in the observed spectra of the normal isotope. This is a key difference between complexes containing CO2 and those containing OCS or N2O. In the recent experimental study of paraH2–CO2,24 8 transitions were observed for the 12C16O2 complex and 10 transitions for 13C16O2 and 12C18O2. These were fitted using an asymmetric rotor Hamiltonian, with results that were very similar to paraH2–OCS20 and –N2O.21 However, the orthoH2–CO2 spectrum was found to be completely different, and no reasonable assignments could be made. It was therefore inferred that orthoH2–CO2 must be unlike orthoH2–OCS and orthoH2–N2O, whose spectra resemble the corresponding paraH2 complex. To our knowledge there is no modern H2–CO2 PES available in the literature for rovibrationally bound state calculations. Theoretical studies based on a 4-D PES are clearly desirable to help explain the ‘mystery’ of the orthoH2–CO2 infrared spectrum.24 The construction of such a potential surface and bound state calculations for H2–CO2 form the main object of the present paper, which also includes further experimental data on orthoH2–CO2.
This paper is organized as follows. The theoretical determination of the ab initio PES and bound state energy levels are described in section II. Details of the experimental infrared spectra of H2–CO2 are reported and compared with theory in section III. Finally, a discussion and brief conclusions are presented in sections IV and V.
II. Ab initio potential energy surface and bound state calculations
A. Ab initio PES
The 4-D intermolecular PES is described by the Jacobi coordinate system (R, θ1, θ2, φ). The molecular axes of the linear molecules H2 and CO2 are denoted as r1 and r2, respectively. As shown in Fig. 1, R is the vector connecting the H2 and CO2 centers of mass, θ1 is the enclosed angle between R and r1, θ2 is the enclosed angle between R and r2, and φ is the torsional angle between the (R − r1) and (R − r2) planes. The H2 and CO2 molecules are approximated as rigid rotors, with their bond lengths fixed at the vibrationally averaged values of 0.7666 17 and 1.1615 6 Å, respectively. | ||
| Fig. 1 Jacobi coordinates for the H2–CO2 complex. R denotes the distance between the H2 and CO2 centers of mass, θ1 (θ2) is the enclosed angle between the R vector and the H2 (CO2) axis, and φ denotes the torsion angle of the H2 axis anticlockwise from the plane formed with the R vector and CO2 axis. | ||
The intermolecular potential energy for a given geometry of the H2–CO2 complex is calculated using the supermolecular approach, with the potential energy expressed as the difference between the energy of the complex, E(H2–CO2) and the sum of the monomer energies, E(H2) + E(CO2). The full counterpoise method25 is applied for basis set superposition error (BSSE) correction. Molecular energies are calculated with the CCSD(T) method,26 using Dunning’s cc-pVQZ basis sets27 with g functions omitted. Tao and Pan’s 3s3p2d bond functions28 are also used in this work , and this bond function (Bf) has proven to be effective in the calculation of intermolecular interactions. By comparing with other larger basis sets (avqz + Bf, v5z(f) + Bf), the current one has been chosen by considering the balance of the accuracy and the cost, with an estimated error of 3% for the well depth. All the calculations are carried out using the Molpro 2002.6 software package.29
The intermolecular potential energies are calculated for geometries with 24 grid points of intermolecular distance ranging from 2.2 to 8.0 Å, with angles θ1 and θ2 varied from 0 to 180° in steps of 15°, and with angle φ varied from 0 to 360° in steps of 30°. By considering symmetry, a total of 6360 discrete data points for the intermolecular potential energy are obtained. The PES is constructed by a combined scheme using the cubic spline interpolation method for the angular part, (θ1, θ2, φ), and the interpolating moving least square (IMLS) method30,31 for the intermolecular distance. A Fortran program to generate the intermolecular potential, and the original ab initio data, are available as supplementary material (see ESI‡).
This potential has a global minimum with a well depth of −211.932 cm−1 at the configuration R = 2.978 Å, θ1 = 90.0°, θ2 = 90.0°, φ = 0.0°, with an equivalent minimum at φ = 180.0°. Saddle points are found between the two global minima corresponding to the configuration R = 2.978 Å, θ1 = 90.0°, θ2 = 90.0°, and φ = 90.0° or φ = 270.0°, with a barrier height of 89.386 cm−1. The H2–CO2 PES appears to be similar to that of H2-OCS,15 which also has a co-planar global minimum with R = 3.23 Å, θ1 = 87.0°, θ2 = 109.4°, φ = 0.0°, and a well depth of 201.67 cm−1.
B. Methodology of the bound state calculations
By approximating the linear molecules H2 and CO2 as rigid rotors, the Hamiltonian of the H2–CO2 system may be written as32,33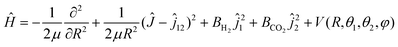 | (1) |
The wave function is expanded as a linear combination of products of the intermolecular distance and angular basis functions,
 | (2) |
 | (3) |
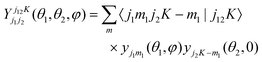 | (4) |
The ARPACK software package34 is applied to solve the eigenvalues and eigenfunctions of the bound states. By considering the symmetry of (ε, j1, j2), there exist 8 symmetry blocks: (+1, para, even), (+1, para, odd), (−1, para, even), (−1, para, odd), (+1, ortho, even), (+1, ortho, odd), (−1, ortho, even), (−1, ortho, odd). Each block can be solved separately. A total of 55 sine basis functions ranging from 3.0 to 15.0 Bohr are used for the R basis set expansion. The size of the rotational basis functions is controlled by the parameters, j1max = 5, j2max = 17, and the energy levels involved in spectroscopic calculation show convergence to 0.001 cm−1 with this basis set.
C. Rovibrational energy levels
The calculated intermolecular vibrational energy levels of para and orthoH2–CO2 are listed in Table 1. As our calculated results showed that the rotation of the H2 in the complex is completely dominated by j1 = 0 and 1 in the para and ortho species, respectively, the intermolecular vibrational energy levels could be labeled with the indices (ns, nb, j1, pm1) by analyzing the wavefunction, where pm1 is a composite index giving the parity of the state and the value of m1, which is the projection of j1 (the H2 angular momentum) on the vector R. When the complex is in its lowest energy equilibrium configuration, R is perpendicular to the O–C–O axis and corresponds to the b inertial axis of the asymmetric rotor model (see below). The quantum number ns denotes the vdW stretching mode. In place of j2 (the CO2 rotation), which is not a very good quantum number, we use a bending label nb, similar to an atom–diatom complex like CO2–He.2 Then for paraH2–CO2 there exist 7 bound vibrational states, labeled as (ns,nb,0,0) in Table 1, with the lowest state bound by 50.383 cm−1, corresponding to a total zero-point energy of 161.549 cm−1. This zero-point energy is over half of the global well depth, similar to other H2-containing vdW complexes.15 Most states correspond to excitations of nb which have relatively low energy consistent with the small rotational constant of CO2. It is interesting to note that label nb has the same parity (even or odd) as j2. The highest vibrational state is assigned to the first excited vdW stretch mode, giving an intermolecular stretching frequency of 47 cm−1.| Even +1 | Even −1 | Odd +1 | Odd −1 |
|---|---|---|---|
| ParaH2–CO2 | |||
| −50.383 (0,0,0,0) | −28.316 (0,1,0,0) | ||
| −23.544 (0,2,0,0) | −20.235 (0,3,0,0) | ||
| −15.116 (0,4,0,0) | −7.107 (0,5,0,0) | ||
| −3.335 (1,0,0,0) | |||
| OrthoH2–CO2 | |||
| −46.472 (0,1,1,1) | −24.993 (0,1,1,−1) | −71.704 (0,0,1,1) | −51.068 (0,0,1,−1) |
| −35.693 (0,3,1,1) | −9.226 (1,1,1,−1) | −37.837 (0,2,1,0) | −16.172 (1,0,1,−1) |
| −25.547 (0,3,1,0) | −31.789 (0,2,1,1) | −4.991 (0,2,1,−1) | |
| −18.368 (0,1,1,0) | −19.099 (1,0,1,0) | ||
| −9.725 (0,5,1,0) | −12.831 (0,4,1,1) | ||
| −5.742 (1,1,1,1) | −7.137 (1,0,1,1) | ||
| −1.786 (1,1,1,0) | −1.215 (1,2,1,0) | ||
For orthoH2–CO2, the vibrational states dominated by (j1 = 1,m1 = 0) are labeled (ns,nb,1,0), and those dominated by (j1 = 1,m1 = ±1) labeled (ns,nb,1,1) for parity = +1 and (ns, nb, 1, −1) for parity = −1, respectively. We note that the ground vibrational state (0, 0, 1, 1) belongs to the (odd, +1) symmetry block, so that nb and j2 have different parity in the ortho species. Labeling of the excited orthoH2–CO2 intermolecular modes is difficult since they are strongly anharmonic and mixed, so only the lower energy orthoH2–CO2 states in Table 1 could be assigned with complete certainty. There are 19 bound intermolecular vibrational states for orthoH2–CO2, almost 3 times more than for the para species. It is important to recall that orthoH2–CO dissociates into the jH2 = 1 channel, so that all states with energies lower than 2BH2 = 118.644 cm−1 are bound. The orthoH2–CO2 ground state is bound by 71.7 cm−1, and so is considerably more stable than that of paraH2–CO2, as also observed in many other vdW complexes containing hydrogen.
Since the available infrared spectra of H2–CO2 involve the CO2ν3 asymmetric stretch mode, rotational energy levels of the complex with CO2 in both the ground state and the v3 state were calculated (differing in the value used for BCO2). Rovibrational energy levels for J > 0 were calculated and it was found that no bound states exist with J beyond 12 and 14 for the para and ortho species, respectively. Tables 2 and 3, for paraH2- and orthoH2–CO2, list all the calculated levels with J = 0 to 4 which lie within 20 cm−1 of the lowest level. More complete lists of calculated rovibrational levels up to dissociation are given in supplementary Tables S1 and S2 (see ESI ‡).
| J | v 3 | Even +1 | Even −1 | Odd +1 | Odd −1 |
|---|---|---|---|---|---|
| 0 | 0 | −50.383 (000) | |||
| 1 | 0 | −49.385 (111) | −49.230 (110) | −49.727 (101) | |
| 2 | 0 | −48.456 (202) | −47.768 (211) | −48.232 (212) | −46.747 (221) |
| 2 | 0 | −46.706 (220) | |||
| 3 | 0 | −44.804 (322) | −46.523 (313) | −45.604 (312) | −46.638 (303) |
| 3 | 0 | −42.702 (331) | −42.695 (330) | −44.616 (321) | |
| 4 | 0 | −44.324 (404) | −42.782 (413) | −44.278 (414) | −42.238 (423) |
| 4 | 0 | −41.745 (422) | −40.047 (431) | −40.093 (432) | −37.245 (441) |
| 4 | 0 | −37.244 (440) | |||
| 0 | 1 | −50.402 (000) | |||
| 1 | 1 | −49.405 (111) | −49.252 (110) | −49.757 (101) | |
| 2 | 1 | −48.487 (202) | −47.801 (211) | −48.259 (212) | −46.770 (221) |
| 2 | 1 | −46.730 (220) | |||
| 3 | 1 | −44.840 (322) | −46.660 (313) | −45.652 (312) | −46.679 (303) |
| 3 | 1 | −42.727 (331) | −42.721 (330) | −44.657 (321) | |
| 4 | 1 | −44.375 (404) | −42.849 (413) | −44.327 (414) | −42.292 (423) |
| 4 | 1 | −41.811 (422) | −40.094 (431) | −40.138 (432) | −37.273 (441) |
| 4 | 1 | −37.272 (440) |
| J | v 3 | Even +1 | Even −1 | Odd +1 | Odd −1 |
|---|---|---|---|---|---|
| 0 | 0 | −71.705 (000) | |||
| 1 | 0 | −70.546 (110) | −71.082 (101) | −70.663 (111) | |
| 2 | 0 | −69.536 (212) | −67.932 (221) | −69.860 (202) | −69.188 (211) |
| 2 | 0 | −67.912 (220) | |||
| 3 | 0 | −67.162 (312) | −68.072 (303) | −66.078 (322) | −67.860 (313) |
| 3 | 0 | −63.689 (330) | −65.976 (321) | −63.691 (331) | |
| 4 | 0 | −65.640 (414) | −63.616 (423) | −65.764 (404) | −64.491 (413) |
| 4 | 0 | −61.200 (432) | −57.926 (441) | −63.334 (422) | −61.185 (431) |
| 4 | 0 | −57.927 (440) | |||
| 0 | 1 | −71.732 (000) | |||
| 1 | 1 | −70.576 (110) | −71.114 (101) | −70.691 (111) | |
| 2 | 1 | −69.571 (212) | −67.963 (221) | −69.899 (202) | −69.228 (211) |
| 2 | 1 | −67.943 (220) | |||
| 3 | 1 | −67.215 (312) | −68.120 (303) | −66.120 (322) | −67.905 (313) |
| 3 | 1 | −63.722 (330) | −66.021 (321) | −63.724 (331) | |
| 4 | 1 | −65.697 (414) | −63.674 (423) | −65.824 (404) | −64.561 (413) |
| 4 | 1 | −61.250 (432) | −57.961 (441) | −63.400 (422) | −61.235 (431) |
| 4 | 1 | −57.961 (440) |
Due to the interchange symmetry of the indistinguishable zero-spin 16O nuclei, the normal isotope of carbon dioxide, 12C16O2, can only have even values of the angular momentum, j2, in its ground vibrational state. The same is true for other symmetric isotopomers containing 16O or 18O (e.g.13C16O2 or 12C18O2), but not for asymmetric forms (e.g.16O12C18O) or for symmetric 17O forms (e.g.17O12C17O). According to our classification, the allowed symmetry blocks (for ν3 = 0) in Tables 1–3 are therefore: (ε, j1, j2) = (+1, para, even), (−1, para, even), (+1, ortho, even), (−1, ortho, even). Analyzing the labels of the paraH2–CO2 rotational levels in Tables 2 and 3, it is found as expected that the allowed rotational levels have (Ka, Kc) = (even, even) or (odd, odd). For orthoH2–CO2 the allowed levels are however found to be (Ka, Kc) = (even, odd) or (odd, even) for the ground state. Thus the lowest allowed level for orthoH2–CO2 is JKaKc = 101, rather than 000, which is forbidden. This turns out to be the key to assigning the orthoH2–CO2 spectrum, as discussed below. When the CO2 asymmetric stretch vibration, ν3, is excited, odd values of j2 are required. In this case, the allowed blocks in Tables 1–3 become: (ε, j1, j2) = (+1, para, odd), (−1, para, odd), (+1, ortho, odd), (−1, ortho, odd).
III. Experimental results and comparison with theory
The only available high resolution spectra of the weakly-bound complex H2–CO2 were recently obtained24 in the mid-infrared region of the CO2ν3 fundamental band, around 2350 cm−1. This experiment was performed using a pulsed supersonic jet expansion and a rapid-scan tunable diode laser probe.35 Both paraH2–CO2 and orthoH2–CO2 transitions were observed, but only the former were analyzed because the correct assignments for the orthoH2 species were not evident. The present theoretical results now enable the orthoH2 assignments to be made successfully, as shown below in section B. However, first we compare the experimental and theoretical results for paraH2–CO2 in the following section.A. paraH2–CO2
A total of 8 transitions were experimentally observed and assigned24 for paraH2–12C16O2, as listed here in the first two columns of Table 4. In order to obtain theoretical values for these transitions from the energy levels in Table 2, we used the expression | (5) |
| J′Ka′Kc′–J″Ka″Kc″ | Observed | Calculated | Obs-Calc |
|---|---|---|---|
| a The calculated band origin was established by fixing the calculated 101 − 000 transition at the observed value (see text). | |||
| 10 1–00 0 | 2349.599 | 2349.599 | —a |
| 11 0–11 1 | 2349.094 | 2349.099 | −0.005 |
| 212–11 1 | 2350.096 | 2350.092 | +0.004 |
| 10 1–20 2 | 2347.664 | 2347.672 | −0.008 |
| 30 3–20 2 | 2350.754 | 2350.744 | +0.010 |
| 11 0–21 1 | 2347.480 | 2347.482 | −0.002 |
| 31 2–21 1 | 2351.082 | 2351.082 | −0.000 |
| 41 4–31 3 | 2351.173 | 2351.162 | +0.011 |
Specifically, we use the JKaKc = 101–000 transition to determine a value of E0 = 2348.966 cm−1 for the para spectrum.36 The third and fourth columns of Table 4 show the resulting theoretical transitions and the deviations between experiment and theory for paraH2–CO2. These deviations are mostly within 0.01 cm−1, with a maximum discrepancy of 0.011 cm−1 for the transition 414–313. This excellent agreement shows that our ab initio PES accounts very successfully for the paraH2–CO2 spectrum.
In order to produce spectroscopic parameters from the theoretical levels, we fit them with the same Hamiltonian used for the experimental data, a Watson asymmetric rotor expression employing the A-type reduction in the Ir representation,2
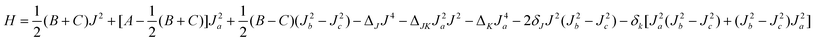 | (6) |
| paraH2–12C16O2 | orthoH2 –12C16O2 | |||
|---|---|---|---|---|
| Experiment | Theory | Experiment | Theory | |
| a Quantities in parentheses correspond to 1 σ from the least-squares fits. b Some parameters were fixed in the fits because of limited data (see text and ref. 24). | ||||
| v 0 | 2348.9452(1) | 2349.0478(2) | ||
| A″ | 0.7558(14) | 0.749 106(39) | 0.7940(55) | 0.789 999(93) |
| B″ | 0.403 96(8) | 0.406 477(57) | 0.373 85(10) | 0.369 33(15) |
| C″ | 0.253 70(7) | 0.249 485(49) | 0.251 86(11) | 0.252 41(13) |
| Δ″K | 0.000 011b | −0.000 518(5) | 0.0015(14) | −0.000 114(12) |
| Δ″JK | 0.002 03(9) | 0.000 969(6) | 0.000 25(2) | 0.000 487(15) |
| Δ″J | −0.000 047(4) | 0.000 016(2) | 0.000 051(2) | −0.000 016(4) |
| δ″K | 0b | 0.000 638(9) | 0.001 59(4) | 0.000 174(34) |
| δ″J | 0b | 0.000 004(1) | −0.000 003(2) | −0.000 006(3) |
| A′ | 0.7558b | 0.749 127(38) | 0.7935(149) | 0.790 061(92) |
| B′ | 0.401 48b | 0.403 202(57) | 0.370 90(11) | 0.366 64(15) |
| C′ | 0.252 27b | 0.248 240(48) | 0.250 47(12) | 0.251 13(14) |
| Δ′K | 0.000 011b | −0.000 508(5) | 0.0015b | −0.000 107(12) |
| Δ′JK | 0.002 03b | 0.000 959(6) | 0.000 25b | 0.000 481(15) |
| Δ′J | −0.000 047b | 0.000 015(1) | 0.000 051b | −0.000 015(4) |
| δ′K | 0b | 0.000 632(9) | 0.001 59b | 0.000 173(35) |
| δ′J | 0b | 0.000 004(1) | −0.000 003b | −0.000 006(3) |
B. orthoH2–CO2
Transitions due to orthoH2–CO2 were clearly observed in the experiments of ref. 24 by recording spectra both with normal H2 (75% ortho, 25% para) in the supersonic expansion gas mix, as well as samples with enriched paraH2 (>99% para). As noted previously for other complexes,20,21 normal H2 gave predominantly orthoH2–CO2 transitions, while the enriched paraH2 sample gave both the para and ortho complexes. This dominance of orthoH2 complexes occurs due to their larger binding energy relative to the corresponding paraH2 complex (e.g. 71.7 vs. 50.4 cm−1 for orthoH2–CO2vs. paraH2–CO2 in the present calculation). However, the orthoH2–CO2 transitions were not rotationally assigned in ref. 24 because they seemed to have a completely different pattern than that observed for paraH2–CO2.The key to the correct assignment is found in the present calculations. Tables 2 and 3 clearly indicate that the allowed ν3 = 0 levels (in the even, +1 and even −1 columns) have (Ka, Kc) = (even, odd) and (odd, even) for orthoH2 as compared to (even, even) and (odd, odd) for paraH2. It is thus no wonder that the orthoH2–CO2 spectrum is different: its transitions are the very ones which are missing from the paraH2–CO2 spectrum (and vice versa)! With this revelation, the observed orthoH2–CO2 transitions can be assigned easily, as given in Table 6. For example, the two most prominent observed lines, at 2350.266 and 2350.399 cm−1, are due to the JKaKc = 202–101 and 211–110 transitions, respectively. Table 6 includes 10 lines from ref. 24, plus 6 additional weaker lines which were located and assigned with the help of the present calculations. One previously reported24 line (at 2349.460 cm−1) still cannot be assigned, and is likely due to something other than H2–CO2. Part of the orthoH2–CO2 spectrum is illustrated here in Fig. 2.
 | ||
| Fig. 2 Part of the observed spectrum of orthoH2–12C16O2 complexes, showing 7 of the 16 assigned transitions. The line marked ‘p’ is due to paraH2–CO2, the line marked ‘h’ is due to He–CO2, and the remaining weak lines are due to carbon dioxide dimers, (CO2)2. | ||
| J′Ka′Kc′–J″Ka″Kc″ | Observed | Calculated | Obs-Calc |
|---|---|---|---|
| a The calculated band origin was established by fixing the calculated 000–101 transition at the observed value (see text). | |||
| 0 0 0–10 1 | 2348.423 | 2348.423 | —a |
| 20 2–10 1 | 2350.266 | 2350.256 | +0.010 |
| 11 1–11 0 | 2348.930 | 2348.927 | +0.003 |
| 21 1–11 0 | 2350.399 | 2350.391 | +0.008 |
| 11 1–21 2 | 2347.912 | 2347.918 | −0.006 |
| 21 1–21 2 | 2349.381 | 2349.381 | +0.000 |
| 31 3–21 2 | 2350.717 | 2350.704 | +0.013 |
| 22 0–22 1 | 2349.060 | 2349.061 | −0.001 |
| 32 2–22 1 | 2350.894 | 2350.884 | +0.010 |
| 20 2–30 3 | 2347.236 | 2347.246 | −0.010 |
| 32 2–30 3 | 2351.008 | 2351.024 | −0.016 |
| 40 4–30 3 | 2351.339 | 2351.320 | +0.019 |
| 21 1–31 2 | 2346.999 | 2347.007 | −0.008 |
| 41 3–31 2 | 2351.688 | 2351.674 | +0.014 |
| 42 2–32 1 | 2351.644 | 2351.648 | −0.004 |
| 31 3–41 4 | 2346.795 | 2346.808 | −0.013 |
Calculated values for the orthoH2–CO2 transition frequencies are given in Table 6. These were determined in a similar manner to paraH2–CO2, with the prominent JKaKc = 000–101 line taken as the standard to establish the vibrational origin. The agreement between observed and calculated frequencies, though slightly worse than for the para species (Table 4), is still excellent, with a maximum deviation of 0.019 cm−1. The parameters resulting from asymmetric rotor fits to the observed spectrum and to the calculated energy levels are given in the last two columns of Table 5 for orthoH2–CO2. In the fit to experiment, the upper and lower state centrifugal distortion parameters were constrained to be equal because of the limited data available. In the fit to the theoretical data (Table 3), all levels with J ≤ 4 were included, both allowed and forbidden, as in the case of paraH2–CO2. There is good agreement between the experimental and theoretical parameters in Table 5, which is not surprising since we know that the observed and calculated line positions agree well. Most trends in Table 5 match well between experiment and theory: that is, there are similar parameter changes between the para and ortho species and between the lower (ν3 = 0) and upper (ν3 = 1) states.
The experimental band origin determined here for orthoH2–CO2 is only slightly red-shifted (−0.096 cm−1) relative to the origin of the free CO2 molecule. Interestingly, the vibrational shifts for H2–CO2 complexes are almost identical to those of H2–OCS complexes, as shown in Table 7. All three family members, CO2, OCS, and N2O show a similar trend, in that the orthoH2 complex is less red-shifted (or more blue-shifted) than the paraH2 complex.
IV. Discussion
A. Average structural parameters
Theoretical average structural parameters, 〈R〉 and 〈θ2〉, determined from the ground state wavefunctions are shown in Table 8. The average value of θ2 is defined as P2(cos 〈θ2〉) = 〈P2(cosθ2)〉, where P2 is the 2nd-order Legendre function. 〈P2(cosθ2)〉 is the average value of the Legendre function for the state of interest.| 〈R〉/Å | 〈θ2〉 | |
|---|---|---|
| paraH2–CO2 Theory | 3.502 | 78.37° |
| paraH2–CO2 Experiment | 3.514 | 80.5° |
| orthoH2–CO2 Theory | 3.384 | 79.53° |
| orthoH2–CO2 Experiment | 3.522 | 76.6 |
It is interesting to observe that the intermolecular distances deviate greatly from the global minimum in the PES, R = 2.978 Å, reflecting the effects of large amplitude motion and zero point energy. Similarly, the deviation of 〈θ2〉 from its equilibrium value of 90° can be thought of as an effect of the zero point librational motion of CO2 within the complex. Estimates of the same structural parameters obtained from the experimental rotational parameters using a simple ‘stick and ball’ model,37 are also shown in Table 8. In the present case, we consider that the theoretical structures are more meaningful than the experimental ones, which rely on a rather crude model. In particular, the vibrationally averaged intermolecular separation 〈R〉 of the ground state of orthoH2–CO2, is found to be somewhat shorter than that of the para species, 3.38 vs. 3.50 Å.
B. Energy level pattern
In this paper, we have focused on the rotational energy levels of the ground intermolecular vibrational state of the H2–CO2 complex. For moderate values of excitation, J < 5, these levels are found experimentally and theoretically to correspond rather well to an asymmetric rotor pattern. This is interesting in itself for a floppy and weakly-bound van der Waals complex, and particularly so for orthoH2–CO2. The lowest excited intermolecular state of paraH2–CO2 is calculated to lie almost 22 cm−1 above the ground state (Table 1), and it is assigned as the first excited CO2 librational state, nb = 1. The J = 0 level of this state is forbidden, but excited rotational levels with (Ka, Kc) = (even, odd) and (odd, even) are allowed.The analogous nb = 1 excited state of orthoH2–CO2 appears at 25.2 cm−1, and is dominated by m1 = ±1 with parity = +1. However the first excited state of orthoH2–CO2 is calculated to lie slightly lower in energy, at 20.6 cm−1 (Tables 1 and S2, see ESI‡). This 20.6 cm−1 state is dominated by m1 = ±1 with parity = −1 and may be a ‘tunneling partner’ of the ground state. The ground and first excited states are thus labeled as (0, 0, 1, 1) and (0, 0, 1, −1), respectively. The fact that all the excited states are separated from the ground state by at least 20 cm−1 probably helps to explain why the ground state levels can be represented by an asymmetric rotor Hamiltonian. It would be very interesting to observe the excited intermolecular vibrations of H2–CO2, but experimental access to these states may be difficult.
Since H2–CO2 is made up of nonpolar components, we do not expect to observe strong pure rotational transitions. However, with sufficient experimental sensitivity it should be possible to detect such transitions, as shown already4 in the case of He–CO2. For the paraH2–CO2 complex, our theoretical results predict the fundamental JKaKc = 111–000 transition to occur in the region of 29931 MHz. For orthoH2–CO2, the most accessible transition may be 110–101, predicted to occur around 16075 MHz. Other possible microwave transitions can be calculated from Tables 2 and 3.
V. Conclusions
In the present work a new 4-D ab initio intermolecular potential energy surface for the H2–CO2 complex has been presented. Energies were calculated using the CCSD(T) method with a large basis set. The PES has a global minimum at two equivalent co-planar configurations (R = 2.978 Å, θ1 = 90°, θ2 = 90°, φ = 0° and 180°) with a well depth of 211.932 cm−1 and a barrier between these two minima with a height of 89.386 cm−1. Bound state calculations have been performed for both para and orthoH2–CO2 species up to high J values. The orthoH2–CO2 ground state is considerably more stable than that of the para species (71.7 vs. 50.4 cm−1). The potential energy surface supports 7 pure intermolecular vibrational states for paraH2–CO2 and 19 for orthoH2–CO2. Calculated infrared transition frequencies are in very good agreement with experimental values for both paraH2- and orthoH2–CO2. For orthoH2–CO2, the allowed ground state energy levels are found to correspond to (Ka, Kc) = (even, odd) or (odd, even) levels, allowing the experimental spectrum to be assigned for the first time, and indicating that the orthoH2 is perpendicular to the intermolecular axis in the complex.Acknowledgements
Minghui Yang was supported by Natural Science Foundation of China (No. 20403029) and Outstanding Overseas Scholar Foundation of Chinese Academy of Sciences. Part of the computations were done on Dawning4000 A of the Shanghai supercomputer center. We are grateful to P. R. Bunker for helpful discussions.References
- J. Tang and A. R. W. McKellar, J. Chem. Phys., 2001, 115, 3053 CrossRef CAS.
- M. J. Weida, J. M. Sperhac, D. J. Nesbitt and J. M. Hutson, J. Chem. Phys., 1994, 101, 8351 CrossRef CAS.
- K. Higgins and W. Klemperer, J. Chem. Phys., 1999, 110, 1383 CrossRef CAS.
- Y. Xu and W. Jäger, J. Mol. Struct., 2001, 599, 211 CrossRef CAS.
- J. Tang and A. R. W. McKellar, J. Chem. Phys., 2002, 117, 2586 CrossRef CAS.
- G. S. Yan, M. H. Yang and D. Q. Xie, J. Chem. Phys., 1998, 109, 10284 CrossRef CAS.
- Y. Z. Zhou and D. Q. Xie, J. Chem. Phys., 2004, 120, 8575 CrossRef CAS.
- F. Paesani and K. B. Whaley, J. Chem. Phys., 2004, 121, 4180 CrossRef CAS.
- Y. Z. Zhou, D. Q. Xie and D. H. Zhang, J. Chem. Phys., 2006, 124, 144317 CrossRef.
- A. R. W. McKellar, J. Chem. Phys., 1998, 108, 1811 CrossRef CAS.
- S. Grebenev, B. Sartakov, J. P. Toennies and A. F. Vilesov, Phys. Rev. Lett., 2002, 89, 225301 CrossRef.
- D. T. Moore and R. E. Miller, J. Phys. Chem. A, 2004, 108, 1930 CrossRef CAS.
- A. R. W. McKellar, J. Chem. Phys., 2005, 122, 084320 CrossRef CAS.
- W. M. Fawzy, G. Kerenskaya and M. C. Heaven, J. Chem. Phys., 2005, 122, 144318 CrossRef.
- F. Paesani and K. B. Whaley, Mol. Phys., 2006, 104, 61 CrossRef CAS.
- P. Jankowski and K. Szalewicz, J. Chem. Phys., 2005, 123, 104301 CrossRef.
- P. Jankowski and K. Szalewicz, J. Chem. Phys., 1998, 108, 3554 CrossRef CAS.
- J. Williams and M. H. Alexander, J. Chem. Phys., 2000, 112, 5722 CrossRef CAS.
- Y. Zhou and D. Q. Xie, J. Chem. Phys., 2005, 123, 134323 CrossRef.
- J. Tang and A. R. W. McKellar, J. Chem. Phys., 2002, 116, 646 CrossRef CAS.
- J. Tang and A. R. W. McKellar, J. Chem. Phys., 2002, 117, 8308 CrossRef CAS.
- Z. Yu, K. J. Higgins, W. Klemperer, M. C. McCarthy and P. Thaddeus, J. Chem. Phys., 2005, 123, 221106 CrossRef.
- D. J. Nesbitt and R. Naaman, J. Chem. Phys., 1989, 91, 3801 CrossRef CAS.
- A. R. W. McKellar, J. Chem. Phys., 2005, 122, 174313 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
- C. Hampel, K. Peterson and H.-J. Werner, Chem. Phys. Lett., 1992, 190, 1 CrossRef CAS.
- D. E. Woon and T. H. Dunning, Jr, J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- F. M. Tao and Y. K. Pan, J. Chem. Phys., 1992, 97, 4989 CrossRef CAS.
- MOLPRO, a package of ab initio programs designed by H.-J.Werner and P.J. Knowles, version 2002.6, R.D. Amos, A. Bernhardsson, A. Berning, P. Celani, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, P. J. Knowles, T. Korona, R. Lindh, A. W. Lloyd, S. J. McNicholas, F. R. Manby, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, G. Rauhut, M. Schütz, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and H.-J. Werner.
- D. H. Mclain, Comput. J., 1974, 17, 318 Search PubMed.
- T. Ishida and G. C. Schatz, Chem. Phys. Lett., 1999, 314, 369 CrossRef CAS.
- D. C. Clary and P. J. Knowles, J. Chem. Phys., 1990, 93, 6334 CrossRef CAS.
- D. H. Zhang, Q. Wu, J. Z. H. Zhang, M. von Dirke and Z. Bacic, J. Chem. Phys., 1995, 102, 2315 CrossRef CAS.
- R. Lehoucq, D. C. Sorensen and C. Yang, ARPACK User’s Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods, SIAM, Philadelphia, PA, 1998, http://www.caam.rice.edu/software/ARPACK Search PubMed.
- M. D. Brookes, C. Xia, J. Tang, J. A. Anstey, B. G. Fulsom, K.-X. Au Yong, J. M. King and A. R. W. McKellar, Spectrochim. Acta, Part A, 2004, 60, 3235 CrossRef.
- The difference (0.021 cm−1) between the present value of E0 and the experimental band origin from ref. 24, is mostly accounted for by the difference in energy (0.019 cm−1) between the theoretical JKaKc = 000 levels for v3 = 0 and 1 in Table 2.
- G. D. Hayman, J. Hodge, B. J. Howard, J. S. Muenter and T. R. Dyke, J. Mol. Spectrosc., 1989, 133, 423 CrossRef CAS.
Footnotes |
| † The HTML version of this article has been enhanced with colour images. |
| ‡ Electronic supplementary information (ESI) available: The ab initio data, a Fortran program to generate the intermolecular potential surface, and a more complete listing of the calculated H2–CO2 bound rovibrational levels. See DOI: 10.1039/b614849b |
| This journal is © the Owner Societies 2007 |
