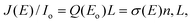Cross sections for low-energy electron scattering from adenine in the condensed phase

Abstract

Measurements of the vibrational and electronic excitation of a sub-monolayer up to a monolayer film of adenine were performed with a high resolution electron energy -loss (HREEL) spectrometer. The integral cross sections (over the half-space angle) for excitation of the normal vibrational modes of the ground electronic state and electronically excited states are calculated from the measured reflectivity EEL spectra. Most cross sections for vibrational excitation are of the order of 10^–17 cm², the largest being the out-of-plane wagging of the amino-group and the six-member ring deformations. A wide resonance feature appears in the incident energy dependence of the vibrational cross sections at 3–5 eV, while a weak shoulder is present in this dependence for combined ring deformations and bending of hydrogen atoms. For the five excited electronic states, at 4.7, 5.0, 5.5, 6.1 and 6.6 eV, the cross sections are of the order of 10^–18 cm², except in the case of the state at the energy of 6.1 eV, for which it is two to three times higher.

---

1. Introduction

Understanding the properties and the functioning of the DNA molecule within and outside the cell is one of the most challenging and inspiring problems in biophysics research. The basic constituents of DNA and RNA, purine (adenine and guanine) and pyrimidine (thymine, cytosine and uracil) bases and their derivatives, are essential elements of genetic information. In a view of the prebiotic conditions on Earth,¹ a certain level of self-assembling property of these compounds could have played a role in the formation of higher-ordered classes of organic molecules. All DNA bases can spontaneously self-assemble into condensed 2-D monolayers.² In the cell, besides being constituents of the DNA, nucleic acid bases are also important elements of its complex metabolic network.^3,4Adenine in particular is a constituent of the essential energy supply molecule, adenosine-tri-phosphate(ATP), whose intercellular concentration reaches the highest level of all nucleotides in the cell. In DNA and RNA molecules adenine is supposed to play a role in the “hole-migration” towards guanine during the process of electron transfer,⁵ which is one of the key problems in nanotechnology, such as in studies of the use of nucleic acids as conducting devices.

A particular research on low-energy electron scattering from DNA bases constituents has been focused on discovering the mechanisms of interaction important in radiotherapy or nanotechnology, for example.^6,7 Abundant secondary low-energy electrons, together with the radicals and ions produced in the subsequent reactions, are responsible for most of the cellular DNA radiolysis in its early stages. Results from measurements on short DNA strands impinged on by 1–30 eV electrons indicate that the damage they induce is due to the chemical nature of the bases and/or their sequence. Fragmentation of biomolecules by these electrons is characterized by multiple mechanisms:⁶ transient negative ions (TNI) formed below the threshold for dipolar dissociation (∼15 eV), which decay into dissociative electronically excited states or into the dissociative electron attachment (DEA) channel; above the threshold for electronic excitation, if the TNI formation takes place, it is observed in high resolution electron energy loss (HREEL) experiments as a peak structure superimposed on continuously rising direct dissociation in the energy dependence of the cross section. The final outcome of the electron–molecule interaction depends on the lifetimes of the TNI states, which are largely determined by the immediate environment of the target molecule. Stable negative ions formed on the DNA bases and base pairs can affect the electron migration along the DNA helix via the stacked bases.⁸ Furthermore, the electron transport in DNA couples to the vibrational motion of the molecular wires formed by hydrogen-bonded and stacked DNA bases.

A majority of the experimental^6–29 studies of nucleic bases, including adenine and nucleosides , focused on photo-processes. Infrared (IR)^21,24 and ultraviolet (UV)^13,22,24 spectroscopy, fluorescence spectroscopy^12,18 and femtosecond laser photo-ionization experiments,^{9,16,19,20,25} prevail, although there are a certain number of gas-phase electron spectroscopy^{11,14,15,17,26,29} and ion-desorption studies^6,7,23 performed recently. Electronically excited states of nucleic bases play an important role in processes of DNA damage, often leading to breaking of the bonds with their counterpart in the double helix or with the sugar moiety along the strand. Transient absorption and time-resolved fluorescence measurements^15,16,43 have shown that the nonradiative decay times (de-excitation viainternal conversion ) of electronic states of adenine are of the order of only a few hundred femtoseconds. This is accommodated by the non-adiabatic coupling of the nπ* and the ππ* electronic states with the vibrational levels of the ground state . Internal conversion (IC ) within the molecule is considered to be an important mechanism for the dissipation of energy received from the UV photons, making the DNA bases photo-stable and protecting the cellular DNA from mutagenesis and possible carcinogenesis. Therefore, possible temporary electron attachment to these states may be of considerable importance to DNA as a possible pathway to its damage.

In theoretical studies^{9,10,21,30–45} the usual method of calculation is density functional theory (DFT), taking into account geometrical properties of the electronically excited states and a consequent change of the molecular dipole moment. For individual adenine base and base pairs, theoretical calculations of properties of the ground and excited states^{30,31,35,37,40–43} and their change in gas and liquid phase have been performed, but only a few treated the targets in the condensed state.^21,45

Desorption studies^6,7,23 of H^–, O^–, OH^–, CN^–, OCN^– and CH₂^– ion yields showed that among all nucleic bases adenine is the least sensitive to damage via DEA, but did not give any information about other dissociative channels. As in previous studies on thymine and pyrimidine,^{14,15,17,28,46} the principal aim of the present study was to investigate a possibility of resonance formation (TNI) in adenine for electrons of incident energy below 12 eV and give the effective cross section values for low-energy electron vibrational and electronic excitation of condensed adenine. Cross sections for excitation of vibrational modes of the ground electronic state and electronically excited states are calculated from reflectivity spectra of thin adenine films, using the HREEL method of measurement. We show the existence of resonance features in the integral cross sections for the important N–H₂ and N–H stretching modes. The effective cross sections for vibrational excitation of the most prominent normal modes in the electron energy -loss spectrum (EEL) range from 10^–17 to 10^–16 cm², while for the electronic excitations they are mostly of the order of 10^–18 cm². Excitation of the singlet ππ* state at 6.1 eV exhibits the largest of the cross sections for electronic excitation, 10^–17 cm². The existence of triplet states in the EEL spectrum is discussed in a view of a recent theoretical study.⁴⁴

2. Experimental

2.1. Apparatus and the deposition procedure

Our measurements were performed using a HREEL spectrometer placed in a cryogenically pumped UHV chamber. The experimental setup and the method of measurement have been described in detail previously,^{14,15,46–48} therefore we will give just a brief description of the main features.

The HREEL spectrometer has a double-spherical energy selector in the monochromator and the analyzer, combined with sets of electrostatic lenses. Both the exit of the monochromator and the entrance of the analyzer have a double-zoom lens, which provides for a nearly uniform electron beam and focus size for incident electron energies from 1 to 20 eV. While the position of the analyzer is fixed at 45° with respect to the normal to the sample, the position of the monochromator is variable from 14 to 65°, at the opposite azimuth. The incident energy E_o was calibrated by measuring the onset of the electron current transmitted through the sample, within ±0.1 eV with respect to the vacuum level. The combined energy resolution of the spectrometer ranged from 15 to 20 meV FWHM, for an incident electron current of 0.77 nA.

The substrate for sample deposition is made of polycrystalline platinum foil, which is cryogenically cooled to a temperature of 18 K. Deposition of the gaseous samples is done using a capillary introducing the gas from a small calibrated volume in front of the substrate, in amount sufficient to achieve the desired layer thickness. Solid samples are deposited following a fast heating–sublimation procedure in front of the cold substrate. The platinum foil is cleaned by resistive heating, reaching temperatures of the red/orange glow (∼1100 °C) within 10 s.

A second vacuum chamber, connected to the main UHV chamber through a gate valve, serves as a load-lock for transferring the solid sample to a ceramic finger, which is then introduced into the main vacuum chamber in order to make film deposition onto the substrate. The base pressure in the main chamber was of the order of 10^–11Torr , while the pressure in the load-lock chamber was two orders of magnitude higher, 0.8–1.5 × 10^–9Torr . The oven placed in the load-lock chamber contains a small crucible. In order to provide clean vacuum conditions for sublimation of sample molecules from this crucible onto the tip of the sample carrier (ceramic finger), and from the carrier onto the substrate in the main UHV chamber, the gate valve between these two vacuum chambers is kept open for only a few minutes. The residual background gas and possible undesirable decomposition of the sample is monitored in the load-lock chamber with a quadrupole mass spectrometer.

The deposition procedure for argon and adenine was the same as in the case of thymine^14,15,17 and pyrimidine⁴⁶ except for the adeninesublimation time and temperature. Argon, with a stated purity of 99.9995% (Matheson Canada Ltd), is condensed on the previously cleaned and cooled Pt substrate by introducing the amount sufficient to make 5–6 layers. Thickness of the film was estimated from the pressure drop in the calibrated volume. The crucible filled with adenine powder with the stated purity of 99.9% (Sigma Aldrich Canada) is heated to a temperature of approximately 60 °C for several hours to eliminate water and other impurities from the sample. This temperature is well below the reported^11,22 temperature for decomposition (250 °C). We considered degassing being completed when the partial pressure of the water in the load-lock chamber, monitored by the quadrupole mass spectrometer, drops down to the level corresponding to adenine-free conditions. The ceramic finger was cleaned before each deposition, by heating to 280 °C for about 15 min. After the ceramic cooled down to room temperature, it is moved at 2 mm distance from the opening of the crucible, which was heated to ∼ 100 °C and descended from the top part of the load-lock chamber. Typical deposition time was 10 min. After this time, the ceramic finger is retracted away from the oven and the oven quickly cooled down to room temperature and lifted to the position where it stayed isolated (by a gate valve) from the rest of the vacuum chamber. In order to deposit adenine onto the substrate in the main vacuum chamber, the ceramic finger was introduced through the opened gate valve to approach the substrate at 5 mm distance and heated to ∼150 °C for 70 s for a sub-monolayer and 90 s for a monolayer to be formed. After the deposition, it was retracted back to the load-lock chamber and the gate valve was closed. In most measurements, the thickness of adenine film was between 0.8 to 1.2 monolayers. The actual number of adenine molecules in the film is estimated based on the results of several studies on orientation and molecule–surface interaction.^2,49–52

It is known from the STM measurements² that the direct deposition of adenine onto the surface (HOPG, MoS₂) can result in a diverse orientation of its molecules and hybridization of the molecular orbitals centred on the atom forming the bond with the substrate. This eventually modifies the vibrations of adenine and its surface coverage , which, on the other hand, influences the intermolecular motion. Temperature programmed studies on structure and desorption dynamics of DNA bases deposited on gold⁵⁰ show that in the case of low-coverage sites adenine molecules are attached to the substrate by their amino-group hydrogen or nitrogen and carbon from the same site, while the rest of the molecule is positioned at an angle with respect to the surface. Only one of four possible orientations of adenine with respect to the surface is horizontal and only at higher temperatures. In the other combined experimental and theoretical studies,^49,51,52 the STM measurement on adenine bilayers formed on graphite by evaporating the saturated aqueous solution^49,51,52 and the low energy electron diffraction ^51,52 results indicate that the upper layer of the bilayer structure shows a structural change compared to the layer adsorbed directly to the graphite. The upper layer is shifted, rotated and less dense than the base layer. Apart from the van der Waals forces , physisorbed monolayer formation involves also an intermolecular hydrogen bonding. It turned out, from modeling the Moiré structure,^49,51 that the molecules are bound tighter to their neighbours in the same row than to those from different rows. The symmetry is p2gg and the vectors of the unit model cell are a = 22 ± 1 Å and b = 8.5 ± 0.5 Å. Each cell contains four adenine molecules, of the approximate area of 48 Ų each,⁵¹ organized as hydrogen-bonded dimers.⁵² Each of adenine molecules is fixed in a network of four adenine bonds of 2.94 ± 0.02 Å. In a LEED study,⁵¹ it was found that the same unit-cell vectors existed for different experiments under various conditions, i.e. vacuum sublimated films as well as adsorbates dried from the solution.

There is no specific experimental evidence for a true position of adenine molecules deposited on solid argon. Taking into account the aforementioned results for deposition on graphite, gold and MoS₂, we assume the same cell structure and even a weaker interaction with the substrate due to the chemical inertness of argon and a very low temperature of the substrate. In our previous experiments argon layers proved to be adequate in preventing the effect of chemical bonding and provided a good base for formation of satisfactory uniform sub- or monolayer film of adenine. Argon was also convenient for the observed energy range from 1.5 to 12 eV because of a large energy gap between the elastic and the first electronically excited state (∼12 eV).

2.2. Method of measurement

As described in a previous study,¹⁵ both the characterization of the target sample and recording energy-loss (EL) spectra rely on the measurement of the transmitted and the backscattered electron current, I_S and J (θ_d), respectively. From extrapolation of the linear relation between J (θ_d) and I_S we can find values of the effective incident current I_o,d‡ and the incident current on the target I_o and then normalize the EL spectrum to obtain the values of the absolute reflectivity. Typical value for I_o was 0.77 ± 0.08 nA. Since the transmitted current, I_S, changes with the incidence angle within only 10%, we consider the ratio J (θ_d)/I_o,d approximately constant over the angles of analysis. Consequently, this ratio is analogous to dividing integral of J (E, θ_d) over the half angular space by the I_o, i.e. it is equal to J (E)/I_o.

Multiple-scattering theory⁴⁸ developed for the interaction of low-energy electrons with molecules in a condensed film can also be applied in the case of electron scattering on very thin films. The relation between the above ratio, calculated from the experimental data and the scattering probability per unit length per unit solid angle and per unit energy range (SPUL) for an electron of energy E_o to lose E–E_o and be deflected from an incident direction θ_o to a back-scattered direction θ_d, Q (E_o, E–E_o), is:

where L is the thickness of the film, n is the molecular density of the target film and σ (E) is the absolute integral cross section. Therefore, to determine σ (E), we need to know the molecular coverage of the target area, nL. The above formula is valid for near normal incidence on an azimuthally disordered molecular coverage, when we assume that the electrons scatter from the film into a near cylindrically symmetric space.

To estimate the thickness of adenine films, on the other hand, we used the fact that the specular reflectivity of the surface is very directional and very sensitive to surface conditions. Therefore, we relied on the attenuation of its value for the argon film after it has been covered by adenine. As it was described in the previous work on thymine,¹⁵ this attenuation is an exponential function of the surface density of the molecular film:

where R is the specular reflectivity and 〈n〉 = N/M is the average number of molecules per adsorption site. Having the same incident current and the reflectivity inherent to certain type of molecules for different coverage, we find that the function ln(I/I_o) vs. I/I_o gives us the number of monolayers in the film.

A well-collimated and focused incident electron beam of energy ranging from 1.5 to 12 eV was aimed at the target at an angle of 15° with respect to the direction perpendicular to the film surface. EL spectra have been recorded by measuring the number of electrons backscattered from the film, at the fixed analyzer angle of 45°. Tuning of the entrance electron lens in the analyzer for each of the incident electron energy provided detection of all electrons scattered from the film at this angle. We have recorded 13 energy-loss spectra, at 1.5, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 eV and additionally at 11.5 eV only for electronically excited states. Exposure times for collecting individual EEL spectra were sufficiently small§ to exclude significant contribution from damaged molecules to the signal. All spectra which exhibited charging or damage effects were discarded.

In order to present the integral cross sections for different vibrational modes, we chose to integrate over the Gaussians of deconvoluted peaks from the EEL spectra, corresponding to the most intense vibrations. For electronic excited states, we applied the same method for the energy-loss ranging from 4.2 to 7.2 eV, at the incident energies of 8, 9, 10, 11, 11.5 and 12 eV.

3. Results and discussion

3.1. Vibrational excitation of the ground electronic state

Adenine (in Fig. 1), or 9H-purine-6-amine, is a two-ring molecule with the amino group attached to the carbon atom in the six-member ring. It has a large dipole moment³⁰ of 2.8 (theoretical value) to 3.0 Debye (experiment). The adiabatic ionization potential is calculated³⁰ to be 8.1 eV and measured to be between 8.3 eV⁵³ and 8.45 eV.⁵⁴ In its ground state adenine has 39 normal vibrational modes, of which 27 lie in the molecular plane. Assignments of these modes (Table 1) are provided through various calculations, such as DFT Kohn–Sham scheme with gradient corrections for exchange and correlation,^21,37 ultra-soft pseudo-potentials⁴⁰ and the ab initio³⁰ method. They provided also the frequencies and intensities of certain modes, as well as a comparison with measurements from IR, Raman^21,24,55 and neutron inelastic scattering spectroscopy.⁵⁶Fig. 2 shows four characteristic vibrational EEL spectra shifted on the intensity scale, in the EEL range from 0 to 0.5 eV, for incident energies of 1.5, 5, 8 and 12 eV. The background contribution from phonons in the argon spacer is marked with the dash line only for the spectrum of 1.5 eV electrons. The linear fit of the background has been shown to be^14,28 a good approximation of the exponential phonon background for low incident electron energies and energy-loss greater than 50 meV. In the EEL spectra there are three distinctive spectral bands among the normal vibrational modes of adenine: at ΔE from 0.06 to 0.13 eV, from 0.15 to 0.21 eV, and from 0.33 to 0.44 eV. We cannot distinguish between vibrational modes at EEL ≤ 0.06 eV due to the proximity of the strong elastic peak.

Fig. 1 Adenine molecule.

Fig. 2 EEL spectra at characteristic incident energies. Bars on the top denote energies of the normal vibrational modes from IR measurements of adenine in the Ar matrix,²¹ in the middle are our values from deconvolution. Background contribution from phonon excitations in the Ar substrate has been approximated by a linear fit (dashed line).

Table 1 Assignment and energy of vibrational modes of adenine in its ground electronic state. The last column contains energies of peaks from deconvolution of electron energy -loss spectra

Calculated values^c
Type of vibration and its symmetry	Energy/meV	Strength	Spectroscopic energy/meV	Electron energy loss from deconvolution/meV
a Exchange–correlation functional DFT.^32 b IR results for adenine in an inert gas matrix.^32 c IR-UV double resonance spectroscopy,^40 and d IR spectra DFT and experiment in matrix isolation .^30
Butt molecule/Out	26 (7.3)	30^b	34^c
Tors molecule/Out	36 (1.0)	39
Wag of H in NH2/Out	63 (227.3)	64	63^c	64
Rock NH2, wag C2–H, C8–H/Out	68 (1.1)	69	70^c
Rock NH2, wag C2–H/Out	69 (6.0)	74
Def R5 and R6/In	74 (1.6)	76
Wag of N9–H and C8–H/Out	79 (202.8)			84
Def R5 and R6; A wag of N9–H and H in NH2/Out	83 (1.0)	85
Def R5/In	106 (8.1)	107		106
Wag C2–H/In	113 (9.2)	112
Def R6; S bend of H in NH2/In	120 (1.9)	119		126
Def R5; A bend C8–H and N9–H/In	130 (26.7)	129
Def R5 & R6; bend of H attached to the rings/In	137 (6.8)	139
Def R5 & R6; S bend of C8–H and N9–H/In	150 (40.8)	152
Def R5 & R6; A bend C8–H and N9–H/In	156 (89.3)	155		154
Def R5 and R6; bend C8–H/In	160 (48.9)	159
Def R5 and R6; bend all H except N10–H12/In	164 (14.5)	163
Def R5 and R6; bend all H/In	168 (14.6)	171
Def R5 and R6; S bend all H/In	176 (36.9)	176		174
Def R5 and R6; bend C2–H, C8–H and C6-NH2/In	179 (11.1)	184	183^c
Def R5 and R6; bend N9–H & N10–H11/In	192 (93.7)	198		194
Def R6; sciss NH2/In	196 (69.3)	202	203^c
Sciss NH2; str C6-NH2	202 (456.8)	204		204
Str C2–H	387 (24.9)	374
Str C8–H	395 (1.3)	387		385
S str of N–H in NH2	434 (78.9)	426	427^d
Str of N9–H	441 (51.4)	432	434^d	435
A str of N–H in NH2	452 (38.7)	440	441^d

---

According to the detailed study of Santamaria et al.,³⁷ both the calculation and the IR measurements show that many modes exist in the low-band part of the spectrum, of which the most intense are two modes at 0.063 and 0.079 eV. They correspond to the wagging of two hydrogen atoms in the amino group and the symmetric wagging of hydrogen atoms at N9 and C8 positions on the five-member ring (Fig. 1). In the intermediate energy range, between 0.118 and 0.210 eV, there are many modes of in-plane ring deformations and of H- bending. Scissoring of H in the amino group appears at the end of this range. According to Table 1, the most intense peaks in the whole spectrum are those at 0.063, 0.079, 0.202 and 0.192 eV and a vibrational mode at 0.156 eV. In the first two bands there is a large contribution from NH₂ scissoring, some ring deformation and stretching of the C6–NH₂. The 0.156 eV peak contains mostly bending of all hydrogen atoms and ring deformations (stretching). The last EEL region, separated from the previous one by ca. 0.140 eV, is the high-band part of the spectrum where two modes should dominate, at 0.434 and 0. 441 eV. The first corresponds to the symmetric stretching of H in the amino group and the other to the N9–H stretching. The remaining modes in this band are also exclusively from stretching of hydrogen bonds.

We performed a spectral deconvolution in these three EEL regions (Fig. 3), taking as a reference calculated and measured energy positions of different modes. The limited energy resolution in our measurements did not allow a distinction between closely spaced vibrational modes around 0.150, 0.174 and 0.44 eV. Therefore, we assumed that each group comprises a single Gaussian peak (Table 1). Furthermore, a small shoulder in the EEL spectra that was reproduced by two Gaussian peaks at 0.335 and 0.355 eV is not predicted by theory nor measured by IR spectroscopy. Both peaks are significantly shifted from the IR measured and DFT calculated vibrational energies in this last band. A possibility of a significant contribution from multiple energy-losses in adenine films is excluded based on the fact that the film is very thin, that the incident angle of the electron beam is near normal to the surface and that there are no peaks which indicate such processes in the background region beyond EL of 0.5 eV. The possibility that the energy shift of the modes in this band is due to the mixed isolated-molecule/dimer and inter-dimer structure of adenine film would affect the assignment of the peaks in the EEL spectrum. Furthermore, there is no shift in the mode at the EL of 0.204 eV, to the contrary of what has been reported in the study of A–T complexes,³⁷ where the similarly strong hydrogen bonds govern the dimer structure. Therefore, these small peaks can be interpreted as possible overtones of 0.171–0.184 eV normal modes. Two other modes, at 0.385 and 0.435 eV are the most significant in the last part of the measured EEL spectra. Following the assignment from Table 1, the first one belongs exclusively to the C8–H stretching and the second is most likely a combined asymmetric stretching of hydrogen atoms in the NH₂ group and the N9–H stretching, while the mode at 0.415 eV is most probably a possible overtone of the 0.204 eV mode, which is also the amino-group vibration, or a combination mode.

Fig. 3 EEL spectrum at the 8 eV incident energy. Twelve Gaussian peaks, each corresponding to individual vibrational modes, are marked by the dotted line. Standard deviation for the peaks is 0.010, except for the peaks at the energy-loss of 0.154 and 0.194 meV, where it was 0.0134 and 0.0113, respectively. The corresponding FWHM are 23, 31 and 26 meV.

The assignment of the peaks to specific vibrational modes was based on the calculations.^24,37 Owing to its dependence on the method applied, except for the mode at the EEL of 0.064 eV, which theory claims with more confidence,²⁴ these assignments should be taken with reserve. According to the theoretical study, the anharmonicity for NH₂ should be taken into account in order to improve accuracy of calculations. However, the resemblance in shape of the integral cross sections dependence on incident energy for a particular vibrational mode may give an estimate of their correct position.

In order to calculate the cross sections corresponding to different vibrational modes, we have integrated the Gaussian functions for each of their EEL values and applied the normalization procedure described in section 2.2. The FWHM of each of the Gaussian functions is 23 meV, which is a little larger than the measured FWHM of our incident beam elastically scattered from the clean substrate, 15–20 meV. Fig. 4A and B shows these cross sections (integrated over a half-angular space) as a function of the incident electron energy . The cross sections are grouped according to the dominant type of vibrations in each band: (A) six- and five-member ring (R6 and R5) deformations with bending and wagging of hydrogen atoms and (B) amino-group deformations and stretching of hydrogen atoms attached to the rings. All cross sections (see the Table 1 in the supplement file) are of the order of 10^–17 cm², the largest being the out-of-plane wagging of the amino-group and the six-member ring (R6) deformations. The uncertainty is within ±35% and is mostly the uncertainty of the number of molecules in the film (±20%) and the uncertainty of the incident current value (10%), with a few percent contributions from the statistical error and the difference between the fitted and measured spectra. As shown in Fig. 4B, cross sections for stretching of hydrogen bonds on the rings are three to four times smaller than for the other modes. The cross section for asymmetric stretching of the amino group hydrogen atoms is showing an enhancement as a possible resonance at 3 eV. This can be an indication that the same structure in the other vibration cross sections, only less pronounced, originates also from the asymmetric stretching of either ring-bonds deformations or hydrogen atoms bound to the rings. At approximately 5 eV, all vibrational modes seem to exhibit an enhancement in the cross section. This is not surprising since the coupling of different vibrations in adenine is very likely. Furthermore, there is numerous evidence for the internal conversion from the nπ* to the ground state , which could result in the vibrational excitation. The energy of this state is very close to the energy of the ππ* state, at 5 eV. A small maximum at 8 eV in the cross section energy function for NH₂ scissoring and C–NH₂ stretching at the EL of 0.204 eV, appears in all other vibrational modes as a small shoulder.

Fig. 4 (A) Integral cross sections for excitation of vibrational states of adenine; five- and six-member ring (R5 and R6) deformations and combined modes. (B) Incident electron energy dependence of the integral cross sections for excitation of vibrational states of adenine; mostly vibrations of the amino-group and the possible overtones.

From the electron-transmission spectroscopy (ETS) measurements and calculations of Aflatooni et al.,¹⁰ we would expect to see in our integral cross sections a shape resonance structure at the vertical attachment energy of 2.17 eV (at the approximately same position as in the (A–H)^– anion yield of Gohlke et al.⁵⁷) and a core excited resonance at 6.28 eV, both leading to the DEA and the (A-H)^– anion yield. In thymine and uracil, for example, H-atoms are released from the N3 site via the coupling between the temporary anion states associated with the π* and σ* valence orbitals owing to the out-of-plane vibrations. This mechanism produces anion yields near the energies of the π* temporary anion states. From the N1 site, on the other hand, hydrogen atoms are ejected via sharp Feshbach resonances created by mixing of the dipole bound negative ion states associated with the lowest unoccupied valence σ* molecular orbital .

Considering that the polarization in an argon substrate is expected to shift the shape resonances positions to smaller energies with respect to those in the gas-phase for about 0.8 eV,⁴⁶ we would expect to see the resonances observed by Aflatooni et al.²⁹ at 1.4 and 5.5 eV. Thus, the broad peak in Fig. 4, around 5 eV, could be associated with the gas-phase 6 eV core-excited resonance. On the other hand, in the present measurements, energy-loss spectra were taken in the 1 eV steps, implying that the measured position of the resonance at 3 eV could be, according to plots in Fig. 4A and B, at an energy shifted for ±0.5 eV. Therefore, the comparison between the gas-phase and condensed phase experimental results, regarding the energy at which the resonances in the integral cross sections appear, is qualitative and should be considered more as an indication than as a definite interpretation of the origin of these structures.

From anion yields of Aflatooni et al.,²⁹ the DEA cross sections for all three bases are of the order of 10^–19 cm². Vibrational Feshbach resonances in adenine are interpreted as arising from the excitation of the N9–H stretching vibration of the dipole bound anion. Their calculations show that the lowest valence orbital is almost entirely localized on this bond, so the dipole-bound electron lies away from the C8–H end of the molecule. There are a few other theoretical calculations as DFT^32,42 and ab initio,^41,43,58 which confirm that adenine forms only dipole-bound anions, that this process is accompanied by the significant changes in molecular geometry and that the negative adenine anion is metastable with respect to an adiabatic attachment.⁴¹ Both studies of Aflatooni et al.²⁹ and Al-Jihad et al.⁴¹ confirm that the negative vertical electron affinity has a consequence on the bridge-assisted, long-range electron transfer along the stack in DNA, becoming hampered by the presence of adenines. Tonzani and Green⁴² indicate possible shape resonances at 2.4, 3.2, 4.4 and 9.0 eV, of the widths: 0.2, 0.2, 0.3 and 0.5 eV, respectively. Since usually theory predicts resonances at higher energies (in this case, the suggested shift was 1.5 eV) than those measured, the structure in the integral cross section at 3 eV in our measurements can be their third resonance. They showed that there is no significant buildup of electron density on hydrogen atoms, meaning that the negative charge stays on the molecular rings and that the H^– is not formed. In principle, breaking of C–C and C–N bonds could be the other possible channels of adenine dissociation after electron attachment . On the other hand, these calculations do not include any vibrational Feshbach resonances, neither the core-excited resonances.

3.2. Electronic excitation

Electrons in adenine occupy a large manifold of molecular π and σ orbitals and can be excited following various pathways to π* and σ* orbitals, whose energies lie close to each other.²⁶ In the adenine monomer, nπ* state dominates the relaxation pathway, while in dimer it is the πσ* state.^9,20 The nearby nπ* and ππ* vibrational coupling is manifested through the out-of-plane vibrations, which causes the quenching of luminescence.³³ In the case of strong coupling, when the Franck–Condon factor associated with the radiationless transition is large, the conversion to the ground state is very fast.

We did not observe a clear vibrational structure in the EL spectrum of the electronically excited states (Fig. 5). According to the study of Mishra et al.,³⁰ this is not surprising since the vibrational frequencies are appreciably reduced in magnitude consequent to excitation in the case where the ground and ππ* singlet excited states modes are the same. Thus, even the most intense vibrational modes of the ground electronic state of adenine might be significantly smaller if they exist in the electronically excited states and the new modes, not strong enough to appear as distinctive peaks. Consequently, deconvolution of the energy-loss spectra for these excited states did not allow resolving possible vibrational modes. Results from calculation for the most intense absorption and the experimental values of energies of these excited states were reported by Preuss et al.,⁴⁰ Mishra et al.,³⁰ Sobolewski and Domcke,³⁶ Dillon et al.,¹¹ and Isaacson²⁷ and are listed in Table 2(a). Sobolewski and Domcke³⁶ have calculated, by ab initio time-resolved DFT, the adiabatic excitation energies of the three lowest excited singlet states –4.75, 4.99 and 5.05 eV, for the ¹nπ* (valence state), ¹πσ* (Rydberg state) and ¹ππ* (valence state). They considered the lowest πσ* state, associated with the azine group, as well as the lowest nπ* and ππ* states, based on the result from Plützer et al.,²⁴ that there are two potentially active centers for hydrogen detachment, the azine (NH) and the amino (NH₂) group. For the purpose of deconvolution of the EEL spectrum from our experiment, energies of the excited states (Table 2) are chosen to be in the range of energies calculated in the theoretical studies^30,36,40 and measured in the experiments.^11,27,30,40 For the excited state in the energy range from 5.7 to 6.1 eV we used two Gaussians of the same width, one at 5.5 eV and the other at 6.1 eV, in order to better reproduce the energy-loss spectrum (Fig. 6). Furthermore, the part of the spectrum beyond the EL of 6.8 eV does not give us an indication where the possible excited states should be, since it is very broad and featureless.

Fig. 5 EEL spectra for the incident electron energies from 8 to 12 eV. Vertical lines indicate the positions of the Gaussian peaks that we used in deconvolution.

Fig. 6 EEL spectrum for 8 eV electrons; excitation of electronic states. Dotted lines represent deconvolution curves corresponding to peaks at the energy—loss of 4.7, 5, 5.5, 6.1 and 6.6 eV.

Table 2 (a) Energies (in eV) of the singlet electronic excited states of adenine. The last column contains energies of the peaks from the deconvolution of our EEL measurements. (b) Calculated⁴⁴ vertical energies for triplet states of adenine and the possible corresponding peaks in our deconvoluted spectrum

(a)
Theory				Experiment
Adiabatic excitation^a	Intense absorption^b	Vertical excitation^c	Vertical excitation^f	Absorption^b	Fluorescence from gas^c	Electron scattering—gas phase^d	Electron scattering—thin film^e	Deconvol. from EEL spectra
	3.93
4.75 (nπ*)	4.71		4.54 (ππ*)		4.59 (ππ*)		4.53 ± 0.18	4.7
					4.77 (ππ*)
4.99 (πσ*)	5.2		5.04 (ππ*)	4.9	5.27 (nπ*)	4.96 (ππ*)		5.0
5.05 (ππ*)
	5.69		6.17 (ππ*)	5.7–6.1	5.76 (ππ*)	6.15 (n → 3s)	5.84 ± 0.18	5.5; 6.1
	6.82	6.6 (ππ*)		6.8		6.5 (ππ*)	6.5 ± 0.18	6.6
		6.73 (ππ*)
	7.51	7.16 (ππ*)		7.7		7.28 (ππ*)	7.71 ± 0.18
		8.19 (ππ*)				8.56 (ππ*)

---

(b)
Vertical excitation	Deconvolution from EEL spectra (this work)
a Ab initio TDDFT by Sobolewski and Domcke.^36 b Plane-wave calculations with ultra-soft pseudopotentials by Preus et al.^40 c Ab initio study for gas phase and aqueous solution and fluorescence measurements by Mishra et al.^30 d Small angle (<10°) scattering of 200 eV electrons by Dillon et al.^11 e High energy (25 keV) electron scattering from solid adenine film by Isaacson.^27 f Combined DF and multireference configuration interaction methods by Marian.^44
3.63	Not observed
4.42	Not included
4.79	4.7
4.81
5.08	5.0
5.10
5.25
5.34
5.54	5.5
5.58

---

The effective cross sections for the excitation of electronic states (see Table S2 in the ESI)† that we included in the deconvolution were calculated using the same method as for the vibrational excitation. The residual value, calculated as the difference between the convoluted curve and the energy-loss spectrum in the EL range from 4.2 to 7.2 eV, is given in a separate column and it comprises the contribution from the electronic states beyond the EL of 6.8 eV. Magnitudes of these cross sections are in the range from 10^–18 to 10^–17 cm², an order of magnitude smaller or the same as in thymine. From the cross section dependence on incident energy (Fig. 7), no core-excited resonance could be indicated supporting the desorption peak at 9 eV. The highest cross section (see Table S2 in the ESI)† belongs to the EL of 6.1 eV (Gaussian width is ∼700 meV). Recent results of negative ion formation in adenine in the gas phase⁵⁹ confirmed the existence of increased probability for H^– production at 6 eV (with the energy resolution of 1 eV). Another recent study⁶⁰ of decomposition of purine nucleobases in the gas phase by very low energy electrons shows a high yield of CN^– and (A-HCN)^– ions from adenine at around 6 eV. Both results give the resonance energy lower than in ion-desorption measurements.^6,7,23 The lowest-lying resonance for desorption of H^– lies at about 9 eV and the suggested interpretation was that it appeared as a consequence of the electron capture by the positive electron affinity of the nπ*, ππ* and nσ* states. According to another theoretical study,⁹ that of the adenine dimer, σ* orbitals are located at the peripheral N–H groups of the two adenine constituents, while no such anti-bonding orbitals exist between the individual parts along the H-bond. If we look further at the consequences of electronic excitation, theoretical study of Mishra et al. found that in the 9H-form of adenine, the C2–N3 and C5–C6 bond lengths (Fig. 1) increase appreciably under both the ππ* and nπ* excitations. The C4–C5 increases under ππ* excitations, while it remains almost unaffected consequent to the nπ* excitation and the C5–N7 bond length decreases under both the ππ* and nπ* excitations. After ππ* excitations, the amino group changes from pyramidal to coplanar with the rings, unlike after nπ* excitations. Therefore, it is extremely difficult to disentangle all these channels and identify an electronic state as certainly leading to a specific bond breaking. It seems plausible that the bond breaking is often a result of simultaneous action on different parts of the molecule. Detailed orbital assignments for the core-excited resonances are yet to be determined.

Fig. 7 Effective cross sections for excitation of the singlet and triplet electronic states in adenine at 5.0, 5.5 and 6.6 eV. The interpolated line serves only to better visualization.

Some increase of the cross section of the ππ* states of 5.0 and 5.5 eV, at 8 eV incident energy and a broad feature in the cross section of the 5.0 and 6.6 eV state at 10 eV may be linked to the peripheral N–H bond breaking and deformations, but we also have to take into account the existence of triplet states and their contribution to the overall picture. Triplet states have been investigated very little.^31,44 In the previous HREEL study²⁸ of thymine, triplet states have been clearly observed at the EL of 3.7 eV (ππ*) and 4 eV (nπ*). In the case of adenine, according to the DFT calculation of Marian,⁴⁴ the lowest lying excited states of adenine are triplet states at 3.63 and 4.4 eV. Positions of higher-lying triplet states, existing in thymine, could not be accurately identified in adenine. Results of the combined DFT and multi-reference configuration interaction methods from a recent theoretical calculation⁴⁴ of the energies of singlet and triplet states of adenine are shown in Table 2(b). It is clear that the proximity of triplet and singlet states above 4 eV does not allow us to distinguish between them in the EL spectrum. The fact that we collect the scattered electrons at the angle which is large enough to make triplet states intensity significant with respect to the singlet states (which would dominate the spectrum at small scattering angles) is not sufficient to isolate the triplet states and analyze their energy dependence with certainty. There are only two other EEL experimental studies analyzing electronic excitation of adenine, available to date: one of 25 keV electrons scattered from a thin polycrystalline film of adenine deposited on graphite, by Isaacson,²⁷ and the other, of 200 eV electrons energy-loss measurements at 3 and 6° from adenine in the gas phase, by Dillon et al.¹¹ Both have observed only ππ* and σσ* singlet transitions. The latter experiment suggested the dissociation is due to the diffuse character of the EEL spectrum. The short lifetime of the first excited state was attributed to the IC to the ground state . Therefore, three of five Gaussian peaks that we used to deconvolute the EL spectrum with energies of 4.7, 5.0 and 5.5 eV, represent both triplet and singlet electronic states.

Conclusions

We presented here the experimental results of the HREEL study of the thin film of adenine within the incident electron energy range from 1.5 to 12 eV. EEL spectra of the vibrational excitation of the ground electronic state and the excitation of electronic states have been analyzed by deconvolution with the Gaussian peaks. We showed that the out-of-plane wagging of hydrogen atoms in the amino-group is the most intense vibrational mode of adenine, in its ground electronic state. The effective cross section over the half-angular space of this vibrational mode is the largest for the incident electron energy of 5 eV, reaching the value of almost 10^–16 cm². This may indicate either an existence of the transient negative ion or possible coupling of the excited nπ* (monomer) or/and πσ* (dimer) states with the ground electronic state as a result of the fast internal conversion , in either of these processes enhancing the vibrational motion of adenine. In thymine, this would have been impossible because the energy gap between the ππ* and πσ* states is larger and this relaxation channel becomes significant only in the presence of some stabilizing factor, such as the presence of water, for example. The resonance at about 3 eV incident electron energy contributes to the enhancement of the probability for excitation of all vibrational modes, but is stronger than the feature at 5 eV only in the case of asymmetric stretching of hydrogen atom in NH₂ and N9–H, at the EL of 0.435 eV. This first feature might be the resonance seen in the gas-phase experiments at 2.17 eV^10,57 and the calculated 4.4 eV resonance shifted down for 1.5 eV, as suggested by Tonzani and Green.⁴²

The effective cross sections of the electronically excited states are typically in the range of 10^–18 cm² and reach one order of magnitude higher values only for the ππ* singlet 6.1 eV state. A weak enhancement of the cross section for the 5 and 5.5 eV states for excitation by 8 eV incident electrons, that could be possibly linked to the core-excited resonance leading to H^– extraction, is not convincing enough to support the resonance at 9 eV from the desorption studies and that at 6.2 eV from the gas-phase measurements. Another weak and broad feature in the 5.0 and 6.6 eV electronic states cross sections at 10 eV incident electron energy may be a more probable indication of the excited states giving rise to the H^–-resonance. On the other hand, contributions from the triplet states at energies close to 4.7, 5.0 and 5.5 eV may completely change the interpretation of the features that we see in each of the cross sections of deconvoluted EEL spectra. Ambiguity in the energy of the singlet and the usually longer lived triplet electronically excited states in the EL spectrum of nucleic bases will remain to be a challenge for the future experimental and theoretical studies.

In the context of adenine within more complex molecules, such as DNA, the conformational changes during vibrational motion of a specific base in the DNA helix could delay, or, more drastically, even prevent binding of an appropriate enzyme, due to the “irregular” shape of the binding site. All deformations of the amino group are of particular importance for understanding the properties of complexes where adenine binds by means of the hydrogen bond. Vibrations of the azine group (NH), in particular, on the N9 site, are also important due to its role in binding to the sugar moiety in DNA and RNA. A study³ of the non-homologous crystal protein-ligand complex structure, where the ligand contains one or two nucleic acid bases, showed that 70–80% of all hydrogen bonds involve the atoms that discriminate between adenine and guanine. These results suggested that proteins evolved to recognize their cognate ligands and that they exhibit a strong preference to bind only to their own ligand and not other similar molecules found in the cell. Ligand atoms involved in recognition are the hydrogen bond donors (N10 in adenine). For example, the amino-acid Asparagin has distinctly higher propensity for adenine binding sites, where it is often found using its amide group to contact both N10 and N1 or N7. In a view of these studies and according to our measurements, the largest enhancement of the effective cross section at energies from 3–5 eV corresponding to the “out-of-plane” vibrations, could significantly affect the DNA functioning.

In summary, the biological relevance of the molecular excitation stems from two processes: firstly, from the molecular fragmentation due to the temporary negative ion formation and secondly, from the geometrical changes caused by the vibrational motion of the molecule. In DNA, conformational change is the signature of specific life-cycle processes and the binding of various enzymes and other metabolically important molecules may largely depend on its shape at the individual binding site. Furthermore, in the quest for better understanding and control of effects of high-energy ionizing radiation on living tissue, the effective cross sections for the electron–molecule interactions are of the ultimate importance. We showed that in the case of adenine these cross sections are of the order of 10^–18 to 10^–16 cm² and that the 3–5 eV electrons induce significant “out-of-plane” vibrational motion of the chemically important amino- and azine group, which may be linked to the H^– detachment from the molecule as well as to the ability of proteins to recognize the correct binding site on DNA. Further studies of adenine clusters with water would be beneficial to unraveling which of the aforementioned excitation processes may be enhanced or quenched in its presence. Such measurements would be a step forward to understanding the electron transfer processes in the aqueous solution and within the cell.

Acknowledgement

This research was financed by the Canadian Institute of Health Research.

References

1. S. J. Sowerby and W. M. Heckl, Origins Life Evol. Biosphere, 1998, 28, 283.
2. S. J. Sowerby, W. M. Heckl and G. B. Petersen, J. Mol. Evol., 1996, 43, 419.
3. I. Nobeli, R. A. Laskowski, W. S. J. Valdar and J. M. Thornton, Nucleic Acids Res., 2001, 29, 4294.
4. B. R. Bochner and B. N. Ames, J. Biol. Chem., 1982, 257, 9759.
5. L. P. Candeias and S. Steenken, J. Am. Chem. Soc., 1993, 115, 2437.
6. L. Sanche, Eur. Phys. J. D, 2005, 35, 367.
7. L. Sanche, Mass Spectrom. Rev., 2002, 21, 349.
8. S. Steenken, Biol. Chem., 1997, 378, 1293.
9. H.-H. Ritze, H. Lippert, E. Samoyolova, V. R. Smith, I. V. Hertel, W. Radloff and T. Schultz, J. Chem. Phys., 2005, 122, 224320.
10. K. Aflatooni, G. A. Gallup and P. D. Burrow, J. Phys. Chem. A, 1998, 102, 6205.
11. M. A. Dillon, H. Tanaka and D. Spence, Radiat. Res., 1989, 117, 1.
12. N. J. Kim, H. Kang, Y. D. Park and S. K. Kim, Phys. Chem. Chem. Phys., 2004, 6, 2802.
13. S. Ulrich, T. Schultz, M. Z. Zgierski and A. Stolow, J. Am. Chem. Soc., 2004, 126, 2262.
14. P. L. Levesque, M. Michaud and L. Sanche, Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 208, 225.
15. P. L. Levesque, M. Michaud, W. Cho and L. Sanche, J. Chem. Phys., 2005, 122, 224704.
16. E. Samoylova, H. Lippert, S. Ulrich, I. V. Hertel, W. Radloff and T. Schultz, J. Am. Chem. Soc., 2005, 127, 1782.
17. W. Cho, M. Michaud and L. Sanche, J. Chem. Phys., 2004, 121(22), 11289.
18. N. J. Kim, G. Jeong, Y. S. Kim, J. Sung, S. K. Kim and Y. D. Park, J. Chem. Phys., 2000, 113(22), 10051.
19. A. Reuther, H. Iglev, R. Laenen and A. Laubereau, Chem. Phys. Lett., 2000, 325, 360.
20. H. Kang, K. T. Lee and S. K. Kim, Chem. Phys. Lett., 2002, 359, 213.
21. M. J. Nowak, L. Lapinski, J. S. Kwiatkowski and J. Leszczyński, J. Phys. Chem., 1996, 100, 3527.
22. C. Desfrançois, H. Abdoul-Carime and J. P. Schermann, J. Chem. Phys., 1996, 104(19), 7792.
23. H. Abdoul-Carime, P. Cloutier and L. Sanche, Radiat. Res., 2001, 155, 625.
24. Chr. Plützer, E. Nir, M. S. de Vries and K. Kleinermanns, Phys. Chem. Chem. Phys., 2001, 3, 5466.
25. H. Kang, B. Jung and S. K. Kim, J. Chem. Phys., 2003, 118, 6717.
26. M. A. Huels, I. Hahndorf, E. Illenberger and L. Sanche, J. Chem. Phys., 1998, 108, 1309.
27. J. Isaacson, J. Chem. Phys., 1972, 56, 1803.
28. P. L. Levesque, M. Michaud and L. Sanche, Rev. Sci. Instrum., 2005, 76, 103901.
29. K. Aflatooni, A. M. Scheer and P. D. Burrow, J. Chem. Phys., 2006, 125, 054301.
30. S. K. Mishra, M. K. Shukla and P. C. Mishra, Spectrochim. Acta, Part A, 2000, 56, 1355.
31. M. T. Nguyen, R. Zhang, P.-C. Nam and A. Ceulemans, J. Phys. Chem. A, 2004, 108, 6554.
32. S. D. Wetmoore, R. J. Boyd and L. A. Eriksson, Chem. Phys. Lett., 2000, 322, 129.
33. A. Broo, J. Phys. Chem. A, 1998, 102, 526.
34. B. Cohen, C. E. Crespo-Hernández and B. Kohler, Faraday Discuss., 2004, 127, 137.
35. M. Meyer and J. Sühnel, J. Biomol. Struct. Dyn., 1997, 15, 619.
36. A. L. Sobolewski and W. Domcke, Eur. Phys. J. D, 2002, 20, 369.
37. R. Santamaria, E. Charro, A. Zacarías and M. Castro, J. Comput. Chem., 1999, 20(5), 511.
38. X. Li, M. D. Sevilla and L. Sanche, J. Am. Chem. Soc., 2003, 125, 8916.
39. P. Możejko and L. Sanche, Radiat. Environ. Biophys., 2003, 42, 201.
40. M. Preuss, W. G. Schmidt, K. Seino, J. Furthmüller and F. Bechstedt, J. Comput. Chem., 2004, 25, 112.
41. I. Al-Jihad, J. Smets and L. Adamowicz, J. Phys. Chem. A, 2000, 104, 2994.
42. S. Tonzani and C. Green, J. Chem. Phys., 2006, 124, 054312.
43. M. D. Sevilla, B. Besler and A.-O. Colson, J. Phys. Chem., 1995, 99, 1060.
44. C. M. Marian, J. Chem. Phys., 2005, 122, 104314.
45. N. Sreerama, R. W. Woody and P. R. Callis, J. Phys. Chem., 1994, 98, 10397.
46. P. L. Levesque, M. Michaud and L. Sanche, J. Chem. Phys., 2005, 122, 094701.
47. M. Michaud and L. Sanche, Phys. Rev. A, 1987, 36, 4672.
48. L. Sanche and M. Michaud, Phys. Rev. B, 1984, 30, 6067–6078.
49. M. M. Reiter, F. Jamitzky, F. Trixler and W. M. Heckl, Phys. Status Solidi A, 2001, 187(1), 171.
50. M. Östblom and B. Liedberg, J. Phys. Chem. B, 2005, 109, 15150.
51. M. Edelwirth, J. Freund, S. J. Sowerby and W. M. Heckl, Surf. Sci., 1998, 417, 201.
52. J. E. Freund, M. Eselwirth, P. Kröbel and W. M. Heckl, Phys. Rev. B, 1997, 55, 5394.
53. From http://webbook.nist.gov/chemistry.
54. S. K. Kim, W. Lee and D. R. Herschbach, J. Phys. Chem., 1996, 100, 1933.
55. S. G. Stepanian, G. G. Sheina, E. D. Radchenko and Y. P. Blagoi, J. Mol. Struct., 1985, 131.
56. Z. Dhaouadi, M. Ghomi, J. C. Austin, R. B. Girling, R. E. Hester, P. Mojzes, L. Chinsky, P. Y. Turpin, C. Coulombeau, H. Jobic and J. Tomkinson, J. Phys. Chem., 1993, 97, 1074.
57. S. Gohlke, H. Abdoul-Carime and E. Illenberger, Chem. Phys. Lett., 2003, 380, 595.
58. A.-O. Colson, B. Besler and M. D. Sevilla, J. Phys. Chem., 1994, 96, 9787.
59. D. Huber, M. Beikircher, S. Denifl, F. Zappa, S. Matejcik, A. Bacher, V. Grill, T. D. Märk and P. Scheier, J. Chem. Phys., 2006, 125, 084304.
60. H. Abdoul-Carime, J. Langer, M. A. Huels and E. Illenberger, Eur. Phys. J. D, 2005, 35, 399.

---

Footnotes

† Electronic supplementary information (ESI) available: Integral cross sections (over the half-space angle) for electron induced vibrational excitation of molecules in a thin film of condensed adenine (Table S1); Integral cross sections (over the half-space angle) for electron induced excitation of molecules in a thin film of condensed adenine (Table S2). See DOI: 10.1039/b612700b

‡ I_o,d can be interpreted as the fraction of the incident electron current backscattered in the direction θ_d by an ideal medium, with the total electron reflectivity of 1.

§ The electron beam of 0.77 nA delivers 4.8 × 10⁹ electrons s^–1 onto the spot of 7.85 × 10^–5 cm². Typical time of exposure of the film was 300 s, except for incident electron energy ≥11 eV, when it was ten times longer. Combining this time with the estimated probability for the electronic excitation of the target, of ∼10^–17 cm² and the number of incident electrons, we obtain that only two out of a thousand (or one hundred for higher energies) electrons are potentially damaging molecules in the film. The average number of adenine molecules in the monolayer spot is 1.64 × 10¹². This means that only a very small number of molecules in the film suffer any damage during exposure to the incident electron beam.

---