Product pair correlation in bimolecular reactions
Kopin
Liu
ab
aInstitute of Atomic and Molecular Sciences (IAMS), Academia Sinica, P.O. Box 23-166, Taipei, 10617, Taiwan
bDepartment of Chemistry, National Taiwan University, Taipei, 10617, Taiwan
First published on 27th November 2006
Abstract
The vast majority of chemical reactions involve polyatomic species as reactants and/or products. The added degree of complexity offers opportunities to address dynamical questions other than those already encountered in a typical atom + diatom reaction. Product pair correlation is one of them. This article introduces the basic concept, outlines the experimental approach we developed and then highlights some of the applications to bimolecular reaction dynamics. Particular emphasis is placed on the information contents and unique insights gained from this type of measurements, which otherwise would have been lost by the conventional approach.
I. Introduction
One of the fundamental goals of physical chemistry is to understand how a chemical reaction—an elusive process whereby old chemical bonds are broken and new bonds are formed—actually takes place at the microscopic level.1 Reaction dynamists address this question from the molecular point of view, i.e., how the atoms rearrange themselves in going from reactants to products. Past decades have witnessed spectacular advances in our fundamental understanding of the detailed dynamics of elementary chemical reactions.2–4 This progress has been driven by a very stimulating and fruitful interaction between theory and experiment, which is the hallmark of the field of reaction dynamics.On the experimental front, the development of modern ultrahigh vacuum technology has extended the universal crossed-molecular beam studies to a wider range of reaction systems.5 The recent implement of the soft ionization technique,6 either by low energy electron impact ionization technique or using photoionization method, enables dynamists to push the capability of the universal machine further—to obtain a complete picture on the branching ratio of all energetically allowed product channels, thus becoming truly universal. While the universal machine is ideal for studying a complex reaction with multiple product channels, its resolution is in general not sufficient to obtain product state-resolved information. Such information, on the other hand, can be acquired by laser spectroscopic methods, most notably laser-induced fluorescence (LIF) and resonance-enhanced multiphoton ionization (REMPI). By exploiting more sophisticated detection schemes of those laser based methods, such as Doppler technique,7 ion time-of-flight (TOF)8 or their combination (Doppler-selected TOF),9 Rydberg H-atom TOF,10 and ion velocity-map imaging technique, etc.,11 even the state-resolved differential cross sections have been demonstrated for a number of benchmark reactions. Theoretical progress over the past decade or so is equally impressive. Tremendous advance in theoretical methodologies and computational capabilities has been made, so that for simple three- and four-atom systems the state-to-state differential cross section can now be simulated by exact quantum dynamics calculations on a fully ab initio potential energy surface (PES). In fact, the state-of-the-art theoretical results for a few benchmark A + BC reactions can even rival the most detailed experimental measurements.12
Remarkable as those achievements are, the advances in our understanding of the dynamics of polyatomic reactions, which often yield two molecular species as products, are handicapped. The conventional product state distribution measurements for one species is blind to the state distribution of its coproduct; yet, the two products are formed together as a colliding pair from each individual reactive encounter. Clearly, the coincident information of the two product state distributions is desirable, which will enable dynamists to gain deeper and heuristic insights applicable to a much wider range of reaction systems of interest to the general chemistry community. This Invited Article gives a pedagogical account of our attempt towards that goal. The concept of product pair correlation will first be presented in section II, followed by our experimental approach in section III. A few systems will then be highlighted in section IV, with the emphasis on how the new or otherwise lost dynamics information can be recovered through this type of measurement. Section V concludes with a very brief comment and outlines several other applications that remain outside the scope of this review.
II. What is the product pair correlation?
More precisely, we are speaking of the quantum state-correlation of the product pair from a bimolecular reaction. Considering a polyatomic reaction yielding two molecular products, say F + CH4 → HF(ν′) + CH3(νi). The product methyl radical CH3 has six vibrational modes (two of them are doubly degenerate), what is the correlation between the vibrational modes of two product molecules? And for a given mode of CH3, what is the quantum number correlation between HF and CH3? In terms of probability theory, what we are seeking is the joint or conditional probability distributions of the quantum states of the two products, i.e., the pair-correlated distribution P(ν′,νi)11,13,14A simple consideration suffices for illustration. Exemplified in Table 1 is a hypothetical 4 × 4 matrix representing the joint probability matrix of the two products from the F + CH4 reaction. The matrix element then gives the pair-correlated probability for finding a HF vibrator coincidently formed in stated ν′ when a CH3 oscillator is in state νi from the same reactive event. The traditional product state distributions P(ν′) and P(νi) are simply averages of P(ν′,νi) according to P(ν′) = ∑νiP(ν′,νi) and, likewise, for P(νi). Because the correlated information P(ν′, νi) is ν′ × νi in dimension (i.e., 4 × 4 = 16 in this example), it can be significantly larger than the sum of the uncorrelated information, ν′ + νi (i.e., 4 + 4 = 8 here). Obviously, it is not feasible to retrieve the full P(ν′,νi) matrix from the information of P(ν′) and P(νi) alone even if both are available.
| ν′, ν″ | 0 | 1 | 2 | 3 | P(ν′) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.01 | 0.01 | 0.02 |
| 1 | 0 | 0.02 | 0.05 | 0.02 | 0.09 |
| 2 | 0.09 | 0.2 | 0.07 | 0.01 | 0.37 |
| 3 | 0.35 | 0.1 | 0.06 | 0.01 | 0.52 |
| P(ν) | 0.44 | 0.32 | 0.19 | 0.05 | 1.0 |
It is instructive at this point to consider two limiting cases. If the two products are completely uncorrelated, namely, if the vibrational distribution of HF is independent of the CH3 state, one has P(ν′,νi) = P(ν′) P(νi). An obvious example is the spectator case in which a group of atoms, say the CH3 moiety, plays a small role in the reaction and becomes one of the products. Another dynamically uncorrelated example is the statistical case, for which the product pair correlation may not convey much additional information about dynamics, as it can be largely predicted by statistical models based on energy and angular momentum constraints.14 If, on the other extreme, the two vibrators are strictly correlated, for example, ν′ = νi + n, with n an integer, the joint probability matrix can then be expressed as P(ν′,νi) = δνi+n,ν′ P(ν′). In both extreme cases, uncorrelated and totally correlated, it suffices to merely measure the averaged probabilities P(νi) and P(ν′). More often, the situation lies between the two limiting cases and a direct determination of P(ν′,νi) will be more telling.
III. How to measure P(ν′,νi)?
The key idea of experimental determination of P(ν′,νi) is in fact rather simple. Consider the reaction F + CH4 → HF(ν′) + CH3(νi) at collisional energy Ec, the conservation of energy leads to | (1) |
with μ denoting the respective product speed in the center-of-mass (c.m.) frame. The conservation of linear momentum in the c.m. frame requires mHFμHF + mCH3μCH3 = 0. Incorporating the momentum conservation into the ET′ expression, one has
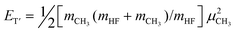 | (2) |
Now, if one performs an experiment with a well-defined Ec and manages to detect one of the products, say CH3, in a state-resolved manner, from eqn (1) one is left with two unknowns, EHF(ν′) and ET′. However, if one goes one step further by simultaneously measuring the speed μCH3 of the state-tagged CH3(νi), then from eqns (1) and (2), the desired state-correlated information of the HF coproduct will be uncovered from the measured CH3-speed distribution.
With the above in mind, we developed a time-sliced ion velocity-imaging technique to make the idea a reality.11,15 We employed crossed molecular beam technique to control the initial collision energy Ec. A (2 + 1) REMPI detection scheme was used to state-selectively tag the methyl radical product.16 Taking advantage of the multiplexity nature of the ion imaging technique, we improved upon the conventional velocity-map approach by incorporating the ion TOF method into the imaging technique, thus, the so-called time-sliced velocity imaging technique.15 The desired pair-correlated distributions are then revealed directly from the raw images. Since the main purpose of this overview is to send the message of the unique opportunity of pair-correlation data in unveiling the “hidden” reaction dynamics, we will leave the technical detail of experiments untouched. The interested readers are referred to ref. 17 for a comprehensive review on the recent developments of ion imaging techniques and ref. 15 for the specific detail of our experimental setup. In the following we will just focus on the new dynamical aspects that have been uncovered from such type of measurements.
IV. What have we been learning?
The motivation for developing the pair-correlation measurement arises from our desire to have better perspective on what happens in the transition state of a polyatomic reaction. Let us elaborate it from the viewpoints of transition state theory (TST). The transition state represents a dividing surface between reactants and products on a reactive PES and acts as a dynamical bottleneck that gates the reactive flux. Thus, the detailed characterization of the transition state has been a long-standing goal in chemical reaction dynamics and kinetics. In the context of TST, one is interested in knowing the energy of the transition state relative to separated reactants, the transition state geometry and the frequencies of the 3N-7 (or 3N-6 for a linear transition state) bound vibrational modes of the transition state that are orthogonal to the reaction coordinate. The involvement of those properties of the transition state in predicting a reaction rate is most clear from Eyring’s formulation of TST.18,19 In this approach, a quasi-equilibrium between transition-state species and reactants is postulated and the emphasis is on the equilibrium distribution in the dividing surface and on the statistical character of the equilibrium approximation. The alternative point of view of TST formulated by Wigner, however, stresses the collisional or dynamical behaviour of the transition state.20,21 In this view, the transition state can be regarded as a dynamical entity and the fundamental factor in governing the chemical reactivity becomes the collective motions of all atoms in the transition state region. Pushing that idea a bit further, we conjectured that in a direct reaction the quantum state- or mode-correlation of the product pair should carry more insightful imprints of the concerted motions of atoms upon old bond rupture and new bond formation. In the remainder of this section a number of reactions will be highlighted to elucidate what mechanistic insights have been revealed through the pair-correlation measurements.A State correlation matrix in F + CD4 → DF(ν′) + CD3(ν2)
This is a fast and very exothermic reaction, ΔHrx = −31.1 kcal mol−1 (or −130.1 kJ mol−1). The thermal rate coefficient for the isotopically analogous reaction F + CH4 can be expressed as k = 1.64 × 10−10 exp(−265/T) cm3 molecule−1 s−1.22 Previous HF infrared chemiluminescence studies established a highly inverted vibrational distribution, peaking at HF(ν′ = 2),23 and a relatively low rotational excitation.24 Time-resolved diode laser absorption spectroscopy was used to probe the CH3 umbrella mode (ν2) excitation. A vibrational distribution of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.36
0.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.15 was found for ν2
= 0, 1 and 2, respectively.25 Hence, the state distributions of both reaction products have been interrogated, which are all one can measure using the conventional experimental approach. Yet, the HF and CH3 products are always formed together as a pair from a single reactive event; thus, their state distribution must be somehow correlated. For example, as CH3 is produced with one quantum excitation of the umbrella mode in a reactive encounter, what is the probability for concomitantly forming HF in a particular vibration state, say ν′
= 1; and how is it different when CH3 is formed in another vibration state?
0.15 was found for ν2
= 0, 1 and 2, respectively.25 Hence, the state distributions of both reaction products have been interrogated, which are all one can measure using the conventional experimental approach. Yet, the HF and CH3 products are always formed together as a pair from a single reactive event; thus, their state distribution must be somehow correlated. For example, as CH3 is produced with one quantum excitation of the umbrella mode in a reactive encounter, what is the probability for concomitantly forming HF in a particular vibration state, say ν′
= 1; and how is it different when CH3 is formed in another vibration state?
Illustrated in Fig. 1 are the raw images of the CD3 products in four different vibration states from the reaction F + CD4 at the collisional energy of 5.37 kcal mol−1.11 A (2 + 1) REMPI scheme was used to probe CD3 in a state-specific manner and the velocity distribution of the state-selected CD3 was then mapped by the time-sliced velocity imaging technique. Superimposed on the images are the velocity vector diagrams (Newton diagrams) of the collision system. The energetics of the reaction are well-defined; thus, by conservation of energy and momentum, the maximum velocities of the coproduct DF, recoiling from the REMPI-selected state of CD3, in different vibration states can be calculated and are represented as dashed lines in Fig. 1. The successive rings on each image can be unambiguously assigned to the vibrational states of the DF coproduct. The intensity around each ring then gives an immediate impression about the preferred scattering direction of the coincidently formed DF states—the state-pair correlated angular distribution or the correlated differential cross section (CDCS).
 | ||
| Fig. 1 Raw images of the state-selected CD3 products from the F + CD4 → DF(ν′) + CD3(ν2) reaction at Ec = 5.37 kcal mol−1. The labeled REMPI band Pnm denotes the mode P with m and n quanta of excitations in the electronically ground and excited states, respectively. The successive rings on each image correspond to the indicated vibrational states of the coincident DF products (adapted from ref. 11). | ||
Several interesting observations are worth noting just from glancing at those raw images. For a given ν′ the decrease of the ring size for the higher CD3 vibration excitaiton is in accord with energetic considerations. In terms of angular distributions, for all CD3 states, the coincidently formed DF in ν′ = 2 is confined within the backward hemisphere. The gradual protrusion of its angular distribution in the sideways direction with higher excited CD3(ν2) coproduct state is reminiscent of the usual trend observed for a typical A + BC reaction proceeding through a direct rebound mechanism.1 The angular distributions for DF(ν′ = 3) spread over all angles, but its dominant feature shifts progressively from sideways to forward as increasingly more energy is deposited into the umbrella mode of the CD3 coproduct. For the DF product in ν′ = 4, the most prominent feature is a very sharp forward-scattered peak. What is truly amazing about Fig. 1 is to see such a rich variety of CDCS of each product pair from the very same chemical reaction.
Another remarkable aspect is the state-correlated population or the correlated integral cross section (CICS), which are summarized in Fig. 2 as the correlation matrices at four different collision energies.26 Shown on the background in each figure is the conventional vibration distribution of DF (or CD3) that is obtained by summing the pair-correlated populations for each fixed vibration state of CD3
(or DF). It is interesting to note that P(ν′)s remain highly inverted at all four Ecs, while P(ν2) changes from a cold distribution at Ec
= 1.5 kcal mol−1 to a slightly inverted one at higher Ec values. More significant is the observation of an anti-correlated excitation of the two product vibrators, i.e., the lower the CD3 vibration excitation, the higher excitation of the DF is, which also proves beyond any doubt that the CD3-moiety is not a spectator in this reaction. The origin of this behavior could largely be kinematic.11,13,26 For a heavy + light-heavy collinear reaction, the mass-weighted skew angle1 is small (β
= 25.5° for the F–D–CD3 reaction) and a strong inertia coupling between the two scaled coordinates is anticipated, which in turn leads to the Polanyi’s rule27 that the reagent translation in excess of the barrier to reaction is deposited mainly into product translation, i.e., ΔEc
→
Δ(ET). The conservation of energy can be expressed as Etotal
=
Ec
−
ΔHrx
=
VCD3
+
RCD3
+
VDF
+
RDF
+
ET, where V and R denote the corresponding vibrational and rotational energies, respectively. The angular momentum conservation dictates that ![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ≈
J
=
NCD3
+
jDF
+
≈
J
=
NCD3
+
jDF
+
![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′, where
′, where ![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′) is the orbital angular momentum of the two reactants (products), J represents the total angular momentum of the reaction system and N and j denote the respective rotational angular momenta. For a light-atom transfer reaction, both the initial and final orbital angular momenta (
′) is the orbital angular momentum of the two reactants (products), J represents the total angular momentum of the reaction system and N and j denote the respective rotational angular momenta. For a light-atom transfer reaction, both the initial and final orbital angular momenta (![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) and
and ![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′) are mainly carried by the orbital motions of the two heavy particles. For a nearly collinear reaction, one often has
′) are mainly carried by the orbital motions of the two heavy particles. For a nearly collinear reaction, one often has ![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ≈
≈
![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′, as demonstrated by Schulten and Gordon.28 Thus, both NCD3 and jDF
(or RCD3 and RDF) are likely to be small, which is exactly what we found experimentally.26 In combination with Ec
→
Δ(ET), thereby the two product vibrators should exhibit anticorrelated excitations.
′, as demonstrated by Schulten and Gordon.28 Thus, both NCD3 and jDF
(or RCD3 and RDF) are likely to be small, which is exactly what we found experimentally.26 In combination with Ec
→
Δ(ET), thereby the two product vibrators should exhibit anticorrelated excitations.
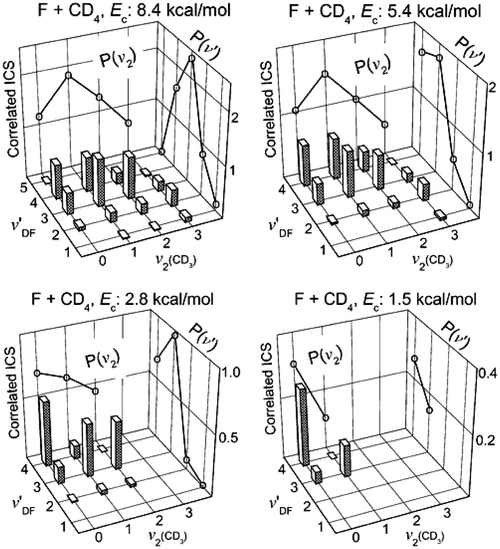 | ||
| Fig. 2 A 3-D representation of the correlated integral cross section (CICS) or the correlated state population of product pairs for F + CD4 → DF(ν′) + CD3(ν2) at four collision energies. All data have been scaled according to the CD3 vibration state distribution from ref. 16. Summing the pair-correlated populations for each fixed vibration state of CD3 (or DF) yields the conventional vibration distribution of DF (or CD3), which is displayed as open circles on the respective background (adapted from ref. 26). | ||
B Stereodynamics of F + CD4 reaction
The above example shows how the pair-correlated information can be used to elucidate the dynamics of vibrational motions that is otherwise lost by conventional, uncorrelated measurements. One of the major conclusions drawn from there is the active role of the CD3vibrator participating in the reaction. What is then the role of CD3-moiety as a rotor in the reaction? As it turns out, the product pair measurements not only provide a clear answer to the question, but also reveal interesting stereodynamics of the reaction.To explore the rotational correlation, we resorted to the N-resolved REMPI spectral feature to interrogate the behavior of the individual CD3N-state. Summarized in Fig. 3 are the pair-correlated angular distributions (CDCSs) derived from rotationally selected CD3(ν = 0, N) product images for the reaction F + CD4 → DF(ν′) + CD3(ν = 0) at the collisional energy of 5.37 kcal mol−1.29 It is amazing that even the total angular distribution (i.e., N-state resolved differential cross section) exhibits such rich variations as well remarkable sensitivities to the individual N state, which provides unequivocal evidence for the active role the CD3 rotor in this reaction. Closer inspection of the individual CDCS also indicates significant variations in the correlated vibration branching with N. Fig. 4a summarizes the results.29 The general trend is quite obvious; the inverted DF vibration distribution becomes more relaxed as the rotational quantum number N of the coincidently formed CD3 increases. This finding is quite intriguing in that the vibrational spacing of DF is around 7.5 kcal mol−1 and the rotational energy difference of CD3 is significantly smaller, e.g. merely 1.07 kcal mol−1 between N = 3 and 9; yet, the product pair of the DF vibrator and the CD3rotor appears highly correlated. Viewing this correlation in a different way provides further insights into its physical origin. Fig. 4b presents the dependence of correlated energy disposal on the CD3(ν = 0) product rotation energy EN.29 All three average energies exhibit a linear dependence on EN. (Note the different energy scales of the left ordinate for 〈VDF〉 and the right ordinate for 〈RDF〉 or 〈ET〉.) From Fig. 4a, a more relaxed vibration distribution for a higher N state yields, of course, less vibration energy of the DF coproduct. On the other hand, an opposite trend is observed for ET, i.e., higher N states give more kinetic energy release. The average energy of the DF rotor shows little variation with the rotation of the CD3 coproduct.
 | ||
| Fig. 3 Correlated differential cross sections (CDCSs) of the product pairs DF(ν′) + CD3(ν = 0, N) from F + CD4 at Ec = 5.37 kcal mol−1. The rotational lines of the REMPI-probe of CD3(ν = 0, N) are indicated. Note the remarkable sensitivities of the angular distributions as well as the vibrational branchings of the DF coproducts to the rotational motions of the CD3 product (adapted from ref. 29). | ||
 | ||
| Fig. 4 (a) Dependence of DF vibrational branchings on the rotational quantum number N of the CD3(ν = 0) coproduct. The result for N = 1 is approximated from the S(1)/R(4) result, which contains about 60% contribution from S(1). Similarly, N = 2 is estimated by S(0)/R(2) that has ∼ 70% from R(2). (b) Dependence of correlated energy disposals on the CD3(ν = 0) product rotational energy EN. All three average energies exhibit a linear dependence on EN. The apparent deviation for N = 2 is attributed to the K dependency (see ref. 29 for detailed account). | ||
In a very illuminating paper, Schechter et al.30 argued convincingly that the usual conversion of reactant orbital angular momentum ![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) to product rotational angular momentum j′ for a heavy + heavy–light system should also hold for other mass combination in collinearly dominated reactions due to the steric requirements of the reaction. Hence, one has j′
≈
α
to product rotational angular momentum j′ for a heavy + heavy–light system should also hold for other mass combination in collinearly dominated reactions due to the steric requirements of the reaction. Hence, one has j′
≈
α![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) under more general conditions, where α is a dimensionless factor accounting for kinematic constraints. For the reaction F + CD4, the transition state is believed to be nearly collinear in F⋯D⋯C geometry.31–36 We asserted analogously j′
≈
α
under more general conditions, where α is a dimensionless factor accounting for kinematic constraints. For the reaction F + CD4, the transition state is believed to be nearly collinear in F⋯D⋯C geometry.31–36 We asserted analogously j′
≈
α![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) for the newly formed DF rotor.37 Recalling that RDF
≈
Bj′2 and
for the newly formed DF rotor.37 Recalling that RDF
≈
Bj′2 and ![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) 2
= 2 μb2Ec, thus 〈RDF〉
∝
Ec, which also implies that 〈RDF〉 is nearly independent of the N state of CD3—exactly as was found experimentally (Fig. 4b). Consideration of the conservation of energy, as the vibrational ground state of CD3 was probed, leads to VDF
+
RCD3
+
ET
=
−ΔHrx
+
Ec
−
RDF. From 〈RDF〉∝
Ec, one has VDF
+
RCD3
+
ET
= const.—or invariant to the selected N states. The linear relationship shown in Fig. 4b, 〈VDF〉
=
−3〈RCD3〉 can then be alternatively expressed as 〈ET〉
≅
C
+ 2EN, where C represents a positive constant.
2
= 2 μb2Ec, thus 〈RDF〉
∝
Ec, which also implies that 〈RDF〉 is nearly independent of the N state of CD3—exactly as was found experimentally (Fig. 4b). Consideration of the conservation of energy, as the vibrational ground state of CD3 was probed, leads to VDF
+
RCD3
+
ET
=
−ΔHrx
+
Ec
−
RDF. From 〈RDF〉∝
Ec, one has VDF
+
RCD3
+
ET
= const.—or invariant to the selected N states. The linear relationship shown in Fig. 4b, 〈VDF〉
=
−3〈RCD3〉 can then be alternatively expressed as 〈ET〉
≅
C
+ 2EN, where C represents a positive constant.
The conservation of angular momentum can be written as ![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ≈
≈
![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′
+
j′
+
N. The assumption of j′
≈
α
′
+
j′
+
N. The assumption of j′
≈
α![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) yields (1 −
α)
yields (1 −
α)![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ≈
≈
![[scr J, script letter J]](https://www.rsc.org/images/entities/b_char_e529.gif) ′
+
N. Squaring it and expressing the terms in the respective energy, one obtains 〈ET〉
≅
C1Ec
−
C2EN
−
C3〈
′
+
N. Squaring it and expressing the terms in the respective energy, one obtains 〈ET〉
≅
C1Ec
−
C2EN
−
C3〈![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′·N〉, where the weak N-dependent parameters have been grouped into three positive constants C1, C2 and C3.37 Comparing it with the above relationship of 〈ET〉
≅
C
+ 2EN and recalling that C is a positive constant, one is led to the conclusion that 〈
′·N〉, where the weak N-dependent parameters have been grouped into three positive constants C1, C2 and C3.37 Comparing it with the above relationship of 〈ET〉
≅
C
+ 2EN and recalling that C is a positive constant, one is led to the conclusion that 〈![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′·N〉 is most likely N-dependent and negative. In other words, N tends to lie antiparallel to
′·N〉 is most likely N-dependent and negative. In other words, N tends to lie antiparallel to ![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′—an alignment in the collisional frame.29,37 Since the structure of the CD3-moiety must be, on average, perpendicular to the F–D–C plane near the transition-state region, the physical implication of the N–
′—an alignment in the collisional frame.29,37 Since the structure of the CD3-moiety must be, on average, perpendicular to the F–D–C plane near the transition-state region, the physical implication of the N–![[small script l]](https://www.rsc.org/images/entities/b_i_char_e146.gif) ′ antiparallelism is that the product of CD3 rotors should be primarily of the tumbling rotation (rotating around a C2 axis) in the molecular frame, rather than the spinning rotation (rotating around the C3 axis). This conclusion is entirely in corroboration of that drawn from the (N,K)-state distribution measurements.16 The driving torque to induce the tumbling motion of CD3 products, however, must arise from, despite an on-avearge collinear transition state, the interactions and/or even exchange between the transferred D atom and the other three “passive” D atoms as the two products recede from each other. This illustrates the requisite in unfolding the detailed reaction dynamics from the concerted motions of all atoms—i.e., more than just the static aspects—in the transition state, a point that has been stressed in the beginning of this section.
′ antiparallelism is that the product of CD3 rotors should be primarily of the tumbling rotation (rotating around a C2 axis) in the molecular frame, rather than the spinning rotation (rotating around the C3 axis). This conclusion is entirely in corroboration of that drawn from the (N,K)-state distribution measurements.16 The driving torque to induce the tumbling motion of CD3 products, however, must arise from, despite an on-avearge collinear transition state, the interactions and/or even exchange between the transferred D atom and the other three “passive” D atoms as the two products recede from each other. This illustrates the requisite in unfolding the detailed reaction dynamics from the concerted motions of all atoms—i.e., more than just the static aspects—in the transition state, a point that has been stressed in the beginning of this section.
Electronically, this reaction is isoelectronic to the above F + CD4 reaction. For the latter reaction, the product DF has one vibrational mode and experimentally only the vibrationally ground and umbrella-excited CD3 products were found to have significant populations; hence, only the quantum-state correlation of the two products has been elucidated, as illustrated above in section IV(A). For the OH + CD4 reaction, the added complexity—a seven atom reaction with two polyatomic products—offers the opportunity to explore the unprecedented mode correlation of product pairs.
Fig. 5 exemplifies three time-sliced raw images of the CD3 products from the OH + CD4 reaction.41 In (a) the ground state CD3(ν = 0) was probed at the collisional energy of 10.0 kcal mol−1. The images shown in (b) and (c) are for the umbrella-mode excited CD3(ν2 = 2) at 10.6 and 13 kcal mol−1, respectively. While all three images display several concentric ringlike features, their appearances are noticeably different. In the case of CD3(ν = 0), the angular distribution is broad and predominantly in the backward hemisphere and on energetic ground, the most intense feature can be assigned to the HOD (200) coproduct [we denote the vibrational level of HOD as (νODνbendνOH)]. On the other hand, the most abundant HOD becomes (100) when CD3(ν2 = 2) was probed at both energies.
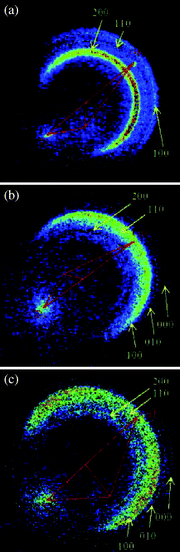 | ||
| Fig. 5 Raw images of the state-selected CD3 from the OH + CD4 → HOD + CD3 reaction. Shown in (a) is for probing CD3(ν = 0) at Ec = 10.0 kcal mol−1, (b) and (c) for CD3(ν2 = 2) at 10.6 and 13.0 kcal mol−1, respectively. Superimposed on each image is the Newton diagram. The dashed circles represent the maximum recoiled speed of the labeled vibrational states (νODνbendνOH) of the coincidently formed HOD. The spots along the CD4 beam are background, thus were discounted in data analysis (adapted from ref. 41). | ||
The qualitative impressions can be quantified after the image analysis.15 The vibration-correlated distributions thus obtained are presented in Fig. 6.41 As summarized in the lower-right panel of Fig. 6, the correlated distribution of HOD in concomitance with CD3(ν = 0) is dominated by the first overtone excitation of OD stretching mode (200) that amounts to two-thirds of total available energy. A small population of bending excitation is found in the combination mode (110). Both findings are in line with an impulsive bond-breaking mechanism based on the theoretical transition state structure:42,43 the HO–DCD3 bond length (1.32 Å) is significantly larger than the D–OH product (0.97 Å) and the angle for D–O–H (97°) at transition state is somewhat smaller than the asymptotic value of 103.4°. The theoretically calculated transition-state eigenvector corresponds primarily to a motion of the D-atom transferring between the C and O centers,43 which could provide the necessary kick-start and thus tends to support the impulsive mechanism. We note in passing that the general pattern of this correlated HOD distributions is strikingly similar to that for the OH + D2 → HOD + D reaction at somewhat lower collision energy of 6.6 kcal mol−1.44 It seems to suggest the spectator role of CD3 when formed in the ground state. This conclusion is in accord with that drawn from the study of the isotope effects of this reaction.45
 | ||
| Fig. 6 The product speed distribution P(μ) derived from the images shown in Fig. 5. The heavy lines are the fitting results and the thin lines are the individual components. The lower right panel summarizes the pair-correlated populations (adapted from ref. 41). | ||
On the other hand, when CD3(ν2 = 2) was probed, the correlated HOD distribution changes dramatically. The dominant state shifts downward to (100)—a state correlation. Similar anticorrelation in quantum numbers of the paired vibrators was illustrated above in section (A) for the F + CD4 reaction. Also note that Fig. 6a and b have the same initial collision energy and CD3(ν2 = 2) at 13 kcal mol−1 has essentially the same available energy for disposal [recalling that E(ν2 = 2) = 2.76 kcal mol−1] as is the case for CD3(ν = 0). Therefore the observed drastic change in pair correlation is not energetic in origin. More remarkable is the pronounced increase in bending excitation—a mode correlation. Fig. 7 elucidates such mode correlation in another way.46 Plotted here are the collisional energy dependencies of the ratio of (bend + stretch/bend combination)/(pure stretch) of the correlated HOD products. While the ratios for CD3(ν = 0) exhibit a clear increase with the increase in Ec, those for CD3(ν2 = 2) are significantly larger with a milder dependence on Ec. Unlike the stretching vibrations, the umbrella and bending motions are nonlocalized and involved the concerted motions of three or more atoms. We surmised the observed mode correlation as an imprint of different collective motions of all atoms in the vicinity of the transition state region. More explicitly, theory predicted a hydrogen-bonded post-reaction complex D3C⋯DOH with a more bent interproduct configuration, i.e., the C⋯D–O angle of 158°.43 The formation of CD3(ν2 = 2) is assumed to involve preferentially larger impact-parameter collisions with wider cone of acceptance, which not only slow down the passage over the transition state region, allowing more time for intramolecular energy flow, but also mediate the colliding pair to attain more readily the transitory complex geometry, which experiences more post-barrier anisotropic interactions, thus enhancing bend-excited CD3.41 The different behaviour of CD3(ν = 0) and CD3(ν2 = 2) shown in Fig. 7 is consistent with the proposed scenario. In other words, the observed mode correlation in this reaction is interpreted as the result of a bifurcation of the subtle reaction pathways driven by dynamics in passing through the transition state region. Once again, what really counts appears to be the collective motions of all atoms in the region of the reaction bottleneck.
 | ||
| Fig. 7 Collisional energy dependencies of the (bend + stretch/bend combination)/(pure stretch) ratio of the correlated HOD products for the two CD3 product states. The error bars encompass the uncertainties from two independent measurements as well as in fitting the P(μ) distributions as exemplified in Fig. 6 (adapted from ref. 46). | ||
D Reactive resonance in the F + CH4 reaction
The discovery of a reactive resonance in this polyatomic reaction stemmed from a puzzling REMPI result, which is exemplified in the left panel of Fig. 8.47 As is shown, the high-energy spectrum of the CH3 product displays a normal spectral pattern—a dominant Q branch with rotational-resolved P, O, R and S branches on either side.16 As the collision energy decreases, the spectral feature of the 111 band prevails and becomes comparable in intensity to that of 000 band at Ec = 0.48 kcal mol−1. The right-panel summarizes the intensity ratios as a function of collisional energy. The ν1 is the symmetric-stretch mode with a high harmonic frequency of 3004 cm−1.48 Its production occurring only near the reaction threshold is counterintuitive and surprising. | ||
| Fig. 8 The left panel shows three typical (2 + 1) REMPI spectra around the 000 band of the CH3 product from the F + CH4 reaction. The rotational features are discernible in the high collision energy spectrum. At lower energies, they gradually disappear, indicating less rotational excitation of the CH3 products and the 111 band pops out. The right panel summarizes the collision energy dependence of the intensity ratio of the 111 band and the 000 Q head. The reactive excitation function for the production of the CH3(ν = 0) is shown in the inset (from ref. 49). Combining these two results, the formation of CH3(ν1 = 1) is significant only near the reaction threshold (adapted from ref. 47). | ||
The underlying mechanism for the unexpected observations was elucidated through the pair-correlated measurements.47 The images shown in Fig. 9a and b are for the probe laser frequency set at the peak of the 111 band, i.e., probing the CD3(ν1 = 1) products. At Ec = 2.65 kcal mol−1, the three concentric rings are discernibe. As shown in Fig. 8a, at this collision energy both 111 and P(4) transition of the 000 band can contribute spectroscopically. By virtue of energy conservation, two CH3 vibrational levels should result in different velocities on the product image. Indeed the three image features can, on energetic ground, be readily ascribed to the product pairs as indicated. The two inner rings dominate the image, reflecting a high specificity of state correlation in product pairs. At Ec = 0.48 kcal mol−1, the production of the HF(ν′ = 3) + CH3(ν = 0, N = 4) pair is energetically closed. Hence, only the feature of the HF(ν′ = 2, j′) + CH3(ν1 = 1) pair remains, for which a forward–backward asymmetric peaking distribution is noted, as the case for Ec = 2.65 kcal mol−1. When the laser frequency was shifted to the peak of the 000 band at Ec = 0.48 kcal mol−1, the resultant image is displayed in Fig. 9c. Far richer features are vividly seen and the successive ring structures can be assigned to the coincidently formed rotational states of the HF(ν′ = 2) coproducts, starting from j′ = 13 for the innermost ring and outward. Inspection of the image reveals a broad rotational distribution up to the energetic limit. Moreover, high j′ states are preferentially scattered in the forward direction, oppositely to the low j′ states. These striking rotational features persist from threshold to about 1.3 kcal mol−1—exactly over the same energy range as that yielding high branching of the ν1-excited CH3 products (see Fig. 8). Such distinct rotational features are also strongly reminiscent of those observed previously for the F + HD → HF(ν′ = 2, j′) + D reaction at low energies,50 for which resonant tunneling has been shown to be the underlying mechanism.51 A similar mechanism is suggested to be at work here.
 | ||
| Fig. 9 The raw images shown in (a) and (b) are for the probe laser frequency set at the peak of the 111 band. Due to the spectral overlap and the opposite energy dependence of the intensities of the 111 band and the P(4) line of the 000 band, the image at Ec = 2.65 kcal mol−1 actually comprises both the contributions from CH3(ν1 = 1) and CH3(ν = 0) and the responsible state-pairs are indicated. Shown in (c) is the image when 000 Q head was probed. The series of ring structures corresponds to the rotationally resolved pairs of HF(ν′ = 2, j′) + CH3(ν = 0). Note that the intense high-j′ states prefer forward scattering, as opposed to the low-j′ states (adapted from ref. 47). | ||
At low collision energies where the product channel HF(ν′ = 3) + CH3(ν = 0) is barely open (threshold at Ec = 0.6 kcal mol−1), the decay of the resonance state can proceed via a vibrationally nonadiabatic predissociation (with a rate 1/τp) into HF(ν′ = 2, j′) + CH3(ν = 0), in analogy to the F + HD reaction.50 Replacing the D-atom in HD by CH3, however, adds additional degrees of freedom. Intramolecular vibration energy redistribution (IVR) within the resonant complex might occur, which opens up new decay channels. The ν1-mode excitation of the CH3-moiety retains the symmetry of collision complex; thus, the coupling between the two vibrationally adiabatic PESs that asymptotically lead to HF(ν′ = 3) + CH3(ν = 0) and HF(ν′ = 2) + CH3(ν1 = 1), respectively, is symmetry allowed. The energy difference between the two product channels is 1.7 kcal mol−1. The anticipated proximity of these two adiabatic surfaces near the transition state region could give rise to a significant coupling strength. However, in order for this new channel to be effective in competition to the predissociation channel, HF(ν′ = 2, j′) + CH3(ν = 0), the lifetime of the resonance state has to be sufficiently long for IVR to occur. The fact that only a specific product pair of vibrational mode/state is observed at low energies implies a highly restricted IVR process with a rate 1/τIVR; thus, τp ∼ τIVR and the resonant complex must decay into products before energy is completely randomized. Since the angular distribution is forward–backward asymmetric, the resonance lifetime should be shorter than the rotational period (τR) of the resonant complex;4,52 hence, τp ∼ τIVR < τR. This is a nice example illustrating how the pair-correlated measurements can help us to decipher the complicated energy flow within the transient resonant complex.
E Reactive resonance in Cl + CH4—a less obvious one
The resonance in F + CH4 seems entirely analogous to that in F + HD, if the methyl moiety is regarded as a pseudo D-atom. Nevertheless, the methyl moiety is not just an innocent spectator. It instead plays a central role in mediating the resonance decay mechanism—thus, providing an unparallel opportunity to unravel the intramolecular vibrational energy flow while the fleeting resonant complex is breaking apart into products. Presented below is the experimental evidence for a resonance of quite different nature in a hitherto unsuspected reaction Cl + CH4 → HCl + CH3.This reaction is slightly endothermic, ΔH00 = 1.21 kcal mol−1, with an appreciable barrier of about 3.8 kcal mol−1 at a linear Cl–H–C configuration. Again, this resonance was discovered through the product pair measurements.53 The upper panel of Fig. 10 displays two typical raw images (in a 3-D representation) of the probed CH3(ν = 0) products from the Cl + CH4 reaction. Both images are dominated by the HCl(ν′ = 0) + CH3(ν = 0) pair that is preferentially sideways-scattered. The middle rings, nearly isotropic at Ec = 9.7 kcal mol−1 and forward peaking at 14.74 kcal mol−1, were ascribed to a spin–orbital nonadiabatic reaction Cl*(2P1/2) + CH4 → HCl(ν′ = 1) + CH3(ν = 0). The innermost structures arise from Cl + CH4 → HCl(ν′ = 1) + CH3(ν = 0) and feature backscattering and predominantly sideways peaking at 9.7 and 14.74 kcal mol−1, respectively.
 | ||
| Fig. 10 The upper panel displays two raw images (in 3-D representation) of the probed CH3(ν = 0) products from the Cl + CH4 reaction at Ec = 9.7 and 14.74 kcal mol−1, respectively. The successive ringlike features on each image correspond to the labeled vibration states of the coincident HCl(ν′) product. The lower panel summarizes the evolution of the state-correlated angular distributions (dσ/d(cosθ)) as a function of collision energies. Note the large disparity in the vertical scales of the two plots and the dramatic differences in their appearance—in particular the ridge structure and the oscillatory, sharp forward–backward peakings for the HCl(ν′ = 1) + CH3(ν = 0) pair. The former is in line with the anticipation of the (stretching) vibrational adiabaticity of the Cl + CH4 reaction. The latter leads to the resonance proposition by pattern recognition (adapted from ref. 53). | ||
By taking 29 images over the energy range from about 2.5 to 20 kcal mol−1 and normalizing the results to the reactive excitation function, the energy dependencies of the correlated angular distribution of three product state pairs were obtained. Two of them are depicted in the lower panel of Fig. 10.53 For the ground state pair, HCl(ν′ = 0) + CH3(ν = 0), the angular distribution evolves slowly from backward near threshold to sideways and into the forward hemisphere with further increase in collision energies. Putting all together, a distinct ridgelike structure is then formed in the I(θ)–θ–Ec plot. Its origin is for the most part via a direct reaction mechanism, reflecting the dominance of large impact-parameter collisions and tunneling through the centrifugal-shifted barrier to reaction. By way of contrast, the energy evolution of the angular distribution for Cl + CH4 → HCl(ν′ = 1) + CH3(ν = 0) appears totally different. Besides the ridge that runs from backward near its energetic threshold (at Ec = 9.45 kcal mol−1) to sideways at higher Ec’s, the oscillatory, sharp forward–backward peaks also develop. We believe that the ridge observed here actually consists of two types: a rapidly evolving resonance ridge51 spanned over a narrow energy range near threshold, which overlaps with a direct, transition-state ridge extended over a much wider energy range than that for the ground state pair. The dramatic changes in general patterns from the two product state pairs signify different reaction mechanisms. Moreover, the pattern for the HCl(ν′ = 1) + CH3(ν = 0) pair is reminiscent of that previously found for the F + HD → HF + D reaction, for which a reactive resonance has been shown to be responsible.50,51 By pattern recognition, we asserted the existence of a reactive resonance for the formation of the HCl(ν′ = 1) + CH3(ν = 0) pair.
How does it come about, or how can we “understand” it? Fig. 11 depicts a schematic of vibrationally adiabatic potential energy curves based on ab initio theoretical studies.54–57 Only the high frequency stretching modes are shown here. The concept of adiabaticity in general has to do with the relative time scales of the motions of concern. The high-frequency modes have shorter oscillating periods, whereas the reaction path is governed by the translational motions of the two heavy species. Hence, like the electronic Born–Oppenheimer approximation, the vibrationally adiabatic PESs for those stretching modes are anticipated to be a reasonable starting point for discussion, at least for regions en route to the transition state as well as in the post barrier regions. As seen from Fig. 11, the ground-state reaction has a barrier of about 3.8 kcal mol−1 in accord with, accounting for tunneling, the experimental findings.58 The interaction of CH4 with an approaching Cl-atom causes a rapid decrease of the CH symmetric stretching frequency, while the frequency of antisymmetric stretch retains a spectator mode. As a result, the vibrationally adiabatic curve for antisymmetric stretch is simply shifted up from the ground state curve. On the other hand, the rapid decrease of symmetric stretching frequency in the transition state region lowers the adiabatic barrier and gives rise to a significant coupling of this mode of excitation to reaction coordinate; thus, further facilitating the colliding pair to surmount the barrier to reaction. The near degeneracy of the two stretching curves would of course cause wavefunction or mode mixings from nonadiabatic coulpings in the entrance channel, blurring the normal mode picture. Nonetheless, the vibrational adiabaticity of the two mixed stretching motions, as a first order approximation, could remain roughly held with respect to the ground-state one, giving rise to an adiabatic (or dynamical) well for the stretch-excited CH4 reaction. Particularly noteworthy is its adiabatic correlation to the HCl(ν′ = 1) + CH3(ν = 0) pair on the product side. Based on the I(θ)–θ–Ec evolution for that product pair (Fig. 10), which is too characteristic to be missed, we suggested that the adiabatic well is deep enough to dynamically support a guasi-bound state, i.e., a reactive resonance.
 | ||
| Fig. 11 Schematic representation of vibrationally adiabatic potential energy curves as a function of reaction coordinate. These curves are roughly sketched in keeping with the theoretically calculated vibration frequencies along the reaction path. The symmetry of each curve is indicated in parentheses in the C3v configuration. The vertical dotted line at s0 locates the saddle point. The horizontal dashed line denotes the proposed resonance state that is dynamically trapped in the vibrationally adiabatic potential well (adapted from ref. 53). | ||
Another interesting aspect of this proposed resonance is about the energy flow. The initial energy in this study is purely translational between Cl and CH4, the formation of this trapped state that is supported by the stretch-excited adiabatic curve requires the T → V energy transfer in the entrance channel. The large disparity in intensities of the two plots shown in the lower panel of Fig. 10 indicates low probability for such an energy transfer process, testifying to the goodness of vibrational adiabaticity in this reaction. Once the resonant complex is formed, its vibrational motions are essentially delocalized, in contrast to the above F + CH4 case for which the vibrational motion is believed to remain primarily in the F–H–C moiety, i.e., an intermolecular complex. As the complex decays, an energy flow from intramolecular mode of excitation to intermolecular mode must then be invoked in forming the HCl(ν′ = 1) + CH3(ν = 0) product pair. Again, this is to be in contrast to the formation of HF(ν′ = 2) + CH3(ν1 = 1) from F + CH4, for which the energy flow, upon resonant complex decays, instead occurs from intermolecular mode of excitation to intramolecular mode, as alluded to in the above section.
F Effects of bending excitation of methane
The above example already hinted on the mode-specificity in chemical reactivity. While the notion of vibrationally adiabatic dynamics might be anticipated for a high-frequency, stretch-excited reagent and can provide an intuitively appealing way to rationalize its mode-specific reactivity, the physical understanding of the effect of bend excitations is less obvious. Generally speaking, bending and torsional modes are of low-frequency vibrations; thus, in terms of the relative time scale, the concept of adiabaticity may not be valid. In addition, unlike the stretching motions (for a hydride molecule) that are by and large localized, the bending/torsional motions always involve nonlocalized, concerted motions of three of more atoms. Yet, theoretical studies predicted that bending excitation of CH4 leads to, when reacting with Cl, a hotter umbrella-mode excitation of CH3 products, which was interpreted as an adiabatic mapping of the bending motion of the CH4 reagent directly onto the analogous motion of the CH3 product.54–57 In other words, umbrella-mode excitation of CH4 was partially preserved in the Cl + CH4 reaction, suggesting a spectator behavior of the CH3 moiety in the reaction.Presented in Fig. 12 are the pair-correlated results for the Cl + CD4 → DCl(ν′) + CD3(ν = 0) reaction.59 The CD3 product kinetic energy releases are displayed for the two CD4 source temperatures of 340 K in (a) and 463 K in (b), while the collisional energies in both cases were maintained at 4.78 kcal mol−1. All three peaks in the distributions turn out to be the DCl(ν′ = 0) coproducts, but originating from the ground-state and bend-excited CD4 reagents in the molecular beam. The notations “0*” and “0**” indicate one-quantum and two-quanta bending excitations of CD4, respectively and, as can be seen, they are in accord with the energetic considerations. The enhancement of the relative contributions from the 0*- and 0**-peaks by heating up the CD4 reagent (Fig. 12b) not only re-enforces the assignments but also provides a way to estimate the relative reactive cross sections to the ground state reaction. The resulted σ*/σ0 and σ**/σ0 for the Cl + CD4 reaction at EC = 4.78 kcal mol−1 are about 3 and 7.5, respectively.59 The reported modest vibrational enhancement factors in reactivity are in sharp contrast to the earlier experimental value of ∼80 for the same reaction.60,61 More recent reinvestigation,62,63 however, revised the old results and is now in quantitative agreement with ours. It is interesting to note that a factor of three for vibrational enhancement factor in reactivity turns out to be about the same as an equivalent amount of additional translation energy;53,58 thus, it appears to be purely energetic in origin and not mode-specific.
 | ||
| Fig. 12 CD3 product speed distributions from the Cl + CD4 reaction at the two CD4 source temperatures (a) 340 and (b) 460 K. The corresponding angular distributions are shown in panels (c) and (d) (adapted from ref. 59). | ||
Also shown in Fig. 12c and d are the corresponding angular distributions, which for both the ground state and bend-excited reactions are predominantly back-scattered.59 Within our experimental uncertainties all three distributions are essentially identical, suggesting the same rebound reaction mechanism and again no mode-specificity.
Similar experiments were performed for the O(3P) + CD4 reactions and the results are presented in Fig. 13.64 This reaction is also slightly endothermic, ΔH00 = 2.47 kcal mol−1, which is nearly the same as Cl + CD4. The reaction barrier, 9–10 kcal mol−1, is however substantially higher.65,66 It is interesting to contrast the effects of bending excitation of this reaction (Fig. 13a) with that for the Cl + CD4 reaction (Fig. 12a and b). While the bend-excited CD4 in the latter case yields the ground state DCl in coincidency with CD3(ν = 0),59 the O(3P) + CD4 (ν2/ν4 = 1) reaction produces mainly the OD(ν′ = 1) + CD3(ν = 0) pair.64 More detailed analysis indicated that the ratio of σ*/σ0 for the reaction shown in Fig. 13a becomes 0.68—less than unity!64 Compared to the translational enhancement factor with an equivalent energy, this factor is substantially smaller.66 Thus, bend-excited CD4 exhibits mode-specific behaviour in suppressing reactivity for the reaction with O(3P), in sharp contrast to the analogous reaction with Cl-atom. Apparently, the extra energy from the bending motion of reagents in O(3P) + CD4 does not channel in the right way to help surmount the reaction bottleneck. This finding also appears to be an interesting counter-example to the Polanyi’s rule,27 which is based on atom + diatom reactions, that vibration is usually more effective in promoting a late-barrier reaction, which is the case for both endothermic reactions considered here.
 | ||
| Fig. 13 Methyl product speed distributions in the center-of-mass frame, the open data points are from the reaction with source temperature at 291 K and the solid points are from a heated source at 433 K. The reactions are (a) O(3P) + CD4 → CD3(ν = 0) + OD, (b) O(3P) + CHD3 → CD3(ν = 0) + OH and (c) O(3P) + CHD3 → CHD2(ν = 0) + OD. The peak features are assigned as the vibrational quantum numbers of the OD or OH coproduct based on energetic grounds. The superscript “≠” indicates the corresponding OD or OH state formed from the bend-excited methane reagent (adapted from ref. 64). | ||
V. Summary
The case studies presented in this paper illustrate the power of the new product pair measurements in elucidating the intimate details of individual reactive molecular collisions. More than often the dynamical information recovered from the pair correlation measurements are unseen by conventional experiments. A common thread that implicates in our attempts to reveal the “hidden” dynamics is an approach of decomposing a complex reaction problem into simpler pieces that preserve the essential physics. That seems to be the most natural way of digesting and decoding the enormous amounts of information encoded in the pair-correlated data. While this approach provides a convenient vehicle enabling us to gain some intuitive insights into reaction dynamics, a deeper understanding will inevitably rely on further theoretical advances in the furture.In this short review we have surveyed only a limited system, which more or less reflects the current state of the pair-correlation measurements in bimolecular reactions. Clearly, more examples for more reactions will come along in the near future. One can also envision several other variants and/or applications. One obvious extension will be the vector correlation in bimolecular reactions.67 Lessons from the analogous studies of photofragmentations68 over the past decade promise fruitful stereodynamical information to be discovered. Another possibility is to explore the mode- and bond-selective chemistry with pair-correlation measurements as the detection scheme, as illustrated in section IV(F).59,64 This is the area to which our effort is currently devoted.69 With delayed ion-extraction technique,70 in conjunction with REMPI-prepared ions,71,72 even the state-selected ion–molecule reaction73 may reveal pair-correlated information.
Acknowledgements
I am greatly indebted to my past and current group members for the works mentioned here. I would also like to gratefully acknowledge the National Science Council of Taiwan for the financial support under NSC 94-2113-M-001-019 and NSC 95-2119-M-001-002.References
- R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics and Chemical Reactivity, Oxford University Press, New York, 1987 Search PubMed.
- Modern Trends in Chemical Reaction Dynamics: Experiment and Theory, ed. X. Yang and K. Liu, World Scientific, Singapore, 2004, Parts 1 and 2 Search PubMed.
- K. Liu, Annu. Rev. Phys. Chem., 2001, 52, 139 CrossRef CAS.
- K. Liu, J. Chem. Phys., 2006, 125, 132307 CrossRef.
- J. J. Lin, D. W. Hwang, S. Harich, Y. T. Lee and X. Yang, Rev. Sci. Instrum., 1998, 69, 1642 CrossRef CAS.
- P. Casavecchia, G. Capozza and E. Segoloni, in Modern Trends in Chemical Reaction Dynamics: Experiment and Theory, ed. X. Yang and K. Liu, World Scientific, Singapore, 2004, Part 2, ch. 7 Search PubMed.
- The Chemical Dynamics and Kinetics of Small Radicals, ed. K. Liu and A. Wagner, World Scientific, Singapore, 1995, Part 2, ch. 16 and 18 Search PubMed.
- A. J. Orr-Ewing and R. N. Zare, in The Chemical Dynamics and Kinetics of Small Radicals, ed. K. Liu and A. Wagenr, World Scientific, Singapore, 1995, Part 2, ch. 20 Search PubMed.
- S.-H. Lee and K. Liu, in The Chemical Dynamics and Kinetics of Small Radicals, ed. X. Yang and K. Liu, World Scientific, Singapore, 2004, Part 2, ch. 1 Search PubMed.
- X. Yang, Int. Rev. Phys. Chem., 2005, 24, 37 CrossRef CAS.
- J. J. Lin, J. Zhou, W. Shiu and K. Liu, Science, 2003, 300, 966 CrossRef CAS.
- For example, (a) F. J. Aoiz, L. Banares and V. J. Herrero, Int. Rev. Phys. Chem., 2005, 24, 119 CrossRef CAS; (b) B. Bussery-Honvault, J. Julien, P. Honvault and J. M. Launay, Phys. Chem. Chem. Phys., 2005, 7, 1476 RSC; (c) D. de Fazio, V. Aquilanti, S. Cavalli, A. Aquilar and J. M. Lucas, J. Chem. Phys., 2006, 125, 133109 CrossRef.
- J. Zhou, J. J. Lin, W. Shiu and K. Liu, J. Chem. Phys., 2003, 119, 4997 CrossRef CAS.
- S. W. North and G. E. Hall, J. Chem. Phys., 1997, 106, 60 CrossRef CAS.
- J. J. Lin, J. Zhou, W. Shiu and K. Liu, Rev. Sci. Instrum., 2003, 74, 2495 CrossRef CAS.
- J. Zhou, J. J. Lin, W. Shiu, S.-C. Pu and K. Liu, J. Chem. Phys., 2003, 119, 2538 CrossRef CAS.
- M. N. R. Ashfold et al., Phys. Chem. Chem. Phys., 2006, 8, 26 RSC.
- H. S. Johnson, Gas Phase Reaction Rate Theory, Ronald, New York, 1966 Search PubMed.
- P. L. Houston, Chemical Kinetics and Reaction Dynamics, McGraw Hill Co., New York, 2001 Search PubMed.
- E. Wigner, Trans. Faraday Soc., 1938, 34, 29 RSC.
- J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice-Hall Inc., New Jersey, 1999 Search PubMed.
- A. Persky, J. Phys. Chem., 1996, 100, 689 CrossRef CAS.
- M. A. Nazar and J. C. Polanyi, Chem. Phys., 1981, 55, 299 CrossRef CAS.
- W. W. Harper, S. A. Nizkorodov and D. J. Nesbitt, J. Chem. Phys., 2000, 113, 3670 CrossRef CAS.
- K. Sugawara, F. Ito, T. Nakanaga, H. Takeo and C. Matsumura, J. Chem. Phys., 1990, 92, 5328 CrossRef CAS.
- J. Zhou, J. J. Lin, W. Shiu and K. Liu, Phys. Chem. Chem. Phys., 2006, 8, 3000 RSC.
- J. C. Polanyi, Science, 1987, 236, 680 CrossRef CAS , and references therein.
- K. Schulter and R. G. Gordon, J. Chem. Phys., 1976, 64, 2918 CrossRef CAS.
- J. Zhou, W. Shiu, J. J. Lin and K. Liu, J. Chem. Phys., 2006, 124, 104309 CrossRef.
- I. Schechter, R. D. Levine and R. G. Gordon, J. Phys. Chem., 1991, 95, 8201 CrossRef CAS.
- D. Troya, J. Chem. Phys., 2005, 123, 214305 CrossRef.
- J. F. Castillo, F. J. Aoiz, L. Banares, E. Martinez-Nunez, A. Fernandez-Ramos and S. Vazquez, J. Phys. Chem. A, 2005, 109, 8459 CrossRef CAS.
- C. Rangel, M. Navarrete and J. Espinosa-Garcia, J. Phys. Chem. A, 2005, 109, 1441 CrossRef.
- D. Troya, J. Millan, I. Banos and M. Sonzalez, J. Chem. Phys., 2004, 120, 5181 CrossRef.
- J. C. Corchado and J. Espinosa-Garcia, J. Chem. Phys., 1996, 105, 3152 CrossRef CAS.
- (a) O. Roberto-Neto, F. B. C. Machado and F. R. Ornellas, Chem. Phys. Lett., 2005, 409, 38 CrossRef CAS; (b) O. Roberto-Neto, F. B. C. Machado and F. R. Ornellas, Chem. Phys., 2005, 315, 27 CrossRef.
- J. Zhou, W. Shiu, J. J. Lin and K. Liu, J. Chem. Phys., 2004, 120, 5863 CrossRef CAS.
- I. M. Campbell, Energy and the Atmosphere, John Wiley & Sons Ltd, London, 1977 Search PubMed.
- A. R. Ravishankara, Annu. Rev. Phys. Chem., 1988, 39, 367 CrossRef CAS.
- N. K. Srinivasan, M.-C. Su, J. W. Sutherland and J. V. Michael, J. Phys. Chem. A, 2005, 109, 1857 CrossRef CAS , and reference therein.
- B. Zhang, W. Shiu, J. J. Lin and K. Liu, J. Chem. Phys., 2005, 122, 131102 CrossRef.
- J. Espinosa-Garcia and J. C. Corchado, J. Chem. Phys., 2005, 112, 5731.
- L. Masgrau, A. Gonzalez-lafont and J. M. Lluch, J. Chem. Phys., 2001, 114, 2154 CrossRef CAS.
- B. R. Strazisar, C. Lin and H. F. Davis, Science, 2000, 290, 958 CrossRef CAS.
- B. Zhang, W. Shiu and K. Liu, J. Phys. Chem. A, 2005, 109, 8989 CrossRef CAS.
- B. Zhang, W. Shiu and K. Liu, J. Phys. Chem. A, 2005, 109, 8983 CrossRef CAS.
- W. Shiu, J. J. Lin and K. Liu, Phys. Rev. Lett., 2004, 92, 103201 CrossRef.
- M. E. Jacox, J. Phys. Chem. Ref. Data, 2003, 32, 1 CrossRef CAS.
- W. Shiu, J. J. Lin, K. Liu, M. Wu. and D. H. Parker, J. Chem. Phys., 2004, 120, 117 CrossRef CAS.
- (a) S.-H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2002, 116, 7839 CrossRef CAS; (b) S.-H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2006, 125, 133106 CrossRef.
- (a) R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2000, 112, 4536 CrossRef CAS; (b) R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, Phys. Rev. Lett., 2000, 85, 1206 CrossRef CAS.
- D. R. Herschbach, Angew. Chem., Int. Ed. Engl., 1987, 26, 1221 CrossRef.
- B. Zhang and K. Liu, J. Chem. Phys., 2005, 122, 101102 CrossRef.
- W. T. Duncan and T. N. Truong, J. Chem. Phys., 1995, 103, 9642 CrossRef CAS.
- D. Troya, J. Millan, I. Banos and M. Gonzalez, J. Chem. Phys., 2002, 117, 5730 CrossRef CAS.
- H.-G. Yu and G. Nyman, J. Chem. Phys., 1999, 111, 6693 CrossRef CAS.
- J. C. Corchado, D. G. Truhlar and J. Espinosa-Garcia, J. Chem. Phys., 2000, 112, 9375 CrossRef CAS.
- J. Zhou, B. Zhang and K. Liu, Mol. Phys., 2005, 103, 1757 CAS.
- J. Zhou, J. J. Lin, B. Zhang and K. Liu, J. Phys. Chem. A, 2004, 108, 7832 CrossRef CAS.
- S. A. Kandel and R. N. Zare, J. Chem. Phys., 1998, 109, 9719 CrossRef CAS.
- Z. H. Kim, A. J. Alexander, H. A. Bechtel and R. N. Zare, J. Chem. Phys., 2001, 115, 179 CrossRef CAS.
- H. A. Bechtel, J. P. Camden, D. J. A. Brown, M. R. Martin, R. N. Zare and K. Vodopyanov, Angew. Chem., Int. Ed., 2005, 44, 2382 CrossRef CAS.
- M. J. Bass, M. Brouard, R. Cireasa, A. P. Clark and C. Vallance, J. Chem. Phys., 2005, 123, 094301 CrossRef CAS.
- B. Zhang and K. Liu, J. Phys. Chem. A, 2005, 109, 6791 CrossRef CAS.
- D. L. Baulch, C. J. Cobs, R. A. Cox, C. E. P. Frank, Th. Just, J. A. Kerr, M. J. Pilling, J. Troe, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 1992, 21, 411 CAS.
- B. Zhang, J. Zhang and K. Liu (unpublished results).
- For example A. J. Alexander, M. Brouard, K. S. Kalogerakis and J. P. Simons, Chem. Soc. Rev., 1998, 27, 405 Search PubMed.
- For example, G. E. Hall and P. L. Houston, Annu. Rev. Phys. Chem., 1989, 40, 375 Search PubMed.
- S. Yan, Y.-T. Wu and K. Liu, Phys. Chem. Chem. Phys., 2006 10.1039/b614307e.
- D. A. Chestakov, S.-M. Wu, G. Wu, D. H. Parker, A. T. J. B. Eppink and T. N. Kistopoulos, J. Phys. Chem. A, 2004, 108, 8100 CrossRef CAS.
- B. Yang, Y. Chiu and S. L. Anderson, J. Chem. Phys., 1991, 94, 6459 CrossRef CAS.
- C. Chang, C.-Y. Luo and K. Liu, J. Phys. Chem. A, 2005, 109, 1022 CrossRef CAS.
- J. Mikosch, U. Fruhling, S. Trippel, D. Schwalm, M. Weidemuller and R. Wester, Phys. Chem. Chem. Phys., 2006, 8, 2990 RSC.
| This journal is © the Owner Societies 2007 |

