Direct observation of the solvent reorientation dynamics in the “twisted” intramolecular charge-transfer process of cyanophenyldisilane–water cluster by transient infrared spectroscopy†‡
Haruki
Ishikawa
*a,
Masuyuki
Sugiyama
b,
Wataru
Setaka
b,
Mitsuo
Kira
b and
Naohiko
Mikami
*b
aDepartment of Molecular Science and Material Engineering, Graduate School of Science and Technology, Rokko-dai, Nada-ku, Kobe, 657-8501, Japan. E-mail: haruki@kobe-u.ac.jp; Fax: +81-78-803-6463; Tel: +81-78-803-6463
bDepartment of Chemistry, Graduate School of Science, Tohoku University, Aramaki, Aoba-ku, Sendai, 980-8578, Japan. E-mail: nmikami@mail.tains.tohoku.ac.jp
First published on 17th November 2006
Abstract
The solvent reorientation dynamics of the intramolecular charge-transfer (ICT) process of the (p-cyanophenyl)pentamethyldisilane–H2O (CPDS–H2O) cluster was investigated by transient infrared (IR) absorption spectroscopy. Transient IR bands of two distinct charge-transfer (CT) states appeared in both the OH and the CN-stretching vibration regions. Analyses of the IR spectra and the time profiles of the transient bands revealed that the ICT process of the CPDS–H2O cluster proceeds in two steps. The first step is a transition from a photo-prepared locally excited (LE) state to the CT state, which is accompanied by a minor reorientation of the H2O moiety. In contrast, the second step is an extensive reorientation process of the H2O molecule in the CT state. These two reorientation processes exhibit very distinct pico- and nano-second time scales. In the latter case, a relatively slow time constant of 2 ns was related to a large geometric change in the orientation.
Introduction
The intramolecular charge-transfer (ICT) process is one of the most fundamental processes in photochemical reactions. Since the first report of a dual emission of p-dimethylaminobenzonitrile (DMABN) in 1955,1 a vast number of spectroscopic studies have been carried out, mainly in condensed phase.2 The stabilization processes of the charge-transfer (CT) state can be described in terms of two main factors. The first is an intramolecular structural change of a reactant. The most accepted mechanism of the intramolecular structural change in the ICT process is the so-called twisted ICT (TICT) model, in which a 90° twist occurs around the single bond between the charge-donating and -accepting groups.3 The second factor is a reorientation process of polar solvent molecules around the reactant, that is, solvent molecules often exhibit rearrangement to reduce the dipole moment of the whole system.We have been carrying out laser spectroscopic studies on the jet-cooled gas phase of (p-cyanophenyl)pentamethyldisilane (CPDS) and its solvated clusters, which are quite suitable for the investigation of molecular-level insights of the ICT process, such as determination of the mechanism, structure of the CT state, microscopic solvation, and so on.4–7 Phenyldisilanes are known to exhibit dual emission in solution.8–17 Much as in the DMABN system, the occurrence of a 90° twist of a disilanyl group with respect to the phenyl ring in the ICT process has been one of the main issues in this system.13 In our previous study based on the electronic transition, we determined that the electronic configuration of the CT state of CPDS is a σSi−Siπ*-type configuration.5 That is, after the photoexcitation of a π-electron of the aromatic ring to the antibonding π* orbital, which is called the locally excited (LE) state, the electronic relaxation of an electron in the σSi−Si orbital of the disilanyl group to the π orbital generates the σSi−Siπ*-type CT state as the ICT process proceeds. However, the equilibrium structure of the CT state was not determined in the paper.5 Since the electronic transition related to the CT state is broad and structure-less, it is very difficult to extract more precise information about the characteristics of the CT state, such as the geometrical structure and electronic properties. Thus, transient IR spectroscopy has been applied to obtain detailed information about the equilibrium structure of the CT state. We have measured transient IR spectra of jet-cooled CPDS in the CH-stretching vibration (νCH) region near 3000 cm−1, and have found that the methyl CH-stretch band pattern of the CT state is very distinct from that of the S0 state.7 This band pattern was well reproduced by ab initio calculation, in which the 90° twist of the disilanyl group was assumed. This result clearly exhibits an occurrence of such a 90° twist during the ICT process.7 Since the charge-donating disilanyl group and the charge-accepting cyanophenyl group are in the same plane in the equilibrium structure of the CT state of CPDS, it appears that the direction of the torsional motion in the ICT process is opposite to that expected in the TICT model of the DMABN system. In the phenyldisilane system, however, the σSi−Si orbital plays the same role as the nonbonding orbital of the dimethylamino group of DMABN. Thus, the ICT process of the disilanyl group is considered to be a variation of the TICT model that maintains the inherent nature of its dynamics.
The problem remaining is the reorientation process of solvent molecules. In solution, generally, it is difficult to measure the IR spectra of solvent molecules near the reactant. Thus, the reorientation process has been discussed mainly based on the temporal profile of CT emission or transient vibrational bands of reactants, so that the detailed orientation process of solvent molecules with respect to the reactant has been unclear. In the case of solvated clusters as prepared in a jet-cooled gas phase, however, we can measure the IR spectra of both reactant and solvent molecules. In addition, a direct comparison with the theoretical results is possible for such a cluster system, since we will be able to regulate the coordination of the solvent molecules without undesired perturbation from others. Thus, we have applied transient IR spectroscopy to solvated CPDS clusters in order to obtain a detailed picture of the reorientation dynamics of solvent molecules in the ICT process.
Reorientation or rearrangement dynamics of solvent molecules in solvated clusters is an attractive topic in cluster chemistry. Photoionization18–20 or photodetachment21-induced solvent reorientation processes have been reported by several groups. In general, the most stable orientation of solvent molecule(s) in the cationic (neutral) state is different from that of the neutral (anionic) state, due to a significant change in the charge distribution upon photoionization or photodetachment. Tachikawa and Igarashi theoretically investigated the photoionization process of benzene–H2O cluster.18 They reported that the reorientation process of the H2O moiety is completed within 1 ps. Recently, Ishiuchi and coworkers observed the movement of an Ar atom in the [phenol-Ar]+ initiated by an ionization of the corresponding neutral species.19 They found that the reorientation process is completed within 10 ps. On the other hand, Zwier and coworkers performed a laser-initiated population transfer between two isomers of trans-formanilide (TFA)-H2O clusters.22 In their experiment, one of the isomers was vibrationally excited by a stimulated emission pumping technique and then cooled down by collision in a supersonic expansion. When the vibrational energy exceeds the barrier height between the two isomers, isomerization from one isomer to the other occurs. In this manner, Zwier and coworkers obtained energy thresholds for the isomerization or reorientation of the H2O moiety in the TFA–H2O cluster. Since such a relaxation of vibrationally excited clusters takes place under a complicated multi-collision process during a supersonic jet expansion, they could not obtain information about the rate of the isomerization.
In the present study, we measured transient IR spectra of the CPDS–H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cluster, being interested in the solvent reorientation dynamics at the molecular level. Since the vibrational frequency shift of OH-stretching (νOH) mode(s) upon hydrogen-bond formation is known to correlate with the bond strength and also with the relative orientation of surrounding molecules around the OH site, it was expected that the νOH frequency of the H2O moiety in the CPDS clusters should sensitively reflect a small change in the electronic and/or structural situation governed by the ICT process. In other words, the νOH should be a good probe for indicating the dynamics of the ICT process. Our viewpoint is to look at what is going on during the ICT process from the solvent side. In addition to νOH of the H2O moiety, a transient IR spectrum in the CN-stretch (νCN) frequency region was measured to probe the reactant side, since it is known that the νCN of DMABN is significantly dependent on the character of their electronic states.23–27
1 cluster, being interested in the solvent reorientation dynamics at the molecular level. Since the vibrational frequency shift of OH-stretching (νOH) mode(s) upon hydrogen-bond formation is known to correlate with the bond strength and also with the relative orientation of surrounding molecules around the OH site, it was expected that the νOH frequency of the H2O moiety in the CPDS clusters should sensitively reflect a small change in the electronic and/or structural situation governed by the ICT process. In other words, the νOH should be a good probe for indicating the dynamics of the ICT process. Our viewpoint is to look at what is going on during the ICT process from the solvent side. In addition to νOH of the H2O moiety, a transient IR spectrum in the CN-stretch (νCN) frequency region was measured to probe the reactant side, since it is known that the νCN of DMABN is significantly dependent on the character of their electronic states.23–27
Here, we report our observations of the reorientation dynamics in the ICT process of the CPDS–H2O cluster by means of ultraviolet–infrared (UV-IR) pump–probe spectroscopy. The movement of the H2O molecule in the CT state is clearly probed by changes in the IR spectra in both the νOH and the νCN frequency regions. The reorientation process is discussed based on our spectroscopic and theoretical results.
Experimental details
In the present study, a conventional supersonic jet apparatus and a nanosecond pulsed laser system were used. CPDS was synthesized using a previously described method.9 CPDS was heated to 350 K to create sufficient vapor pressure. The CPDS vapor seeded in He gas was supersonically expanded into a vacuum chamber through a pulsed nozzle with an orifice of 0.8 mm in diameter. A frequency-doubled output of a tunable dye laser (LAS 20505) pumped by a Nd:YAG laser (Continuum Surelite III) was used for the excitation of the jet-cooled CPDS. The light pulse irradiated the jet at a point 10 mm downstream of the nozzle orifice. The fluorescence was collected with a lens placed at a right angle to both the jet stream and the laser beam, and was detected by a photomultiplier tube (Hamamatsu 1P28). The signal was integrated by a boxcar averager (EG&G Par 4420) and processed by a microcomputer.Transient IR spectra were recorded by an ultraviolet (UV)-infrared (IR) double resonance technique28 as follows. First, the UV laser pulse excites the CPDS clusters to the LE (ππ*) state. Then, the IR light pulse is irradiated to the photo-prepared clusters by the UV excitation. When the IR absorption by the electronically excited molecule occurs, the fluorescence yield decreases due to some non-radiative decay processes, such as internal conversion, intersystem crossing and vibrational predissociation in the vibrationally excited levels. Thus, the IR absorption of the electronically excited clusters can be detected as a depletion of the fluorescence intensity. In this study, only the CT emission from the clusters was monitored. Since the CT state is generated after passing through the photo-generated LE state, a population decrease in the LE state induced by the IR excitation also causes a decrease in the fluorescence intensity from the CT state. Thus, we could observe IR bands of both the LE and the CT state by our method. When IR spectra of the S0 state were measured, the IR light pulse was introduced ∼20 ns prior to the UV light pulse. In this case, vibrational excitation by the IR light was detected as a decrease in the fluorescence intensity, which also reflects the population of the vibrational ground level of the S0 state.
The IR light pulse was generated by a difference frequency mixing by a LiNbO3 crystal between the second harmonics of the Nd:YAG (Continuum Powerlite 8000) and the output of a dye laser (Continuum ND6000). In measuring IR spectra in the CN-stretching region, we used the output of an IR-OPO (LaserVision) pumped by the Nd:YAG laser (Continuum Powerlite 8000). IR laser wavenumbers were calibrated based on the IR absorption spectra of H2O vapor (3500–3800 cm−1) and CO gas (2100–2250 cm−1).29 The temporal pulse widths of the UV and IR pulses were ∼3 and ∼4 ns, respectively. The delay time between the UV and the IR pulses was controlled by a digital delay generator (SRS DG535).
Results and discussions
Fluorescence excitation and dispersed fluorescence spectra of CPDS–H2O cluster
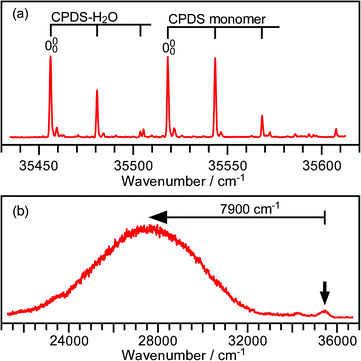
Before reporting the results of the present study, we will briefly review our previous spectroscopic study on the ICT process of the CPDS–H2O cluster.6Fig. 1a shows a fluorescence excitation spectrum of the CPDS–H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cluster. The origin band appears at 35 456.5 cm−1, which is shifted by −62.5 cm−1 compared with that of the CPDS monomer. As seen in the figure, a clear progression similar to that of the CPDS monomer appears. The low frequency vibration forming this progression was assigned as a torsional motion of the disilanyl group with respect to the phenyl ring. The appearance of a very similar torsional progression suggests that the H2O molecule is bound to the cyano group side, and thus has no significant influence on the Si–Si bonding site of the molecule. No progression assignable to an intermolecular vibrational motion appeared in the spectrum. This indicates that the relative orientation between the CPDS and the H2O moieties in the LE state is quite similar to that in the S0 state. Fig. 1b shows a dispersed fluorescence spectrum measured by exciting the origin band of the CPDS–H2O cluster. The spectrum consists of very weak LE and intense CT emissions. The Stokes shift of the CT emission was found to be about 7900 cm−1. This value is 1100 cm−1 larger than that of the monomer, which roughly corresponds to the stabilization energy by the microscopic solvation. The decay time constant of the CT emission was found to be 7.1 ns. Since the LE emission intensity is very weak, the ICT reaction rate should be very fast.
1 cluster. The origin band appears at 35 456.5 cm−1, which is shifted by −62.5 cm−1 compared with that of the CPDS monomer. As seen in the figure, a clear progression similar to that of the CPDS monomer appears. The low frequency vibration forming this progression was assigned as a torsional motion of the disilanyl group with respect to the phenyl ring. The appearance of a very similar torsional progression suggests that the H2O molecule is bound to the cyano group side, and thus has no significant influence on the Si–Si bonding site of the molecule. No progression assignable to an intermolecular vibrational motion appeared in the spectrum. This indicates that the relative orientation between the CPDS and the H2O moieties in the LE state is quite similar to that in the S0 state. Fig. 1b shows a dispersed fluorescence spectrum measured by exciting the origin band of the CPDS–H2O cluster. The spectrum consists of very weak LE and intense CT emissions. The Stokes shift of the CT emission was found to be about 7900 cm−1. This value is 1100 cm−1 larger than that of the monomer, which roughly corresponds to the stabilization energy by the microscopic solvation. The decay time constant of the CT emission was found to be 7.1 ns. Since the LE emission intensity is very weak, the ICT reaction rate should be very fast.
 | ||
| Fig. 1 Fluorescence excitation (a) and dispersed fluorescence (b) spectra of the CPDS–H2O cluster. The dispersed fluorescence spectrum was measured exciting the origin band. The arrow indicates the excitation wavenumber. | ||
Transient IR spectra of the CPDS–H2O cluster in the νOH region
IR spectra in the OH-stretching region of the CPDS–H2O cluster are shown in Fig. 2. The UV laser was tuned to the origin band of this cluster. The IR spectrum of the S0 state is displayed in the top trace for comparison. The bands at 3730.3 and 3617.1 cm−1 are assigned as the anti-symmetric and the symmetric OH-stretch vibration (ν3 and ν1), respectively. In the local mode picture, the ν3 and ν1 modes of hydrogen-bonded H2O are frequently referred to as a dangling and a hydrogen-bonded (H-bonded) OH-stretching vibration, respectively. In this paper, we use the normal mode labeling (ν3 and ν1) rather than the local mode one, since the former labeling makes our discussion clear, as will be described later. The observed frequency shifts of the ν3 and ν1 cluster bands from the corresponding bands of a bare H2O molecule are known to be −25.5 and −40.0 cm−1, respectively.30 The IR band pattern of the CPDS–H2O cluster is quite similar to that of the benzonitrile–H2O cluster where the H2O molecule is attached to the side of the cyano group,31 and thus a similar structure is expected in the case of CPDS–H2O.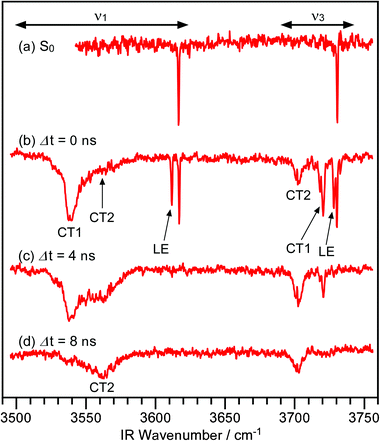 | ||
| Fig. 2 IR spectra of the CPDS–H2O cluster in the OH-stretching vibration region. Trace (a) is an IR spectrum of the S0 state, whereas traces (b)–(d) are transient IR spectra. The delay times between the UV and IR laser pulses are indicated in the figure. | ||
Transient IR spectra of the CPDS–H2O cluster are shown in Fig. 2b–d. In the case of Fig. 2b, IR and UV light pulses were introduced simultaneously. Since both pulses have a width of few nanosecond, the clusters can absorb either the IR light prior to the UV light or the IR light after the UV light. In the former case, IR bands of the S0 states appear in the spectrum, whereas transient bands appear in the latter case. As clearly seen in the figure, three bands other than that of the S0 state appear in both the ν3 and ν1 frequency regions. The relative intensity ratio among these bands changes drastically with the time propagation. The ν3 and ν1 bands at 3728.2 and 3611.7 cm−1 are very sharp and their frequencies are very close to those of the S0 state. Moreover, these bands decay within 4 ns after the UV excitation. Therefore, they have unambiguously been assigned as the ν3 and ν1 bands of the LE state. The small difference in frequency indicates that the orientation of the H2O to the CPDS moieties does not change significantly between the LE and the S0 states. This is consistent with the fact that there is no intramolecular vibration band in the fluorescence excitation spectrum.
In addition to the transient bands of the LE state, two additional bands, designated CT1/2, appear in both the ν3 and the ν1 frequency regions. Both CT1/2 bands in the ν1 region exhibit a substantial low-frequency shift. Considering that the cyanophenyl group acts as an electron acceptor in the CT state, both of these bands are assigned as the ν1 bands of states having a CT character. The relative intensity ratio between these bands evolves with time, but the positions of these bands stay unchanged. This means that there are two stable states or local minima involved in the CT state. According to the time dependence, we can conclude that there is a set of bands at 3720.5 and 3539.3 cm−1 and another set of bands at 3702.5 and 3561.8 cm−1, and that these sets correspond to different structures. The former set of bands appears and decays faster than the latter. Hereafter, the state corresponding to the former set is assigned to the ν1 and ν3 band of the fast decaying CT state, called the CT1 state, whereas the latter is assigned to the ν1 and ν3 bands of the other state, the CT2 state.
The width of the ν1 band of the CT2 state is extremely broad. The CT2 state is the most stable state among the LE, the CT1, and the CT2 states. Thus, the clusters in the CT2 state should be vibrationally excited. This broad band width should be related to a fast intramolecular vibrational energy redistribution (IVR) process in the CT2 state. In this respect, we have succeeded in probing the ICT process by the transient IR spectroscopy of solvent molecules rather than that of the reactant. The transient IR spectra of the solvent H2O moiety should provide us with detailed information about the reorientation of solvent molecules in the ICT.
Time profiles of the LE, CT1, and CT2 states
Fig. 3a shows typical time profiles of the IR bands associating with the LE, CT1, and CT2 states. The intensities of these bands reflect populations of the corresponding states. To avoid any contribution of overlapping bands, the ν1 band intensity was used for the LE state, whereas the ν3 band intensities were used for the CT1 and the CT2 states. By measuring the time profiles using different IR laser powers, we confirmed that an undesirable saturation effect did not appear in our measurements. The profiles of the LE and the CT1 states are similar, but there is a definitive difference in the onset and the peak position. On the other hand, the profile of the CT2 state rises and evolves with a substantially slower time profile compared with those of the bands of the LE and CT1 states. These three profiles were well reproduced based on the scheme shown in Fig. 3b. Since the CT2 state population rises at the same rate as the decay of the CT1 state population, we assumed that the backward transition from the CT2 to CT1 state was neglected in the present analysis. The following differential equations represent the population change of these states: | (1) |
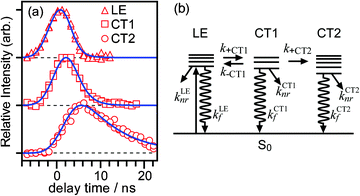 | ||
| Fig. 3 (a) Time profiles of the LE, the CT1, and the CT2 states measured by the transient IR spectroscopy in the νOH region. Open symbols represent the data observed in each trace. Each profile was normalized so that the maximum intensity is equal to 1.0. Solid lines are simulated time profiles for these states according to the kinetic model schematically shown in (b). Details are described in the text. | ||
k Afl: fluorescence decay rate of the state A,
k Anr: non-radiative decay rate of the state A,
k +CT1: formation rate of the CT1 state from the LE state,
k −CT1: backward transition rate from the CT1 state to the LE state, and
k +CT2: formation rate of the CT2 state from the CT1 state.
After solving these equations, the time profiles of these states can be described using three rate constants, λ1, λ2, and λ3. The analytical expressions of these rate constants and the time profiles of each state involved are described in the Appendix. The LE state evolves with the time constants, 1/λ1 and 1/λ2, while the CT1 state rises with 1/λ1 and decays with 1/λ2. The CT2 state rises as the CT1 state decays and finally decays with 1/λ3. As shown in the figure, all the time profiles were well reproduced by the scheme introduced above. The values of the time constants 1/λ1, 1/λ2, and 1/λ3 obtained by the analysis were 0.6 ± 0.2 ns, 2.0 ± 0.2 ns, and 8.3 ± 0.6 ns, respectively. The time profile of the CT emission was reproduced as a rise-and-decay-type profile.6 The rise time constant of the CT emission of 0.6 ns coincides with 1/λ2, while the decay constant of 7.1 ns is coincident with 1/λ3 obtained in the transient IR measurement. This means that the CT1 and the CT2 states cannot be discriminated by CT emission measurement alone, and that the transition from the CT1 to the CT2 state can evidently be identified by transient IR spectroscopy.
Transient IR spectra of the CPDS–H2O cluster in the νCN region
In order to obtain additional information about the character of the CT1 and the CT2 states, transient IR spectra of the CPDS–H2O cluster in the νCN frequency region were measured and are shown in Fig. 4. In the case of νCN, two transient bands other than that of the S0 state (2238.0 cm−1) appeared in the region of 2150–60 cm−1. Although these bands partially overlap, each spectrum can be decomposed by two Gaussian profiles as shown in the inserts in Fig. 4. By this convolution, the center frequencies of these bands are found to be 2155.2 and 2160.0 cm−1. The νCN frequency of the CT state of the CPDS monomer is found to be 2157.1 cm−1, which is just in the middle of these values. | ||
| Fig. 4 IR spectra of the CPDS–H2O cluster in the CN-stretching vibration region. Trace (a) is an IR spectrum of the S0 state, whereas traces (b)–(d) are transient IR spectra. The delay times between the UV and IR laser pulses are indicated in the figure. The inserted spectra exhibit a decomposition of two overlapped bands by the fit using two Gaussian profiles centered at 2155.2 and 2160.0 cm−1. | ||
The time profiles of these two bands are displayed in Fig. 5. Based on a comparison between the time profiles of these bands and those of the OH-stretching bands, the νCN bands of the CT1 and the CT2 states are assigned as shown in Fig. 4. The difference in the νCN frequency between the CT1 and the CT2 states is very small (4.8 cm−1). Thus, it is verified that these two states have the same electronic characteristics, and such a small shift suggests that the difference is due to a coordination change of the attachment of the water molecule onto CPDS. In other words, the CT2 is an isomeric form of the CT1 and vice versa. The transition from the CT1 to the CT2 states observed in the present study is an isomerization of the CPDS–H2O cluster in the CT state. That is, our result is a real time observation of the isomerization of CPDS–H2O.
 | ||
| Fig. 5 Time profiles of the 2155.2 and 2160.0 bands. Open symbols indicate the observed data. Each profile was normalized so that the maximum intensity is equal to 1. Solid lines are simulated time profiles of the CT1 and the CT2 states obtained based on the time profiles of the OH stretching bands. | ||
In the transient IR spectra of the νCN region, we have noticed several features. First, the CN-stretching band of the LE state did not appear in our spectrum. It is expected that the IR transition intensity of the CN-stretching band of the LE state will be too small to be measured by our transient IR spectroscopy. In the case of DMABN, the CN-stretching band of the LE state was only measured by Raman scattering spectroscopy.23 In this respect, the situation of CPDS should be quite similar to that of DMABN. The second feature is that the IR transition intensity of the CN-stretching vibration of the CT state is substantially stronger than that of the S0 state. The widths of the νCN bands of the CT state are much narrower than that of the ν1 band, while they are two or three times broader than that of the νCN band of the S0 state. Thus, the νCN bands of the CT states are considered to be broadened by the IVR process, as in the case of the ν1 band. Since the H-bonded OH stretching is considered to couple with intermolecular vibrations, the broad width should come from relatively large anharmonicities between the ν1 and intermolecular vibrations. However, the anharmonicity between the νCN and intermolecular vibrations seems to be small. Thus, the width of the νCN band turns out to be much narrower than that of the ν1 band.
Possible orientations of the H2O molecule in the CT state
In order to determine the coordination of the H2O moiety on CPDS in the CT state, ab initio calculations (CASSCF(8,8)/cc-pVDZ) of the CPDS–H2O clusters were carried out by using the Gaussian 03 program package.32 The π, σSi−Si, π*, and dπ orbitals were chosen as active orbitals in the calculations. In our previous study, we determined the equilibrium structure of the CT state of CPDS. The H2O moiety is expected to attach to CPDS by hydrogen bonding as well as electric dipole–electric dipole interaction. Based on these interactions, the five isomers shown in Fig. 6 were found. Each of these isomers is labeled according to the orientation of the H2O moiety. In the case of side isomer (a), H2O makes a weak hydrogen bond to the in-plane π-electron cloud of the cyano group. In the linear isomer (b), a strong hydrogen bond is formed between one of the H atoms of H2O and one of the non-bonding orbitals of the nitrogen atom. In the case of the on-ring isomers (c) and (d), on the other hand, H2O attaches to CPDS by the dipole–dipole interaction. In the on-ring 1 structure (c), H2O is directed to the middle of the Si–Si bond, while in the on-ring 2 structure (d), H2O is directed to the Si atom attached to the phenyl ring. In the disilanyl-side isomer (e), H2O should be attached to the disilanyl group through a weak charge–dipole interaction, since the disilanyl group is partially polarized to δ+. The relative energies and dipole moments of these isomers are listed in Table 1. Considering the level of our calculations, one cannot rely on the relative energies among the isomers (a)–(d). Details of results of the calculation, such as the coordinates of each atom in the clusters, are described in the ESI.‡ | ||
| Fig. 6 Isomeric structures of CPDS–H2O in the CT state obtained by a theoretical calculation. | ||
| Isomer | CT1(obs.) | CT2(obs.) | Side | Linear | On-ring 1 | On-ring 2 | Disilanyl-side |
|---|---|---|---|---|---|---|---|
| a Not available. | |||||||
| ΔE/kcal mol−1 | —a | —a | +1.05 | +1.21 | 0.0 | +0.85 | +8.95 |
| ΔE0/kcal mol−1 | —a | —a | +1.46 | +1.86 | 0.0 | +1.15 | +9.24 |
| μ/Debye | —a | —a | 16.4 | 18.8 | 14.4 | 13.4 | 18.6 |
| ν 3/cm−1 | 3720.5 | 3702.5 | 3717 | 3711 | 3704 | 3721 | 3735 |
| ν 1/cm−1 | 3539.3 | 3561.8 | 3629 | 3597 | 3592 | 3615 | 3635 |
| ν CN/cm−1 | 2160.0 | 2155.2 | 2161 | 2160 | 2178 | 2179 | 2163 |
To compare the calculated and observed results, vibrational frequencies of these isomers were examined. Since the number of electrons and atoms is very large, there was a limitation of the basis set used here. We used basically 6-31G(d) basis set and 6-31G(d,p) especially for H atoms in the H2O moiety for a better description of the hydrogen bonding. The vibrational frequencies obtained in the calculations are displayed with the observed spectrum in Fig. 7, in which calculated frequencies are scaled with a factor of 0.876 for the OH-stretch bands and 0.861 for the CN-stretch band. These scale factors were obtained by comparing the vibrational frequencies of the S0 state of CPDS–H2O cluster between the observed and the calculated values. Based on the comparison with the theoretical results, it seems that the CT1 isomer corresponds to the linear-type structure (b), whereas the CT2 corresponds to the on-ring 1 isomer (c). The disilanyl-side isomer can be excluded from the candidates, since its electronic energy is much higher than those of the others.
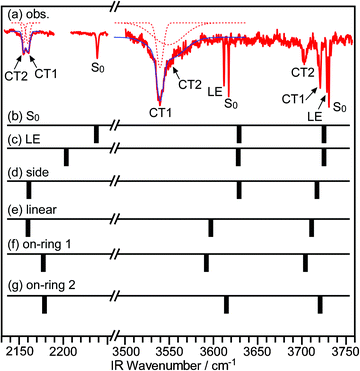 | ||
| Fig. 7 IR spectra of the CPDS–H2O cluster. (a) Observed spectrum. (b)–(g) Calculated spectra. The scaling factor for the OH-stretch vibrations is 0.876, whereas it is 0.861 for the CN-stretch vibration. | ||
However, it is difficult to make a definitive assignment based only on the comparison between the experimental and theoretical frequencies. One of the reasons for this is the insufficient level of calculations. An inclusion of diffuse functions in the basis set should provide us with more reliable results. However, such calculations require very high performance computer facilities, and we cannot carry out such calculations at this stage. Thus, we examined the assignment of the cluster structure not only by the calculated results but also from another viewpoint as described below.
Determination of the orientation of the H2O in the CT1 and CT2 isomers
First, we will examine the linear-type isomer, and consider a typical feature of clusters involving H2O, expressed as HOH-B, where one of the H atoms of the H2O moiety is hydrogen bonded to a proton acceptor site (B). In most cases with an ordinary bond strength, the OHB angle is expected to be close to 180°, since the other hydrogen and the oxygen sites are left free from any intermolecular interaction with the other site(s). In hydrogen-bonded clusters of such linear type, we can often find a good correlation between the observed frequencies of ν3 and ν1, as shown in Fig. 8a. In the figure, ν1 values of several linear-type clusters are plotted against their ν3. Though the experimental data33–36 in the figure are rather limited, there is a good correlation. This correlation can be rationalized as given below. | ||
| Fig. 8 Correlation between the ν3 and the ν1 frequencies of linear-type clusters. (a) Comparison with the experimental vibrational frequencies.33–36 (b) Comparison with the vibrational frequencies obtained by the theoretical calculation. Vibrational frequencies were obtained by the B3LYP/6-31+G(d,p) level of calculations. Vibrational frequencies plotted were scaled by 0.955. Broken lines represent the simulation based on the simplest model, whereas solid lines are the results of the modified model. See details in the text for the simulation. Abbreviations are as follows: BN, benzonitrile; TN, p-tolunitrile; ABN, p-aminobenzonitrile; Cl−, chlorine anion; I−, iodine anion; BN−, benzonitrile anion; and CT1, CT2: isomers of the CPDS–H2O cluster. | ||
In the local mode picture, symmetric (ν1) and anti-symmetric (ν3) OH-stretch vibrational modes are expressed as repelling between the two equivalent OH-stretching vibrational levels by an intramolecular interaction, H′, as schematically shown in Fig. 9a. The value of H′ can be obtained from the difference between the ν1 and ν3 of free H2O. When a hydrogen bond is formed, a zero-order vibrational level energy of one of the OH-stretch mode (νHBOH) shifts to a lower frequency side. In the most naive treatment, it is assumed that neither the energy level of the free OH-stretching vibration (νfeeOH) nor the intramolecular interaction undergoes change. That is, νfreeOH = ν0OH. Vibrational levels (ν3 and ν1) are formed by the intramolecular interaction from these two zero-order states, as shown in Fig. 9b. The energies of the ν3 and ν1 can be calculated as follows.
 | (2) |
 | ||
| Fig. 9 Schematic description of the relation between the normal and local mode pictures in expressing the OH-stretch vibrational level of H2O in (a) free molecule and (b) H-bonded cases. | ||
Fig. 8b exhibits a comparison between our simple model and ν1 and ν3 frequencies obtained by density functional theory calculation (B3LYP/6-31+G(d,p)). Our model well reproduced the correlation between the ν1 and ν3. The deviation increases along with the increase in the shift by the hydrogen bonding. Fig. 8a shows the comparison between the simulated and experimental ν1 and ν3 frequencies. In this case, our model reproduced the trend of a correlation between the ν1 and ν3, but the deviation is much larger in the case shown in Fig. 8b. We slightly modified our model. In the simple model, the νfreeOH is assumed to be unaffected by the hydrogen bonding of the other OH. We modified this assumption. When one of the OH is involved in the hydrogen bonding, the νfreeOH should slightly shift to the lower frequency side. We assumed that the change in the zero-order vibrational level energy of the free OH (ΔνfreeOH = ν0OH − νfreeOH) is a few % of that of the H-bonded one (ΔνHBOH = ν0OH − νHBOH). In this case, the ν3 ant ν1 frequencies are expressed as follows.
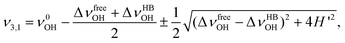 | (3) |
This slight modification gives us a better agreement, as shown in the figure. In the case of the simulation shown in Fig. 8b, we assumed that the value of ΔνfreeOH was 1.2% of the ΔνHBOH, whereas we found that it was 3% in the case of Fig. 8a. Thus, this simple and intuitive model can interpret the correlation between the ν1 and ν3 frequencies.
In Fig. 8a, data points for the CT1 and CT2 states of the CPDS–H2O cluster are also plotted. It can be clearly seen that the point corresponding to the CT1 state is very close to the correlation line, indicating that the hydrogen-bonding feature would be similar to others with a linear type. This correlation provides us with firm support for the linear form assignment above from an experimental viewpoint, and the assignment of the structure type also agrees with the expectation based on the theoretical calculation mentioned above. Therefore, we concluded that the structure of the CT1 state is of the linear type.
The side-type orientation is a common structure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cluster of benzonitrile derivatives with H2O in the S0 state.31,33,37 Several sets of data of ν3 and ν1 are available for several clusters in both the S0 and the S1 states.33,37 The ν3 are in the range from 3732 to 3728 cm−1, whereas the ν1 are in the range from 3619 to 3609 cm−1, as listed in Table 2. It seems that the OH-stretch frequencies of the side-type isomer are not substantially affected by the electronic excitation. In this orientation, the H atom mainly interacts with the πCN orbital of the CN bond, which is located in the same plane as the phenyl ring. This side πCN orbital does not contribute to the conjugation with the phenyl π system. Thus, the charge distribution of this side πCN orbital is expected not to change substantially in the ππ* or the σSi−Siπ* excitations. Therefore, the hydrogen-bonding strength is not affected significantly by the electronic excitation. Our calculation also exhibited a small frequency change among the CT, the LE, and the S0 states in the side orientation. Thus, the side isomer should not be a candidate for the CT2 isomer.
1 cluster of benzonitrile derivatives with H2O in the S0 state.31,33,37 Several sets of data of ν3 and ν1 are available for several clusters in both the S0 and the S1 states.33,37 The ν3 are in the range from 3732 to 3728 cm−1, whereas the ν1 are in the range from 3619 to 3609 cm−1, as listed in Table 2. It seems that the OH-stretch frequencies of the side-type isomer are not substantially affected by the electronic excitation. In this orientation, the H atom mainly interacts with the πCN orbital of the CN bond, which is located in the same plane as the phenyl ring. This side πCN orbital does not contribute to the conjugation with the phenyl π system. Thus, the charge distribution of this side πCN orbital is expected not to change substantially in the ππ* or the σSi−Siπ* excitations. Therefore, the hydrogen-bonding strength is not affected significantly by the electronic excitation. Our calculation also exhibited a small frequency change among the CT, the LE, and the S0 states in the side orientation. Thus, the side isomer should not be a candidate for the CT2 isomer.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
ν 3/cm−1 | ν 1/cm−1 | Ref. |
|---|---|---|---|
| a There are two isomers for the 1-CNN-H2O cluster. This isomer B has the same geometric configuration as BN. b There are two isomers for the 2-CNN-H2O cluster. Both of the isomers have the same geometric configuration as BN. | |||
| CPDS(S0) | 3730.3 | 3617.1 | This work |
| CPDS(LE) | 3728.2 | 3611.7 | This work |
| BN(S0) | 3732 | 3619 | 37 |
| BN(S1) | 3730 | 3613 | 37 |
| ABN(S0) | 3731 | 3612 | 33 |
| 1-CNN(S0) (B)a | 3731 | 3619 | 37 |
| 1-CNN(S1) (B)a | 3731 | 3617 | 37 |
| 2-CNN(S0) (A)b | 3730 | 3617 | 37 |
| 2-CNN(S1) (A)b | 3728 | 3609 | 37 |
| 2-CNN(S0) (B)b | 3732 | 3618 | 37 |
| 2-CNN(S1) (B)b | 3729 | 3609 | 37 |
The remaining candidate for the CT2 state is the on-ring 1 structure. As shown in Fig. 7, the calculated OH vibrational frequencies were acceptable, though there were two discrepancies between the calculated and observed IR spectra. One was the relative intensity between the ν3 and the ν1. The observed IR spectra indicate that the transition intensity of the ν1 is much stronger than that of the ν3. However, the calculation predicts that the intensity of the ν1 band will be the similar to or less than that of the ν3 band. The other discrepancy was a disagreement in regard to the νCN frequency. That is, the νCN of the on-ring isomer was calculated to be somewhat higher than those of the other isomers. The most probable reason for these discrepancies is an insufficient level of calculation. However, despite these minor discrepancies, we can safely conclude that the orientation of H2O for the CT2 state is an on-ring-type orientation.
Reorientation dynamics of the H2O moiety
Based on our transient IR spectroscopy, we have revealed the detailed dynamics of the ICT process in the CPDS–H2O system. The structural changes in the ICT process and corresponding time constants are graphically illustrated in Fig. 10. Since the H2O moiety is located at the side position of the cyano group in the LE state, the reorientation of the H2O should start from the side configuration. As the CT state is generated form the LE state, the H2O moiety moves from the side position to the linear configuration, followed by the further dynamics of the H2O moiety to the on-ring orientation.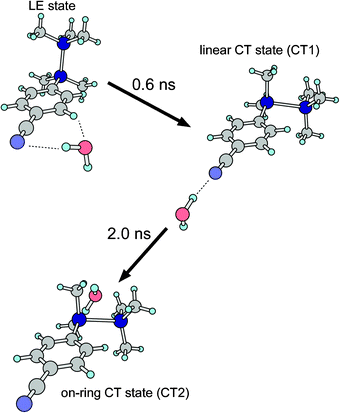 | ||
| Fig. 10 Graphical illustration of the ICT process of the CPDS–H2O cluster. | ||
It should be noted that the first step consists of two dynamics; one is the electronic transition from the LE to the CT states and the other is the movement of the H2O moiety from the side to the linear configuration. Since the time resolution of our study was limited by the pulse widths of our nanosecond lasers, it was difficult to resolve the initial parts of the fast dynamics with the present transient IR spectroscopy. Thus, the reorientation dynamics of the H2O moiety from the side to the linear configuration is expected to be very fast, presumably with a picosecond time scale, which is too fast to detect a short lived isomer in our transient IR spectroscopy. If this reorientation process proceeds in a nanosecond time scale, the rise of the transient IR intensity of the linear isomer would be delayed compared to the rise of the CT emission intensity. However, the rise time constant of the CT emission intensity coincides with that of the transient IR band within our experimental uncertainty. This fact supports our estimation that the reorientation from the side to the linear configuration proceeds within our experimental time resolution.
In the time profile analysis, we ignored the backward transition from the CT2 to the CT1 isomers. This assumption corresponds to the following condition. As our calculation showed, there are at least two local minima in the on-ring configuration. Thus, it is expected that a potential energy surface around the on-ring configuration is very shallow or nearly flat, and that the density of state in the CT2 state should be very high. Therefore, the effective backward transition rate is negligible. In contrast to the first step of the ICT process of the CPDS–H2O cluster, the second step proceeds very slowly, with a time constant of 2.0 ns. Such a slow rate can be related to either a relatively high barrier in this process or a large geometric difference in the orientation between the CT1 and the CT2 states. Our preliminary calculation showed that the barrier height of the reorientation from the linear to the on-ring 1 configuration is on the order of 1 kcal mol−1. In such a case of reorientation with a potential barrier, the reorientation rate would depend significantly on the overlap between the vibrational wave functions in both potential wells. Therefore, the relatively slow time constant observed for the reorientation should be due to a small overlap in the wave functions of intermolecular vibrations between the CT1 and CT2 states.
It is revealed that there are two distinct time scales, pico- and nanosecond, of the reorientation dynamics in the ICT process of the CPDS–H2O cluster. One of the origins of such a significant difference should be a topological difference in the paths of the potential energy surface. As mentioned above, the barrier height between the isomers is not very high in either of the steps. The major difference should be overlaps in the wave functions of the intermolecular vibrations between the corresponding isomers. In any case, very detailed reorientation dynamics could be obtained by applying the transient IR spectroscopy to a molecular cluster system.
Conclusion
We have carried out the transient IR spectroscopy of the CT state of the CPDS–H2O cluster. By using such a solvated cluster, the transient IR spectroscopy enabled us to obtain information about the coordination dynamics of the solvent molecule occurring under the evolution of the ICT process. It was revealed that the reorientation dynamics of the ICT process proceeds in two steps. The first step is a reorientation from the side to the linear configuration, while the second step is a reorientation from the linear to the on-ring configuration. It should be noted that the time scales of these steps are very distinct: pico- vs. nanosecond. This variation in the dynamics rates arises mainly from the differences in the overlaps of the vibrational wave functions between the corresponding isomers. As graphically shown in Fig. 10, the H2O molecule travels across a very wide region around the CPDS moiety. The transition from the CT1 to CT2 can also be treated as an isomerization of the CPDS–H2O cluster. In other words, the observations in this report represent a real-time probe of the isomerization. To our knowledge, this is the first report of such a direct observation, probing the vibrations of solvent molecule(s), of the isomerization in the cluster systems. The reorientation dynamics revealed here cannot be obtained by the analysis of the time profile of the CT emission. By applying the transient IR spectroscopy to the solvated cluster, we could obtain a very detailed picture of the reorientation dynamics in the ICT process, including detailed orientations of the solvent molecule as well as the time constants. Although our system is a simple 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cluster, the dynamics we revealed is found not to be a simple process. Our observation of the reorientation process of the solvent molecule in the ICT process should provide new insights into the ICT process.
1 cluster, the dynamics we revealed is found not to be a simple process. Our observation of the reorientation process of the solvent molecule in the ICT process should provide new insights into the ICT process.
Appendix
The time profiles of the LE, the CT1, and the CT2 states can be expressed analytically as follows. | (A1) |
 | (A2) |
 | (A3) |
 | (A4) |
 | (A5) |
Acknowledgements
This work was partially supported by a Grant-in-Aid for Scientific Research (No. 16550004) by J.S.P.S. Some of the theoretical calculations in the present study were performed using supercomputing resources at the Information Synergy Center, Tohoku University, Japan. M.N. acknowledges the financial support of a Grant-in-Aid for specially promoted research from MEXT (Project No. 16002006).References
- (a) E. Lippert, Z. Naturforsch., 1955, 10a, 541 Search PubMed; (b) E. Lippert, W. Lüder and H. Boos, in Advances in Molecular Spectroscopy, ed. A. Mangini, Pergamon, New York, 1962, p. 443 Search PubMed.
- For a recent review, see: Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899 Search PubMed.
- K. Rotkiewicz, K. H. Grellmann and Z. R. Grabowski, Chem. Phys. Lett., 1973, 19, 315 CrossRef CAS.
- Y. Tajima, H. Ishikawa, T. Miyazawa, M. Kira and N. Mikami, J. Am. Chem. Soc., 1997, 119, 7400 CrossRef CAS.
- H. Ishikawa, Y. Shimanuki, M. Sugiyama, Y. Tajima, M. Kira and N. Mikami, J. Am. Chem. Soc., 2002, 124, 6220 CrossRef CAS.
- H. Ishikawa, M. Sugiyama, Y. Shimanuki, Y. Tajima, W. Setaka, M. Kira and N. Mikami, J. Phys. Chem. A, 2003, 107, 10781 CrossRef CAS.
- H. Ishikawa, M. Sugiyama, I. Baba, W. Setaka, M. Kira and N. Mikami, J. Phys. Chem. A, 2005, 109, 8959 CrossRef CAS.
- H. Sakurai, H. Sugiyama and M. Kira, J. Phys. Chem., 1990, 94, 1837 CrossRef CAS.
- M. Kira, T. Miyazawa, H. Sugiyama, M. Yamaguchi and H. Sakurai, J. Am. Chem. Soc., 1993, 115, 3116 CrossRef CAS.
- M. Kira and T. Miyazawa, in The chemistry of organic silicon compounds, ed. Z. Rappoport and Y. Apeloig, John Wiley & Sons, Chichester, 1998, vol. 2, ch. 22 Search PubMed.
- H. Shizuka, H. Obuchi, M. Ishikawa and M. Kumada, J. Chem. Soc., Chem. Commun., 1981, 405 RSC.
- H. Shizuka, Y. Sato, M. Ishikawa and M. Kumada, J. Chem. Soc., Chem. Commun., 1982, 439 RSC.
- H. Shizuka, H. Y. Sato, Y. Ueki, M. Ishikawa and M. Kumada, J. Chem. Soc., Faraday Trans. 1, 1984, 80, 341 RSC.
- H. Shizuka, H. Obuchi, M. Ishikawa and M. Kumada, J. Chem. Soc., Faraday Trans. 1, 1984, 80, 383 RSC.
- H. Shizuka, K. Okazaki, M. Tanaka, M. Ishikawa, M. Sumitani and K. Yoshihara, Chem. Phys. Lett., 1985, 113, 89 CrossRef CAS.
- H. Hiratsuka, Y. Mori, M. Ishikawa, K. Okazaki and H. Shizuka, J. Chem. Soc., Faraday Trans. 2, 1985, 81, 1665 RSC.
- M. Yamamoto, T. Kudo, M. Ishikawa, S. Tobita and H. Shizuka, J. Phys. Chem. A, 1999, 103, 3144 CrossRef CAS.
- H. Tachikawa and M. Igarashi, J. Phys. Chem. A, 1998, 102, 8648 CrossRef CAS.
- S. Ishiuchi, M. Sakai, Y. Tsuchida, A. Takeda, Y. Kawashima, M. Fujii, O. Dopfer and K. Müller-Dethlefs, Angew. Chem., Int. Ed., 2005, 44, 6149 CrossRef CAS.
- M. Gerhards, A. Jansen, C. Unterberg and A. Gerlach, J. Chem. Phys., 2005, 123, 074320 CrossRef CAS.
- (a) T. Sanford, D. Andrews, J. Rathbone, M. Taylor, F. Muntean, M. Thompson, A. B. McCoy, R. Parson and W. C. Lineberger, Faraday Discuss., 2004, 127, 383 RSC; (b) F. Muntean, M. S. Taylor, A. B. McCoy and W. C. Lineberger, J. Chem. Phys., 2004, 121, 5676 CrossRef CAS; (c) M. S. Taylor, J. Barbera, C.-P. Schulz, F. Muntean, A. B. McCoy and W. C. Lineberger, J. Chem. Phys., 2005, 122, 054310 CrossRef.
- J. R. Clarkson, E. Baquero, V. A. Shubert, E. M. Myshakin, K. D. Jordan and T. S. Zwier, Science, 2005, 307, 1443 CrossRef CAS.
- W. M. Kwok, C. Ma, D. Phillips, P. Matousek, A. W. Parker and M. Towrie, J. Phys. Chem. A, 2000, 104, 4188 CrossRef CAS.
- C. Chudoba, A. Kummrow, J. Dreyer, J. Stenger, E. T. J. Nibbering, T. Elsaesser and K. A. Zachariasse, Chem. Phys. Lett., 1999, 309, 357 CrossRef CAS.
- W. M. Kwok, C. Ma, P. Matousek, A. W. Parker, D. Phillips, W. T. Toner, M. Towrie and S. Umapathy, J. Phys. Chem. A, 2001, 105, 984 CrossRef CAS.
- J. Dreyer and A. Kummrow, J. Am. Chem. Soc., 2000, 122, 2577 CrossRef CAS.
- D. Rappoport and F. Furche, J. Am. Chem. Soc., 2004, 126, 1277 CrossRef CAS.
- T. Ebata, N. Mizuochi, T. Watanabe and N. Mikami, J. Phys. Chem., 1996, 100, 546 CrossRef CAS.
- Tables of wavenumbers for the calibration of infrared spectrometers, ed. International Union of Pure and Applied Chemistry, Commission on Molecular Structure and Spectroscopy, Butterworths, London, 1961 Search PubMed.
- G. Herzberg, Molecular Spectra and Molecular Structure, Vol. III—Electronic Spectra and Electronic Structure of Polyatomic Molecules, Van Nostrand, New York, 1966 Search PubMed.
- S. Ishikawa, T. Ebata and N. Mikami, J. Chem. Phys., 1999, 110, 9504 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 program package (Revision C.02), Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- K. Sakota, N. Yamamoto, K. Ohashi, M. Saeki, S. Ishiuchi, M. Sakai, M. Fujii and H. Sekiya, Chem. Phys., 2002, 283, 209 CrossRef CAS.
- P. Ayotte, C. G. Bailey, G. H. Weddle and M. A. Johnson, J. Phys. Chem. A, 1998, 102, 3067 CrossRef CAS.
- J.-H. Choi, K. T. Kuwata, Y.-B. Cao and M. Okumura, J. Phys. Chem. A, 1998, 102, 503 CrossRef CAS.
- T. Maeyama, I. Yagi, Y. Murota, A. Fujii and N. Mikami, J. Phys. Chem. A Search PubMed , submitted.
- (a) R. Yamamoto, T. Ebata and N. Mikami, Symposium on Molecular Structure, Kobe, 2002 Search PubMed; (b) R. Yamamoto, Ph.D. thesis, Tohoku University, 2003.
Footnotes |
| † The HTML version of this article has been enhanced with colour images. |
| ‡ Electronic supplementary information (ESI) available: Cartesian coordinates of optimized structure of five isomers of CPDS–H2O clusters. See DOI: 10.1039/b612758d. |
| This journal is © the Owner Societies 2007 |
