Using blood hemoglobin for blood analysis†
Vanesa
Sanz
,
Susana
de Marcos
and
Javier
Galbán
*
Analytical Biosensors Group, Analytical Chemistry Department, Faculty of Sciences, University of Zaragoza and Institute of Nanotechnology, Zaragoza, 50009, Spain. E-mail: jgalban@unizar.es
First published on 6th November 2006
Abstract
This paper demonstrates that the spectrophotometric properties of blood hemoglobin (Hb) can be used for the direct determination of biochemical compounds in blood. Glucose is used as a model, but the methodology can be applied to many other compounds (only a previous enzymatic reaction producing H2O2 is needed). In order to develop the method, a model relating the Hbabsorbance variation during the reaction with the glucose concentration has been developed to provide theoretical support for the method and to predict its application to other compounds. In addition, clear blood samples need to be prepared without pre-treatment and lateral reactions of H2O2 with other blood constituents need to be blocked; this has been achieved with 100 : 1 v/v blood dilution in bi-distilled water and azide addition. The linear response range of the method can be fitted between 2 and 540 mg dL–1glucose relative to the original blood sample (RSD about 4%, 70 mg dL–1). The analyte concentration can be obtained by an absolute calibration method or by the standard addition method; both have been applied for direct glucose determination in several blood samples and good correlations with those obtained by an automatic analyzer have been obtained.
Introduction
The development of analytical methods for the determination of molecular species in biological (including human) fluids continues to be one of the most important tasks facing analytical chemistry. Not only do such methods represent substantial business for the clinical chemistry industry, they also act as a spearhead for many other kinds of analytical fields; methods for which viability is demonstrated for biological fluids (enzymatic methods, immunoassay methods, DNA analysis) are quickly implemented in other branches of chemistry (environmental, toxicology or food, among others).Most routine analytical methods currently in use (i.e., for blood sample analysis) assume that all molecular species accompanying the analyte in the sample are either interferences (which have to be eliminated) or innocuous species (and can therefore remain in the sample during analysis); for this reason, most methods require a previous interference elimination step (for blood analysis, usually of cells and proteins) and in consequence are not fully reversible in essence. This idea is impractical for current and future needs and trends in chemistry, such as sensor designs, lab-on-a-chip philosophy or continuous analysis. A leading research line in analytical methodology (begun and developed by several groups such as those of Hellinga,1,2 Cass,3,4 Daunert,5 Lakowick,6 and our own,7,8 among others9), alternative to synthetic receptors, deals with methods trying to be both compatible with fluid samples and reversible. Such methods are based on the use of spectrochemical analytical signals (mainly fluorescence or molecular absorption) generated by the proteins themselves. The idea is to try to increase the method selectivity by transforming all the chemical species in the sample (except the analyte) into innocuous species.
However, in this paper we propose a new approach consisting of using molecular species present in the sample itself as reagents. In blood analysis using molecular spectrochemical methods, the human hemoglobin (Hb) represents a strong spectral and chemical interference. In this new approach we take advantage of the spectrochemical properties of Hb and use the reaction between Hb and H2O2 (which is previously generated in an enzymatic reaction) for the determination of blood components; in this way an interference is converted to a reagent.
The basis of this derives from the fact that, like other heme proteins,10Hb is composed of an active heme group—in this case ferrous—and its amino acidic surround. During its reaction with H2O2, changes are observed in its molecular absorption spectrum owing to the formation of species in which the heme group presents different oxidation states; if the H2O2 is produced in a previous enzymatic reaction, the variation of the Hb absorption can be used to determine the substrate of the previous enzymatic reaction; the classical enzymatic oxidation of glucose with glucose oxidase (GOx) (giving H2O2) is used as a model for this new methodology. To achieve our aim, two aspects need to be dealt with: (a) a clear blood sample needs to be obtained without pre-treatment and lateral reactions of H2O2 with other blood constituents need to be blocked, and (b) a mathematical model relating the Hbabsorbance variation during the reaction with the glucose concentration has to be developed to provide theoretical support for the method and to predict its application to other compounds. Both aspects are considered in the paper.
The main aim of the work is not only to present a new method for glucose determination in blood (in fact this method, slightly modified, can be used for the determination of lactate, cholesterol or many other substances), but to introduce a new approach which tries to avoid the idea of destructive methods, and might be considered as a new step towards a kind of “sustainable analytical chemistry”.
Experimental
Instruments
The molecular absorption measurements were carried out in a Hewlett-Packard 8452A diode-array spectrometer and in a Perkin–Elmer Lambda 5 spectrometer (2 nm bandwidth). Quartz cells of 1 cm optical pathway.Software
The scientific software Origin 6.0® was used for fitting the experimental data to the theoretical equations.Materials
A0 Human Hemoglobin (A0-Hb) (Sigma H-0267) of 46% (w/w) purity was used. Glucose oxidase (GOx) was taken from Aspergillus Níger, E.C. 1.1.3.4 (Sigma G-7141), and was of 157 IU mg–1 of lyophilised solid. Protein solutions were prepared by dissolving the solid in bi-distilled water (except where indicated).Glucose (G) stock solutions were prepared by dissolving the appropriate amount of β-D-(+)-glucose (Sigma G-5250) in bi-distilled water.
Azide solutions were prepared by dissolving the appropriate amount of sodium azide (Sigma S-8032) in bi-distilled water. Sodium azide may be fatal if swallowed or absorbed through skin and harmful if inhaled. When it is mixed with water, sodium azide changes rapidly to a toxic gas.
The H2O2 or glucose calibration experiments and the study of the effect of hemoglobin on ΔAbs experiments were carried out using A0-Hb. The rest of the experiments were performed by using blood. Blood as a reagent was obtained from volunteers. After punction the glucose concentration was determined by using a Reflotron®.
Procedure for glucose determination
Bi-distilled water (1860 µL) is placed in the measurement cuvette. Immediately after finger punction, 20 µL blood is collected and added to the cuvette, which is then stirred for about 30 seconds until the hemolysis (erythrocyte lyses and Hb liberation) is over, which is detected by the disappearance of the initial turbidity observed in the cuvette. Then 100 µl of a 0.2 M sodium azide solution is added and the absorbance value (Absλ,0) at the wavelength selected (typically 576 nm; Abs576,0) is measured. Finally, 20 µL GOx solution (typically 5.10–4 M, 12.2 U µL–1) is added and the absorbance is monitored as a function of time. The parameter used for quantification is:| ΔAbs576,90 = Abs576,90 – Abs576,0 |
Abs576,90 being the absorbance at 576 nm after 90 s from the beginning of the reaction. In the standard addition method a second sample is prepared in the same conditions but replacing the bi-distilled water with a 0.80 mg dL–1glucose solution.
Theoretical models, results and discussion
Reaction between Hb and H2O2
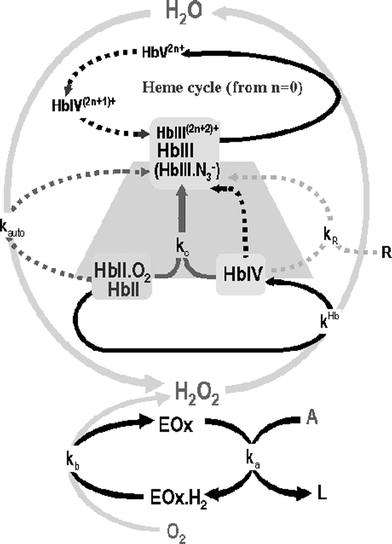 | ||
| Fig. 1 The Hb/H2O2 cycle. Throughout the paper the conventional nomenclature for hemoglobin is being used: Hb(X) refers to the total concentration of an oxidation state of the heme group and HbX refers to a particular species. The superscript charge refers to the number of amino acids which become oxidized (for example; in HbIV+ the heme group is in Fe(IV) oxidation state and one electron has been transferred from the shell to the heme). The arrows represent: black dotted line: intramolecular reduction; grey dotted line: autoxidation; grey solid line:comproportionation; light grey dotted line: external reducer; black solid line: oxidation with H2O2. Shaded zone corresponding to the reaction mechanism in the presence of azide. | ||
Because electrons can be transferred from these amino acids to the heme group of the same protein (intramolecular redox process) or other neighboring proteins (intermolecular redox process), the formal oxidation state of this shell is represented by a n+ superscript (see Fig. 1 caption); these properties confer a very significant redox activity to the molecule as a whole.
The heme group of the protein in +2 oxidation state (HbII; in blood this oxidation state is mainly linked to O2, giving oxyhemoglobine HbII.O2) reacts with H2O2 producing +4 oxidation state (HbIV, ferrylhemoglobin). The HbIV is very reactive and can be reduced to Hb(III) according to three processes: by the surrounding amino acid part of the hemoglobin (inter- and intramolecular redox processes), by comproportionation (kc) with another HbII.O2 molecule or by external reducers (R). This last reaction, which is not really of interest for this paper, could in fact increase the analytical possibilities of the system towards R species determination; examples of R species are reducing compounds found in biological fluids, such as uric acid or ascorbic acid, which can reduce Hb(IV) at a kinetic constant (kR) of about 150 M–1 s–1 and 15 M–1 s–1, respectively. The main HbIV reduction process depends on the value of the kinetic constants, the Hb/H2O2 ratio11 and the pH; in the conditions used throughout the paper (the Hb concentration ranges from being higher to slightly lower than that of H2O2 and a pH about 6), the comproportionation reaction is the most important.
In this situation, and when there is an excess of H2O2, the inner redox cycle of Hb starts (Fig. 1). In this cycle, the HbIII formed is ready to react with another H2O2 molecule forming the HbV species which is more reactive than HbIV so it very quickly decays by intramolecular reduction, firstly to HbIV+ and subsequently (in the absence of an external reducer) to HbIII2+; this molecule is again ready to react with another H2O2 and a new cycle begins.
Finally the HbII.O2 can also suffer autoxidation, which can be considered as the oxidation of HbII by the linked O2; this is a radical mediated process giving HbIII and H2O2, which is very dependent on the pH.
 | ||
| Fig. 2 Absorption spectrum of hemoglobin species during the reaction with H2O2. (a) HbII.O2; (b) HbIII.N3–, obtained as the complete conversion of HbII.O2 after a stoichiometric addition of H2O2 to HbII.O2 in the presence of azide; (c) Hb(IV), obtained after the addition of H2O2 1.77 × 10–3 M to HbIII 10–4 M (an excess of H2O2 over HbIII is necessary to ensure the complete conversion of HbIII to HbIV because of the slowness of the reaction); (d) Hb(III), obtained as the complete conversion of HbII.O2 after a stoichiometric addition of H2O2 to HbII.O2. | ||
In order to use blood hemoglobin as a reagent it is necessary to achieve hemolysis (for Hb liberation) without coagulation (to avoid Hb losses and light dispersion). This depends on the blood handling after extraction. In our experience, blood dilution with bi-distilled water at a level of 50 : 1 (v/v, water : blood) or higher fulfils these conditions; a 100 : 1 v/v is a good choice considering the blood concentrations of glucose, hemoglobin and the potential interferences with the Hb/H2O2 reaction.
These diluted solutions are stable for about 1 day (about 24 h) in a closed vessel, out of the light and at room temperature; Fig. 3 shows the results of a stability study. Diluted blood samples kept with azide are stable for at least the same time. According to other authors17 and our own experiments, dilutions made with buffers can also provide stable solutions when the concentration of the buffer is kept below 10–2 M.
 | ||
Fig. 3 Stability study of the hemolysed blood samples. Blood is diluted in bidistilled water 100 : 1 v/v. (♦) HbII.O2 and ( ) glucose concentrations as a function of time after punction; both are determined by the methods proposed in this paper. The blood diluted sample was kept in a closed vessel out of the light and at room temperature between measurements. ) glucose concentrations as a function of time after punction; both are determined by the methods proposed in this paper. The blood diluted sample was kept in a closed vessel out of the light and at room temperature between measurements. | ||
2GSH + H2O2 ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (GP) (GP)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) > glutathione disulfide + 2H2O > glutathione disulfide + 2H2O |
However the possible interference of this reaction can be discarded because the GSH levels in blood are low relative to Hb (about 10–3 M18) and the activity of GP is lower than catalase (the GP activity in blood is about 1% than that of catalase).19GSH may act as a reducer of Hb(IV) but, in the light of the kinetic constants and the levels of GSH and HbIIO2 in blood,11 the comproportionation reaction (HbII.O2 as reducer) is faster. Furthermore, GSH may consume H2O2 through the reaction with GP, but the literature19,20 and our experimental results shows that the main H2O2 consuming reaction is catalase; so, the addition of iodoacetamide which inhibits GP by reacting with GSH does not modify the consumption of H2O2 by Hb. These two facts make GSH interference negligible. Catalase catalyses the disproportionation of H2O2 according to:
H2O2 ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (catalase) (catalase)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) > ½O2 + H2O > ½O2 + H2O |
This enzyme is another heme-protein (with the Fe of the heme group in the 3+ oxidation state) but with a very high activity. This is the reason why, in order to observe the Hb/H2O2 reaction, it is necessary to block the human catalase activity, which can be achieved by sodium azide (NaN3) addition.
Azide inhibits catalase because it forms an inactive redox compound with the Fe(III)21,22 of the heme group. Azide also affects the HbIII molecular absorption spectrum (Fig. 2 shows that the HbIII.N3– complex presents a molecular absorption spectra significantly different from that of the HbIII) and the Hb mechanism; in its presence the Hb/H2O2 reaction stops when the Hb reaches the HbIII state (Fig. 1, trapezoidal shaded zone) as can be deduced from Fig. 4, which shows how the molecular absorption spectra of the blood changes during the reaction in the presence of azide, indicating that the isosbestic point HbII.O2/HbIII.N3– is conserved.
 | ||
| Fig. 4 Variation of the absorption spectrum of blood during the enzymatic reaction (blood dilution 1 : 100, 1 × 10–5 M glucose oxidase and 0.01 M azide in bi-distilled water). The absorption spectra were recorded before addition of GOx (t = 0) and every 50 seconds after glucose oxidase addition. Note that two isosbestic points are observed during the reaction, corresponding to the HbII.O2/HbIII.N3– transition (526 and 586 nm, see Fig. 1). Inset: absorbance variation at 576 nm as a function of time. | ||
As Fig. 2 show, the maximum difference in the molar absorptivity coefficients between HbII.O2 and HbIII.N3– appears at 576 nm (this is the reason why this wavelength was chosen for kinetic and analytical purposes). Additional tests have shown that azide does not react with HbII.O2 nor Hb(IV) species.
Fig. 5 shows the effect of the azide concentration on the absorbance variation during the Hb/H2O2 reaction. The absorbance variation measured (ΔAbs576,500) is the difference between the initial absorbance and the absorbance at a time t (t = 500 s) from the beginning of the reaction; given that at the wavelength selected (576 nm) εHbII.O2 > εHbIII.N3–, an absorbance decrease is observed. In the absence of azide, no changes in absorbance are observed because the H2O2 only reacts with catalase. As the azide concentration increases, the absorbance variation of Hb also increases (blood catalase is partially inhibited), while for an azide concentration higher than 0.01 M, the absorbance variation becomes independent of the azide concentration revealing that all the catalase has been inhibited.
 | ||
| Fig. 5 Azide effects on: (■) ΔAbs576,500 during the blood Hb and H2O2 reaction as a function of azide concentration. Blood diluted in bidistilled water to give a hemoglobin concentration 1.0 × 10–4 M and pH 6. The H2O2 concentration was 7.0 × 10–5 M; (♦) Kinetic constant of the GOx reaction (ka). The kinetic constants were obtained from several calibration curves with glucose and GOx (5.0 × 10–8 M) using a fluorometric method described elsewhere.23 | ||
The HbII.O2 autoxidation works against the Hb/H2O2 reaction. However this process is highly dependent on the pH (see ESI, page ESI-2† ). When blood is diluted in water, the resulting pH is about 6, so the autoxidation is negligible.
Analytical model
The mathematical model for the Hb/GOx/Glucose reaction will be better understood if the Hb/H2O2 reaction is first considered. The key to the mathematical model is the mass balance for the Hb and H2O2 in the presence of azide. According to Fig. 1 (shaded zone):| [Hb]0 = [HbII.O2]t + [HbII]t + [HbIV]t + [HbIII.N3–t]t ≈ [HbII.O2]t + [HbIII.N3–]t | (1) |
 | (2) |
In addition to the fact that the vast majority of HbII is in the HbII.O2, the mass balances (1) and (2) assume the HbIV concentration during the reaction is very low; this can be deduced from Fig. 2B, which shows how the molecular absorption spectra of the blood change during the reaction in the presence of azide, indicating that the isosbestic point HbII.O2/HbIII.N3– is conserved.
Before the reaction the absorbance (Absλ,0) is only due to HbII.O2. As the HbII.O2 is the majority species in blood, then:
| ΔAbsλ,0 = εIIλ[HbII.O2]0 = εIIλ[Hb]0 | (3a) |
During the reaction, a part of the HbII.O2 is transformed into HbIII.N3–, so that at any time during the reaction the absorbance (Absλ,t) is due to the concentration of both species. The absorbance change (the optical pathlength will be considered to be 1 cm throughout the paper) during the reaction at any wavelength is then given by:
| ΔAbsλ,t = Δελ[HbIII.N3–]t | (3b) |
εIIλ and  being the molar absorptivity of the HbII.O2 and HbIII.N3– species respectively. To express the [HbIII.N3–]t as a function of the reactants, the following two kinetic considerations should be taken into account:
being the molar absorptivity of the HbII.O2 and HbIII.N3– species respectively. To express the [HbIII.N3–]t as a function of the reactants, the following two kinetic considerations should be taken into account:
(1) The variation of [HbIII.N3–]t is given by:
 | (4) |
(2) The steady state approximation can be applied to [HbIV]:
 | (5) |
A combination of eqn (1), (4) and (5) yields:
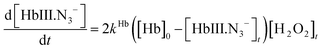 | (6) |
 | (7) |
 | (8) |
Finally considering that the measurements are made at 576 nm , the combination of eqn (8) and eqn (3b) yields:
 | (9) |
Fig. 6 shows the ΔAbs576,t changes obtained after submitting different aliquots of a HbII.O2 solution (A0-Hb reagent) to the reaction with aliquots of different concentrations of H2O2. The figure also shows the graph obtained by fitting the results to a function as that indicated in eqn (9) (Origin™ software was used). From these fitting the kHb could be obtained giving 14 ± 1 M–1 s–1.
 | ||
| Fig. 6 ΔAbs576,t change as a function of time for different H2O2 concentrations: (a) 2.5 × 10–5 M, (b) 4.5 × 10–5 M, (c) 6.5 × 10–5 M, (d) 8.5 × 10–5 M, (e) 1.8 × 10–4 M and (f) 3.0 × 10–4 M. Reaction conditions: 4.4 × 10–5 M hemoglobin, 0.01 M azide pH 6. Grey lines are the theoretical curves. | ||
Eqn (9) admits several simplifications depending on the measurement times considered (see ESI, page ESI-3 for discussion† ).
For glucose determination, as the whole Hb/GOx process consists of two enzymatic cycles, different considerations have to be applied depending on the relative rate of both. When the H2O2/HbII.O2 is the limiting step of the process, all the analyte (glucose, G) is quickly converted to H2O2 at the very beginning of the reaction, so that:
| [H2O2]0 = [G]0 | (10) |
Under these conditions, the model described by eqn (9) can be directly applied by substituting [H2O2]0 by [G]0.
 | (11) |
This can be achieved by adequately increasing the GOx concentration. However, two important matters should first be taking into account.
In conclusion, a GOx concentration high enough should be chosen to fulfil eqn (10) and low enough to avoid its reaction with Hb. In that condition, Fig. 7 shows the ΔAbs576,t obtained for different initial glucose concentrations in these conditions and how these curves fit the theoretical model (eqn (11)).
 | ||
| Fig. 7 ΔAbs576,tversus time for different glucose concentrations under eqn (11) fulfilment: (a) 2.6 × 10–5 M, (b) 4.5 × 10–5 M, (c) 6.6 × 10–5 M, (d) 8.5 × 10–5 M and (e) 1.8 × 10–4 M. Reaction conditions: 4.3 × 10–5 M Hb, 5.0 × 10–6 M GOx and 0.01 M azide. The grey lines correspond to the theoretical curves (eqn (11)). | ||
Eqn (11) admits several simplifications depending on the measurement time considered. Table 1 shows the most important simplifications for analytical purposes. The kHb values were also obtained and also match very well with the previously obtained average values.
| t interval | Simplification applied | Mathematical model | K Hb/M–1 s–1 | |||
|---|---|---|---|---|---|---|
| a e([Hb]0 – 2[G]0)kHbt ≈ 1 + ([Hb]0 – 2[G]0)kHbt. b 1 + [Hb]0kHbt ≈ 1. | ||||||
| Full record | None |
|
16 ± 1 | |||
| >2000 s | [Hb]0 > 2[G]0 |
|
||||
| [Hb]0 < 2[G]0 |
|
|||||
| <500 s | Polynomial approach to (11)a |
|
15 ± 2 | |||
| <150 s | Low time approximation to (13)b |
|
14 ± 1 | |||
From the analytical point of view eqn (14) is the most advantageous. The time interval indicated in Table 1 in which each equation is fulfilled is given for guidance only. In practice, the shorter the measurement time, the higher the glucose concentration range in which it can be applied. However, shorter measurement times also imply lower method sensitivity (slope of eqn (14)). For this reason, different calibration studies for glucose determination were performed in order to experimentally establish the upper limit of the linear response range as a function of the measurement time. Table 2 shows the results obtained.
| Measurement time/s | 90 | 250 | 500 | 750 | 1000 | 1250 | 1500 |
|---|---|---|---|---|---|---|---|
| Linear range/M | 1 × 10–5 | 5.1 × 10–6 | 3.1 × 10–6 | 2 × 10–6 | 1.6 × 10–6 | 1.2 × 10–6 | 1.1 × 10–6 |
| 3 × 10–4 | 2.5 × 10–4 | 1.5 × 10–4 | 6.5 × 10–5 | 4.5 × 10–5 | 2.5 × 10–5 | 1.3 × 10–5 |
The best measurement time as a function of the glucose concentration to be determined can be obtained from this table. Finally 90 s was considered a good choice, considering the glucose level in blood. Other analytical parameters of interest studied by using this measurement time were:
(a) The analytical reproducibility . A value of about 4% (relative standard deviation, RSD) was obtained for 10 replicates of the same blood sample (average glucose concentration 92 mg dL–1).
(b) The % recovery . This was measured after addition of known amounts of glucose (75 mg dL–1) to aliquots of the blood sample (average glucose concentration, 72 mg dL–1). For 10 replicates the average recovery obtained was 99 (±4)%.
Direct determination of glucose in blood
Starting from eqn (14), two quantification methods have been tested.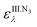 values are obtained from stock solutions prepared from the HbII.O2, HbIII and azide; from these the Δε576 is determined. The [Hb]0 has to be experimentally obtained beforehand. This is done using eqn (3a):
values are obtained from stock solutions prepared from the HbII.O2, HbIII and azide; from these the Δε576 is determined. The [Hb]0 has to be experimentally obtained beforehand. This is done using eqn (3a):
Eqn (14) then yields:
[G]S being the glucose concentration in the sample. By replacing the constants indicated by their corresponding values the following expression is obtained
 | (15) |
| (ΔAbs576,t)1 = 2Δε576[Hb]okHb[G]st |
| (ΔAbs576,t)2 = 2Δε576[Hb]okHb([G]s + [G]ad)t |
 | (16) |
The [G]s can be obtained only from the absorbance values, avoiding the uncertainty involved in the kHb and molar absorptivity values.
Both methods have been validated by analysing a set of real blood samples and comparing the results with those obtained using a Reflotron® clinical analyser. Both the self calibration and the standard addition methods were validated. Fig. 8 shows the results obtained.
 | ||
Fig. 8 Correlation graph between hemoglobin method and Reflotron® method: (black ♦) results obtained by the self-calibration method; (grey  ) results obtained by the addition standard method. ) results obtained by the addition standard method. | ||
The correlation graph between the methods is:
| [G]Reflotron = 1.07 [G]Hb method – 1.94, r = 0.98 |
As the slope and intercept of this line are statistically equal to 1 and 0 respectively, it can be concluded that both methods give equivalent results.
Conclusions
The main general contribution is to demonstrate a new approach consisting of using molecular species in the sample itself as reagents; this could be considered as a new step towards “sustainable analytical chemistry”. This approach means that the interference elimination step is not required, implying non-destructive, faster and more reproducible analysis and the design of reversible methods. This is important in view of future needs and trends in chemistry. Given that the analytical signal is obtained after addition of the enzyme which generates H2O2 from the analyte of interest, the methodology can be used for sensor designs. The theoretical basis enables this methodology to be applied to many other metabolites or biochemical compounds giving H2O2. Finally, the interaction between Hb and GOx also points to a new alternative in the design of analytical procedures for the determination of proteins.Acknowledgements
This work was supported by the Ministerio de Educación y Ciencia (MEC) of Spain, project CTQ 2005-05761. V.S. thanks the MEC for a grant.References
- L. L. Looger, M. A. Dwyer, J. J. Smith and H. W. Hellinga, Nature, 2003, 423, 185 CrossRef CAS.
- M. A. Dwyer, L. L. Looger and H. W. Hellinga, Science, 2004, 304, 1967 CrossRef CAS.
- A. Wada, M. Mie, M. Aizawa, P. Lahoud, A. E. G. Cass and E. Kobatake, J. Am. Chem. Soc., 2003, 125, 16228 CrossRef CAS.
- J. E. Noble, P. Ganju and A. E. G. Cass, Anal. Chem., 2003, 75, 2042 CrossRef CAS.
- L. G. Puckett, E. Dikici, S. Lai, M. Madou, L. G. Bachas and S. Daunert, Anal. Chem., 2004, 76, 7263 CrossRef CAS.
- K. Aslan, I. Gryczynski, J. Malicka, E. Matveeva, J. R. Lakowick and C. D. Geddes, Curr. Opin. Biotechnol., 2005, 16, 55 CrossRef CAS.
- J. Galbán, O. Sánchez-Monreal, Y. Andréu, S. de Marcos and J. R. Castillo, Anal. Biochem., 2004, 334, 207 CrossRef CAS.
- V. Sanz, S. de Marcos, J. R. Castillo and J. Galbán, J. Am. Chem. Soc., 2005, 127, 1038 CrossRef CAS.
- E. R. Goldman, I. L. Medintz, J. L. Whitley, A. Hayhurst, A. R. Clapp, H. T. Uyeda, J. R. Deschamps, M. E. Lassman and H. Mattousi, J. Am. Chem. Soc., 2005, 125, 1038.
- W. E. Blumberg, J. Peiscich, B. A. Wittenberg and J. A. Wittenberg, J. Biol. Chem., 1968, 243, 1854 CAS.
- C. Giulivi and K. J. A. Davies, J. Biol. Chem., 1990, 265, 19453 CAS.
- D. A. Svistunenko, R. P. Patel, S. V. Voloshchenko and M. T. Wilson, J. Biol. Chem., 1997, 272, 7114 CrossRef CAS.
- T. Brittain, A. R. Baker, C. S. Butler, R. H. Little, D. J. Lowe, C. Greenwood and N. Watmough, J. Biochem., 1997, 326, 109 CAS.
- M. Tsuruga, A. Matsuoka, A. Hachimori, Y. Sugawara and K. Shikama, J. Biol. Chem., 1998, 273, 8607 CrossRef CAS.
- T. Egawa, H. Shimada and Y. Ishimura, J. Biol. Chem., 2000, 275, 34858 CrossRef CAS.
- D. G. Pina, A. V. Shnyrova, F. Gavilanes, A. Rodriguez, F. Leal, M. G. Roig, I. Y. Sakharov, G. G. Zhadan, E. Villar and V. L. Shnyrov, Eur. J. Biochem., 2001, 268, 120 CrossRef CAS.
- K. Chen, K. Ballas, R. R. Hantgan and D. B. Kim-Shapiro, Biophys. J., 2004, 87, 4113 CrossRef CAS.
- E. Karg, I. Németh, M. Horányi, S. Pintér, L. Vécsei and S. Hollán, Blood Cells Mol. Dis., 2000, 26, 91 CrossRef CAS.
- S. Mueller, H. D. Riedel and W. Stremmel, Blood, 1997, 90, 4973 CAS.
- E. Nagababu, F. J. Chrest and J. M. Rifkind, Biochim. Biophys. Acta, 2003, 1620, 211 CrossRef CAS.
- N. Masuoka, H. Kodama, T. Abe, D. Wang and T. Nakano, Biochim. Biophys. Acta, 2003, 1637, 46 CAS.
- T. Brittain, J. Inorg. Biochem., 2000, 81, 99 CrossRef CAS.
- J. F. Sierra, J. Galbán and J. R. Castillo, Anal. Chem., 1997, 69, 1471 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: pH effect on the autooxidation kinetic, H2O2 calibration lines and the Hb/GOxelectron transfer . See DOI: 10.1039/b613335e |
| This journal is © The Royal Society of Chemistry 2007 |





