Soft contact: measurement and interpretation of contact angles
Abraham
Marmur
Department of Chemical Engineering, Technion – Israel Institute of Technology, 32000 Haifa, Israel. E-mail: marmur@technion.ac.il; Fax: +972 4 829 3088
First published on 25th November 2005
Abstract
The measurement and interpretation of contact angles deceptively appear to be simple. This paper attempts to summarize the pitfalls in the field, and how to avoid them. First, the fundamental underlying theory that is necessary in order to properly measure and interpret contact angles is discussed, emphasizing recent developments. Then, the practical implications of these theoretical aspects are presented. In addition, the discussion highlights the missing pieces of the picture that need to be completed through future research.
Introduction
Wetting systems are ubiquitous.1–3 Wetting is an essential component in many applications and processes, such as transport in soil, development of biocompatible surfaces, control of biofouling, printing, membranes, and more. Fig. 1 shows a wetting system consisting of a liquid drop on a solid surface, immersed in a fluid. The latter could be a gas or another liquid. There are many other possible configurations of solid–liquid–fluid systems, such as a liquid inside a porous medium, or a particle floating on a liquid–fluid interface. In all such systems, the most important, measurable characteristic is the contact angle, θ, which is defined as the angle between the tangent to the liquid–fluid interface and the tangent to the solid interface at the contact line between the three phases. The contact angle is usually measured on the liquid side.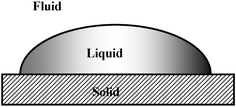 | ||
| Fig. 1 A wetting system. | ||
The measurement of contact angles appears to be simple and straightforward. Unfortunately, this impression is very deceptive, and leads to many misunderstandings. From a technical point of view, the sessile drop method is frequently used, since this is the most convenient method; however, other contact angle measurement methods are used as well, such as the captive bubble (a fluid bubble floating in a liquid underneath the solid surface), and the Wilhelmy plate (a plate of the solid immersed in the liquid). From a theoretical point of view, some important questions are still open, while some recently answered questions have not yet been widely applied to contact angle measurement.
The objective of this paper is to convey the author's view regarding the experimental and theoretical status of the characterization of wetting systems by contact angle measurement. The theoretical aspects are summarized first, in order to lay the foundation for understanding the requirements for meaningful measurement and interpretation. Then, the practical implications of the theoretical conclusions are summarized. The main emphasis is on the sessile drop method, however some fundamental conclusions are applicable to any contact angle measurement method.
The ideal contact angle
A three-phase wetting system is characterized by three interfacial tensions: liquid–fluid, σlf, solid–liquid, σsl, and solid–fluid, σsf. The pioneering correlation between the contact angle and the interfacial tensions is the Young equation4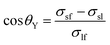 | (1) |
In principle, there is reason to believe that the Young equation needs to be modified, even for an ideal solid surface. This is so, since the three interfacial tensions may be influenced by each other at the contact line, due to the effect that one phase may have on the interaction between the other two phases. Especially, the molecules of the solid may interfere with the interaction between the liquid and the fluid, thus affecting the value of the liquid–fluid interfacial tension very close to the contact line. This possibility was recognized by Gibbs, who suggested that this three-phase mutual interaction be accounted for by a “line tension.” The value of line tension has been a controversial issue for many years, however it is clear now that it may affect the contact angle of drops only when they are extremely small.5–7 Therefore, for all practical purposes related to the measurement of contact angles of macroscopic drops, line tension effect on the YCA is negligible. Thus, the YCA is indeed considered to practically be the ICA.
One of the important applications of contact angle measurement is the assessment of the surface tension of a solid surface, σs (for simplicity, it will be assumed within the present context that the surface tension of the solid and its Gibbs surface energy per unit area are synonymous). In most applications, it is the contact angle that determines the behavior of the wetting system rather than the surface tension of the solid. However, the assessment of this surface tension is essential for the following reason. The liquid used to measure the contact angle in a specific system is not necessarily the same as the liquid applied in practice. For example, it is better to characterize a printing substrate by using a pure liquid rather than using the ink to be applied in the printing process. Thus, in order to “translate” the contact angle measured with the pure liquid into the contact angle that is applicable to the actual wetting process (using the Young equation), the surface tension of the solid must be known.
Practically, σs is the value of σsf, when the fluid is a gas; therefore, the measurement is usually done under a gaseous environment. The value of σs may be affected by the nature of the gas, if some components from the gas phase adsorb to the solid surface. Thus, it should be remembered that the value of σs, which is calculated from contact angle measurements, refers to the conditions of the measurement. For clarity and simplicity, the following discussion refers only to systems for which the fluid is a gas. The Young equation for such systems, written in terms of σs as the unknown, reads
| σs = σlcosθY + σsl | (2) |
A major problem that is encountered when trying to calculate σs from eqn. (2) is that σsl is unknown, since it cannot be measured directly. Thus, assuming that the YCA and σl are known, σs can be calculated from eqn. (2) only if σsl can be predicted based on additional information. To solve this problem, semi-empirical correlations between the interfacial tension, σsl, and surface tensions, σs and σl, can be used.8–11 The choice of the proper correlation is still an open problem that is difficult to settle in the absence of ability to measure σsl directly. To demonstrate the application of such correlations, and the problems involved, the following family of correlations will be used below12–14
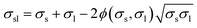 | (3) |
| σ = σd + σp | (4) |
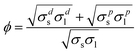 | (5) |
The example represented by eqns. (3)–(5) demonstrates that the number of unknowns that need to be determined in order to assess the surface tension of a solid from a measured YCA is higher than one. This is so, since in order to express the seemingly single unknown σsl in eqn. (2), additional information needs to be known about the various contributions to the values of the surface tensions σs and σl. In order to be able to solve a higher number of unknowns, the contact angle needs to be measured more than once, with various liquids.10,15 However, much care needs to be exercised in choosing the proper liquids, otherwise the mathematical properties of the equations may lead to very erroneous results.16 This point, though crucial, will not be further dealt in the present paper, since the main emphasis is put here on the correct measurement and interpretation of the contact angle itself. The following discussion refers to these questions first from a theoretical point of view. Then, the practical implications will be presented.
Contact angles on real surfaces—theoretical aspects
Actual and apparent contact angles
Having discussed the problem of the value of σsl, the next fundamental problem with respect to eqn. (2) is the elucidation of the YCA, θY. In principle, it can be measured only on ideal surfaces; however, obviously, such surfaces rarely exist in real applications. Solid surfaces are usually rough and chemically heterogeneous to some extent. Therefore, the main question that needs to be answered is: how can the YCA be determined from measurements on real surfaces?The first step in answering this question is the distinction between the actual and apparent contact angles. Fig. 2 schematically demonstrates these definitions for a rough surface. The actual contact angle is the angle between the tangent to the liquid–fluid interface and the actual, local surface of the solid. The apparent contact angle is the angle between the tangent to the liquid–fluid interface and the line that represents the nominal solid surface, as seen macroscopically. Obviously, the difference between the two contact angles may be very large. It turns out,17–19 that the actual contact angle equals the Young contact angle, if line tension is negligible. So, the actual contact angle is the one needed for the assessment of surface tension of solid surfaces. However, it is yet experimentally inaccessible on rough surfaces. On smooth, but chemically heterogeneous surfaces it may vary from one point to another, again making its measurement very difficult.
 | ||
| Fig. 2 The actual contact angle (ACCA) and the apparent contact angle (APCA). | ||
The contact angle that is currently amenable to measurement is the apparent contact angle (APCA). Therefore, the question posed above should now be rephrased: how can the YCA be determined from APCA measurements on real surfaces? In order to answer this question, it is necessary first to find out if the APCA has a single, unique value for a given solid surface (as does the YCA); then, the correlation between the APCA and the YCA for various types of surface should be discussed.
Contact angle hysteresis
The major difficulty underlying contact angle interpretation is the observation that on real surfaces there may exist a wide range of practically stable APCAs.20 Experimentally, when the volume of a drop is increased, the contact line seems to be pinned, while the APCA increases (Fig. 3a). The APCA eventually reaches a maximum value, which is referred to as the “advancing contact angle” (ADCA). If the drop volume is further increased, the contact line advances. Therefore, the motion of the contact line is sometimes described as a “stick–slip” motion. Similarly, when the drop volume is decreased (Fig. 3b), the contact line appears to be pinned, while the APCA decreases until it reaches a minimal value termed the “receding contact angle (RCA).” Further reduction in the volume of the drop causes the contact line to recede. The difference between the advancing and receding contact angles, which is termed “the hysteresis range,” may be very large.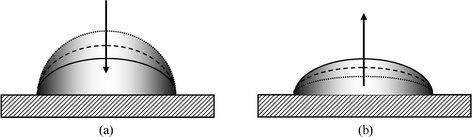 | ||
| Fig. 3 Contact angle hysteresis: (a) measuring the advancing contact angle; (b) measuring the receding contact angle. | ||
Contact angle hysteresis stems from the fact that the Gibbs energy curve for a drop on a real surface is characterized by multiple minima points (Fig. 4).20–23 This is in contrast with the ideal surface case, for which this curve has a single minimum. Thus, many metastable APCAs exist for a real surface. In principle, the system tends to get to the most stable state, which corresponds to the global minimum in energy (Fig. 4). However, in order to move from one local minimum to the next, the drop has to overcome an energy barrier (defined as the energy difference between a local minimum and an adjacent local maximum, see Fig. 4). It is important to note that the energy barriers increase as the drop gets nearer to the global minimum.
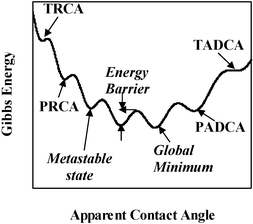 | ||
| Fig. 4 Schematics of the Gibbs energy curve for a real wetting system: multiplicity of minima that define metastable states. TRCA, theoretical receding contact angle; PRCA, practical receding contact angle; TADCA, theoretical advancing contact angle; PADCA, practical advancing contact angle. | ||
The physics behind the multiplicity of the minima in the Gibbs energy curve for a real solid surface can be explained as follows.23 The surface tension of the solid may change from point to point due to chemical heterogeneity; similarly, the inclination of the solid surface may vary from one location to the other because of roughness. Thus, in principle, at each point along the solid surface there may exist a different APCA, such that the actual contact angle conforms to the locally required YCA. However, the fulfilment of this necessary thermodynamic equilibrium condition is insufficient. The sufficient condition is that the APCA also conforms to the shape of the drop, from a geometrical point of view. For a given drop volume, the contact radius determines a geometrical contact angle, based on the shape of the drop. Only at locations where this geometrical contact angle coincides with the one required by the thermodynamic equilibrium condition, a local minimum exists.
Based on this theoretical picture, the theoretical ADCA can be defined as the highest angle for which there is a local energy minimum (Fig. 4). Similarly, the theoretical RCA is the lowest angle for which there exists a local energy minimum. In practice, the system is always subject to some external energy input, for example, via vibrations in its environment. This energy input may assist in overcoming energy barriers up to a certain level. Therefore, the ADCA in practice is somewhat lower than the theoretical ADCA (see Fig. 4). Likewise, the practical RCA is higher than the theoretical one.
While the theoretical qualitative reasoning behind contact angle hysteresis is relatively well understood, the quantitative correlation between the ADCA, RCA, and the YCA is yet unknown. It is also not clear whether any universal correlation may exist between these contact angles. An assumption sometimes made in the literature is that the ADCA approximates the YCA. This assumption may be misleading, in the absence of theoretical reasoning, since it is impossible yet to experimentally prove such a hypothesis. Thus, a more promising way to get information about the YCA is via the most stable contact angle (at the global minimum in the Gibbs energy), as described in the following section.
The most stable apparent contact angle
In 1936, Wenzel24 developed the following equation for the APCA, θW, on a rough surface| cosθW = rcosθY | (6) |
The Wenzel equation was developed in a rather intuitive way, averaging the fine details of the roughness. A recent, fundamental analysis of the problem25 revealed some interesting theoretical conclusions that may be applied to the measurement and interpretation of contact angles. It turns out that the Wenzel equation is an approximation that becomes better as the drop becomes larger in comparison with the scale of roughness. The question of how large the drop should be in order for the Wenzel equation to apply has not yet been fully answered. However, based on some simulations,26 and preliminary experimental data, it seems that if the drop is larger than the roughness scale by two to three orders of magnitude, the Wenzel equation applies. In addition, it has been established25 that the Wenzel contact angle represents the most stable APCA, namely the contact angle that is associated with the global minimum in the Gibbs energy of the system. So, eqn. (6) gives the required correlation between the YCA and the most stable APCA. Finally, it has been proven25 that at the state of global energy minimum the drop is axisymmetric.
Similar conclusions have been reached regarding the APCA on chemically heterogeneous solid surfaces.26 On such surfaces, the surface tension varies from one location to another. Accordingly, the YCA has a different value at each location. The starting point is the Cassie equation for the APCA, θC, on a heterogeneous solid surface,27 which was developed for the case of a surface with only two different chemistries
| cosθC = x1cosθY1 + x2cosθY2 | (7) |
In this equation, x is the area fraction characterized by a given chemistry, and the subscripts 1 and 2 indicate the two different surface chemistries. This equation can be generalized to state that the cosine of the Cassie contact angle is the weighted average of the cosines of all the YCAs that characterize the surface. The weighted averaging is done according to the area fraction of each chemistry.
Like in the case of the Wenzel equation, the Cassie equation is also an approximation that becomes better when the drop size becomes larger with respect to the scale of chemical heterogeneity.26 Also, it has been demonstrated that the Cassie contact angle represents the most stable APCA, and that at the state of global energy minimum the drop is axisymmetric.26
As mentioned above, under some roughness conditions, air bubbles may be trapped in the roughness grooves, under the liquid.28 In this case, the solid surface may be considered chemically heterogeneous, and the Cassie eqn. (7) may be applied in the following form:
| cosθCB = frfcosθY − (1 − f) | (8) |
This equation was developed by Cassie and Baxter (CB),29 considering air to be the second chemistry in eqn. (7). In eqn. (8), θCB is the CB apparent contact angle, f is the fraction of the projected area of the solid surface that is wet by the liquid, and rf is the roughness ratio of the wet area. When f = 1, rf = r, and the CB equation turns into the Wenzel equation. The transition from homogeneous wetting (Wenzel equation) to heterogeneous wetting (CB equation) has been recently analyzed.30 It has been found to depend not only on the roughness ratio, but also on the specific geometry, in terms of the second derivative of (rff) with respect to f.
Contact angles on real surfaces—measurement and interpretation
As will be summarized below, the problem of contact angle measurement and interpretation is not yet completely solved. Therefore, it is of utmost importance to fundamentally understand the difficulties that are involved, in order to choose the best possible path for a specific application.The measurement problem consists of a few issues, but is relatively simple to solve by applying the necessary precautions and equipment modification. The first issue is the symmetry of the drop: on real surfaces, which may be rough and chemically heterogeneous, the drop may not be axisymmetric. Obviously, it is meaningless to measure the contact angle of a non-axisymmetric drop. However, the most common method of measuring contact angles is by taking a side-view picture of a drop and evaluating the contact angle from this picture. This method does not allow checking whether the drop is axisymmetric; at most it allows comparing the two APCAs at the two sides of the drop. Therefore, a top-view is also necessary. Actually, the contact angle can be calculated from a top view picture, if the drop volume is exactly known.31
Moreover, according to theory and simulations,25,26 in order for a drop to be axisymmetric, it has to be sufficiently large compared with the scale of roughness or heterogeneity. Thus, only large drops should be used for contact angle measurements. This should not pose a major difficulty for rough surfaces, since a typical scale of roughness is of the order of magnitude of microns, while typical drops are of the order of magnitude of millimetres. The spatial length scale of chemical heterogeneity may vary, and needs to be checked for each specific case.
Another critical measurement issue, which is closely related with the interpretation method, is the question of which contact angle is to be measured. One approach is to try to directly measure the most stable APCA. Another approach is to measure the hysteresis range extremes, namely the ADCA and the RCA. In the latter case, the equipment needs to allow increase and decrease of the drop volume in a quasi-static way.32 In addition, relatively large drops should be used also to minimize the effect of drop volume on the results (an experimental indication for the drop being sufficiently large is minimal “stick–slip” behavior of the contact line).22–23 A useful implication of a theoretical observation is that the sessile drop method is preferable for low contact angles, while the captive bubble technique is better for high contact angles.23 This is so, since such choice minimizes the dependence of the practical advancing and receding contact angles on the drop volume.
If the most stable APCA is sought after, a means to experimentally reach and identify it is necessary. A promising technique that can be used for this purpose is the induction of vibrations in the system,31,33–34 in order to overcome the energy barriers between the metastable states. The question that remains unsolved is how the most stable state can be identified. A working hypothesis that has been suggested31 is to use the property of symmetry at the most stable state. As has been theoretically shown, a drop at the most stable state is axisymmetric.25 Though the opposite statement has not been proven, the best that can be done is to follow the shape of the drop while vibrating it, and take contact angle measurements only when the drop is sufficiently axisymmetric. This approach cannot ensure that the drop is indeed at its most stable state; however, it does ensure that it is possibly at this state.
Whatever the measurement approach is, the ultimate objective is the elucidation of the YCA, since its value is the key to calculating the surface tension of the solid surface from eqn. (2). The only existing theories for calculating the YCA, eqns. (6–8) are based on the most stable APCA (the application of the theory is straightforward in the case of a rough surface, since the roughness ratio is measurable; this is not the case for chemically heterogeneous surfaces). So far, there is no theory that directly relates the advancing or receding contact angles to the YCA. Therefore, the key issue is the elucidation of the most stable APCA.
In the most stable APCA approach, the most stable APCA is directly attempted to be measured, as described above. In the hysteresis approach, the advancing and receding contact angles, θa and θr, are measured, and the most stable APCA, θms, may be estimated either by33
| cosθms = (cosθa + cosθr)/2 | (9) |
| θms = (θa + θr)/2 | (10) |
Unfortunately, none of the above approaches has been sufficiently studied and substantiated.
Summary and conclusions
The correct measurement and interpretation of contact angles are important objectives in regard to many essential applications. However, there exist theoretical as well as experimental difficulties on the way to achieve these objectives. The following is a concise, practical summary of the main points that need to be considered.Two measurement approaches may be taken: (a) direct assessment of the most stable APCA; and (b) measurement of the advancing and receding contact angles. If the latter is preferred, the most stable APCA may be estimated by either eqn. (9) or eqn. (10). Hopefully, future work will help to decide which of these equations (or a different one) is to be preferred.
With respect to the measurement technique, a few important points should be kept in mind. First, it is essential to use large drops. This assures the validity of the Wenzel and Cassie equations, enables axisymmetry, and minimizes the dependence of the advancing and receding angles on the drop volume. Second, a top view is preferred, to assure axisymmetry. Also, vibrations should be applied, either to overcome energy barriers and get to the most stable state, or just to assure axisymmetry (in the hysteresis approach).
Once the most stable APCA is assessed, the YCA needs to be calculated. This may be relatively simple for a rough surface that is chemically uniform: one needs to measure the roughness ratio (using a profilometer or an AFM), then use eqn. (6). The problem is much more difficult with chemically heterogeneous surfaces, since they are characterized by more than one YCA. For smooth, chemically heterogeneous surfaces, it may be best to simply treat the most stable APCA as an average YCA, in the sense of eqn. (7).
When the YCA (or its average value) is known, eqn. (2) with equations such as (3) and (5) may be used to assess the surface tension of the solid. Usually, the process has to be repeated more than once, with various liquids, in order to be able to solve for the required number of unknowns in eqn. (3).
In order to further improve our ability to assess the surface tension of solid surfaces, it seems that progress needs to be made in three main directions: (a) the understanding of the relationship between the advancing/receding contact angles and the most stable APCA; (b) the understanding of the dependence of the interfacial tension of the solid–liquid interface on the surface tensions of the solid and the liquid; and (c) the development of standard surfaces for comparing and calibrating contact angle measurements.
References
- E. B. V. Dussan, Ann. Rev. Fluid Mech., 1979, 11, 371 Search PubMed
.
- A. Marmur, Adv. Colloid Interface Sci., 1983, 19, 75 CrossRef CAS
.
- P. G. DeGennes, Rev. Mod. Phys., 1985, 7, 827 CrossRef
.
- T. Young, Philos. Trans. R. Soc. London, 1805, 95, 65 CrossRef
.
- A. Marmur and B. Krasovitski, Langmuir, 2002, 18, 8919 CrossRef CAS
.
- T. Pompe, A. Fery and S. Herminghaus, J. Adhes. Sci. Technol., 1999, 13, 1155 CrossRef CAS
.
- A. Marmur, J. Colloid Interface Sci., 1997, 186, 462 CrossRef CAS
.
- C. A. Ward and A. W. Neumann, J. Colloid Interface Sci., 1974, 49, 286 CrossRef
.
- C. J. Van Oss and R. J. Good, J. Dispersion Sci. Technol., 1990, 11, 75 CrossRef
.
-
J. C. Berg, in Wettability, ed. J. C. Berg, Marcel Dekker, Inc., New York, 1993, pp. 75 Search PubMed
.
- N. T. Correia, J. J. Moura Ramos, B. J. V. Saramago and J. C. G. Calado, J. Colloid Interface Sci., 1997, 189, 361 CrossRef CAS
.
- L. A. Girifalco and R. J. Good, J. Phys. Chem., 1957, 61, 904 CrossRef CAS
.
- F. M. Fowkes, J. Phys. Chem., 1963, 67, 2538 CrossRef CAS
.
- D. K. Owens and R. C. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741 CrossRef CAS
.
- C. Della Volpe and S. J. Siboni, J. Colloid Interface Sci., 1997, 195, 121 CrossRef
.
- S. Shalel-Levanon and A. Marmur, J. Colloid Interface Sci., 2003, 262, 489 CrossRef CAS
; S. Shalel-Levanon and A. Marmur, J. Colloid Interface Sci., 2003, 268, 272 CrossRef CAS
.
- L. Boruvka and A. W. Neumann, J. Chem. Phys., 1977, 66, 5464 CrossRef CAS
.
- G. Wolansky and A. Marmur, Langmuir, 1998, 14, 5292 CrossRef CAS
.
- P. S. Swain and R. Lipowsky, Langmuir, 1998, 14, 6772 CrossRef CAS
.
-
R. E. Johnson, Jr. and R. H. Dettre, in Surface and Colloid Science, ed. E. Matijevic, Wiley-Interscience, New York, 1969, vol. 2, p. 85 Search PubMed
.
- A. Marmur, J. Colloid Interace Sci., 1994, 168, 40 Search PubMed
.
- A. Marmur, Adv. Colloid Interface Sci., 1994, 50, 121 CrossRef CAS
.
- A. Marmur, Colloids Surf., A, 1998, 136, 209 CrossRef CAS
.
- R. N. Wenzel, Ind. Eng. Chem., 1936, 28, 988 CrossRef CAS
.
- G. Wolansky and A. Marmur, Colloids Surf., A, 1999, 156, 381 CrossRef CAS
.
- S. Brandon, N. Haimovich, E. Yeger and A. Marmur, J. Colloid Interface Sci., 2003, 263, 237 CrossRef CAS
.
- A. B. D. Cassie, Discuss. Faraday Soc., 1948, 3, 11 RSC
.
- M. Callies and D. Quéré, Soft Matter, 2005, 1, 55 RSC
.
- A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546 RSC
.
- A. Marmur, Langmuir, 2003, 19, 8343 CrossRef CAS
.
- T. S. Meiron, A. Marmur and I. S. Saguy, J. Colloid Interface Sci., 2004, 274, 637 CrossRef CAS
.
- C. N. C. Lam, R. H. Y. Ko, L. M. Y. Yu, A. Ng, D. Li, M. L. Hair and A. W. Neumann, J. Colloid Interface Sci., 2001, 243, 208 CrossRef CAS
.
- C. Andrieu, C. Sykes and F. Brochard, Langmuir, 1994, 10, 2077 CrossRef CAS
.
- E. L. Decker, B. Frank, Y. Suo and S. Garoff, Colloids Surf., A, 1999, 156, 177 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2006 |
