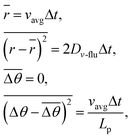Simulating molecular shuttle movements: Towards computer-aided design of nanoscale transport systems

Abstract

Molecular shuttles based on the motor protein kinesin and microtubule filaments have the potential to extend the lab-on-a-chip paradigm to nanofluidics by enabling the active, directed and selective transport of molecules and nanoparticles. Based on experimentally determined parameters, in particular the trajectory persistence length of a microtubule gliding on surface-adhered kinesin motors, we developed a Monte-Carlo simulation, which models the transport properties of guiding structures, such as channels, rectifiers and concentrators, and reproduces the properties of several experimentally realized systems. Our tool facilitates the rational design of individual guiding structures as well as whole networks, and can be adapted to the simulation of other nanoscale transport systems.

---

Introduction

Active, nanoscale transport on surfaces by single-molecule nanocars,^1,2 molecular shuttles,^3,4 or domesticated bacteria⁵ enables new approaches to a variety of engineering challenges.^6–12 Ultimately, these transporters will move along complex networks of tracks connecting different workstations, thus extending the lab-on-a-chip paradigm to the nanoscale.

For molecular shuttles powered by the motor proteins kinesin or myosin,¹³ a wide variety of fabrication techniques^14–23 and structural motives^24–26 (junctions, concentrators, rectifiers, etc.) for tracks has been described. However, due to the lack of simulation tools the efficiency of a particular design can only be predicted using a general understanding of the physics of the system,²⁷ so that each design has to be implemented and evaluated experimentally.²⁸ Efficient, large-scale design of complex networks ideally would replicate the success of electronic design automation software, such as the Cadence platform (Cadence Inc.).

Here, we describe Monte-Carlo simulations²⁹ of the movement of kinesin-powered molecular shuttles through track motifs which replicate the observed characteristics, such as rectifying efficiency. The two-dimensional simulation assumes that the forward movement of the shuttle experiences small, random fluctuations in direction and velocity in each time step, so that the unrestricted trajectory can be characterized by an average velocity, motional diffusion coefficient, and persistence length, parameters which have been experimentally determined for this system.³⁰ These parameters are complemented by a rule describing the interaction with a track boundary, in this case prescribing the alignment of the direction of movement with the boundary according to experimental observations.^18,24 Modification of the parameters and interaction rule enable, in principle, the adaptation to myosin-powered shuttle systems,¹⁵ bacterial transporters,⁵ and other nanosystems displaying active movement.^31,32

Simulations of active movement have been utilized to explain quite different phenomena, including aggregation³³ and foraging³⁴ of bacteria, cell migration,^35,36 and wound healing.³⁷ A complete modeling of the movement of molecular shuttles would similarly have to integrate subsystems at multiple scales, interactions between agents, and a complex environment. However, our very basic model has the advantage of very few, experimentally accessible parameters, can be directly validated, and can focus on the design of interconnected structures.

Methods

We describe microtubule (MT) movement within microfabricated patterns in terms of the trajectory of the MT leading tip, since it is retraced by the rest of the microtubule. We model the movement as a two-dimensional random walk having a fixed persistence length and being confined within a region surrounded by a set of predefined linear and/or circular segments. The set of segments describes the boundaries of the region accessible to MTs, that is, the region within the microfabricated patterns. The random walk is generated by an off-lattice Monte Carlo simulation. The step distance (r) and angular change (Δθ) during a time step (Δt) are normally distributed random variables. Their means and variances are given by
where v_avg is time-averaged velocity, D_v-flu is motional diffusion coefficient, L_p is persistence length of the MT trajectory. These values have been experimentally determined to be 0.85 ± 0.02 µm s⁻¹, 2.0 ± 0.4 × 10⁻³ µm² s⁻¹, and 111 (92–132) µm, respectively.³⁰ In our simulation, the values of v_avg, D_v-flu and L_p are set accordingly to be 0.85 µm s⁻¹, 2.0 × 10⁻³ µm² s⁻¹, and 111 µm, respectively. The time step is set to be 100 ms, corresponding to the time required for 10 elementary steps of a motor and an order of magnitude smaller than the time required to traverse the smallest structure studied. The normal random numbers are generated with the Box–Muller method from uniform pseudorandom numbers, which are generated with a linear congruent method. Our trajectory generation procedure has been checked for consistency by analyzing 30 computer-generated MT trajectories on planar surfaces according to the method described in ref. 30 (5 s sampling intervals) and obtaining v_avg = 0.85 µm s⁻¹ (SEM = 5.0 × 10⁻⁴ µm s⁻¹), D_v-flu = 1.9 ± 0.2 × 10⁻³ µm² s⁻¹ (avg. ± SEM), L_p = 116 (110–124) µm. When simulating MT movements on a track (Fig. 1A), we check for each newly generated location if any one of the boundary segments defining the track has been crossed. If no segment is crossed, the location is employed as the next location. If a segment is crossed, the guiding rule is applied (we assume that no MT escapes from the track); the segment of the microtubule trajectory outside of the boundary is folded onto the boundary, and the direction of the microtubule movement is set to be tangential with the boundary segment. We neglected any possible interaction between microtubules. The programming language used is Fortran90. For the simulation of straight channels, MT trajectories several millimetres in length were generated in straight channels of varying width (1.5, 2.5, and 5.5 µm), so that more than one thousand wall collisions occurred. The MTs were initially placed in the center of the channel. For the simulation of track motifs other than straight channels, MTs were initially located 100 µm from the center of the structure (except for networks; see below). Movements of 1000 MTs were investigated for each one of five simulations.

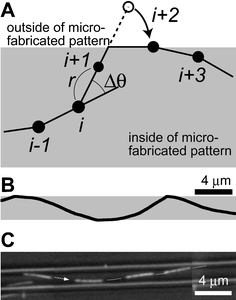Fig. 1 (A) A schematic of the simulation method. The position of a MT leading end is generated according to the off-lattice Monte Carlo simulation employing experimentally determined parameters, until it crosses a boundary of a microfabricated pattern. When it crosses a boundary, the position is folded onto the boundary as shown for point (i + 2). (B) A computer simulated trajectory of a MT moving within a 2.5 µm width channel from left to right. (C) A typical movement of a MT within a microfabricated straight channel. Reproduced with permission from Langmuir, 2003, 19, 1738–1744. Copyright 2003 American Chemical Society.

Results

In the following sections, we describe our simulation results for movements of molecular shuttles in straight channels, orthogonal cross junctions, reflector arms, circular concentrators, and rectifiers. We first validate our simulation method by comparing these results to experimental studies. Then, we discuss simulations of molecular shuttle movements in simple networks, which enable simulations of molecular shuttle systems integrated into lab-on-a-chip devices.

Straight channel

The simulated trajectories were similar to those observed in experiments (Fig. 1B; experimental data by Clemmens et al.¹⁸). Employing the guiding criteria introduced by Clemmens¹⁸ (collisions were only counted for multiple collisions if MTs traveled at least 0.5 µm away from the boundary or traveled more than 20 µm along the boundary), the average distance between two wall collisions of the simulated MT trajectories were 14.5 ± 7.3 µm (number of wall collisions N = 1159, experiment: 16.6 ± 7 µm, avg. ± σ), 18.3 ± 9.2 µm (N = 1136, experiment: 17 ± 8 µm) and 28.3 ± 14.4 µm (N = 1457, experiment: 24 ± 14 µm) for channel width w = 1.5, 2.5, and 5.5 µm, respectively. Collision angles against the channel walls were 17.7 ± 7.9° (experiment: 11 ± 7°), 20.1 ± 9.1° (experiment: 17 ± 9°), and 24.6 ± 11.8° (experiment: 28 ± 21°) for w = 1.5, 2.5, and 5.5 µm, respectively. These results were in good agreement with the results reported by Clemmens et al., given the accuracy with which the trajectory persistence length is known. For example, within a 5.5 µm wide straight channel, the average distance between collisions and the average collision angle varied from 26.6 ± 13.5 µm and 26.6 ± 12.3° (N = 1542) to 30.2 ± 15.7 µm and 23.7 ± 11.2°(N = 1369) as L_p was set to 92 µm and 132 µm (the extremes of our confidence interval), respectively. Reducing the time step to 10 ms had no influence on our simulation results (w = 1.5 µm, N = 1157; 14.5 ± 7.7 µm, 17.9 ± 7.5°).

Orthogonal cross junction, reflector junction, and concentrator

For the orthogonal cross junction, we found that most MTs moved straight through the intersection (72.7 ± 1.4%; fraction ± standard deviation; experiment: 82 ± 2%) (Fig. 2; experimental data by Clemmens et al.²⁶). Some MTs collided with the walls of the crossing track to follow the track to the right or left (27.2 ± 1.3%; experiment: 19 ± 2%). Only once did a MT collide with the walls to go back to the original channel (0.1 ± 0.1%).

Fig. 2 MT trajectories in an orthogonal cross junction, a circular concentrator, and reflector junctions.

For the reflector junction, a MT approaching from the inlet would generally bend 45° toward the outlet rather than turning 135° into the reflector arm (98.5 ± 0.4% vs. 1.5 ± 0.4%; experiment: 97% vs. 3%). MTs entering from the outlet most often traveled into the reflector arm rather than turning 45° into the inlet (82.6 ± 1.5% vs. 17.4 ± 1.5%; experiment: 67% vs. 33%).

For the concentrator, most MTs entering a circular concentrator were trapped in it (96.0 ± 0.2% trapped 10³ s after entering).

Rectifier A

A majority of MTs entering the rectifier from the wrong direction turned around (62.2 ± 0.9%, experiment: 51 ± 5%), while the rest passed through (Fig. 3; experimental data by Hiratsuka et al.²⁴). All MTs coming into the rectifier from the right direction went through the rectifier.

Fig. 3 Rectifier designs and MT trajectories in the rectifiers. The majority of MTs entering from the upper channel (wrong direction) is rectified and exits through the same channel (dark trajectories), while the rest went through the rectifier (bright trajectories). Practically all MTs entering from the lower channel (right direction) pass through the rectifier and exit through the upper channel (dark trajectories). Only very rarely did MTs collide with the walls and go back to the same channel (bright trajectories). Probabilities of MT rectified (wrong direction) and those of MT going through the rectifiers (right direction) are shown in the figure for each rectifier design.

Rectifier B

Most MTs coming into the rectifier from the wrong direction turned around (91.4 ± 0.9%; experiment: 79 ± 3% – escaping MTs discounted) (Fig. 3; experimental data by van den Heuvel et al.²⁸). Rarely did MTs go through the rectifier (8.6 ± 0.9%). Practically all MTs coming into the rectifier from the right direction went through the rectifier (99.9 ± 0.1%; experiment: 98 ± 1%).

Rectifier C

Introducing an offset of 5.0 µm between the inlet and outlet of rectifier B did not improve the rectifying efficiency much (92.8 ± 0.7%; experiment: 92 ± 3% – escaping MTs discounted) (Fig.3; experimental data by van den Heuvel et al.²⁸). Practically all MTs coming into the rectifier from the right direction went through the rectifier (99.9 ± 0.1%; experiment: 100%).

Further, increasing the offset to 10.0 µm (simulation only) improved the rectifying efficiency to 94.8 ± 0.6%. Practically all MTs coming into the rectifier from the right direction went through the rectifier (99.9 ± 0.1%).

Circular track with multiple rectifiers

As an initial condition, MTs were placed in the circular track (Fig. 4) at random locations and with random orientations. Fig. 4 shows the time evolution of the fraction of MTs moving counter-clockwise, a process which can be described by a rate equation (see Appendix; experimental observations by Hiratsuka et al.²⁴). The rates of MTs changing their direction from clockwise to counter-clockwise were 5.4 ± 0.1 × 10⁻³ s⁻¹, and 9.8 ± 0.7 × 10⁻³ s⁻¹ for a circular track with two and four rectifiers, respectively. After 1000 s, practically all MTs moved counter-clockwise, as observed by Hiratsuka et al.

Fig. 4 Simulated time evolution of the fractions of MT moving counter-clockwise in circular tracks with two or four rectifiers. Solid lines are least-square fits through the simulation data with the formulae derived in the Appendix. The designs of the networks are shown in the figure.

Discussion

While an important aspect of the presented simulations is their validation by experimental results, the potential for new insights and the generation of testable hypotheses also becomes apparent. Measuring the trajectory persistence length of actin filaments gliding on myosin motors, for example, is straightforward, and enables quantitative predictions for actin filament guiding in microfabricated structures, starting again with straight channels.

The design of structural motifs, such as crossings, rectifiers and concentrators, can be tremendously improved, if design iterations can be performed in silico, reducing the need for prototypes fabricated by e-beam lithographically and largely manual analysis of device performance.

The explanatory power of the simulations is illustrated by the rectifier results: Just like the experiments show and common sense suggests, in the simulations circular sections at the bottom of the rectifier are superior to straight sections, since they direct MTs towards the outlet. However, it is much less obvious even though experimentally observed, that due to the angular distribution in the direction of movement at the entrance of the channel a lateral offset between entrance and exit channel does not have a large impact on the rectifying efficiency.

Simulation of the time evolution of the state of devices is particularly helpful for the design of experiments, since it points out transitory and stable states of the device, reducing the guesswork involved in choosing observation times.

It has been suggested earlier²⁶ that experimentally determined transmission ratios for specific structural motifs can be combined to model device characteristics in a matrix approach, as utilized in optics. In contrast, these Monte-Carlo simulations are more akin to a “ray-tracing” approach to modeling, with the concomitant increase in computational cost, but improved ability to model complex situations. Ultimately, a matrix approach relying on a library of transmission matrices of computer-designed and experimentally validated structural elements may be the most efficient way to model a large number of devices.

Conclusions

Taking advantage of measurements of the MT trajectory persistence length and of observations of the interaction of a MT with a guiding structure, we have successfully developed an off-lattice 2-D Monte Carlo simulation method for active transport by kinesin/microtubule-based molecular shuttles. This simulation reproduced the experimental results of three different research groups with an error of less than 20%, which confirms the validity of our simulation. Further, the simulation of MT movements in networks of components, demonstrated for simple networks, enables computer-aided design for lab-on-a-chip devices utilizing molecular shuttles.

Clearly, further developments are needed. From a practical point of view, “imperfectness” should be implemented, such as pinning of MTs and escape of MTs from micropatterns. Following pinning due to defective motors, MTs proceed in random directions. This lowers the performance of a rectifying device or reduces the transmission of a channel. The escape of MTs into solution primarily due to wall collisions with a high approach angle leads to the loss of cargo. Future implementation of these effects is straightforward, and will most likely result in an improved quantitative agreement with experiments, but at the cost of an increasing number of parameters. Importantly, it will permit the development of more robust designs.

Moreover, in principle, our simulation method is applicable to other nanoscale transportation systems, such as actin/myosin-based shuttles, bacteria and nanocars, if the required parameters are determined and a suitable guiding rule is formulated. Our results on kinesin/microtubule-based molecular shuttles are indicating the potential value of this simulation for the other nanoscale transportation systems.

Appendix

Calculation of rate of MTs changing their direction from clockwise to counter-clockwise in a circular track with multiple rectifiers (Fig. 4). We assume that when a MT enters a rectifier moving counter-clockwise, it always passes through the rectifier without a change in direction; if a MT enters a rectifier moving clockwise, it is changing direction to counter-clockwise with a probability w_rectify or continues moving clockwise with a probability of w_through = 1 − w_rectify. Thus, the time evolution of the probability of a MT moving clockwise is given by

P_CW(n) = (w_through)ⁿP_CW(0),

where n is the number of times with which the MT has encountered the rectifiers. With

P_CCW = 1 − P_CW,

and expressing the equation in terms of time (t), we obtain

P_CCW(t) = 1 − P_CW(0) exp(−kt),

with
where τ is the duration taken for a MT to travel from a rectifier to the next one. Using our simulations, we can determine w_through = 0.325 ± 0.021, τ_A = 191 ± 6 and τ_B = 96 ± 5 s for the tracks of design A and design B, respectively. The resulting rates k_A = 5.9 ± 0.5 × 10⁻³ and k_B = 1.2 ± 0.1 × 10⁻² s⁻¹ are in good agreement with the fits to our simulation results (Fig. 4).

Acknowledgements

We thank Dr Yasuhiro Inoue, Prof. Koji Nemoto, and Prof. Wendy Thomas for valuable discussions. We thank Dr Yuichi Hiratsuka for providing information on the design of his rectifier. We gratefully acknowledge financial support from Advancing Researcher Support Program (Gifu University, Faculty of Engineering), and the DARPA Biomolecular Motors Program (AFOSR FA 9550-05-1-0274 & FA 9550-05-1-0366).

References

1. M. Porto, M. Urbakh and J. Klafter, Phys. Rev. Lett., 2000, 84, 6058–6061.
2. Y. Shirai, A. J. Osgood, Y. Zhao, K. F. Kelly and J. M. Tour, Nano Lett., 2005, 5, 2330–2334.
3. J. R. Dennis, J. Howard and V. Vogel, Nanotechnology, 1999, 10, 232–236.
4. H. Hess and V. Vogel, Rev. Mol. Biotechnol., 2001, 82, 67–85.
5. Y. Hiratsuka, M. Miyata and T. Q. P. Uyeda, Biochem. Biophys. Res. Commun., 2005, 331, 318–324.
6. H. Hess, J. Clemmens, J. Howard and V. Vogel, Nano Lett., 2002, 2, 113–116.
7. H. Hess, J. Howard and V. Vogel, Nano Lett., 2002, 2, 1113–1115.
8. S. Diez, C. Reuther, C. Dinu, R. Seidel, M. Mertig, W. Pompe and J. Howard, Nano Lett., 2003, 3, 1251–1254.
9. H. Hess, J. Clemmens, C. Brunner, R. Doot, S. Luna, K.-H. Ernst and V. Vogel, Nano Lett., 2005, 5, 629–633.
10. L. Ionov, M. Stamm and S. Diez, Nano Lett., 2005, 5, 1910–1914.
11. S. Ramachandran, K.-H. Ernst, G. D. Bachand, V. Vogel and H. Hess, Small, 2006, 2, 330–334.
12. G. D. Bachand, S. B. Rivera, A. Carroll-Portillo, H. Hess and M. Bachand, Small, 2006, 2, 381–385.
13. J. Howard, Mechanics of Motor Proteins and the Cytoskeleton, Sindauer, Sunderland, MA, 2001.
14. H. Suzuki, K. Oiwa, A. Yamada, H. Sakakibara, H. Nakayama and S. Mashiko, Jpn. J. Appl. Phys., Part 1, 1995, 34, 3937–3941.
15. H. Suzuki, A. Yamada, K. Oiwa, H. Nakayama and S. Mashiko, Biophys. J., 1997, 72, 1997–2001.
16. D. V. Nicolau, H. Suzuki, S. Mashiko, T. Taguchi and S. Yoshikawa, Biophys. J., 1999, 77, 1126–1134.
17. H. Hess, J. Clemmens, D. Qin, J. Howard and V. Vogel, Nano Lett., 2001, 1, 235–239.
18. J. Clemmens, H. Hess, J. Howard and V. Vogel, Langmuir, 2003, 19, 1738–1744.
19. H. Hess, C. M. Matzke, R. K. Doot, J. Clemmens, G. D. Bachand, B. C. Bunker and V. Vogel, Nano Lett., 2003, 3, 1651–1655.
20. R. Bunk, J. Klinth, L. Montelius, I. A. Nicholls, P. Omling, S. Tagerud and A. Mansson, Biochem. Biophys. Res. Commun., 2003, 301, 783–788.
21. R. Bunk, M. Sundberg, A. Mansson, I. A. Nicholls, P. Omling, S. Tagerud and L. Montelius, Nanotechnology, 2005, 16, 710–717.
22. S. G. Moorjani, L. Jia, T. N. Jackson and W. O. Hancock, Nano Lett., 2003, 3, 633–637.
23. L. J. Cheng, M. T. Kao, E. Meyhofer and L. J. Guo, Small, 2005, 1, 409–414.
24. Y. Hiratsuka, T. Tada, K. Oiwa, T. Kanayama and T. Q. Uyeda, Biophys. J., 2001, 81, 1555–1561.
25. H. Hess, J. Clemmens, C. M. Matzke, G. D. Bachand, B. C. Bunker and V. Vogel, Appl. Phys. A: Mater. Sci. Process., 2002, A75, 309–313.
26. J. Clemmens, H. Hess, R. Doot, C. M. Matzke, G. D. Bachand and V. Vogel, Lab Chip, 2004, 4, 83–86.
27. J. Clemmens, H. Hess, R. Lipscomb, Y. Hanein, K. F. Boehringer, C. M. Matzke, G. D. Bachand, B. C. Bunker and V. Vogel, Langmuir, 2003, 19, 10967–10974.
28. M. G. van den Heuvel, C. T. Butcher, R. M. Smeets, S. Diez and C. Dekker, Nano Lett., 2005, 5, 1117–1122.
29. N. Metropolis and S. Ulam, J. Am. Stat. Assoc., 1949, 44, 335–341.
30. T. Nitta and H. Hess, Nano Lett., 2005, 5, 1337–1342.
31. A. K. Schmid, N. C. Bartelt and R. Q. Hwang, Science, 2000, 290, 1561–1564.
32. K. Y. Kwon, K. L. Wong, G. Pawin, L. Bartels, S. Stolbov and T. S. Rahman, Phys. Rev. Lett., 2005, 95, 166101.
33. A. Stevens, SIAM J. Appl. Math., 2000, 61, 172–182.
34. Y. Liu and K. M. Passino, J. Optim. Theor. Appl., 2002, 115, 603–628.
35. B. Rubinstein, K. Jacobson and A. Mogilner, Multiscale Model. Simul., 2005, 3, 413–439.
36. F. A. Meineke, C. S. Potten and M. Loeffler, Cell Proliferation, 2001, 34, 253–266.
37. D. C. Walker, G. Hill, S. M. Wood, R. H. Smallwood and J. Southgate, IEEE Trans. Nanobiosci., 2004, 3, 153–163.

---