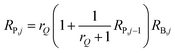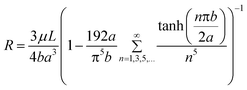DOI:
10.1039/B516401J
(Paper)
Lab Chip, 2006,
6, 871-880
A microfluidic device for continuous, real time blood plasma separation
Received
18th November 2005
, Accepted 5th April 2006
First published on 19th April 2006
Abstract
A microfluidic device for continuous, real time blood plasma separation is introduced. The principle of the blood plasma separation from blood cells is supported by the Zweifach–Fung effect and was experimentally demonstrated using simple microchannels. The blood plasma separation device is composed of a blood inlet, a bifurcating region which leads to a purified plasma outlet, and a concentrated blood cell outlet. It was designed to separate blood plasma from an initial blood sample of up to 45% inlet hematocrit (volume percentage of cells). The microfluidic network was designed using an analogous electrical circuit, as well as analytical and numerical studies. The functionality of this device was demonstrated using defibrinated sheep blood. During 30 minutes of continuous blood infusion through the device, all the erythrocytes (red blood cells) traveled through the device toward the concentrated blood outlet while only the plasma was separated at the bifurcating regions and flowed towards the plasma outlet. The device has been operated continuously without any clogging or hemolysis of cells. The experimentally determined plasma selectivity with respect to blood hematocrit level was almost 100% regardless of the inlet hematocrit. The total plasma separation volume percent varied from 15% to 25% with increasing inlet hematocrit. Due to the device’s simple structure and control mechanism, this microdevice is expected to be used for highly efficient continuous, real time cell-free blood plasma separation from blood samples for use in lab on a chip applications.
Introduction
Most biological sample analyses require either the removal of cells from a biological fluid, such as the removal of blood cells from whole blood to leave purified plasma, or cell concentration for downstream analyses. For instance, when performing blood analysis in medical laboratories, the blood cells are separated from the whole blood collected from a patient by centrifugation and the blood plasma is analyzed for electrolyte concentration, glucose, lactate, total cholesterol, etc. These sequential procedures on single batch blood collections can take up to several hours. Recently, the iSTAT system has been introduced as a point of care diagnostic device1 for blood analysis for both bedside and outpatient monitoring and has removed some of the laboratory bottlenecks. However, there is a need for a system, which can separate blood plasma from whole blood and measure the concentration of the clinically relevant proteins in continuous, real time fashion. For example, according to several studies,2–10 cardiac surgery can produce systemic inflammatory responses in a variety of ways, especially when cardiopulmonary bypass (CPB) is used. CPB induces complex inflammatory responses characterized by complement, neutrophil, and platelet activation, and the release of pro-inflammatory cytokines. In general, exposure of blood to nonphysiological surfaces of the heart–lung machine, hypothermia, surgical trauma, and ischemia–reperfusion of the involved tissues are considered as main factors causing postoperative complications. These complications include vital organ dysfunction that can lead to multi-organ failure and even death.8,10,11 The intensity of the inflammatory response appears to be directly correlated with the severity of CPB-related morbidity.2,8,10–13 Currently, there is no effective method for preventing this systemic inflammatory response syndrome in cardiac surgery patients undergoing CPB. Therefore, there is an unmet medical need to develop safe and effective therapeutic diagnostics to monitor this inflammatory response in real time, while the surgery is proceeding to better understand how CPB and surgical or anesthetic procedures might be modified to prevent its occurrence. Current technology provides measurements of the effects of cardiopulmonary bypass on activation of complements, neutrophils, platelets, and cytokines hours or days post-surgery. More immediate measurements would aid in understanding the mechanisms of cellular activation, and modify surgical and perfusion protocols for minimizing adverse effects of cardiopulmonary bypass. To accomplish immediate measurements of the clinically relevant proteins, such as cytokines and complements, two functions have to be obtained in a continuous, real time fashion: blood plasma separation and detection of proteins. The objective of this study is to develop a microfluidic device for continuous, real time blood plasma separation14 for the application of the online monitoring of inflammatory responses (cytokines, complements) during the CPB procedure. Research activities involving on-chip biological cell or fluid separations exist and are based on a variety of working principles (e.g. Brownian ratchet,15 dielectrophoresis,16 deterministic lateral displacement,17 field flow fractionation,18 microfiltration,19 acoutic standing waves,20etc.). In this report plasma separation is accomplished by designing a simple microfluidic network based on the Zweifach–Fung effect. Particle or cell separations considering the local microflow profile and hydrodynamic forces on particles has been demonstrated21–25 but has not been applied to blood plasma separation for continuous, real time monitoring techniques.
Bifurcation law (Zweifach–Fung effect)
The principle of the plasma separation device is based on the bifurcation law,26–28 also called the Zweifach–Fung effect. The bifurcation law describes that, in the microcirculation, when erythrocytes (red blood cells) flow through a bifurcating region of a capillary blood vessel, they have a tendency to travel into the daughter vessel which has the higher flow rate leaving very few cells flowing into the lower flow rate vessel. The critical flow rate ratio between the daughter vessels for this cell separation is approximately 2.5 ∶ 1 when the cell-to-vessel diameter ratio is of the order of one. As described in Fig. 1(a), the reason for this apportioning is that cells are drawn into the higher flow rate vessel because they are subjected to a higher pressure gradient (ΔPh > ΔPl). In addition, the asymmetric distribution of shear forces (γcell_wall_high_flow > γcell_wall_low_flow) on the surface of the cell produces a torque on the cell, pulling it towards the faster flow rate vessel. The stagnation point of the flow is a critical streamline (see the dashed line on Fig. 1(b)) within the flow field. If the centroid of the cell is located away from the lower flow rate area beyond the critical streamline, it will flow towards the higher flow rate branch. Therefore, the higher the flow rate ratio between the two daughter branches, the closer to the low flow rate branch the critical streamline occurs as shown in Fig. 1(b). The background flow pattern shown in Fig. 1(b) shows streaklines for a 4 ∶ 1 flow rate ratio between high and low flow rate channels. Each particle and line overlaid on the flow pattern represents the expected flow path of the particles depending on their position within the channel.
 |
| | Fig. 1 (a) Schematic of the Zweifach–Fung effect; red blood cells have a tendency to travel into the higher flow rate daughter vessel with no cells travelling to the lower flow rate daughter vessel when the flow rate ratio is more than 2.5 and the cell-to-vessel diameter ratio is of the order of 1. The primary reason for this effect are because of differential pressure drops and shear forces acting on a cell. (b) An illustration of the critical streamline; A particle (I) whose centroid is beyond the critical streamline will travel into the high flow rate channel. A particle (II) whose centroid is within the critical streamline will travel into the low flow rate channel. A particle (III) whose centroid is on the critical streamline will travel into the high flow rate channel because of the Zweifach–Fung effect. | |
Experimental methods
Throughout this study, a variety of particles were used. The initial demonstration of the Zweifach–Fung effect in microfluidic channels utilized two types of particles: 16 µm diameter fluorescent polystyrene divinylbenzene (DVB) microspheres (Duke Scientific Corp., CA, USA) and human C8161 melanoma cells. C8161 cells were cultured in DMEM media supplemented with Pen/Strep, glutamine and 10% Fetal Bovine Serum (FBS). After culturing, they were stained and incubated with calcein acetoxymethyl (AM) at a concentration of 1 µl calcein AM per 1 ml media for 3 minutes. Calcein AM enters the cell cytoplasm and is cleaved by intracellular esterases, generating a fluorescent signal in live cells with no fluorescence generation for dead cells. After cells reached confluency, the cells were trypsinized (0.025% trypsin) and were stored in 1X phosphate buffer saline (10 mM phosphate buffer, pH 7.4, 140 mM NaCl, 3 mM KCl) solution for use in experiments. The measured diameter of the melanoma cells were between 8 to 10 µm when they were suspended in the PBS solution. The separation experiment were conducted within 15 minutes of trypsinization to ensure that cells remained alive throughout the experiments.
In blood plasma separation experiments, two types of particles were used for flow visualization: 0.85 µm diameter fluorescent microspheres (Duke Scientific Corp., CA, USA) and defibrinated sheep blood at 36% hematocrit (Hemostat Labs, Inc., CA, USA). The blood was used within 3 weeks of harvest and stored at 4 °C. Prior to experiments the blood was diluted in PBS to a known hematocrit level (10%, 15%, 20%, 25%, 30%, 35% hematocrit).
The microfluidic device has been fabricated in polydimethylsiloxane (PDMS) using the conventional soft lithography process.29,30 After preparing the device, it was mounted on an inverted microscope (Olympus IX71).for visualization. Then, the particles were infused through the device using a syringe pump (KDS210, KD Scientific Inc., MA, USA). Although, the microfluidic network can handle flow rates as high as 5 µl min−1, all blood plasma experiments were conducted at a flow rate of 10 µl h−1 to allow accurate imaging and analysis of the individual blood cells with minimal streaking. The particles in the microchannels were imaged using two different types of CCD cameras. The first was a conventional NTSC CCD camera, which has a 640 × 480 pixel resolution and a frame rate of a 30 frames s−1. The other was a high resolution (1376 × 1040 pixel) CCD Camera (Cooke SensiCam QE, MI, USA) at a 10 frames s−1 and variable shutter time. For blood plasma separation experiments, the shutter is allowed to remain open for 20 µs frame−1. After obtaining images, they were analyzed using an image processor program to obtain the hematocrit change between upstream and downstream of the separation region as well as the particle motion at the bifurcation.
Results and discussion
I. The demonstration of the Zweifach–Fung effect in microchannels
The initial demonstration of the Zweifach–Fung effect in microchannels used a simple device containing a single bifurcation. Fig. 2 (a) shows a schematic of the device. The inlet channel was 35 µm wide by 35 µm deep and the two daughter channels have varying downstream channel widths to introduce flow rate ratios (1 ∶ 1 to 8 ∶ 1) between the two daughter channels. The particle recovery efficiency with respect to the flow rate ratios between the two daughter channels was studied using the rigid 16 µm fluorescent beads and 8–10 µm human C8161 melanoma cells. Fig. 2 (b) shows a series of fluorescent images overlaid on the bright field channel image, while a human melanoma cell travels through the device with a 4 ∶ 1 flow rate ratio. Due to the higher pressure drop and a higher shear force acting on the cell in the higher flow rate channel, the human C8161 melanoma cell travels into the higher flow rate channel. The cell diameter to inlet channel width ratio is between 0.23–0.29. The recovery efficiency for this experiment was 98.9%. As shown in Fig. 3, the larger flow rate ratio yields the higher particle recovery efficiency. As a result of the Zweifach–Fung effect, there is a 100% particle recovery efficiency for flow rate ratios larger than 6 ∶ 1. A greater than 15% increase in particle recovery over that predicted by the simple flow rate distribution is also seen.
 |
| | Fig. 2 (a) Schematic of the single bifurcation microchannel to demonstrate Zweifach–Fung effect; an inlet channel is 35 × 35 µm2 and the outlet channels have different channel widths in the downstream region to introduce different flow rate ratios (1 ∶ 1 to 8 ∶ 1) between the two daughter channels. The dashed box represents the observation window of the moving cells. (b) A series of fluorescent images of the calcein AM dye stained human C8161 melanoma cell; the human cell is heading for higher flow rate channel. The cell diameter/channel width is about 0.23–0.29 and the flow rate ratio is 4 ∶ 1. The recovery efficiency was 98.9%. | |
 |
| | Fig. 3 Percentage recovery efficiencies with respect to flow rate ratios; due to the Zweifach–Fung effect, there is more than 15% improvement in the recovery efficiency predicted by the asymmetric flow distribution regardless of the particle type. | |
A. 16 µm diameter fluorescent particles (particle diameter/channel width = 0.46)
For the 16 µm diameter fluorescent particles, 87.2% recovery efficiency was obtained for a 2.5 ∶ 1 flow rate ratio. In order to obtain a 100% particle recovery efficiency for the 2.5 ∶ 1 flow rate ratio, a particle diameter to inlet channel width ratio of 0.57 is estimated as the minimum flow rate ratio required to place all of the particle centroids beyond the critical streamline. The actual particle to the inlet channel width is about 0.46 so the 87.2% particle recovery experimentally observed is considered reasonable. For the 4 ∶ 1 flow rate ratio, a 95.68% recovery efficiency was obtained. This result is somewhat lower than the 100% particle recovery expected. The reason for this discrepancy may be from the statistical size distribution of the fluorescent particle diameters. However, 100% particle recovery efficiency was achieved using 6 ∶ 1 and 8 ∶ 1 flow rate ratios. In general, to improve particle recovery efficiencies at lower flow rate ratios, a higher particle diameter to channel width ratio is needed.
B. 8–10 µm diameter human C8161 melanoma cells (cell diameter/channel width = 0.23–0.29)
For the 8–10 µm diameter human C8161 melanoma cells, for the 2.5 ∶ 1 and 4 ∶ 1 flow rate ratios, 88.7% and 98.9% particle recovery efficiencies were obtained respectively. 100% particle recovery efficiency was also achieved using 6 ∶ 1 and 8 ∶ 1 flow rate ratios. The recovery efficiencies are higher than those of the 16 µm diameter fluorescent particles case, even though the cell diameter to channel diameter ratio is lower and is expected to lead the lower recovery efficiency. However, a deformable particle within a channel tends to have an equilibrium position closer to the center of the channel than a rigid particle does because of shear induced migration of particles.31 This means that deformable cells are not evenly distributed across the channel as is expected with a rigid particle, but distributed closer towards the middle of channel (beyond the critical streamline), yielding an even higher particle recovery efficiency than those of 16 µm diameter rigid particles. For both experiments, a 6 ∶ 1 flow rate ratio is required to obtain 100% particle recovery and it is set as a minimum flow rate ratio for subsequent designs for blood plasma separation.
II. Design of a microfluidic device for continuous, real time blood plasma separation
To successfully design a blood plasma separation device based on the Zweifach–Fung effect, a series of design techniques were incorporated to determine the optimal channel geometries to skim off cell free plasma within the microfluidic network. The optimal channel geometries were determined using an analogous electrical circuit analysis, verified using computational simulation (CFD), and demonstrated experimentally. The blood plasma separation device was designed to have a whole blood inlet, a purified plasma outlet, and a concentrated blood cell outlet as shown in Fig. 4(a). The main channel (15 µm wide) is fed by the whole blood inlet and leads to the blood plasma separation region. Each channel extending from the separation region to an outlet is 5 mm in length. The individual plasma skimming channels are each 9.6 µm wide (Fig. 4(b)). The channel depth for the entire device is 10 µm. Since 100% particle recovery could be achieved when 6 ∶ 1 flow rate ratio between two daughter channels this device was designed to separate plasma from defibrinated sheep blood with hematocrit levels up to 45% and achieve flow rate ratios around 8 ∶ 1 between the main channel and plasma channels. At this flow rate ratio, the critical separation streamline is placed 1.67 µm from the main channel wall for a 15 µm wide channel. In order to increase the total plasma volume which could be separated from the main channel, five parallel plasma channels are placed within the device rather than a single bifurcating region. To obtain a consistent flow rate ratio (8 ∶ 1) at each bifurcating point, the flow resistance ratios between main (blood) and each branch (plasma) channels were used as a control parameter in the design since the flow rate in a channel is inversely proportional to its flow resistance.
 |
| | Fig. 4 Schematic diagrams of a microfluidic blood plasma separation device; (a) an overview of a device. This device is designed to have a whole blood inlet, a purified plasma outlet, and a concentrated blood cell outlet. Each channel is 5 mm in length. (b) A zoomed-in view of the blood plasma separation region. The main blood channel width is 15 µm, while all plasma skimming channels have widths of 9.6 µm. The channel depth for the entire device is fixed as 10 µm deep. The bifurcation positions are indexed from 5 (upstream) to 1 (downstream). | |
A. Analogous electrical circuit studies for the blood plasma separation device
In order to design a complex fluidic circuit, it is essential to have an efficient way to determine channel geometries that meet specific criteria. Since the fluid network contains many channels in parallel and series, the pressure-flow relationship at each network node is inherently coupled and cannot be described analytically. Each portion of the network is therefore described by an analogous electrical circuit to obtain optimal resistance ratios between the main and plasma channel. In a manner analogous to an electrical current, fluidic flow rate (Q) can be defined bywhere R is the fluid flow resistance and ΔP is a pressure drop. Thus, the flow rate ratio at each bifurcation can be determined by controlling flow resistance ratio between the main channel and a plasma channel at each bifurcation. In order to determine the flow resistance of each channel, an analogous electrical circuit is analyzed where the flow rate is modulated by the current and the flow resistance is modulated by an electrical resistance. It is assumed that capacitance (compliance) of the system is negligible because the channel dimensions and pressure within the channels are small. If the flow rate ratio is assumed to be rQ, the resistance relationship between the main and plasma channels at each node should satisfy the criteria that| | 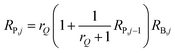 | (2) |
where, RP,j is the resistance of a plasma channel at the jth node and j = 2, 3, 4,…, n. RP,1 = rQ·RB,1. Based on eqn (2) and verified by PSpice simulation (Cadence Design, NY, USA), in order to maintain a 8 ∶ 1 flow rate ratio at each bifurcation, the resistances of the plasma channels have to be from 120 to 102 times larger than that of the individual segments of the main channel except at the concentrated blood cell channel (RB,1), which requires a resistance 15 times larger than that of the main channel.
B. Analytical studies for the blood plasma separation device
Once the optimal flow resistance ratios were obtained from the electrical circuit analysis, an analytical study was conducted to determine optimal fluid channel dimensions, which meet the flow resistance ratio requirement. Eqn (3) describes the analytical solution of flow resistance within a rectangular duct32| | 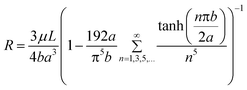 | (3) |
where μ is the fluid viscosity, L is the channel length, a is the half width of the channel, and b is the half depth of the channel. The actual channel dimensions were analytically determined by combining eqn (2) and (3). All channels’ depth was assumed to be 10 µm deep. To obtain a resistance 15 times larger than in the main channel, a 154 µm wide concentrated blood cell channel is required. For the plasma channels, channels widths ranging from 9.6 to 10.4 µm wide are required to obtain a resistance 120 to 102 times larger in the plasma channels than that in the main channel. However, due to the lithographic resolution of the mask aligner used to fabricate the device, it is very difficult to control the variation of the plasma channel width with 0.1 µm resolution. Therefore, all plasma channel widths were fixed 9.6 µm wide to obtain more consistent channel widths during device fabrication. Thus, the flow rate ratio between the main and plasma channels varies between 8 ∶ 1 to 9.2 ∶ 1 as shown in Table 1. However, since the flow rate ratios are still above 6 ∶ 1, 100% plasma separation is expected.
Table 1 Resistance values in the blood plasma separation device
| Bifurcation index |
R
B/Rm |
R
P/Rm |
Flow rate ratio (Qm/Qp) |
| 5 |
1 |
120 |
9.2 |
| 4 |
1 |
120 |
9.0 |
| 3 |
1 |
120 |
8.7 |
| 2 |
1 |
120 |
8.4 |
| 1 |
15 |
120 |
8.0 |
C. Numerical studies for the blood plasma separation device
After determining the optimal channel geometries based on the analogous electrical circuit and the analytical studies, the performance of the microfluidic device was estimated using computational fluid dynamic (CFD) simulation. For this numerical study, CFDACE + (CFD Research Corp., AL, USA) was used. In all simulations, the blood is assumed to be a homogeneous Newtonian fluid because blood behaves as a Newtonian fluid in high shear rate conditions (∼1850 s−1, Q (inlet flow rate) =10 µl h−1). The hemolysis of cells were ignored even at high shear rate condition (∼1850 s−1) because the average shear stress (∼134 dynes cm−2 for 45% inlet hematocrit) is lower than required for hemolysis (>1000 dynes cm−2)33 and the blood exposure time to the device is short (<1 s). It is also assumed that the hematocrit level changes gradually as blood travels through the main channel region due to the increase in hematocrit as the plasma is separated at each bifurcation region. All viscosity values with respect to hematocrit levels used in numerical studies were obtained from measurement (RotoVisco 1 viscometer, Rheology Solutions, Victoria, Australia). Fig. 5(a) shows the velocity magnitude contour at the separation region for a 45% hematocrit level obtained from the numerical simulation. Due to the plasma skimming at each bifurcation, the velocity gradually decreases as blood flows downstream to satisfy the conservation of mass (Fig. 5(a), (b)). Fig. 5(c) plots the flow rate ratio at each bifurcation with respect to hematocrit levels and is compared with the analogous electrical circuit result. For a 45% hematocrit, the flow rate ratio at each bifurcation is well matched with the result obtained from the analogous electrical circuit study. However, as the hematocrit level decreases, the flow rate ratio increases due to the decrease in fluidic resistance because of the decrease in blood viscosity in the main channel, while maintaining the same fluidic resistance in the plasma channel. Thus, the flow rate ratio between the main channel and plasma channels increases as the hematocrit level decreases.
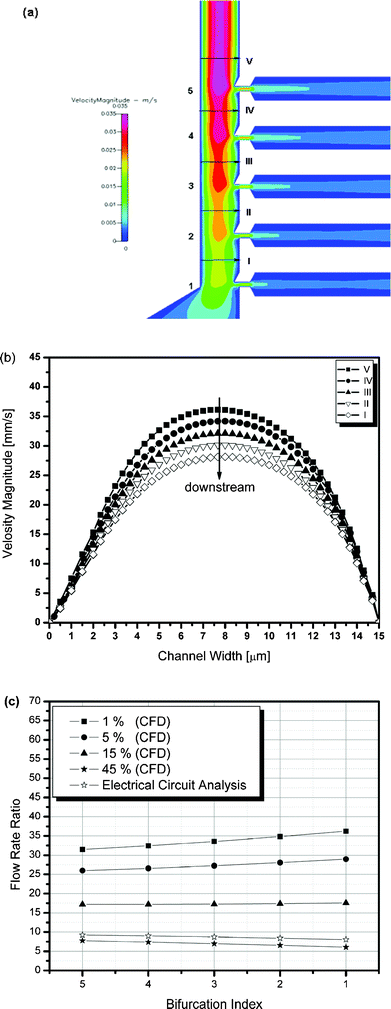 |
| | Fig. 5 Numerical simulation results showing (a) the velocity magnitude contour at the separation region, (b) the velocity magnitude obtained at I to V, (c) the flow rate ratio at each bifurcation with respect to the microchannel hematocrit levels. | |
III. Experimental verification of the device (Blood plasma separation experiments)
In the first stage of the experiment, 0.85 µm diameter fluorescent particles were infused through the whole blood inlet at 10 µl h−1 to investigate flow pattern at the bifurcation regions. It was assumed that 0.85 µm diameter fluorescent spherical particles were small enough to follow flow streamlines and would not experience preferential separation as seen with blood cells. As shown in Fig. 6(a), 0.85 µm diameter fluorescent spherical particles flow into both the concentrated blood cell outlet and the plasma outlet because the centroid of the fluorescent particle (0.425 µm) is located within the critical streamline (1.47–1.67 µm). Due to the high particle velocity (∼18.5 mm s−1), the particles appear as streak lines at 10 frames s−1. From these studies, the critical streamline for preferential separation is visualized at the flow stagnation point.
 |
| | Fig. 6 (a) A fluorescent photograph (40× magnification, 1376 × 1040 pixels) of the separation region after infusing 0.85 µm diameter fluorescent particles at a flow rate of 10 µl h−1. (b) A photograph (20× magnification, 640 × 480 pixels) of the blood plasma separation region after infusing defibrinated sheep blood (36% Hct) through the whole blood inlet at a flow rate of 10 µl h−1. (c) Another snapshot of same region taken using a higher resolution (40× magnification, 1376 × 1040 pixels) CCD camera with shorter shutter open time (20 µs). | |
In the second stage of the experiment, the blood plasma separation experiment was conducted at a 10 µl h−1 input flow rate using commercially available defibrinated sheep blood with a 36% initial hematocrit. Since red blood cells have a discoid shape, it is obvious that the minimum distance between the centroid of the blood cell and the main channnel wall is a strong function of the orientation of the blood cell. However, in this study, the blood cells are constrained in orientation by the height of the device because the channel depth (∼10 µm) is shallower than the channel width (∼15 µm) and they appear to flow through with the central axis of the disc parallel to the top and bottom of the microchannel. Thus, the minimum distance between the centroid of the blood cell and the main channel wall is 2.5 µm for a sheep blood cell that is 5 µm in diameter and 2 µm thick.34 This minimum distance is farther than that of the critical streamline position (1.47–1.67 µm) from the main channel. Thus, no cells are expected to travel into the plasma channels. Fig. 6(b) shows an image obtained using a standard NTSC CCD camera, where the blood cells are flowing through the device. These streaklines are seen in the main channel, but not in the plasma channel. This image demonstrates that blood cells flow only towards the concentrated blood cell outlet and not into the plasma channels and also supports the idea of the preferential orientation of the blood cells.
To observe individual blood cell dynamics, images were acquired using a higher resolution (1376 × 1040 pixels) CCD camera with a shorter shutter speed (20 µs) at 40× magnification. In Fig. 6(c), the individual blood cells flowing through the device are clearly observed. Again, no cells are observed in the plasma channels. In addition, severe deformation of red blood cells was not observed throughout the experiment. During a total of 30 minutes of continuous blood infusion at a variety of inlet hematocrit levels, only few blood cells flowed into the purified plasma outlet. Therefore, only plasma was skimmed into the purified plasma outlet. In addition, no clogging or hemolysis of cells was observed. These results experimentally demonstrate that the continuous, real time blood plasma separation could be accomplished by simply controlling the flow rate ratio at each bifurcation.
Once blood plasma separation in the microfluidic device was demonstrated, the performance of the device was quantified by determining the total plasma separation volume percent from the total plasma volume and the plasma selectivity. The plasma selectivity (σ) is defined as
| |  | (4) |
where
Hp and
Hmu are the hematocrit levels in the plasma channel and upstream of the separation region, respectively. A plasma selectivity of 100% implies that no cells travel into the plasma channels. The total plasma separation volume percent out of total plasma volume (
η) is also defined as
| |  | (5) |
where
Hmd is the hematocrit level downstream of the separation region. In order to determine hematocrit levels at each local position of the device, more than 200 successive images were taken using the 1376 × 1040 pixel resolution
CCD camera at a 10 frames s
−1 and a 20 µs frame
−1 shutter time and were analyzed to determine the hematocrit distribution upstream and downstream of the separation region. Standard instrumentation for hematocrit measurement, such as a coulter counter or centrifuge-based equipment, usually require the collection of relatively large blood samples and do not allow an understanding of dynamic behaviour of hematocrit changes at the region of interest. Therefore, by developing an image analysis program, information on hematocrit changes at the region of interest and continuous, real time monitoring without sample collection can be achieved. For image processing, a “hemocytometer” program was prepared using LabVIEW 7.0 (National Instruments Corporation, TX, USA). The hemocytometer was designed to find particles within a given region of interest (ROI) (
Fig. 7(a)) and to count the number of particles (
Fig. 7(b), (c)). To convert the number of cells found in a given ROI into a hematocrit level, a red blood cell volume was experimentally determined by counting the number of red blood cells per unit volume (Coulter Counter ZM, Hialeah, FL, USA) and measuring the sample hematocrit level (Autocrit Ultra3 Centrifuge, Clay Adams, Parsippany, NJ, USA). Using an experimentally determined RBC volume of 48 µm
3, which is slightly larger than one previously reported,
34 the hematocrit level within a known ROI volume is determined. To maintain the same sampling conditions, the same ROI areas were used at both upstream and downstream positions.
Table 2 shows a significant change in the hematocrit level distributions between the upstream and downstream of the separation region for an inlet hematocrit of 36%. The mean hematocrit levels at upstream (
Hmu) and downstream (
Hmd) of the separation region are significantly different (p < 0.001) between the upstream (10.69%) and downstream (13.70%) positions. It should be noted that the measured hematocrit upstream of the separation region (15 µm wide) is much lower than the infused hematocrit (10.69% versus 36%). This is due to the Fahraeus effect,
35 in which, when blood of a constant hematocrit flows from a large feed inlet into a small channel, the average hematocrit in the channel decreases as the channel diameter decreases.
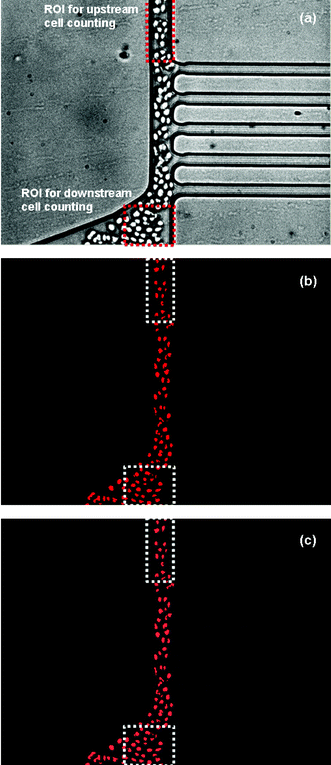 |
| | Fig. 7 A sequence of image processing used in determination of the total plasma separation volume%; (a) a representative original image used in image processing, (b) after finishing image processing, (c) an overlay image of (a) and (b). | |
Table 2 Statistical summary of hematocrit distributions obtained from the image processing
| Sample |
N
a
|
Mean Hb (%) |
SDc |
SEd |
|
Number of images analyzed.
Hematocrit level.
Standard deviation.
Standard error.
|
| Upstream |
210 |
10.69123 |
0.73756 |
0.0509 |
| Downstream |
210 |
13.69921 |
0.71345 |
0.04923 |
To investigate the total plasma separation volume percent out of the total plasma volume as well as the plasma selectivity, the blood (Hin = 10%–35%) was infused into the device and the images of the separation region was recorded every two minutes for 30 minutes. In each data collection, 210 images were taken for 21 seconds (10 frames s−1). The total number of images analyzed was 3360 for each case. The acquired images were then analyzed using the “Hemocytometer” image processing program (Fig. 7). Fig. 8 shows representative behaviours of the microchannel hematocrit with respect to data collection time. In both 10% and 35% inlet hematocrits, the hematocrit level changes significantly (P < 0.05) between upstream (Hmu) and downstream (Hmd) of the separation region. A higher inlet hematocrit level (Hin) produces a higher upstream hematocrit level (Hmu). As a result, a higher downstream hematocrit level (Hmd) is produced. Since the plasma separation volume percent is represented by the difference between Hmu and Hmd as described in eqn (5), a larger upstream hematocrit produces the larger plasma separation volume percent. In other words, the larger the upstream hematocrit level, the lower the flow rate ratio between the main and plasma channels is established so that a higher fluid volume flows into the plasma channels.
 |
| | Fig. 8 Microchannel hematocrit changes with respect to time. | |
Fig. 9 analyzes the Fahraeus effect observed in the device by plotting the upstream microchannel hematocrit (Hmu) as a function of the inlet hematocrit (Hin). The upstream microchannel hematocrit level is linearly dependent on the inlet hematocrit level and is consistent with measured tube hematocrits reported in the blood rheology literature.35
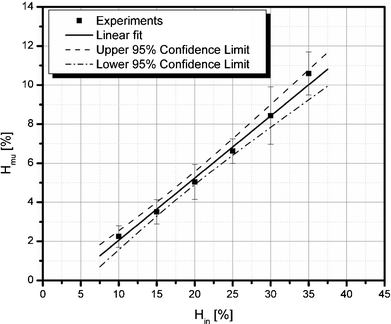 |
| | Fig. 9 Fahraeus effect in a 15 µm wide microchannel. | |
Using the results obtained in Fig. 8, the plasma selectivity was calculated and plotted in Fig. 10. The plasma selectivity with respect to the blood hematocrit level is almost 100% regardless of the hematocrit levels. This result implies that no cells travel toward the plasma channels for lower inlet hematocrit levels (Hin < 25%) and only a few cells at higher inlet hematocrit levels (Hin > 30%).
 |
| | Fig. 10 Plasma selectivity with respect to microchannel and inlet hematocrit levels; The digits shown above each data point represent the inlet hematocrit levels. | |
Fig. 11 shows a comparison of the experimental and CFD simulation results of the total plasma separation volume percent with respect to the upstream microchannel hematocrit level. The total plasma separation volume percent varies from about 15% to 25% depending on the inlet hematocrit level. To obtain a larger plasma separation percent, additional plasma channels may be placed in parallel. The experimental results are well matched with the CFD predictions. Thus, it is clear that the series of design techniques used in this study are very useful in designing a complex fluid circuit for particle separation.
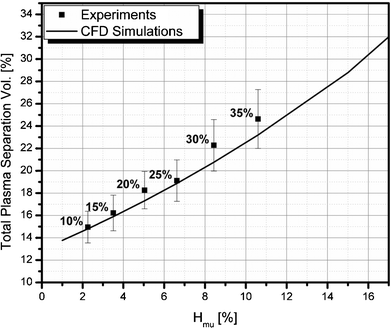 |
| | Fig. 11 A comparison of the experimental and CFD simulation results of the total plasma separation volume percent with respect to the upstream microchannel hematocrit level; The digits shown above each data point represent the inlet hematocrit levels. | |
Conclusions
A microfluidic device for continuous, real time blood plasma separation based on the Zweifach–Fung effect was successfully designed and experimentally demonstrated using commercially available sheep blood. By studying the Zweifach–Fung effect in a simple bifurcating microfluidic channel, a 6 ∶ 1 minimum flow rate ratio to obtain successful blood plasma separation was determined. To design a complex fluidic circuit, the combination of various design techniques, including an analogous electrical circuit, analytical, and numerical simulations, was introduced and successfully supported by experimental results. The plasma selectivity obtained from experiments was close to 100% regardless of the inlet hematocrit levels. The total plasma separation volume percent out of the total plasma volume varied from 15% to 25% depending on the inlet hematocrit levels.
As a preliminary study for future clinical application, the blood plasma separation device has been successfully integrated with a CPB pump at flow rates of 3–4 µl min−1. Observed device performance is also similar to that reported in this paper. Since clinical trials are beyond the scope of this paper, this data is not presented here. Also, depending on clincial tests, additional plasma channels can be placed in parallel to increase the total plasma separation volume.
Acknowledgements
The authors would like to thank Herbert H. Lipowsky for helpful discussions of blood rheology. This project is funded, in part, under a grant with the Pennsylvania Department of Health using Tobacco Settlement Funds. The department specifically disclaims responsibility for any analyses, interpretations or conclusions.
References
- E. Jacobs, E. Vadasdi, L. Sarkozi and N. Coman, Clin. Chem., 1993, 39(6), 1069–1074 CAS.
- G. Asimakopoulos, Perfusion, 1999, 14, 269–277 CAS.
- I. Birdi, M. Caputo, M. Underwood, A. Bryan and G. Angelini, Eur. J. Cardiothorac. Surg., 1999, 16, 540–545 CrossRef CAS.
- E. Fosse, T. Mollnes and B. Ingvalden, J. Thorac. Cardiovasc. Surg., 1987, 93, 860–866 CAS.
-
Cardiac Surgery, ed. J. Kirklin and B. Barratt-Boyes, Elsevier Sciences, New York, 1993 Search PubMed.
- J. Kirklin, D. Chenoweth and D. Naftel, Ann. Thorac. Surg., 1986, 41, 193–199 CAS.
- J. K. Kirklin, S. Westaby, E. H. Blackstone, J. W. Kirklin, D. E. Chenoweth and A. D. Pacifico, J. Thorac. Cardiovasc. Surg., 1983, 86, 845–857 CAS.
- F. Moore, Jr, K. Warner and S. Assousa, Ann. Surg., 1988, 208, 95–103 CAS.
- J. B. Steinberg, D. P. Kapelanski and J. D. Olson, J. Thorac. Cardiovasc. Surg., 1993, 106, 1008–1016 CAS.
- S. Westaby, Intensive Care Med., 1987, 13, 89–95 CAS.
- M. Seghaye, J. Duchateau and R. Grabitz, J. Thorac. Cardiovasc. Surg., 1993, 106, 978–987 CAS.
- G. Schlag, H. Redl and S. Hallstrom, Resuscitation, 1991, 21, 137 CrossRef CAS.
- J. R. Utley, J. Card. Surg., 1990, 5, 177–189 Search PubMed.
- S. Yang, A. Ündar and J. D. Zahn, ASAIO J., 2005, 51(5), 585–590 Search PubMed.
- R. D. Astumian, Science, 1997, 276, 917–922 CrossRef CAS.
- P. Gascoyne, C. Mahidol, M. Ruchirawat, J. Satayavivad, P. Watcharasit and F. F. Becker, Lab Chip, 2002, 2(2), 70–75 RSC.
- L. Huang, E. Cox, R. Austin and J. Sturm, Science, 2004, 5673, 304, 987–900 Search PubMed.
- J. Yang, Y. Huang, X. B. Wang, F. F. Beker and P. R. C. Gascoyne, Biophys. J., 2000, 78(5), 2680–2689 CrossRef CAS.
- T. A. Crowley and V. Pizziconi, Lab Chip, 2005, 5, 922–929 RSC.
- F. Petersson, A. Nilsson, C. Holm, H. Jönsson and T. Laurell, Lab Chip, 2004, 5, 20–22 Search PubMed.
- R. Ditchfield and W. L. Olbricht, J. Biomech. Eng., 1996, 118(3), 287–294 CrossRef CAS.
- B. W. Roberts and W. L. Olbricht, AIChE J., 2003, 49(11), 2842–2849 CrossRef CAS.
- M. Yamada, M. Nakashima and M. Seki, Anal. Chem., 2004, 76(18), 5465–5471 CrossRef CAS.
- M. Yamada and M. Seki, Lab Chip, 2005, 5, 1233–1239 RSC.
- B. W. Roberts and W. L. Olbricht, AIChE J., 2006, 52(1), 199–206 CrossRef CAS.
- Y. C. Fung, Microvasc. Res., 1973, 5, 34–48 CrossRef CAS.
- G. W. Schmid-Schönbein, R. Skalak, S. Usami and S. Chien, Microvasc. Res., 1980, 19, 18–44 CrossRef CAS.
- R. T. Yen and Y. C. Fung, Am. J. Physiol., 1978, 235(2), H251–H257 Search PubMed.
- D. Duffy, J. McDonald, O. Schueller and G. Whitesides, Anal. Chem., 1998, 70(23), 4974–4984 CrossRef CAS.
- Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184 Search PubMed.
- Y. Zhao and M. K. Sharp, J. Biomech. Eng., 1999, 121(2), 148–152 CrossRef CAS.
-
Laminar Boundary Layer, ed. L. Rosenhead, New York, Dover Publications, inc., 1963 Search PubMed.
-
J. D. Hellums and P. A. Hardwick, Response of Platelets to Shear Stress - A Review, in The Rheology of Blood, Blood Vessels and Associated Tissue, ed. G. Hwang, Sijthoff & Noordhoff, Rockville, MD, 1981, pp. 160 Search PubMed.
- S. Chien, S. Usami, R. J. Dellenback and C. A. Bryant, Biorheology, 1971, 8, 35–57 CAS.
- J. H. Barbee and G. R. Cokelet, Microvasc. Res., 1971, 3, 6–16 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2006 |
Click here to see how this site uses Cookies. View our privacy policy here.